Plan
Comptes Rendus
no. 7-8

Degradation of the herbicide isoproturon by a photocatalytic process
[Dégradation de l’herbicide isoproturon par un procédé photocatalytique]
Sébastien Thomas1 ; Abir Alatrache1, 2 ; Marie-Noëlle Pons1 ; Orfan Zahraa1 
1 Laboratoire Réactions et Génie des Procédés, UMR CNRS 7274, université de Lorraine, ENSIC, 1, rue Grandville, BP 20451, 54001 Nancy cedex, France
2 Laboratoire RMN Physique 01 UR 13-04, ENSIT, université de Tunis, 5, avenue Taha-Hussein, BP 56, 1008 Bab Menara, Tunis, Tunisia
Comptes Rendus. Chimie, Volume 17 (2014) no. 7-8, pp. 824-831.

Résumé

In this study, the adsorption and photocatalytic degradation of isoproturon (one of the most widely used herbicides in agriculture) was investigated in an annular photoreactor packed with a TiO2 photocatalyst. The results highlighted that the monolayer Langmuir adsorption isotherm model was well obeyed. The isoproturon adsorption equilibrium constant was determined experimentally. The codegradation of isoproturon and of other copollutants such as salicylic acid and phenol occurred, demonstrating that within the catalyst, the same type of sites can be involved in the adsorption of the two pollutants. The heat of adsorption fell in the range of 20 to 50 °C and was found to be ∼43 kJ/mol. As expected, the adsorption constant Ka decreased with increasing the fluid flow due to the temperature rise. The kinetics of the photocatalytic degradation of isoproturon revealed a first-order reaction for initial concentrations between 3 and 43 ppm. In our experimental conditions, no by-products were detected and total disappearance of isoproturon was observed.

Supplementary Materials:
Supplementary material for this article is supplied as a separate file:

Métadonnées
Reçu le :
Accepté le :
Publié le :
DOI : 10.1016/j.crci.2014.04.002
Mots clés : Isoproturon, Adsorption, Annular reactor, Kinetics, Photocatalytic degradation, Codegradation
Sébastien Thomas 1 ; Abir Alatrache 1, 2 ; Marie-Noëlle Pons 1 ; Orfan Zahraa 1

1 Laboratoire Réactions et Génie des Procédés, UMR CNRS 7274, université de Lorraine, ENSIC, 1, rue Grandville, BP 20451, 54001 Nancy cedex, France
2 Laboratoire RMN Physique 01 UR 13-04, ENSIT, université de Tunis, 5, avenue Taha-Hussein, BP 56, 1008 Bab Menara, Tunis, Tunisia 
@article{CRCHIM_2014__17_7-8_824_0,
     author = {S\'ebastien Thomas and Abir Alatrache and Marie-No\"elle Pons and Orfan Zahraa},
     title = {Degradation of the herbicide isoproturon by a photocatalytic process},
     journal = {Comptes Rendus. Chimie},
     pages = {824--831},
     publisher = {Elsevier},
     volume = {17},
     number = {7-8},
     year = {2014},
     doi = {10.1016/j.crci.2014.04.002},
     language = {en},
}
TY  - JOUR
AU  - Sébastien Thomas
AU  - Abir Alatrache
AU  - Marie-Noëlle Pons
AU  - Orfan Zahraa
TI  - Degradation of the herbicide isoproturon by a photocatalytic process
JO  - Comptes Rendus. Chimie
PY  - 2014
SP  - 824
EP  - 831
VL  - 17
IS  - 7-8
PB  - Elsevier
DO  - 10.1016/j.crci.2014.04.002
LA  - en
ID  - CRCHIM_2014__17_7-8_824_0
ER  - 
%0 Journal Article
%A Sébastien Thomas
%A Abir Alatrache
%A Marie-Noëlle Pons
%A Orfan Zahraa
%T Degradation of the herbicide isoproturon by a photocatalytic process
%J Comptes Rendus. Chimie
%D 2014
%P 824-831
%V 17
%N 7-8
%I Elsevier
%R 10.1016/j.crci.2014.04.002
%G en
%F CRCHIM_2014__17_7-8_824_0
Sébastien Thomas; Abir Alatrache; Marie-Noëlle Pons; Orfan Zahraa. Degradation of the herbicide isoproturon by a photocatalytic process. Comptes Rendus. Chimie, Volume 17 (2014) no. 7-8, pp. 824-831. doi : 10.1016/j.crci.2014.04.002. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2014.04.002/

Version originale du texte intégral

1 Introduction

The pollution of ground or surface water has been a major environmental problem for many years. Most of these organic pollutants come from pesticides used in agriculture. The diversity of these compounds, as well as the lack of knowledge about their toxicity to human health, are important factors favoring the study of means for their elimination.

Various remediation processes already exist, such as chlorination or treatment on activated carbon. However, those processes do not allow satisfactory elimination of all chemical species: chlorination induces the production of toxic by-products [1,2], and adsorption on activated carbon results in pollutant transfer and not in pollutant elimination [3]. An ideal treatment method for pesticide wastes would be a non-selective one that could achieve rapid and complete degradation into inorganic products and could be suitable for small-scale treatment units [4]. Among the so-called advanced oxidation processes (AOPs), photocatalytic methods in the presence of artificial or solar light, like heterogeneous photocatalysis (TiO2/UV-A), have been proven to be effective for the degradation of various contaminants found in industrial or domestic wastewaters [5].

In the present study, the photocatalytic decomposition and mineralization of pollutants was studied with a TiO2/UV system. The pollutant used is an herbicide (isoproturon) that is widely used in the treatment of cereal crops in particular. Its elimination was then compared with that of atrazine, another pesticide that is commonly studied in the laboratory. The influence of experimental conditions such as flow rate, temperature and the presence of other pollutants in the treated solution was also investigated.

2 Photocatalysis principle

A photochemical reaction is characterized by an activation related to the absorption of at least one photon by a molecule. The range of wavelengths generally used in photochemistry is in the UV/visible region (wavelength 200 to 700 nm). However, this is not always sufficient for suitable pollutant remediation. Thus, oxidants such as O3, H2O2 and/or a catalyst are often used.

Semiconductors are characterized by a certain non-stoichiometry, unlike oxides such as MgO or Al2O3, which are insulators. Indeed, their electronic structure is characterized by a filled valence band and an empty conduction band. If a photon provides an energy hν equal to or higher than the gap band energy, an electron of the valence band moves to the conduction band as shown in Fig. 1. As a consequence, this leads to the appearance of a positive hole in the valence band and of a negative charge in the conduction band. Thus, the catalyst becomes very reactive while also gaining redox capacity [6,7].

Fig. 1

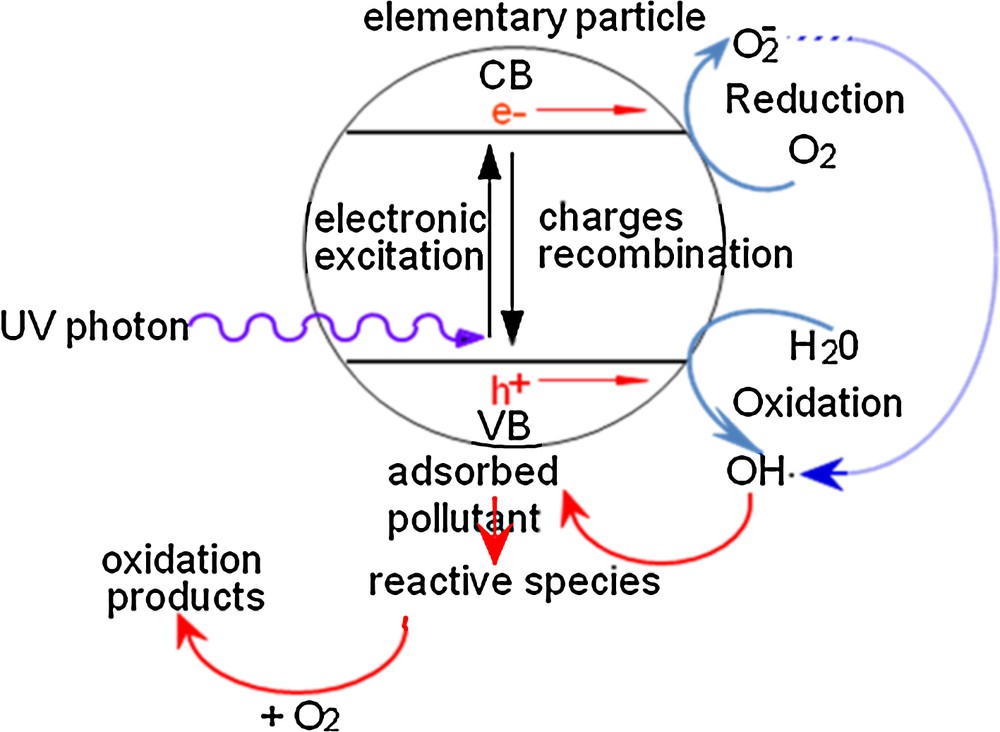
The principle of the photocatalytic process.

The most commonly used semiconductor is TiO2, due to its performance, stability, low cost and resistance to corrosive conditions. Its gap energy is 3.2 eV, which corresponds to 308 kJ/mol. The exposure of this material to an UV irradiation emitted at 365 nm is sufficient to supply this amount of energy. TiO2 can be used for the degradation of most organic pollutants, such as alkenes, olefin hydrocarbons, aliphatic compounds, phenols, chlorinated organic compounds [8], pesticides, and herbicides [9].

Two types of photocatalytic decomposition can take place:

  • • by direct reaction on the created electron-hole after the absorption of photons: h+Rad→Rad+•;
  • • by reaction with OH• radicals generated on the surface of the catalyst: OH•+RHad→Rad•+H2O.

These radicals can be generated via several pathways:

  • • interfacial charge transfer with H2O and/or OH–:
    • ∘ h++H2Oad→OH•+H+,
    • ∘ h++OHad→OH•;
  • • hydrogen peroxide action:
    • ∘ hydrogen peroxide is formed using oxygen present in the medium according to the following pathway (O2 is indeed the principal acceptor of e- in the medium):
      • – e−+O2→O2−,
      • – O2−•+H+→HO2•,
      • – HO2•+HO2•→H2O2+O2,
      • – O2−•+HO2•→HO2−+O2,
      • – HO2−+H+→H2O2,
    • ∘ then, hydrogen peroxide is broken up to yield OH• radicals:
      • – e−+H2O2→OH•+OH−,
      • – H2O2+O2−•→OH•+OH−+O2.

3 Elimination of isoproturon

Isoproturon, or 3-(4-isopropylphenyl)-1,1-dimethylurea, is one of the most-used herbicides in the world, in particular on cereal crops. It can be absorbed by plants, mainly by their roots. It acts primarily on annual graminaceous weeds. Its developed formula is:

Isoproturon's LD50 toxicity for rats is 1,826 mg/kg (oral) or >2,000 mg/kg (skin); these values are rather low. In spite of its substantial use, it is only found in relatively small quantities in ground or surface water. This is because it can be hydrolyzed or biodegraded in the natural environment. Indeed, enzymatic and microbial action can lead to the formation of aniline 4 (2-hydroxyisopropyl):

Isoproturon can also be photodegraded to yield:

3(4-isopropylphenyl)-1-methylurea
3(4-isopropylphenyl)-urea
and 4-4’-diisopropyl-azobenzene

Its half-life is approximately 40 days in moderate climates and 15 days in tropical climates. The concentrations in surface water or groundwater can reach values up to 0.15 μg/L. The French standard is the same for all pesticides (namely 0.1 μg/L), and this concentration is often detected in surface waters [10].

An earlier study examining the adsorption of pesticides on activated carbon showed that compounds belonging to the family of substituted urea, to which isoproturon belongs, were very well retained. This process should thus be developed for the elimination of this type of pesticide [11].

The photodegradation of isoproturon in water has been investigated in the presence and absence of oxygen. The irradiation of isoproturon at 290 nm in water containing dissolved organic matter showed that photolysis in the absence of oxygen was faster during the first minutes of the irradiation period. Later on, the transformation seemed to slow down more gradually than in normal conditions, showing an increase in the half-life of isoproturon in water [12].

4 Materials and methods

4.1 Experimental set-up and procedures

Experiments were performed in a 2-liter annular reactor (92 cm height, and inner and outer diameters of 3.2 and 4.2 cm, respectively). A MAZDA 36 W (1.20 m long and 26 mm in diameter, reference TWFN) black light was placed along the reactor's central axis; according to the manufacturer, the lamp's radiation has a λ-distribution between 340 and 400 nm, centered at 366 nm. The isoproturon solution was circulated in the system using a centrifugal pump and entered the reactor from the bottom after passing through a well-stirred tank. Thus, the system works in a closed loop and the reactor can be approximated as a batch reactor. The flow rate of the circulating effluent was controlled by a flow meter as described elsewhere [9].

During the photocatalytic experiments, 15 L of the isoproturon solution were mechanically stirred while the solution was continuously circulated through the reactor and flowed past the catalyst in the dark until adsorption equilibrium was reached. One hour later, the light was turned on, and at specific time intervals, samples were withdrawn and analyzed by HPLC.

The flow was adjusted to 10 L/min, which corresponds to a fluid velocity of 4.6 m/min. Thus, the Reynolds number can be calculated as, Re=ρudμ with d=4×sectionactual perimeter where u is the fluid velocity (m/s), ρ is the fluid density, μ is the fluid viscosity and d is the mean diameter of the reactor. The obtained Reynolds number was approximately 1500, indicating that the system was in turbulent flow.

4.2 Catalyst

The photocatalyst consisted of TiO2 deposited on a fiberglass sheet (Ahlstrom, Pont-l’Évêque, France). The total loading rate was 20 g/m2. According to the manufacturer, the specific surface area was 250 m2/g. However, as TiO2 was deposited on the fiberglass, the actual contact area was obviously different from the specific surface area and difficult to predict. The apparent surface of the catalyst in contact with the liquid in the described set-up was 0.24 m2, which corresponds to a mass of 4.8 g TiO2 or 2.4 g/L of TiO2 per unit volume of the reactor. The glass fibers were assembled between them by a binder, as shown by SEM in Fig. 2.

Fig. 2

SEM images of Ahlstrom paper a) without TiO2, b) with TiO2.

The sheet of catalyst-deposited fiberglass was rolled up and placed in the reactor so that it was plated on the inside of the external cylinder. However, both faces of the sheet were in contact with the liquid and were sensitive to light, as the paper was permeable to both liquid and light. The paper was first rinsed in order to remove all of the weakly attached TiO2 particles.

4.3 Chemicals

The following chemicals were used: isoproturon ISOYUARD (isoproturon 500 g/L from Garder Chemicals Ltd) and atrazine ATRAPHYTEL (atrazine 500 g/L from Sipcam-Phyteurop). Demineralized water was used without any further purification. Salicylic acid and phenol were purchased from Fluka and were used without any further purification. Methanol was purchased from Prolabo and was used without any further purification.

4.4 Analytical methods

Isoproturon concentrations were measured throughout the experiment using a High-Performance Liquid Chromatograph (HPLC) equipped with a UV SPD-10A Shimadzu detector and Lichosorb C18 column. The details of the apparatuses have been given in an earlier study [13]. The wavelengths at which the absorption of the chosen compounds was monitored were 240 nm for isoproturon, 295 nm for salicylic acid, 220 nm for atrazine and 270 nm for phenol.

5 Results and discussion

5.1 Rate expression

The experimental set-up was comparable to a closed batch reactor system; a similar system has been described elsewhere [14].

The following notations will be used:

  • • Cr and Cs are the concentrations in the tank and on the outlet side of the reactor, respectively (in mol/L);
  • • Vr and Vs are the volume for each flow rate s in the tank and the reactor, respectively (in L);
  • • Q is the volumetric flow rate of the fluid circulating throughout the reactor (in L/min);
  • • r is the rate of degradation (in mol/L/min).

The mass balance of each pollutant at steady state in the reactor, assuming perfect mixing and batch operation, is as follows:

In the tank:

Vr=dCrdt=−QCr−Cs(1)

In the reactor:

−Q   dCV,t=r   dV(2)
with the boundary conditions C = Cr for V = 0 and C = Cs for V = Vs. The photocatalytic reactions generally follow the Langmuir–Hinshelwood kinetic model, in which the rate can be written as follows:
r=−k   Ka   C1+Ka   C(3)
where Ka is the adsorption constant (in L/mol), and k is the rate constant of degradation (in mol/L/min) (with respect to the reactor's volume). Combining (2) and (3), we obtain the following relation:
lnCrCs+KaCr−Cs=Ka   k   ts(4)
where ts (min) is the residence time in the reactor.

Since, in our case, the conversion and therefore the contact time is low, it can be assumed that the concentration is uniform throughout the system. Then, we can write:

Vr+Vs   dC=−r   Vs   dt(5)

Using Eq. (1) and Eq. (5), we could solve the problem numerically and determine Cr. However, in order to get an expression of Cr as a function of time, it will be necessary to make an assumption. By combining Eq. (5) and Eq. (3), a differential equation describing the concentration can be obtained:

Vr+VsdCdt=k   Ka   C1+KaCVs(6)

Before solving this equation, it is essential to consider the possible boundary conditions:

  • • KaC >> 1 (high concentration), which would yield a zero-order reaction:
    Cr=C0−VsVr+Vs;(7)
  • • KaC << 1 (low concentration) which would yield a first-order reaction:
    Cr=C0   e−VsVr+Vsk   Kat.(8)

It is worthwhile to mention that the present study was performed at low concentrations, therefore leading to an exponential decay of the isoproturon concentration.

5.2 Kinetics of isoproturon degradation

In this study, each experiment was repeated three times, and the experimental values in all figures represent the mean values of three replicates, with standard deviations < 10%.

The analysis of the isoproturon solution by HPLC at different irradiation times under our experimental conditions yielded no detectable by-products. Indeed, only the isoproturon absorption peak was present. This might be due to the mineralization of isoproturon or to its decomposition into non-aromatic fragments undetectable by UV [15]. The evolution of isoproturon disappearance is given in Fig. 3.

Fig. 3

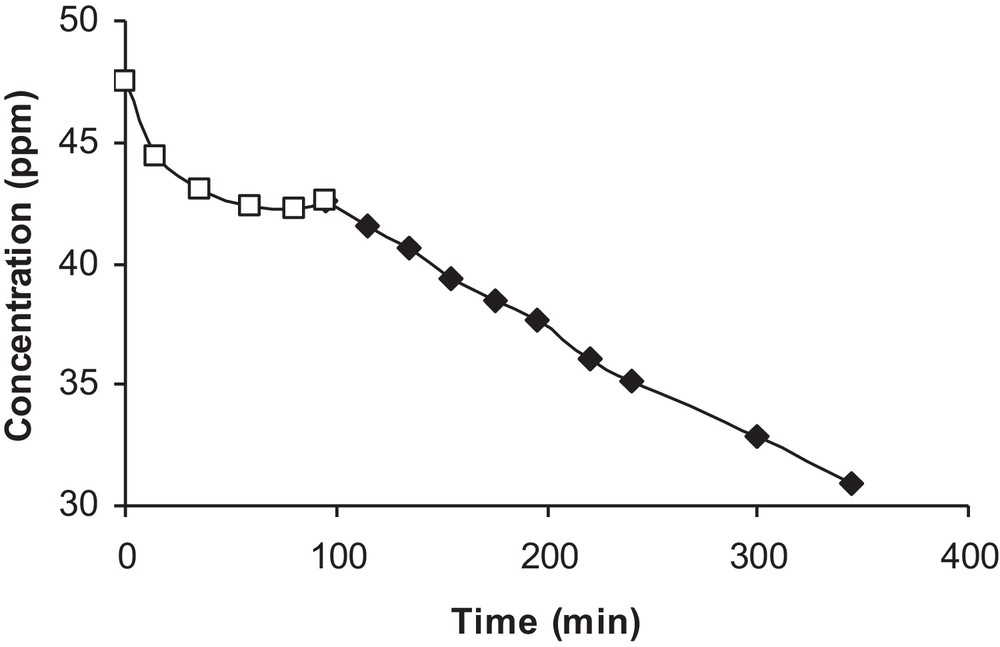
Photocatalytic degradation of isoproturon in the presence of light and catalyst (□) lamp off (♦) lamp on.

A rapid decrease in the pollutant concentration was observed during the adsorption period, and then equilibrium was reached in one hour. At the moment when the lamp was turned on, a small increase in concentration appeared due to isoproturon desorption induced by the rise in temperature. Thus, the initial concentration considered for photocatalytic degradation was that measured at equilibrium.

The kinetic behavior of the photocatalytic degradation of isoproturon was monitored, indicating that degradation proceeded as a first-order reaction: when the term ln(C/C0) is plotted against the time of irradiation, a straight line results, as can be observed in Fig. 4.

Fig. 4

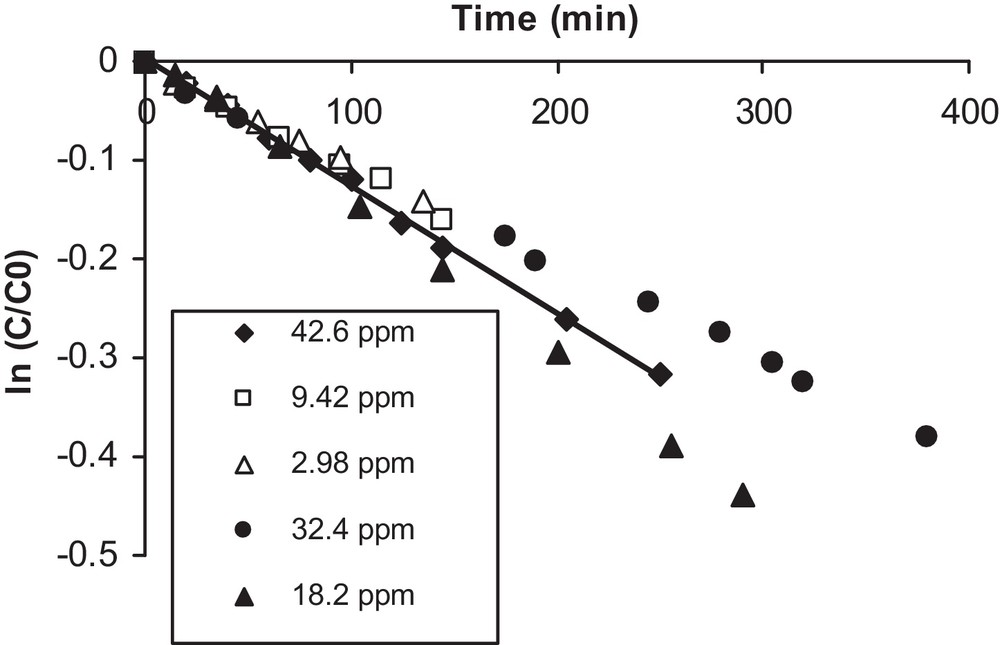
Determination of the kinetic constant.

A first-order reaction behavior was also observed for different initial concentrations ranging from 3 to 43 ppm. Moreover, the value of the apparent rate constant is simply the slope of the straight line. Pseudo-first-order kinetics have also been observed for the solar photocatalytic degradation of isoproturon [16]; the authors used TiO2 supported on H-mordenite, in an attempt to identify degradation intermediates and to achieve complete mineralization of isoproturon in aqueous solution. Furthermore, several intermediates in the reaction suspension at pH 3.8 have been identified by LC–ESI–TOF–MS analyses, and a degradation mechanism has been proposed [17].

The values of the kinetic constants obtained at different initial concentrations are given in Table 1. It can be seen from this table that the values of the experimentally obtained rate constants are on the same order, with an average value equal to 1.1·10−3 min−1.

Table 1

Values of rate constants at different initial concentrations.

C0 (ppm)k (min−1)
42.61.27 10−3
32.41.01 10−3
18.21.49 10−3
9.421.10 10−3
2.981.06 10−3

It should be mentioned that the obtained value of k at 18.2 ppm in the above table is slightly higher than the others, because the sample was withdrawn at the reactor outlet.

The temperature of the solution was stabilized at 32 °C after the UV lamp was turned on. Thus, the kinetic parameters were determined based on this condition. In order to obtain k Ka, expression Eq. (8) can be written (for 32 °C) as:

−VsVr+Vsk   Ka=−1.1⋅10−3min−1(9)

with

Vr=13 L   and   Vs=2 L,   then   k   Ka=8.3   10−3min−1(10)

5.3 Adsorption isotherm of isoproturon

The adsorption of this herbicide can be explained by the formation of hydrogen bonds between the O, N and H atoms of the isoproturon molecule and the TiO2 surface. From the values of the initial concentration C0 and those obtained at the adsorption equilibrium concentration C, the specific adsorbed amount of isoproturon was calculated according to the following equation:

q=VC0−C/m(11)
where V is the volume of the equilibrium solution and m is the mass of TiO2. An adsorption isotherm was then established as shown in Fig. 5, which corresponds to the specific quantity of adsorbed pollutant (in mol/g) as a function of the concentration at equilibrium.

Fig. 5

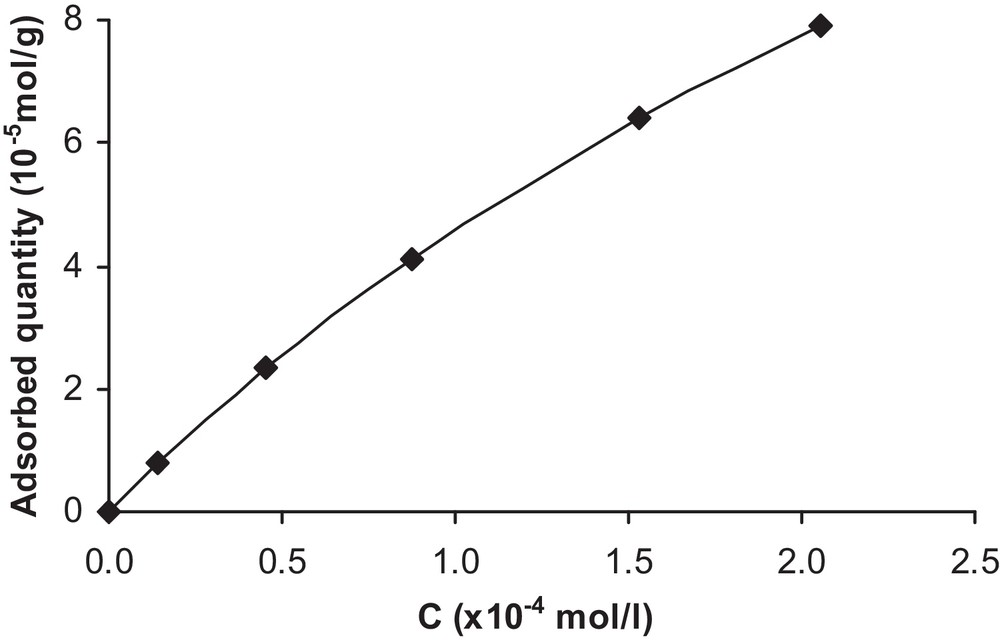
Adsorption isotherm of isoproturon on TiO2.

Assuming monolayer adsorption (Langmuir isotherm), the adsorption equilibrium constant can be determined as follows:

Ka=ka/kd(12)
where ka (L/min·g) and kd (mol/min·g) correspond to the rate constants of adsorption and desorption. By introducing qmax (mol/g), the maximum number of sites per gram of catalyst; m (g), the mass of catalyst; and C0 and C (mol/L), the initial concentration of the pollutant and its concentration at equilibrium, we obtain the Langmuir isotherm equation [18]:
q=qmax   Ka   C1+Ka   C(13)

In this expression, q (mol/g) corresponds to the quantity of adsorbed isoproturon per gram of catalyst. Rewriting Eq. (13), we obtain:

1q=1qmax1+1Ka   C(14)

Indeed, when plotting 1/q versus 1/C as in Fig. 6, a straight line is obtained and the Langmuir isotherm provides a good fit of the data (at 20 °C). However, the type of isotherm may be different, since it is strongly influenced by the properties of the solute itself, by the composition of the adsorbent, and by the chemistry of the solution. Similarly, the investigations of Ertli and coworkers on the adsorption of isoproturon on several natural adsorbents have revealed the presence of multistep adsorption isotherms [11].

Fig. 6

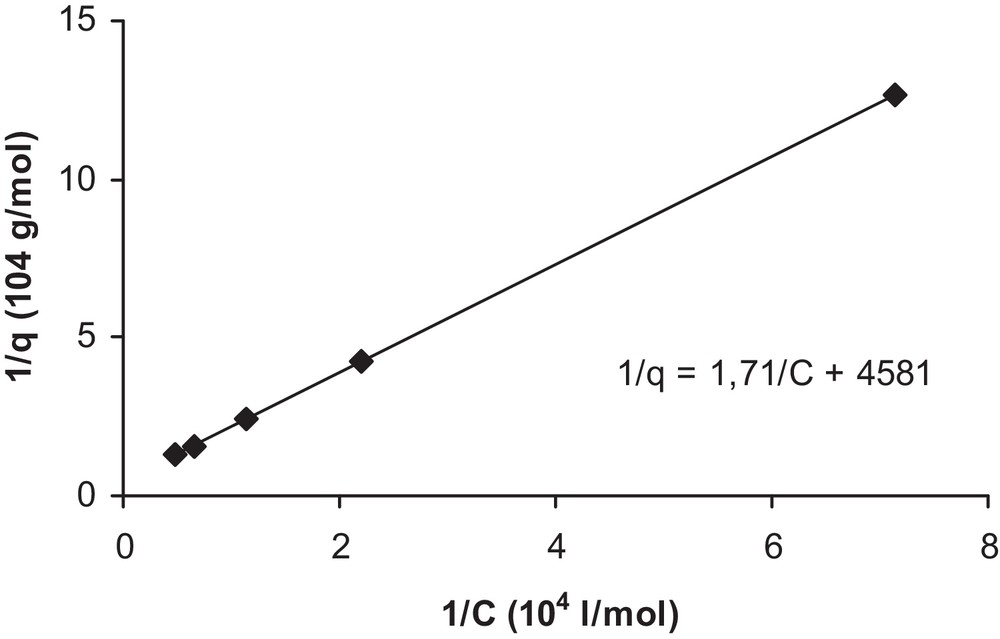
Determination of Langmuir isotherm constants Ka and qmax.

Therefore, the following constants were determined: Ka = 2,7·103 L/mol and qmax = 2.2·10−4 mol/g. However, by considering the dependence of Ka on temperature, the following equation is obtained:

Ka32°C=Ka20°CeQR1305.15−1293.15(15)
where Q is the heat of adsorption, which has been determined experimentally and is equal to 42.6 kJ, and R is the ideal gas constant (8.31 J/mol/K). The adsorption constant can then be calculated as: Ka (32 °C) = 1.4·103 L/mol. Then, from relation Eq. (10), the rate constant can also be deduced: k (32 °C) = 6.2·10−6 mol/L/min. This rate constant is comparable to the value obtained by Parra et al. (8·10−6 mol/L/min) for the photocatalytic degradation of isoproturon carried out using TiO2 supported on glass rings, in a coaxial rector [19]. At a 1.5 L/min flow rate, they achieved almost complete mineralization in 120 minutes. In this work, in the same period, only 25% of the isoproturon was eliminated since the flow rate was 10 times faster in our conditions.

5.4 Codegradation

Ground and surface water can be contaminated simultaneously by a variety of organic pollutants including pesticides; as a result, the degradation of isoproturon could be affected in the presence of other substances. In their work using solar illumination, Miranda-Garcia et al. have examined, in addition to isoproturon, the degradation of 14 emerging contaminants in a mixture [20], observing that some contaminants can degrade faster than the others. Since the photocatalytic process depends on the accessibility of the surface sites of the catalyst, additional or competitive degradation may occur among the pollutants. In order to examine this phenomenon, the degradation of a binary mixture of isoproturon with salicylic acid or phenol as a copollutant was carried out using similar concentrations of isoproturon and the copollutant (approximately 50 μmol/L). The experimental evolution of the relative isoproturon concentration (C/C0) under these conditions is plotted in Figs. 7 and 8, where salicylic acid and phenol are the copollutants, respectively.

Fig. 7

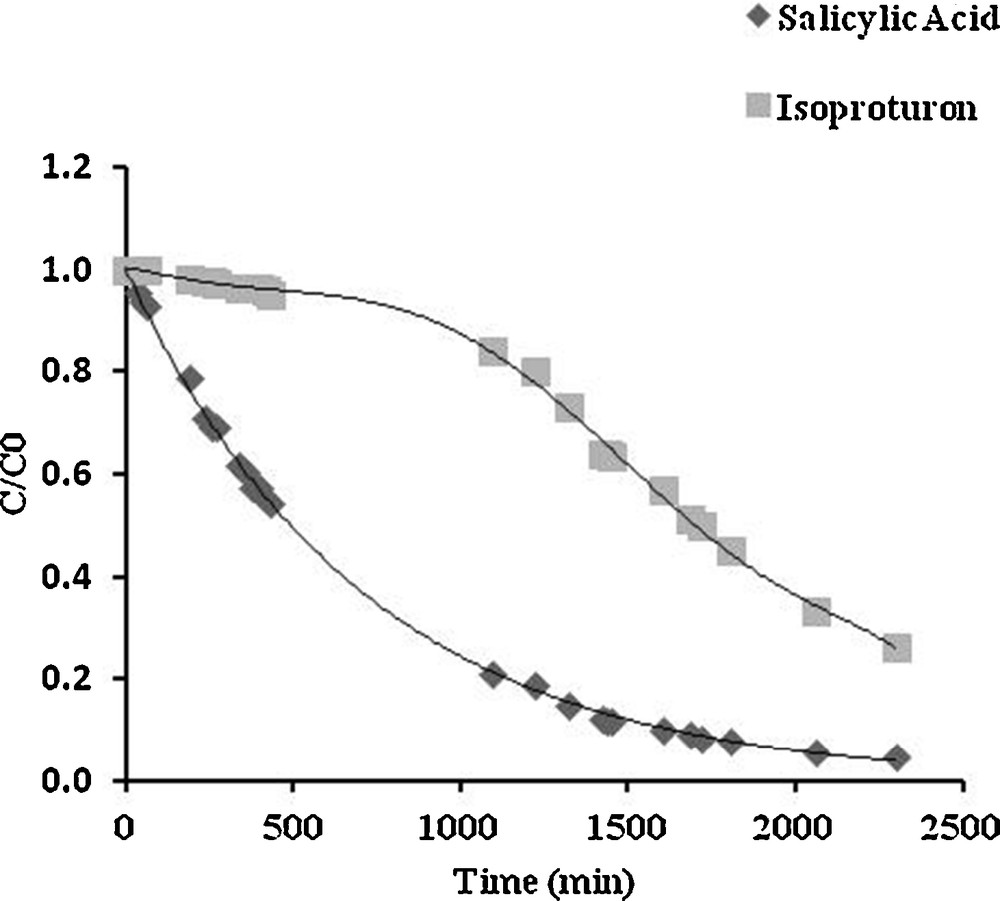
Competitive photocatalytic degradation of isoproturon and salicylic acid. Initial concentrations: isoproturon 48 μmol/L; salicylic acid 46 μmol/L.

Fig. 8

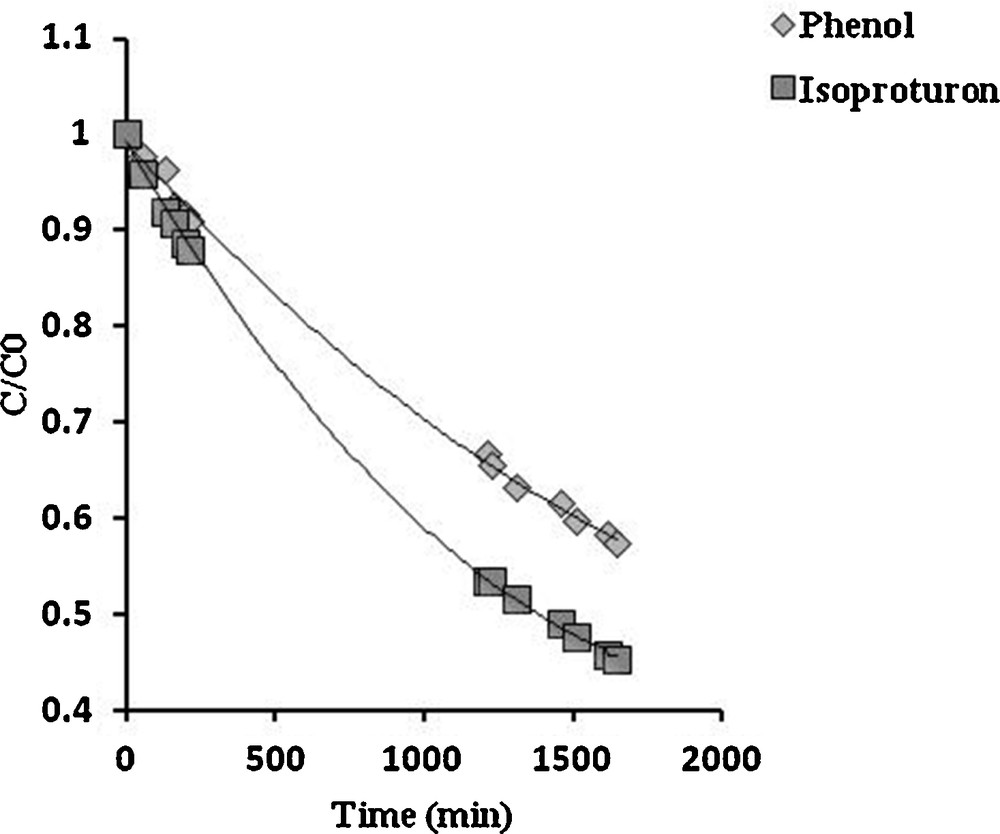
Competitive photocatalytic degradation of isoproturon and phenol. Initial concentrations: isoproturon 48 μmol/L; phenol 50 μmol/L.

Fig. 8 shows that in isoproturon–phenol codegradation, both isoproturon and phenol degradation occurs simultaneously, without mutual inhibition; in this case, it seems that isoproturon and phenol do not compete for the same type of active site. However, an important effect can be observed in isoproturon–salicylic acid codegradation (Fig. 7), where isoproturon degradation was inhibited by the strong adsorption of salicylic acid. The degradation of isoproturon occurred once the copollutant had mostly been degraded. Obviously, both pollutants participate in competitive adsorption at the same type of site on the surface of TiO2, with (in this particular case) a higher affinity of salicylic acid molecules toward the surface. A similar behavior has been reported in systems containing 4-hydroxybenzoic acid (4-HBz) and benzamide (Bz) [21], as well as in the degradation of a mixture of volatile organic carbons (VOCs) [22]. These observations suggest that competitive adsorption might be the most critical process in the competition for degradation. Thus, taking into account the effects of competitive adsorption, the rate of isoproturon degradation can be written as follows [18]:

r=kdeg   KLH   C1+KLH   C+K'LHC'(16)
where K’LH is the adsorption constant, and C’ is the concentration of the copollutant. This situation can be simulated by an approximate model in which the copollutant inhibits isoproturon degradation; however, the pesticide does not significantly alter the degradation of salicylic acid, as shown in an earlier work [9].

5.5 Influence of flow rate and temperature

The effect of temperature elevation (due to the increased flow rate) on the adsorption constant was studied and will be discussed in this section. The photocatalytic degradation of isoproturon mainly depends on its adsorption on TiO2. In addition, it is well known that the adsorption constant is dependent on temperature [18]. Thus, the effect of flow rate on TiO2 particles was investigated, and the adsorption constant of isoproturon was measured. Two series of experiments were carried out, first by lowering the flow from 17 to 7 L/min, and then by increasing it from 5 to 22 L/min. At each flow rate, the adsorption constants were calculated from the Langmuir adsorption isotherm, the results of which are plotted in Fig. 9 as a function of the corresponding flow rate.

Fig. 9

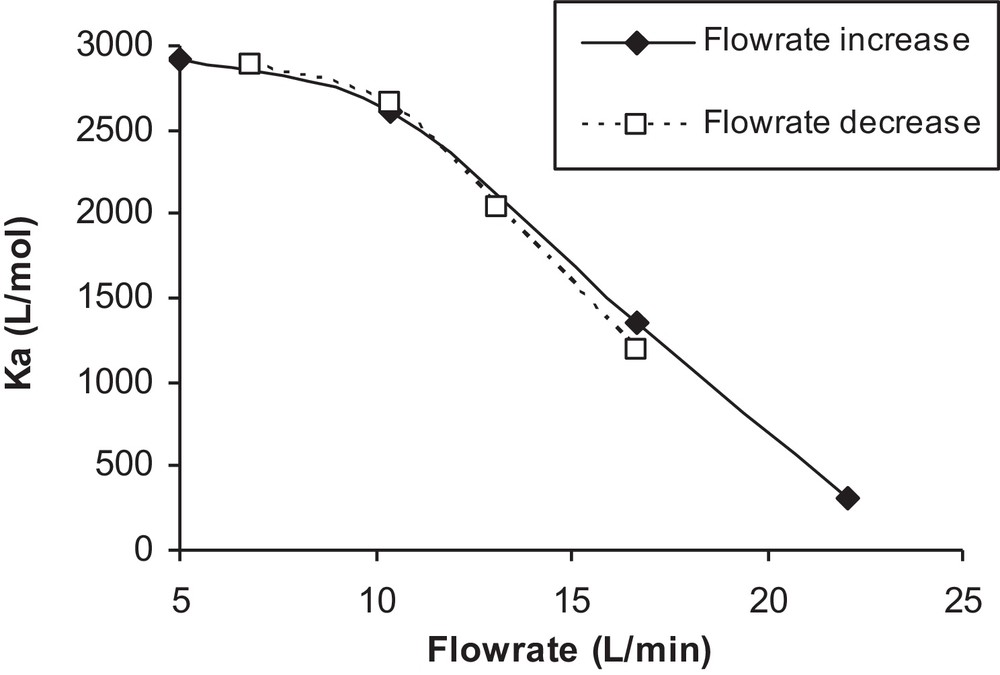
Influence of flow rate on the adsorption constant.

The observed variation of Ka in this figure is surprising because the thermodynamic constant of adsorption cannot depend only on the flow. One possible assumption can be made, i.e. to consider that the increase in the flow is accompanied by an increase in temperature, which would explain the decrease of isoproturon adsorption on the surface of TiO2. This assumption can be verified by the drastic increase in the temperature of the solution with an increase in flow rate observed in a separate experiment, as shown in Fig. 10. In the literature, numerous studies have been conducted on the dependence of photocatalytic reactions on the reaction temperature [23,24].

Fig. 10

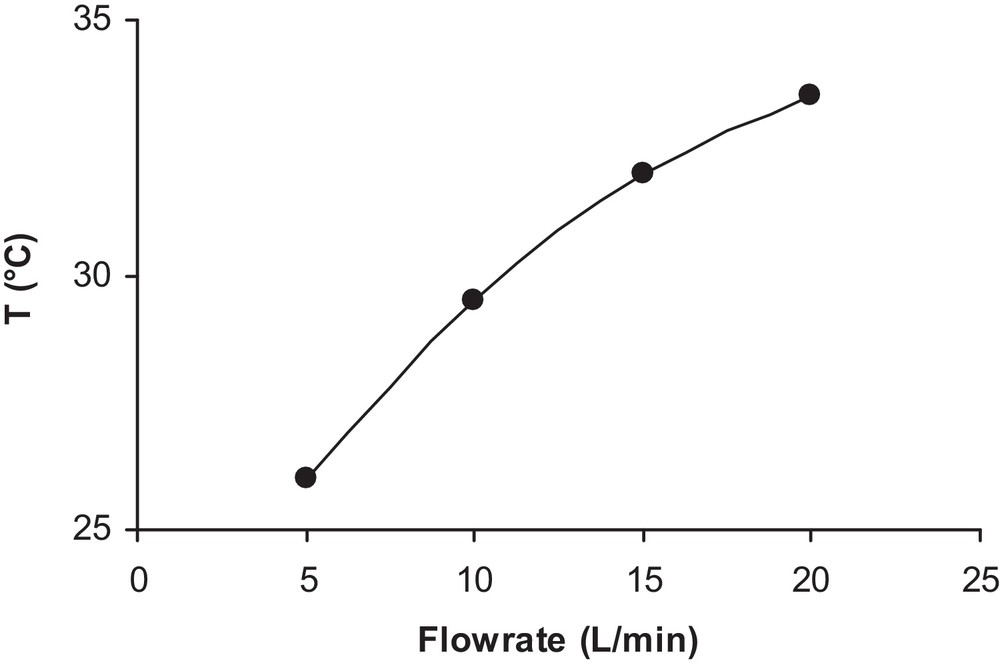
Fluid temperature variation with flow rate.

In the present study, the effect of temperature on the adsorption constant was investigated by varying the temperature of the isoproturon solution from 20 to 50 °C. The adsorbed quantity and adsorption constant of the pollutant were then determined at four different temperatures, allowing the evolution of the adsorption constant with temperature to be determined, as seen in Fig. 11. Therefore, heat energy is inadequate to activate the TiO2 surface. Most previous investigations have stated that an increase in the photocatalytic reaction temperature (> 80 °C) promotes the recombination of charge carriers and deters the adsorption of organic compounds onto the TiO2 surface [25]. A further change in temperature down to 0 °C would cause an increase in the apparent activation energy. As a consequence, the optimum reaction temperature for photo-mineralization is reported to be in the range of 20 to 80 °C [26].

Fig. 11

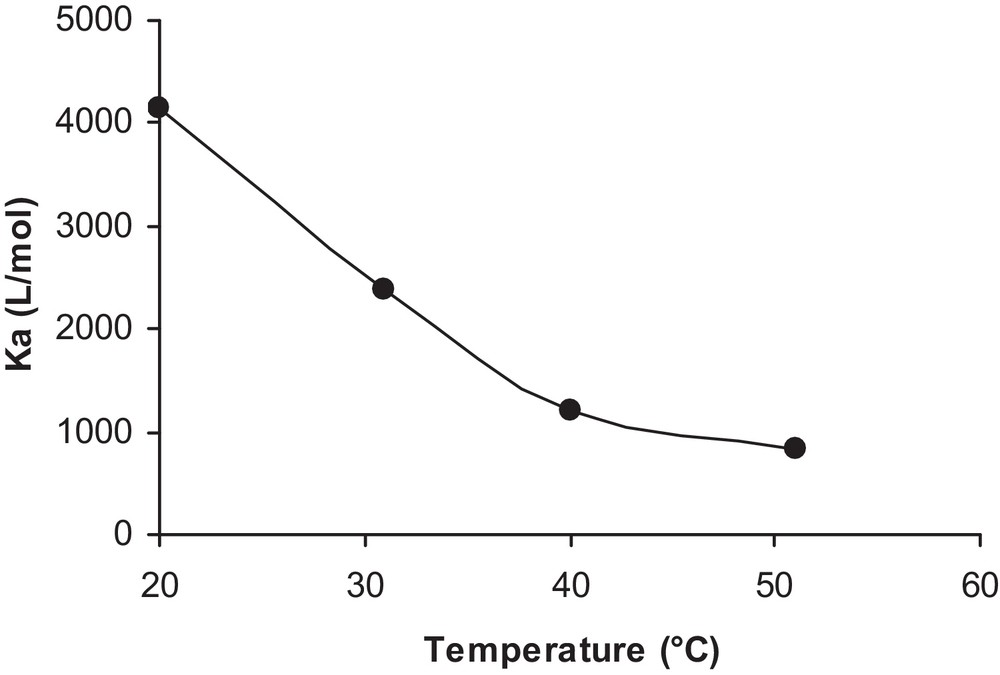
Influence of the temperature on the adsorption constant.

The heat of adsorption Q can then be deduced, knowing that the adsorption constant can be expressed in the form:

Ka=K0   eQRT(17)
where Q is the heat of adsorption (in J/mol), K0 is a constant (in L/mol), and R is the ideal gas constant (J/mol/K).

The logarithm of Ka is:

lnKa=lnK0+QRT(18)

Thus, by plotting ln (Ka) vs. (1/T) in Fig. 12, the heat of adsorption Q can be deduced within this temperature range as Q = 42.6 kJ/mol.

Fig. 12

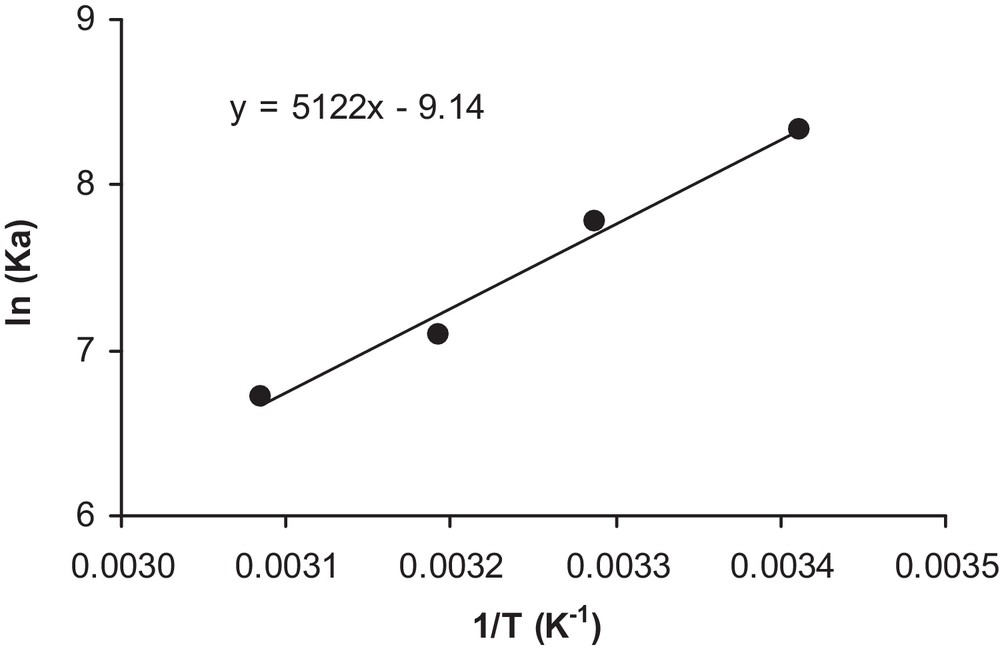
Determination of the heat of adsorption.

Two observations can be made at this stage: the obtained heat of adsorption seems to be high enough for a phenomenon such as physisorption (maximum of 50 kJ in general), and, in the case of a solar reactor, it would be important to use a cooling system in order to avoid low adsorption.

6 Conclusions

The results in this study highlighted the adsorption of isoproturon on a catalyst surface, The Langmuir isotherm was verified, and the adsorption parameters Ka and qmax were found to be 2.7·103 L/mol and 2.2·10−4 mol/g, respectively. Competitive adsorption might be the critical process in the codegradation of isoproturon and other copollutants. Moreover, the effect of temperature on adsorption was determined, and the heat of adsorption Q was found to be on the order of 43 kJ/mol. The photocatalytic degradation of isoproturon occurred following the Langmuir–Hinshelwood kinetic model. Thus, the apparent rate constant and the reaction order with respect to the pollutant were also determined.

In order to improve the effectiveness of the reaction, additional treatments should be considered for either the catalyst or the solution. Moreover, the kinetic results obtained in this work, along with other data characteristic of irradiation, could be used to scale up an appropriate photocatalytic reactor, leading to herbicide mineralization.

Bibliographie

[1] Chemistry of Wastewater Technology (R.L. Jolley; W.W. Pitt; A.J. in Rubin, eds.), Ann Arbor Science Publishers, Ann Arbor, MI, 1978

[2] A. Lopez; G. Mascolo; R. Ciannarella; G. Tiravanti Chemosphere, 45 (2001), pp. 269-274

[3] J.W. Patterson Industrial wastewater treatment technology, Butterworth, Boston, 1985

[4] J. Blanco; S. Malato Solar detoxification, UNESCO, Natural Sciences, World Solar Programme 1996-2005, 2001 http://www.unesco.org/science/wsp ([chapter 2])

[5] P.J. Robertson; D.W. Bahnemann; J.M.C. Robertson; F. Wood, Springer-Verlag, Berlin, Heidelberg (2005), pp. 367-423 ([vol. 2, Part M])

[6] O. Legrini; E. Oliveros; A.M. Braun Chem. Rev., 93 (1993), pp. 67-698

[7] M. Hoffmann; S. Martin; W. Choi; D. Bahnemann Chem. Rev., 95 (1995), pp. 69-96

[8] V. Carlin; C. Minero; E. Pelizetti Environ. Technol., 11 (1990), pp. 919-926

[9] O. Zahraa; L. Sauvanaud; G. Hamard; M. Bouchy Int. J. Photoenergy, 2 (2003), pp. 87-93

[10] Gharda Chemicals Limited, 2008, www.gharda.com/products/agrochemicals/herbicides_isoproturon.html.

[11] T. Ertli; A. Marton; R. Földényi Chemosphere, 57 (2004), pp. 771-779

[12] M. Mansour; E.A. Feicht; A. Behechti; I. Scheunert Chemosphere, 35 (1997), pp. 39-50

[13] O. Zahraa; S. Maire; F. Évenou; C. Hachem; M.N. Pons; A. Alinsafi; M. Bouchy Int. J. Photoenergy (2006), pp. 1-9 ([Article ID 46961])

[14] G. Chester; M. Anderson; H. Read; S. Esplugas J. Photochem. Photobiol. A: Chem., 71 (1993), pp. 291-297

[15] G. Mascolo; A. Lopez; H. James; M. Fielding; G. Mascolo; A. Lopez; H. James; M. Fielding Water Res., 35 (2001), pp. 1695-1704

[16] M.V.P. Sharma; V. Durgakumari; M. Subrahmanyam Solar photocatalytic degradation of isoproturon over TiO2/H-MOR composite systems, J. Hazard Mater., Volume 160 (2008), pp. 568-575

[17] M.J. López-Munoz; A. Revilla; J. Aguado Catal. Today, 209 (2013), pp. 99-107

[18] G. Scacchi; M. Bouchy; J.-F. Foucaut; O. Zahraa Cinétique et catalyse, Tec & Doc, Lavoisier, Paris, 1996

[19] S. Parra; S. Malato; C. Pulgarin Appl. Catal. B: Environ., 36 (2002), pp. 131-144

[20] N. Miranda-García; M. Ignacio Maldonado; J.M. Coronado; S. Malato Catal. Today, 151 (2010), pp. 107-113

[21] D. Robert; A. Piscopo; J.V. Weber Solar Energy, 77 (2004), pp. 553-558

[22] F. Moulis; J. Krysa Catal. Today, 209 (2013), pp. 153-158

[23] E. Evgenidou; K. Fytianos; I. Poulios Appl. Catal. B: Environ., 59 (2005), pp. 81-89

[24] N. Doucet; F. Bocquillon; O. Zahraa; M. Bouchy Chemosphere, 65 (2006), pp. 1188-1196

[25] U.I. Gaya; A.H. Abdullah J. Photochem. Photobiol. C: Photochem. Rev., 9 (2008), pp. 1-12

[26] S. Malato; P. Fernandez-Ibanez; M.I. Maldonado; J. Blanco; W. Gernjak Catal. Today, 147 (2009), pp. 1-59

☆ Thematic issue dedicated to François Garin.

Commentaires - Politique

Ces articles pourraient vous intéresser

Fe–TiO 2 composite beads driven hybrid process of photocatalysis and photo-Fenton for the degradation of isoproturon

Steffi Talwar; Alisha Shandil; Anoop Kumar Verma; ...

C. R. Chim (2020)

Antibacterial inactivation of spiramycin after titanium dioxide photocatalytic treatment

Rahma Hendili; Abir Alatrache; Mossadok Ben-Attia; ...

C. R. Chim (2017)

Editorial Board - English

C. R. Chim (2014)