1 Introduction
Mordenite zeolites are often presented as catalytic materials [1] and they are also used as membrane layers for pervaporation or fuel cell applications [2]. The reason why mordenite is also used as a membrane is because zeolites present some interesting characteristics and properties, as for example uniform and molecular-sized pores, surface acidity, inter-crystalline porosity, hydrophobicity. Mordenite is a zeolite that has a low Si/Al ratio, with an ideal composition of the unit cell corresponding to Na8[Al8Si40O96]·nH2O. Synthetic mordenite is characterized by a Si/Al ratio ranging from 5 to 10, which directly depends on the chemical composition of the reagents mixture. Mordenite was synthesised for the first time by Barrer et al. [3] in 1948, and it was used as a membrane active layer by Suzuki et al. [4] in 1990. Due to its composition, mordenite presents a hydrophilic behaviour and its catalytic properties directly depend on the Si/Al ratio related to Brønsted and Lewis acidities [5–7]. The Na–mordenite system presents uniform and molecular-sized pores and a surface negatively charged, which both induce a high retention of organic molecules and a particular selectivity for the filtration of salts [8]. In a previous work [9], we showed that Na–mordenite membranes could also be used for the separation of halide salt mixtures. These results were obtained with a Na–mordenite membrane synthesized by sol–gel methodology and impregnated onto a tubular ceramic alumina support. The active layer of the membrane presented a double porosity: mesopores (corresponding to the inter-crystallinity of the mordenite crystals) and nanopores (corresponding to the intra-crystalline porosity of the mordenite framework). We observed that the use of these membranes required a previous step, corresponding to the stabilization of the membrane permeability, obtained by the filtration of pure water at a constant transmembrane pressure and a constant temperature. As shown by Weber et al. with different ceramic membranes [10], the stabilization of membrane permeabilities, corresponding to the conditioning phase, depends on the filtration active layer and/or the support of the membrane.
The hydration phenomenon of mineral porous surfaces and more particularly those of mordenite is not trivial, and it has been little described in the literature. Especially, Demuth et al. [11] presented that the water molecule could be adsorbed in two different ways on an acid mordenite surface: the water molecule may be physisorbed at the Brønsted acid sites of the zeolite, and it can be also adsorbed after the formation of a hydroxonium cation (H3O+). Ab initio investigations showed that the physisorbed form is stabilized by the existence of two hydrogen bonds, while the adsorption of the hydroxonium cation does not lead to a stable structure [11–13]. It may correspond more to a transition state than to a steady state of the water molecule on the mordenite surface. Maurin et al. [12] studied the hydration phenomenon in a Na+–mordenite zeolite by using the dielectric relaxation spectroscopy (DRS) methodology coupled with molecular dynamics simulations (MDS). They showed that Na+ cations were situated half in the 8 T channels (small ones) and half in the 12 T channels (big ones). They simulated different hydration levels of the unit cell, from 1 to 24 water molecules. The results showed that, if the Na+ cation located in the small channels was not affected by the presence of water, the mobility of the Na+ cation situated in the main channel increased and that this cation was shifted to another position in the channel. Then, the mobility of this Na+ cation increased a lot after the introduction of more than two molecules of water, leading to a weak interaction between this cation and the zeolite framework. These results [11,12] indicate that the water molecules may interact both with the zeolite surface and adsorb on different sites, but also with the Na+ cations present in the channels (cation hydration).
Even if the diffusion rate of a nanoconfined water molecule remains low, it increases in nanopores by the complete destruction of the hydrogen-bonded networks, as presented by Zhu et al. [13]. The presence of Na+ cations inside the mordenite pores is also important because water molecules may hydrate the Na+ cations and also be physisorbed on the mordenite surface, as shown previously. In another work, Li et al. [14] showed that the hydraulic permeability of ceramic membranes could be predicted by the Carman–Kozeny equation at the steady state. Their results indicated that the hydraulic permeability is controlled by the pore size, the thickness and the porosity of the membrane. This result indicates that there is a relation between the membrane microstructure and the membrane permeability.
It is essential to note that before performing the filtration tests with the different Na–mordenite membranes, the permeation flux must be stabilized, which means that the membranes must be conditioned with water (surface hydration). This point is very important in order to reach the membrane permeation equilibrium. The phenomena that take part in Na–mordenite membrane surface stabilization are complex because many parameters must be taken into account. Only few works have studied and reported the evolution of the hydraulic permeability of mineral membranes during the stabilization phase (conditioning step) [10,15].
The purpose of this work is to study the hydration phenomena that operate during the conditioning step of different ceramic membranes. Actually, the water permeation flux observed at the beginning of the membrane life is maximal, and stabilises at a lower value at the end of the conditioning step. The decrease of the permeation flux is significant in the first hours of the conditioning step and becomes lower after several hours. This observation can be interpreted by several hydration phenomena acting with different kinetics. During this work, we study the evolution of the membrane hydraulic permeability all along the conditioning step, and an empirical identification of the different hydration contributions is proposed in order to find some correlations between the active layer properties and the hydraulic permeability. Na–mordenite membranes that were prepared in the laboratory are conditioned as well as a commercial TiO2 membrane, morphologic and textural properties of these membranes are also studied. This work is original, because there is no work that presents or explains the conditioning step of ceramic membranes and also the physical description of this phenomenon.
2 Experimental part
2.1 Materials
The Na–mordenite gel was prepared by the same way as that detailed by Hincapie et al. [16]. After obtaining the gel, a set of five Na–mordenite membranes was prepared by the impregnation of the gel inside different commercial alumina tubular supports (provided by Pall Exekia company, Bazet, France). The spin-coating method was carried out with the injection of 5 mL of the gel at 800 rpm, and then the rotation speed was increased to 1500 rpm (horizontal orientation of the rotating engine) to obtain a homogeneous gel layer all over the inlet tube surface. This procedure was chosen because the implementation was easy and not so expensive. The alumina tube used in this study present a length of 25 × 10−2 m and an internal radius of 3.5 × 10−3 m before the impregnation step. Then, a hydrothermal synthesis was carried out in an autoclave at 155 °C for 41 h. The protocol of preparation was verified on the membrane M4, and it showed both a good reproducibility of the conditioning process as well as a stabilised permeability.
A part of the gel prepared for each membrane was reserved to obtain at the same time Na–mordenite powder for characterizing the matter, which forms the membrane active layer. The membranes and the powders were simultaneously calcined between 300 °C and 500 °C for 4 h in a furnace. In the present study, five Na–mordenite membranes and a commercial one were studied, after calcination at different temperatures. All the experimental data are given in Table 1.
References, nature and calcination temperatures of the different ceramic membranes used in this work.
| References | Active layer | Temperature of calcination (°C) |
| M1-300 | Na–mordenite | 300 |
| M2-400 | Na–mordenite | 400 |
| M3-300 | Na–mordenite | 300 |
| M4-400 | Na–mordenite | 400 |
| M5-500 | Na–mordenite | 500 |
| M6-400 | TiO2 | 400 |
M1, M2, M3, M4 and M5 membranes have been fully prepared (gel, impregnation, hydrothermal synthesis and calcination) in our laboratory. M3, M4 and M5 membranes have been made according the same protocol than M1 and M2, except that the precursor used to prepare the gel was not the same (different mordenite sowing germs). Finally, M6 is an ultrafiltration (low cut-off: 1 kD) TiO2 commercial membrane also supplied by the Pall Exekia company.
A Micromeritics ASAP 2000 apparatus was used to study the textural properties (microporous volume and surface area) of the different samples (Na–mordenite and TiO2). Nitrogen adsorption experiments were performed at 77 K, the surface area was estimated by the Brunauer–Emmett–Teller (BET) methodology, while the microporous volume was estimated by the t-plot methodology. The structural and composition properties of the different Na–mordenite samples were characterized by X-ray diffraction (XRD) using a PANanalytical X’Pert Pro diffractometer with Cu Kα (1.542 Å) radiation and RTMS X’celerator detector. X-ray diffractograms were recorded from 5 to 90°. SEM observations of the membrane surfaces were performed using a FEI MEB FEG XL30 microscope. TiO2 powder was supplied by the Pall Exekia Company in order to perform nitrogen adsorption experiments.
2.2 Methods
The experimental set-up utilized to follow the evolution of the membrane water permeability is a laboratory pilot-plant (TIA, Bollène, France) described in a previous work [17] (see Fig. 1). Water permeabilities are investigated by cross-flow rate experiments (constant flow rate of 700 L/h using a volumetric pump) at a pressure of 5 bar. The flow rate was measured with an electromagnetic flowmeter, pressure is controlled upstream and downstream of the membrane cage and is manually set. A constant temperature (25 °C) of the filtered water is maintained all along the filtration period. The feed tank of the experimental unit has a volume capacity of 5 L. The membrane water flux is achieved at a constant transmembrane pressure (5 bar) in order to follow the evolution of its hydraulic performances. The hydraulic permeability of the different membranes is directly extracted from equation (1):
| (1) |
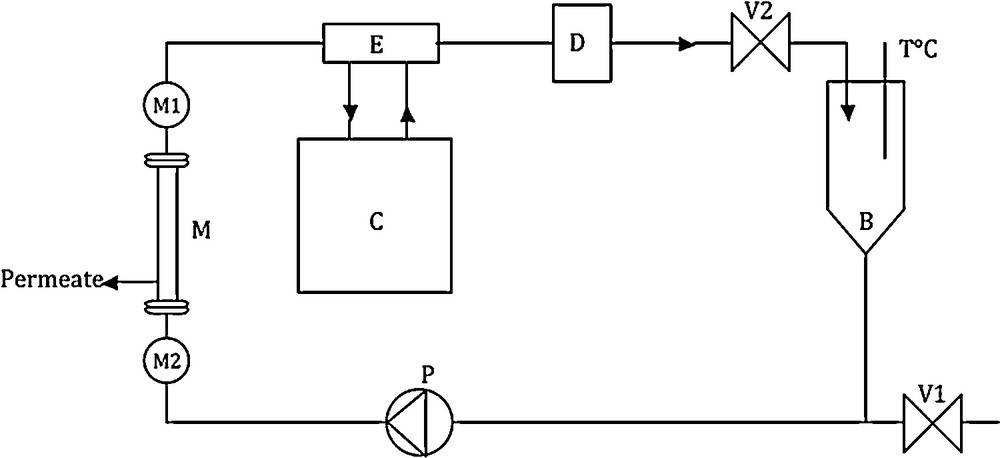
Description of the ultrafiltration/nanofiltration experimental set-up used in this work. B: feed tank; C: frigorific unit; D: flowmeter; E: counter-current heat exchanger; M: membrane; M1 and M2, manometers; P: volumetric pump; V: waste outlet gate; V2: pressure control gate.
Ultrapure water is used during the conditioning step, in order to avoid the development of a biofilm, which could also strongly modify membrane permeability. In order to verify that no contaminant was present during the conditioning step, we also introduce square alumina platelets (4 cm2) in the feed tank, which were analysed by confocal microscopy at the end of the conditioning step. For each experiment, we did not observe the presence of bacteria on the alumina sample.
3 Results
The different samples of Na–mordenite obtained by the sol–gel method (3.8 Na2O·Al2O3·18.6 SiO2·481·7 H2O) are analyzed by X-ray diffraction (XRD) before the calcination step in order to control the structure and the crystallinity of the zeolite. The reflection intensities observed on the XRD patterns (not shown here) obtained with the different Na–mordenite samples confirm the presence of a structure corresponding to mordenite (22.3°; 25.7°; 26.3°; 27.9°; 30.8°). SEM photograph (Fig. 2a) shows a cross section of a Na–mordenite membrane. The active layer is 80–100-μm thick (upper layer in Fig. 2a). Fig. 2b and c correspond to enlargements of the membrane's active layer as observed in Fig. 2a. They show an agglomeration of Na–mordenite crystals, whose sizes are close to 2 μm in length and 0.5 μm in width. Finally, Fig. 2d and e show a cross section of the TiO2 commercial membrane, which presents a very thin active layer (2 μm of thickness) recovering the surface of the alumina macroporous support (three alumina layers presenting different porosities). A SEM photograph of the TiO2 surface (Fig. 2f) indicates that this surface consists of an agglomeration of spheroidal particles with diameters from 20 to 80 nm.

SEM observations: (a) cross section of the Na–mordenite membrane, (b) and (c) agglomeration of Na–mordenite crystals at the surface of the membrane with different enlargements, (d) cross section of the commercial TiO2 membrane, (e) observation of the commercial TiO2 membrane thickness, (f) agglomeration of TiO2 nanoparticles at the surface of the commercial TiO2 membrane.
The textural properties (BET and BJH methods) were carried out with the five Na–mordenite powders [18] as well as with the TiO2 powder (not shown) by nitrogen adsorption experiments. For the different Na–mordenite samples, we obtained a H4 type isotherm corresponding to solids consisting of an agglomeration of particles (see Fig. 2b and c) with uniform pore shape. The isotherm of TiO2 (type H2) corresponds to the agglomeration of spheroidal particles having pores with uniform shape and size, which was previously observed by SEM. From these results, we extracted the textural properties of the different membrane layers, which are presented in Table 2.
Textural properties of the different membrane layers obtained by nitrogen adsorption and hydraulic permeabilities obtained after the conditioning step (stabilized values).
| References | Specific area (m2·g−1) | Mean pore radius (nm) | Microporous volume (cm3·g−1) | Hydraulic permeability (10−14 m3·m−2) |
| M1-300 | 175.4 | 15.5 | 0.089 | 2.96 |
| M2-400 | 261.5 | 17.3 | 0.139 | 4.6 |
| M3-300 | 31.5 | 17.6 | 0.020 | 0.78 |
| M4-400 | 19.8 | 8.4 | 0.160 | 5.6 |
| M5-500 | 14.3 | 15.1 | 0.050 | 5.34 |
| M6-400 | 231 | 3.8 | 0.019 | 4.4 |
The significant difference of specific surface areas and hydraulic permeabilities between membrane 1 and 2 can be explained by a difference of agitation time during the preparation of the gel. There is a slight decrease in these values after the treatment (surface area of 300 m2·g−1 before the thermal treatment). The surface area of Na-mordenite comes from the existence of both external and porous surfaces. The Na-mordenite porosity is associated to the presence of micropores (diameter < 2 nm) and mesopores (2 < diameter < 50 nm), corresponding to the intra and inter-crystallinity of the Na-mordenite crystals respectively. This result was expected, while SEM photographs and nitrogen adsorption experiments showed that the Na–mordenite layers consist in an agglomeration of small crystals, which generates a mesoporosity (inter-crystallinity).
First, the permeability of the different Na–mordenite membranes was stabilized during water permeation experiments. Figs. 3 and 4 show the hydraulic permeability evolution of respectively three Na–mordenite membranes and the TiO2 membrane according to time.
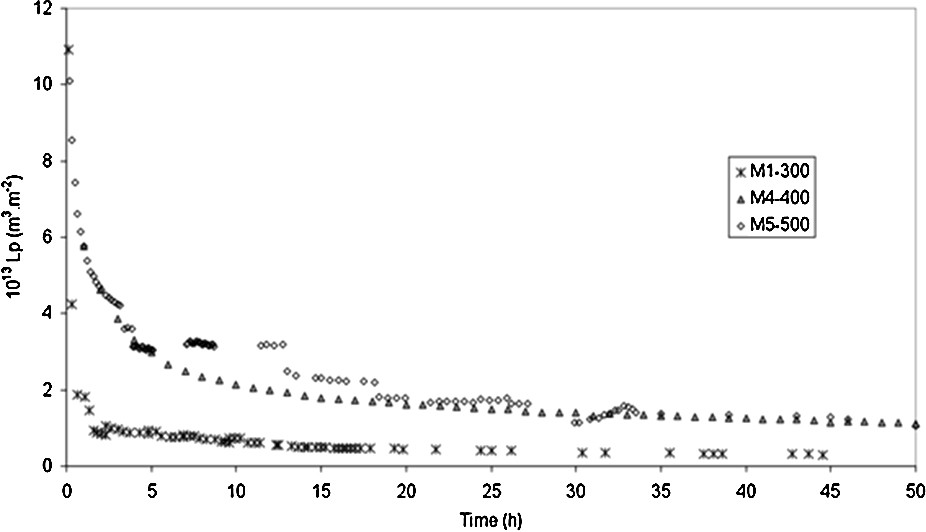
Evolution of the hydraulic permeability according to time during the conditioning step performed at 25 °C for three different Na–mordenite membranes calcined at 300 °C (×), 400 °C (), 500 °C (○).
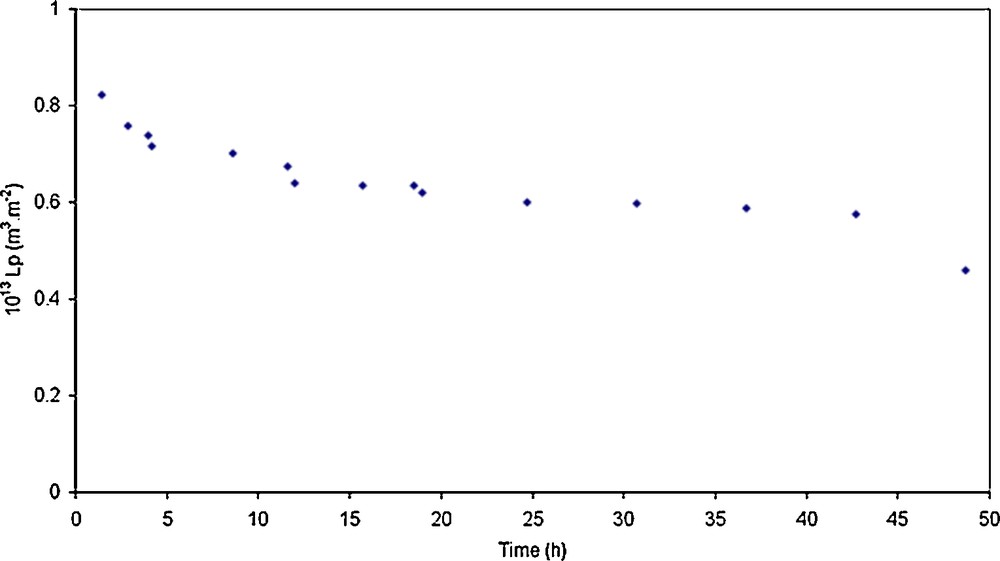
Evolution of the hydraulic permeability according to time during the conditioning step performed at 25 °C for the TiO2 membrane.
Fig. 3 only shows three curves for the sake of clarity, but the shapes of the curves obtained with the last two membranes are similar. The hydraulic permeability of the Na–mordenite membranes decreases significantly at the beginning of the conditioning step and at the same time, that of the TiO2 membrane decreases a little. Actually, the hydraulic permeabilities of all the Na–mordenite membranes are ten times lower that their initial values after the stabilization step.
It seems that there are two separate phases during the membrane stabilization process. First, a fast decrease of permeability is observed during the beginning of the conditioning step and second, it slows down, indicating a diffusive transfer. This behaviour may be explained by both the accessibility of water molecules to the Na–mordenite surface, and the reorientation of water molecules after their adsorption [9].
External and inter-crystalline surfaces may be more accessible than intra-crystalline ones for water molecules, then the hydration phenomena of Na–mordenite global surface must be described by the combination of two parallel kinetics (Eq. (2)). In order to verify this hypothesis for each permeation experiment, we calculate:
| (2) |
Fig. 5 shows the evolution of the hydraulic permeability (with a logarithm form) during the conditioning step for the membrane M1 calcined at 300 °C (as an example). This figure shows two parts: at the beginning of the conditioning step, we observe a fast decrease in the hydraulic permeability. After 1 to 5 h, the decrease of the hydraulic permeabilities slows down and becomes quasi linear with a low slope.
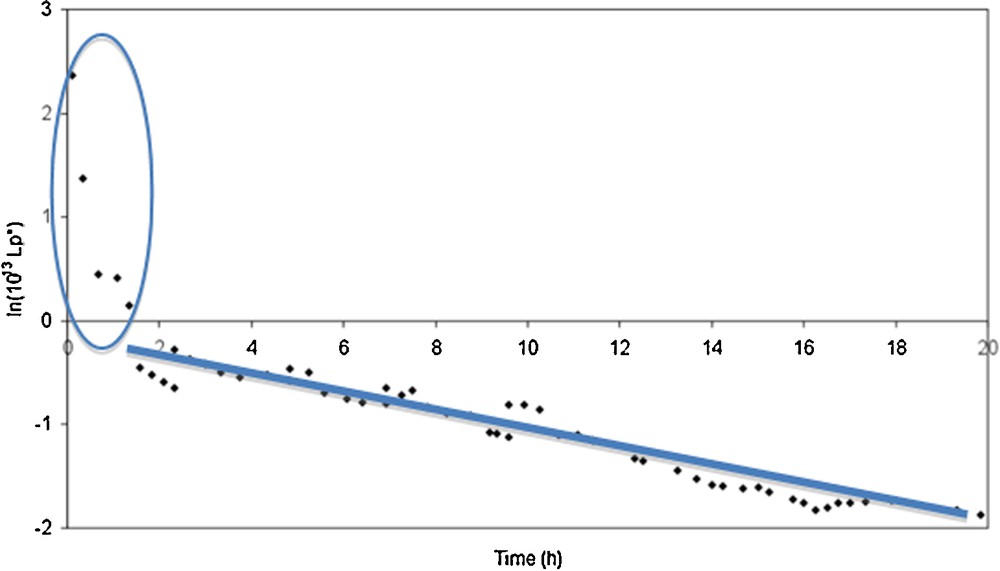
Evolution of the logarithm of the hydraulic permeability according to time during the conditioning step performed at 25 °C for a Na–mordenite membrane (M1) calcined at 300 °C.
Taking into account this observation, the function ln(1013 Lp*) is numerically approximated by a function (Eq. (3)), which results from two contributions: a linear one f1(t) and a second one f2(t) to fit the beginning of the conditioning step:
| (3) |
Table 3 shows the different values obtained for the parameters a, b, c and d of equation (3) for all the experiments carried out. With regard to these results, all the stabilization curves can be well approximated by the same equation, which is the sum of two contributions.
Best-fitted parameters a, b, c, d of equation (3) obtained for the different membranes.
| Membranes/parameters | a | b | c | d |
| M1-300 | –0.3 | –0.075 | 0.6 | 0.15 |
| M2-400 | –0.02 | –0.115 | 1.76 | 0.5 |
| M3-300-400 | –0.97 | –0.025 | 5 | 0.7 |
| M4-400 | 0 | –0.1 | 0.67 | 0.34 |
| M5-500 | 1.23 | –0.042 | 0.74 | 1.35 |
| M6-TiO2 | –1.5 | –0.018 | 0.8 | 0.34 |
Fig. 6 presents the experimental points and the fitted data calculated with equation (3) for two membranes and the simulation curves obtained with the two contributions. The non-linear contribution f2(t) describes the first part of the stabilization curve (first hour of the conditioning part), f1(t) describes the linear contribution corresponding to the last part of the curve, and the sum of f1(t) and f2(t) allows the description of the non-linear part (from 1 to 5 h).
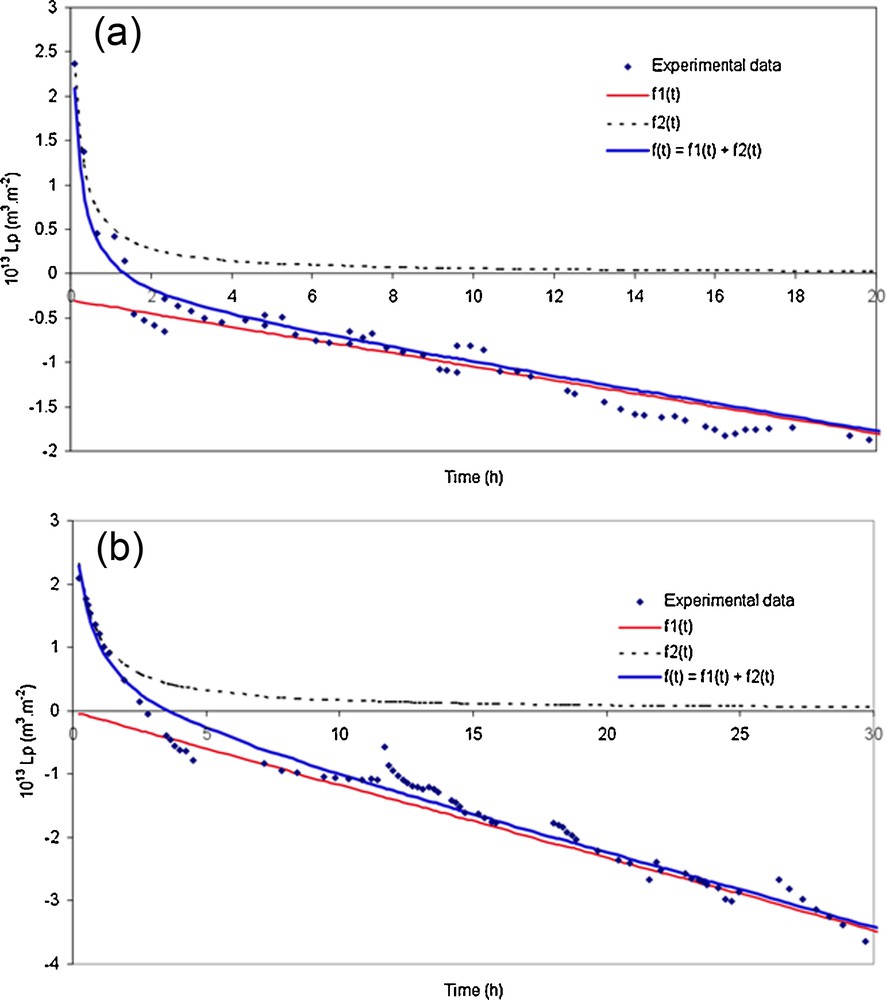
(Color online.) Experimental and simulated curves obtained with the equation (3) and the two contributions [f1(t) and f2(t)] for, respectively, (a) an Na–mordenite membrane calcined at 300 °C (M1) and (b) an Na–mordenite membrane calcined at 400 °C (M2).
It seems that f2(t) represents rapid hydration phenomena that should be a surface hydration of Na–mordenite membrane, including both external and mesoporous (inter-crystalline) surfaces, and also the reorientation of the Na–mordenite crystals [19]. The function f1(t) describes the slow-acting phenomena of hydration as the hydration of the intra-crystalline structure of the Na–mordenite membrane, which is longer, maybe because of the presence of Na+ cations in the cavities of the crystal lattice. Actually, Maurin et al. [20] have shown by atomistic simulation, that there are different cation (Na+) behaviours. The cations situated in the main channels of mordenite are progressively extracted from their initial sites upon hydration. The cation displacements from their initial sites are function of the hydration level of the material. In the same way, Yamazaki and Tsutsumi [21] concluded that the crystal layer formed in the initial stage of the synthesis of the mordenite membrane contains deformed pores capable of exclusively adsorbing water.
For the TiO2 membrane, the function f(t) is quasi linear ≈ f1(t), with a little slope. As it is able to anticipate for the TiO2 membrane, there are no inter-crystalline surfaces and, consequently, the surface hydration phenomena are much lower than for Na–mordenite membrane. Only the intra-crystalline hydration phenomenon operates without the presence of the compensation cation (with different behaviour), but in greater pores.
The expression of the evolution of
| (4) |
The comparison between these contributions and the results obtained with nitrogen adsorption experiments shows that the contribution relative to pore hydration is proportional to the microporous volume.
Fig. 7 shows the estimated parameter b and the microporous volume of all the studied membranes. These six points are quasi lined up. The best linear fit is a straight line with a slope equal to –1.32 cm3·g−1 and an interception equal to 0. These results are in good agreement with the suggestion previously done. Actually, the contribution of the pore hydration to the loss of permeability must be directly proportional to the microporous volume.
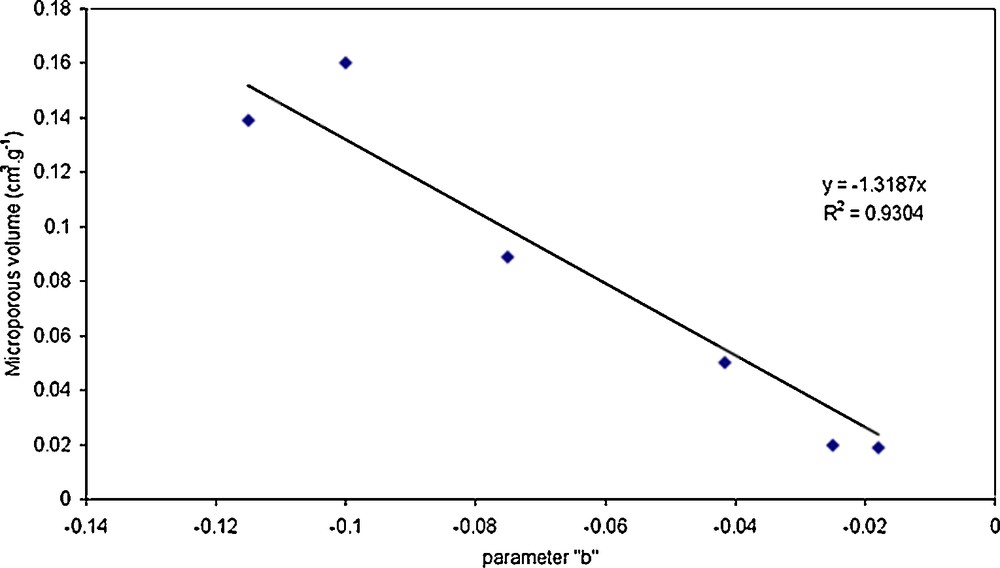
Representation of the best-fitted parameter b according to the active layer microporous volume of the different membranes.
4 Conclusions
The hydration of the zeolite surface is an important point, especially when it is used as a filtration material. This study shows that due to their specific structure and composition, Na–mordenite membranes need a long time to be stabilized. First the surface and the porous surfaces are hydrated. Water seems to diffuse very slowly in the intra-crystalline structure of Na–mordenite. This phenomenon may be identified with a numerical approach by fitting the experimental data of the hydraulic permeability with an algebraic function that is defined as the sum of three contributions, which respectively represent the initial hydraulic permeability of the membrane, the loss of hydraulic permeability due to surface hydration, and the loss of hydraulic permeability due to the hydration of the intra-crystalline structure of the zeolite. Moreover, the contribution of hydraulic permeability loss due to pore hydration seems to be directly proportional to the microporous volume obtained by nitrogen adsorption experiments. This last observation allows us to envisage the estimation of the microporous volume of the zeolite membranes by studying water permeability evolution during the conditioning step.
Acknowledgements
The authors are grateful to Mulhouse Alsace Agglomération (M2A) for supporting this research and financing the filtration unit set-up.



Vous devez vous connecter pour continuer.
S'authentifier