1 Introduction
In a recent publication, Bernal and Watkins [1] reviewed the entire contents of the Cambridge Crystallographic Database [2] for examples of hydronium cations and found approximately 1500 of them which were available by February 2014 and which were analyzed in detail. Among the many species described in that publication, easily one of the most interesting ones is that referenced as WIZPAX [3] which is pictured in Fig. 1. Among the 1500 crystal structures of hydronium ions examined this one is unique.
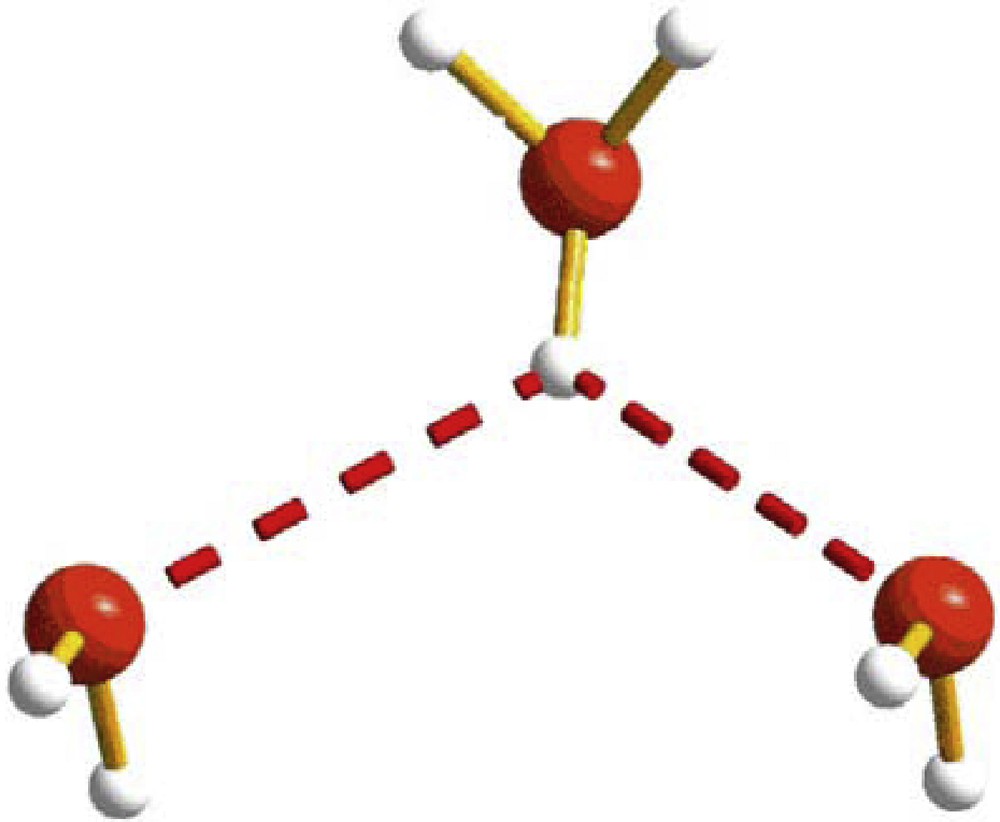
(Color online.) The experimental geometry of an ion H2O-(H3O+)-H2O from the Cambridge data base (WIZPAX [3]).
This cation has the same composition and a similar relative arrangement of the oxygen atoms as that shown in Fig. 2, both sharing the formula H2O-(H3O+)-H2O.

(Color online.) The experimental geometry of an ion H2O-(H3O+)-H2O from the Cambridge data base (XUMQIF [4]).
In the case of the ion pictured in Fig. 2 the central hydronium moiety is the same as that in Fig. 1 but it differs in that it has the “normal” or “expected” hydrogen bonding displayed by hydronium ions familiar to crystallographers for many years. In contrast to that, the crystal's hydronium ion pictured in Fig. 1 has a bifurcated hydrogen bond connecting to a pair of adjacent water molecules. Previous work [5] has shown that crystal forces are capable of capturing protonated water structures that are highly unusual. However when the unusual protonated structures are removed computationally from the crystal environment in which they have been captured, and then subjected to theoretical calculations in the gas phase, their structure changes dramatically to one corresponding to their minimized energy geometry.
Against that experience it occurred to us to remove the bifurcated hydrogen bond structure of Fig. 1 from its crystal environment and subject it to theoretical analysis since it would be of interest to ascertain the relative stabilities of the two structures pictured in Figs. 1 and 2. If the classical structure of Fig. 2 were to be the more stable it could be expected that optimization of the bifurcated hydrogen bond structure, upon energy optimization, would revert to that classical geometry. On the other hand it was also an open possibility that the structure of Fig. 1 corresponded to an optimized minimum energy structure. As it happened however, calculations show that the optimized geometry of the bifurcated hydrogen bond structure of Fig. 1 corresponds to a transition state, with a single imaginary vibrational frequency, which appears to be unusual.
Stated differently, it appears that crystal forces have captured an hydronium ion in a geometry that would otherwise be unstable and very short-lived except for its appearance within the crystal. Such a crystallographic bifurcated hydrogen bond hydronium species has never been described previously to the best of our knowledge. Considerable calculations have been invoked to test adequately the result that the structure of Fig. 1 is a transition state in the gas phase. The existence of such a transition state associated with protonated water structures may well be related to the motion of protons though the liquid state, with a possibly wide range of importance in experimental biology and material science.
2 Results
2.1 Energy and geometry
The geometrical parameters of the H7O3+ bifurcated hydrogen bond as it exists in the crystal structure are given in Fig. 3. The two hydrogen bonds associated with the bifurcation are perfectly symmetrical both corresponding to inter-nuclear distances to the neighboring oxygen equal to 2.351 Å. The angle subtended by the pair of hydrogen bonds is 102.7°. We optimized the geometry, and calculated the optimized energy of the H7O3+ complex, using Gaussian 09 program [6]. In Table 1 that energy is given for several chemical models, HF [7], B3LYP [8,9], MP2 [10], and CCSD [11] in which both the basis functions, 6-311G [12], 6-311G(d,p) [13], 6-311+G(d,p) [14], 6-311++G(3df,3pd), and the approximation for solution of the Schrodinger equation were varied.
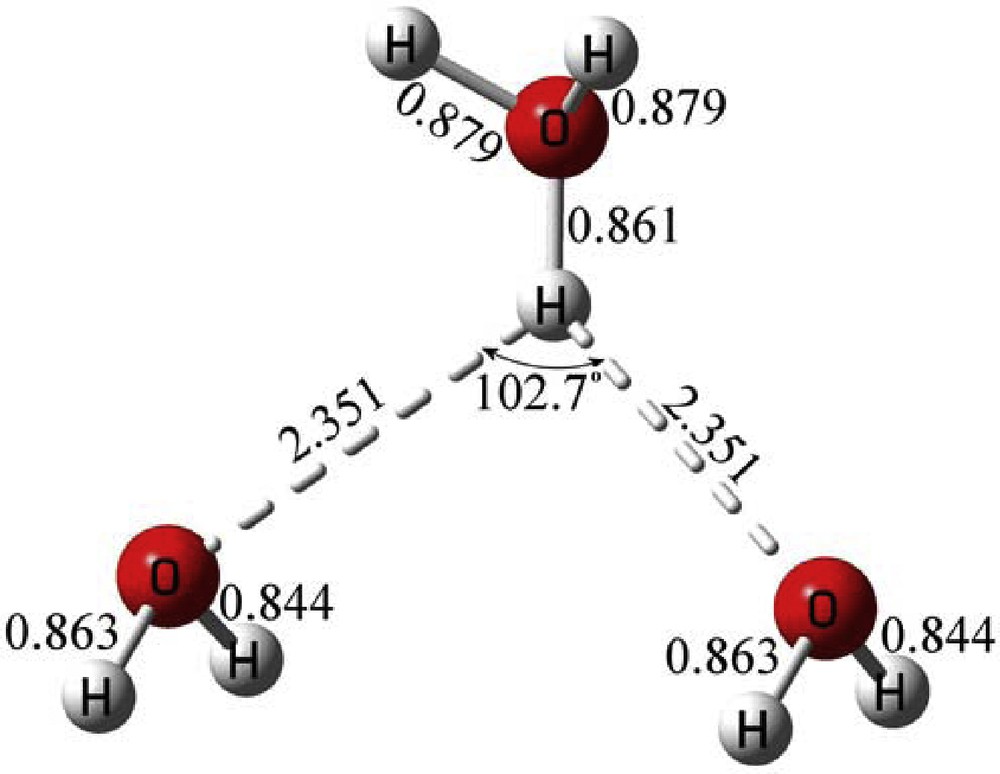
(Color online.) Geometrical parameters of H7O3+ as it exists in the crystal.
Energy of the bifurcated H7O3+ complex at the crystallographic geometry before (single point, or SP) and after geometry optimization (OPT) for different chemical models.
| Energy (a.u.) | HF | B3LYP | MP2 | CCSD | ||||
| SP | OPT | SP | OPT | SP | OPT | SP | OPT | |
| 6-311G | −228.24529 | −228.41014 | −229.43991 | −229.63312 | −228.64182 | −228.83120 | – | – |
| 6-311G(d,p) | −228.36473 | −228.49802 | −229.54632 | −229.70684 | – | – | – | – |
| 6-311+G(d,p) | −228.37266 | −228.50529 | −229.56011 | −229.71922 | – | – | – | – |
| 6-311++G(3df,3pd) | −228.39201 | −228.51937 | −229.57873 | −229.73213 | −229.16237 | −229.31282 | −229.16835 | −229.32977 |
The energy of the molecule is equal to –229.16835 atomic units (a.u) at crystal coordinates in the most accurate of the chemical models, viz., CCSD/6-311++G(3df,3pd), which stands for coupled clusters with singles and doubles excitations and a 6-311G basis set supplemented by diffuse function, 3 sets of d functions and 1 set of f functions for polarization on the heavy atoms, and supplemented by 3 sets of p functions and 1 set of d functions for polarization on hydrogens. When the same chemical model is used to energy optimize the molecule, Fig. 4, in the gas phase the total energy is equal to –229.32977 a.u. The geometry changes with the symmetrical hydrogen bonds becoming equal to 1.873 Å, and the angle subtended by them expanding to 116.0°.

(Color online.) Geometrical parameters of energy optimized H7O3+ by CCSD/6-311++G(3df,3pd).
Notice however, comparing H7O3+ in its crystal geometry and energy optimized gas phase geometry, its overall appearance, including its topology and symmetry are unchanged. The mathematical characterization of a transition state (TS) is such that the vibration frequencies associated with its optimized geometry must all be real, except for exactly one which is imaginary. For this CCSD calculation mentioned above the imaginary frequency is 514.4 i cm−1. All the optimizations we have carried out for all chemical models applied to H7O3+ satisfy that criterion. The single imaginary frequency obtained for each of the chemical models is listed in Table 2. We emphasize that all the quantum calculations listed in Tables 1 and 2 indicate definitively that the optimized geometry corresponding to the bifurcated hydrogen bond is a transition state for the molecule.
Imaginary frequencies (harmonic, unscaled) of the bifurcated H7O3+ transition state complex for different chemical models.
| Frequency (cm−1) | HF | B3LYP | MP2 | CCSD |
| 6-311G | 500.0i | 567.3i | 533.4i | – |
| 6-311G(d,p) | 457.9i | 541.6i | – | – |
| 6-311+G(d,p) | 448.0i | 532.5i | – | – |
| 6-311++G(3df,3pd) | 463.6i | 547.4i | 536.0i | 514.4i |
Every transition state is connected to a reactant and a product. In the case of the transition state of this paper the geometry of the reactant and product are simply obtained from that of the transition state by a 60° rotation of the central H3O+. This breaks the bifurcated hydrogen bonds emanating from one hydrogen atom and converts them into two single hydrogen bonds arising from two separate hydrogen atoms. The relation of the reactant, transition state, and product is indicated in Fig. 5. The activation barrier calculated by CCSD/6-311++G(3df,3pd) to the “pinwheel” rotation to the transition state is 15.1 kcal/mol.

(Color online.) The activation energy barrier connecting reactant and product to the transition state (TS), using CCSD/6-311++G(3df,3pd). (R = reactants, P = products, a.u. = atomic units).
2.2 Topology of the electron density
To further emphasize the true existence and the nature of the bifurcated hydrogen bonds in the H7O3+ molecule topological calculations were carried out in accordance with the quantum theory of atoms in molecules (QTAIM) [15,16]. It occurs that a volume in a molecule occupied by an atom is fixed by a surface that is defined by the vanishing of the electron density gradient vector field flux across that surface, i.e., a surface satisfying:
| (1) |
We have calculated the bond paths associated with the H7O3+ complex at the CCSD/6-311++G(3df,3pd) level of theory. Fig. 6 shows the bond paths associated with the molecular coordinates taken directly from the crystal structure through a frozen geometry single point (SP) calculation. Notice first of all, along the bond paths the magnitudes of the density at the bond critical points ρb are indicated and are equal to 0.01 a.u. The values of the ρb are also indicated for the covalent bonds in the molecule, and these are increased by an order of magnitude as would be expected because of the relative strengths of the bonds in question, i.e., covalent bonds versus hydrogen bonds.

(Color online.) The molecular graph of the H7O3+ complex based upon coordinates as it exists in the crystal at the CCSD/6-311++G(3df,3pd) level of theory. The small green dots indicate the positions of the bond critical points (BCP), where the gradient of the density vanishes along the bond path labeled with the values of the electron density at these points (ρb) in a.u.
Fig. 7 shows the corresponding collection of bond paths (the molecular graph) associated with the same complex but optimized at the CCSD level of theory. The calculations show the bifurcated hydrogen bonds analogous to those which occur with the crystal coordinates. The values of ρb are larger, equal to 0.03 a.u., consistent with an increase in the strengths of these bonds with energy minimization.
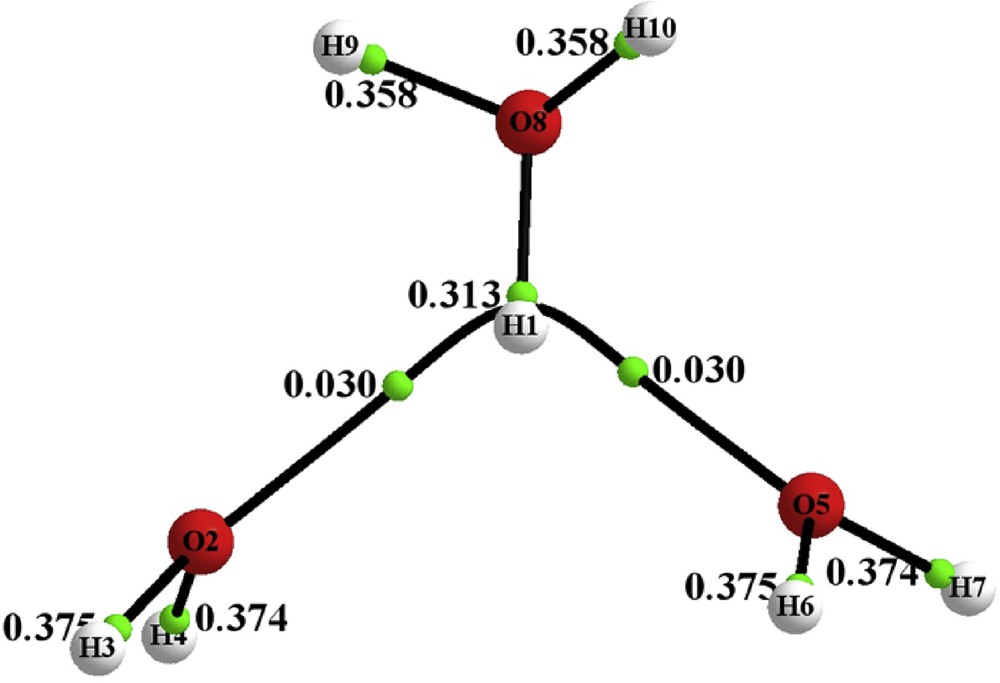
(Color online.) The molecular graph of the H7O3+ complex based upon energy optimized coordinates at the CCSD/6-311++G(3df,3pd) level of theory. The small green dots indicate the positions of the bond critical points (BCP), where the gradient of the density vanishes along the bond path labeled with the values of the electron density at these points (ρb) in a.u.
3 Discussion and conclusions
The principal result of this paper is the discovery of a hydronium cation, unique among all crystallographic such ions of the Cambridge Database. The cation has a bifurcated hydrogen bond. From a central H3O+ moiety a single hydrogen bond donor extends to two adjacent water molecules.
Surprisingly perhaps, quantum chemical calculations indicate the bifurcated hydrogen bond structure is that of a transition state for the H7O3+ cation. Thus one may say that crystal forces have captured the ion in what would otherwise be a short-lived and unstable transition state geometry. In the crystal the ion is surrounded by atoms of a coordination compound and is stabilized by a number of hydrogen bonds to and from the coordination compound fragments acting as hydrogen receptors (bases) or hydrogen donors (acids). It may be noted that because of the accuracy of the crystallographic experiment [3] which contains the hydronium ion there is no doubt about the overall accuracy of the H7O3+ coordinates as it exists in the crystal. The crystal structure was determined at 293 K and achieved the accuracy associated with an R-factor equal to 1.63%.
Given the crystal coordinates of H7O3+, the ion was subjected to energy minimization. We found the overall geometrical symmetry and outline of the molecule remained unchanged from its appearance as a fragment within the crystal. The detailed magnitudes of distances and angles changed slightly to accommodate the energy minimization process but, the overall appearance of the ion was unchanged. When the vibration frequencies associated with the energy minimum were calculated, exactly one imaginary frequency occurred in the results, indicating that the ionic complex is in a transition state.
This was sufficiently surprising that it was deemed worthwhile to carry out several additional calculations based upon a variety of chemical models to ensure that the result was not an artifact of one particular model choice. The variety of these results are contained in Tables 1 and 2, and Figs. 3–6. Also in the Supplementary Information Figs. S1 and S2 the geometry and bond paths of all the chemical model calculations are illustrated in condensed form. All calculations yield the same conclusion, viz., that this H7O3+, containing a hydronium ion displaying a bifurcated hydrogen bond, is in a transition state. Restated, the crystal-field appears to have inverted what is in vacuum an activation energy barrier into a well, that is, into a crystal-field-stabilized bound state. It remains to be seen how relevant are these findings to possible mechanisms of charge transfer in proton wires.
Acknowledgements
Funding for this project was provided by the Office of Naval Research (ONR) through the Naval Research Laboratory's Basic Research Program - (L.H.), by the Natural Sciences and Engineering Research Council of Canada (NSERC), Canada Foundation for Innovation (CFI), and Mount Saint Vincent University - (C.F.M.), the US Naval Research Laboratory (project # 47203-00 01) and by a PSC CUNY Award (project # 63842-00 41) - (L.M.).
Appendix A Supplementary data
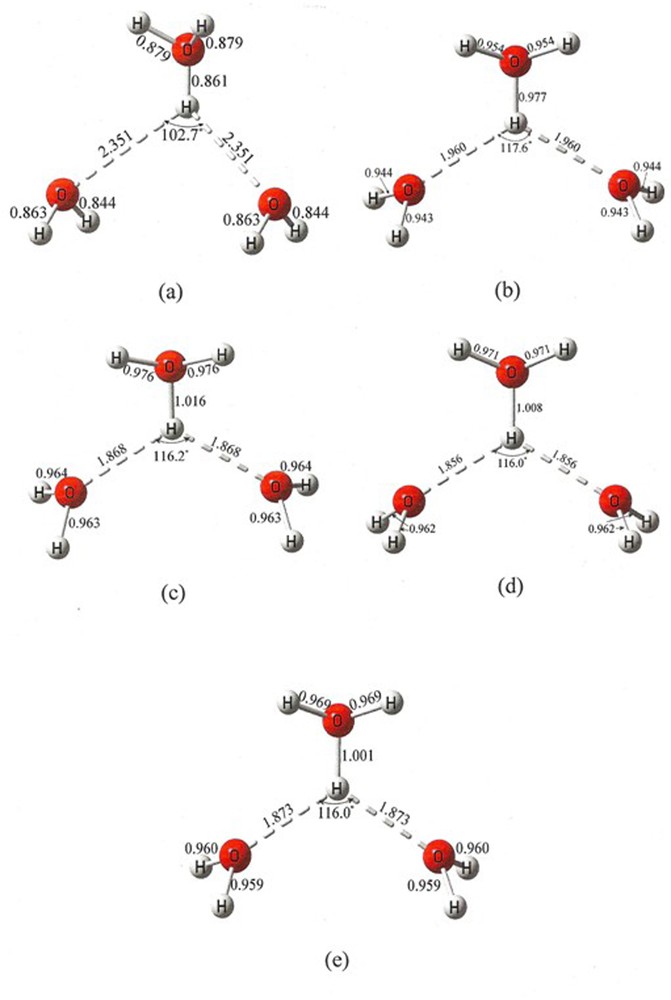
Geometry of the crystal (a), and optimized structures: HF (b), B3LYP (c), MP2 (d) and CCSD (e).
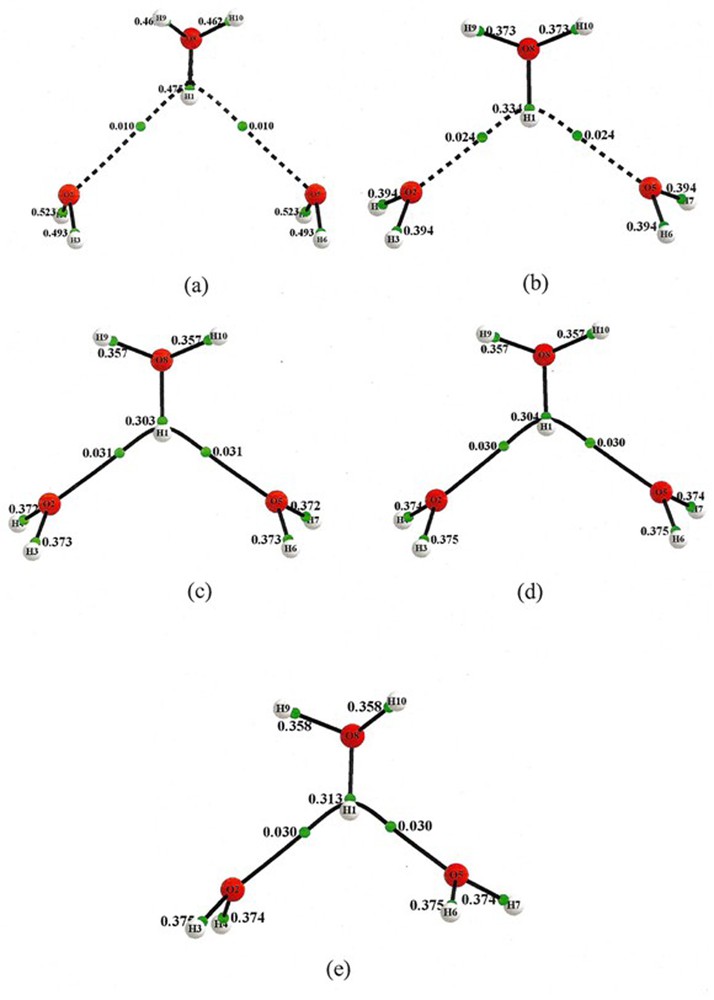
QTAIM calculations for the crystal (a), and optimized structures: HF (b), B3LYP (c), MP2 (d) and CCSD (e).



Vous devez vous connecter pour continuer.
S'authentifier