Population of triplet states in acetophenone: A quantum dynamics perspective

Miquel Huix-Rotllant; Irene Burghardt; Nicolas Ferré

doi:10.1016/j.crci.2015.10.002

Population of triplet states in acetophenone: A quantum dynamics perspective

Miquel Huix-Rotllant ^1,² ; Irene Burghardt ¹; Nicolas Ferré ²

¹ Institut für Physikalische und Theoretische Chemie, Göethe-Universität Frankfurt, D-60439 Frankfurt am Main, Germany
² Aix-Marseille Université, CNRS, Institut de Chimie Radicalaire, 13397 Marseille Cedex 20, France

Comptes Rendus. Chimie, Emerging Chemistry in France, Volume 19 (2016) no. 1-2, pp. 50-56.

Abstract

When initially excited to its first singlet excited state, acetophenone, a prototypical aromatic ketone, is characterized by a singlet to triplet conversion quantum yield close to 100%. In this work, the time evolution of photo-excited acetophenone is theoretically investigated using quantum dynamics simulations based on the Multi Configuration Time Dependent Hartree (MCTDH) method. A model Hamiltonian, comprising both electronic and vibronic terms, is defined and its parameters are fitted to available data obtained by high-level quantum chemical calculations. An exploratory MCTDH dynamics shows a sequential mechanism S₁→T₂→T₁. The population in the triplet manifold is distributed evenly among the two states, explaining the origin of acetophenone rich photochemistry.

Initialement excité vers son premier état excité singulet, l’acétophénone, une cétone aromatique typique, est caractérisée par une conversion singulet vers triplet proche de 100%. Dans ce travail, l’évolution temporelle de l’acétophénone photo-excitée est étudiée de fa,on théorique par dynamique quantique basée sur la méthode Multi Configuration Time Dependent Hartree (MCTDH). Un Hamiltonien modèle, comprenant des termes électroniques et vibroniques, est défini et ses paramètres sont déterminés à partir de données obtenues par des calculs de chimie quantique de haut niveau. La dynamique MCTDH exploratoire montre un mécanisme séquentiel S₁→T₂→T₁. La population est distribuée également dans les deux états triplet, expliquant l’origine de la photochimie riche de l’acétophénone.

Compléments :
Des compléments sont fournis pour cet article dans le fichier séparé :

mmc1.pdf

Metadata

Received: 2015-02-26
Accepted: 2015-10-01
Published online: 2016-01-01

DOI: 10.1016/j.crci.2015.10.002

Mots-clés : Photochemistry, Femtochemistry, Chromophores, Aromatic ketones, Quantum chemistry, Conical intersections, Molecular dynamics, Photochimie, Femtochimie, Chromophores, Cétones aromatiques, Chimie quantique, Intersections coniques, Dynamique moléculaire

Author's affiliations:

Miquel Huix-Rotllant ^{1, 2}; Irene Burghardt ¹; Nicolas Ferré ²

¹ Institut für Physikalische und Theoretische Chemie, Göethe-Universität Frankfurt, D-60439 Frankfurt am Main, Germany
² Aix-Marseille Université, CNRS, Institut de Chimie Radicalaire, 13397 Marseille Cedex 20, France

@article{CRCHIM_2016__19_1-2_50_0,
     author = {Miquel Huix-Rotllant and Irene Burghardt and Nicolas Ferr\'e},
     title = {Population of triplet states in acetophenone: {A} quantum dynamics perspective},
     journal = {Comptes Rendus. Chimie},
     pages = {50--56},
     publisher = {Elsevier},
     volume = {19},
     number = {1-2},
     year = {2016},
     doi = {10.1016/j.crci.2015.10.002},
     language = {en},
}

TY  - JOUR
AU  - Miquel Huix-Rotllant
AU  - Irene Burghardt
AU  - Nicolas Ferré
TI  - Population of triplet states in acetophenone: A quantum dynamics perspective
JO  - Comptes Rendus. Chimie
PY  - 2016
SP  - 50
EP  - 56
VL  - 19
IS  - 1-2
PB  - Elsevier
DO  - 10.1016/j.crci.2015.10.002
LA  - en
ID  - CRCHIM_2016__19_1-2_50_0
ER  -

%0 Journal Article
%A Miquel Huix-Rotllant
%A Irene Burghardt
%A Nicolas Ferré
%T Population of triplet states in acetophenone: A quantum dynamics perspective
%J Comptes Rendus. Chimie
%D 2016
%P 50-56
%V 19
%N 1-2
%I Elsevier
%R 10.1016/j.crci.2015.10.002
%G en
%F CRCHIM_2016__19_1-2_50_0

Miquel Huix-Rotllant; Irene Burghardt; Nicolas Ferré. Population of triplet states in acetophenone: A quantum dynamics perspective. Comptes Rendus. Chimie, Emerging Chemistry in France, Volume 19 (2016) no. 1-2, pp. 50-56. doi : 10.1016/j.crci.2015.10.002. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2015.10.002/

Version originale du texte intégral

1 Introduction

Acetophenone, like many other aromatic ketones, features energetically close excited singlet and triplet states, even in the Franck–Condon region [1–3]. The relatively fast triplet state population makes photo-excited aromatic ketones very efficient molecular systems for hydrogen abstraction, double bond addition or bond cleavage. More specifically, acetophenone is characterized by a lowest singlet state (of n→π^∗ character) experimentally estimated at 3.38 eV above the electronic ground state and calculated (adiabatically) at 3.44 eV [3]. It is noteworthy that two (lowest) triplet states of n→π^∗ and π→π^∗ characters are quasi-degenerate with the singlet excited state. This peculiarity opens the possibility to efficiently populate both triplet states immediately upon light absorption. This efficient singlet to triplet decay is further enhanced by the existence of an extended region of near-degeneracy which culminates with the presence of the so-called 3-state crossing.

While static mechanistic details have been reported elsewhere [1,3], the photochemical path is summarized in Fig. 1. Examination of this picture shows that the two triplet states have phosphorescence light emission at similar wavelengths, such that it is experimentally difficult to assess which state(s) is(are) photoactive. However this knowledge is of tremendous importance to understand, for instance, the photoreduction properties of acetophenone, which can in turn be modulated by external factors like the presence of chemical substituents or polar solvents. As a matter of fact, recent near infra-red spectroscopy studies have shown that triplet states of substituted acetophenones are in “thermal” equilibrium, finding that their respective populations remain unaffected by the above-mentioned factors [4]. Moreover, the same work concludes that the ${}^{3}π π^{*}$ photoreduction activity is zero. However, the ordering of the triplet states in these molecular systems appears to be sometimes inverted with respect to bare acetophenone.

Fig. 1
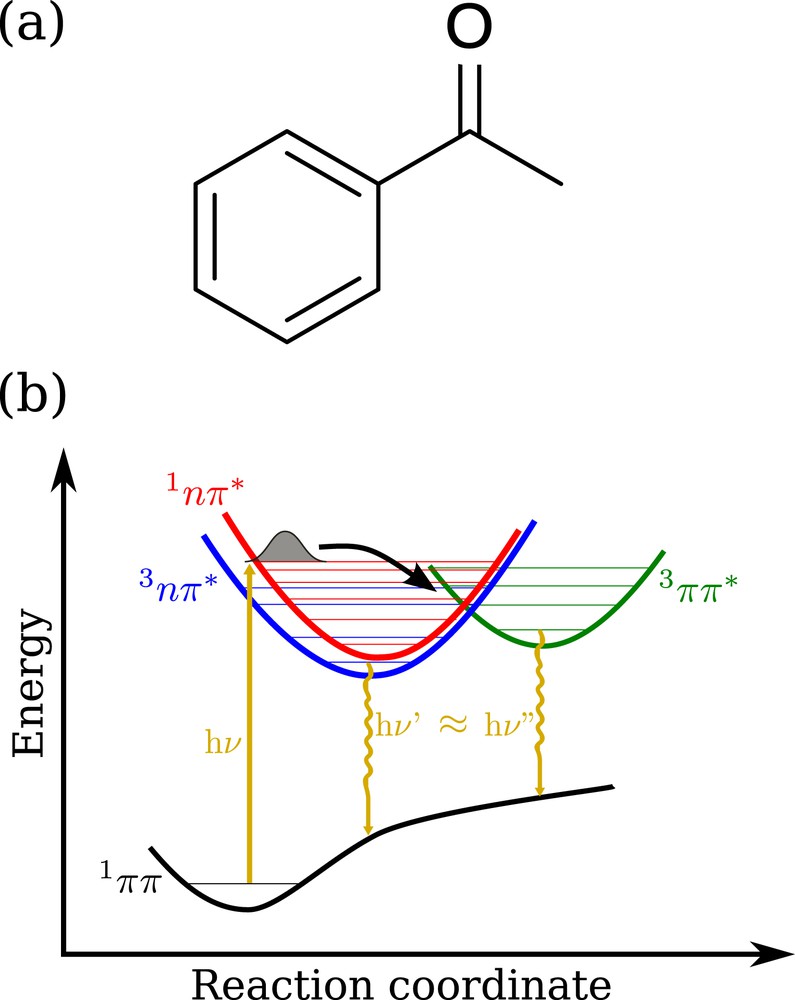
(a) Acetophenone chemical structure; (b) Schematic representation of the ${}^{1}n π^{*}$ -based photochemistry of acetophenone, including ${}^{3}n π^{*}$ and ${}^{3}π π^{*}$ triplet populations and eventually phosphorescence.

The kinetics of the intersystem crossing of acetophenone have not been reported to the best of our knowledge, but there are reports on the closely related benzaldehyde molecule [5, 6]. Ultrafast electron diffraction experiments by Zewail and co-workers showed a lifetime of the first singlet excited state of 42 ps [5], whereas theoretical Marcus theory estimates by Ou and Subotnik predicted a four times faster process [6]. Accordingly, the dynamical mechanism of the acetophenone populated triplet states remains an open question and the central aim of the present contribution.

The computational investigation of excited state populations and, by extension, the calculation of quantum yields, is still in its infancy for at least two main reasons [7]. First, the selected theoretical model must be flexible enough to describe with the same accuracy some (or many) electronic states, their couplings and crossings. Second, the statistical nature of the property under consideration imposes to sample a large portion of the phase space, including the possibility to jump (hop) from one state to another. While direct quantum dynamics simulations propagating a wavepacket with the time-dependent Schrödinger equation would be an ideal method of choice (the so-called standard method) [8], its computational cost remains prohibitive for most systems of interest. On the other hand, cost efficient semi-classical molecular dynamics simulations (Ehrenfest, surface-hopping, etc.) are cost-effective approaches which do not require the a priori knowledge of the (electronic) potential energy surface [9–11]. Nevertheless, the classical propagation of the nuclear degrees of freedom implies to perform a statistical sampling over several trajectories, which turns out to be difficult to converge when several branchings and crossings are implied in the photochemical process.

Here, we have chosen to perform full quantum dynamics simulations employing the multi-configuration time-dependent Hartree (MCTDH) method [12–14]. This approach has proven to be very accurate, especially when strong non-adiabatic effects are present [15–18]. In MCTDH, the vibronic wavepacket is represented by the time-dependent wavefunction

Ψ ({Q_{i}}, t) = \overset{N_{1}}{\sum_{j_{1}}} \dots \overset{N_{n}}{\sum_{j_{n}}} A_{j_{1} \dots j_{n}} (t) \overset{f}{\prod_{k = 1}} ϕ_{j_{k}}^{(k)} (Q_{k}, t),

(1)

in which Q_k are combined nuclear coordinates and

A_{j_{1} \dots j_{k}} (t)

are the multi-configuration expansion coefficients of the Hartree-products,

ϕ_{j_{k}}^{(k)} (Q_{k}, t)

are the time-dependent single particle functions. The Ansatz is inserted into the Dirac-Frenkel variational principle,

〈 δ Ψ (t) | \hat{H} - i ℏ \frac{\partial}{\partial t} | Ψ (t) 〉 = 0

, from which a set of equations of motion for the propagation of the time-dependent expansion coefficients and single-particle-functions is derived. The variational principle implies that one gets a systematic better description of the wavepacket with additional single particle functions, and thus the wavepacket can be systematically converged. In practice, efficient implementations of the real-time propagation of the MCTDH equations-of-motion are possible by making use of several numerical techniques, such as numerical integrators, discrete variable representation of operators and function, and the factorization of the Hamiltonian in product form [14]. Still, the computational effort depends on a balanced choice of single particle functions and the number of degrees of freedom. This balance is motivated by computational effort, and the problem at hand.

Here, we perform MCTDH simulations to study the singlet/triplet conversion and the triplet population distribution of acetophenone. First, we present the definition and the parametrization of a model Hamiltonian suitable for describing the excited states of acetophenone. Then, we perform an exploratory quantum dynamics simulation using the MCTDH showing that, despite the relatively weak spin–orbit couplings, significant population transfer occurs between the singlet excited state and triplet state. Phosphorescence origin versus reactive decay paths are sketched in conclusion.

2 Computational details

MCTDH simulations have been performed with the Heidelberg MCTDH package [19]. The numerical propagation of the MCTDH equations-of-motion employs three integrators: (i) a variable constant mean field for the mean field matrices with 0.5 fs of initial time interval and an accuracy threshold of 10⁻⁸, (ii) a Bulirsch-Stoer extrapolation integrator for the single particle functions of maximal order 7, initial accuracy threshold of 10⁻⁸ and initial step size of 2.50·10⁻⁸, and (iii) a SIL integrator for the coefficient matrix A with maximal order 5, and accuracy 10⁻⁸. This combination ensures an error in the norm of the wavefunction of less than 10⁻⁷ along the whole propagation time (see Supporting Information). The number of single particle and discrete variable representation functions is described in the next section. This combination of numerical integrators ensures a good convergence of the wavepacket propagation, but the computational cost is high. Therefore, an initial momentum has been given to the wavepacket (see below). A longer time dynamics with a smaller convergence criteria with longer propagation times is added in the Supporting Information.

MCTDH dynamics require that the electronic Hamiltonian is in diabatic form. For obtaining the diabatic couplings, we have employed the 4-fold way quasi-diabatization scheme of Truhlar et al. for complete-active space self-consistent field (CASSCF) wavefunctions [20–23], as implemented in the GAMESS-US [24]. This method requires quasi-diabatic reference orbitals and configuration state functions, which have been taken at the C_s ground-state geometry as calculated with second-order extended multi-configuration quasi-degenerate perturbation theory (XMCQDPT2) [25]. The active space used for the CASSCF calculations comprises 10 electrons in 9 occupied orbitals (6 π orbitals of phenyl, 2 π orbitals of the carboxyl group and the oxygen lone pair.) We have employed the Pople 6-31+G* basis set throughout [26]. XMCQDPT2 calculations have been performed with Firefly [27].

3 Results and discussion

3.1 Parametrization of the model

The MCTDH approach, as an indirect dynamics method, requires that model Hamiltonian matrix elements are fitted to contain all the information of the potential energy surfaces along the considered photochemical pathway. The general form of a vibronic coupling Hamiltonian [28] is taken as

\hat{H} = {\hat{H}}_{e l} + {\hat{H}}_{e l - p h},

(2)

in which

{\hat{H}}_{e l}

is the purely electronic part and

{\hat{H}}_{e l - p h}

includes the bath modes and the vibronic couplings.

The main minimum energy structures and crossing points of the lowest states of acetophenone have C_s symmetry [3]. The ${}^{1}n π^{*}$ and the ${}^{3}n π^{*}$ states belong to A” symmetry, whereas the ${}^{3}π π^{*}$ state belongs to A’ symmetry. Simple symmetry considerations can be used to predict the type of coupling that occurs between such states. On the one hand, El-Sayed's rule implies that there exists a strong spin–orbit coupling between the singlet ${}^{1}n π^{*}$ and the triplet ${}^{3}π π^{*}$ , whereas this coupling is zero for the states belonging to the same irreducible representation [29]. On the other hand, the triplet intersection is of accidental symmetry-allowed type. This implies that the in-plane vibrations, that conserve the planar symmetry, are tuning modes in the direction of the derivative gradient difference, whereas the out-of-plane vibrations are coupling modes, which break the symmetry, allow the mixing between the two triplets and thus point in the direction of the non-adiabatic coupling.

Accordingly, the electronic Hamiltonian contains the relative energies of the three considered states ( ${}^{1}n π^{*}$ , ${}^{3}n π^{*}$ , ${}^{3}π π^{*}$ ), and the spin–orbit coupling,

{\hat{H}}_{e l} = E_{{}^{1}n π^{*}} |^{1} n π^{*} 〉 〈^{1} n π^{*} | + E_{{}^{3}n π^{*}} |^{3} n π^{*} 〉 〈^{3} n π^{*} | + E_{{}^{3}π π^{*}} |^{3} π π^{*} 〉 〈^{3} π π^{*} | + λ_{S O} (|^{1} n π^{*} 〉 〈^{3} π π^{*} | + h . c .),

(3)

in which

E_{{}^{3}n π^{*}}

,

E_{{}^{3}π π^{*}}

and

E_{{}^{1}n π^{*}}

are the diabatic energies and λ_SO is the spin–orbit coupling. The spin–orbit coupling is taken as the mean value for the three triplet components (M_s = −1,0,1).

The parameters used for the electronic part of the model Hamiltonian are reported in Table 1. All energies are relative to the lowest state and the diabatic energies have been calculated by considering the spectrum in the Franck–Condon region. We have taken these values from our previous study of the photochemistry of acetophenone (see Ref. [3],) in which the electronic spectrum was calculated at the CASSCF(9,10)/XMCQDPT2/6-31+G* level of theory on structures optimized at the XMCQDPT2 level. The quasi-diabatic spin-free electronic states are also diabatic with respect to the total vibronic Hamiltonian containing the spin–orbit coupling.

$E_{{}^{1}n π^{*}}$	$E_{{}^{3}π π^{*}}$	$E_{{}^{3}n π^{*}}$	λ_SO
0.1360	0.050	0.000	0.006

The spin–orbit coupling has been calculated using the one-electron part of the Breit-Pauli Hamiltonian [30] at the CASSCF(9,10)/6-31+G* level on the XMCQDPT2-optimized ground-state geometry. At this planar geometry, the ${}^{1}n π^{*} / {}^{3}n π^{*}$ coupling vanishes by symmetry. The ${}^{1}n π^{*} / {}^{3}π π^{*}$ instead is 0.006 eV. We have calculated the spin–orbit coupling along the normal coordinates, and found that this value remains essentially constant, similar to what was previously found in Ref. [6]. Therefore, we keep this value constant and independent of the vibrations. While the ${}^{1}n π^{*} / {}^{3}π π^{*}$ spin–orbit coupling is relatively weak, it allows the singlet population to transfer to ${}^{3}π π^{*}$ on a given but still unknown time scale.

The vibronic Hamiltonian ( ${\hat{H}}_{e l - p h}$ ) part of the model Hamiltonian is considered up to linear vibronic coupling (LVC) [28]. The LVC Hamiltonian is sufficient to capture the interstate couplings for acetophenone, since we suppose a sequential process ( ${}^{1}n π^{*} \to {}^{3}π π^{*} \to {}^{1}n π^{*}$ ). Higher order vibronic coupling models would be necessary in case of non-harmonic potential energy surfaces. In the present case, we have performed potential energy surface (PES) cuts for some selected vibrational coordinates, confirming that the potential energy surfaces are essentially harmonic or only slightly anharmonic. Therefore, the LVC Hamiltonian can be used to fit such potential energy surfaces to good accuracy. The actual form of the LVC Hamiltonian considered in this work is of the form.

{\hat{H}}_{e l - p h} = \overset{N_{v}}{\sum_{i}} \frac{1}{2} ω_{i} ({\hat{p}}_{i}^{2} + {\hat{q}}_{i}^{2}) + \overset{N_{v}^{o p}}{\sum_{i}} λ_{i} {\hat{q}}_{i} |^{3} n π^{*} 〉 〈^{3} π π^{*} | + \overset{N_{v}^{i p}}{\sum_{i}} {\hat{q}}_{i} (κ_{i}^{{}^{1}n π^{*}} |^{1} n π^{*} 〉 〈^{1} n π^{*} | + κ_{i}^{{}^{3}n π^{*}} |^{3} n π^{*} 〉 〈^{3} n π^{*} | + κ_{i}^{{}^{3}π π^{*}} |^{3} π π^{*} 〉 〈^{3} π π^{*} |)

(4)

in which N_v is the total number of vibrations,

N_{v}^{i p}

and

N_{v}^{o p}

are, respectively, the number of in-plane and out-of-plane vibrations, ω_i is the frequency of the normal mode,

{\hat{p}}_{i}

and

{\hat{q}}_{i}

are the coordinates in mass-and-frequency weighted (MFW) linear momentum and normal mode coordinate operators.

κ_{i}^{{}^{1}n π^{*}}

,

κ_{i}^{{}^{3}n π^{*}}

and

κ_{i}^{{}^{3}π π^{*}}

are the diagonal vibronic couplings between vibrations and the corresponding electronic states, and λ_i is the off-diagonal vibronic coupling between out-of-plane vibrations and the triplet states.

The frequencies and MFW normal coordinates have been obtained at the minimum of the ${}^{1}n π^{*}$ state obtained at the CASSCF(9,10)/6-31+G* level of theory. The same set of vibrational coordinates has been used for all states. The linear vibronic couplings are defined as

κ_{i} = \frac{\partial V ({q_{i}})}{\partial q_{i}} .

(5)

In the harmonic approximation, these couplings can be related to the displacements of one harmonic potential with respect to the reference Δq_i, according to the formula

κ_{i} = - ω_{i} Δ q_{i} .

(6)

These displacements have been computed by expanding the geometry of the minima of each of the corresponding excited states optimized at the XMCQDPT2 level with the ground-state geometry, and projecting it in the space of the normal modes of the ${}^{1}n π^{*}$ state.

For the sake of interpretation, it is convenient to compute the spectral densities which, in the harmonic approximation, take the form

J (ω) = \sum_{i}^{N_{v i b}} κ_{i}^{2} δ (ω - ω_{i}) .

(7)

The spectral densities of all states are plotted in Fig. 2 in which Dirac δ functions have been substituted by Lorentzian functions with a broadening of 30 cm⁻¹. The spectral density of the ${}^{3}π π^{*}$ state is around 10 times larger than the corresponding spectral densities of the ${}^{1}n π^{*}$ and ${}^{3}n π^{*}$ states. This is easily understood by noticing that both singlet and triplet nπ^∗ minima are close to the ground-state geometry, whereas the ${}^{3}π π^{*}$ minimum structure differs considerably (see Ref. [3]). This implies that the displacements and thus the reorganization energies for the ${}^{3}π π^{*}$ state are considerably larger (Fig. 1).

Fig. 2
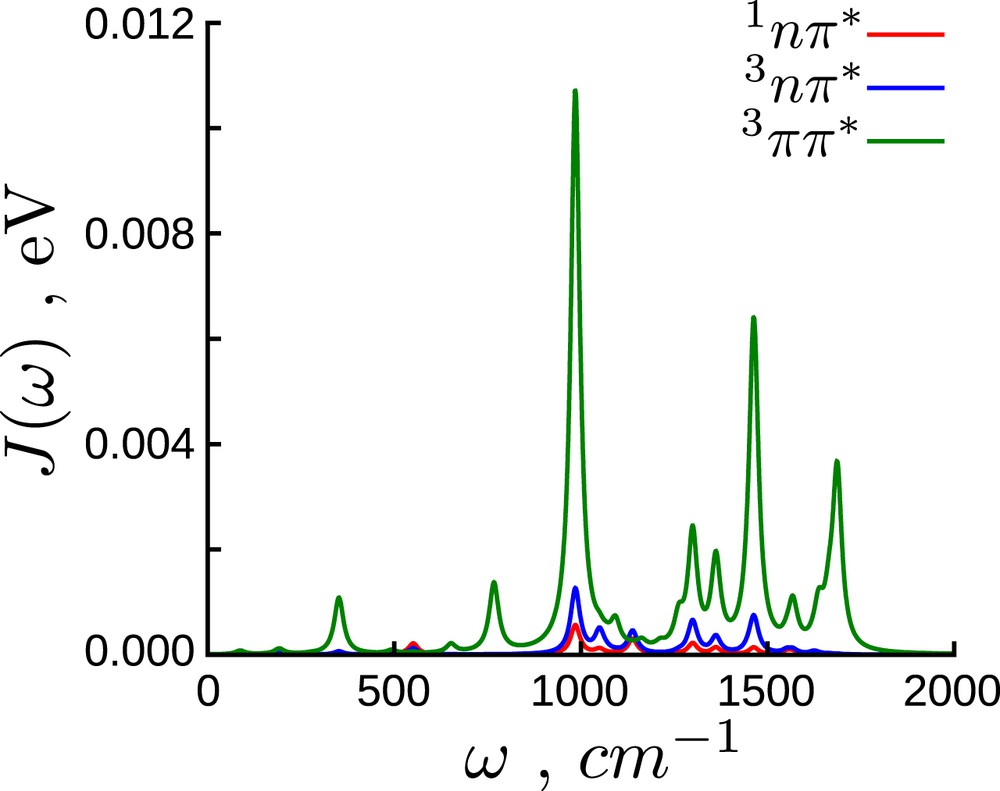
Spectral density for the ${}^{1}n π^{*}$ , ${}^{3}n π^{*}$ and ${}^{3}π π^{*}$ states.

The structure of the spectral densities is similar in the three cases. The large peaks around 400 cm⁻¹, 700 cm⁻¹ and 1000 cm⁻¹ correspond to different types of in-plane vibrations of the carboxyl bond and the methyl groups, also delocalized on the phenyl ring. The peak around 1470 cm⁻¹ corresponds to the carboxyl-phenyl bond stretching and the peak around 1600 cm⁻¹ corresponds to the CC double bond stretching in the phenyl ring. This is in line with our previous assumption, that the CO bond length and the phenyl ring distortions are both relevant reaction coordinates to connect the excited state minima [3].

The out-of-plane modes induce off-diagonal diabatic coupling between the two triplet states, which allow their interconversion. For calculating the off-diagonal elements for the coupling modes, we have used the 4-fold way quasi-diabatization scheme of Truhlar and co-workers [20–22] for the CASSCF(9,10) triplet states along all out-of-plane modes at the Franck–Condon geometry. Table 2 summarizes the results for the triplet couplings. The couplings have been obtained by calculating the slope of a linear fitting of the quasi-diabatic couplings along the selected coordinate. The R² correlation coefficient further indicates that the LVC model is suitable for describing acetophenone. The absolute mean value of the triplet coupling is 0.0019 eV, similar to the spin–orbit coupling intensity. Still, there are 12 modes which act as coupling modes, and therefore, the population distribution might happen in an ultrafast scale.

Mode	Frequency	Coupling (λ)	R²
1	87.36	0.00136	0.993
2	150.72	0.00074	0.998
3	188.69	0.00168	0.991
5	277.81	0.00315	0.975
7	482.00	−0.00273	0.990
9	531.80	0.00171	0.996
12	702.28	0.00315	0.966
13	748.63	0.00525	0.997
15	836.17	−0.00111	0.991
16	861.74	−0.00177	0.999
17	938.89	−0.00061	0.998
18	975.60	−0.00017	0.950

3.2 Quantum dynamics

The acetophenone nuclear structure is defined by 45 internal degrees of freedom in total. In order to keep the computations tractable, we have excluded the high frequency modes (8 modes with frequencies larger than 3000 cm⁻¹) corresponding to hydrogen stretching. These modes could contribute at the fast-time dynamics, but they are probably not active owing to the negligible vibronic coupling observed (see below). Furthermore, we have used the mode combination approach, by which several internal degrees of freedom are combined in one [14]. This procedure does not involve any approximation, but allows to reduce the total number of degrees of freedom that are propagated in the MCTDH equations. In Table 3, we summarize the mode combination scheme and the single-particle functions and primitive functions necessary for a reasonable convergence of the wavepacket. At the end of the propagation, the population both at the edges of the primitive grid and the last single-particle function is less than 10⁻²–10⁻³.

Mode	Frequencies	SPF^a	DVR^b
${}^{3}n π^{*}$	${}^{3}π π^{*}$	${}^{1}n π^{*}$
1	87, 150, 188	3	3	2	32
3	193, 351, 551	3	3	2	32
3	227, 482, 531	3	3	2	32
4	493, 652, 767	3	3	2	32
5	702, 748, 836	3	3	2	32
6	891, 938, 975	3	3	2	32
7	985, 1050, 1067	3	3	2	32
8	1092, 1138, 1162	3	3	2	32
9	1212, 1262, 1299	3	3	2	32
10	1361, 1452, 1463	3	3	2	32
11	1552, 1567, 1616	3	3	2	32
12	1625, 1637	3	3	2	32
13	1665, 1686	3	3	2	32

^a Number of single particle functions.

^b Number of primitive functions for the discrete variable representation.

The MCTDH wavepacket, initially localized in the singlet excited state, has been propagated for 1.3 ps, reaching the point where about 60% of the population has been transferred in the triplet manifold. The evolution of diabatic populations is shown in Fig. 3. No Poincaré recurrences have been observed during the propagation times [28]. In this exploratory dynamics, the wavepacket has been given an initial impulsion of +5 au in all dimensions. This accelerates the dynamics and makes the simulations feasible in a reasonable time, since the convergence criterion for the numerical integrators and the combination of single particle and primitive functions is computationally demanding. Even though, the mechanistic conclusions extracted here are similar to a longer time dynamics with less well convergence criteria (see Supporting Information).

Fig. 3
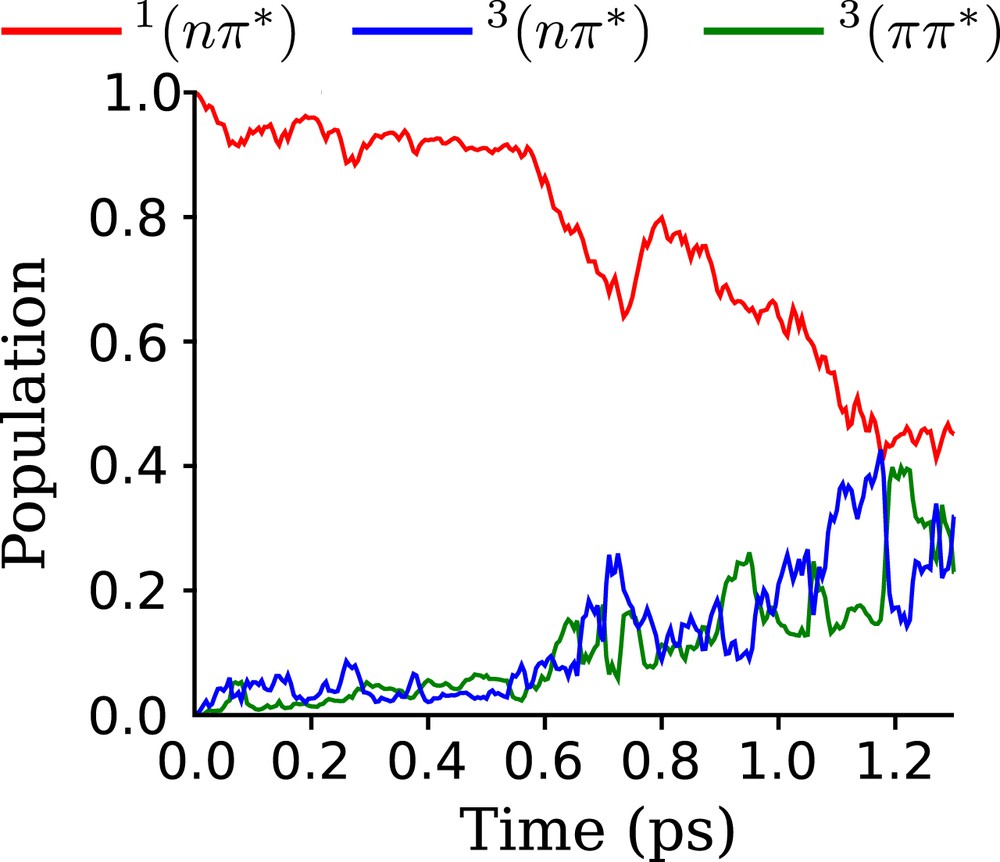
Quantum dynamics simulation of the evolution of population in the diabatic states. Initially, the wavepacket is located only in the singlet excited state.

The full quantum dynamics can be divided into three different time scales: (i) the first 0.6 ps is characterized by a relatively slow transfer from ${}^{1}n π^{*}$ towards ${}^{3}π π^{*}$ ; this triplet is immediately equilibrated with the ${}^{3}n π^{*}$ , implying that out-of-plane vibrations get active fast; (ii) From 0.6 ps to 0.8 ps, a sudden large transfer occurs, lowering the ${}^{1}n π^{*}$ population from 95% to 65%, and a concomitant increase of both the ${}^{3}π π^{*}$ and ${}^{3}n π^{*}$ populations; (iii) From 0.8 ps to 1.2 ps, a monotonic decrease of the singlet population occurs, which leads to strong Rabi-type oscillations between the two triplets.

From these results, we can easily interpret that the nuclear wavepacket evolves initially by means of an internal conversion process in the electronic singlet state. Its characteristic time is relatively long due to the small vibronic couplings in acetophenone. At around 0.6 ps, the wavepacket reaches a region of stronger non-adiabatic coupling, and thus, a non-adiabatic coupling between the ${}^{1}n π^{*}$ and ${}^{3}π π^{*}$ states starts to act. The transferred population remains essentially constant from 0.6 ps to 0.9 ps, with an average value of 65% of the population in the ${}^{1}n π^{*}$ state. The evolution of the ${}^{3}π π^{*}$ population is concomitant with the singlet one, due to the direct coupling between these two states. The ${}^{3}n π^{*}$ population, which is not directly coupled to the singlet state, gets population mainly through vibronic couplings with the ³ππ^∗ triplet through out-of-plane modes, which get activated from the beginning of the triplet manifold dynamics.

The fast population of the ${}^{3}π π^{*}$ state is a clear indication that non-adiabatic couplings are fully active through out-of-plane nuclear displacements, which in turn activate the coupling between the triplet states. As a matter of fact, the ${}^{3}π π^{*}$ state seems to be always equilibrated with the ${}^{3}n π^{*}$ one. In the present exploratory dynamics, the full population transfer from ${}^{3}π π^{*}$ to ${}^{3}n π^{*}$ is not fully observed. In longer time dynamics (see Supporting Information), the population transfer to the ${}^{3}n π^{*}$ is almost complete, where the ${}^{3}π π^{*}$ state can be seen as an intermediate tube in a quantum equivalent of a Japanese bamboo rocking fountain: it needs to accumulate population before releasing it to the more stable lowest triplet state. Closing this discussion, notice that effects beyond the harmonic approximation used in this study [31] could even lead to faster ${}^{3}n π^{*}$ population through direct transfer from ${}^{1}n π^{*}$ .

Comparing the calculated time evolution of acetophenone with the reported μs phosphorescence time scale [4], acetophenone probably emits light from the ${}^{3}n π^{*}$ state mainly, without excluding the possibility of ${}^{3}π π^{*}$ emission at a similar wavelength. Much longer simulations would be required to determine if the experimentally proposed triplet equilibrium [4] is theoretically confirmed. However, at the shorter time scale in which triplet photochemical reactions take place, both ${}^{3}n π^{*}$ and ${}^{3}π π^{*}$ states are expected to contribute. This finding explains the origin of the rich photochemistry acetophenone and other aromatic ketones.

4 Conclusions

In the present study, we have reported results of full quantum dynamics simulations of acetophenone after initial excitation to its first singlet excited state. The quantum dynamics have been performed using the MCTDH approach, which requires a model Hamiltonian in diabatic form. We have shown that the linear vibronic coupling Hamiltonian is a suitable model to take into account the interstate couplings of acetophenone.

We have shown the parametrization procedure of the model Hamiltonian with high-level quantum mechanical calculations. For the electronic part, we have used XMCQDPT2 results for energetics, and a quasi-diabatization procedure for CASSCF wavefunction to calculate the diabatic couplings between the triplet states. The vibrational modes have been classified in tuning modes (keeping the molecular symmetry) and coupling modes (breaking the molecular symmetry), and vibration-dependent triplet couplings have been calculated. This adds information on the triplet conical intersection in the dynamics. The singlet–triplet diabatic coupling has been estimated by a CASSCF calculation of spin–orbit coupling. We found that the spin–orbit coupling has a negligible dependence on the vibrational coordinates.

The quantum dynamics simulations indicate that the decay process is initially dominated by internal conversion, and only after the intersystem crossing occurs. The latter becomes increasingly important after the initial internal conversion time of 0.6 ps. Then acetophenone needs only 0.6 ps to transfer about 60% of the singlet population to the triplet manifold.

From the present results, we can tentatively sketch how the triplet states of other aromatic phenones are populated. In the case of rigid aromatic phenones (like quinones) that feature small (out-of-plane) non-adiabatic couplings, the ISC-based conversion will be slow. In such cases, the triplet population will end up mainly in the state directly coupled to the initially excited singlet state. In contrast, in molecules which can more easily break the planar symmetry (such as benzophenone), the lowest triplet state will be populated swiftly, because of the stronger non-adiabatic couplings. As acetophenone shows an intermediate behavior between these two limiting cases, interest in such a peculiar photochemistry will not vanish.

Acknowledgments

MHR acknowledges the Alexander von Humboldt Foundation for a post-doctoral research fellowship. This work was granted access to the HPC resources of Aix-Marseille Université financed by the project Equip@Meso (ANR-10-EQPX-29-01) of the program “Investissements d’Avenir” supervised by the Agence Nationale pour la Recherche.

References

[1] W.-H. Fang; D. Phillips Chem. Phys. Chem., 3 (2002), p. 889

[2] G. Cui; Y. Lu; W. Thiel Chem. Phys. Lett., 537 (2012), p. 21

[3] M. Huix-Rotllant; D. Siri; N. Ferré Phys. Chem. Chem. Phys., 15 (2013), p. 19293

[4] S. Yamabuto; S. Shigeto; Y.-P. Lee; H.o. Hamaguchi Ang. Chem. Int. Ed., 49 (2010), p. 9201

[5] S.T. Park; J.S. Feenstra; A.H. Zewail J. Chem. Phys., 124 (2006), p. 174707

[6] Q. Ou; J.E. Subotnik J. Phys. Chem. C, 117 (2013), p. 19839

[7] J. Eng; C. Gourlaouen; E. Gindensperger; C. Daniel Acc. Chem. Res., 48 (2015) no. 3, pp. 809-817

[8] Molecular Quantum Dynamics: From Theory to Applications (F. Gatti, ed.), Springer, 2014

[9] M. Barbatti; G. Granucci; M. Persico; M. Ruckenbauer; M. Vazdar; M. Eckert-Maksic; H. Lischka J. Photochem. Photobiol. A: Chem., 190 (2007), pp. 228-240

[10] M. Richter; P. Marquetand; J. Gonzalez-Vazquez; I. Sola; L. Gonzalez J. Chem. Theory Comput., 7 (2011) no. 5, pp. 1253-1258

[11] E. Tapavicza; G.D. Bellchambers; J.C. Vincent; F. Furche Phys. Chem. Chem. Phys., 15 (2013), pp. 18336-18348

[12] H.-D. Meyer; U. Manthe; L.S. Cederbaum Chem. Phys. Lett., 165 (1990), pp. 73-78

[13] M. Beck; A. Jäckle; G. Worth; H.-D. Meyer Phys. Rep., 324 (2000), pp. 1-105

[14] Multidimensional Quantum Dynamics: MCTDH Theory and Applications (H.-D. Meyer; F. Gatti; G. Worth, eds.), Wiley-VCH, 2009

[15] I. Burghardt; E. Gindensperger; L.S. Cederbaum Mol. Phys., 104 (2006), p. 1081

[16] E. Gindensperger; I. Burghardt; L.S. Cederbaum J. Chem. Phys., 124 (2006), p. 144103

[17] E. Gindensperger; I. Burghardt; L. Cederbaum J. Chem. Phys., 124 (2006), p. 144104

[18] E. Gromov; A.B. Trofimov; F. Gatti; H. Köppel J. Chem. Phys., 133 (2010), p. 164309

[19] G.A. Worth; M.H. Beck; A. Jäckle; H.-D. Meyer The MCTDH Package, Version 8.2, 2000 http://mctdh.uni-hd.de H.-D. Meyer, Version 8.3(2002), Version 8.4 (2007). Current version: 8.4.10 (2014)

[20] H. Nakamura; D.G. Truhlar J. Chem. Phys., 115 (2001), pp. 10353-10372

[21] H. Nakamura; D.G. Truhlar J. Chem. Phys., 117 (2002), pp. 5576-5593

[22] H. Nakamura; D.G. Truhlar J. Chem. Phys., 118 (2003), pp. 6816-6829

[23] Z. Li; R. Valero; D. Truhlar Theor. Chem. Acc., 118 (2007), pp. 9-24

[24] M.W. Schmidt; K.K. Baldridge; J.A. Boatz; S.T. Elbert; M.S. Gordon; J.H. Jensen; S. Koseki; N. Matsunaga; K.A. Nguyen; S. Su; T.L. Windus; M. Dupuis; J.A. Montgomery J. Comput. Chem., 14 (1993), pp. 1347-1363

[25] A.A. Granovsky J. Chem. Phys., 134 (2011), p. 214113

[26] M.M. Francl; W.J. Pietro; W.J. Hehre; J.S. Binkley; D.J. DeFrees; J.A. Pople; M.S. Gordon J. Chem. Phys., 77 (1982), pp. 3654-3665

[27] A.A. Granovsky Firefly version 7, 2013 http://classic.chem.msu.su/gran/firefly/index.html

[28] H. Köppel; W. Domcke; L.S. Cederbaum Adv. Chem. Phys., 57 (1984), p. 59

[29] M.A. El-Sayed Acc. Chem. Res., 1 (1968), p. 8

[30] H. Bethe; E. Salpeter Quantum Mechanics of One- and Two-Electron Atoms, Plenum Press, 1977

[31] M. Etinski; V. Rai-Constapel; C.M. Marian J. Chem. Phys., 140 (2014) no. 11, p. 114104

Comments - Policy