<i>In silico</i> receptor-based drug design of X,Y-benzenesulfonamide derivatives as selective COX-2 inhibitors

David J. Pérez; Orlando Sarabia; Manuel Villanueva-García; Kayim Pineda-Urbina; Ángel Ramos-Organillo; Jorge Gonzalez-Gonzalez; Zeferino Gómez-Sandoval; Rodrigo Said Razo-Hernández

doi:10.1016/j.crci.2016.05.015

In silico receptor-based drug design of X,Y-benzenesulfonamide derivatives as selective COX-2 inhibitors

David J. Pérez ¹ ; Orlando Sarabia ¹ ; Manuel Villanueva-García ² ; Kayim Pineda-Urbina ¹ ; Ángel Ramos-Organillo ¹ ; Jorge Gonzalez-Gonzalez ¹ ; Zeferino Gómez-Sandoval ¹ ; Rodrigo Said Razo-Hernández ^1,³

¹ Facultad de Ciencias Químicas, Universidad de Colima, kilómetro 9 carretera Colima-Coquimatlán, Col., México, C.P. 28400, Mexico
² Asociación de Jubilados de la Universidad de Guanajuato, Paseo de la Presa No 77, Guanajuato, Gto., México, C.P. 36000, Mexico
³ Laboratorio de Dinámica de Proteínas y Ácido Nucleicos, Centro de Investigación en Dinámica Celular, Instituto de Investigación en Ciencias Básicas y Aplicadas, Universidad Autónoma del Estado de Morelos, C.P. 62209 Cuernavaca, Mexico

Comptes Rendus. Chimie, Volume 20 (2017) no. 2, pp. 169-180.

Résumé

COX-2 is a widely studied biological target, since its activity is directly related to the inflammation response. The design of COX-2 selective inhibitors is an ongoing topic in drug design. We performed a quantitative structure–activity relationship and docking studies over a series of benzenesulfonamide derivatives on their inhibition towards COX-1 and COX-2, in order to rationalize their selectivity towards COX-2. Constitutional, topological and molecular property descriptors for the QSAR models and molecular docking calculations were employed. The mathematical model highlighted that lipophilic character and size are the most important features for COX-2 inhibition by benzenesulfonamides. A second QSAR model revealed that the dipole moment, the number of hydrogen bond donors and lipophilicity descriptors of benzenesulfonamides are crucial for their binding to COX-1. Moreover, artificial neural networks were employed to improve the prediction power of the COX-1 inhibition QSAR model. In this sense, we proposed new selective potential inhibitors by introducing different halogens into the benzenesulfonamide scaffold, improving their interactions with key residues of COX-2.

Supplementary Materials:
Supplementary material for this article is supplied as a separate file:

mmc1.docx

Métadonnées

Reçu le : 2016-03-08
Accepté le : 2016-05-12
Publié le : 2016-06-22

DOI : 10.1016/j.crci.2016.05.015

Mots clés : QSAR, Docking, Cyclooxygenase, Benzenesulfonamides, Drug design, Artificial neural networks

Affiliations des auteurs :

@article{CRCHIM_2017__20_2_169_0,
     author = {David J. P\'erez and Orlando Sarabia and Manuel Villanueva-Garc{\'\i}a and Kayim Pineda-Urbina and \'Angel Ramos-Organillo and Jorge Gonzalez-Gonzalez and Zeferino G\'omez-Sandoval and Rodrigo Said Razo-Hern\'andez},
     title = {\protect\emph{In silico} receptor-based drug design of {X,Y-benzenesulfonamide} derivatives as selective {COX-2} inhibitors},
     journal = {Comptes Rendus. Chimie},
     pages = {169--180},
     publisher = {Elsevier},
     volume = {20},
     number = {2},
     year = {2017},
     doi = {10.1016/j.crci.2016.05.015},
     language = {en},
}

TY  - JOUR
AU  - David J. Pérez
AU  - Orlando Sarabia
AU  - Manuel Villanueva-García
AU  - Kayim Pineda-Urbina
AU  - Ángel Ramos-Organillo
AU  - Jorge Gonzalez-Gonzalez
AU  - Zeferino Gómez-Sandoval
AU  - Rodrigo Said Razo-Hernández
TI  - In silico receptor-based drug design of X,Y-benzenesulfonamide derivatives as selective COX-2 inhibitors
JO  - Comptes Rendus. Chimie
PY  - 2017
SP  - 169
EP  - 180
VL  - 20
IS  - 2
PB  - Elsevier
DO  - 10.1016/j.crci.2016.05.015
LA  - en
ID  - CRCHIM_2017__20_2_169_0
ER  -

%0 Journal Article
%A David J. Pérez
%A Orlando Sarabia
%A Manuel Villanueva-García
%A Kayim Pineda-Urbina
%A Ángel Ramos-Organillo
%A Jorge Gonzalez-Gonzalez
%A Zeferino Gómez-Sandoval
%A Rodrigo Said Razo-Hernández
%T In silico receptor-based drug design of X,Y-benzenesulfonamide derivatives as selective COX-2 inhibitors
%J Comptes Rendus. Chimie
%D 2017
%P 169-180
%V 20
%N 2
%I Elsevier
%R 10.1016/j.crci.2016.05.015
%G en
%F CRCHIM_2017__20_2_169_0

David J. Pérez; Orlando Sarabia; Manuel Villanueva-García; Kayim Pineda-Urbina; Ángel Ramos-Organillo; Jorge Gonzalez-Gonzalez; Zeferino Gómez-Sandoval; Rodrigo Said Razo-Hernández. In silico receptor-based drug design of X,Y-benzenesulfonamide derivatives as selective COX-2 inhibitors. Comptes Rendus. Chimie, Volume 20 (2017) no. 2, pp. 169-180. doi : 10.1016/j.crci.2016.05.015. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2016.05.015/

Version originale du texte intégral

1 Introduction

Cyclooxygenase (COX) enzyme catalyzes the conversion of arachidonic acid into prostaglandins (PGs), which are endogenous compounds that play several and important functions within the cells [1,2]. At least two isozymes of COX are well identified: COX-1, the constitutive isoform, which is mostly expressed under normal conditions and COX-2, which is mainly expressed during inflammatory responses [2,3]. Therefore, COX-2 has become one of the biological targets of anti-inflammatory drugs. Non-Steroidal Anti-Inflammatory Drugs (NSAIDs) inhibit COX isozymes in a non-selective manner [2–4]. This lack of selectivity towards COX-2 is related to undesired side effects: dyspepsia, ulceration and bleeding due to the use of NSAIDs [2]. Side effects are due to COX-1 inhibition, which implies the deletion of its physiologic functions [1–4].

The pursuit of selective inhibition of COX-2 led to the discovery of the COX-2 selective inhibitors, for instance celecoxib, rofecoxib and valdecoxib (called COXIBS) [2].

However, chronic use of these drugs is associated with cardiovascular side effects; therefore, the search for safer COX-2 selective inhibitors is an ongoing topic in drug design [3]; COXIBS are diaryl compounds that contain sulfonamide or methyl sulfone groups. Besides COXIBS and NSAIDs, some other compounds have been identified as COX inhibitors derived from natural sources, for instance resveratrol [5] and amarogentin [6].

By modifying the resveratrol structure [5], a series of 31 benzenesulfonamide derivatives (BzSAD) that showed an increase in selectivity towards COX-2 with respect to that of resveratrol were reported (Fig. 1). Quantitative Structure–Activity Relationship (QSAR) models are able to predict the biological activity of compounds—even before they are synthesized—improving the rational drug design and facilitating the comprehension of the mechanism of the action and pharmacokinetics of biologically active compounds [7].

Fig. 1
Benzenesulfonamide derivatives previously synthesized and tested as COX-2 selective inhibitors [5]. These compounds were employed in this work.

QSAR studies employ the algorithms and techniques developed by the computer sciences, like Genetic Algorithms (GA) and Artificial Neural Networks (ANN) [8–10]. The GA method is inspired by Darwin's evolution concept and consists of a stochastic generation of individuals (mathematical models), followed by a random selection of two individuals which will generate a new one. In order to express the best parents' characteristics (biological activity), this new individual must inherit the right genes (molecular descriptors). The ANN technique seeks to mimic the human brain mechanism. Its architecture consists of a set of interconnected neurons (basic units) that generates a response (physicochemical properties or biological activity) according to the environmental stimuli (molecular descriptors) [10].

The exchange of a Ph with a Ph–X is as useful a strategy in drug design that increases binding affinity and improves the pharmacodynamic profile; such an exchange favors halogen bonding [11]. Halogen bonding refers to short contact interactions seen in drugs bearing the group Ph–X, (F, Cl, Br, and I) where X acts as a Lewis acid allowing the interaction with the carbonyl within residues, which acts as a Lewis base [12]. Halogen bonding is explained on the basis of “σ-hole” caused by the uneven electronic distribution of the Ph–X functionality, forming a positively charged region that interacts with a nucleophile such as carbonyl observed in protein backbones [13].

Several QSAR studies of COX-2 inhibitors have been done on a wide variety of molecular structures [14–22], including studies on compounds that contain sulfonamide and methyl sulfone groups [23,24]. In these studies, BzSAD, phenylazobenzenesulfonamide [23] and resveratrol derivatives [24] were considered for obtaining a structure–activity relationship in a global context.

In this work, we performed a QSAR study using only BzSAD previously reported [5] due to their improved selectivity towards COX-2. Additionally, a molecular docking calculation was made in order to rationalize the BzSAD selectivity towards COX-2. Furthermore, we used molecule 2 as a scaffold (Fig. 1) to construct novel and more potent COX-2 selective inhibitors based on the halogen bonding approach [11–13].

2 Computational details

2.1 Molecules preparation

The 31 benzenesulfonamide derivatives previously synthesized [5] and three reference drugs (celecoxib, resveratrol and NS398) were employed in this work. Full geometry optimizations, without symmetry constraints, for the 34 neutral compounds were performed with the PM3 [25] semi-empirical method implemented in the SPARTAN'08 program [26]. Harmonic frequency analysis was performed for all the compounds, in order to ensure that their geometric are minima on the potential energy surface.

Scior et al. discuss the many pitfalls that QSAP/QSPR models have and the options that one as a researcher possess to bypass them [27]. For instance, in order to avoid the use of unnecessary descriptors that poorly describe the biological activity and may correlate fortituisly, they suggest to perform an exhaustive descriptor selection prior to the construction of the mathematical model [27,28]. Thus in this study, only constitutional, topological, and molecular properties and quantum molecular descriptor families, from the optimized geometry of the BzSAD, were calculated with the DRAGON ‘05 [29] and SPARTAN'08 [26] packages (Table 1). By selecting these descriptor families, we attempted to correlate the lipophilicity, chemical group accounts (number of carbons, nitrogens, rings, etc.), molecular size and electronic distribution of the BzSAD with their inhibitory activity. The lipophilicity and molecular size are molecular properties that determine the selectivity towards COX-2 due to its bigger and more lipophilic active sites in comparison to that of COX-1 [2,3]. Hence, for this study, we calculated all the molecular descriptors (available in DRAGON) that are related to lipophilicity: the hydrophilic factor ( $H y$ ), topological polar surface area ( $T P S A$ ), linear and quadratic Moruguchi octanol–water coefficients of partition ( $M L O G P$ and $M L O G P^{2}$ ), and linear and quadratic Ghose–Crippen–Viswanadhan octanol–water partition coefficients ( $A L O G P$ and $A L O G P^{2}$ ). The $L O G P$ quadratic term has been successfully used before to explain the inhibitory activity of several compounds (barbiturates, alkyl-benzimidazoles, aliphatic primary amines, etc.) and their selectivity towards P450 isoforms [30]. On the other hand, the electronic character of sulfonamide derivatives and its correlation with its inhibitory activity over the acetylcholinesterase protein has been properly studied by using quantum chemical descriptors, such as HOMO, LUMO, dipole moment, etc. [31]; hence, they were included in the descriptor pool used in this study.

Program	Descriptor	Type
DRAGON	$\begin{array}{l} A M W, S v, M v, n A T, n S K, n B T, n B O, n B M, S C B O \\ A R R, n C I C, n C I R, R B N, R B F, n D B, n A B \end{array}$	Constitutional
	$\begin{array}{l} Z M 1 V, Z M 2, Z M 2 V, Q i n d e x, S N a r, H N a r, G N a r, X t, \\ D z, R a m, P o l, L P R S, V D A, M S D, S M T I, S M T I V, G M T I G M T I V, X u, S P I, W, W A, H a r, H a r 2, Q W, T I 1, \\ T I 2, S T N, H y D p, R H y D p, w, P W 2, P W 3, P W 4, P W 5 \end{array}$	Topological
	$\begin{array}{l} U i, H y, T P S A (T o t), M L O G P, M L O G P^{2}, \\ A L O G P, A L O G P^{2} \end{array}$	Molecular properties
SPARTAN	$D i p o l e, H O M O, L U M O, M o l e c u l a r V o l u m e (M V o l), P S A, M W, H B D, G º$	Quantum-Chemical

2.2 Mathematical model construction and validation

For the construction of the mathematical models, the genetic algorithms technique (GA) was employed and carried out in the MobyDigs 01 program [32]. All of the molecular descriptors and the half maximal inhibitory concentration ( $I C_{50}$ ), of the BzSAD, were used as the independent variables ( $X$ ) and the dependent variable ( $Y$ ), respectively. In order to inspect all the possible mathematical models, a variety of transformations over the dependent variable ( $1 / Y$ , $l o g Y$ , ${(Y + 1)}^{2}$ , $- (1 / l o g Y)$ , $1 / l o g Y$ , $1 / Y + 1$ ) were tested. The molecules were separated into training and validation groups. 80% of all the molecules were randomly selected for the training process, and the rest 20% was used for the validation stage. The top 10 mathematical models, based on its $Q^{2}$ value, were chosen. The model with the best $Q^{2}$ values was selected and validated statistically by the QUIK rule.

To validate the QSAR model, we employed the QUIK rule, which allows the rejection of models with high predictor co-linearity that can lead to casual correlation [33]. This rule is based on the K multivariate correlation index that measures the total correlation of a set of variables, defined as:

K = \frac{\sum_{j} [\frac{λ_{j}}{\sum_{j} λ_{j}} - \frac{1}{p}]}{\frac{2 (p - 1)}{p}} j = 1, \dots \dots, p and 0 \leq K \leq 1

(1)

where

λ_{j}

is the data from the joint

X (n, p)

matrix eigenvalues,

n

is the number of objects and

p

is the number of variables in the model. The total correlation in the set given by the descriptors (

X)

plus the response

Y

(

K_{X Y}

) should always be greater than that measured only in the set of descriptors (

K_{X}

); if

K_{x y} - K_{x} < Δ K

, the model is rejected; Δ

K

may have values between 0.01 and 0.05 (in our case,

Δ K = 0.01

In addition, the standard deviation ( $s$ ) and Fisher test ( $F$ ) values were calculated [33]. These parameters gave information about how the correlation between the experimental and calculated activities is affected by the number of molecules in the study (Equation (2)), and what the probability is for the mathematical model to casually occur (Equation (3)).

s = \frac{\sum_{i = 1}^{n} {({\hat{y}}_{i} - y_{i})}^{2}}{n - 2}

(2)

In Eq. (2), the $n$ variable represents the number of molecules in the study, ${\hat{y}}_{i}$ represents the experimental activity and $y_{i}$ is the calculated activity from the QSAR model.

F = \frac{\sum_{i = 1}^{n} {({\hat{y}}_{i} - \bar{y})}^{2} / d f_{M}}{\sum_{i = 1}^{n} {({\hat{y}}_{i} - y_{i})}^{2} / d f_{E}}

(3)

where

d f_{M}

and

d f_{E}

refer to the degrees of freedom of the model (molecular descriptors in the model) and error, respectively. Also,

{\hat{y}}_{i}

\bar{y}

and

y_{i}

refer to the experimental, average value of experimental and calculated activities, respectively.

d f_{E} = n - p - 1

(4)

In the mathematical model, $s$ and $F$ should have the smallest and largest possible values, respectively, to ensure that the QSAR model is reliable.

To evaluate the internal predictive ability of our models, the leave one out technique was employed [34]. This technique consists of evaluating each molecule within the training set to determine as to how it corresponds to the validation set. One by one, each molecule is evaluated and its $Y$ value is calculated (Eq. (5)):

Q_{L O O}^{2} = 1 - \frac{\sum_{i = 1}^{n} {(y_{i} - {\hat{y}}_{\frac{i}{i}})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}

(5)

As mentioned above, to test our model more rigorously in terms of the predictive aspect, an evaluation of the estimated error was performed on all the molecules that were excluded from the training process.

2.3 Molecular docking methodology

Molecular docking calculations were performed by using a Molegro Virtual Docker (MVD) 6.0 [35]. We used the crystal structures of the COX-1 and COX-2 complexes with celecoxib PDB:3KK6 [36] and PDB:3LN1 [37], respectively. All water molecules were removed from the crystal. The potential binding sites (defined as cavities) of both COX-1 and COX-2 were detected by the expanded van der Waals sphere method. The cavities found for COX-1 (87.5 Å³) and for COX-2 (84.5 Å³), where all the binding calculations were performed, correspond to each isoform binding site. We employed the minimal geometries of all the BzSAD as a starting point. The partial charges used were set from the PM3 calculations (electrostatic type). The residues within a distance of 6 Å were set as flexible totaling 20 for COX-1 and 15 for COX-2. If one of these residues had four or more free rotating bonds, a zero strength factor was assigned; for the rest of flexible residues, a one strength factor was set.

A Moldock SE (Simplex Evolution) search function for both COX-1 & COX-2 that uses genetic algorithm during the search for the best binding site of a given enzyme or receptor was employed. A 2000 minimization steps for each flexible residue and 2000 steps of global minimization per run were set. For the Moldock SE, a total of 20 runs with a maximum of 2000 iterations using a population of 100 individuals per run. For calculating the binding energy, we used the scoring function Moldock Score [GRID]. We performed a rigid docking approach. For both isoforms, the scoring function GRID was set at 0.2 Å, the search sphere fixed as 15 Å radius. For the energy analysis of the ligand, the electrostatic internal interactions, internal Hydrogen bonds and the sp²–sp² torsions were considered for the scoring calculation.

The method was validated by reproducing the experimental binding mode of the reference inhibitor, with a Root Media Square Deviation (RMSD) of 0.77 Å for COX-1 and 0.52 Å for COX-2 (Figs. S1 and S2, see supporting information). Rather than analyzing the overall biding energies, we followed the method reported previously [38], and searched for interactions with residues that are considered key to selectively binding to each isoform.

All the structures of the proposed inhibitors COX-2 based on 2 scaffold were fully optimized by the method described previously (vide supra). In the same manner, the docking methodology used for the proposed inhibitors was the same that the one described above.

3 Results and discussion

3.1 QSAR model for COX-2

The mathematical model that described the half maximal inhibitory concentration ( $I C_{50}$ ) of the benzenesulfonamide derivatives over the COX-2 is shown below:

1 / I C_{50} = - 4.36483 [A L O G P] + 0.83506 {[A L O G P]}^{2} + 0.00137 [M V o l] + 5.44596

(6)

In Eq. (6), $A L O G P$ is the Ghose–Crippen–Viswanadhan octanol–water partition coefficient [39] and $M V o l$ is the molecular volume obtained by a space-filling model, intended to represent molecular shape and size [26]. The $Δ K$ value for the QSAR model was 0.073, satisfying the QUIK rule. According to the Pearson's correlation matrix, the molecular descriptors of the model were not lineally dependent among them (see Table S1, Supplementary data). The values of $R^{2}$ =94.23 and $Q_{L O O}^{2}$ =91.61 indicate a good correlation and prediction ability of the QSAR model, while $s$ and $F$ values (0.16 and 136.10, respectively) confirmed the reliability of the statistical model.

All the molecular descriptors values that conforms the mathematical models of the BzSAD are shown in Table 2. Molecule 15 was identified as the most potent COX-2 inhibitor according to the $I C_{50}$ data, while also possessing the lowest $A L O G P$ value of all the compounds.

Molecule	$A L O G P$	$A L O G P^{2}$	$M V o l$	$D i p o l e$	$H B D$	COX-1 $I C_{50}$	COX-2 $I C_{50}$
1	2.25	5.08	253.84	4.38	1	108.34	2.87
2	2.46	6.05	258.67	2.66	1	159.07	2.22
3	2.11	4.45	301.51	1.50	1	183.5	2.73
4	2.15	4.62	275.76	4.52	1	141.25	3
5	2.15	4.62	275.75	7.82	1	105.63	6.75
6	2.42	5.84	303.97	5.95	1	195.74	3.36
7	1.99	3.95	260.81	5.01	2	148.20	3.42
8	3.20	10.22	286.19	3.99	1	182.19	4.60
9	2.74	7.51	271.71	5.85	1	190.47	4.94
10	2.24	5.01	280.65	5.21	1	313.83	9.88
11	2.24	5.01	280.70	4.59	1	383.36	5.45
12	1.99	3.95	260.86	6.54	2	38.20	2.78
13	1.72	2.96	268.10	7.72	3	23.15	2.85
14	1.97	3.88	288.43	4.92	2	78.20	2.95
15	1.59	2.53	288.74	7.64	3	85.13	0.74
16	2.32	5.38	306.87	5	2	47.91	3.69
17	1.97	3.88	288.57	4.46	2	43.80	3.50
18	2.22	4.94	307.76	5.59	1	110.27	3.09
19	2.22	4.94	307.71	4.45	1	109.69	3.40
20	2.21	4.86	335.31	4.24	1	167.69	2.93
21	1.95	3.82	315.36	4.58	2	155.95	2.71
22	2.25	5.08	253.69	4.91	1	63.59	3.11
23	2.46	6.05	258.51	3.57	1	80.20	4.38
24	2.74	7.51	271.7	5.31	1	63.22	4.62
25	3.20	10.22	286.21	2.89	1	43.89	6.54
26	2.42	5.84	303.88	5.24	1	64.42	1.95
27	1.99	3.95	260.44	5.13	2	51.83	5.09
28	2.24	5.01	280.66	4.81	1	60.74	4.14
29	2.22	4.94	308.89	4.34	1	31.27	4.28
30	1.84	3.40	306.18	3.56	2	23.99	3.13
31	2.11	4.45	300.93	2.74	1	56.73	3.72
Celecoxib	4.55	20.72	336.21	3.71	1	23.47	0.30
Resveratrol	3.01	9.08	237.06	0.51	3	4.12	34.61
NS398	3.96	15.72	231.77	3.42	1	35.68	0.61

All the values of the reciprocal experimental activity “IC₅₀” ( $1 / Y_{e x p}$ ), the reciprocal calculated and predicted activity ( $1 / Y_{c a l}$ and $1 / Y_{p r e d}$ ) by the QSAR model are presented in Table 3.

Molecule	$1 / Y_{e x p}$	$1 / Y_{c a l}$	$r e s i d u a l_{c a l}$	$1 / Y_{p r e d}$	$r e s i d u a l_{p r e d}$
1	0.35	0.20	0.15	0.18	0.17
2	0.45	0.12	0.33	0.09	0.36
3	0.37	0.37	0	0.37	0
4	0.33	0.30	0.03	0.30	0.03
5	0.15	0.3	0.15	0.31	0.16
6	0.30	–	–	0.19	0.11
7	0.29	0.43	0.14	0.45	0.16
8	0.22	0.42	0.20	0.47	0.25
9	0.20	0.13	0.07	0.12	0.08
10	0.10	0.25	0.15	0.25	0.15
11	0.18	0.25	0.07	0.25	0.07
12	0.36	0.43	0.07	0.44	0.08
13	0.35	–	–	0.78	0.43
14	0.34	0.48	0.14	0.49	0.15
15	1.35	1.01	0.34	0.82	0.53
16	0.27	0.23	0.04	0.23	0.04
17	0.28	0.48	0.20	0.50	0.22
18	0.32	0.29	0.03	0.29	0.03
19	0.29	0.29	0	0.29	0
20	0.34	0.34	0	0.34	0
21	0.37	–	–	0.54	0.17
22	0.32	0.20	0.12	0.19	0.14
23	0.23	0.12	0.11	0.11	0.12
24	0.22	0.13	0.09	0.12	0.10
25	0.15	–	–	0.42	0.27
26	0.51	0.19	0.22	0.16	0.35
27	0.20	0.43	0.23	0.46	0.26
28	0.24	0.25	0.01	0.25	0.01
29	0.23	0.29	0.06	0.30	0.07
30	0.32	–	–	0.66	0.34
31	0.27	0.37	0.10	0.38	0.11
Celecoxib	3.33	3.34	0.01	3.36	0.03
Resveratrol	0.03	0.20	0.17	0.25	0.23
NS398	1.64	1.59	0.05	1.55	0.09

In addition, the absolute value of the differences between $1 / Y_{e x p}$ and both $1 / Y_{c a l}$ & $1 / Y_{p r e d}$ , are represented by the $r e s i d u a l_{c a l}$ and $r e s i d u a l_{p r e d}$ term respectively.

The ( $1 / Y_{p r e d}$ ) versus $(1 / Y_{e x p})$ activity plot is shown in Fig. 2. The squared correlation coefficient (R²) includes the molecules used for the external validation.

Fig. 2
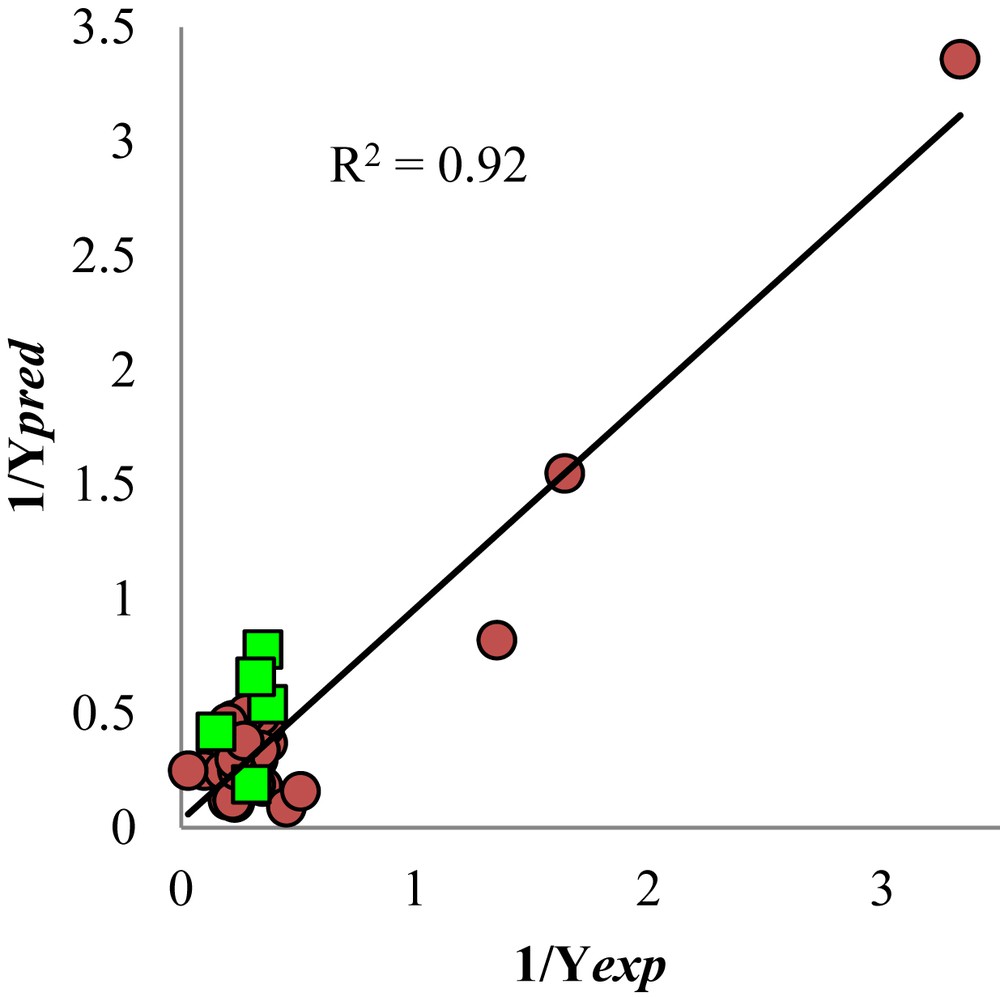
Reciprocal of the predicted activity versus the reciprocal of the experimental activity. The squares represent molecules used of external validation of the QSAR model.

The presence of $A L O G P$ and $M V o l$ descriptors in the QSAR model indicates that lipophilic character and molecular size are crucial for the COX-2 inhibition by the BzSAD. This is in accordance to the experimental data provided by the X-ray crystallographic structure of COX-2 [40], where its active site mainly differs from that of COX-1 in one residue, Val523 for the former and Ile523 for the latter [4]. This subtle difference translates to a more hydrophobic character and a larger volume in the active site of COX-2. According to our QSAR model, the relationship between the biological activity ( $I C_{50}$ ) and the lipophilicity of the molecule was exponential ( $A L O G P^{2}$ ).

However, due to the negative coefficient of the linear term, the $A L O G P$ of a molecule must be higher than one but lower than two ( $1 < A L O G P > 2$ ) in order to be a potent COX-2 inhibitor, thus, minimizing the negative contribution of the $A L O G P$ linear term. On the other hand, the QSAR model indicated that an inhibitor based on the BzSAD scaffold could nullify the negative effect of high lipophilicity with a large molecular volume ( $M V o l$ ). The positive coefficient of $M V o l$ in the QSAR model suggested that an increase in the volume of a molecule will increase its COX-2 inhibitory potency ( $283 \leq M V o l \geq 500$ ); the $M V o l$ value range is in accordance with Lipinski rules [41].

3.2 QSAR model for COX-1

The mathematical model for the inhibition of COX-1 ( $I C_{50}$ ) by the BzSAD is the following,

- log (1 / I C_{50}) = 0.06757 [D i p o l e] - 0.44141 [H B D] - 0.27199 [A L O G P] + 2.86343

(7)

where the molecular dipole (

D i p o l e

), number of hydrogen bond donors (

H B D

) and the lipophilicity are present. The statistical parameters for this model are

R^{2}

=54.36,

Q_{L O O}^{2}

=39.70,

s

=0.29,

F

=9.9 and

Δ K

=0.03. Although the predictive ability of the QSAR model was deficient, it was improved by incorporating back propagation artificial neural network (BPANN). This method was previously used by our group to combine the characteristics of the GA (for descriptor selection) and the prediction ability of BPANN [10].

All the values of the negative logarithm of the experimental $- l o g (\frac{1}{Y_{e x p}})$ , calculated $- l o g (\frac{1}{Y_{c a l}})$ , and predicted $- l o g (\frac{1}{Y_{p r e d}})$ activities by the multi-linear QSAR model and the predicted activity $- l o g (\frac{1}{Y_{p r e d A N N}})$ by the BPANN are shown in Table 4. In addition, $r e s_{c a l}$ , $r e s_{p r e d}$ and $r e s_{p r e d A N N}$ are displayed. These terms represent the absolute value of the differences between $- l o g (\frac{1}{Y_{e x p}})$ and $- l o g (\frac{1}{Y_{c a l}})$ , $- l o g (\frac{1}{Y_{p r e d}})$ and $- l o g (\frac{1}{Y_{p r e d A N N}})$ , respectively.

Molecule	$- l o g (\frac{1}{Y_{e x p}})$	$- l o g (\frac{1}{Y_{c a l}})$	$r e s_{c a l}$	$- l o g (\frac{1}{Y_{p r e d}})$	$r e s_{p r e d}$	$- l o g (\frac{1}{Y_{p r e d A N N}})$	$r e s_{p r e d A N N}$
1	2.03	–	–	2.10	0.07	2.03	0
2	2.20	1.93	0.27	1.90	0.30	2.06	0.14
3	2.26	1.95	0.31	1.85	0.41	2.17	0.09
4	2.02	2.14	0.12	2.14	0.12	2.08	0.06
5	2.15	–	–	2.37	0.22	1.97	0.18
6	2.29	2.17	0.12	2.15	0.14	1.99	0.30
7	2.17	1.78	0.39	1.75	0.42	1.85	0.32
8	2.26	1.82	0.44	1.78	0.48	2.00	0.26
9	2.28	2.07	0.21	2.05	0.23	2.17	0.11
10	2.50	–	–	2.17	0.33	2.09	0.41
11	2.58	2.12	0.46	2.09	0.49	2.03	0.55
12	1.58	1.88	0.30	1.92	0.34	1.75	0.17
13	1.36	1.59	0.23	1.69	0.33	1.48	0.12
14	1.89	1.78	0.11	1.77	0.12	1.94	0.05
15	1.93	1.62	0.31	1.50	0.43	1.77	0.16
16	1.68	1.69	0.01	1.69	0.01	1.73	0.15
17	1.64	1.75	0.11	1.75	0.11	1.69	0.05
18	2.04	2.20	0.16	2.21	0.17	2.14	0.10
19	2.04	2.12	0.08	2.12	0.08	2.01	0.03
20	2.22	2.11	0.11	2.10	0.12	2.00	0.22
21	2.19	1.76	0.43	1.73	0.46	1.90	0.39
22	1.80	–	–	2.14	0.34	2.06	0.36
23	1.90	1.99	0.09	2	0.10	2.02	0.12
24	1.80	2.04	0.24	2.06	0.26	2.13	0.33
25	1.64	1.75	0.11	1.76	0.12	1.75	0.11
26	1.81	–	–	2.12	0.31	2.02	0.21
27	1.71	1.79	0.08	1.79	0.08	1.86	0.15
28	1.78	2.14	0.36	2.16	0.38	2.04	0.26
29	1.49	2.11	0.62	2.15	0.66	2.01	0.52
30	1.38	1.72	0.34	1.76	0.38	1.56	0.18
31	1.75	2.03	0.28	2.08	0.33	1.89	0.14
Celecoxib	1.37	1.43	0.06	1.49	0.12	1.36	0.01
Resveratrol	0.61	0.75	0.14	0.98	0.37	0.64	0.03
NS398	1.55	1.57	0.02	1.58	0.03	1.57	0.02

The reciprocal of the predicted activity against the experimental biological activity is shown in Fig. 3. The R² in the graphic represents the squared correlation coefficient between the $- l o g (\frac{1}{Y_{p r e d A N N}})$ and the $- l o g (\frac{1}{Y_{e x p}})$ , where the molecules used for the external validation are included.

Fig. 3
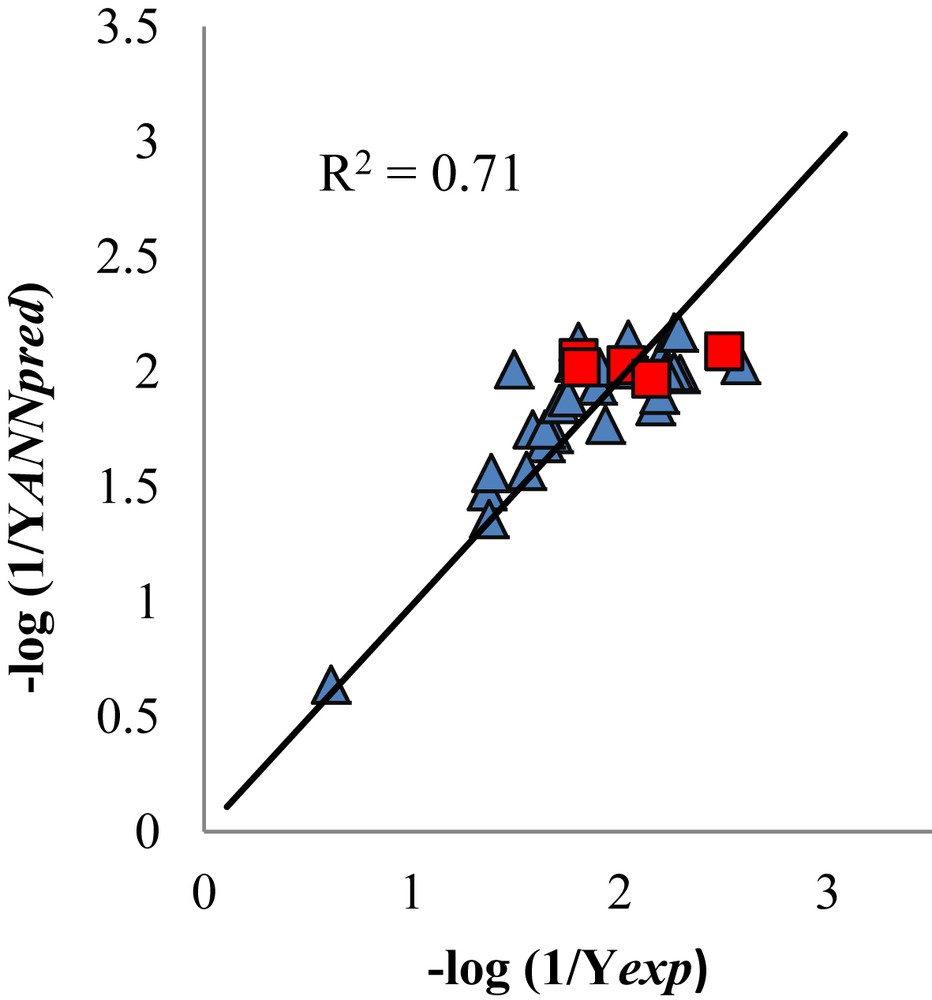
Values of the negative logarithm of the reciprocal predictive activity by BPANN versus the negative logarithm of the reciprocal experimental activity. The squares represent the molecules used to external validation of the QSAR model.

The coefficient of the HBD descriptor in the QSAR model, indicated that this feature is crucial for the inhibition of COX-1. Consequently, a COX-1 inhibitor must possess HBD groups. The negative sign in the coefficient of the $A L O G P$ descriptor was related to the HBD value, which precludes the addition of “too many” HBD groups; the molecule must have an equilibrium between its hydrophobic and hydrophilic character in order to diffuse well in blood and across the cell membrane. Finally the increase of the dipole moment—a large dipole is related to a low lipophilicity—will negatively affect the inhibitory activity of this type of compounds. The descriptors gleaned from the previously reported QSAR models are similar to our results [23,24]. However, our QSAR model found descriptors that provided insights into the pharmacodynamic profile of the BzSAD compounds.

3.3 Molecular docking

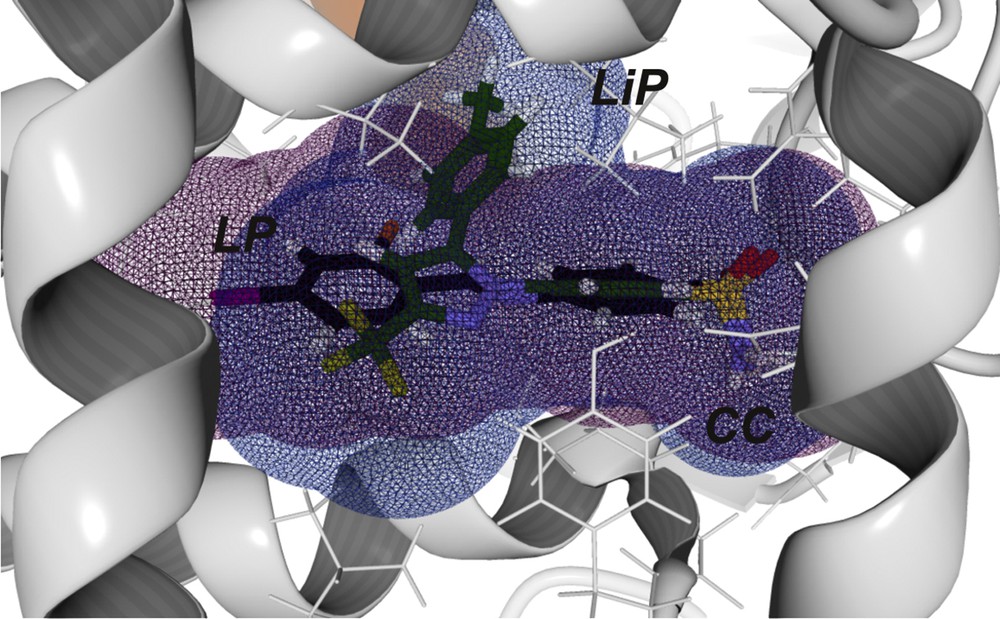
We discussed the interactions with the residues located in the regions that are relevant to the selectivity towards both isoforms: the Lateral Pocket (LP: Ala527, Leu531, Ser530 & Val349), Constriction Channel (CC: Arg120, Glu524 & Tyr355), Lipophilic Pocket (LiP: Val523), and with Arg513 & His90 [42,43]. We compared the interactions of BzSAD 2 and 15 with LP, CC, LiP, Arg513 & His90 to those of celecoxib and NS-398, and to resveratrol (Table 5). The interactions of 15 with the LP were more favorable than those of celecoxib, which explains its increase in COX-2 selectivity index. Specifically the interaction of 15 with Leu531 was −7.27 whereas that of celecoxib was −1.45 (kcal/mol). In the same manner, molecule 2 showed a more favorable interaction with Leu531 (−4.21 kcal/mol) than celecoxib.

Residues	Cel.	15	2	NS-398	Resve.
Ala527	−14.77	−21.23	−12.73	−12.12	−5.3
Arg120	−2.53	−3.02	–	−8.22	–
Arg513	−4.61	−4.42	−4.42	–	−4.21
Glu524	−0.45	–	–	–	–
His90	−9.16	−6.8	−7.12	−2.05	−7.87
Leu531	−1.45	−7.27	−4.12	−0.90	–
Ser530	−2.22	−5.33	−5.04	−2.80	−4.7
Tyr355	−10.68	−3.92	−4.07	−8.99	−7.2
Val349	−8.98	−10.73	−10.6	−9.05	−0.9
Val523	−20.68	−11.21	−11.25	−17.20	−14.5

Since Leu531 is a key residue – its correct conformational arrangement allows the substrates and inhibitors to accommodate into COX-2 active site – the interaction value of 15 with this residue provided a rationale to its increased selectivity index [44]. The binding modes of 15, 2, celecoxib and resveratrol are shown in Fig. 4.

Fig. 4
Binding modes of 15 (A), 2 (B), celecoxib (C) and resveratrol (D) into COX-2. Hydrogen bonds are depicted as blue dashed lines. Residues are colored according to their hydropathy index value; red represent hydrophilic residues, blue hydrophobic and purple amphiphilic.

The sulfonamide moiety within 2, 15 and celecoxib was oriented similarly, which allowed the electrostatic interactions with Arg513 and His90 and the formation of HB to several residues. Binding mode of 15 (Fig. 4A) is stabilized by the formation of HB to Ala527, Ile517, Leu352, Gln192, Phe518 and Ser353. On the other hand, molecule 2 and celecoxib (Fig. 4B and C) formed a HB to Gln192, Ile517, Leu352 and Ser353. Additionally celecoxib formed a HB to His90. Neither the BzSAD nor celecoxib formed HB to CC residues. This is in agreement with the reported data regarding COX-2 selective inhibitors, which are less prone to form HB to CC residues [3,4,45].

The presence of Val523 in COX-2 forms a lipophilic pocket whose access is controlled by His90 [42]. Hence, a COX-2 selective inhibitor needs to interact with His90 and Arg513 to gain access to the LiP and interact with Val523. The energy (kcal/mol) of the interactions of 15 (11.21) and 2 (11.25) with Val523 are less favorable than those of celecoxib (20.68). However, their electrostatic interactions with His90 and Arg513 imply a tight and durable binding to COX-2; such interactions are only achieved by non-time dependent inhibitors such as COXIBS [42,45]. In comparison with celecoxib, compounds 2 and 15 formed less favorable electrostatic interactions with His90; however, their interactions with Arg513 are similar in energy; these two important interactions provided a rationale to their selectivity towards COX-2. The interaction energy of 2 and celecoxib with Arg513 helped to explain why molecule 2 is akin to celecoxib in terms of COX-2 selectivity.

The interactions of molecules 2, 15 and reference ligands (celecoxib, NS-398 and resveratrol) with the residues that form the LP, CC and Ile523, which are relevant to the selectivity towards COX-1 [3], are presented in Table 6; their binding modes are shown in Fig. 5.

Residues	Cel.	15	2	NS-398	Resv.
Ala527	−14.19	−21.45	−14.0	−12.80	−7.59
Arg120	−1.88	−2.46	–	−10.30	–
Glu524	−0.49	–	–	0.50	–
Ile523	−23.03	−15.17	−16.70	−17.30	−21.41
Leu531	−2.70	−6.36	−4.43	−4.20	–
Ser530	−1.88	−4.51	−6.13	−1.00	−1.44
Tyr355	−12.1	−6.82	−7.18	−11.70	−5.45
Val349	−6.63	−7.87	−6.89	−5.80	−1.67

Fig. 5
Binding modes of 15 (A), 2 (B), celecoxib (C) and resveratrol (D) in COX-1 active site. Hydrogen bonds are depicted as blue dashed lines. Residues are colored according to their hydropathy index values; red, blue and purple represent hydrophilic, hydrophobic and amphiphilic residues.

The interaction energy of molecule 2 and 15 with LP and CC residues showed important differences: molecule 15 formed a HB to Ala527 and also interacted more energetically with Leu531, Val349 and Arg120 than 2 (Fig. 5A–B). Binding of compounds 15 and 2 to COX-1 was ruled out by the formation of HB; in accordance with our QSAR COX-1 model where dipole and HBD groups defined the selectivity towards COX-1. The interaction energy achieved by 15 with Ile523 was 7.86 kcal/mol less favorable than that obtained by celecoxib with the same residue. This provided a rationale to the increase in the selectivity index (SI=115) of 15 in comparison to that of celecoxib (SI=78). Celecoxib, which is a more potent COX-1 inhibitor (IC₅₀=23.47) than 2 and 15, showed the highest interaction energy with Ile523 (−23.03 kcal/mol), the interaction of 2 with Ile523 was −16.7 kcal/mol (IC₅₀=159.07), in contrast to 15 (IC₅₀=85.13) whose interaction value was −15.77 kcal/mol. According to the docking calculations, comparison of 2 and 15 to resveratrol (−21.4 kcal/mol and IC₅₀=4.12) also correlated with experimental data. Molecules 15 and 2 interacted less energetically than resveratrol (6.0 kcal/mol and 4.7 kcal/mol, respectively) with the Ile523.

COX-1 inhibition is ruled out by a conformational change achieved by Ile523, which requires a high energy spend, that allows an inhibitor to bind into the active site of COX-1 [46]. In this regard, celecoxib is a non-competitive and reversible COX-1 inhibitor and a tight time-dependent COX-2 inhibitor.

3.4 Structure based design of new COX-2 selective inhibitors

We designed new selective COX-2 inhibitors based on the compound 2 scaffold, found in the COX-2 QSAR model—in which the lipophilicity and $M V o l$ define the selectivity towards COX-2, whereas Dipole and HBD define that towards COX-1—and docking results. Also, we have selected molecule 2 due to (i) its similarities to celecoxib in binding orientation to the COX-2 active site (Fig. 6) and that (ii) it possesses less HBD groups than molecule 15. The expanded van der Waals sphere representation of molecule 2 and celecoxib (Fig. 6), depicts that the former occupies a smaller volume than the latter.

Fig. 6
Binding modes of molecule 2 (black) & celecoxib (green) into COX-2. Celecoxib conformation corresponds to the one experimental binding from its complex with COX-2.

Conformation of molecule 2 is the one obtained by molecular docking calculations. The expanded van der Waals surfaces are shown as a purple grid for 2 and a blue grid for celecoxib. Celecoxib is filling the three pockets that are key to the selective inhibition of COX-2. Another important feature observed in molecule 2 was the presence of a Ph–F moiety (where F can be exchanged with Cl, Br, and I). Fluorine has been defined as the only halogen that may present electronic repulsion with a carbonyl backbone; thus, its exchange with iodine, bromine or chlorine is an accepted improvement in drug design [13]. On this basis, we proposed compounds (36–53) as new COX-2 selective inhibitors (Table 7). We have docked 36–54 molecules into COX-1 and COX-2 active sites.

Molecules	X	Y	COX-2	COX-1
E_total	LE	E_internal	E_total	LE	E_internal
36	Cl	H	−144.9	−7.6	−4.6	−97.4	−5.1	13.3
37	Br	H	−143.9	−7.6	−3.7	−141.9	−3.5	−7.5
38	I	H	−142.2	−7.5	−4.2	−135.9	−7.2	−4.2
39	F	F	−159.7	−8.0	−11.9	−147.8	−7.4	−12.6
40	F	Cl	−155.7	−7.8	−8.2	−149.1	−7.5	−8.0
41	F	Br	−150.7	−7.5	−4.1	−141.7	−7.1	−4.0
42	F	I	−150.4	−7.5	−2.6	−138.4	−6.9	−2.4
43	Cl	F	−153.7	−7.7	−6.7	−145.5	−5.0	−7.3
44	Cl	Cl	−151.3	−7.6	−4.6	−141.3	−7.3	−8.5
45	Cl	Br	−149.9	−7.5	−3.5	−138.4	−6.9	−3.3
46	Cl	I	−150.5	−5.8	−3.1	−139.0	−6.9	−4.1
47	Br	F	−149.5	−7.5	−3.17	−137.2	−6.9	−5.1
48	Br	Cl	−148.0	−7.4	−0.82	−140.0	−7.0	−4.7
49	Br	Br	−148.7	−6.2	−7.4	−137.4	−6.7	−7.3
50	Br	I	−152.7	−7.6	−6.6	−143.3	−7.2	−7.7
51	I	F	−147.1	−5.8	−3.15	−138.4	−5.0	−2.4
52	I	Cl	−147.4	−7.4	−4.9	−129.7	−6.5	0.2
53	I	Br	150.0	−7.5	−7.5	−142.0	−7.4	−14.6
54	I	I	−150.7	−7.5	−6.4	−149.3	−7.5	−7.6
2	F	H	−150.0	−7.9	−7.1	−143.0	−7.5	−7.1
Cele	—	—	−195	−7.5	0.8	−168.4	−6.5	−2.1

Our results demonstrated that the exchange of fluorine for chlorine and the addition of iodine in 52 increased the energy interaction with COX-2 and lowered that of COX-1. Another important feature observed in molecule 2 was the presence of a Ph-F moiety (where F can be exchanged with Cl, Br, and I). Fluorine has been defined as the only halogen that may present electronic repulsion with a carbonyl backbone; thus, its exchange with iodine, bromine or chlorine is an accepted improvement in drug design [13]. On this basis, we proposed compounds (36–53) as new COX-2 selective inhibitors, Energy interaction values (E_total) between the proposed inhibitors and COX isoforms are presented in Table 7. Also the internal energy of ligands (E_internal) – i.e. the energy held by ligand conformation due to the interaction with the target – and the ligand efficiency (LE, the ratio of E_total and number of heavy atoms, excluding hydrogen's, of the ligand) are displayed.

It can be appreciated that celecoxib showed the highest E_total value for COX-2 and COX-1 (Table 7). Nonetheless, LE of celecoxib for COX-2 ranges within the lowest values; this means that it is not the best in terms of efficiency per atom interaction. In addition, its E_internal value is higher than those of some the proposed inhibitors 36, 39, 41, 42, 46, 50, 52, 53, 54 and molecule 2; which implies that celecoxib is less energetically “comfortable” into COX-2 active site than the mentioned proposed inhibitors. We selected the “best proposed inhibitor” based on differences (Δ) between the interaction energies of COX-2 and COX-1 (Eqs. (8)–(10)). According to Table 8, we selected compound 52 because of its value of ΔE_total and ΔLE. Also, compound 52 possessed a negative ΔE_internal, which means that the molecule was more “comfortable” bound to COX-2 than to COX-1.

Δ E_{t o t a l} = E_{t o t a l - C O X - 2} - E_{t o t a l - C O X - 1}

(8)

Δ L E = L E_{- C O X - 2} - L E_{- C O X - 1}

(9)

Δ E_{i n t e r n a l} = E_{i n t e r n a l - C O X - 2} - E_{i n t e r n a l - C O X - 1}

(10)

Molecules	ΔE_total	ΔLE	ΔE_internal
36	−3.7	−0.2	1.5
37	−2.0	−0.1	−0.2
38	−6.3	−0.33	−0.03
39	−11.9	−0.6	0.6
40	−6.7	−0.3	−0.2
41	−8.9	−0.4	−0.1
42	−12.0	−0.6	−0.2
43	−8.2	−0.4	1.6
44	−10.0	−0.5	1.3
45	−11.5	−0.2	−0.6
46	−11.2	−0.6	1.0
47	−12.3	−0.6	1.9
48	−8.0	−0.4	3.9
49	−11.4	−0.6	1.1
50	−9.5	−0.5	1.1
51	−5.2	−0.04	−0.3
52	−17.7	−0.9	−5.1
53	−8.0	−0.4	−5.0
54	−1.4	−0.1	1.2
2	−7.1	−0.4	0.03
Cele	−27.1	−1.0	2.9

The binding of molecule 52 into COX-2 (Fig. 7) showed that its sulfonamide moiety is oriented similarly to that of celecoxib and compound 2 (Fig. S3 and Table S2).

Fig. 7
Binding modes of 52 (black) & celecoxib (green) into COX-2. Celecoxib conformation corresponds to the experimental binding from its complex with COX-2. Conformation of 52 (in black) was the one obtained by molecular docking calculations; iodine is represented in purple and chlorine in orange. The expanded van der Waals surfaces are shown as a grid: purple for 52 and as a blue for celecoxib.

The van der Waals sphere representation of molecule 52, with COX-2 (Fig. 7), depicts that it was able to reach a similar volume to that of celecoxib, occupying the “three interaction points” (i.e. the three key binding pockets: LP, LiP and CC). The exchange of fluorine to iodine and the addition of chlorine (in Y substituent) is inherently related to an increase in $M V o l$ . The increase in affinity (a lower E_total) towards COX-2 of molecule 52 is in accordance with our QSAR model, which defines $M V o l$ as a key descriptor to achieve COX-2 selectivity. Another important feature introduced by the addition of a halogen functionality is a moderate increase in lipophilicity due to the presence of iodine [13], which is also related to COX-2 selectivity [3,4].

The binding mode of molecule 52 into the COX-1 active site (Fig. 8 and Fig. S4) showed that its interactions with Leu531 and Ile523 diminished (3.93 kcal/mol and 1.40 kcal/mol) with respect to those displayed by molecule 2 (Table S3). The van der Waals sphere representation of compound 52, with COX-1, depicted that it possessed a similar volume to that of celecoxib, occupying the three interaction points. The orientation of iodine towards the LP explained why the interaction with Leu531 diminished.

Fig. 8
Binding modes of 52 (black) & celecoxib (green) compounds into COX-1. Celecoxib conformation corresponds to the experimental binding from its complex with COX-1. Conformation of molecule 52 is the one obtained by molecular docking calculations; iodine is represented in purple and chlorine in orange. The expanded van der Waals surfaces are shown as a grid: purple for 52 and blue for celecoxib.

In contrast to COX-2 the binding orientation of molecule 52 with COX-1, showed that chlorine orients and sees the CC, which favored the interaction with Tyr355 and Arg120 (−0.70 and −6.9 kcal/mol).

While the newly proposed inhibitors may be conceived as resveratrol-scaffold based compounds, they differ from it in two key structural aspects: (i) the imine bond instead of an olefin and (ii) the lack of hydroxyl groups bound to the phenyl rings. Recent studies have documented compounds known as Pan Assay Interference Compounds (PAINS) that cannot be considered as good leads or scaffolds for drug design; resveratrol is among them [47]. PAINS may display a variety of biological activities; however, they are not specific or selective to any biological target, rather they display such activities by other mechanisms. Resveratrol is a stilbene that bears hydroxyl groups resembling a polyphenol moiety and displays antioxidant activity, which relies on such groups [48]. The OH groups are bound to the phenyl rings of resveratrol and make it prone to form reactive quinones that may interfere in biological assays; the plethora of biological activities attributed to resveratrol are related to its antioxidant activity [47]. The exchange of hydroxilhydroxyl groups may account to reduce that promiscuity in biological assays and broadens the utilization of stilbene as a drug scaffold [48]. Studies reporting on the synthesis of new compounds based on resveratrol scaffolds suggest that such compounds may be viable in drug design [48,49].

4 Conclusion

According to the COX-2 QSAR model, selective inhibition exhibited by BzSAD is ruled out by the $A L O G P$ term, where an increase in the hydrophobic character of a molecule is disadvantageous to its inhibition. However, the combination of certain lipophilic characters ( $1 < A L O G P > 2$ ) with an appropriate molecular volume ( $283 Å^{3} \leq M V o l \geq 500 Å^{3}$ ) results in a selective COX-2 inhibitor. The COX-1 QSAR model indicates that the presence of HBD determines COX-1 inhibition because of the importance of the formation of HB to Arg120, as anti-inflammatory drugs commonly do. From a theoretical point of view, the presence of iodine and chlorine within molecule 52 increased its selectivity towards COX-2. The binding features of molecule 52 corroborates that a drug based on the selected scaffold represents an important candidate to be considered in the design of new selective COX-2 inhibitors. In addition, the results showed as to how the insertion of halogens within BzSAD scaffold may be a useful approach to improve drug-candidate COX-2 inhibitory properties. We leave the synthesis and biological experiments of the proposed derivatives as a future endeavor.

Acknowledgments

The authors gratefully thank David Neilson for his valuable revisions. D.J.P. and O.S. gratefully acknowledge CONACYT fellowships 229124 and 307323, respectively. R.S.R.H thanks SEP-PRODEP for a postdoctoral scholarship.

Bibliographie

[1] C.A. Rouzer; L.J. Marnett J. Lipid Res., 50 (2009), p. S29

[2] D.L. Simmons; R.M. Botting; T. Hla Pharmacol. Rev., 56 (2004), p. 387

[3] A.L. Blobaum; L.J. Marnett J. Med. Chem., 50 (2007), p. 1425

[4] A.L. Blobaum; M.J. Uddin; A.S. Felts; B.C. Crews; C.A. Rouzer; L.J. Marnett ACS Med. Chem. Lett., 4 (2013)

[5] S.-J. Lin; W.-J. Tsai; W.-F. Chiou; T.-H. Yang; L.-M. Yang Bioorg. Med. Chem., 16 (2008), p. 2697

[6] S. Shukla; K. Bafna; D. Sundar; S.S. Thorat PLoS One, 9 (2013) (e90637)

[7] F. Martínez-Martínez; R. Razo-Hernández; A. Peraza-Campos; M. Villanueva-García; M.T. Sumaya-Martínez; D. Cano; Z. Gómez-Sandoval Molecules, 17 (2012), p. 14882

[8] NeuroShell Predictor Reference Manual, Ward Systems Group, Inc., Frederick, MD, USA, September 2008

[9] Genetic Algorithms in Search, Optimization and Machine Learning (D.E. Goldberg, ed.), Addison-Wesley, Massachusetts, MA, 1989

[10] J.A. Valcarcel; R.S. Razo-Hernández; L.L. Valdez-Velázquez; M.V. García; Á.A. Ramos-Organillo; O.F. Vázquez-Vuelvas; M.A. García Ruiz; Z. Gómez-Sandoval Inorg. Chim. Acta, 392 (2012), p. 229

[11] L.A. Hardegger; B. Kuhn; B. Spinnler; L. Anselm; R. Ecabert; M. Stihle; B. Gsell; R. Thoma; J. Diez; J. Benz; J.-M. Plancher; G. Hartmann; D.W. Banner; W. Haap; F. Diederich Angew. Chem., Int. Ed., 50 (2011), p. 314

[12] R. Wilcken; M. Zimmermann; A. Lange; S. Zahn; F. Boeckler J. Comput.-Aided Mol. Des., 26 (2012), p. 935

[13] R. Wilcken; M.O. Zimmermann; A. Lange; A.C. Joerger; F.M. Boeckler J. Med. Chem., 56 (2013), p. 1363

[14] K. Arvind; K.A. Solomon; S.S. Rajan Med. Chem. Res., 23 (2014), p. 1789

[15] N. Baurin; J.-C. Mozziconacci; E. Arnoult; P. Chavatte; C. Marot; L. Morin-Allory J. Chem. Inf. Comput. Sci., 44 (2004), p. 276

[16] R. Bhatiya; A. Vaidya; S.K. Kashaw; A.K. Jain; R.K. Agrawal J. Saudi Chem. Soc., 18 (2014), p. 977

[17] P. Datar Mod. Chem. Appl., 3 (2015), p. 148

[18] A. Dwivedi; A.K. Srivastava; A. Singh Med. Chem. Res., 23 (2014), p. 1865

[19] A. Dwivedi; A.K. Srivastava; A. Singh Med. Chem. Res., 24 (2015), p. 714

[20] R. Garg; A. Kurup; S.B. Mekapati; C. Hansch Chem. Rev., 103 (2003), p. 703

[21] H.X. Liu; R.S. Zhang; X.J. Yao; M.C. Liu; Z.D. Hu; B.T. Fan J. Comput.-Aided Mol. Des., 18 (2004), p. 389

[22] K. Singh; Monika; N. Verma Int. J. Res. Med. Sci., 2 (2014), p. 612

[23] B.K. Sharma; P. Singh; M. Shekhawat; P. Pilania Eur. J. Med. Chem., 45 (2010), p. 2389

[24] S. Soltani; H. Abolhasani; A. Zarghi; A. Jouyban Eur. J. Med. Chem., 45 (2010), p. 2753

[25] J.J.P. Stewart J. Comput. Chem., 10 (1989), p. 209

[26] WAVEFUNCTION, SPARTAN‘08, 2009, June-24 (Irvine, California, USA)

[27] T. Scior; J.L. Medina-Franco; Q.-T. Do; K. Martínez-Mayorga; J.A. Yunes Rojas; P. Bernard Curr. Med. Chem., 16 (2009), p. 4297

[28] A. Tropsha Mol. Inf., 29 (2010), p. 476

[29] Talete DRAGON for Windows (Software for Molecular Descriptor Calculations), 2006 (Milan, Italy)

[30] D.F.V. Lewis; Y. Ito; B.G. Lake J. Enzyme Inhib. Med. Chem., 25 (2010), p. 679

[31] E. Eroğlu; H. Türkmen; S. Güler; S. Palaz; O. Oltulu Int. J. Mol. Sci., 8 (2007), p. 145

[32] R. Todeschini; D.C. Ballabio; V. Mauri MobyDigs-Version 1.0, 2004 (Milan, Italy)

[33] R. Todeschini; V. Consonni; A. Mauri; M. Pavan Anal. Chim. Acta, 515 (2004), p. 199

[34] M. Baroni; S. Clementi; G. Cruciani; G. Costantino; D. Riganelli; E. Oberrauch J. Chemom., 6 (1992), p. 347

[35] R. Thomsen; M.H. Christensen J. Med. Chem., 49 (2006), p. 3315

[36] G. Rimon; R.S. Sidhu; D.A. Lauver; J.Y. Lee; N.P. Sharma; C. Yuan; R.A. Frieler; R.C. Trievel; B.R. Lucchesi; W.L. Smith Proc. Natl. Acad. Sci. U.S.A., 107 (2010), p. 28

[37] J.L. Wang; D. Limburg; M.J. Graneto; J. Springer; J.R.B. Hamper; S. Liao; J.L. Pawlitz; R.G. Kurumbail; T. Maziasz; J.J. Talley; J.R. Kiefer; J. Carter Bioorg. Med. Chem. Lett., 20 (2010), p. 7159

[38] R.S. Razo-Hernández; K. Pineda-Urbina; M.A. Velazco-Medel; M. Villanueva-García; M.T. Sumaya-Martínez; F.J. Martínez-Martínez; Z. Gómez-Sandoval Cent. Eur. J. Chem. (2014), p. 1

[39] A.K. Ghose; V.N. Viswanadhan; J.J. Wendoloski J. Phys. Chem. A, 102 (1998), p. 3762

[40] B.J. Orlando; M.J. Lucido; M.G. Malkowski J. Struct. Biol., 189 (2014), p. 62

[41] C.A. Lipinski J. Pharmacol. Toxicol. Methods, 44 (2000), p. 235

[42] A.A.M. Abdel-Aziz; K.E.H. ElTahir; Y.A. Asiri Eur. J. Med. Chem., 46 (2011), p. 1648

[43] G.H. Hegazy; H.I. Ali Bioorg. Med. Chem., 20 (2012), p. 1259

[44] A.J. Vecchio; D.M. Simmons; M.G. Malkowski J. Biol. Chem., 285 (2010), p. 22152

[45] M.A.A. El-Sayed; N.I. Abdel-Aziz; A.A.M. Abdel-Aziz; A.S. El-Azab; Y.A. Asiri; K.E.H. ElTahir Bioorg. Med. Chem., 19 (2011), p. 3416

[46] R.S. Sidhu; J.Y. Lee; C. Yuan; W.L. Smith Biochemistry, 49 (2010), p. 7069

[47] J.B. Baell J. Nat. Prod., 79 (2016), p. 616

[48] F.S. Aldawsari; C.A. Velázquez-Martínez Invest. New Drugs, 33 (2015), p. 775

[49] F.S. Aldawsari; O.H. Elshenawy; M.A.M. El Gendy; R. Aguayo-Ortiz; S. Baksh; A.O.S. El-Kadi; C.A. Velázquez-Martínez J. Enzyme Inhib. Med. Chem., 30 (2014), p. 884

Commentaires - Politique

Ces articles pourraient vous intéresser

QSAR of the free radical scavenging potency of selected hydroxybenzoic acids and simple phenolics

Miloš Filipović; Zoran Marković; Jelena Đorović; ...

C. R. Chim (2015)

Molecular docking investigation of cytotoxic phenanthrene derivatives

Habiba Guédouar; Hanane Zaki; Mohammed Bouachrine; ...

C. R. Chim (2020)

Electrocatalytic multicomponent assembling of phthalhydrazide, aldehydes and malononitrile: An efficient approach to 1H-pyrazolo[1,2-b]phthalazine-5,10-diones

Hassan Kefayati; Shadi Homayoon Amlashi; Reyhaneh Kazemi-Rad; ...

C. R. Chim (2014)