1 Introduction
It is well known that α-oxo-ketenes can usually react as 1-oxadienes in the oxa-Diels–Alder (oxa-DA) cycloadditions with inverse electron demand. For example, α-oxo-ketenes can react with ketones or aldehydes to give 1,3-dioxinones [1]. α-Oxo-ketenes can also react as dienophiles in microwave-assisted aza-DA cycloadditions in the presence of 1-aza-dienes [2]. Despite several interesting examples of [2+2] reaction between acylketenes and thiazolines to produce β-lactams [3], α-oxo-ketenes rarely participate in [2+2] cycloadditions.
Pyrazolidinones have shown antibacterial properties and some are effective organocatalysts [4]. In 2011, a microwave-assisted reaction for the stereoselective synthesis of pyrazolidin-3-one C from hydrazone 1 and the α-oxo-ketene 3 was described by Coquerel et al. (Scheme 1) [5]. In this process, a unique reactivity of α-oxo-ketene was reported which acts as a dipolarophile. For this purpose, the initial step involves the formation of azomethine imine 2, as a dipole, from hydrazone 1 with a 1,2-hydrogen shift, followed by a 1,3-dipolar cycloaddition (1,3-DC) reaction with α-oxo-ketene 3, leading to the pyrazolidinone C (see Scheme 1) [5]. In the absence of 1,2-hydrogen shift in hydrazone 1, there are two possible DA reaction pathways. For one pathway, α-oxo-ketene 3 acts as a diene (pathway A, Scheme 2) and in another it would be a dienophile (pathway B, Scheme 3). Herein, as a part of our theoretical and experimental research program on the 1,3-DC reactions [6] and to achieve a deeper insight into α-oxo-ketene reactions, a full theoretical study on the mechanism of this reaction was carried out.
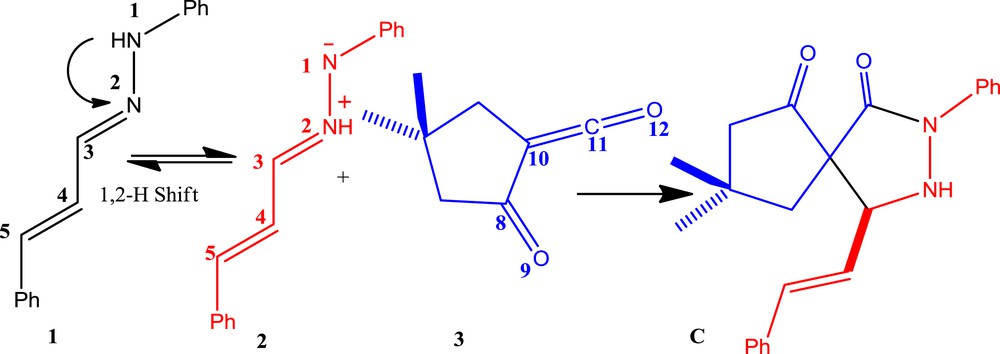
1,3-Dipolar cycloaddition of azomethine imine 2 and α-oxo-ketene 3 [5].
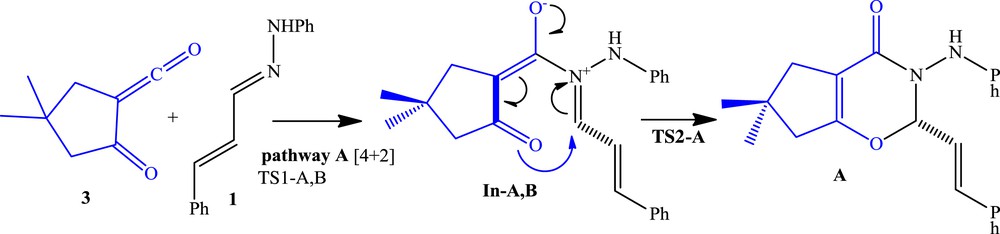
Possible reaction pathway A.
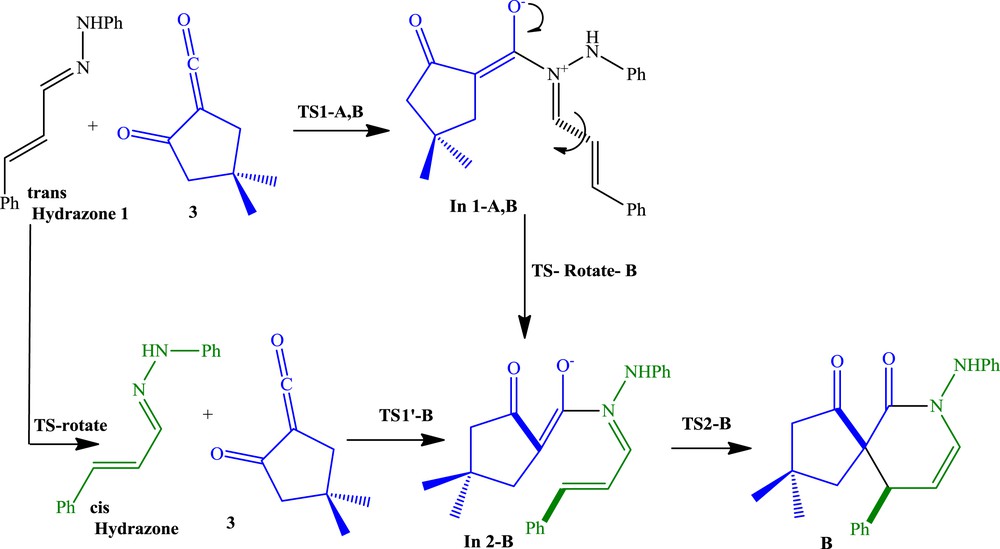
Possible reaction pathways B and B′.
2 Computational details
All calculations were performed at the B3LYP/6-311+G(d,p) and M06-2X/6-31G(d,p) levels as implemented in the Gaussian 09 program package [7]. No symmetrical restriction was applied through geometrical optimizations. The stationary points were confirmed as minima (zero imaginary frequencies) or transition states (one imaginary frequency) by frequency calculations at the same theory levels as the geometry optimizations. The intrinsic reaction coordinate (IRC) calculations were performed to verify each transition state (TS) connecting with the two associated minima of the proposed mechanism [8]. The reported energies are Gibbs free energies, which include zero-point vibrational corrections and thermal and entropy corrections at 298 K. The electron localization function (ELF) study was performed with the TopMod program using the corresponding M06-2X/6-31G(d,p) monodeterminantal wave functions of the selected structures along the IRC curve [9].
3 Results and discussion
In this study, the highest occupied molecular orbital (HOMO)–lowest unoccupied molecular orbital (LUMO) energy gaps suggest that the HOMOazomethine imine (hydrazone)–LUMOα-oxo-ketene interaction controls the cycloaddition reactions. To better imagine the frontier molecular orbital (FMO) approach, two probable interactions for each reaction are shown in Fig. 1.
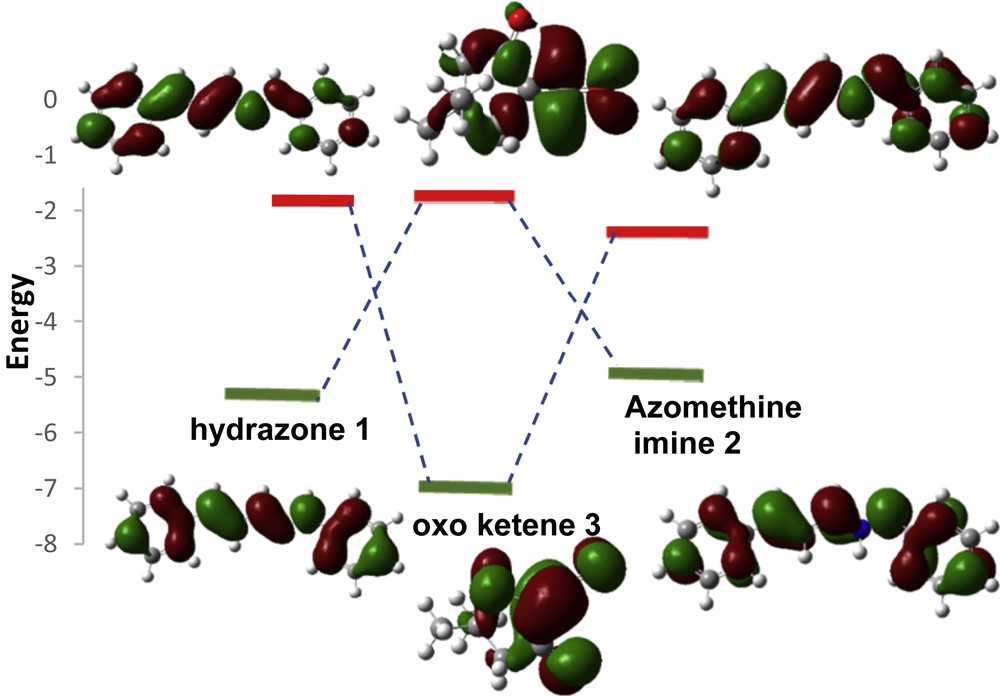
HOMO and LUMO energies of hydrazone 1, azomethine imine 2, and α-oxo-ketene 3 calculated at the B3LYP/6-311+G(d,p) level.
The global electrophilicity index, which measures the total ability to attract electrons, is the ratio ω = μ2/(2η) [10], where μ is the electronic chemical potential and η is the chemical hardness. Both quantities may be approached in terms of the one electron energies of the frontier molecular orbital HOMO and LUMO, EHOMO and ELUMO, μ is defined as the mean value of HOMO and LUMO energies [μ = (EHOMO + ELUMO)/2] and η is the difference between the HOMO and LUMO energies [η = (ELUMO − EHOMO) [11].
In Table 1 global indices, named the electronic chemical potential, chemical hardness, and global electrophilicity index, and Fukui indices are displayed for the reagents. The electronic chemical potentials, μ, of the azomethine imine (−0.135 au) and hydrazone (−0.133 au) at B3LYP/6-311+G(d,p) are higher than those for the α-oxo-ketene (−0.160), which is in agreement with the preferred HOMO–LUMO interactions. The α-oxo-ketene can be considered as a strong electrophile, because it possess a high electrophilicity index at B3LYP (ω = 3.26) [12]. Therefore, the global electron density in these pericyclic reactions will flux from the azomethine imine (hydrazone) toward the α-oxo-ketene. FMO results reveal that the DA pathway A is an inverse electron demand reaction and the DA pathway B and 1,3-DC (pathway C) are normal electron demand reactions. As shown in Table 1, the M06-2X results agree with B3LYP.
The calculated global properties and Fukui indices of hydrazone 1, cis-hydrazone, azomethine imine 2, and α-oxo-ketene 3 at B3LYP/6-311+G(d,p) and M06-2X/6-31G(d,p) levels given in parenthesis.
| Structure | EHOMO (eV) | ELUMO (eV) | μ (au) | η (au) | ω (eV) | S | Site | fk+ | fk− |
| Hydrazone 1 | −5.320 (−6.449) | −1.896 (0.354) | −0.133 (−0.125) | 0.123 (0.224) | 1.96 (0.949) | 4.065 (2.232) | N2 | 0.133 (0.110) | 0.067 (0.044) |
| C3 | 0.002 (0.269) | 0.004 (0.043) | |||||||
| Azomethine imine 2 | −4.950 (−5.660) | −2.384 (−1.143) | −0.135 (−0.125) | 0.094 (0.166) | 2.62 (1.28) | 5.302 (3.012) | N2 | 0.011 (−0.043) | 0.013 (−0.037) |
| N1 | 0.082 (0.070) | 0.126 (0.141) | |||||||
| C3 | 0.032 (0.027) | 0.002 (0.087) | |||||||
| C4 | 0.125 (0.011) | 0.047 (−0.025) | |||||||
| C5 | 0.288 (0.051) | 0.098 (0.068) | |||||||
| α-Oxo-ketene 3 | −6.985 (−8.027) | −1.735 (−0.082) | −0.160 (−0.149) | 0.108 (0.292) | 3.26 (1.03) | 4.645 | C10 | 0.683 (0.013) | 0.169 (0.162) |
| C11 | 0.938 (0.299) | 0.064 (0.147) | |||||||
| C8 | 0.241 (0.045) | 0.031 (0.001) |
The 1,3-DC and DA reactions can take place with two orientations, leading to two regioisomeric adducts. The regioselectivity of these reactions can be predicted with the analysis of the nucleophilic Fukui functions, fk−, at the nucleophile together with the analysis of the local electrophilicity, ωk+, at the electrophile [13–15]. As presented in Table 1, in 1,3-DC reaction, the interaction between N1 at the azomethine imine and C11 at the α-oxo-ketene will be favored, and for DA reactions, local Fukui functions predict the most probable interaction between N2 at the hydrazone and C11 at the α-oxo-ketene. The Fukui functions correctly predict the experimental finding for 1,3-DC.
Recently, Domingo et al. have suggested that the Parr functions are viable to predict the most favorable nucleophilic–electrophilic interaction in polar processes [16]. The electrophilic Parr functions, Pk+, and nucleophilic Parr functions, Pk−, are obtained from atomic spin density (ASD) at the radical anions and the radical cations of the reagents, respectively [16–21]. Fig. 2 shows the ASD maps of the radical anion and the local electrophilic Parr function values and ASD maps of the radical cation and the local nucleophilic Parr function values of azomethine ylide 2 and α-oxo-ketene 3. Analysis of the nucleophilic Parr functions, Pk−, at the azomethine ylide 2 indicates N1 is the most nucleophilic center of this species. On the other hand, the electrophilic Parr functions, Pk+, of α-oxo-ketene 3 revealed that the C11 carbon is the most electrophilic center. Therefore, for the 1,3-DC reaction, the nucleophilic attack of azomethine ylide 2 on α-oxo-ketene 3, the most favorable electrophile–nucleophile interaction will take place between N1 and the C11 in accordance with experiment.
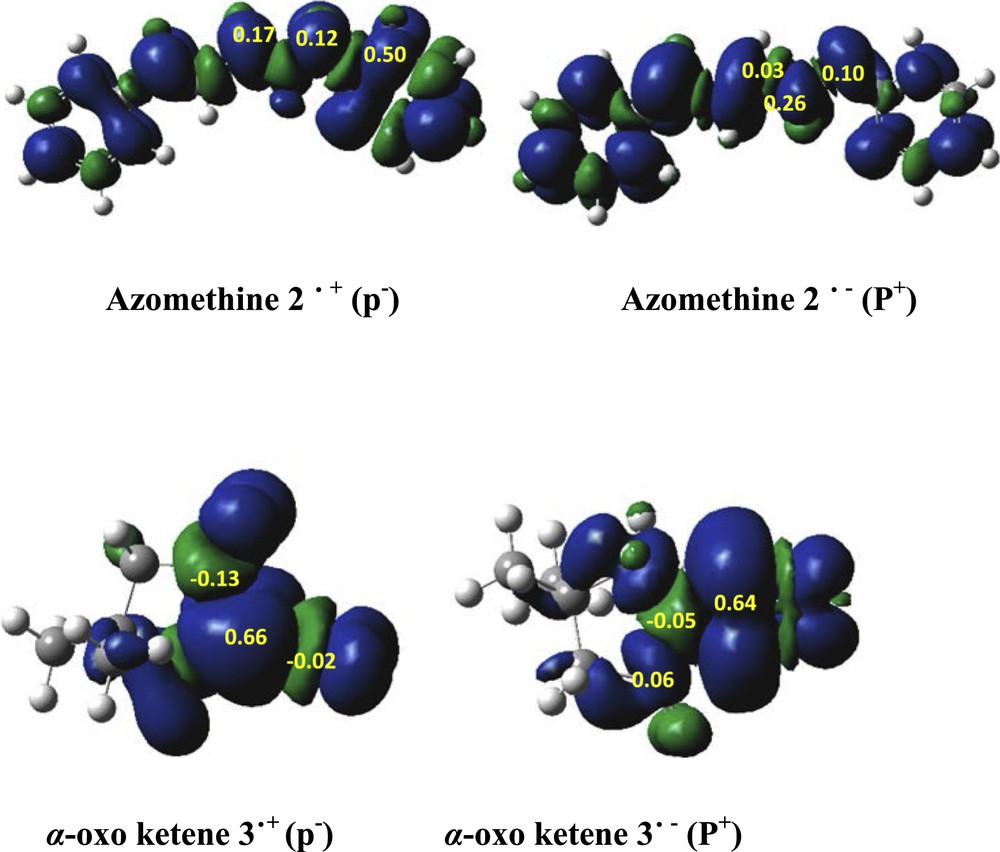
Atomic spin density maps of the radical anion and radical cation, the local electrophilic Parr function values, and the local nucleophilic Parr function values of azomethine ylide 2 and α-oxo-ketene 3 at M06-2X/6-31G(d,p).
We investigated mechanisms of the three possible reaction pathways. The DA pathways are shown in Schemes 2 and 3, respectively. Relative Gibbs free energies (ΔG in kcal/mol) and enthalpies (ΔH in kcal/mol) of TSs, intermediates, and products involved in DA pathways A, B, and B′ are given in Table 2. In pathway A, α-oxo-ketene 3 acts as a diene, whereas in pathway B it acts as a dienophile. The relative free energy and relative enthalpy profiles for the model DA reactions are shown in Figs. 3 and 4. Gibbs free energies are higher than enthalpies because of the undesirable activation entropies associated with two consecutive steps of these reactions.
B3LYP/6-311+G(d,p) and M06-2X/6-31G(d,p) relativea Gibbs free energies (ΔG in kcal/mol) and enthalpies (ΔH in kcal/mol) of TSs, intermediates, and products involved in Diels–Alder pathways A, B, and B′.
| Structure | ΔG | ΔH | ||
| B3LYP | M06-2X | B3LYP | M06-2X | |
| TS1-A,B | 18.7 | 9.2 | 5.4 | −5.2 |
| In-A,B | 16.2 | 4.2 | 1.7 | −11.5 |
| TS2-A | 19.9 | 7.0 | 4.4 | −10.0 |
| A | 6.4 | −17.2 | −8.7 | −31.7 |
| TS-rotate-B | 29.6 | 14.5 | 14.0 | −2.1 |
| In2-B | 28.7 | 11.3 | 14.0 | −5.1 |
| TS2-B | 33.5 | 19.4 | 17.1 | 2.1 |
| B | −0.3 | −29.9 | −17.1 | −47.5 |
| TS-rotate | 9.8 | 9.7 | 9.3 | 8.3 |
| cis-Hydrazone + 3 | 3.3 | 3.6 | 3.1 | 2.9 |
| TS1′-B | 30.3 | 16.4 | 16.5 | 0.2 |
a Relative to reactants 1 and 3.
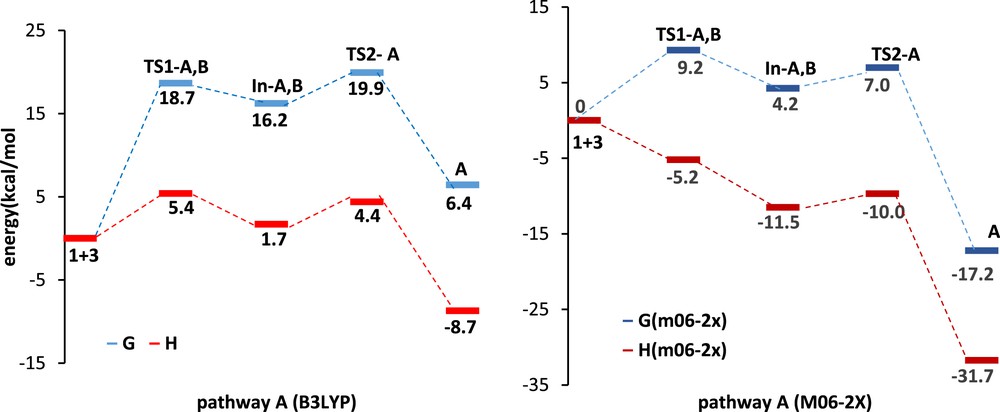
The relative energy and relative enthalpy profiles of Diels–Alder pathways A (kcal/mol).
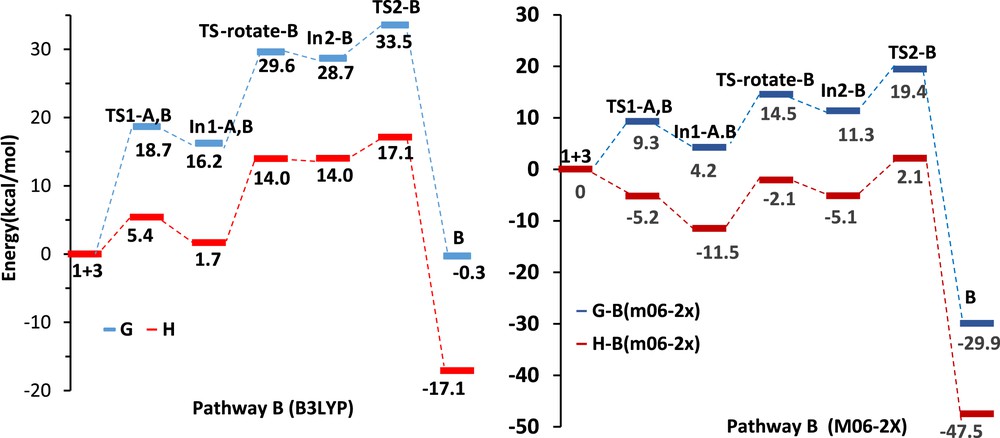
The relative free energy and relative enthalpy profiles of Diels–Alder pathways B (kcal/mol).
In pathway A, s-trans-hydrazone 1 attacks the α-oxo-ketene 3, generating the zwitterion intermediate In-A,B. Then the CO bond formation from In-A,B generates the product A (Scheme 2 and Fig. 3). It can be seen that the activation barrier for the nucleophilic attack of the nitrogen of hydrazone on the carbonyl group of the α-oxo-ketene is higher than the ring formation in the stepwise DA pathway A. Therefore, the first step is the rate-determining step in the model reaction A. The activation free energy associated with this step via TS1-A at B3LYP/6-311+G(d,p) level is 18.7 kcal/mol; formation of corresponding intermediate In-A,B is endergonic by 16.2 kcal/mol. The energy barrier for ring formation from In-A,B is 3.7 kcal/mol via TS2-A, and this step has been found to be exergonic by 9.8 kcal/mol. The B3LYP energies predict an endergonic overall reaction (ΔG = 6.4 kcal/mol) for pathway A and low stability of the intermediate with respect to the reactants. This is also consistent with the experimental observation that only 1,3-DC product is formed in the reaction (Table 2 and Fig. 3).
It is well known that the stabilization gained by π–π interactions are not well treated by density functional theory (DFT) calculations [22]. One strategy to overcome this deficiency is to augment the conventional density functionals with ad hoc addition of nonbonded pairwise interaction semiempirically by a large number of free parameters in the functional. M06 functional is parameterized for “medium-range” electron correlation [23]. This has encouraged us to perform studies on the mechanism of these cycloaddition reactions at M06-2X. Therefore, the geometries of the reactants, TS, intermediates, and products of the three possible reactions were also optimized at M06-2X method using 6-31G(d,p) basis set.
For pathway A, the activation free energy associated with the first step via TS1-A at M06-2X/6-31G(d,p) level is 9.2 kcal/mol; formation of corresponding intermediate In-A,B is endergonic by 4.2 kcal/mol. The energy barrier for ring formation from In-A,B is 2.8 kcal/mol via TS2-A, and this step has been found to be exergonic by 13.0 kcal/mol. Finally, overall reaction is exergonic by 17.2 kcal/mol (Table 2 and Fig. 3).
The first step of the pathway B is similar to pathway A, although intermediate In-A,B requires rotation around the CC bond to form a cis-double bond (shown in Scheme 3). Therefore, the first activation barrier at B3LYP/6-311+G(d,p) level, similar to pathway A, is 18.7 kcal/mol and the following step, rotation around the CC bond, proceeds with typical activation energy of about 13.4 kcal/mol to form less stable In2-B (12.5 kcal/mol less stable than In 1-A,B) (Table 2 and Fig. 4).
As shown in Fig. 4, the first step activation barrier of pathway B at M06-2X/6-31G(d,p) level is 9.3 kcal/mol, and this step has been found to be endergonic by 4.2 kcal/mol and the following step, rotation around the CC bond, proceeds with activation energy of about 10.3 kcal/mol to form In2-B and this step is endergonic by 7.1 kcal/mol. Analysis of the free energy profiles of pathway B in Fig. 4 indicates that the M06-2X activation barrier for the first step is half of B3LYP/6-311+G(d,p) result, whereas for rotating step, it is 3.1 kcal/mol lower than the later. Therefore, the rate determining step has changed from the first step, the nucleophilic attack of the nitrogen of hydrazone on the carbonyl group of the α-oxo-ketene, at B3LYP/6-311+G(d,p) level results to rotating step at M06-2X/6-31G(d,p) level (Table 2). The relative energy of In2-B at M06-2X/6-31G(d,p) level is 17.4 kcal/mol lower than that at B3LYP/6-311+G(d,p) level. Finally, the activation barrier of ring formation is 8.1 kcal/mol at M06-2X/6-31G(d,p) level versus 4.8 kcal/mol at B3LYP/6-311+G(d,p) level, and this step is exergonic by 18.6 kcal/mol at M06-2X/6-31G(d,p) level, whereas it is endergonic by 8.1 kcal/mol at B3LYP/6-311+G(d,p) level (Table 2 and Fig. 4).
At the B3LYP/6-311+G(d,p) level, the enthalpy associated with the nucleophilic attack of hydrazone on the central carbon atom of α-oxo-ketene is 1.7 kcal/mol; rotation around the CC single bond is 12.3 kcal/mol and formation of the compound B from intermediate In2-B is −31.3 kcal/mol. The overall reaction is exothermic by 17.1 kcal/mol (Table 2). However, at M06-2X/6-31G(d,p) level, the enthalpies associated with three steps of pathway B are −11.5, 3.1, and −42.5 kcal/mol, respectively, and the overall reaction is exothermic by 47.5 kcal/mol (Table 2 and Fig. 4).
In2-B can be also formed through rotation around the CC bond in the former hydrazone 1 (Scheme 3, pathway B′). Rotation around single bonds of the s-trans-hydrazone 1 leads to s-cis-hydrazone with an activation barrier 9.8 kcal/mol at B3LYP/6-311+G(d,p) level and 9.7 kcal/mol at M06-2X/6-31G(d,p) level, whereas the s-cis conformer is less stable of about 3–4 kcal/mol than s-trans (Fig. 5 and Table 2). The first step of DA pathway B′ has been found 25.6 kcal/mol endergonic with an energy barrier of 27.2 kcal/mol at B3LYP/6-311+G(d,p) level and 7.7 kcal/mol endergonic with an energy barrier of 12.8 kcal/mol at M06-2X/6-31G(d,p) level. The energy barrier of ring-forming process at B3LYP/6-311+G(d,p) level is 4.8 kcal/mol, and the process is exergonic by 29.0 kcal/mol relative to the In2-B and 0.3 kcal/mol relative to the isolated reactants. At M06-2X/6-31G(d,p) level, the energy barrier of ring-forming process is 8.1 kcal/mol, and the process is exergonic by 18.6 kcal/mol relative to the In2-B and 29.9 kcal/mol relative to the isolated reactants (Table 2 and Fig. 5). In the pathway B′, attack of the s-cis-hydrazone to the α-oxo-ketene 3 is rate determining step.
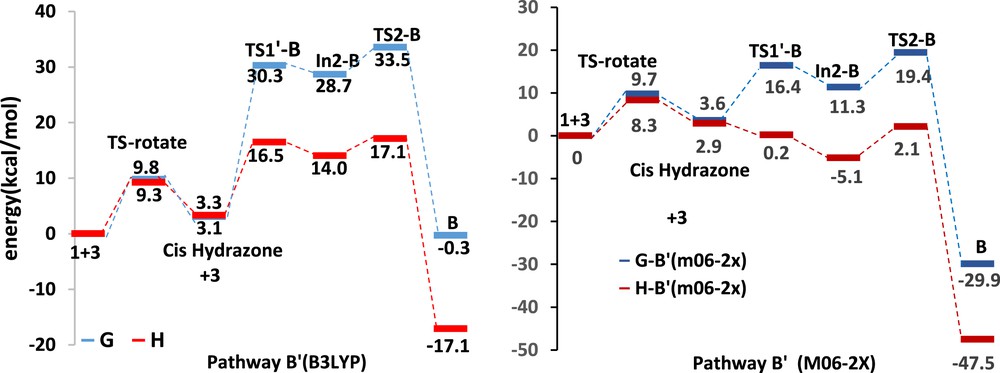
The relative free energy and relative enthalpy profiles of Diels–Alder pathways B′ (kcal/mol).
Our calculations at B3LYP/6-311+G(d,p) and M06-2X/6-31G(d,p) levels show that B is more stable than A and the activation energy of rate-determining step of pathway B′ is higher than pathways A and B. On the other hand, formation of B is more exothermic than A. Despite the fact that the pathway B requires more rotation energy, it seems more favorable than B′. The B3LYP/6-311+G(d,p) geometries of the TSs corresponding to the pathways A, B, and B′ are shown in Fig. 6.
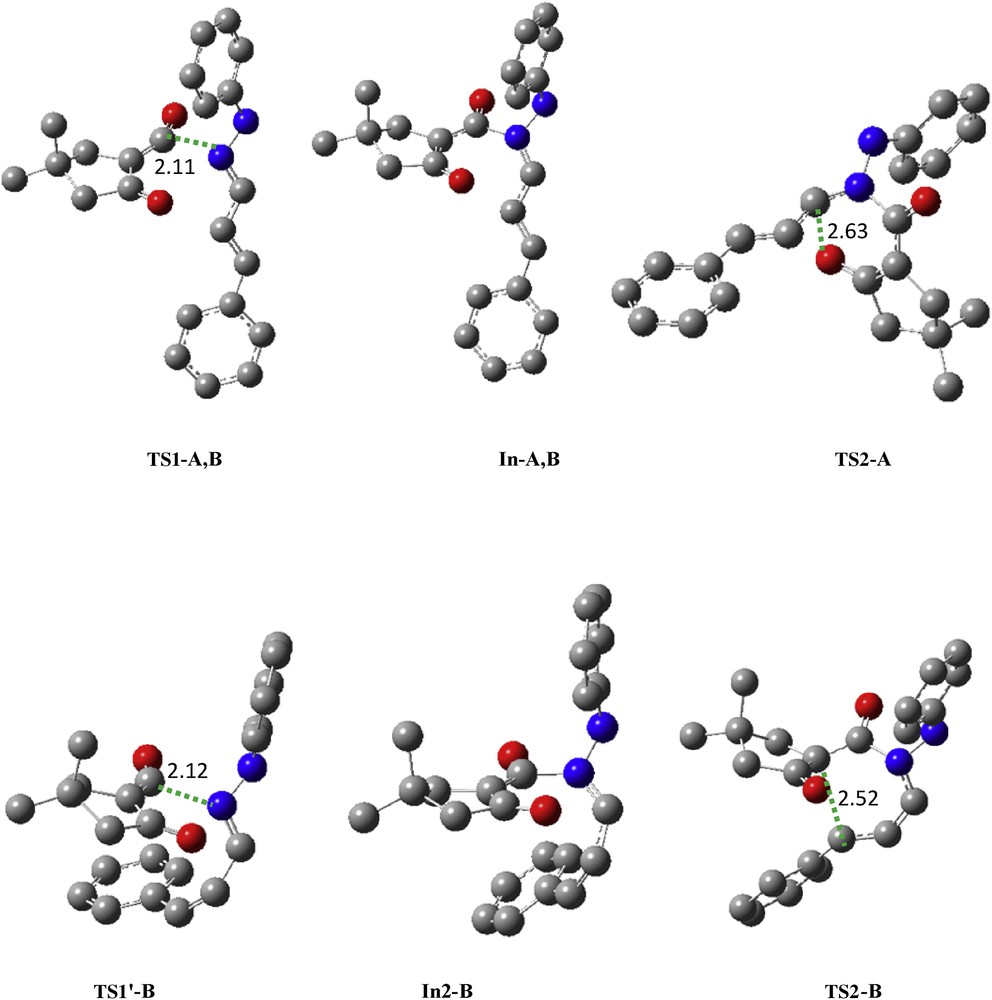
Transition structures corresponding to the pathways B and B′ at B3LYP/6-311+G(d,p) level. The bond lengths directly involved in the reaction are given in angstroms. Hydrogen atoms have been omitted for clarity.
The calculated activation enthalpies associated with the nucleophilic attack steps, in all possible pathways, with respect to the sum of the enthalpies of the separated reagents are negative at M06-2X (Figs. 3–5 and 7). It is well known that a van der Waals precomplex which is energetically more stable than the separated reactants, is formed at an appropriate distance between reactants. Then this precomplex, instead of separated reactants, involves in the TS formation [24].
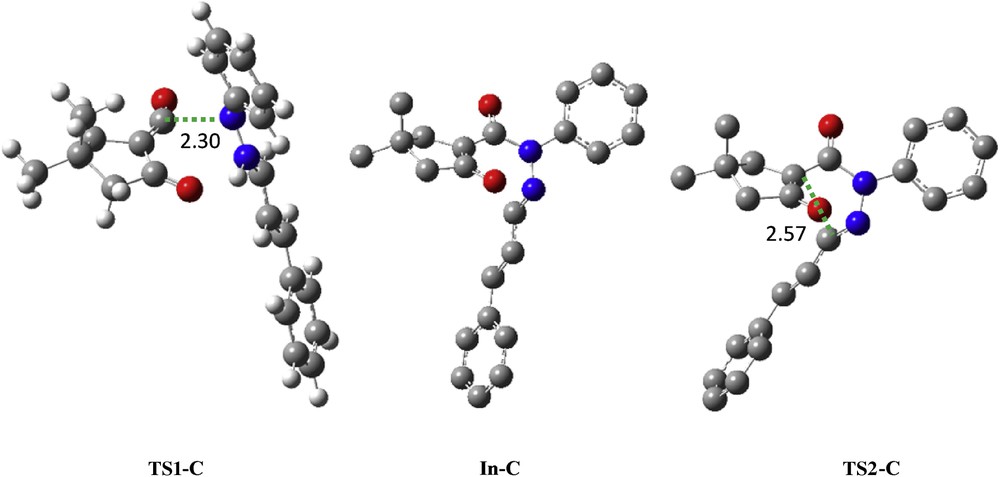
Transition structures corresponding to the pathway C. The bond lengths directly involved in the reaction are given in angstroms. Hydrogen atoms have been omitted for clarity.
In pathway C, the azomethine imine 2 is accessible from hydrazone 1, by migration of a proton from N1 to N2, in a so-called 1,2-prototropic shift (Scheme 4). The barriers for intramolecular 1,2-hydrogen transfer in all the reactions are found to be very large [25]. As expected, the barrier to intramolecular 1,2-hydrogen shift in hydrazone 1 is too large (58.1 and 60.1 kcal/mol at B3LYP and M06-2X, respectively). It is known that singlet carbenes such as dialkylcarbene, alkylchlorocarbene, and benzylchlorocarbene undergo intramolecular 1,2-sigmatropic hydrogen shifts [26–37]. Recently, Karmakar and Datta [38] have shown that at room temperature, 1,2-hydrogen-transfer reactions of N-heterocyclic carbenes occur almost entirely (>90%) by quantum mechanical tunneling (QMT). From the experimental results of temperature and isotope effects, it was shown that the 1,2-sigmatropic hydrogen shift in the photorearranged intermediate of N-acetylpyrrole also proceeds via QMT processes under experimental conditions [39]. The theoretical considerations for the tunneling mechanism have been described by Formosinho and co-workers [40–45].
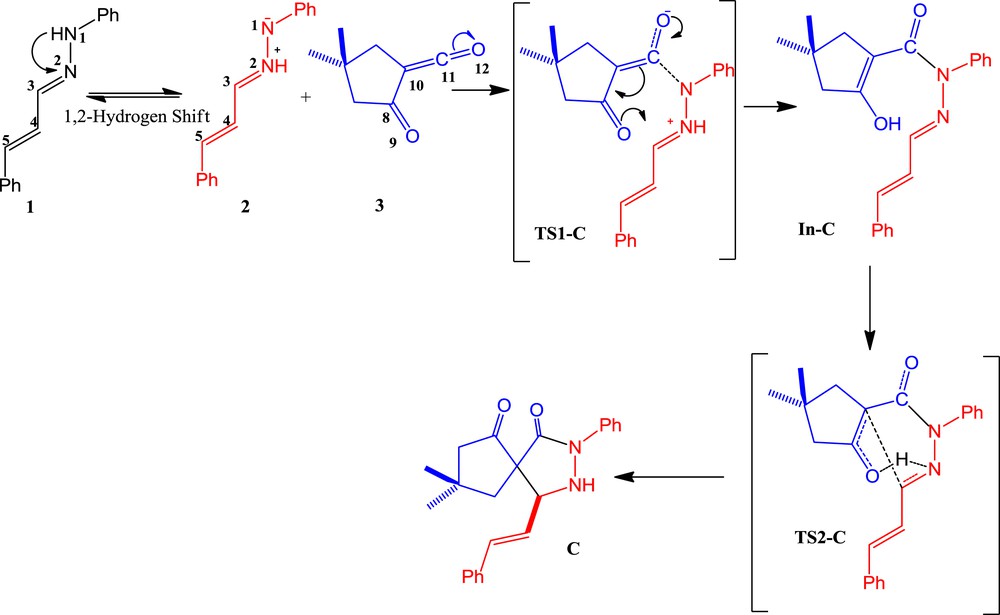
Reaction pathway C.
It is interesting here that the 1,3-DC reaction is favored over the DA pathways, in spite of the high-energy barrier for 1,2-sigmatropic hydrogen shift. This suggests that 1,2-sigmatropic hydrogen shift in hydrazone 1 probably proceeds via the QMT in the electronically ground state. Because the tunneling effect decreases the barrier of the reaction in comparison with the classical path, this mechanism can be verified experimentally from reaction kinetics.
An analysis of the gas-phase results for the reaction between the azomethine imine 2 and α-oxo-ketene 3 shows that the 1,3-DC reaction takes place by a stepwise process. Therefore, two TSs, TS1-C and TS2-C, an intermediate In-C, and the corresponding [3+2] cycloadduct C were located and characterized. The different stationary points of this cycloaddition are depicted in Scheme 4 together with the atom numbering, whereas the geometries of the TSs and intermediate are presented in Fig. 7. Relative Gibbs free energies (ΔG in kcal/mol) and enthalpies (ΔH in kcal/mol) of TSs, intermediate, and product involved in 1,3-DC pathway C are reported in Table 3.
B3LYP/6-311+G(d,p) and M06-2X/6-31G(d,p) relativea Gibbs free energies (ΔG in kcal/mol) and enthalpies (ΔH in kcal/mol) of TSs, intermediate, and product involved in 1,3-DC pathway C.
| Structure | ΔG | ΔH | ||
| B3LYP | M06-2X | B3LYP | M06-2X | |
| TS1-C | 14.9 | 4.6 | 1.6 | −8.7 |
| In-C | −6.0 | −26.1 | −20.6 | −40.1 |
| TS2-C | 9.8 | −9.2 | −6.2 | −24.7 |
| C | 16.1 | −44.6 | −31.7 | −60.6 |
a Relative to reactants 2 and 3.
The global electron-density transfer [46] was computed for TS1-C and TS2-C by the natural bond orbital [47] analysis between the nucleophilic and electrophilic frameworks. At TS1-C and TS2-C, the global electron-density transfer that fluxes from the azomethine imine 2 framework toward α-oxo-ketenes 3 is 0.12e and 0.41e, respectively. This behavior agrees with the analysis of the global reactivity indices and preferred HOMO–LUMO interactions.
Fig. 8 shows the enthalpy and Gibbs free energy profiles of 1,3-DC reaction of azomethine imine 2 with α-oxo-ketene 3 at B3LYP/6-311+G(d,p) and M06-2X/6-31G(d,p) levels. The first step involves a carbon–nitrogen bond formation leading to the intermediate In-C. At B3LYP/6-311+G(d,p) and M06-2X/6-31G(d,p) levels, this step has a barrier of 14.9 and 4.6 kcal/mol and is exergonic by 6.0 and 26.1 kcal/mol, respectively. The formation of the final five-membered ring from In-C, occurring through TS2-C, has 15.8 and 16.9 kcal/mol barrier, and the reaction is exergonic by 10.1 and 18.5 kcal/mol at B3LYP/6-311+G(d,p) and M06-2X/6-31G(d,p) levels, respectively (Table 3). The overall 1,3-DC reaction leading to final product C, starting from azomethine imine 2 and α-oxo-ketene 3, is exergonic by as much as 16.1 kcal/mol at B3LYP/6-311+G(d,p) level and 44.6 kcal/mol at M06-2X/6-31G(d,p) level.
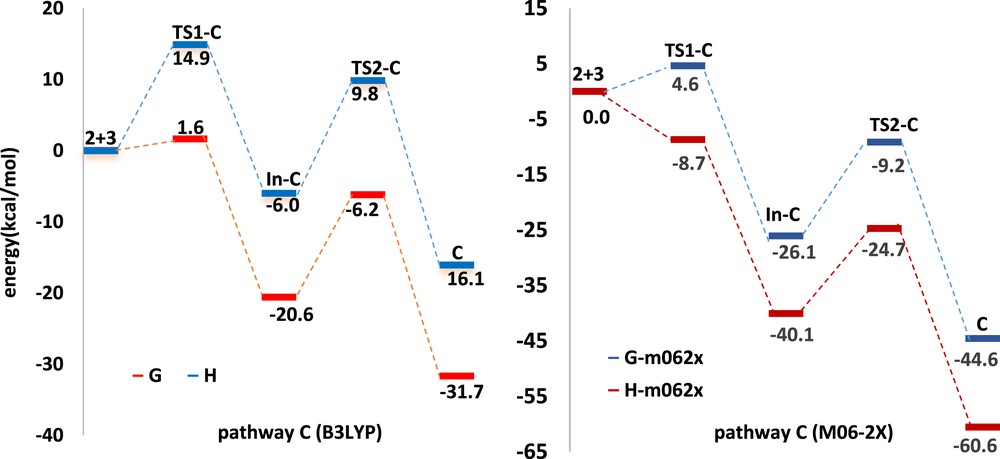
Calculated free energy and enthalpy profile for the reaction mechanism of azomethine imine 2 and α-oxo-ketene 3 (pathway C).
The activation enthalpy associated with nucleophilic attack of azomethine imine 2 on the C1 of α-oxo-ketene via TS1-C at B3LYP/6-311+G(d,p) level is very low (1.6 kcal/mol) and formation of the intermediate In-C is exothermic by 20.6 kcal/mol. From intermediate In-C, formation of spiro compound C via TS2-C presents activation enthalpy, 14.4 kcal/mol, and this step is exothermic by 11.1 kcal/mol (Table 3). The overall 1,3-DC reaction is actually exothermic by 31.7 kcal/mol. At M06-2X/6-31G(d,p) level, the formations of the intermediate In-C and spiro compound C are exothermic by 40.1 and 20.5 kcal/mol, respectively (Fig. 8). The overall 1,3-DC reaction is strongly exothermic by 60.6 kcal/mol, which agrees with B3LYP results.
As shown in Fig. 8, the second step of cycloaddition reaction (formation of the pyrazolidinone C from In-C) is the rate-determining step. Considering the lowest barrier according to the B3LYP/6-311+G(d,p) (15.8 kcal/mol) and the most stable intermediate and product among all the other possible structures, pathway C is the most favorable pathway in accordance with the experimental observation that only C is formed in the reaction. It seems that the M06-2X/6-31G(d,p) level overestimates the stability of intermediates and products (Table 3 and Fig. 8). Therefore, despite highly negative reaction free energies, it estimates that 1,3-DC reaction has the highest activation barrier of rate-determining step.
3.1 ELF topological analysis of the mechanism of the 1,3-DC reaction of azomethine imine 2 with α-oxo-ketene 3
The ELF is a powerful tool to investigate the bonding changes along an organic reaction [48]. In this section, an ELF topological analysis of the M06-2X/6-31G(d,p) wave functions of the structures involved in the IRC curves of the stepwise 1,3-DC reaction of azomethine imine 2 with α-oxo-ketene 3 was performed to characterize the electronic aspects of this 1,3-DC reaction in more detail. Schematic representation of ELF attractors of selected points of IRC path of the 1,3-DC reaction is shown in Fig. 9. Valence basin populations of the most relevant valence basins calculated from the ELF of the 1,3-DC reaction are listed in Table 4.
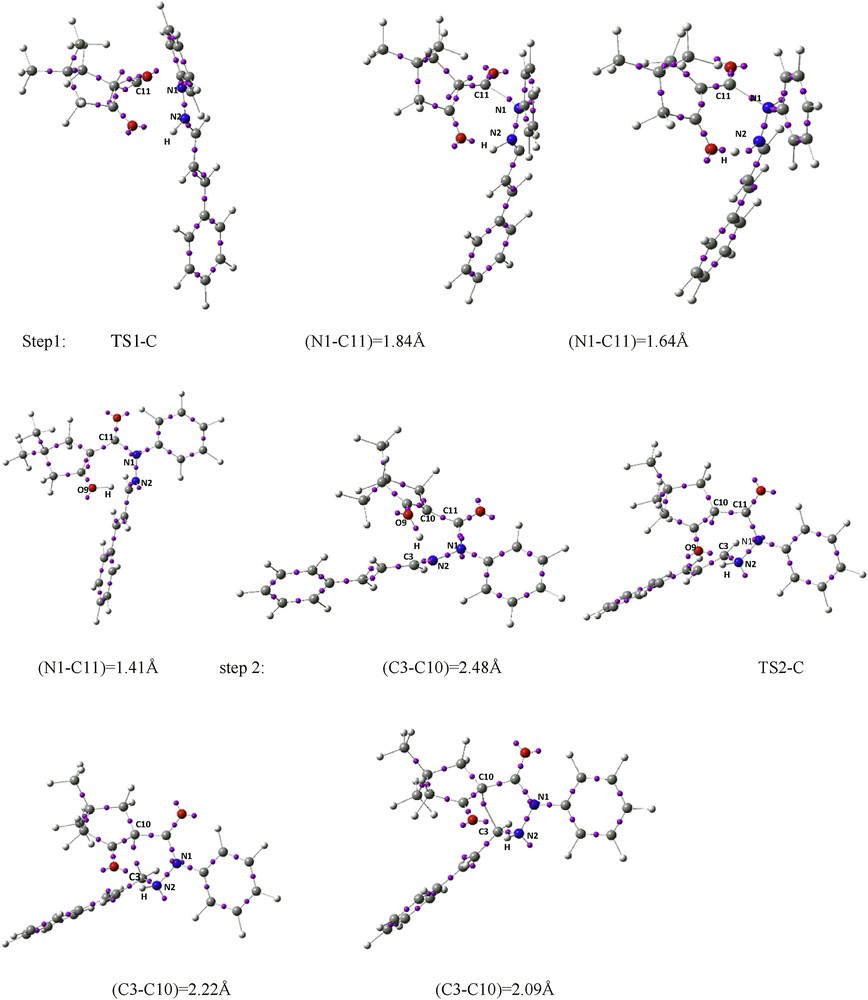
Schematic representation of ELF attractors of selected points of IRC path of 1,3-DC reaction of azomethine imine 2 and α-oxo-ketene 3.
Valence basin populations of the most relevant valence basins calculated from the ELF of the 1,3-DC reaction of azomethine imine 2 and α-oxo-ketene 3.
| Step (I) | Step (II) | ||||||||||
| N1–C11 (Å) | C3–C10 (Å) | ||||||||||
| Basins | 2+3 | TS1-C | 1.98 | 1.84 | 1.64 | 1.60 | In-C | 2.48 | TS2-C | 2.22 | 2.09 |
| V(O12) | 2.35 | 4.76 | 4.94 | 2.96 | 2.53 | 2.63 | 2.67 | 2.68 | 2.68 | 2.68 | 2.71 |
| 2.34 | 2.11 | 2.66 | 2.55 | 2.70 | 2.70 | 2.70 | 2.70 | 2.65 | |||
| V(C11,O12) | 1.51 | 2.89 | 2.71 | 2.55 | 2.48 | 2.50 | 2.34 | 2.34 | 2.33 | 2.34 | 2.35 |
| 1.40 | |||||||||||
| V(C11) | – | – | 0.18 | – | – | – | – | – | – | – | – |
| V(N1,C11) | – | – | – | 1.39 | 1.66 | 1.69 | 1.86 | 1.87 | 1.82 | 1.86 | 1.91 |
| V(C10,C11) | 1.69 | 1.63 | 2.93 | 2.79 | 2.53 | 2.46 | 2.30 | 2.30 | 2.32 | 2.27 | 2.23 |
| 1.65 | 1.50 | ||||||||||
| V(C10) | 0.36 | 0.39 | 0.42 | 0.41 | – | – | – | – | 0.65 | 0.82 | – |
| 0.39 | 0.50 | 0.50 | 0.47 | ||||||||
| V(C3) | 0.19 | – | – | – | – | – | – | – | – | 0.26 | – |
| V(C3,C10) | – | – | – | – | – | – | – | – | – | – | 1.29 |
| V(C10,C8) | 2.13 | 2.33 | 2.54 | 2.54 | 3.57 | 3.46 | 1.72 | 3.63 | 2.82 | 2.49 | 2.36 |
| 2.03 | |||||||||||
| V(C8,C9) | 2.41 | 2.25 | 2.15 | 2.08 | 1.83 | 1.68 | 1.56 | 1.69 | 1.95 | 2.17 | 2.24 |
| V(H) | – | – | – | – | 0.35 | – | – | 0.47 | – | – | – |
| V(O9,H) | – | – | – | – | – | 1.92 | 1.80 | – | – | – | – |
| V(O9) | 2.69 | 2.78 | 2.89 | 3.00 | 3.98 | 4.18 | 4.38 | 4.47 | 3.09 | 2.93 | 2.77 |
| 2.64 | 2.62 | 2.58 | 2.53 | 1.69 | 1.17 | 2.51 | 2.69 | 2.61 | |||
| V(N1) | 3.39 | 3.48 | 3.50 | 2.45 | 2.27 | 1.86 | 0.99 | 1.04 | 1.08 | 1.08 | |
| 2.70 | 1.35 | 1.41 | 1.34 | 1.28 | |||||||
| V(N1,N2) | 1.85 | 1.72 | 1.62 | 1.58 | 1.46 | 1.41 | 1.41 | 1.37 | 1.36 | 1.87 | 1.34 |
| V(N2,H) | 2.19 | 2.25 | 2.30 | 2.36 | – | – | – | – | 2.01 | 2.07 | 2.07 |
| V(N2,C3) | 3.32 | 3.61 | 3.59 | 3.55 | 3.00 | 3.00 | 2.94 | 2.67 | 2.41 | 2.09 | 1.97 |
| V(N2) | – | – | – | 2.72 | 2.82 | 2.90 | 3.18 | 1.80 | 1.97 | 2.07 |
The analysis of the gradient field of ELF for TS1-C reveals that there are not disynaptic basins associated with the region of N1–C11 forming bond. A monosynaptic basin emerges with a population of 0.18e after TS1-C at a N–C distance of 1.98 Å, and it is associated with the C11 center (Fig. 8b). However, at a N–C distance of 1.84 Å, the population associated with disynaptic V(C10,C11) and V(C11,O12) basins decreases slightly, whereas the V(N1,C11) basin emerges with a populations of 1.39e. Interestingly, at a N–C distance of 1.64 Å, one monosynaptic attractor appears on the hydrogen atom of NH with a population of 0.35e, whereas disynaptic V(N,H) basin decays and the population associated with the V(C8,C10) basin increases and V(C10,C11) basin decreases. Then, a disynaptic V(O9,H) basin is observed with the populations of 1.92e at the NC, OH, and NH distances of 1.60, 1.01, and 1.51 Å, respectively. In other words, after passing TS1-C, at first N1–C11 bond formation takes place and then hydrogen atom of NH of azomethine imine migrates to O9 in α-oxo-ketene 3, which leads to the enol intermediate In-C. The basin populations associated with the V(C8,C10), V′(C8,C10), V(C8,O9), and V(O9,H) regions for In-C are 2.03, 1.72, 1.56, and 1.80e, respectively (Fig. 9).
Remarkably, the ELF topological analysis of the second step of pathway C, ring-forming process from In-C, shows that before TS-C disynaptic V(O9,H) basin decays and a monosynaptic V(H) basin appears (0.47e) at the C3–C10, O9H, and N2H distances of 2.48, 1.09, and 1.40 Å, respectively. The unique relevant change found at the ELF of TS2-C is regeneration of a disynaptic V(N2,H) attractor with a population of 2.01e, whereas the populations associated with the V(C8,C10) and V(N2) basins decrease and V(C8,O9) basin increases. The creation of two pseudoradical centers characterized by the presence of V(C3) and V(C10) monosynaptic basins takes place at a C3–C10 distance of 2.22 Å with decreasing V(C3,N2) basin population. Finally, spiro compound 3 is generated by merging V(C3) and V(C10) monosynaptic basins into a V(C3,C10) disynaptic basin with a population of 1.29e at a C3–C10 distance of 2.09 Å (Fig. 9).
4 Conclusions
The molecular mechanisms of the probable reactions of α-oxo-ketene 3 with hydrazone 1, experimentally studied by Coquerel et al. [5], have been investigated using DFT methods at the B3LYP/6-311+G(d,p) and M06-2X/6-31G(d,p) computational levels. Three possible reaction pathways have been studied including two DA pathways, A and B and a 1,3-DC pathway C. Mechanisms of the reactions have been studied in terms of global and local reactivity indices and characterization of relevant TS. In addition, a DFT method evaluation at the cycloaddition reaction studies was carried out. Analysis of the nucleophilic Parr functions Pk−, at the azomethine ylide 2 and electrophilic Parr functions, Pk+, at α-oxo-ketene 3 indicates that N1 is the most nucleophilic center and C11 represents the most electrophilic center of these species, respectively, which is in clear agreement with the observed regioselectivity.
The first step of the model reactions A and B, nucleophilic attack of hydrazone on the central carbon atom of α-oxo-ketene, is the rate-determining step at B3LYP/6-311+G(d,p) level. However, the rate-determining step of pathway B has changed from the first step to second step rotating along the C3–C4 single bond at M06-2X/6-31G(d,p) level. In the case of 1,3-DC reaction pathway, ignoring the initial 1,2-hydrogen shift step in hydrazone 1 to form azomethine imine 2, formation of pyrazolidinone C from In-C involves the rate-determining step at both levels of theory. Thermodynamic calculations indicate that reaction pathway C is most energy favorable among the three reaction pathways; hence, it should be the main reaction channel, which agrees with the experimental results. To clarify interesting points about the molecular mechanism of 1,3-DC reaction, the ELF analysis was performed. In this way, the details of hydrogen transfer and electron delocalization within the pathway C have been characterized.
Acknowledgments
The author acknowledges the University of Jouybar for financial support of this research.


