1 Introduction générale
La production d'énergie durable, combinée à des pratiques de consommation modérées, représentent un défi pour notre civilisation [1–8]. Au cours de cette dernière décennie, l'augmentation continue de la demande énergétique mondiale et la prise de conscience collective de la problématique du réchauffement climatique ont conduit à un fort développement des moyens de production d'énergie électrique à partir de sources renouvelables. Cette évolution est amenée à se poursuivre pendant la décennie à venir, notamment dans l'Union européenne (Fig. 1), qui s'est fixé pour objectif d'atteindre une part des énergies renouvelables dans le mix énergétique européen de 20%, soit une part d'environ 35% de la production d'électricité [9]. À l'horizon 2050, les scénarios envisagés par les différents organismes du secteur énergétique prévoient un pourcentage de sources renouvelables dans le mix énergétique, français et européen, compris entre 40 et 75% [10].
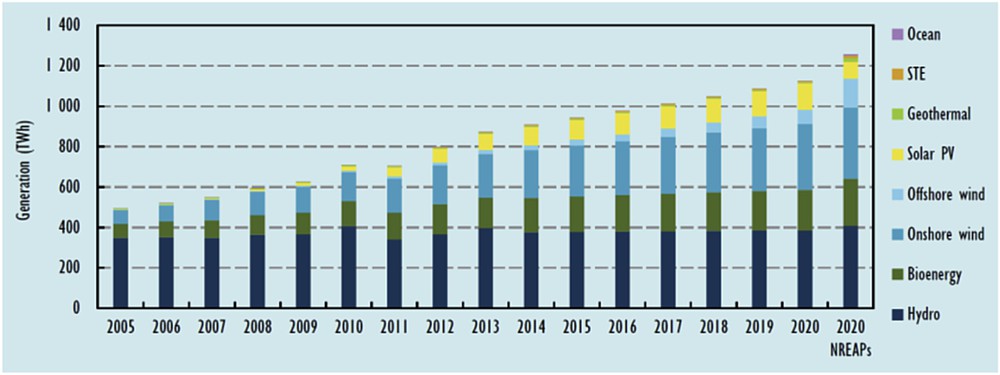
Évolution de la production d'électricité à partir de sources renouvelables dans l'Union européenne de 2005 à 2013 et prévisions de l'Agence internationale de l'énergie (AIE) et de la Commission européenne (NREAPs : National Renewable Energy Action Plans) [9].
Cette intégration massive de sources d'énergie renouvelables dans le paysage énergétique se heurte toutefois à la problématique de la gestion des réseaux électriques. La nature intermittente et localisée de la plupart de celles-ci, notamment de l'éolien et du solaire, compliquent à tout instant l'équilibrage de ces réseaux, entre la production et la demande en énergie électrique. Afin de permettre cette intégration, les gestionnaires recherchent des solutions permettant une gestion flexible des réseaux électriques comme la modulation de la demande, l'optimisation de l'exploitation, et, en particulier, des moyens de stockage de très grande capacité.
Les besoins futurs de stockage d'énergie électrique pourront ainsi atteindre des capacités de plusieurs TWh et des durées de stockage de plusieurs jours à plusieurs dizaines de jours, correspondant à des périodes d'excès de productions prolongées (Fig. 2). Les moyens de stockage actuels, dont notamment le pompage-turbinage hydraulique, moyen de stockage le plus massif disponible, ne permettent de stocker que des quantités limitées d'énergie et répondent à des besoins qui s'étendent sur de courtes durées, quelques jours tout au plus. Ces technologies en place aujourd'hui ne suffiront donc pas à couvrir les besoins de stockage à l'horizon 2030, et une augmentation de leur capacité ne pourra être que limitée dans les pays développés du fait des contraintes géographiques et sociétales de certains d'entre eux.
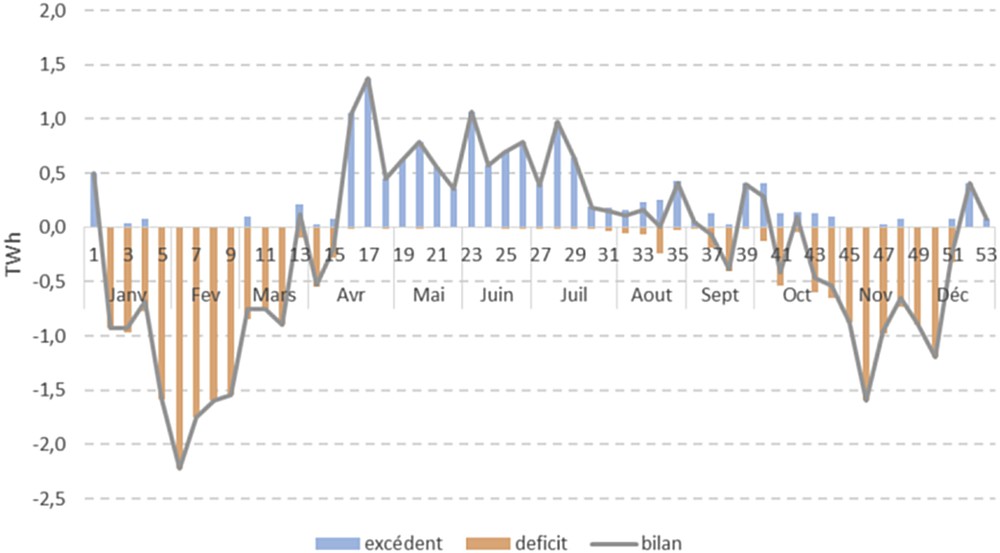
Excédents et déficits de la production électrique hebdomadaire française en 2030, d'après les prévisions de l'Ademe [10].
Depuis quelques années, l'idée d'un moyen de stockage alternatif aux technologies traditionnelles a émergé et propose d'utiliser les énergies entrant en jeux lors de transformations chimiques. Ce moyen de stockage, appelé power to gas, propose ainsi de convertir l'énergie électrique en gaz, hydrogène ou méthane, utilisé comme vecteur de stockage et pouvant être injecté dans les réseaux de gaz naturels, dont les infrastructures, déjà existantes, offrent des capacités de stockage et de transport pouvant permettre de répondre aux besoins futurs (Fig. 3). Considérer uniquement le power to gas sous cet angle serait toutefois trop restrictif. La conversion de l'énergie électrique en gaz offre de nombreuses possibilités d'utilisation finale de cette énergie, comme le chauffage domestique, l'usage industriel ou encore la mobilité des personnes, et ne rend donc pas obligatoire le retour à l'électricité de cette énergie transformée. Plus qu'un simple moyen de stockage, il permet de relier réseaux électriques et gaziers afin de créer de la flexibilité et des synergies entre les deux (Fig. 4).
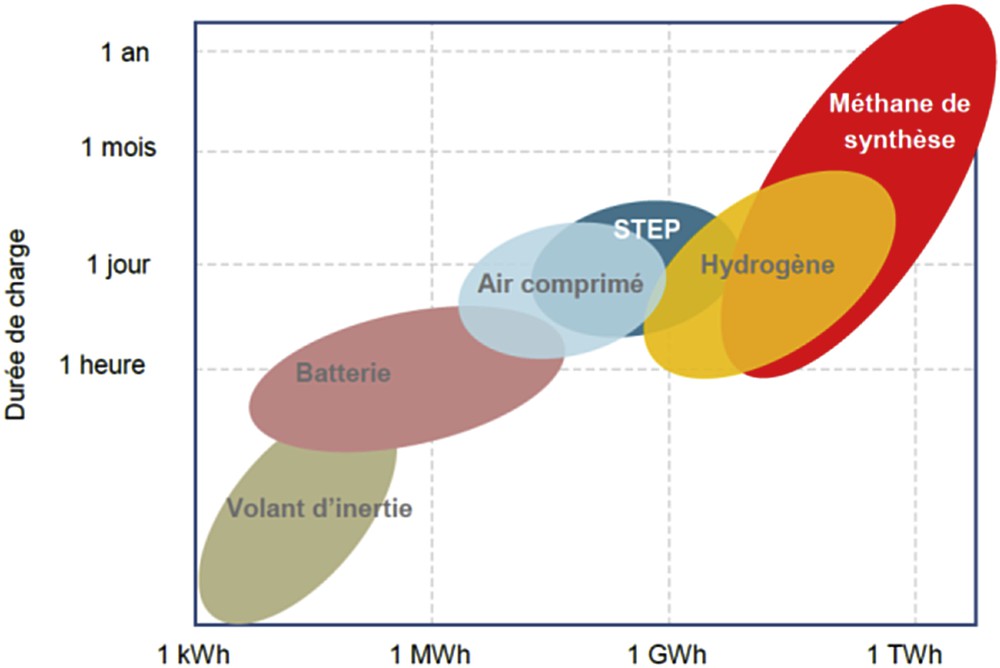
Durée et capacité de différentes technologies de stockage [10].
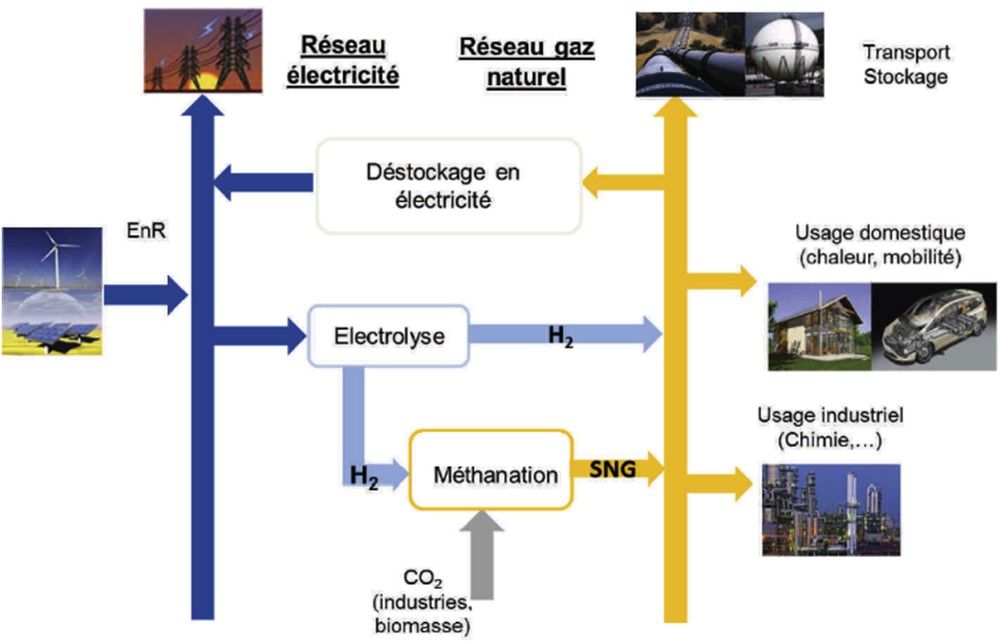
Illustration du concept du power to gas.
Le procédé power to gas consiste en une ou deux étapes de conversion essentielle selon le vecteur de stockage final choisi. Ce vecteur peut être, soit l'hydrogène (power to hydrogen), produit par l'électrolyse de l'eau, soit le méthane (power to methane), produit dans une seconde étape dite de méthanation ; conversion d'hydrogène et de dioxyde de carbone. En plus de permettre la valorisation d'un CO2 « déchet », la réalisation de cette étape supplémentaire permet de limiter les contraintes et le coût de l'adaptation des stockages, de la distribution et de l'utilisation finale du vecteur énergétique. Ceci au prix d'une baisse de l'efficacité énergétique du procédé, celle-ci passant d'environ 75% pour l'étape d'électrolyse seule à 60% PCS (pouvoir calorifique supérieur) pour un procédé power to methane [11].
L'injection d'hydrogène dans les réseaux de gaz naturels est en effet contrainte par les spécifications de ces derniers, dont un extrait est fourni dans le Tableau 1a. En particulier, celle portant sur la composition du gaz et son pouvoir calorifique restreignent le cadre d'application du power to hydrogen, le limitant par conséquent aux installations de faibles puissances, pour lesquelles les possibilités de dilution par les réseaux de gaz seront suffisantes. L'utilisation du vecteur méthane représente une voie plus adaptée à long terme. Cette voie nécessite toutefois l'optimisation des technologies concernées pour le cahier des charges du power to gas.
Quelques spécifications techniques des réseaux de gaz naturels français [12]. (L'indice de Wobbe est défini comme le rapport entre le PCS et la racine carrée de la densité du gaz.)
| Caractéristique | Spécificiation du réseau |
| Pouvoir calorifique supérieur (PCS) | Gaz de type H: entre 10,7 et 12,8 kWh/Nm3 |
| Gaz de type B: entre 9,5 et 10,5 kWh/Nm3 | |
| Indice de Wobbe | Gaz de type H: entre 13,64 et 15,70 kWh/Nm3 |
| Gaz de type B: entre 12,01 et 13,06 kWh/Nm3 | |
| Composition | CO2 < 2,5% |
| H2 < 6% | |
| CO < 2% |
Les procédés d'électrolyse, principalement la technologie alcaline, sont au stade commercial et peuvent permettre de répondre de manière satisfaisante à ce cahier des charges. Les développements en cours et les réductions de coûts attendus dans les années à venir font que cette technologie ne constitue pas le verrou actuel sur la faisabilité technologique du power to gas. A contrario, le retour d'expérience à l'échelle industrielle, pour la méthanation du CO2, est très limité, malgré la découverte de cette réaction il y a plus d'un siècle par le prix Nobel Paul Sabatier [13]. Ceci s'explique principalement par le faible intérêt porté à cette réaction dans le domaine industriel et dans celui de la production d'énergie, mais également par sa problématique complexe liée à ses caractéristiques [1,2,4,5,7,8,14–16]. Il s'agit d'une réaction fortement exothermique et équilibrée, c'est-à-dire à conversion limitée aux températures élevées, ce qui pose le problème de la gestion thermique de la réaction. Cette réaction nécessite également l'utilisation de catalyseurs solides, dont les performances peuvent décroître dans le temps ; on parle alors de désactivation du catalyseur, celle-ci étant également liée à la gestion thermique de la réaction dans le réacteur. Les solutions industrielles existantes sont issues de procédés développés dans les années 1970–1980 pour la mise en œuvre de la méthanation du syngas (mélange CO/H2/CO2) pour la production continue de méthane à partir de charbon et pour lesquels seule la conversion du CO est réellement significative. Ces solutions sont traditionnellement constituées d'une succession de réacteurs adiabatiques séparés par de nombreux échangeurs de chaleur utilisés pour refroidir les gaz et favoriser la recherche de hauts rendements de conversion atteignables à basse température. L'intégration de l'échange thermique au sein des réacteurs a également été abordée, mais s'est presque exclusivement restreinte à l'utilisation de réacteurs à lit fluidisé pour contrôler la forte exothermicité de la réaction. Ces deux types majeurs de procédés ne sont guère adaptés au cadre nouveau du power to gas, où les dimensions des installations sont plus faibles, où les contraintes de coûts sont plus importantes et où la flexibilité est cruciale. Le développement de nouvelles technologies de réacteurs, adaptées à la méthanation du CO2, dits « réacteurs-échangeurs », combinent la réaction chimique et l'échange thermique afin de réduire les coûts, la taille des installations et d'améliorer leur modularité. Ceci semble donc être une nécessité pour le développement du power to gas.
2 Méthanation du dioxyde de carbone
La réaction d'hydrogénation, ou méthanation, du dioxyde de carbone, encore appelée réaction de Sabatier [13], conduit à la production de méthane et d'eau à partir de CO2 et d'hydrogène. Sa principale caractéristique est d'être équilibrée et fortement exothermique.
Son équation est :
| (1) |
Cette réaction peut également être vue comme la combinaison de la réaction dite Reverse Water Gas Shift (RWGS) et de la réaction d'hydrogénation du monoxyde de carbone. Cette combinaison est parfois nommée « voie indirecte » dans la méthanation du CO2. Elle s'écrit :
| (2) |
| (3) |
En phase gazeuse, la molécule de CO2 est d'une grande stabilité, liée à celle de ses liaisons oxygène–carbone, le carbone étant dans son état d'oxydation maximal. En conséquence, la mise en œuvre de la réaction de méthanation du CO2 nécessite le recours à un catalyseur afin de rendre cette molécule plus réactive.
2.1 Évolution du système réactionnel à l'équilibre thermodynamique
L'étude de l'équilibre thermodynamique permet de représenter l'état du système réactionnel à l'équilibre, c'est-à-dire celui qu'il atteindrait à des échelles de temps (ou temps de passage dans un réacteur) très grandes. Ce genre d'étude ne rend pas compte des différentes vitesses des réactions pouvant se produire, et donc de la réalité de la production. Il indique les limites de la conversion possible. Lors de la mise en œuvre de la réaction de méthanation du dioxyde de carbone, plusieurs réactions, impliquant les réactifs et/ou les produits de la réaction, peuvent avoir lieu [1,3,15,17–20]. Parmi ces réactions (Tableau 1b) se trouvent les voies directe et indirecte de méthanation (R1, R2 et R5), ainsi que des réactions conduisant à la formation de carbone solide, comme la réaction de Boudouard (R4), ou au craquage du méthane (R6), ou encore à la décomposition des oxydes de carbone (R7–R8). Enfin, les réactions de Fischer–Tropsch (R9–R10) et la réaction inverse du reformage à sec (R3) sont également thermodynamiquement envisageables. Dans le cas de la méthanation du CO2, en conditions stœchiométriques (rapport H2/CO2 = 4), il a été calculé [20] que le carbone solide et les molécules possédant plusieurs atomes de carbone ne sont présents qu'à l'état de traces à l'équilibre thermodynamique. Celui-ci a été calculé par une méthode de minimisation de l'énergie de Gibbs pour des pressions comprises entre 1 et 100 bar et des températures situées entre 200 et 800 °C. Les calculs montrent cependant que, dans la limite des espèces prises en compte, le carbone solide est présent à l'équilibre thermodynamique pour des ratios H2/CO2 égaux à 2 et pour des pressions de 1 et 30 atm et des températures inférieures à 600 °C.
Principales réactions pouvant entrer en jeu lors de la méthanation du CO2 [20,21].
| Réaction | Formule | Nom de réaction | ||
| R1 | Méthanation de CO | −206,1 | −141,8 | |
| R2 | Méthanation de CO2 | −165 | −113,2 | |
| R3 | Inverse du reformage à sec | −247,3 | −170,4 | |
| R4 | Réaction de Boudouard | −172,4 | −119,7 | |
| R5 | Gaz à l'eau | −41,2 | −28,6 | |
| R6 | Craquage du méthane | 74,8 | −50,7 | |
| R7 | Réduction du CO | −131,3 | −91,1 | |
| R8 | Réduction du CO2 | −90,1 | −62,5 | |
| R9 | Réaction de Fischer–Tropsch | – | – | |
| R10 | Réaction de Fischer–Tropsch | – | – |
En utilisant les résultats obtenus par Gao et al. [21] ils ont supposé que cet équilibre peut être représenté en considérant les réactions R1, R2, R3 et R5. Parmi ces réactions, seules deux sont indépendantes, les réactions R2 et R5 ont, par exemple, été utilisées. L'écriture de l'équilibre thermodynamique de ces réactions conduit à la définition de constants d'équilibre, Kj,eq, permettant de représenter l'état du système à l'équilibre en fonction des conditions (T, P) considérées.
| (4) |
Le taux de conversion du CO2, , et la sélectivité en méthane, , sont définies comme :
| (5) |
| (6) |
Les Figs. 5 et 6 montrent l'évolution de ces deux grandeurs avec la température et la pression dans les conditions de l'équilibre thermodynamique. Les données thermodynamiques nécessaires au calcul sont issues de la référence [22]. Les gaz sont considérés parfaits dans les gammes de température et de pression étudiées.
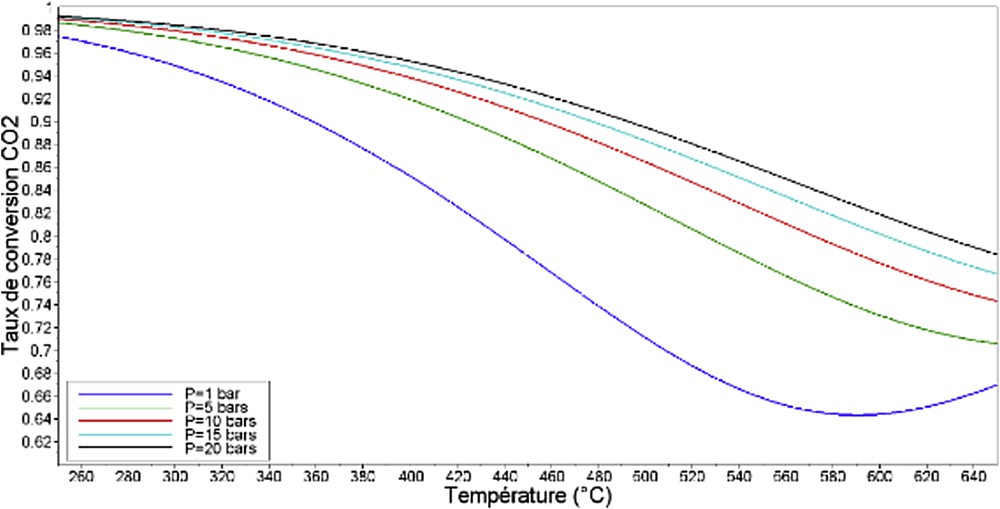
Évolution du taux de conversion du CO2 à l'équilibre thermodynamique pour un mélange stœchiométrique en fonction de la température, à différentes pressions opératoires.
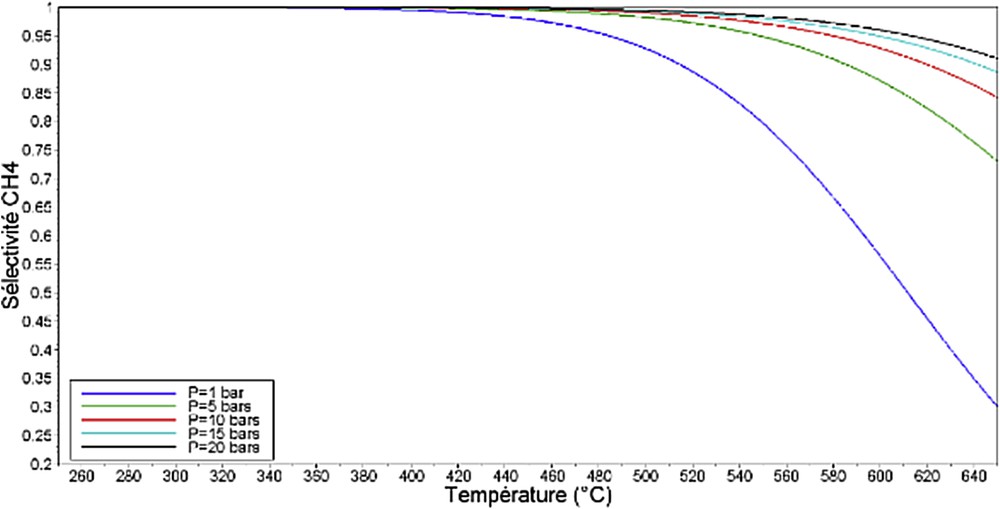
Évolution de la sélectivité en CH4 à l'équilibre thermodynamique pour un mélange stœchiométrique en fonction de la température, à différentes pressions opératoires.
L'obtention d'un taux de conversion et d'une sélectivité en méthane élevés nécessite une pression opératoire élevée et une température relativement basse. Cette observation est conforme aux règles de modération de Van't Hoff et de Le Chatelier, la réaction de méthanation étant exothermique et entraînant une diminution du nombre de moles gazeuses. La sélectivité en méthane, à l'équilibre, est proche de 100% dès lors que la température est inférieure à 450 °C. Le taux de conversion est davantage sensible à la température. L'obtention d'un taux supérieur à 95% requiert des températures inférieures à 430 °C, voire de l'ordre de 320 °C, par exemple, pour un fonctionnement à la pression atmosphérique. Si le déplacement de l'équilibre thermodynamique est notable lorsque la pression augmente de 1 à 5 bar, il devient moins évident au-delà. Le gain de conversion entre une pression de 5 et 20 bar n'est, par exemple, que de 1,5% à 350 °C, celle-ci passant alors de 97% à 98,5%. L'utilisation d'une pression supérieure à 15 bar ne semble donc pas justifiée d'un point de vue thermodynamique pour l'obtention de taux de conversion élevés, compte tenu de l'impact de celle-ci sur le coût d'une installation.
Il peut être noté qu'une première problématique liée à la mise en œuvre de la méthanation du CO2 est remarquée. À la température à laquelle l’équilibre thermodynamique est atteint, les taux de conversion (conversion totale) et les sélectivités maximaux sont réalisés. De basses températures seront donc nécessaires à l’obtention de fortes conversions (en produits désirés) et sélectivités, alors que l'on sait que les cinétiques de réaction augmentent avec la température d’après la loi d'Arrhenius. En effet, en abaissant la température, la sélectivité augmente, car l’importance des réactions « parasites » sera diminuée (ces réactions étant presque toujours irréversibles, elles ont des énergies d'activation élevées). Donc la conversion en produit attendu augmentera. La maîtrise des températures opératoires, c'est-à-dire la gestion thermique de la réaction, apparaît donc d'une importance capitale. Ceci est d'autant plus vrai que l'exothermicité de la réaction est forte et qu'en conséquence l'évacuation de la chaleur dégagée par la réaction est difficile.
2.2 Les catalyseurs utilisés et les mécanismes de réaction
Afin que la molécule de CO2 soit réactive, l'énergie de la liaison carbone-oxygène doit diminuer. Ceci est réalisable en ayant recours à un catalyseur. Ces catalyseurs sont généralement constitués d'une phase active métallique, siège de la réaction, qui est dispersée sur un support poreux ou non poreux, de nature oxyde comme l'alumine (Al2O3), la silice (SiO2) ou la cérine (CeO2). Les métaux de transition du groupe VIII B comme Ru, le Rh, le Pd, le Pt, le Co, le Fe, le Mn, le W, ou encore Ni, sont utilisés comme phase active du catalyseur [14–20,23–38]. Le nickel est le plus largement utilisé, en raison de son plus faible coût. Ces éléments présentent des activités, ou capacité à convertir les réactifs, différentes selon l'importance de leurs interactions avec les molécules réactives. Ces différences peuvent être représentées sous forme de courbes volcaniques en fonction de l'énergie de dissociation de la molécule sur la phase active. Un exemple de courbe volcanique est présenté dans la Fig. 7 dans le cas de la méthanation du CO [39]. Ces courbes mettent en évidence le rôle de la phase active dans l'acte catalytique. Pour les éléments se trouvant à la droite de cette courbe, l'activité est limitée par une barrière énergétique de dissociation très élevée, tandis que, pour les éléments se trouvant sur la gauche de cette courbe, elle est limitée par une trop grande énergie d'adsorption entre le métal et les molécules adsorbées. Le catalyseur doit ainsi interagir avec la molécule afin d'assister la dissociation, mais ne doit pas la stabiliser, ou fixer à sa surface les atomes issus de la dissociation.
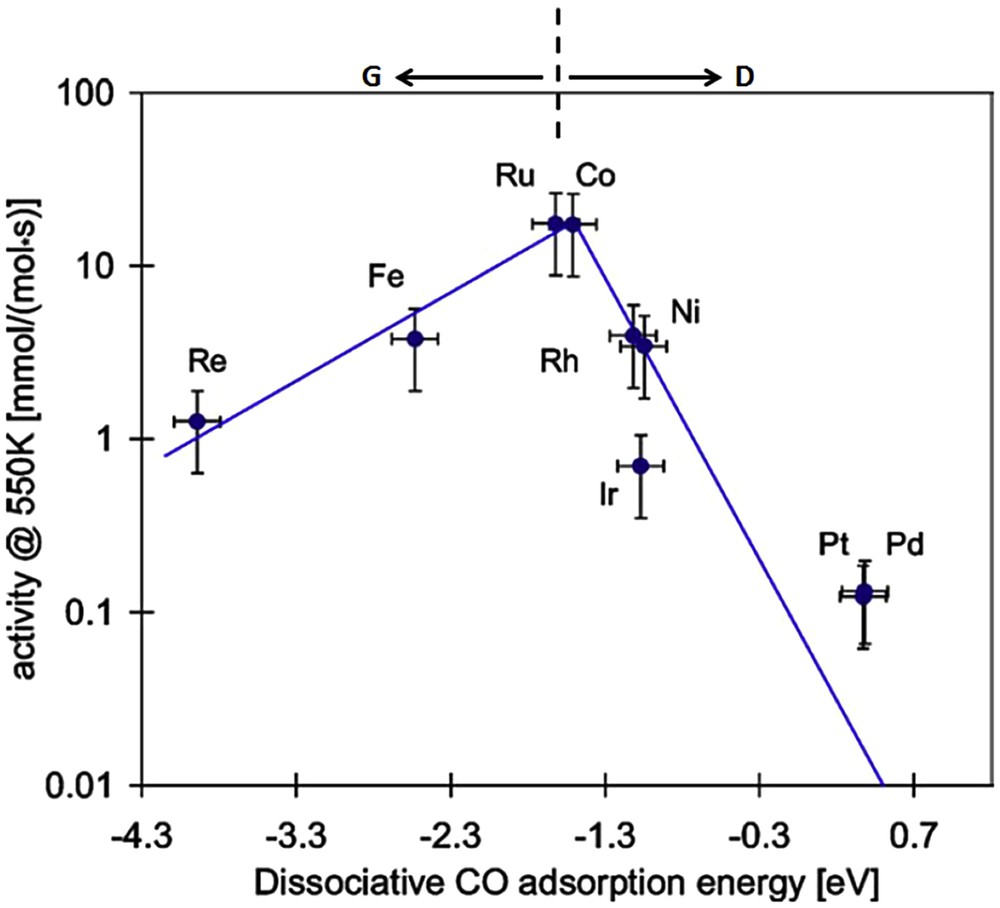
Exemple de courbe « volcanique » dans le cas de la méthanation du CO [39].
Le support du catalyseur joue également un rôle important sur les performances du catalyseur, de par ses interactions avec la phase active métallique et de par la surface spécifique qu'il déploie, sur laquelle est dispersée la phase active. Selon ses propriétés, le support peut également interagir de manière significative avec certains réactifs et ainsi influencer le mécanisme de la réaction. La méthode de préparation du catalyseur est également importante, car elle conditionne aussi les interactions entre le support et la phase active. La nature du support et la méthode de préparation influencent ainsi l'activité, la sélectivité et la stabilité du catalyseur [20,40]. Le choix du support du catalyseur est aussi lié à des contraintes de stabilité mécanique, thermique et de coût.
Le mécanisme catalytique de la réaction de méthanation du CO2 a fait l'objet de plusieurs études approfondies [41–68]. Deux types de mécanismes sont aujourd'hui évoqués : le premier suppose le passage par le CO comme intermédiaire, qui serait ensuite converti en méthane via le mécanisme de la méthanation du CO. Le second suppose la conversion directe du CO2 en méthane via la formation de carbonates et de formiates à la surface du support du catalyseur. Ces deux mécanismes peuvent, de plus, coexister sur le catalyseur. Dans tous les cas, l'hydrogène est adsorbé et dissocié à la surface de la phase active. Les deux mécanismes sont schématisés dans la Fig. 8 [15].
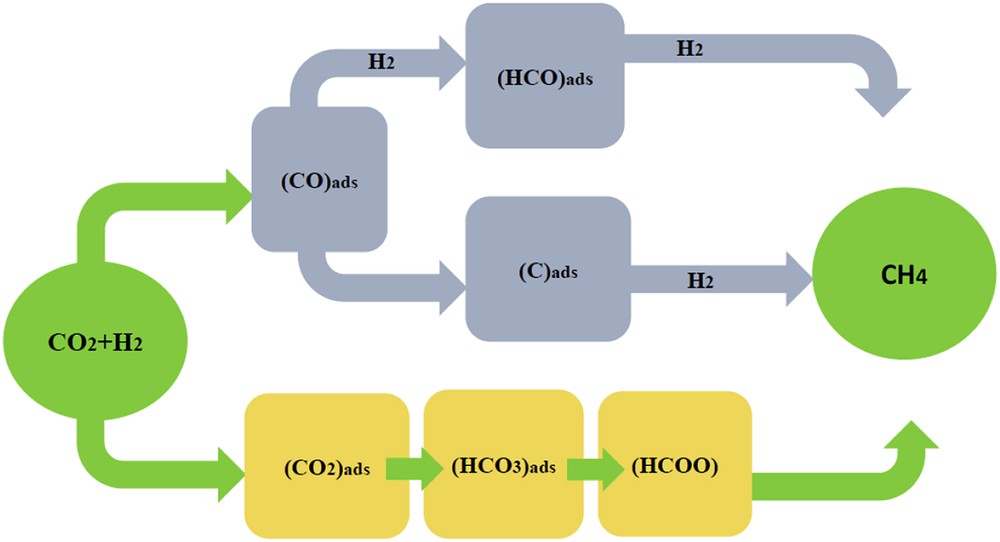
Les mécanismes pour la méthanation du CO2 [15].
Dans le premier mécanisme, le CO2 est tout d'abord adsorbé, puis dissocié à la surface de la phase active du catalyseur pour former un intermédiaire CO adsorbé (ou mono-carbonyle) [62,69]. Après cette étape de dissociation, l'hydrogénation du CO2 suit le même mécanisme que l'hydrogénation du CO. Le mécanisme de la méthanation du monoxyde de carbone ne fait toutefois pas consensus [24,70,71]. Une première famille de mécanismes, assistée par hydrogène, suppose une adsorption du CO suivie d'une dissociation en carbone à la surface de la phase active du catalyseur, tandis qu'une seconde famille de mécanismes propose un intermédiaire de réaction de type CHxO (x = 1,2) sans passer par un carbone adsorbé. La nature exacte du mécanisme de la réaction semble différer selon la phase active du catalyseur et les conditions de réaction [20]. Les mécanismes de la dissociation du CO peuvent également faire intervenir différents sites d'adsorption selon la structure locale de la phase active. Il est ainsi possible de différencier les sites dits de « terrasse » ou de « marche » d'un catalyseur, les sites de marche étant plus favorables à la dissociation du CO [60,72]. Cette différenciation énergétique des sites d'adsorption de la phase active peut ainsi expliquer la sensibilité des réactions d'hydrogénation du CO2 et du CO vis-à-vis de la structure de la phase active et, en particulier, de la taille de ses cristallites [73].
2.3 Les phénomènes de désactivation des catalyseurs
2.3.1 Empoisonnement des catalyseurs
L'empoisonnement des catalyseurs a lieu lorsqu'un composé s'adsorbe fortement, et de façon quasi-irréversible, à la surface du catalyseur. La désactivation du catalyseur est alors due à l'occupation des sites actifs du catalyseur par ce composé, limitant le nombre de sites réactifs disponibles pour la réaction. La désactivation est également due à une modification électronique des sites réactifs voisins, ce qui diminue leurs interactions avec les molécules réactives et les rend moins actifs. Dans le cas d'un catalyseur à base de nickel, les principaux poisons sont le phosphore, l'arsenic, ou encore, plus couramment, le soufre [74]. L'empoisonnement des catalyseurs à base de nickel par le soufre est d'autant plus important que son état d'oxydation est faible et qu'il se dissocie facilement à la surface du nickel. Il est ainsi plus important lorsque le soufre est présent sous la forme H2S que SO2. L'empoisonnement se produit à des très faibles teneurs en sulfure d'hydrogène, de l'ordre de la dizaine de partie par milliards (ppb). La Fig. 9 montre ainsi l'évolution de l'activité de différents catalyseurs pour la méthanation du CO en fonction de la concentration en sulfure d'hydrogène dans le gaz.
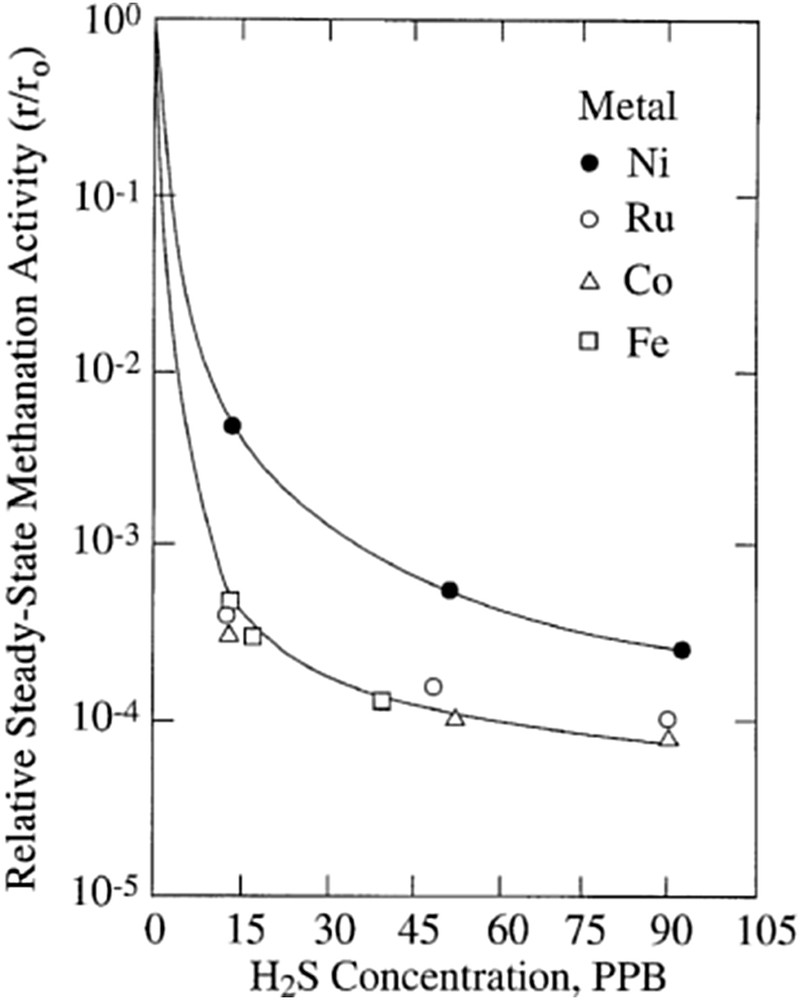
Évolution de l'activité relative de différents catalyseurs pour la méthanation du CO en fonction de la teneur du gaz en H2S (1 bar, 400 °C, 1% CO dans H2 pour Co, Fe et Ru ; 4% CO dans H2 pour Ni) [74].
La sensibilité des catalyseurs à l'empoisonnement au soufre peut toutefois être réduite par l'ajout de molybdène ou de bore, le soufre s'adsorbant préférentiellement sur ces éléments. La seule manière d'empêcher totalement l'empoisonnement des catalyseurs semble, cependant, l'élimination des traces de poisons potentiels présentes dans le gaz d'alimentation. Paradoxalement, ces poisons peuvent être utilisés pour effectuer un prétraitement des catalyseurs afin de limiter la présence d'autres phénomènes entraînant leur désactivation. Par exemple, des catalyseurs de reformage peuvent être exposés à une certaine quantité de soufre afin de limiter la formation de dépôts de carbone, au prix d'une activité catalytique réduite [75].
2.3.2 Désactivation due à la formation de dépôts de carbone
Les dépôts de carbone entraînent un encrassement et souvent une désactivation des catalyseurs. La formation de dépôts de carbone, aussi appelé « cokage », peut avoir plusieurs origines. Les dépôts de carbone peuvent être issus : (i) de la réaction de dismutation du CO, également appelée réaction de Boudouard, (ii) de la réduction des oxydes de carbone à la surface du catalyseur, ou encore (iii) du craquage du méthane (réactions R4, R6, R7 et R8 dans le Tableau 1b). Les termes « dépôts de carbone » et « coke » sont généralement équivalents, bien qu'ils soient parfois utilisés selon l'origine du carbone, le terme dépôts de carbone étant utilisé pour la dismutation du CO et le terme coke pour la décomposition d'hydrocarbures [74]. Plusieurs formes de carbone peuvent être formées à la surface des catalyseurs (Fig. 10). La première est une forme de carbone atomique adsorbé, ou carbone α, directement issu des réactions précédemment citées. Le carbone α est également considéré comme un intermédiaire de réaction de la méthanation du CO dans certains mécanismes, comme cela a été discuté dans la section précédente. Le carbone α est parfois appelé carbone réactif, car il est relativement facile à réoxyder ou ré-hydrogéner. Ce carbone peut ensuite réagir et polymériser sous la forme de film de carbone polymérique β qui, à haute température (>500–600 °C), peut se transformer en carbone graphitique, ou pyrolytiques, peu réactif, voire inerte. Le carbone α peut également réagir avec le nickel pour former du carbure de nickel ou diffuser dans les cristallites de nickel et former des fibres de carbone [74].
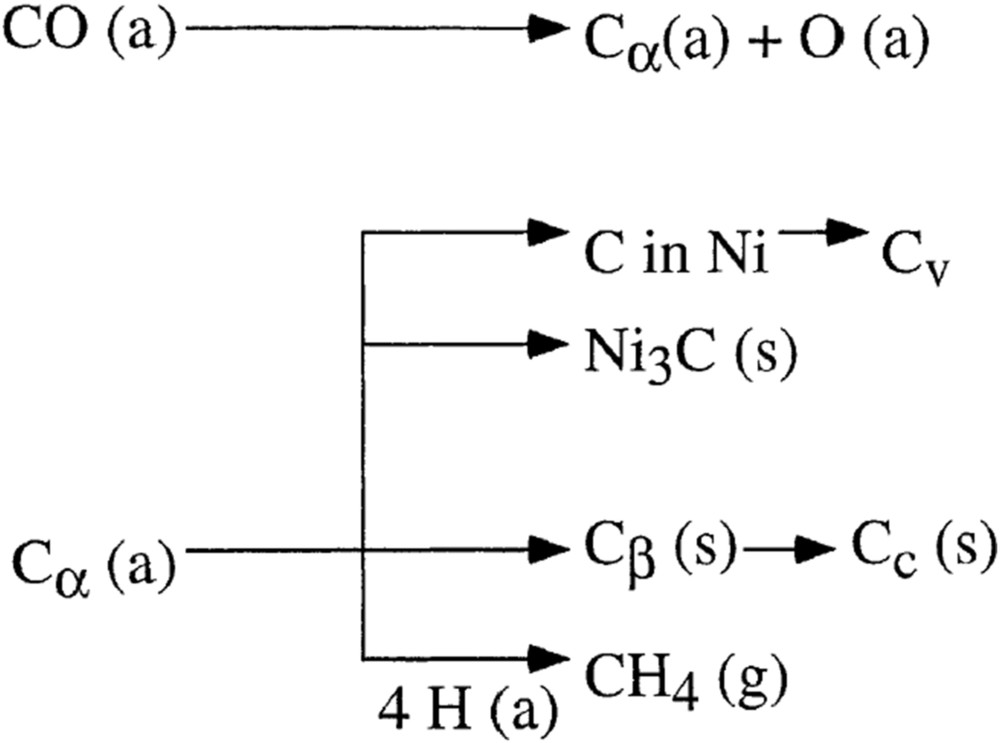
Mécanisme de formation et de transformation des dépôts de carbone à partir de la dissociation du CO [74].
Les conséquences de la formation de ces dépôts de carbone sont multiples. L'accumulation de carbone à la surface du catalyseur bloque l'accès aux sites actifs du catalyseur et conduit donc à une baisse d'activité. La formation de polymères ou de films (principalement de carbone β et de carbone graphitique) peut causer l'encapsulation des cristallites de la phase active et l'obstruction des pores du support. Enfin, la formation de fibres de carbone à l'interface entre le support et les cristallites de nickel peut entraîner la perte de la phase active par détachement, ainsi qu'une fragilisation du support pouvant causer la destruction du catalyseur [76].
Pour un catalyseur donné, la vitesse de formation, voire l'existence, de ces dépôts de carbone est très dépendante des conditions opératoires et de l'atmosphère réactionnelle, en particulier de la présence d'hydrogène et de vapeur d'eau. D'un point de vue thermodynamique, les conditions propices aux dépôts de carbone peuvent être représentées par des zones de stabilité dans des diagrammes ternaires C,H,O. Un exemple de diagramme, calculé par minimisation de l'énergie de Gibbs, est donné dans la Fig. 11. À titre d'exemple, les points correspondant aux conditions de méthanation du CO2 et CO ont été représentés. Pour ces calculs, l'hypothèse des gaz parfaits a été faite et les propriétés thermodynamiques du carbone solide utilisées sont celles du carbone graphite. Ce diagramme a été établi en considérant les propriétés thermodynamiques d'un grand nombre d'espèces contenant des atomes d'hydrogène, de carbone et/ou d'oxygène. La présence de dépôts de carbone dans des conditions de méthanation, c'est-à-dire avec de fortes proportions d'hydrogène (partie gauche du diagramme), est favorisée par une augmentation de la température, avec un déplacement de la limite de stabilité du carbone graphite vers les plus faibles fractions de carbone. Dans ces conditions, une augmentation de la pression défavorise ces dépôts, excepté à basse température (300 °C), où elle ne semble n'avoir aucune influence. L'influence de la température et de la pression sont toutefois inversées lorsque l'on considère de faibles fractions d'hydrogène (partie droite du diagramme). Dans les hypothèses du calcul, la méthanation du CO2 dans des conditions stœchiométriques semble épargnée par la formation de ces dépôts dans les conditions de température et de pression considérées, ce qui n'est pas le cas de la méthanation du CO stœchiométrique. Les compositions à l'équilibre thermodynamique sont cependant influencées par les interactions du catalyseur avec le carbone, ce qui modifie les conditions de stabilité de ce dernier en comparaison de la considération du carbone graphite seul. D'après Pedersen et al. [77], la limite de formation du carbone à la surface d'un catalyseur à base de nickel est ainsi déplacée vers des conditions plus sévères. Cet effet dépend cependant de la nature et la structure du catalyseur, ainsi que de la forme du carbone considéré, et semble favorisé par de faibles tailles de cristallites de nickel.
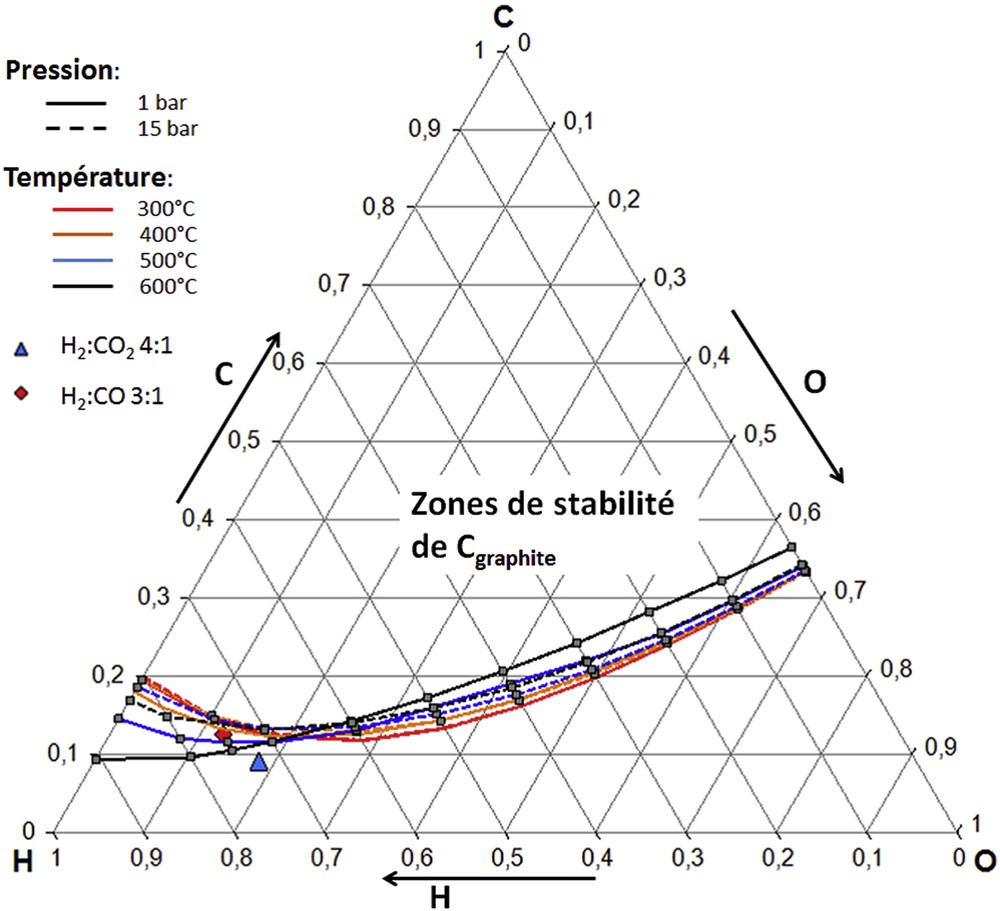
Diagramme ternaire C,H,O représentant les zones de stabilité du carbone graphite pour différentes températures et pressions.
Dans la réalité, c'est-à-dire dans le cas d'un système hors équilibre thermodynamique, l'analyse des aspects cinétiques est essentielle pour la compréhension des phénomènes de dépôt de carbone. La présence des différentes formes de carbone ne sera en effet possible que si leur vitesse de formation respective est supérieure à leur vitesse de disparition.
La Fig. 12 présente, par exemple, les différentes vitesses de formation et d'hydrogénation du carbone atomique adsorbé Cα et polymérique Cβ lors de la mise en œuvre de la méthanation du CO sur un catalyseur à base de nickel. Dans cet exemple, la vitesse de formation du carbone Cα est inférieure à la vitesse d'hydrogénation de celui-ci lorsque la température est inférieure à 325 °C. L'accumulation de cette forme de carbone à la surface du catalyseur est donc faible, voire inexistante. De même, la vitesse d'hydrogénation du carbone Cβ est supérieure à sa vitesse de formation lorsque la température est supérieure à 425 °C ; ce carbone sera donc peu présent à la surface du catalyseur dans ces conditions. En revanche, lorsque la température est intermédiaire, la vitesse d'hydrogénation du carbone Cα est inférieure à sa vitesse de formation ; ce dernier s'accumulera à la surface du catalyseur et pourra polymériser en carbone « C », à une vitesse supérieure à celle d'hydrogénation du carbone Cβ. Dans ces conditions, le carbone Cα et surtout le carbone Cβ peuvent par conséquent s'accumuler à la surface du catalyseur et causer la désactivation de ce dernier, alors que le carbone solide n'est thermodynamiquement pas stable. Ce phénomène, lié aux différentes cinétiques de réaction, a été observé [77] dans le cas de la méthanation du CO à des températures inférieures à 330 °C. Dans ce cas, le dépôt de carbone aboutit à la formation d'un film d'encapsulation de carbone Cβ qui cause la désactivation du catalyseur. La formation de ce film d'encapsulation peut toutefois être encore observée à des températures légèrement supérieures selon le catalyseur utilisé [78]. Cette désactivation, parfois appelée « β désactivation », ne se produit toutefois qu'avec des pressions partielles de CO suffisamment élevées. La méthanation du CO2 semble de plus être épargnée par ce type de dépôt dans ces conditions de température.
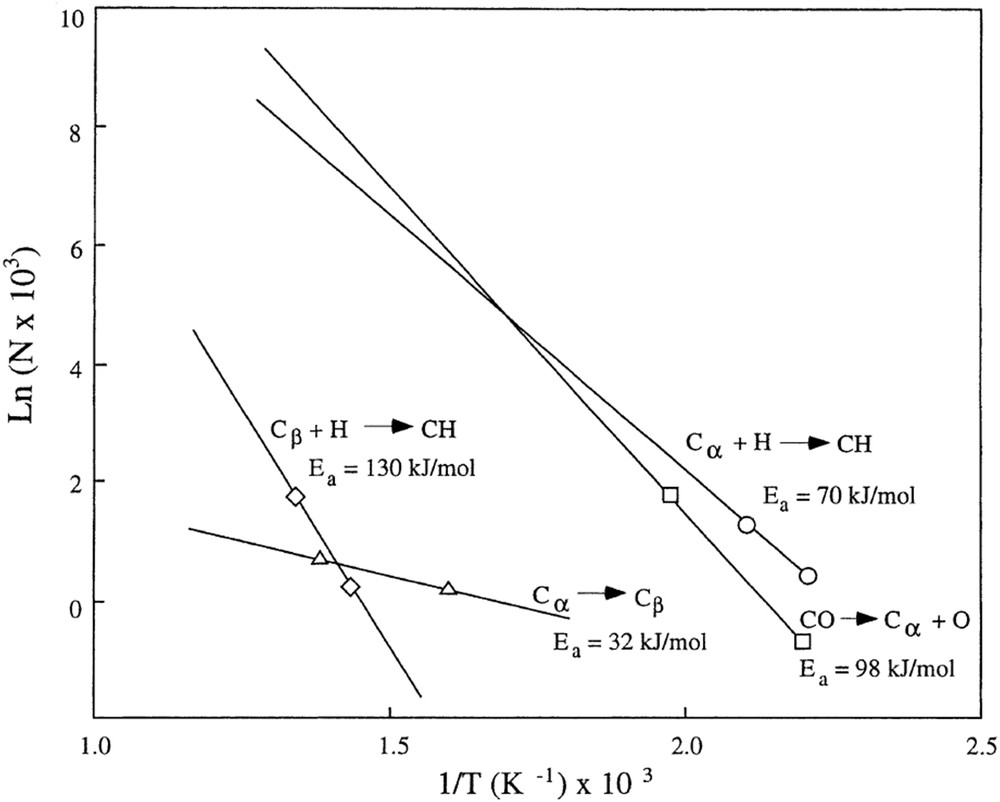
Vitesses de formation et d'hydrogénation des carbones α et β lors de la méthanation du CO sur un catalyseur à base de nickel [74].
Le Tableau 2 regroupe ainsi les gammes de températures de formation et d'hydrogénation des différentes formes de carbone. Ces valeurs dépendent toutefois des conditions opératoires, en particulier des pressions partielles d'eau, d'hydrogène et de molécules carbonées, ainsi que de la nature et de la structure du catalyseur.
Températures de formation et d'hydrogénation des différentes formes de dépôts de carbone [42].
| Forme de carbone | Températures de formation (°C) | Température du maximum d'hydrogénation (°C) |
| Carbone adsorbe (Cα) | 200–400 | 200 |
| Carbone polymérique (Cβ) | 250–500 | 400 |
| Carbone filamenteux, fibres (Cv) | 300–1000 | 400–600 |
| Carbure de nickel | 150–250 | 275 |
| Carbone graphitique (Ce) | 500–550 | 550–850 |
La prévention des phénomènes de dépôt de carbone peut être faite en modifiant les conditions opératoires de la réaction. Une augmentation des quantités d'hydrogène et/ou d'eau par rapport à celles des espèces carbonées a pour effet de réduire ces dépôts. L'utilisation de promoteurs tels que l'iridium ou le platine permet également de réduire leur formation. L'ajout d'alcalins au support a également pour effet de les réduire en augmentant l'adsorption de l'eau [42]. De plus, la taille des cristallites de nickel influence la formation de dépôts de carbone, cette dernière étant défavorisée par des petites particules [76]. La régénération des catalyseurs ayant subi une désactivation par dépôts de carbone peut être effectuée par hydrogénation ou par oxydation de ces dépôts par un traitement sous H2, H2O, O2 ou encore CO2. L'hydrogénation du carbone α peut être effectuée par un traitement sous hydrogène à des températures relativement basses, entre 200 et 400 °C. Celle du carbone polymérique β peut être effectuée à des températures comprises entre 400 et 700 °C, la vitesse d'hydrogénation étant plus élevée à haute température. L'utilisation de températures élevées (>500 °C) est également nécessaire pour l'hydrogénation du carbone graphitique. En comparaison, l'oxydation des dépôts de carbone sous oxygène peut être réalisée à des températures plus basses, de l'ordre de 300 °C. La régénération complète des catalyseurs est toutefois difficile à obtenir pour différentes raisons. Tout d'abord, la totalité du carbone présent à la surface du catalyseur n'est pas toujours éliminée. De plus, les traitements effectués pour régénérer les catalyseurs peuvent entraîner des modifications de la structure de ce dernier, notamment aux températures élevées au cours du traitement. Ceci est notamment le cas pour les traitements oxydants, les réactions d'oxydation étant fortement exothermiques. Enfin, la régénération des catalyseurs peut s'accompagner de pertes de masse de la phase active. Cette perte est principalement due à la présence de carbone sous forme de fibres, ou filaments entre le support et les cristallites, leur élimination entraînant le détachement des cristallites de la phase oxyde [42,79].
En conclusion, la limitation de la formation de dépôts de carbone est possible grâce à un contrôle des conditions opératoires et de la composition du gaz réactif. En particulier, la diminution de la proportion d'espèces carbonées devant celles d'espèces contenant des atomes d'hydrogène ou d'oxygène peut permettre d'éviter l'apparition de ces phénomènes. Ceci est possible par ajustement du ratio CO2/CO/H2 en amont du réacteur, par une réaction de Water Gas Shift par exemple, et par l'ajout de vapeur d'eau aux gaz réactifs. Dans le cas de la méthanation du CO2 stœchiométrique, la composition du gaz ne devrait pas conduire à la formation de dépôts de carbone à basse température, contrairement à la méthanation du CO. Malgré les compositions calculées à l'équilibre thermodynamique, il n'est pas acquis que la formation de ces dépôts soit évitée, en particulier à haute température. Il peut donc s'avérer essentiel d'assurer un certain contrôle des températures au sein du réacteur de méthanation afin de s'affranchir de ces phénomènes.
2.3.3 Les phénomènes de frittage
Les phénomènes dits de frittage décrivent principalement la croissance des cristallites de la phase active du catalyseur qui sont dispersées à la surface de la phase support. L'utilisation de ce terme peut également faire référence aux modifications structurelles pouvant être subies par le support du catalyseur. Le frittage des cristallites de la phase active est piloté par la réduction de l'énergie de surface des cristallites. Ce phénomène se produit généralement à haute température (>500 °C) et peut se produire selon différents mécanismes : par migration des cristallites à la surface du support et coalescence de ces dernières ou par migration d'atomes émis par une cristallite qui migrent à la surface du support du catalyseur et sont captés par une autre cristallite de plus grande taille (Fig. 13). La température influence grandement le mécanisme de frittage prépondérant. La croissance par migration et coalescence de cristallites est, par exemple, prépondérante à des températures inférieures à 600 °C sous des atmosphères H2/H2O, alors que le mécanisme par migration atomique devient majoritaire au-delà [80]. De manière générale les vitesses d'augmentation de la taille des cristallites métalliques, dMétal, peuvent s'écrire sous la forme [73] :
| (7) |
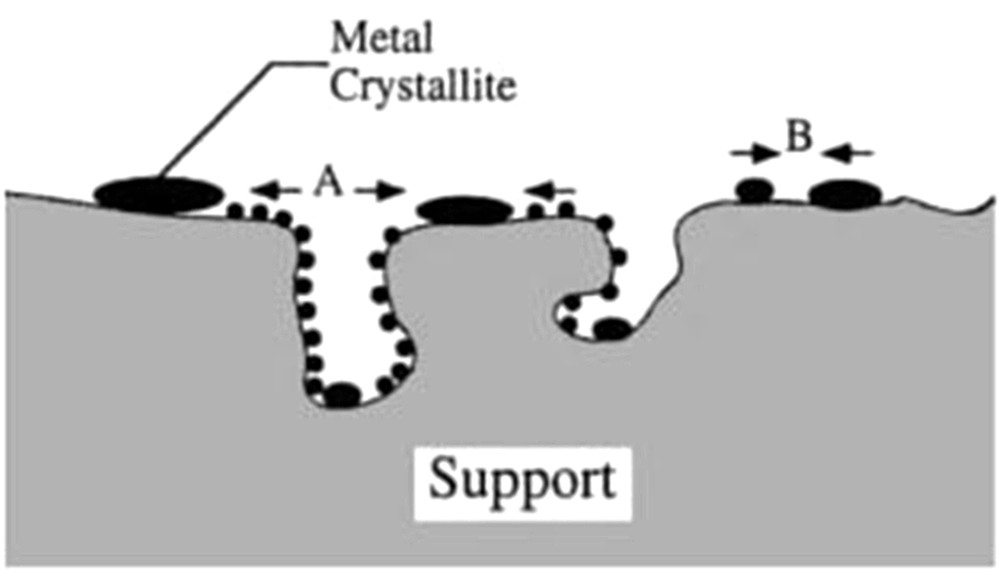
Illustration des mécanismes de frittage des cristallites métalliques : (A) – par migration atomique ; (B) – par migration et coalescence des cristallites [74].
À haute température, la phase support peut elle aussi être concernée par des phénomènes regroupés sous le terme frittage du support. Ils incluent des mécanismes de diffusion en surface, d'évaporation/condensation d'atomes volatils, de croissance de grains par diffusion aux joints de grains ou encore de changement de phase [74].
Les conséquences directes des phénomènes de frittage sont une diminution de la surface spécifique de la phase active et parfois aussi de celle du support. Ces diminutions sont dues, d'une part à la croissance des cristallites métalliques, et d'autre part à la fermeture des pores du support pouvant piéger des cristallites à l'intérieur de ces derniers. Il est intéressant de noter que la croissance des cristallites métalliques ne semble pas être limitée par la taille des pores du support du catalyseur, une réorganisation de la structure du catalyseur support-cristallite pouvant s'opérer lorsque la taille des cristallites devient supérieure à la taille des pores [80]. La modification de la surface active du catalyseur et de celle du support affecte obligatoirement la réactivité du catalyseur. Dans le cas de la méthanation du CO sur un catalyseur à base de nickel [73], il a été montré que la perte de surface active s'accompagne d'une perte d'activité catalytique. En reliant l'activité catalytique, dans des conditions de référence (250 °C, 1 bar, 1% de CO dans H2) à la surface spécifique de nickel, les auteurs ont, de plus, montré que cette perte d'activité n'était pas proportionnelle à l'évolution de cette surface (Fig. 14). D'après ces résultats, la diminution de l'activité spécifique du catalyseur est d'environ 60% pendant les 2000 premières heures, puis ralentit, pour atteindre une diminution globale de plus de 80% au bout de 8000 heures. Au regard de l'activité du catalyseur dans les conditions de référence décrites précédemment, la diminution est d'environ 94% sur cette même durée (Tableau 3). Cette forte sensibilité de la réaction de méthanation du CO à la taille des cristallites de nickel est attribuée à la proportion de sites d'adsorption dits de « marches », plus actifs, par rapport aux sites dits de « terrasses », la proportion des sites de « marches » diminuant lorsque la taille des cristallites augmente.
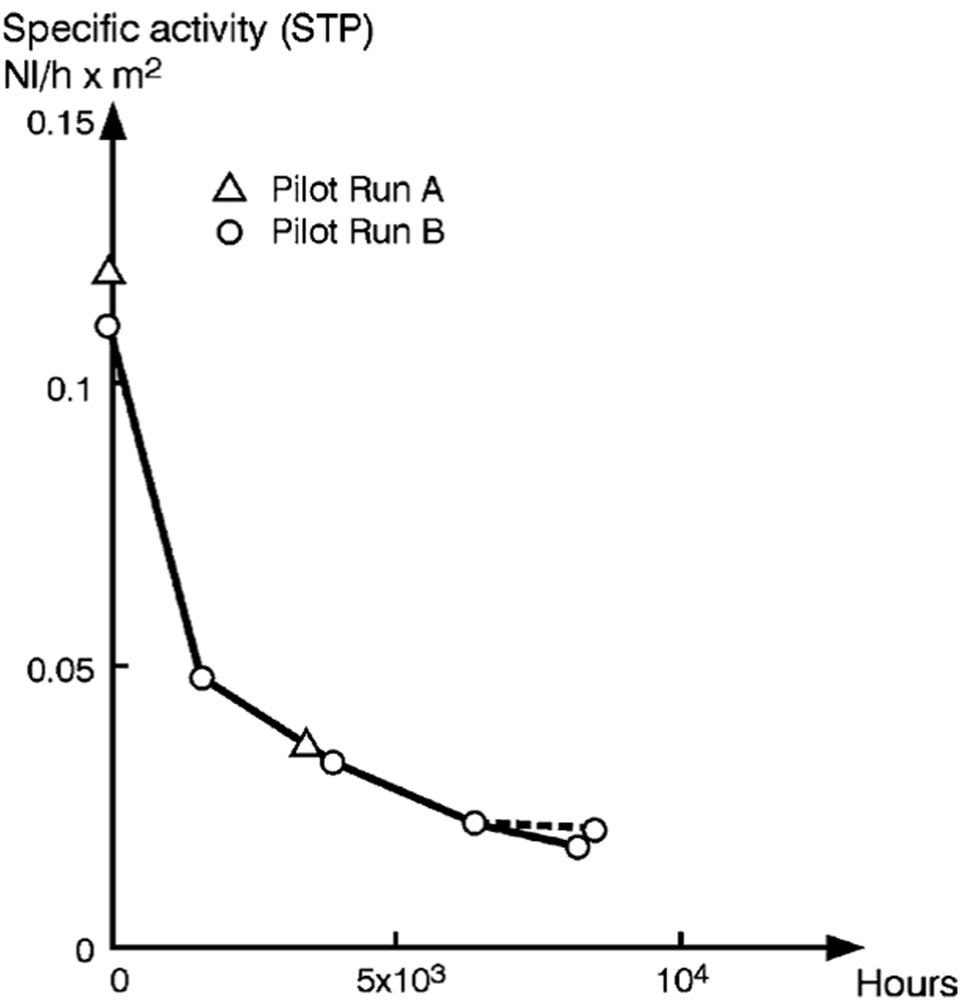
Activité spécifique d'un catalyseur à base de nickel en fonction du temps d'utilisation dans un procédé de méthanation [73].
Évolution temporelle de l'activité dans des conditions de référence, de la surface active et de la taille moyenne des cristallites métalliques d'un catalyseur à base de nickel [73].
| Temps d'utilisation (h) | ro (250 °C) Nl/h/g | Surface active H2 (m2/g) | dNi (Surface active H2) (nm) |
| 0 | 0,85 | 7,9 | 19,4 |
| 1612 | 0,21 | 4,6 | 33,3 |
| 3862 | 0,12 | 3,8 | 40,4 |
| 6350 | 0,065 | 3,0 | 51,1 |
| 8127 | 0,042 | 2,5 | 61,4 |
| 8450 | 0,055 | 2,8 | 54,8 |
Comme énoncé précédemment, les phénomènes de frittage sont favorisés lorsque la température augmente, car la mobilité des cristallites et/ou atomes métalliques, ou du support, augmente. L'atmosphère réactive possède également un rôle important dans ces phénomènes, ces derniers étant favorisés par des atmosphères oxydantes, notamment en présence de vapeur d'eau, comme présenté dans la Fig. 15. Dans cet exemple, les lignes pleines correspondent à une évolution décrite par une équation de la forme de l'équation (7) pour un mécanisme de migration et coalescence de cristallites. On remarquera que cette équation ne représente pas l'évolution temporelle à des températures supérieures à 550 °C, ce qui indique un changement dans le mécanisme de frittage [80]. Cette forte influence de la pression partielle d'eau est attribuée à la formation de complexes avec le nickel Ni2OH, qui sont plus mobiles que les atomes de nickel. Les phénomènes de frittage dépendent également de la structure du catalyseur. De petites tailles de cristallites montrent ainsi une meilleure aptitude au frittage, car elles sont plus mobiles, ce qui explique le comportement asymptotique de la désactivation liée à ces phénomènes. Le support du catalyseur, et en particulier les interactions entre le support et le métal, influence également la croissance des cristallites en limitant leur mobilité. Les interactions métal–support sont, par exemple, généralement plus élevées pour l'alumine que pour la silice. Les interactions métal-support sont également affectées par la présence de promoteurs ou d'impuretés. Les oxydes de baryum et de calcium, ou encore la cérine CeO2, sont, par exemple, des agents réducteurs de la mobilité de la phase active. À l'inverse, la présence de soufre, de plomb ou encore de potassium peut augmenter cette mobilité, et donc la croissance des cristallites [74]. Il est à noter qu'une certaine régénération est possible. La redispersion des cristallites de nickel peut être effectuée par un traitement sous oxygène et/ou dichlore à des températures supérieures à 500–550 °C [74]. Il est cependant peu probable que cette redispersion permette la totale récupération de l'activité initiale du catalyseur.
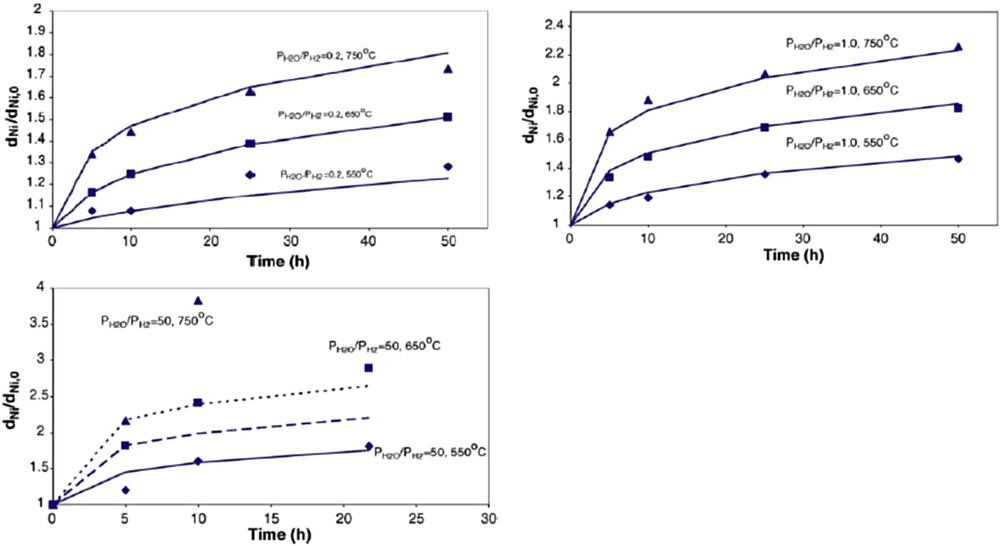
Effet et de la température et de la pression partielle d'eau (pression totale de 1 bar) sur l'évolution de la taille moyenne des cristallites pour un catalyseur Ni/Al2O3 [80].
Il apparaît que les phénomènes de frittage ne peuvent que difficilement être évités autrement que par la recherche d'une température opératoire la plus basse possible. La diminution de la teneur en eau dans le gaz est également favorable, mais difficilement réalisable, car l'eau est un produit de la réaction. La formulation de catalyseurs plus stables face à ces phénomènes représente également un moyen de lutter contre ces derniers et peut permettre d'élever la limite des températures admissibles. La maîtrise des températures au sein des réacteurs demeure donc, là aussi, essentielle.
2.3.4 Autres causes de désactivation liées à des réactions chimiques ou à des dégradations mécaniques
La dégradation de catalyseurs à base de nickel supporté sur de l'alumine peut également être due à la réaction du nickel avec l'alumine pour former de l'aluminate de nickel selon la réaction :
| (8) |
Cette réaction est favorisée à haute température et sous atmosphère oxydante, notamment en présence de vapeur d'eau. L'ajout de MgO au support (MgAl2O4) ou encore de potassium permet de limiter l'occurrence de cette réaction. Le potassium possède cependant le désavantage d'accélérer le frittage des cristallites de nickel [80]. Certaines atmosphères peuvent aussi entraîner la perte de la phase métallique en phase gazeuse. Outre leur effet sur le frittage, les carbonyles de nickel pouvant être formés sous des pressions partielles de CO élevées peuvent entraîner une perte de nickel du fait de leur volatilité plus importante (Fig. 16). La formation de tétra-carbonyles Ni(CO)4 peut causer la volatilisation du nickel, entraînant la perte de masse active du catalyseur, évacuée sous forme gazeuse.
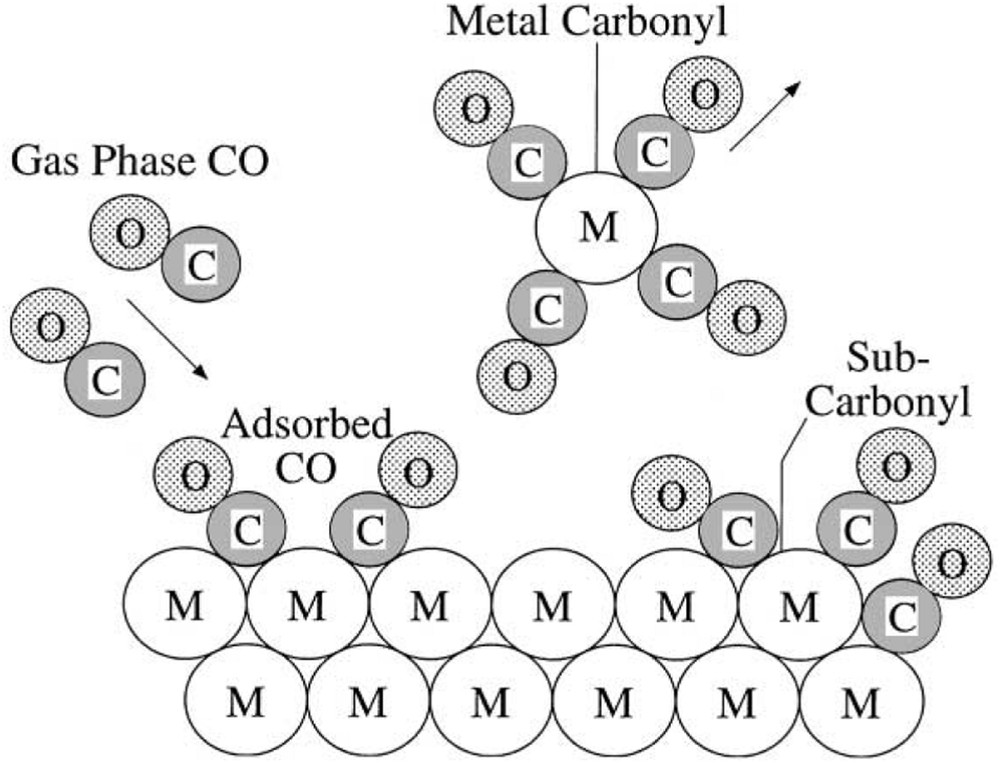
Mécanisme de formation de carbonyle de nickel (M) en présence de CO [74].
La désactivation apparente du catalyseur peut également être d'origine mécanique. Elle peut être due au broyage du catalyseur, lors du remplissage d'un réacteur par exemple, à l'attrition de celui-ci en fonctionnement ou encore à l'érosion d'un dépôt de catalyseur. Si la première cause est commune aux principaux types de réacteurs, les deux dernières concernent avant tout les réacteurs à lits fluidisés et à slurry pour l'attrition des catalyseurs.
3 Les procédés et démonstrateurs industriels de méthanation
Les réactions de méthanation ont été, pendant longtemps, principalement utilisées pour l'élimination de traces de CO dans le procédé de synthèse de l'ammoniac. Les premiers procédés de méthanation, utilisés pour la production de gaz naturel de synthèse (SNG), à partir de la gazéification du charbon, ont vu le jour en Allemagne lors de la seconde guerre mondiale. Ce n'est cependant qu'à partir des années 1960–1970, à la suite d'une forte hausse du prix du gaz, que la synthèse de SNG à partir de charbon a reçu un réel intérêt industriel. Dans ce cadre, de nombreux procédés de synthèse de SNG ont ainsi été développés au cours de la période située entre les années 1960 et 1980. L'intérêt porté à la méthanation du CO2 est apparu, quant à lui, plus récemment, notamment avec l'émergence du concept power to gas. Ces procédés, dédiés pour la plupart à la gazéification du charbon, visent toutefois le traitement en continu de grands débits de gaz et mettent principalement en œuvre la méthanation du CO. Ils répondent donc à des problématiques éloignées de celles d'un procédé power to gas. L'unique démonstrateur de méthanation du CO2, dans le cadre du power to gas développé par la société Etogas, sera également détaillé.
3.1 Les procédés de méthanation utilisant des réacteurs adiabatiques à lit fixe
Parce qu'il représente la structure, la plus simple, de réacteur catalytique, le réacteur adiabatique à lit fixe a été largement utilisé dans les procédés de production de SNG à partir de la gazéification du charbon. Ce type de réacteur n'étant pas directement refroidi, les procédés l'utilisant font appel à une série de réacteurs adiabatiques, chacun étant suivi d'un échangeur thermique qui évacue la chaleur générée par la réaction et refroidit le gaz produit.
3.1.1 Le procédé Lurgi
Le procédé Lurgi (Fig. 17), développé dans les années 1930 en Allemagne pour la production de SNG à partir du charbon, fut l'un des premiers procédés de production de SNG commercialisés dans les années 1960–1970. L'unité de méthanation est composée de deux réacteurs adiabatiques à lit fixe, séparés par des échangeurs de chaleur permettant de refroidir les gaz issus du premier réacteur et de récupérer la chaleur produite par la réaction. Un recyclage du gaz issu du premier réacteur est opéré pour limiter la température au sein de celui-ci, au prix d'un surcoût énergétique lié à la compression des gaz. Dans le premier réacteur adiabatique, du fait du déplacement d'équilibre généré par l'ajout de produits de la réaction, le recyclage du gaz permet d'augmenter la capacité calorique du gaz entrant ainsi que de limiter la conversion obtenue, et donc la chaleur dégagée.
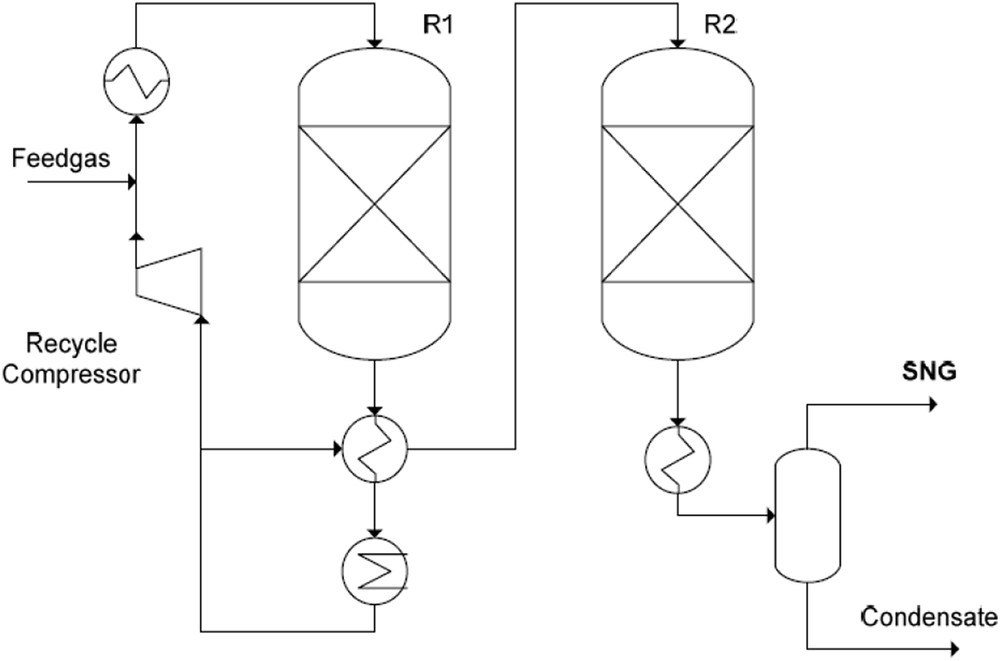
Schéma du procédé de méthanation Lurgi [79].
Les conditions opératoires typiques de ce procédé sont résumées dans le Tableau 4. Il sera noté que les compositions sont exprimées en gaz sec, malgré la présence d'eau dans les gaz. Dans ces conditions, près de 90% du gaz issu du premier réacteur sont recyclés afin de limiter la température à 450 °C. Du fait de la forte conversion déjà atteinte, l'élévation de température est plus limitée (élévation de 55 °C) au sein du second réacteur et ne nécessite pas de mesures particulières. À la sortie du second réacteur, le monoxyde de carbone est presque entièrement converti, contrairement au CO2, dont la proportion est encore très élevée. Le gaz produit par ce procédé n'est donc pas compatible avec une injection sur un réseau gazier. Une étape de purification est par conséquent nécessaire, ce qui entraîne un coût d'installation plus élevé.
Conditions opératoires typiques du procédé de méthanation Lurgi [79].
| Gaz d'alimentation | Réacteur à lit fixe R1 | Réacteur à lit fixe R2 | |||
| Entrée | Sortie | Entrée | Sortie | ||
| Temp., °C | 270 | 300 | 450 | 260 | 315 |
| Flux gazeux (humide), | 18,2 | 96,0 | 89,6 | 8,2 | 7,9 |
| Composition du gaz sec, vol % | |||||
| H2 | 60,1 | 21,3 | 7,7 | 7,7 | 0,7 |
| CO | 15,5 | 4,3 | 0,4 | 0,4 | 0,05 |
| CO2 | 13,0 | 19,3 | 21,5 | 21,5 | 21,3 |
| CH4 | 10,3 | 53,3 | 68,4 | 68,4 | 75,9 |
| C2+ | 0,2 | 0,1 | 0,05 | 0,05 | 0,05 |
| N2 | 0,9 | 1,7 | 2,0 | 2,0 | 2,0 |
Lors des essais réalisés, la température d'équilibre de 450 °C dans le premier réacteur est atteinte en utilisant 20% du lit fixe après 120 h de fonctionnement. Ce point se déplace ensuite dans le réacteur du fait de la désactivation du catalyseur pour finalement se situer à 32% du lit après 4000 h de fonctionnement (Fig. 18). Le surdimensionnement des réacteurs adiabatiques permet de disposer de suffisamment de catalyseur pour compenser sa désactivation et augmenter la durée de vie des lits catalytiques. En comparaison avec le catalyseur neuf, la surface de nickel du catalyseur après 4000 heures de fonctionnement a diminué de 50%, et la taille des cristallites de nickel a augmenté de 4 à 7,5 nm, signe de la désactivation du catalyseur par des phénomènes de frittage. Ce procédé de méthanation est utilisé depuis 1984 dans l'installation de production de SNG à partir du charbon « Great Plains » aux États-Unis. Dans cette installation, le procédé de méthanation est dédié exclusivement à la méthanation du CO, le CO2 présent dans le gaz étant séparé en amont de l'étape de méthanation. La production de cette installation fut de 3,5 millions de Nm3/jour jusqu'en 1992, puis augmentée à 4,8 Nm3/jour grâce à des améliorations continues [79].
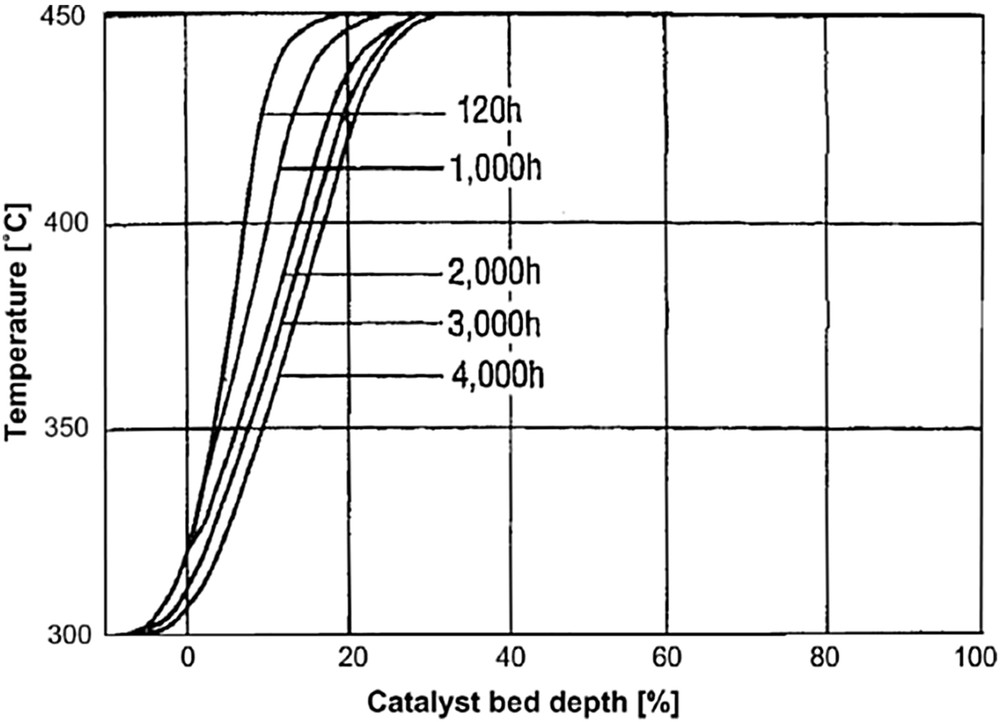
Profil de température dans le premier réacteur du procédé de méthanation Lurgi en fonction du temps d'utilisation [79].
3.1.2 Le procédé HICOM
Le procédé HICOM (Fig. 19), développé par la British Gas Corporation, utilise également une stratégie de recyclage pour limiter la température maximale dans le premier réacteur de méthanation. La particularité de ce procédé est cependant d'effectuer une réaction de Water Gas Shift (WGS) dans le réacteur de méthanation pour ajuster le ratio H2/CO, trop faible en sortie du gazéifieur, afin d'éviter la formation de dépôt de carbone. Pour cela, de la vapeur d'eau est ajoutée au gaz d'alimentation en amont du procédé.
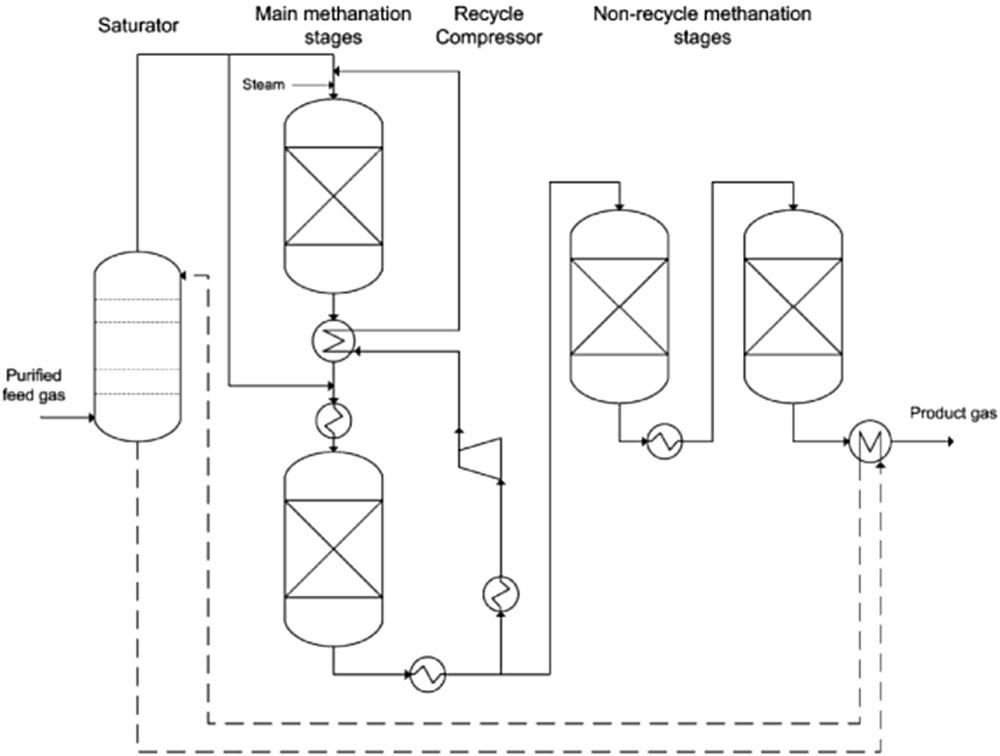
Schéma du procédé de méthanation HICOM [79].
Ce procédé fait intervenir deux premiers réacteurs de méthanation, suivi de un ou de plusieurs réacteurs fonctionnant à plus basse température pour achever la conversion. Des échangeurs de chaleur sont présents entre chaque réacteur pour refroidir les gaz. L'ajout de vapeur d'eau en amont du réacteur présente plusieurs avantages, outre la combinaison de la réaction de Water Gas Shift à la réaction de méthanation. Il permet tout d'abord de contribuer à la réduction des températures au sein des réacteurs en raison de la forte capacité calorifique de la vapeur d'eau et du déplacement de l'équilibre thermodynamique qu'il entraîne. Cet ajout permet également de réduire la formation de dépôts de carbone, en favorisant la gazéification de ces derniers. En contrepartie, l'ajout de vapeur d'eau favorise les dégradations du catalyseur par frittage et réduit le rendement énergétique du procédé. La vapeur d'eau devant être produite est surchauffée à partir de la chaleur de réaction dans le procédé HICOM. Le gaz utilisé pour effectuer le recyclage est prélevé à la sortie du second réacteur et injecté en amont du premier. Par ailleurs, l'alimentation du gaz issu de la gazéification est étagée entre les deux premiers réacteurs, ce qui permet de réduire le taux de recyclage et la quantité de vapeur d'eau ajoutée pour limiter la température dans le premier réacteur. Plusieurs essais, d'une durée allant jusqu'à 2000 h, ont été réalisés avec des catalyseurs de 3,2 et 5,4 mm de diamètre. Les conditions opératoires et compositions typiques des gaz sont données dans le Tableau 5. Ce procédé a été employé dans une unité semi-industrielle en Écosse permettant de convertir 5300 m3 de syngas par heure.
Exemple de conditions opératoires du procédé de méthanation HICOM [79].
| Gaz d'alimentation | Gaz produit | |
| Température à l'entrée (°C) | 230 | 320 |
| Pression (bar) | 25 | 70 |
| Temp. maximale (°C) | 460 | 640 |
| Composition du gaz sec (vol.%) | ||
| H2 | 11,7 | 5,5 |
| CO | 12,6 | 1,1 |
| CO2 | 43,0 | 53,1 |
| CH4 | 31,7 | 39,3 |
| N2 | 1,0 | 1,1 |
3.1.3 Le procédé RMP
Contrairement aux procédés présentés précédemment, le procédé RMP (Fig. 20), développé par la Ralph M. Parsons Company, n'utilise pas de recyclages internes pour contrôler la température dans les réacteurs de méthanation. La température atteinte dans les réacteurs est réduite par l'ajout de vapeur d'eau en amont du premier réacteur et par une alimentation étagée du syngas entre les trois premiers réacteurs. La température en sortie des premiers réacteurs est très élevée, de l'ordre de 770 °C. Le gaz passe ensuite dans une série de plusieurs autres réacteurs pour assurer la conversion souhaitée. Les avantages et inconvénients de ce procédé sont les mêmes que dans le procédé HICOM concernant l'ajout de vapeur d'eau.
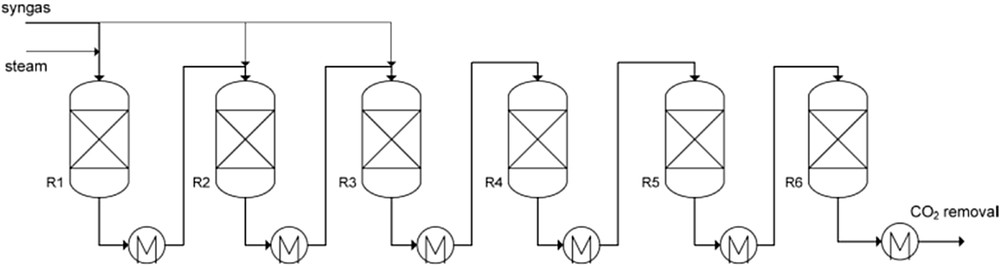
Schéma d'un procédé de méthanation RMP à six réacteurs [79].
Plusieurs essais furent menés avec des pressions et des compositions de gaz variables ; le Tableau 6 fournit les conditions opératoires pour un essai réalisé à 27 bar. Encore une fois, la proportion élevée de CO2 dans le gaz produit nécessite une étape de capture pour obtenir un SNG admissible sur un réseau de gaz naturel. Un procédé similaire, utilisant trois réacteurs adiabatiques en série, a été développé par l'Imperial Chemical Industrie (Grande-Bretagne). De la même manière, de la vapeur d'eau est ajoutée en amont du premier réacteur pour limiter la température à 750 °C. L'alimentation n'est cependant pas étagée : la quantité d'eau introduite pour limiter la température est par conséquent supérieure à celle dans le procédé RMP : environ 48% du débit total du gaz d'alimentation pour ce dernier contre environ 67% pour le procédé ICI. Le catalyseur utilisé a été spécialement développé pour cette application. Ce catalyseur présente un fort chargement en nickel, environ 60% massique en oxyde de nickel, et a montré une bonne activité et sélectivité en méthane pendant un essai de 1500 h [79].
Conditions opératoires du procédé RMP à 27 bar [79].
| Entrée | Sortie | ||||||
| R1 | R1 | R2 | R3 | R4 | RS | R6 | |
| Temp., °C (entrée) | 482 | 538 | 538 | 538 | 316 | 260 | |
| Temp., °C (sortie) | 482 | 773 | 779 | 773 | 717 | 604 | 471 |
| Pression, bar | 27,3 | 26,7 | 25,6 | 24,6 | 23,6 | 22,6 | 21,5 |
| Syngas, vol % (entrée) | 40 | 30 | 30 | – | – | – | |
| Vapeur/gaz | 1,20 | 0,88 | 0,56 | 0,43 | 0,50 | 0,65 | 0,83 |
| Composition du gaz sec (vol. %) | |||||||
| H2 | 49,8 | 53,5 | 48,1 | 43,1 | 36,9 | 22,9 | 9,3 |
| CO | 49,8 | 14,0 | 18,5 | 20,6 | 15,3 | 5,6 | 0,88 |
| CO2 | 0,1 | 25,8 | 24,0 | 23,6 | 29,2 | 39,9 | 46,8 |
| CH2 | 0,5 | 5,7 | 9,4 | 12,6 | 18,6 | 31,6 | 43,0 |
3.1.4 Le procédé TREMP
Le procédé de méthanation TREMP (Topsøe Recycle Energy Efficient Methanation Process) a été développé par Haldor Topsøe (Fig. 21) dans les années 1970–1980 dans le cadre du projet « NFE – Nuclear long-distance energy transportation », au Danemark et en Allemagne. Ce projet visait à récupérer et transporter la chaleur produite par un réacteur nucléaire à haute température.
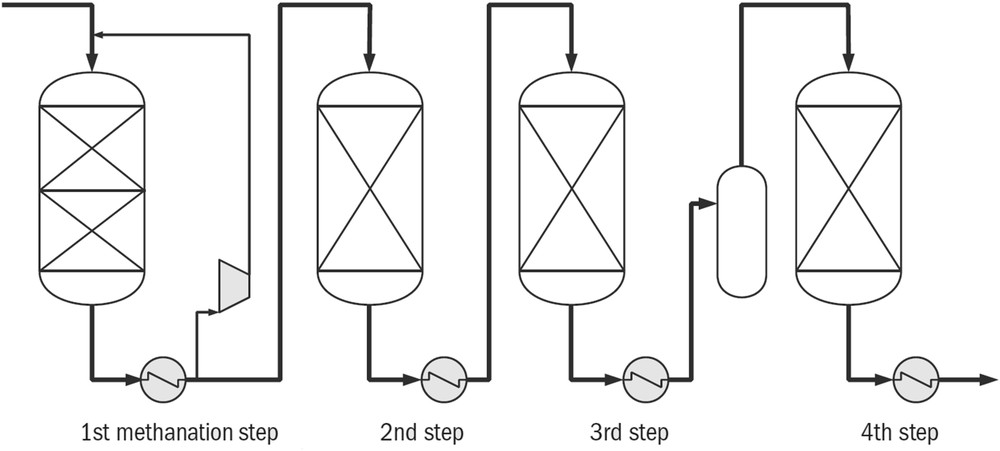
Schéma du procédé TREMP avec quatre réacteurs et une étape de condensation intermédiaire [81].
Le procédé consistait en une première étape de vaporeformage de méthane (pilote EVA), suivie d'une étape de méthanation du mélange H2 et CO formé (pilote ADAM). Le procédé TREMP est constitué d'une succession de trois ou quatre réacteurs adiabatiques avec des échangeurs de chaleur intercalés entre chaque réacteur. Selon les cas, une étape de condensation peut être effectuée avant le dernier réacteur (Fig. 21). Comme pour le procédé Lurgi, l'élévation de température au sein du premier réacteur est limitée par un recyclage du gaz. Le procédé TREMP utilise cependant une température plus élevée en sortie de premier réacteur (entre 600 et 700 °C) afin de produire de la vapeur surchauffée. L'utilisation d'une température plus élevée permet de plus de réduire le taux de recyclage en aval du premier réacteur : environ 70% pour une température de 600 °C (Tableau 7). Un exemple de conditions opératoires de ce procédé dans le cadre du pilote ADAM I est donné dans le Tableau 7. D'après cet exemple, le GHSV (Gas Hourly Space Velocity), défini comme le ratio entre le débit de gaz et le volume du réacteur, du procédé de méthanation global n'est que d'environ 744 h−1. Afin de travailler à ces températures élevées, un catalyseur à base de nickel (MCR-2X) a été spécialement développé par Haldor Topsøe. Ce catalyseur contient 22% de nickel déposé sur une structure céramique « stabilisée », dont la nature n'est pas précisée. Sa surface spécifique est d'environ 55 m2/g et la taille des cristallites de nickel est de l'ordre de 20 nm. Ce catalyseur présente une bonne résistance aux dépôts de carbone se produisant lors de la méthanation du CO à 330 °C et aux phénomènes de frittage des cristallites de nickel [78,81].
Conditions opératoires du procédé TREMP pour le pilote ADAM I, constitué de trois réacteurs adiabatiques [82].
| Alimentation (syngas) | R1 Entrée | R1 Sortie | R2 Sortie | R3 Sortie | Produit | |
| Température (°C) | 300 | 604 | 451 | 303 | 23 | |
| Pression (bar) | 27,3 | 27,2 | 27,1 | 27,05 | 27 | 27 |
| Débit (Nm3/h) | 535 | 1416 | 1255 | 348 | 334 | 119 |
| Composition (%) | ||||||
| H2 | 65,45 | 36,88 | 20,96 | 8,10 | 1,77 | 3,11 |
| CO | 9,84 | 4,28 | 1,17 | 0 | 0 | 0 |
| CO2 | 8,96 | 6,13 | 4,46 | 2,07 | 0,95 | 1,67 |
| CH4 | 11,3 | 28,12 | 37,44 | 44,36 | 47,28 | 82,95 |
| H2O | – | 19,19 | 29,82 | 38,84 | 43,06 | 0,10 |
| N2 | 4,4 | 5,41 | 6,15 | 6,64 | 6,93 | 12,16 |
| GHSV (h−1) | – | 4453 | 3946 | 3823 | 4021 | – |
Dans les années 1980, la stabilité du procédé TREMP a été démontrée sur des durées de plusieurs milliers d'heures. Une certaine désactivation du catalyseur est cependant observée et se traduit par le déplacement du front réactif au sein du réacteur (Fig. 22). De récents développements menés par Haldor Topsøe semblent avoir rendu le catalyseur MCR-2X plus stable, comme le montrent les profils de températures mesurés à différents temps d'utilisation présentés dans la Fig. 22.
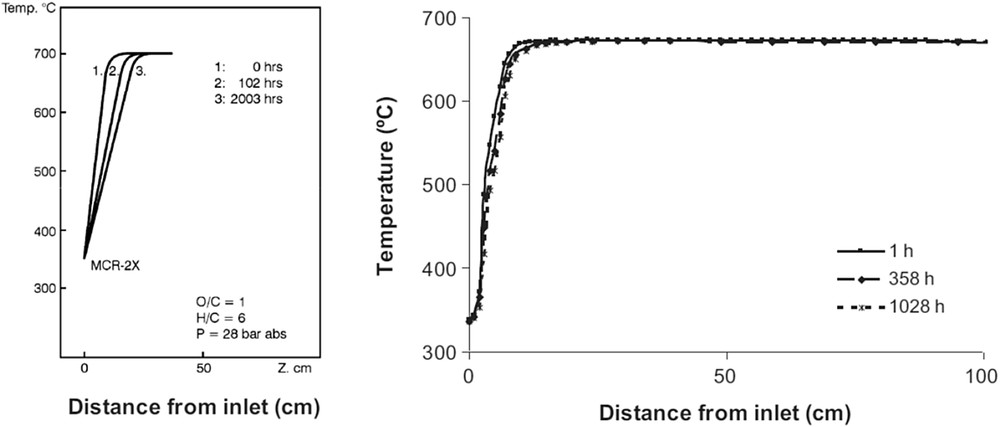
Profils de température mesurés en fonction du temps dans un réacteur adiabatique avec le catalyseur MCR-2X : procédé TREMP dans les années 1980 (gauche) [73,78,82].
Le procédé TREMP peut fonctionner avec des températures d'alimentation basses (entre 200 et 300 °C) pour la mise en œuvre de la méthanation du CO, sans risquer de désactivation accélérée grâce à la combinaison du catalyseur MCR-2X et d'un autre catalyseur sans nickel (catalyseur Cu/Zn/Al). Ce catalyseur est alors placé au début du réacteur afin de réaliser la conversion nécessaire pour élever la température à une valeur compatible avec l'utilisation de catalyseur à base de nickel (environ 330 °C) [81,83]. Le procédé TREMP est aujourd'hui utilisé dans les usines de gazéification du charbon et de biomasse dont l'usine de Quinghua en Chine, permettant la production de 1,4 milliards de Nm3 de SNG par an à partir du charbon [83]. Haldor Topsøe participe également à un projet power to gas au Danemark, visant la production de 10 Nm3/h à partir de CO2 issu d'un procédé de méthanisation.
3.2 Les procédés de méthanation utilisant des réacteurs-échangeurs à lit fixe ou fluidisé
Parce qu'ils permettent de combiner les fonctions réactionnelles et le refroidissement des gaz, les réacteurs-échangeurs ont également été utilisés pour la production de SNG à partir de la gazéification de charbon. Cette combinaison des fonctions permet de réduire le nombre d'équipements nécessaire pour obtenir des conversions élevées, et donc de réduire la taille de l'installation et l'investissement par rapport aux procédés utilisant des réacteurs à lit fixe adiabatique. Parce que ces contraintes d'encombrement et de coûts sont très présentes dans la problématique power to gas, les réacteurs-échangeurs sont étudiés pour cette application. L'utilisation de réacteur-échangeur à lit fixe se heurte néanmoins aux problèmes posés par la gestion thermique de la réaction en lien avec la dégradation des catalyseurs ; c'est pourquoi un certain nombre de procédés ont été conçus avec des réacteurs à lit fluidisé, procurant de meilleures performances thermiques. Dans la plupart des cas, l'utilisation seule de ce type de réacteur ne suffit pas à résoudre le problème de la gestion thermique et nécessite, comme pour les réacteurs à lit fixe, la prise de mesures visant à réduire la chaleur générée par la réaction.
3.2.1 Le procédé Linde
Ce procédé développé par Linde AG utilise deux réacteurs à lits fixes, le premier étant adiabatique, l'autre étant un réacteur-échangeur permettant un fonctionnement quasi-isotherme. Afin de permettre ce type de fonctionnement, le réacteur dit « isotherme » comporte un grand nombre de tubes de refroidissement directement noyés dans le lit fixe. Un schéma de ce type de réacteur est donné sur la Fig. 23. Le procédé de méthanation Linde permet de répartir les réactifs à travers ces deux types de réacteurs, voire d'envoyer les gaz issus du réacteur isotherme dans le réacteur adiabatique afin d'augmenter la conversion du syngas. De la vapeur d'eau, produite dans le circuit de refroidissement du réacteur isotherme, est surchauffée en sortie du réacteur adiabatique, et peut être mélangée aux réactifs afin de mieux contrôler la température et limiter l'apparition de dépôts de carbone (voir Fig. 24).
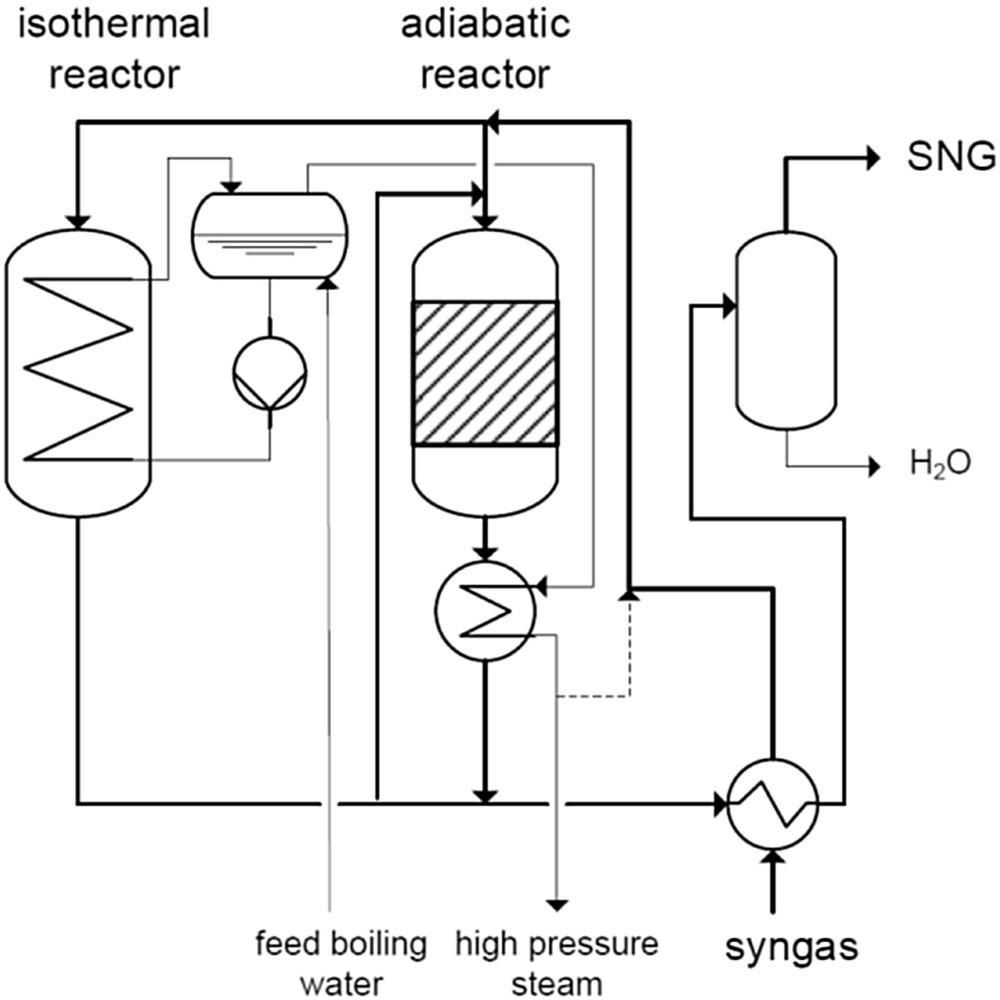
Schéma du procédé de méthanation Linde avec un réacteur isotherme et un réacteur adiabatique [79].
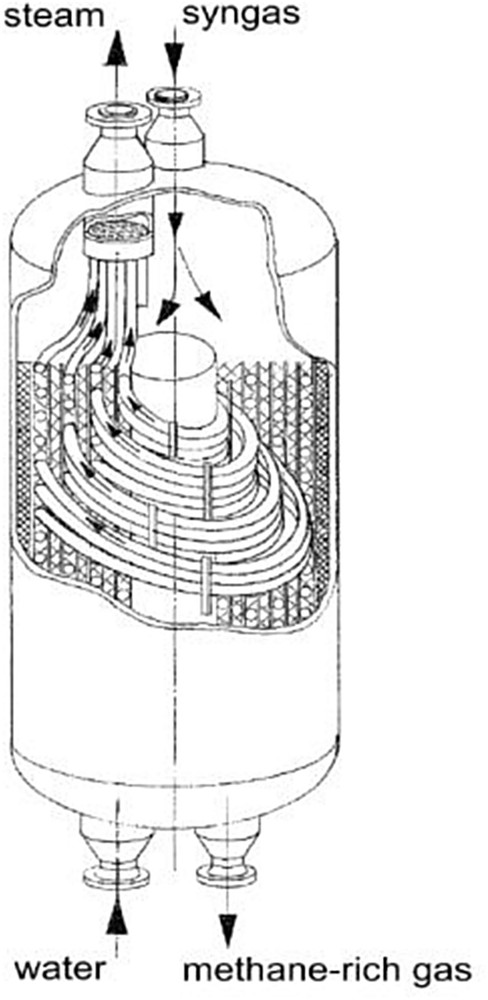
Schéma du réacteur isotherme de Linde [79].
L'utilisation du réacteur isotherme permet ici d'obtenir une bonne conversion des réactifs en un seul étage. Dans ce type de réacteur, la température demeure en effet suffisamment basse pour qu'on ne soit pas limité par la conversion imposée par l'équilibre thermodynamique, contrairement aux procédés à lits fixes adiabatiques, qui nécessitent plusieurs réacteurs séparés par des échangeurs de chaleur. Elle permet également d'intégrer la production du SNG et de la vapeur d'eau dans un seul équipement. Toutefois, la difficulté de la gestion thermique de la réaction conduit à une conception de réacteur complexe afin de réduire les résistances thermiques présentes dans le lit catalytique pour obtenir un fonctionnement quasi isotherme. Aucune information sur les conditions opératoires de ce procédé n'a toutefois été trouvée. Ce réacteur est aujourd'hui toujours commercialisé, pour la production de méthanol notamment.
3.3 Procédés utilisant des réacteurs à lit fluidisé
La recherche du contrôle thermique de la réaction a conduit au développement de plusieurs procédés utilisant des réacteurs à lit fluidisé. L'avantage principal de ce type de réacteur est de présenter une très bonne homogénéité des températures au sein du lit, grâce au mélange généré par la fluidisation, ainsi que de meilleurs échanges en paroi en comparaison de ceux obtenus dans des réacteurs à lit fixe. Un autre avantage est de permettre l'utilisation de grains de catalyseur de très petites dimensions (de quelques dizaines à quelques centaines de micromètres), permettant de limiter les résistances de diffusion à l'intérieur des grains, sans conduire à des pertes de charges rédhibitoires. L'attrition des catalyseurs générée par le mouvement des grains reste cependant un problème majeur pour cette technologie et nécessite un étage aval de séparation/filtration des particules fines et un remplacement fréquent du catalyseur. Cette technologie de réacteur ne procure cependant qu'une relative flexibilité au débit de gaz, du fait de la nécessité de fluidiser le lit de catalyseur. De plus, le comportement hydrodynamique de ces réacteurs rend plus difficile l'accès aux très hauts taux de conversion du fait des rétro-mélanges générés par la circulation du catalyseur. Cette technologie de réacteurs est ainsi plus adaptée pour la production continue de SNG à partir de la gazéification du charbon que pour une application power to gas. Deux démonstrations de production de SNG à partir du charbon en lit fluidisé ont été développées aux États-Unis entre les années 1950 et 1960 par le Bureau of Mines et la Bituminous Coal Research Inc. (BCR) avec le projet Bi-Gas. Le premier réacteur à lit fluidisé développé par le Bureau of Mines possède un diamètre de lit catalytique de 19 mm et une hauteur d'environ 1,8 m. Malgré ce faible diamètre, des élévations de température d'environ 100 °C ont été mesurées. Un second réacteur, possédant un diamètre de lit de 25,4 mm, a ensuite été conçu avec une alimentation étagée afin d'améliorer la gestion thermique de la réaction. Le réacteur présent trois points d'injection de réactif, ce qui permet de limiter à environ 20 °C l'élévation de température (Fig. 25).
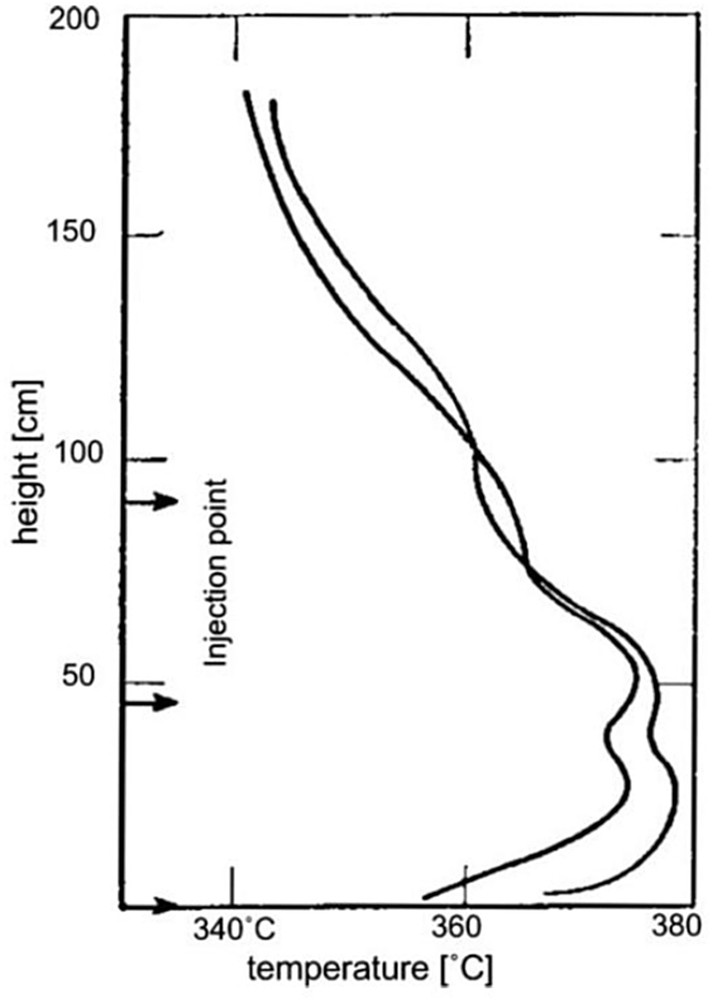
Profils de températures mesurées dans le réacteur à lit fluidisé développé par le Bureau of Mines (États-Unis) [79].
Le réacteur conçu par la BCR (Fig. 26) dans le projet Bi-Gas possède un diamètre nettement supérieur, d'environ 150 mm, pour une hauteur de 4,5 m, la hauteur de la zone réactive du réacteur étant de 2,5 m. Afin de contrôler l'exothermicité de la réaction, le refroidissement est directement inséré à l'intérieur du lit fluidisé, avec une surface d'échange interne de 3 m2. L'alimentation des réactifs est également étagée avec un point d'injection intermédiaire. Ce réacteur pouvait fonctionner à très haute pression, entre 69 et 87 bar, et permettait l'obtention de taux de conversion en CO supérieurs à 96%.
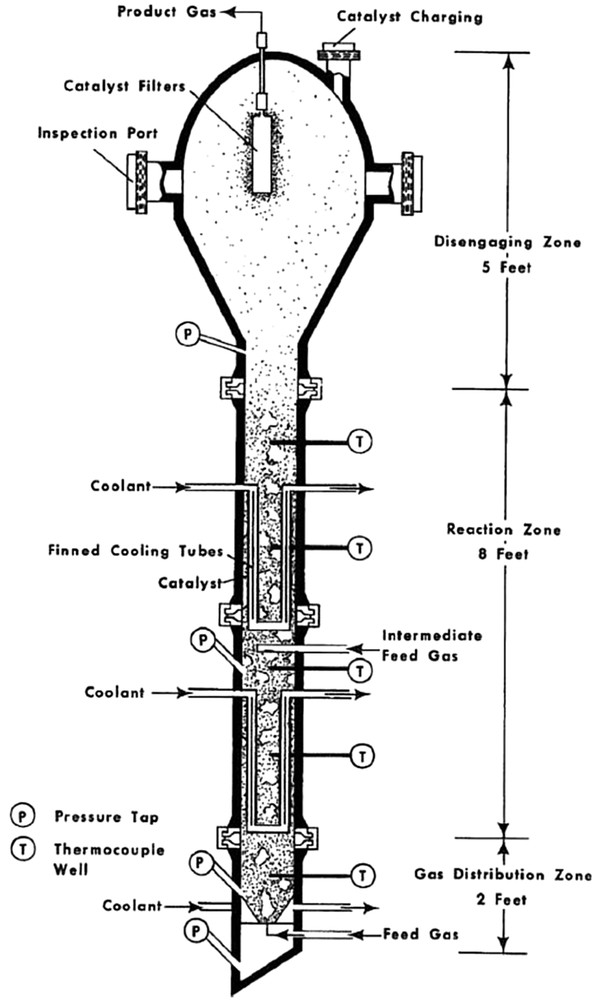
Schéma du réacteur à lit fluidisé développé par la BCR [79].
Entre 1975 et 1986, la société Thyssengas GmbH, en Allemagne, a développé le procédé Comflux pour la production de SNG à partir du charbon. Le réacteur de méthanation à lit fluidisé (Fig. 27), avec refroidissement interne, combine, de la même manière que le procédé à lits fixes adiabatiques HICOM, la réaction de water gas shift à la méthanation grâce à l'ajout de vapeur d'eau aux gaz réactifs. Cet ajout d'eau facilite également la gestion thermique de la réaction. Un démonstrateur du procédé Comflux a été construit en 1981 avec un réacteur à lit fluidisé d'un mètre de diamètre pour une production de 2000 Nm3/h de SNG.
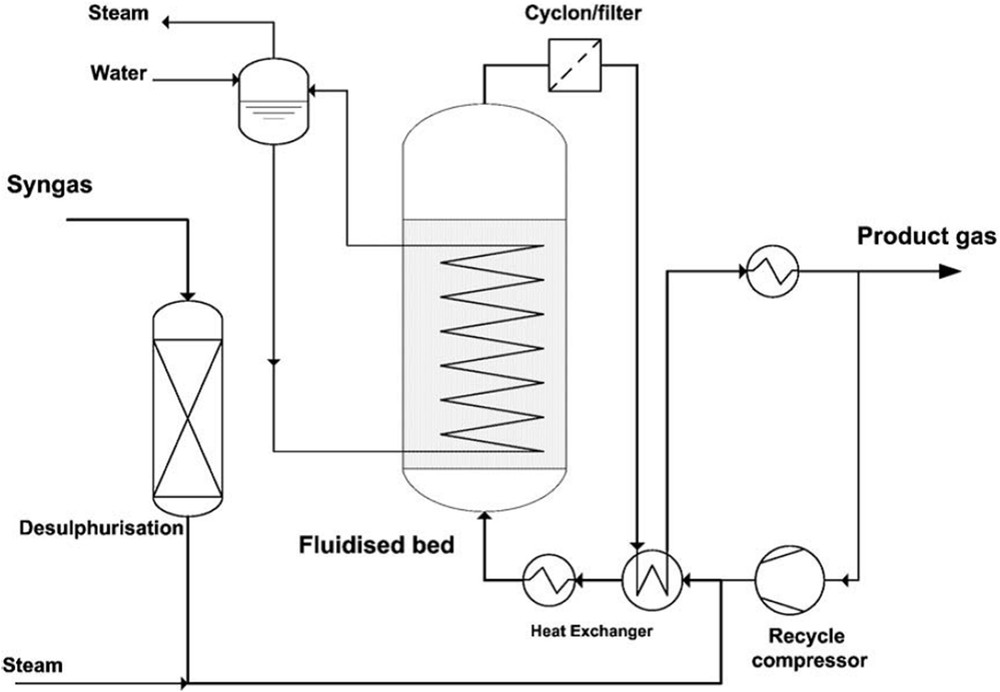
Schéma de la partie méthanation du procédé Comflux [79].
L'institut Paul-Scherrer (PSI, Suisse) a mis au point un procédé de méthanation pour la production de SNG à partir de biomasse. Ce procédé a été validé au cours du projet européen Bio-SNG (2009) et a été choisi pour les projets Gaya, en France et GoBiGas, en Suède.
3.4 Les premiers démonstrateurs de power to SNG
Depuis la fin des années 2000, la société Etogas (par exemple, Solarfuel), en partenariat avec le Zentrum für Sonnenergie und Wasserstoff Forshung (ZSW), a entrepris la réalisation de plusieurs démonstrateurs de procédé power to gas mettant en œuvre la méthanation du CO2 [84]. Le premier démonstrateur à petite échelle fut construit en 2009 pour une puissance électrique d'électrolyse de 25 kW, soit une production de 1,25 Nm3/h de CH4. La technologie d'électrolyseur retenue est l'électrolyse alcaline. L'étage de méthanation est constitué de deux réacteurs-échangeurs en lit fixe multitubulaires en série, séparés par une étape de condensation intermédiaire. Il n'existe que peu d'informations disponibles sur la structure précise des réacteurs utilisés. Il est probable que ces réacteurs soient issus des travaux de ZSW dans lesquels un réacteur de méthanation, refroidi par plusieurs circuits caloporteurs de sels fondus, a été testé (Fig. 28). La température de ces sels fondus décroît de 500 à 250 °C avec l'avancement dans le réacteur. Ce démonstrateur, comme les procédés à lits fixes adiabatiques, utilise un recyclage de gaz afin de contrôler la température au sein des réacteurs-échangeurs. Ceci montre, une fois de plus, l'importance de la gestion thermique de la réaction et les difficultés qu'elle pose, malgré l'utilisation de réacteurs-échangeurs multitubulaires. De la vapeur d'eau est également ajoutée en amont des réacteurs afin d'éviter la formation de dépôts de carbone [84]. Ce procédé de méthanation du CO2, présenté dans la Fig. 29, permet d'obtenir, après condensation de l'eau produite, un gaz pouvant contenir jusqu'à 92% de méthane. Il a cependant été reporté que le comportement dynamique du procédé est relativement limité, ce qui est probablement lié à l'utilisation d'un recyclage du gaz.
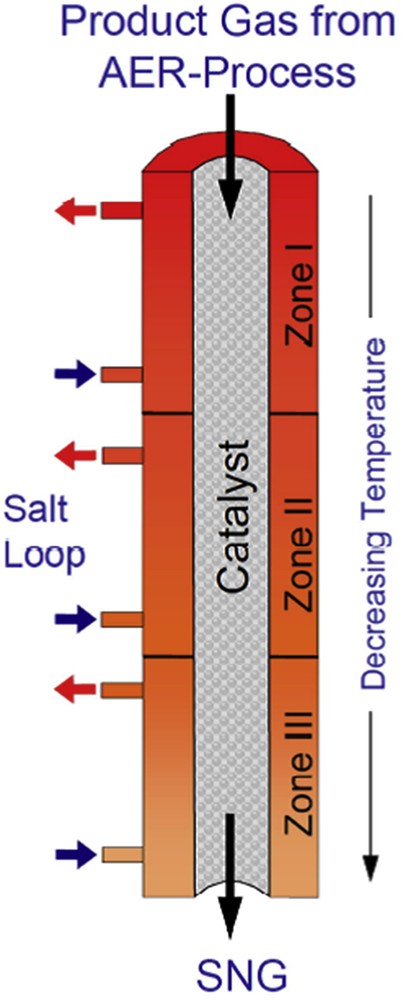
Schéma du réacteur de méthanation développé par ZSW [85].
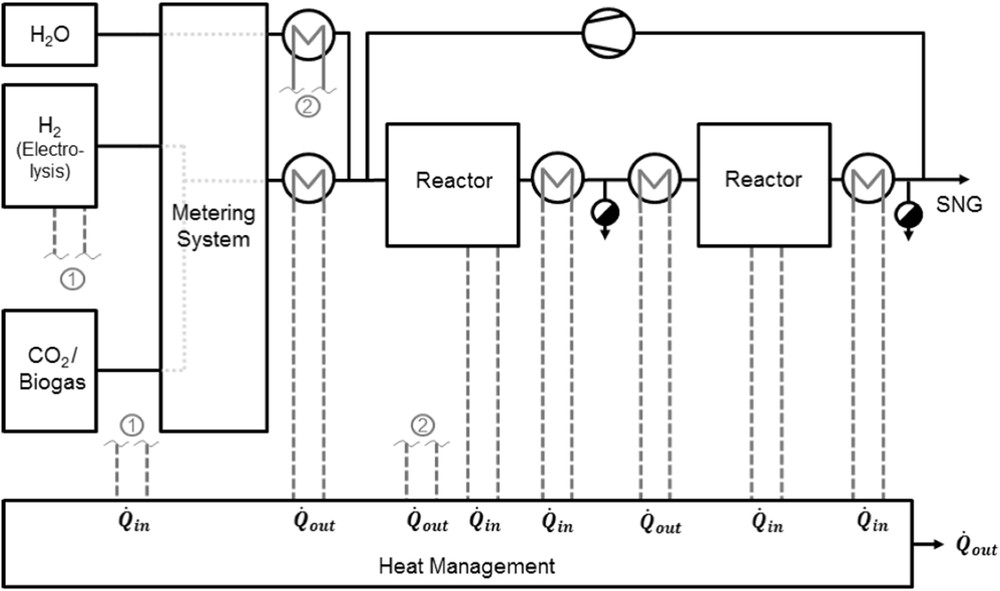
Schéma du procédé power to SNG d'Etogas dans le démonstrateur de 25 kW (2009) [84].
Un second démonstrateur a ensuite été construit pour une puissance de 250 kW électriques. Ce démonstrateur utilise deux réacteurs de méthanation différents, placés en parallèle et refroidis par des sels fondus ou de l'eau, liquide ou vapeur. Aucune information n'a cependant été trouvée concernant ces réacteurs. Cette fois, aucun recyclage du gaz n'est effectué, et de la vapeur d'eau n'est ajoutée que dans le cas de la méthanation du biogaz (mélange CO2 et CH4). Les gaz issus du premier réacteur peuvent toutefois être envoyés vers le second, après condensation. Une ultime étape de séparation membranaire permet enfin de purifier le gaz produit pour atteindre des compositions en méthane allant jusqu'à 99%. Les gaz éliminés dans cette séparation sont recyclés vers l'amont du procédé. Contrairement au démonstrateur 25 kW, le comportement dynamique de ce procédé est compatible avec un procédé power to gas [84]. Un démonstrateur à grande échelle a finalement été construit en 2013 pour Audi dans le cadre de son projet « e-gas ». La puissance électrique installée de ce démonstrateur est de 6 MW et le CO2 est issu d'un piégeage sur un procédé de méthanisation de biomasse. Le procédé de méthanation (Fig. 30) ne comporte qu'un seul réacteur multitubulaire en lit fixe refroidi par des sels fondus. Le contrôle de la température est effectué sans recyclage du gaz, grâce à une alimentation étagée des réactifs au sein du réacteur. Il n'y a pas non plus d'injection de vapeur d'eau en amont du réacteur. Ce procédé permet enfin de produire un gaz contenant 92% de méthane, conforme avec les spécifications des réseaux gaziers allemands [84].
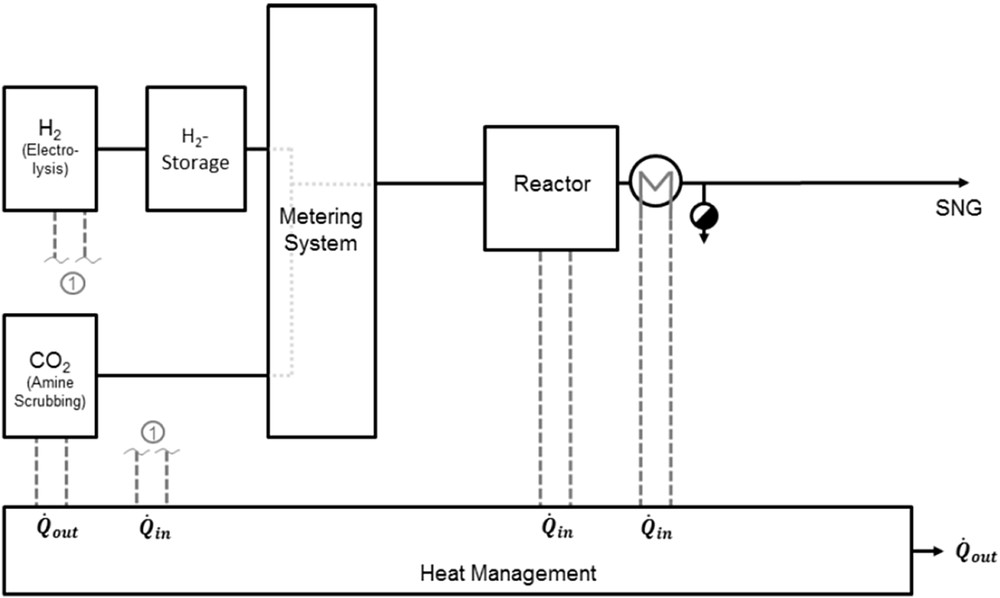
Schéma du procédé power to SNG dans le démonstrateur « e-gas » [84].
Le réacteur multitubulaire (Fig. 31) de ce procédé est fabriqué par la société Man Diesel et Turbo SE [86,87]. Ce réacteur est constitué de nombreux tubes contenant le catalyseur où sont placés des inserts servant à étager l'alimentation des réactifs et à diminuer le diamètre hydraulique des tubes contenant le catalyseur (typiquement entre 10 et 22 mm). Le réacteur est refroidi par deux circuits de sels fondus fonctionnant à des températures différentes : plus élevées dans le circuit situé en entrée de réacteur afin d'avoir une bonne activité catalytique, et plus basses en fin de réacteur afin d'augmenter la conversion finale. L'utilisation de ces deux circuits permet ainsi de se rapprocher d'un profil de température dit « optimal », compromis entre les cinétiques de réaction favorisées à hautes températures et la conversion limite, imposée par l'équilibre thermodynamique, plus grande à basse température. L'alimentation des gaz réactifs est uniquement étagée dans la première partie du réacteur refroidie par le circuit de caloporteur le plus chaud, qui représente 15 à 40% de la longueur totale du réacteur (longueur de la partie réactive). La pression opératoire de ce réacteur est inférieure à 20 bar. Le GHSV est typiquement de quelques milliers d'h−1 : 5000 h−1 d'après [86,87]. La méthanation du CO2 pur est effectuée en léger défaut d'hydrogène, avec un rapport H2/CO2 de 3,85 environ [86] (see Fig. 32).
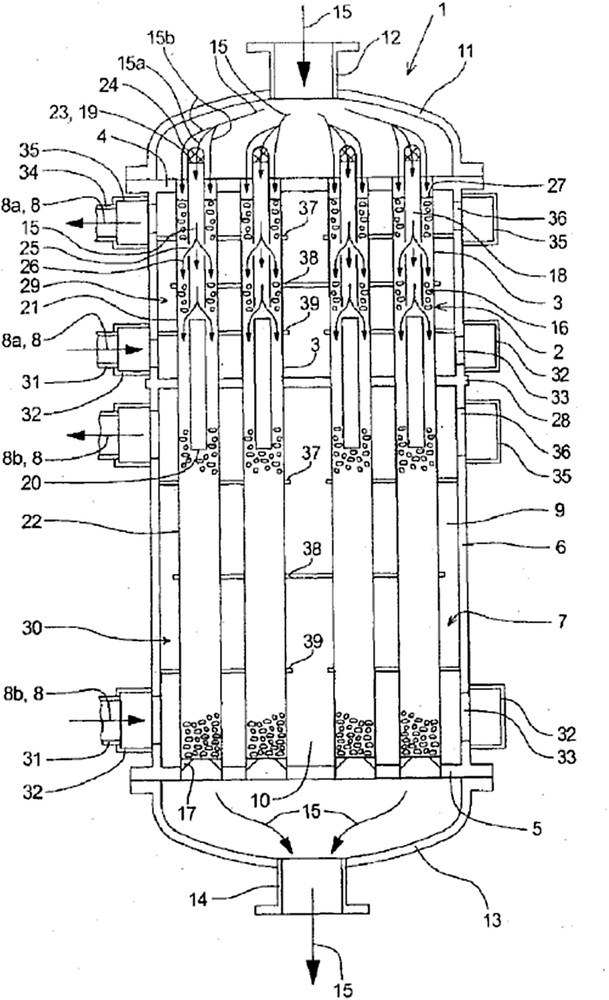
Schéma du réacteur de méthanation utilisé dans le démonstrateur « e-gas » [86].
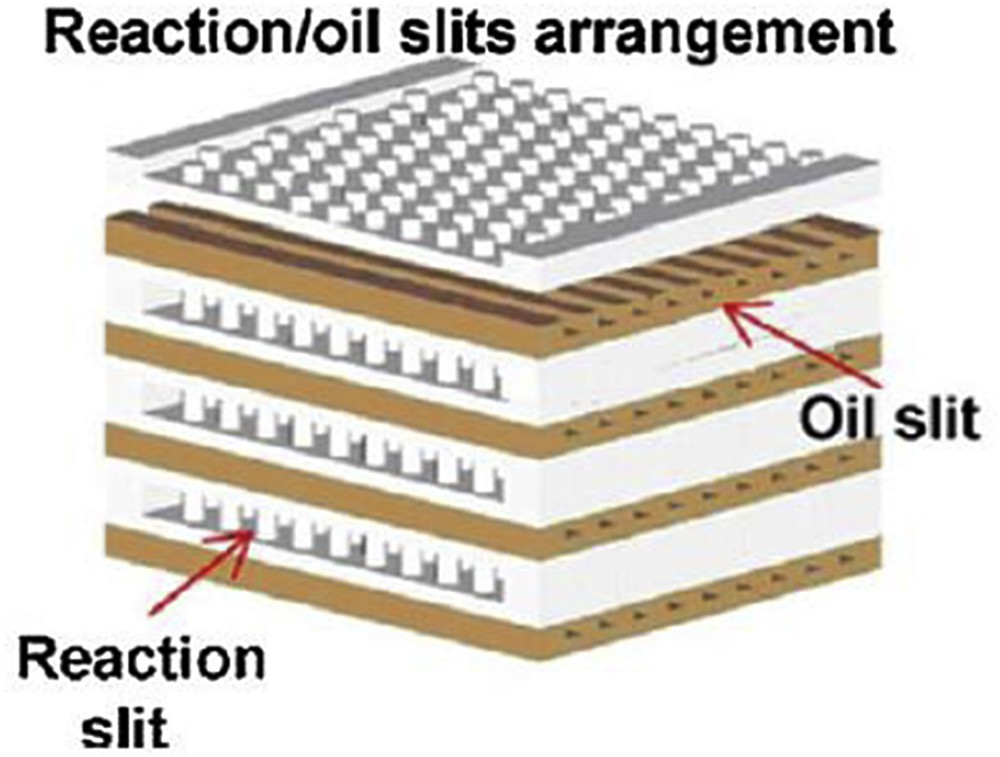
Schéma d'un réacteur milli-structuré à lit fixe utilisé pour la synthèse de diméthyl-éther [88].
Il est important de comprendre que ces premiers démonstrateurs power to gas sont confrontés à des problématiques nouvelles et différentes de celles des procédés de synthèse de SNG à partir de la gazéification du charbon. Ils opèrent avec un gaz entrant différent (mélange d'H2 et de CO2) et doivent répondre à des contraintes de flexibilité, d'encombrement et de coûts plus élevés, et pour des tailles d'installations relativement faibles. Bien que toujours confrontés aux problèmes de gestion thermique en lien avec la durée de vie du catalyseur, les procédés power to gas représentent un tournant dans les procédés de production de SNG, en s'éloignant du contexte classique de la gazéification du charbon : fonctionnement continu, coût de l'entrant (charbon) relativement faible et productions importantes. Ce nouveau cadre d'utilisation des réacteurs catalytiques de méthanation requiert de nouveaux réacteurs et procédés de méthanation, représentés aujourd'hui par l'exemple de l'unique réacteur du démonstrateur « e-gas ».
3.5 Les développements actuels de réacteurs-échangeurs pour les réactions catalytiques athermiques
Depuis la fin des années 2000, de nombreuses voies de développement pour les réactions de méthanation ont été étudiées. Ces divers développements concernent tous les stades de la mise en œuvre de ces réactions : de l'activation de la réaction, par la formulation de nouveaux catalyseurs ou par apport d'énergie externe, à la conception de réacteurs de méthanation innovants. Cette partie se restreint toutefois aux principaux développements concernant la structuration et la gestion de réacteurs-échangeurs de méthanation. Ces développements dépassent toutefois le cadre des réactions de méthanation, et peuvent s'étendre, par exemple, aux réactions catalytiques fortement athermiques et/ou équilibrées.
3.5.1 Systèmes et réacteurs visant à améliorer la gestion thermique des réactions catalytiques
3.5.1.1 Réacteurs-échangeurs à lit fixe milli-structurés
Une voie de développement abordée dans le but d'améliorer la gestion thermique des réactions de méthanation est l'amélioration des transferts thermiques au sein du lit catalytique. Cette amélioration de la gestion thermique permet d'éviter, ou au moins de limiter, le recours à des mesures visant à diminuer les performances du catalyseur (dilution des gaz par recyclage, ajout d'eau, alimentation étagée, dilution du catalyseur…). Une solution usuelle pour diminuer les résistances thermiques est la réduction des dimensions caractéristiques de transfert. S'inspirant des échangeurs de chaleur à plaques, des réacteurs-échangeurs utilisant des dimensions caractéristiques de canaux réactifs de l'ordre du millimètre au centimètre ont été étudiés pour diverses applications, comme le reformage de méthane ou encore la synthèse de Fischer–Tropsch [88]. Ces réacteurs se présentent sous la forme de plaques gravées et empilées, certaines formant des nappes de canaux réactifs et d'autres accueillant les nappes de canaux réservés au fluide caloporteur. La réduction des dimensions caractéristiques des canaux réactifs et des grains de catalyseurs permet d'intensifier les transferts de chaleur, réduisant ainsi la formation de points chauds et également les transferts d'espèces, notamment à l'intérieur des pores du catalyseur. Ces réacteurs à lits fixes milli-(ou micro) structurés peuvent permettre d'obtenir de plus grandes performances et de meilleures durées de vie du catalyseur, du fait d'une gestion thermique et chimique améliorée. Cette structure permet de plus de conserver les avantages liés au catalyseur en grains, notamment une relative facilité de mise en œuvre et une densité de catalyseur rapportée aux canaux réactifs élevée. En contrepartie, l'utilisation de grains de catalyseur de plus petites dimensions peut entraîner des pertes de charge élevées, pénalisantes pour l'efficacité énergétique globale du procédé. Ces pertes de charge peuvent toutefois être compensées par des longueurs de réacteur plus faibles, obtenues grâce à l'amélioration des performances du réacteur.
Le principal verrou à l'utilisation de cette structure de réacteur reste finalement d'ordre technologique, avec la production à grande échelle de ce type d'équipements. Les méthodes de fabrication usuelles n'étant pas adaptées, techniquement et/ou économiquement, à la fabrication de réacteurs pouvant comporter plusieurs dizaines, voire centaines de plaques formant les canaux de réactifs et de caloporteur. De nouveaux procédés d'assemblage par soudage-diffusion, basées sur la diffusion des atomes constituant l'acier à travers les interfaces à hautes températures (environ 1000 °C) et pression (environ 1000 bar), peuvent répondre aux contraintes de fabrication de ces réacteurs, en permettant notamment d'assembler ceux-ci en une seule étape. Ces techniques d'assemblage restent cependant à perfectionner, notamment au niveau de la maîtrise de la déformation des canaux au cours de l'assemblage. Un exemple de réalisation industrielle est celui des réacteurs de synthèse de Fischer–Tropsch de la société Velocys, aux États-Unis. Les dimensions des canaux réactifs en lit fixe du pilote décrit par Deshmukh et al. [89] sont de l'ordre de 1 mm de largeur et 3 mm de hauteur, la taille du catalyseur est de 200 à 300 μm de diamètre. Le refroidissement s'effectue avec des canaux disposés entre les nappes de canaux réactifs, et en courants croisés. Cette configuration de réacteur permet un fonctionnement isotherme à 210 °C.
3.5.1.2 Réacteurs-échangeurs utilisant un catalyseur déposé en paroi
L'intensification des transferts de chaleur et de masse au sein des réacteurs-échangeurs catalytiques a également conduit à l'étude de microréacteurs. Comme pour les réacteurs millistructurés à lits fixes, ces réacteurs sont constitués d'un empilement de plaques portant les canaux des réactifs et les canaux destinés au fluide caloporteur. La taille des canaux des réactifs est cependant plus faible, généralement inférieure au millimètre. Le catalyseur se présente sous la forme d'un dépôt, dont l'épaisseur est typiquement de quelques dizaines de micromètres, situé sur les parois de ces canaux. Dans cette structure de réacteur, le catalyseur est donc directement au contact de la paroi, elle-même en contact sur son autre face avec le fluide caloporteur. L'échange de chaleur au sein des canaux des réactifs s'effectue donc directement entre le catalyseur et la paroi et non via des échanges entre les grains de catalyseurs et le fluide réactif, comme dans le cas de réacteurs à lit fixe. De plus, étant donné les petits diamètres hydrauliques des canaux réactifs, les résistances au transfert de masse sont fortement diminuées, tout comme celles présentes au sein des pores du catalyseur, celui-ci présentant une taille caractéristique (épaisseur du dépôt) plus faible que dans un lit fixe. Enfin, les pertes de pression dans ces réacteurs sont beaucoup plus faibles en comparaison de celles d'un réacteur à lit fixe. Ces réacteurs permettent d'obtenir de très bonnes gestions thermique et chimique, avec une utilisation quasi totale du catalyseur (peu limitée par la diffusion interne). Il en résulte des performances améliorées, avec une masse de catalyseur réduite. La gestion thermique intensifiée de ces réacteurs permet, de plus, un fonctionnement dans des conditions où les réacteurs à lits fixes présenteraient un fort emballement thermique (notamment à pressions plus élevées). Le contrôle des températures au sein des réacteurs permet également une gestion accrue des phénomènes responsables de la désactivation des catalyseurs. Dans leurs travaux, Liu et al. [90] rapportent ainsi l'obtention de résultats de méthanation du CO à des pressions allant jusqu'à 30 atm. En utilisant un catalyseur de nickel/alumine déposé sur des plaques de FeCrAlloy formant le microréacteur utilisé (constitué d'un unique canal), les auteurs ont ainsi obtenu de très bonnes conversions du CO pour des GHSV allant jusqu'à 71,000 h−1 sous une pression de 30 atm et à des températures comprises entre 400 et 550 °C, comme le montre la Fig. 33. La température indiquée est toutefois celle du four où est placé le réacteur, aucune mesure in situ n'ayant été effectuée. Bien que la gestion thermique de ces réacteurs soit très bonne, il reste néanmoins possible qu'une légère élévation de température se produise. Ces résultats montrent toutefois la nécessité d'utiliser des températures élevées (>400 °C) pour obtenir de bonnes performances à de tels GHSV. À ces températures, la désactivation du catalyseur, du fait du frittage des cristallites de nickel, a été observée par les auteurs. Ce type de réacteur ne présente toutefois que de faibles masses de catalyseur rapportées au volume de canaux réactifs, ou au volume de réacteur, par rapport aux lits fixes. L'alternance de canaux réactifs et de canaux de caloporteur peut, de plus, générer un volume de parois important qui réduit la compacité des réacteurs. En comparaison avec d'autres types de réacteurs, il n'est pas toujours assuré que l'amélioration des performances obtenues compense le volume de réacteur plus important induit par des densités de catalyseur plus faibles. La fabrication de ces réacteurs utilisant de très petites tailles de canaux constitue également une difficulté. Enfin, la réalisation d'un dépôt de catalyseur, son remplacement, et surtout sa tenue mécanique dans le temps restent des aspects à maîtriser [91,92].
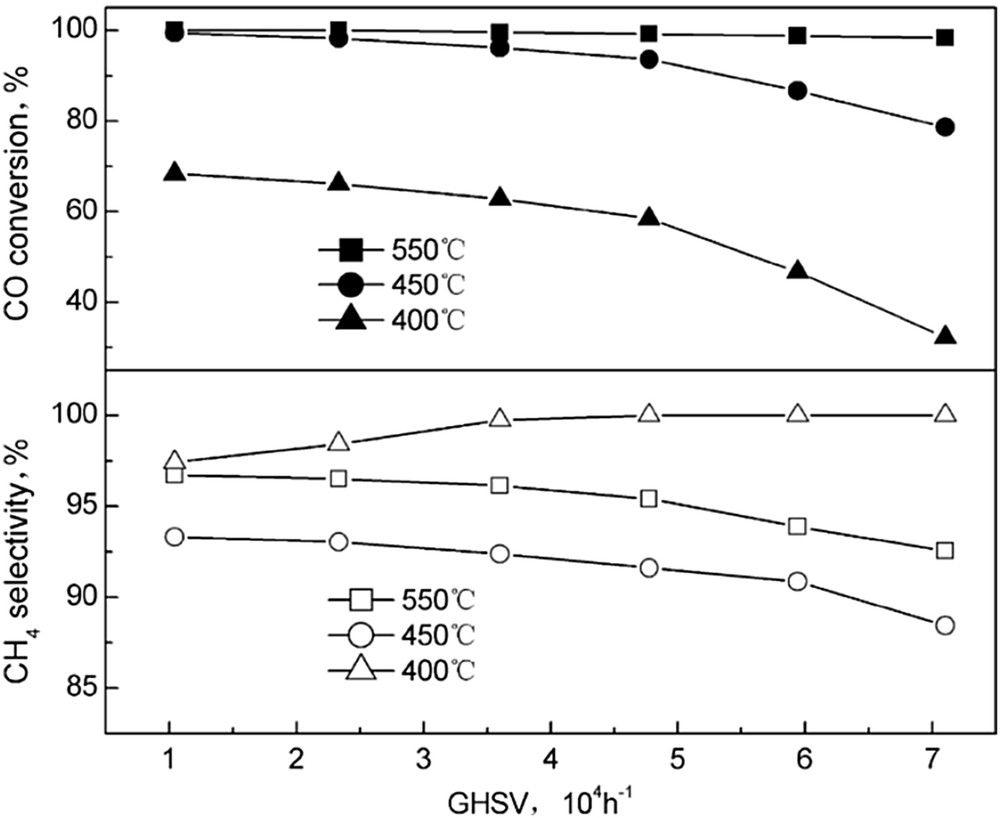
Taux de conversion du CO et sélectivités en CH4 obtenus à différents GHSV dans un micro-canal avec un dépôt de Ni/alumine (P = 30 atm, H2/CO = 3,1) [90].
L'utilisation d'un catalyseur, sous forme déposée, est également possible sur des structures monolithiques. Du fait de leur forte porosité, typiquement entre 70 et 95%, ces structures offrent de très faibles pertes de pression par rapport aux catalyseurs en lit fixe. Elles peuvent se présenter sous différentes configurations, comme le nid d'abeille, ou encore sous la forme de structures cellulaires, plus couramment appelées mousses (Fig. 34). Deux catégories de monolithes peuvent être distinguées, d'une part les monolithes dits conducteurs ne présentant pas de porosité interne, pouvant être en céramiques (alumine, SIC) mais surtout métalliques (aluminium, cuivre), et d'autre part les structures moins conductrices en raison des porosités internes qu'elles présentent. Le catalyseur est déposé (washcoat) sur la surface externe des monolithes conducteurs, alors que dans le cas de monolithes présentant des porosités internes, la structure monolithique peut servir directement de support céramique à la phase active du catalyseur. Ces structures poreuses en céramiques peuvent ainsi présenter de plus grands chargements en phase active du catalyseur et éliminent les problèmes d'adhérence du dépôt de catalyseur à la paroi, au prix de conductivités thermiques bien plus faibles. Parmi ces structures monolithiques, les mousses cellulaires semblent particulièrement intéressantes. Contrairement aux structures monolithiques formant des canaux rectilignes, où le profil d'écoulement est laminaire, le brassage de l'écoulement améliore les transferts de chaleur et de masse entre le fluide et le catalyseur (micro-mélange). Sous certaines conditions, ces transferts peuvent même être supérieurs à ceux présents dans les lits fixes, notamment à faible vitesse de fluide. Ce brassage génère cependant des pertes de pression plus élevées qu'un monolithe à canaux rectiligne, mais toujours nettement inférieures à celles d'un lit fixe. L'importance des transferts dans le fluide circulant à travers une mousse, ainsi que celle des transferts entre le fluide et le catalyseur, dépend des propriétés géométriques de celle-ci, principalement de leur porosité et de la taille des cellules. Une propriété descriptive de ces structures ainsi que le nombre de cellules par unité de surface, exprimé en nombre de pores par pouces (PPI : pores per inch), se situant typiquement entre 10 et 40 (see Fig. 35).

Exemple de monolithes : mousse métallique (haut) et nids d'abeille extrudés en cuivre et aluminium (bas) [93].
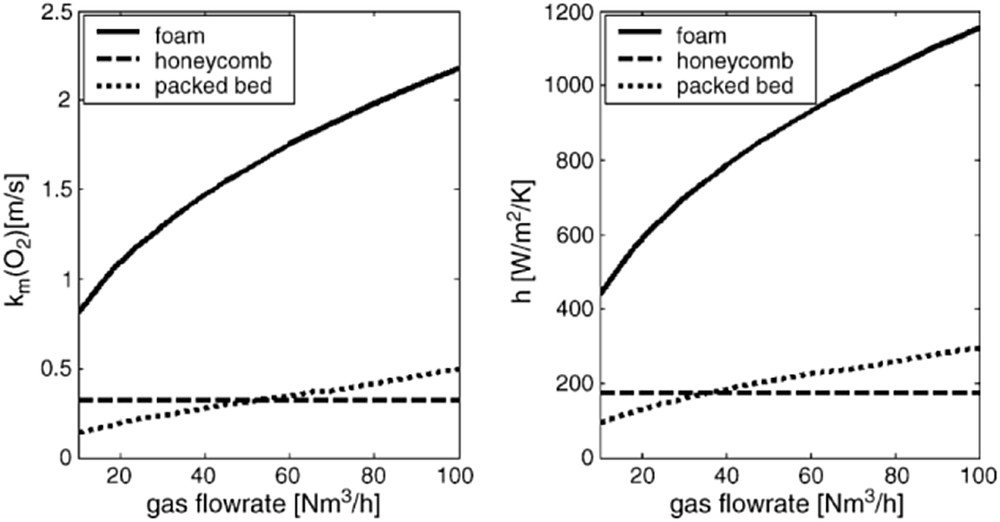
Comparaison des transferts de matière (gauche) et thermique (droite), estimés par corrélations, entre différentes structures en fonction du débit de gaz (Dréacteur = 8,5 cm). Mousse : '' = 0,8–25 PPI (pores per inch) ; nid d'abeille : '' =0,7–400 cpsi (cell per square inch) ; lit fixe : '' = 0,4–dp =1,3 mm [96].
Les mousses cellulaires conductrices offrent, de plus, de bonnes conductivités thermiques, notamment celles en aluminium ou en cuivre, qui peuvent atteindre des conductivités de plusieurs W/m/K [94]. En comparaison, la conductivité thermique apparente d'un lit fixe de catalyseur poreux rempli de gaz dépasse difficilement 1 W/m/K. Le transfert thermique à la paroi peut également être satisfaisant [95].
L'utilisation de ce type de structure pour la méthanation du CO2 a été à plusieurs reprises étudiée par la Nasa dans la perspective de missions habitées sur Mars ; le CO2 de l'atmosphère de la planète servirait alors à produire du CH4 à partir d'hydrogène généré par l'électrolyse de l'eau embarquée [97–99]. Les contraintes de masse et d'encombrement liées à cette application ont orienté les études vers l'utilisation de ce type de réacteur. Un catalyseur à base de ruthénium est ainsi déposé sur des feutres (structures filaires non organisées) de FeCrAlloy servant de structure monolithique et insérés dans les canaux d'un réacteur-échangeur. Dans les essais réalisés [98], les feutres ont une épaisseur de 2,5 mm. Les résultats obtenus à 400 °C sous une pression proche de la pression atmosphérique montrent que ces structures permettent d'atteindre le taux de conversion à l'équilibre thermodynamique pour des temps de contact (ou de passage) supérieurs à 400 ms, soit pour des GHSV inférieurs à 9000 h−1, comme le montre la Fig. 36. Les conversions restent cependant élevées (>70%) pour des GHSV de l'ordre de 50 000 h−1.
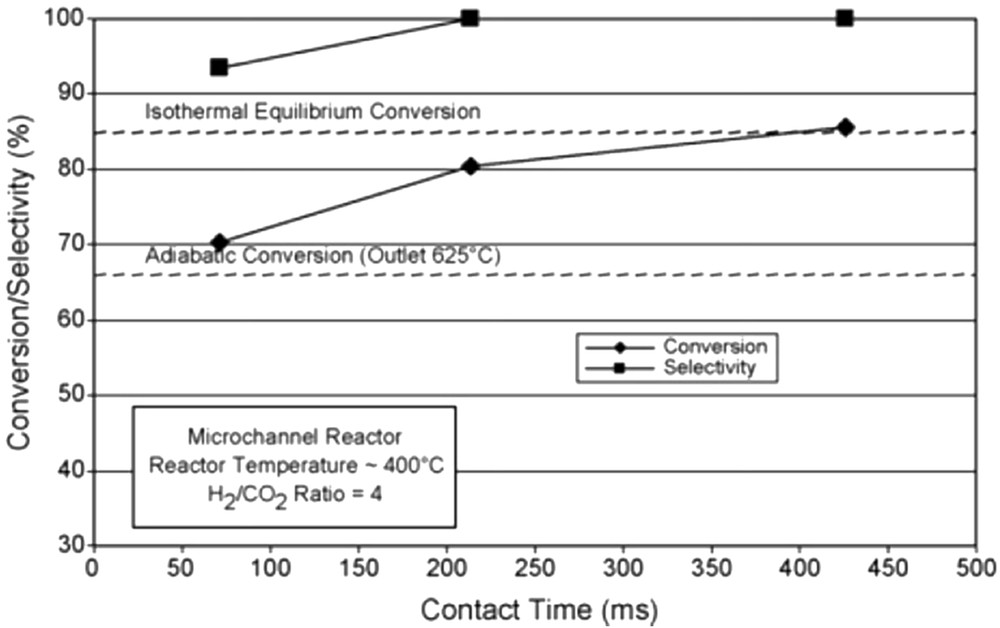
Taux de conversion du CO2 et sélectivité en CH4 obtenu dans un réacteur à inserts monolithiques avec un catalyseur à base de Ru en fonction du temps de contact des réactifs [98].
Les auteurs ont cependant mesuré des élévations de températures de l'ordre de 20 à 30 °C au sein du réacteur, signe de la forte exothermicité de la réaction. Ils ont également observé la désactivation du catalyseur avec le temps, attribuée aux phénomènes de frittage du catalyseur. Comme pour les microréacteurs relativement isothermes, les réacteurs à structures monolithiques nécessitent des températures relativement élevées (>400 °C) afin d'obtenir de bonnes performances de production, mais l'utilisation de températures trop élevées nuit à la stabilité du catalyseur. Le développement de catalyseurs plus actifs à basse température présente donc un intérêt certain pour ce type de structure.
3.5.1.3 Réacteurs triphasiques
L'utilisation d'un réacteur triphasique contenant les réactifs gazeux, le catalyseur et un fluide servant de caloporteur permet d'améliorer la gestion thermique des réactions de méthanation grâce au contact direct du caloporteur avec le catalyseur. Ces réacteurs peuvent contenir le catalyseur sous forme de grains en suspension ; on les appelle alors réacteur slurry (Fig. 37), mais le catalyseur peut également être déposé sur un support. Les fluides caloporteurs utilisés sont généralement des huiles minérales où circulent les gaz réactifs sous forme de bulles. Le refroidissement du liquide peut être effectué par une enveloppe extérieure ou par un circuit inséré au sein du liquide. Ces réacteurs ressemblent ainsi fortement aux réacteurs à lit fluidisé, mais utilisent un catalyseur en suspension plutôt qu'un lit en mouvement, ce qui permet de réduire les phénomènes d'attrition et autorise une plus grande plage de débits de fonctionnement. Bien que l'utilisation d'un fluide caloporteur directement au contact du catalyseur permette une très bonne gestion thermique du réacteur, elle comporte cependant plusieurs désavantages. D'une part, la présence d'un liquide autour du catalyseur induit des résistances de transfert de masse entre les réactifs gazeux et les catalyseurs, qui réduisent les vitesses globales de réaction. Ces résistances sont présentes au sein des bulles de gaz, entre le gaz et le liquide, au sein du liquide et enfin entre le liquide et le solide, en plus de la diffusion interne au sein du catalyseur. D'autre part, la température dans ces réacteurs est limitée par la température d'ébullition du fluide utilisé. Dans le cas d'huiles minérales, celle-ci dépasse difficilement 350 °C. De plus, l'entraînement du caloporteur, en phase liquide (phénomène de primage) ou en phase gazeuse (du fait de la pression de vapeur saturante) par le gaz issu du réacteur impose le recours à des étapes de séparation et de purification après la sortie du réacteur.
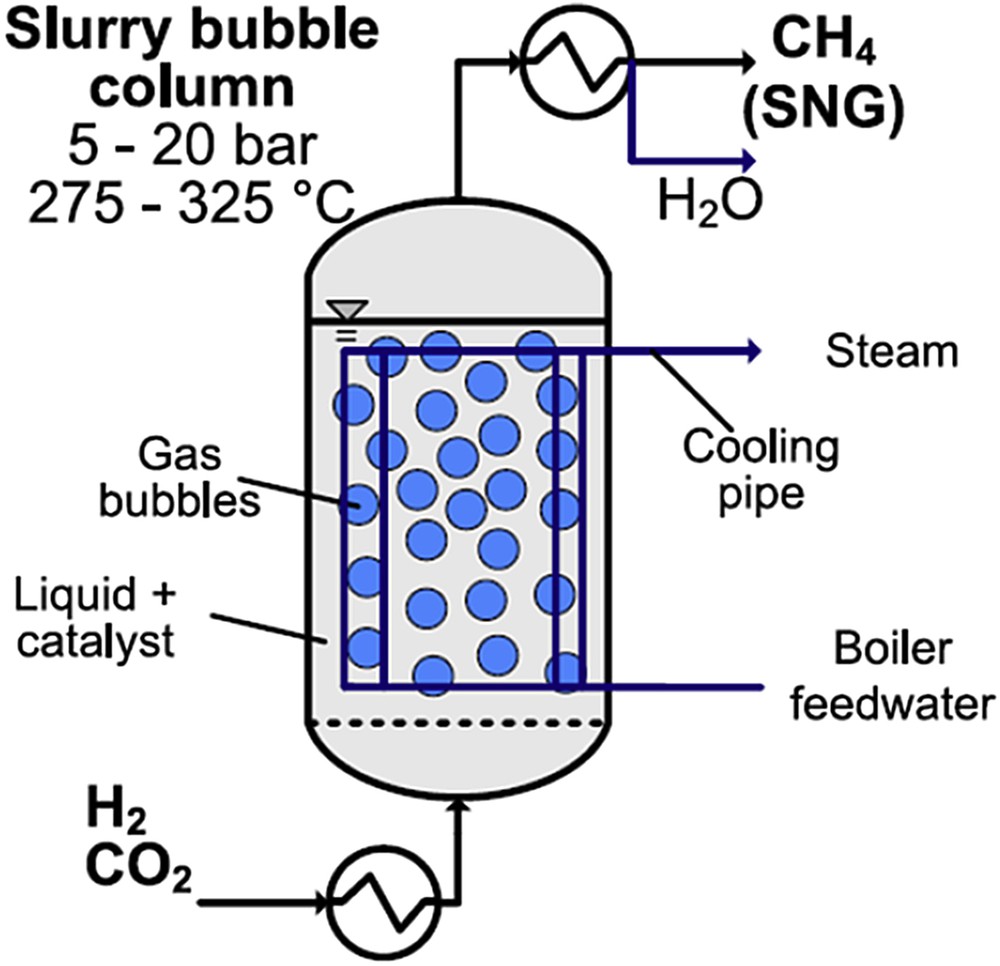
Schéma d'un réacteur slurry à bulles [100].
Un réacteur slurry à bulles pour la méthanation du CO2 avec un catalyseur à base de nickel déposé sur alumine a été étudié [100]. Des conversions de l'ordre de 80% ont pu être obtenues pour des températures de réacteur entre 300 et 325 °C et des pressions allant jusqu'à 20 bar. La concentration en volume du catalyseur dans la suspension est inférieure à 10%. Dans ces conditions opératoires, aucune désactivation du catalyseur n'a été observée par les auteurs. Le GHSV dans ces réacteurs est cependant très faible. Dans leurs essais, les auteurs ont utilisé des GHSV de l'ordre de 100 h−1 pour des conversions de l'ordre de 80%. Ces faibles valeurs sont, en partie, dues aux basses températures utilisées, mais surtout à la faible concentration de catalyseur au sein du liquide. Rapportés au volume de catalyseur, ces GHSV sont compris entre 1000 et 2000 h−1. L'utilisation de concentrations de catalyseur plus importantes peut permettre d'augmenter les GHSV opératoires, mais cela entraîne également la formation de bulles de gaz plus grandes, ce qui réduit l'efficacité des transferts de matière. Dans leurs travaux, les auteurs ont trouvé une concentration optimale de seulement 6,5% en volume, comme le montre la Fig. 38.
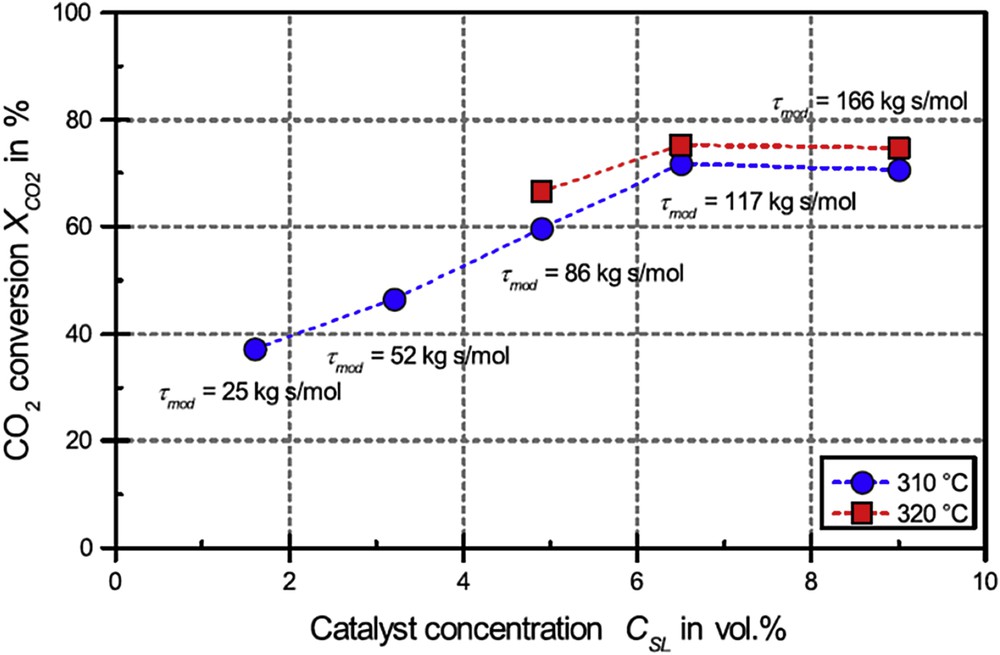
Influence de la concentration du catalyseur dans la suspension sur la conversion du CO2 dans un réacteur slurry [100].
Ces réacteurs présentent de très bonnes performances de gestion thermique ; cependant, leur compacité est très médiocre, en raison des diverses limitations par les transferts de matière et des températures opératoires relativement basses imposées par l'utilisation d'une suspension de catalyseur dans un liquide qui doit être capable de solubiliser les gaz réactifs.
3.5.2 Systèmes et réacteurs spécifiques visant à améliorer la gestion chimique des réacteurs
Hormis les problèmes de gestion thermique que sa mise en œuvre entraîne, un autre aspect de la réaction de méthanation du CO2 est la limitation de la conversion par l'équilibre thermodynamique, qui restreint l'accès aux très hauts taux de conversion, pourtant nécessaires, pour l'injection du SNG dans les réseaux gaziers. Afin de lever ce verrou, il est possible de déplacer l'équilibre thermodynamique dans le sens des conversions plus élevées en élevant la pression opératoire ou en extrayant un produit de la réaction, ici le méthane ou l'eau. Dans les procédés industriels, ce déplacement est effectué grâce à l'utilisation de pressions opératoires élevées (>10–20 bar), ce qui rend plus difficile le contrôle des températures au sein du réacteur, et/ou par la réalisation d'une étape de condensation entre deux réacteurs, ce qui augmente le nombre d'équipements du procédé. De récentes études se sont cependant intéressées à de nouvelles possibilités de séparation de produits in situ. Cette séparation peut, par exemple, être réalisée en utilisant des phénomènes d'adsorption. L'adsorbant peut être mélangé au catalyseur, de manière homogène ou non, afin de piéger un des produits de réaction. L'adsorption du CO2 lors de la méthanation du CO, combinée à la réaction de Water Gas Shift a, par exemple, été étudiée sur un lit de catalyseur Ni/MgAl2O4 mélangé à un adsorbant CaO/MgAl2O4 [101]. Des gains de conversion en CO de plusieurs dizaines de pourcents ont été reportés avec, par exemple, l'obtention d'une conversion en CO quasi-totale avec adsorbant à une température de 500 °C, conditions dans lesquelles le catalyseur seul ne permet d'obtenir qu'un taux de 80%. Dans le cas de la méthanation du CO2, l'adsorption in situ de l'eau produite peut être réalisée en utilisant des zéolithes. Dans de récentes études [102,103], des zéolithes sont directement utilisées comme support du catalyseur à base de nickel. Dans ce cas, les gaz réactifs réagissent à la surface du nickel déposé, mais l'eau reste piégée dans les cellules de la zéolithe (Fig. 39). L'utilisation d'un support assurant directement la fonction d'adsorbant présente, de plus, l'avantage de ne pas réduire la compacité du lit catalytique par la dilution du catalyseur par un adsorbant.
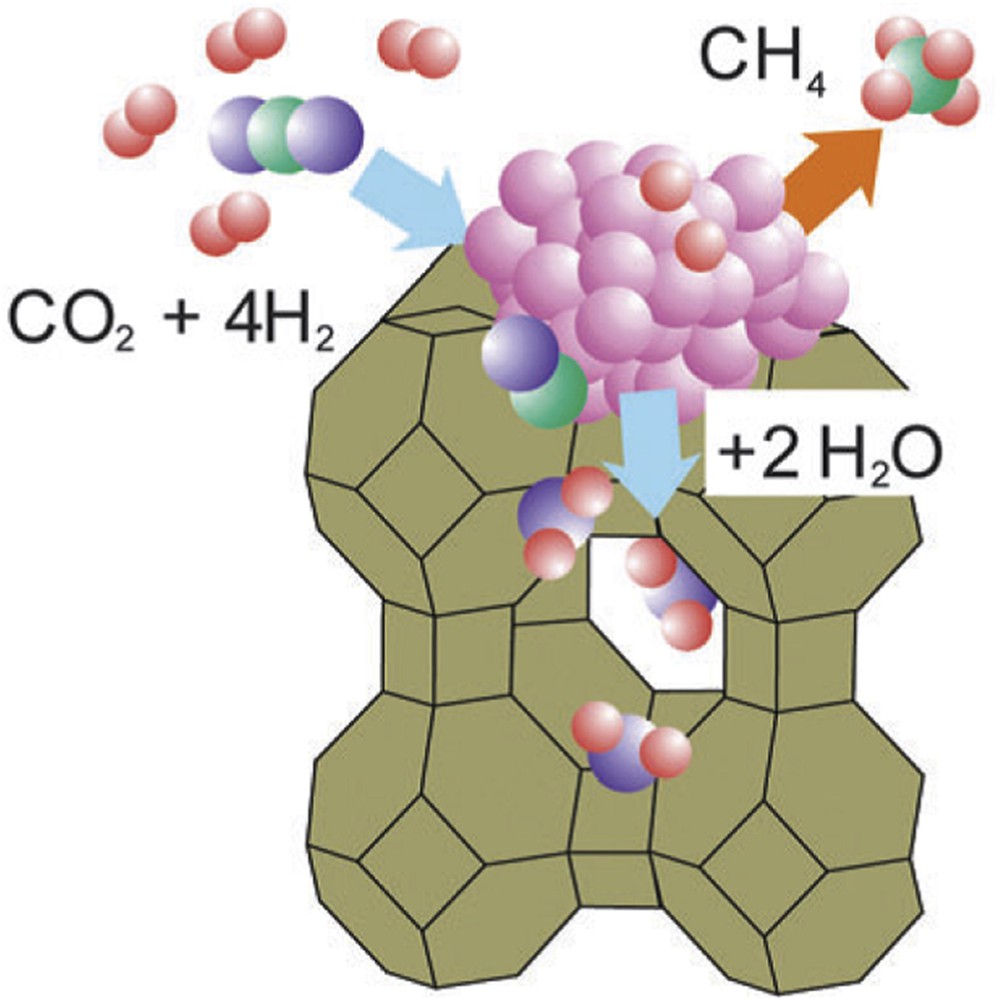
Schéma de principe de l'adsorption de l'eau sur un catalyseur Ni/zéolithe [102].
Grâce à cette adsorption, des productions exclusives de méthane, avec des conversions du CO2 presque totales, ont pu être obtenues à 170 °C, pour un GHSV de 1000 h−1 sous une pression de 1,2 bar [102]. Cet effet d'adsorption n'est toutefois que temporaire, la zéolite ayant une capacité d'adsorption limitée (Fig. 40).
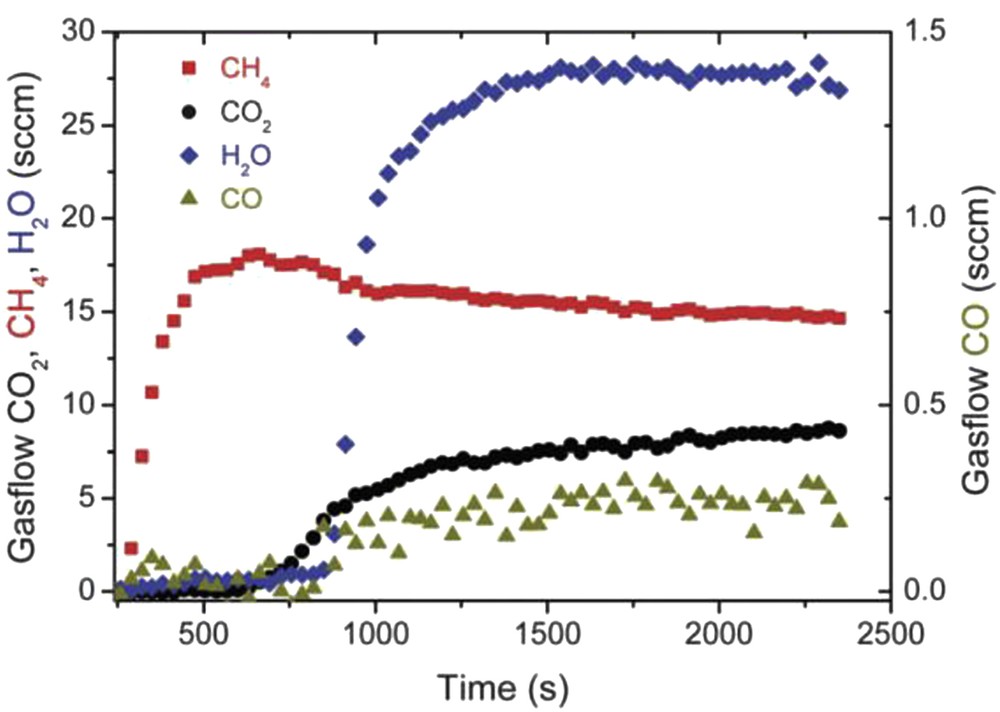
Comportement transitoire de l'adsorption d'eau sur zéolithe : une production exclusive de méthane est observée pendant environ 500 s avant que l'adsorbant ne soit saturé [102].
Ce type de catalyseur implique, par conséquent, d'effectuer des cycles de régénération de l'adsorbant et requiert ainsi la disposition de plusieurs réacteurs en parallèle pour assurer un fonctionnement continu. Le déplacement d'équilibre par captation de l'eau produite peut également être opéré de manière continue à travers des membranes sélectives. A ainsi été proposée [104] l'utilisation d'une membrane sélective à l'eau au sein d'un lit catalytique annulaire avec un catalyseur à base de ruthénium. L'eau passant à travers la membrane est évacuée par pompage. Des gains de conversions de l'ordre de 10% (d'environ 85 à 95%) ont, par exemple, été reportés à une température de 300 °C avec l'utilisation de cette membrane. Bien que très sélective à la vapeur d'eau, la membrane utilisée n'est pas totalement imperméable aux autres gaz présents dans le réacteur, ce qui engendre une perte de productivité. Ces réacteurs membranaires présentent l'intérêt d'un fonctionnement continu, mais la réalisation technique des structures de réacteurs, et surtout des membranes, demeure un verrou à leur utilisation. La dépense énergétique pour assurer l'évacuation de l'eau et la différence de pression nécessaire de part et d'autre de la membrane sont d'autres inconvénients des réacteurs membranaires. Une solution technique a été proposée par Air Liquide, appliquée à la réaction inverse de gaz à l'eau (Reverse Water Gas Shift). Dans cette solution, le lit catalytique est placé dans un tube dont les parois sont perméables aux gaz réactifs. Un système de chauffage est inséré à l'intérieur du lit. Le tube membranaire est lui-même placé dans un réacteur refroidi par ses parois externes. L'eau traversant la membrane est alors condensée sur la paroi froide du réacteur et évacuée sous forme liquide [105].
4 Modélisation des réacteurs catalytiques et de la cinétique de la réaction de méthanation du dioxyde de carbone
4.1 Problématique de la modélisation des milieux poreux
4.1.1 Description générale des milieux poreux
Un milieu poreux est constitué d'une phase solide présentant des interstices, ou pores, au travers desquels un fluide, liquide ou gaz, peut s'écouler. La phase solide peut être consolidée, comme c'est le cas avec les mousses cellulaires réticulées, ou non consolidée, comme par exemple avec un empilement de grains constituant un lit fixe.
La caractéristique descriptive principale d'un milieu poreux est sa porosité, définie comme le rapport entre le volume vide (non solide) et le volume total du milieu :
| (9) |
La porosité d'un lit fixe dépend de nombreux paramètres, comme la distribution de taille et la forme des grains, mais aussi de la qualité du remplissage d'un réacteur ; il est alors question de porosité tassée ou non. Dans le cas de lits fixes, constitués d'empilements de grains, la porosité varie généralement entre 0,3 et 0,4. La valeur de porosité minimale pour un empilement compact de grains sphériques monodispersés est de 0,26. La porosité est plus homogène dans le cas d'une mousse cellulaire qu'avec des lits fixes. Sa valeur est généralement comprise entre 0,8 et 0,95. Lorsque la phase solide est poreuse, comme par exemple avec des grains de catalyseur, deux porosités sont distinguées dans le milieu : la porosité externe, où circule le fluide, et la porosité interne, où le mouvement des constituants du fluide sera plutôt diffusionnel. De plus, si des pores internes du catalyseur sont fermés, il faut distinguer la porosité interne totale et celle accessible au fluide. Contrairement aux mousses cellulaires dont la structure est réticulée, les lits fixes ne présentent pas une porosité homogène, notamment à proximité de la paroi en raison de l'arrangement des grains à proximité de cette paroi. Deux régions sont considérées : une zone dite « cœur », où la porosité est globalement plus faible, et une zone dite « en proche paroi », où la porosité est plus élevée du fait des contacts entre les grains et la paroi. Cette porosité plus élevée à la paroi entraîne une modification locale des propriétés du lit fixe. Il est généralement considéré que la dimension caractéristique de cette zone est de l'ordre du diamètre des grains. La fraction de volume qu'elle représente, et par conséquent son influence sur le comportement du milieu poreux, est d'autant plus faible que le ratio entre le diamètre du réacteur et celui des grains est élevé (see Fig. 41).
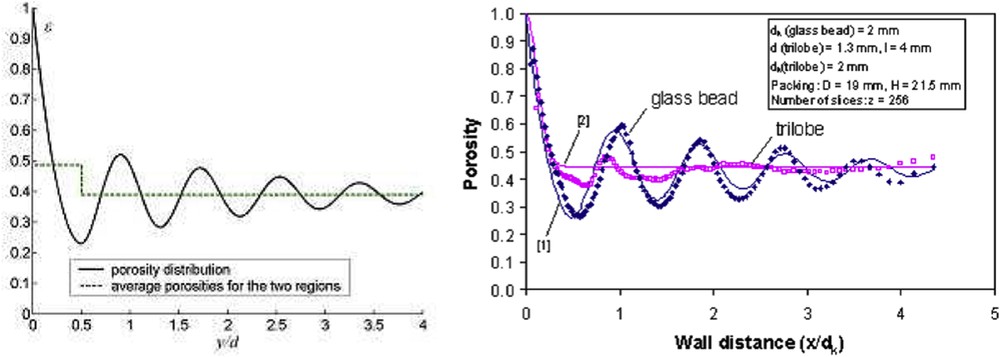
Exemple de profils de porosité: (gauche) modèle proposé par Martin [108] ; (droite) profils expérimentaux obtenus par N. L. Nguyen [109], issu de Fiers [110].
Plusieurs modèles de représentation de la distribution de porosité d'un lit fixe ont été établis dans la littérature. Ces modèles sont généralement issus d'imagerie ou de modélisation donnant accès à la porosité en tout point du réacteur. La distribution de porosité est alors moyennée axialement et orthoradialement pour ne dépendre que du rayon du lit fixe. Certains de ces modèles considèrent une porosité décroissante à partir de la paroi jusqu'à atteindre une valeur constante dans la zone à cœur [106,107]. D'autres modèles considèrent des oscillations de porosité dans cette zone [108]. Enfin, une troisième vision consiste à considérer une zone à cœur et en proche paroi avec chacune des porosités constantes. Les profils de porosité sont cependant très dépendants de la forme des grains utilisés ; ainsi, un lit de sphères présente une porosité oscillante alors qu'un lit de trilobes présente une porosité relativement constante dans la zone à cœur [109].
Les mousses cellulaires ne présentent a priori pas de porosité plus élevée à la paroi, du fait de leurs structures réticulées. Ce point dépend toutefois de la nature de l'ajustement entre la mousse et la paroi du réacteur, et en particulier s'il existe un espace résiduel (jeu) entre elles. Une autre caractéristique d'un milieu poreux est sa surface spécifique, représentant la surface développée par la phase solide par unité de volume total. Comme pour la porosité, il est possible de considérer la surface spécifique externe, intervenant dans les transferts entre la phase fluide et le grain, et la surface spécifique interne, développée par le support d'un catalyseur pour accueillir sa phase active. La surface spécifique externe d'un lit de billes sphériques est donnée par :
| (10) |
La surface spécifique externe d'un lit fixe dépend de la forme et de la taille des grains et de la porosité du lit. Pour des grains de plusieurs millimètres de diamètre, cette grandeur est de l'ordre de 1000 m2/m3. La surface spécifique externe des mousses cellulaires est généralement comprise entre 500 et 2000 m2/m3, selon leurs propriétés [94,111].
La surface spécifique interne d'un catalyseur s'exprime généralement en m2/g. Elle peut par exemple atteindre quelques centaines de m2/g pour un catalyseur avec un support alumine. Lorsqu'un fluide s'écoule dans les porosités d'un milieu poreux, le chemin moyen Le parcouru réellement par le fluide est supérieur à la longueur L de ce milieu, car les lignes de courants contournent les grains (ou fibres) de la phase solide. Cet allongement du trajet moyen du fluide est représenté par un facteur de tortuosité du milieu poreux :
| (11) |
Cette définition est relativement claire lorsque les pores du milieu sont assimilés à des capillaires courbes ; elle l'est cependant moins pour un milieu poreux complexe présentant des tailles de pores hétérogènes et à plusieurs échelles [110]. Dans le cas d'un lit fixe ou d'une mousse cellulaire, ce facteur est généralement compris entre 1 et 3. Les pores internes d'un catalyseur (grain ou dépôt) peuvent également être représentés par un facteur de tortuosité. La tortuosité interne est typiquement comprise entre 2 et 3. Les facteurs de tortuosité sont toutefois difficilement accessibles de manière directe et incluent souvent toute la méconnaissance de la structure du milieu poreux. Enfin, une dernière grandeur permettant de caractériser l'écoulement d'un fluide au sein d'un milieu poreux est sa perméabilité K, représentant sa capacité à laisser un fluide le traverser.
La perméabilité peut être définie grâce à la loi de Darcy, reliant, en l'absence de tout effet inertiel, la perte de pression linéique au sein du milieu poreux au débit de fluide (ou à la vitesse superficielle) le traversant [112] :
| (12) |
Cette relation n'est toutefois vérifiée qu'à faible vitesse superficielle (nombre de Reynolds particulaire Rep < 10). La formulation présentée ici est vérifiée pour un fluide incompressible (liquide), ou pour un gaz si les pertes de pression dans le milieu sont faibles. La perméabilité d'un milieu poreux ne dépend que des propriétés géométriques de ce milieu, comme sa porosité, principalement externe, ou sa surface spécifique, définies précédemment. Elle est typiquement comprise entre 10−11 et 10−9 m2 pour des empilements de grains et de l'ordre de 10−7 m2 dans le cas de mousses cellulaires à forte porosité [113].
4.1.2 La nécessité d'une représentation simplifiée des milieux poreux : la méthode d'homogénéisation par prise de moyenne volumique
La modélisation du comportement d'un milieu poreux, et a fortiori celle d'un réacteur-échangeur catalytique, est un problème multi-physique défini sur plusieurs échelles. Il est possible de distinguer l'échelle macroscopique du réacteur, l'échelle des pores externes du milieu poreux et, enfin, l'échelle microscopique des pores internes du catalyseur. La résolution rigoureuse de ce problème complexe, décrit par les équations de Navier–Stokes et les équations de conservation de masse et de l'énergie, au sein du fluide à l'échelle de chaque pore du milieu poreux, nécessite tout d'abord la description de la structure géométrique multi-échelle du milieu poreux. En particulier la description des dimensions inhomogènes et de la connectivité des pores sont nécessaires afin de décrire les différents transferts de masse et d'énergie au sein du milieu. Même si les technologies actuelles d'imagerie permettent un accès à cette représentation, certains paramètres demeurent difficilement accessibles, comme par exemple les propriétés associées aux contacts thermiques entre les différents grains d'un lit fixe. La résolution de ces problèmes multi-physiques à l'échelle d'un réacteur entier demande, de plus, des capacités de calcul énormes pour être raisonnablement applicable. Dans le cas d'un réacteur-échangeur catalytique, l'échelle du grain de catalyseur, siège de la réaction chimique, doit également être précautionneusement décrite. Une fois encore, une description géométrique de la structure est nécessaire. La seconde difficulté majeure est la représentation de l'acte catalytique, celle-ci étant le résultat d'une série d'étapes d'adsorption et de réactions chimiques. Cette représentation est d'autant plus difficile que les mécanismes précis de la réaction demeurent encore méconnus. La résolution directe du problème de la modélisation d'un réacteur-échangeur catalytique est trop coûteuse en ressources pour être applicable à une problématique d'étude, et hors d'atteinte du fait de l'impossibilité de décrire fidèlement les paramètres nécessaires à cette résolution. La méthodologie généralement utilisée vise à représenter le milieu poreux finement divisé par un milieu continu équivalent, à une échelle supérieure à celle des microstructures. Ceci peut être réalisé par la méthode d'homogénéisation par prise de moyenne volumique, ou « méthode du V.E.R. ». Des descriptions détaillées de cette méthode peuvent être trouvées dans la littérature spécialisée [114–116].
Notre présentation se limitera au principe de cette méthode conduisant aux équations de conservation utilisées dans la pratique. Cette méthode consiste à définir le milieu poreux, c'est-à-dire ses propriétés géométriques et physiques, à partir de valeurs moyennes prises au sein d'un milieu représentatif, appelé « volume élémentaire représentatif ». Le principe de cette méthode d'homogénéisation est illustré dans la Fig. 42. Le volume élémentaire représentatif (ou « V.E.R ») doit être suffisamment grand pour lisser les fluctuations locales des propriétés du milieu poreux, comme sa porosité, et suffisamment petit devant l'échelle d'évolution des gradients des grandeurs caractéristiques des milieux (température, pression, composition …) afin que les grandeurs au sein du V.E.R. conservent un caractère local.
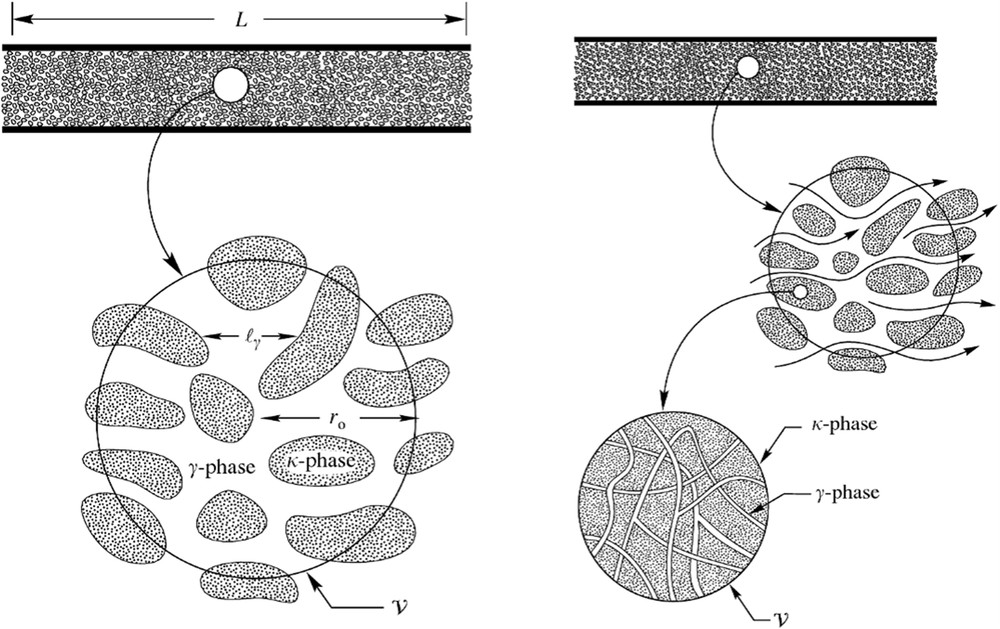
Représentation graphique de la méthode d'homogénéisation par prise de moyenne volumique à l'échelle du milieux poreux (gauche) et étendue à l'échelle du grain de catalyseur (droite) [115].
L'échelle du V.E.R doit donc être grande devant celle des pores du milieu et petite devant celle du réacteur :
| (13) |
Si ces contraintes sont généralement satisfaites à l'échelle des réacteurs industriels, il n'en est pas de même à celle du laboratoire [117]. Les récents développements portant sur l'intensification des transferts au sein de réacteurs catalytiques basés sur la réduction des dimensions caractéristiques de ces réacteurs sont également en opposition avec la satisfaction de ces contraintes. Pour ce type de réacteurs, comme le réacteur-échangeur milli-structuré, cette méthode de résolution est tout à fait critiquable. Elle demeure cependant la seule méthode réellement accessible et applicable. Son application aux équations de conservations locales au sein du fluide permet alors de transposer ces équations à l'échelle du V.E.R. et permet la description du milieu poreux à une échelle macroscopique et continue. Après le processus d'homogénéisation, certains phénomènes de transfert ne sont plus directement résolus, ou sont regroupés avec d'autres sous forme de termes ou coefficients apparus lors du processus d'homogénéisation. Il en va de même pour la structure géométrique du milieu poreux qui n'est plus directement représentée. Ces phénomènes de transfert, représentés de manière simplifiée, regroupent par exemple tous les phénomènes de dispersion au sein du milieu poreux, c'est-à-dire les phénomènes responsables de la dispersion spatiale d'une quantité au sein de ce milieu. Ces phénomènes sont liés à l'écoulement du fluide au sein des pores du milieu poreux dont la structure géométrique est inhomogène. Ils sont par exemple dus au frottement du fluide à la surface des grains (ou de la mousse) du milieu poreux, à la variation de la taille des pores qui induisent des champs de vitesses différents ou encore aux variations des lignes de courant de fluide autour de la phase solide du milieu poreux. L'importance de ces phénomènes de dispersion dépend de la direction considérée par rapport à la direction macroscopique de l'écoulement.
D'autres transferts sont également concernés par cette simplification, comme par exemple les propriétés de conduction thermique des différentes phases du milieu poreux, les échanges de masse et d'énergie à l'interface entre le fluide et le catalyseur, ou encore le transfert thermique entre le milieu poreux et la paroi du réacteur.
L'expression exacte de ces termes est toutefois relativement complexe et fait même parfois encore débat.
L'application de la méthode d'homogénéisation par prise de moyenne volumique permet de transposer les équations de conservation, valables dans le fluide, au sein du milieu poreux finement décrit à une échelle macroscopique, définissant un milieu continu représentatif équivalent. Le processus d'homogénéisation entraîne par principe la « perte d'information » due à la disparition de certains transferts qui ne sont représentés que sous forme de coefficients, dits de « fermeture ». La résolution du problème requiert donc des modèles ou équations descriptifs de ces coefficients que l'on appelle des « équations de fermeture ». Du fait de la complexité du problème à résoudre due, d'une part, au couplage des différentes physiques intervenant et, d'autre part, à la géométrie compliquée du milieu poreux, la définition de ces équations de fermeture est une difficulté majeure de la représentation homogénéisée des milieux poreux. Ces équations dépendent fortement des systèmes considérés, en particulier lorsque les contraintes sur les dimensions du V.E.R ne sont pas rigoureusement respectées. Une détermination expérimentale de ces équations de fermeture est souvent requise pour obtenir un modèle représentatif du milieu poreux utilisé. Cette méthode d'homogénéisation est appliquée à l'échelle du lit catalytique, mais il est également possible de la décliner à l'échelle d'un grain ou d'un dépôt de catalyseur (Fig. 42) afin de modéliser les différentes échelles du réacteur catalytique. Dans la pratique, il existe deux grands types de modèles. Tout d'abord le modèle dit « hétérogène », issu de la méthode du V.E.R. appliquée à l'échelle du réacteur et du catalyseur. Ce modèle permet ainsi de distinguer les deux échelles de porosité du milieu poreux et de représenter les différents transferts de masse et de chaleur au sein du catalyseur. Le second modèle, appelé modèle « homogène », suppose que les transferts entre ces deux échelles sont à l'équilibre. La température du catalyseur et la composition du fluide dans les pores internes du catalyseur sont alors égales à celles du fluide autour du catalyseur.
4.2 Transferts de masse, d'énergie et de quantité de mouvement au sein d'un lit fixe ou d'une mousse cellulaire
Cette partie est consacrée à l'écriture des équations de conservation, permettant de décrire les différents transferts liés à l'écoulement d'un fluide au sein d'un milieu poreux, obtenues à partir de l'homogénéisation par prise de moyenne volumique des équations de conservation locales. Les équations de conservation de la matière, de l'énergie et de la quantité de mouvement seront exprimées en régime stationnaire. Les différences de représentation des modèles homogène et hétérogène, décrits précédemment, seront mises en évidence. Une attention particulière sera portée aux équations de fermeture, permettant de déterminer les paramètres représentant les phénomènes non directement résolus, et aux difficultés rencontrées pour établir ce genre de lois de manière générique.
4.2.1 Équation de conservation de la quantité de mouvement
La conservation de la quantité de mouvement au sein d'un milieu poreux, en négligeant les forces gravitationnelles, s'écrit de la manière suivante [112] :
| (14) |
Le terme à gauche de cette équation est issu de l'application formelle de la prise de moyenne volumique à l'équation de Navier–Stokes et représente les forces inertielles au sein du fluide. La présence de ce terme est toutefois critiquée [112]. Ce terme est de plus souvent négligeable devant les autres termes de l'équation de conservation de la quantité de mouvement. Les termes à droite de l'équation (14) correspondent à la loi de Darcy dans sa variante locale, et à ses différentes « extensions ». La loi de Darcy originelle (1858), déjà présentée dans l'équation (12), peut en effet être appliquée localement à l'échelle d'un V.E.R. [112]. Cette loi n'est cependant valable qu'à faible vitesse de fluide ou faible nombre de Reynolds. Elle s'exprime de la manière suivante :
| (15) |
Lorsque la vitesse du fluide au sein du milieu poreux augmente, la loi de Darcy ne permet plus de décrire l'écoulement en raison de l'apparition de phénomènes non linéaires. Ces phénomènes ne sont pas liés à une transition du régime d'écoulement du régime laminaire au régime turbulent [112], mais plutôt aux traînées formées autour des obstacles solides, qui ne sont alors plus négligeables. Ces effets inertiels sont représentés par l'équation de Forchheimer, première extension de la loi de Darcy :
| (16) |
Le terme est parfois regroupé sous la forme d'un coefficient unique β, appelé traînée de Forchheimer.
La perméabilité et la traînée de Forchheimer ont, par exemple, été identifiées [118] dans le cas d'un lit de particules. Ces coefficients ont été reliés à la porosité du lit et à un diamètre équivalent dp des particules. Le diamètre équivalent utilisé ici est le diamètre équivalent de Sauter, c'est-à-dire le diamètre de la sphère équivalente possédant le même rapport volume sur surface que les grains ou particules constituant le milieu poreux :
| (17) |
La dernière extension de la loi de Darcy a été proposée par Brinkman [119] afin de prendre en compte les forces de cisaillement au sein du fluide, notamment à la paroi d'un lit fixe :
| (18) |
Il existe deux manières d'exprimer le tenseur de contraintes visqueuses.
La première, proposée par Brinkman, s'inspire de la formulation de ce tenseur pour un écoulement uniaxial, qui conduit à :
| (19) |
La viscosité, , utilisée dans le terme représentant les cisaillements est une viscosité effective qui, bien que supposée égale à celle du fluide par Brinkman, peut en être différente. L'application de la méthode d'homogénéisation du V.E.R. entraîne une relation directe entre la viscosité du fluide et la viscosité effective :
| (20) |
Une dépendance de la viscosité effective vis-à-vis du nombre de Reynolds de l'écoulement a cependant été observée par Giese et al. [120] dans le cas de particules sphériques :
| (21) |
La seconde manière d'exprimer ce tenseur est d'utiliser la loi de viscosité de Newton généralisée, présentée dans Bird et al. [121], qui conduit à l'équation suivante :
| (22) |
Lorsque ces effets de parois sont négligés et que la porosité peut être supposée constante, une condition limite de glissement entre le lit et la paroi doit être utilisée. Il a été montré qu'on doit recourir à une condition de frottement aux parois lorsqu'un profil de porosité est considéré [122].
4.2.2 Équation de conservation de la matière
L'équation de conservation de la matière d'un constituant i, transposée à l'échelle d'un V.E.R., s'écrit, en régime stationnaire, de la manière suivante :
| (23) |
Cette équation lie la variation du flux massique de l'espèce i à un flux de diffusion, ou de dispersion, ji et au un terme source si.
La somme des équations de conservation sur les différents constituants d'un mélange conduit à l'équation de conservation de la masse globale, ou équation de continuité. En absence de terme source de masse extérieure, cette équation devient :
| (24) |
4.2.2.1 Expression du flux de diffusion, ou de dispersion, au sein d'un milieu poreux pour un mélange multi-constituants
Comme énoncé précédemment, le flux de diffusion au sein d'un milieu poreux ne représente pas uniquement la diffusion pure de l'espèce i dans les pores, mais intègre également les phénomènes de dispersion hydrodynamiques induits par la structure du milieu. Sans compter la définition de ce coefficient de dispersion, l'expression rigoureuse du flux dispersif est problématique lorsque le fluide contient plus de deux constituants, dont aucun n'est largement majoritaire par rapport aux autres. On parle alors de mélange concentré. Dans ce cas, les propriétés de densité massique et moléculaires ne peuvent être considérées constantes.
Par définition, le flux de matière totale en masse d'un constituant, Ni, peut s'exprimer de deux manières, selon la vitesse de référence employée [121] :
| (25) |
| (26) |
Les coefficients de diffusion (ou, le cas échéant, de dispersion) Di et Di*, sont identiques dans le cas de mélanges binaires, ce qui n'est plus vrai dans le cas de mélanges multi-constituants.
Le flux de diffusion peut donc être exprimé avec, pour référence, la vitesse superficielle moyennée par les fractions molaires, en utilisant la densité moléculaire, ou concentration molaire. Il peut aussi être exprimé, avec pour référence la vitesse superficielle moyennée massique, en utilisant la densité massique du constituant.
En toute rigueur, la vitesse moyennée massique est celle décrite par l'équation de conservation de la quantité de mouvement présentée précédemment. Lorsque les espèces sont diluées dans un solvant majoritaire, ces deux vitesses peuvent être considérées égales à la vitesse du solvant. Ce n'est cependant pas vrai lorsque le mélange est dit concentré. Dans ce cas, le flux dispersif recherché est le flux massique, ji, défini par rapport à la vitesse moyennée massique.
Comme évoqué précédemment, les coefficients Di et Di* définis dans l'équation (25) peuvent être séparés en deux composantes. D'une part, le coefficient de diffusion effectif, indépendant de l'écoulement du fluide et prenant en compte la porosité et la tortuosité du milieu. Dans le cas d'un réacteur catalytique, le régime de diffusion dans les pores externes est généralement régi par la diffusion moléculaire. D'autre part, une composante de dispersion, liée à l'écoulement du fluide, est :
| (27) |
Les phénomènes de dispersion n'étant pas isotropes, ces coefficients sont exprimés sous la forme de tenseurs.
Ces coefficients de dispersion sont généralement issus de corrélations provenant de caractérisations expérimentales. Il convient alors de prêter une attention particulière aux conditions d'obtention de ces corrélations et, notamment, d'examiner par rapport à quels gradient et vitesse sont définis les coefficients qu'ils décrivent.
La plupart des corrélations utilisées ont été établies dans des conditions où les espèces sont diluées [123–125]. Ces coefficients de dispersion sont généralement corrélés pour l'expression du flux molaire, par rapport au gradient de la concentration, ce qui pose le problème de leur utilisation dans l'expression du flux de dispersion massique exprimé par rapport à la vitesse moyennée massique (équation (25)).
En admettant que ces coefficients soient utilisables par rapport au gradient de fraction molaire (et représenteraient donc les Di*), il est possible de définir le flux ji en recourant à certaines hypothèses. Il est, par exemple, possible d'utiliser l'hypothèse du mélange moyenné, qui considère tous les autres constituants différents de i comme un représentant d'un seul corps.
Il devient alors possible d'utiliser les formules démontrées pour des mélanges binaires (A/B), en particulier :
| (28) |
| (29) |
L'utilisation de telles hypothèses entraîne cependant la perte de la nullité de la somme des flux de diffusion, ou de dispersion, et ne permet donc pas de respecter l'équation de conservation de la masse. Ce problème est généralement contourné en omettant la résolution du bilan de matière d'une espèce, dont la composition est alors définie par rapport aux compositions des autres constituants [126].
4.2.2.2 Expression du terme source de matière dans le cas du modèle hétérogène
Le terme source, si, de l'équation (23) représente l'échange entre la phase fluide et la phase solide du milieu poreux. Dans la formulation du modèle hétérogène, ce terme est exprimé comme étant proportionnel à la différence de concentration du composé dans le fluide et à la surface du solide, via un coefficient d'échange.
| (30) |
La concentration à la surface du solide, est quant à elle, calculée à partir de l'équation de conservation de la matière écrite à l'échelle du catalyseur à l'aide de la méthode du V.E.R. Le problème est ici un problème de pure diffusion, exprimé ici en fonction des concentrations au sein des pores internes, Ci,s.
| (31) |
Le terme représente le terme source de l'espèce i lié aux réactions chimiques se produisant dans le catalyseur et doit s'exprimer ici par rapport au volume du catalyseur. Ce terme est alors défini par les lois cinétiques des réactions.
Le problème de la définition du coefficient de diffusion pour un mélange multi-constituants est à nouveau posé. À l'intérieur des pores d'un catalyseur, le régime de diffusion peut, de plus, ne pas être régi par la diffusion moléculaire. Le régime de diffusion dépend en effet de la taille des pores (dpores) par rapport au libre parcours moyen des molécules.
Le libre parcours moyen d'une molécule est fonction des conditions de pression et de température, ainsi que de son diamètre σ :
| (32) |
Dans les conditions de la méthanation du CO2, le libre parcours moyen des molécules est typiquement de l'ordre de 10−7 à 10−8 m.
On définit alors le nombre de Knudsen comme le rapport entre ces deux grandeurs (Kn = lp/dpores).
Lorsque Kn << 1, la diffusion dans les pores est régie par la diffusion moléculaire, où les chocs entre les molécules sont prépondérants. En revanche, lorsque Kn >> 1, les chocs contre les parois des pores sont prépondérants, on parle alors d'écoulement raréfié, ou de régime de Knudsen.
Le coefficient de diffusion à utiliser est alors le coefficient de Knudsen, défini par :
| (33) |
Quel que soit le régime de diffusion considéré, le coefficient de diffusion doit être corrigé d'un facteur pour tenir compte de la porosité du catalyseur et de la tortuosité de ses pores.
4.2.2.3 Expression du terme source de matière dans le cas du modèle homogène
Par définition, le modèle homogène suppose que les phénomènes de diffusion à l'intérieur du catalyseur et les transferts entre le fluide et ce dernier ne sont pas limitants ; on parle alors de régime chimique. La composition du fluide au sein des pores du catalyseur est, par conséquent, homogène et égale à celle du fluide autour du catalyseur. Le terme source de l'équation (23) peut alors simplement s'exprimer en fonction des vitesses de réactions, calculées par rapport à la composition du fluide et exprimée par unité de volume du milieu poreux.
4.2.3 Equation de conservation de l'énergie
L'application de la méthode du V.E.R. aux équations de conservation de l'énergie, qui se déclinent pour les systèmes étudiés en équations de la chaleur, conduit à la définition d'un modèle à deux températures, celle de la phase solide et celle du fluide. Ce modèle est cependant très complexe et fait intervenir de nombreux paramètres [128]. Une forme simplifiée de ce modèle ne représentant qu'une seule température lui est ainsi souvent préférée.
Ce modèle à une seule température n'est cependant valable que sous l'hypothèse de l'équilibre thermique local, stipulant l'égalité des températures moyennes au sein d'un V.E.R. :
| (34) |
Il est évident que cette condition ne peut être que difficilement respectée lors de la mise en œuvre d'une réaction athermique au sein du catalyseur.
Le modèle à une température s'écrit de la manière suivante:
| (35) |
| (36) |
Cette représentation globale (équations (35) et (36)), souvent appelée modèle « λ–h », est cependant critiquée dans le cas d'un lit fixe par différents auteurs [129,130]. L'une des raisons évoquée est qu'elle localise les résistances thermiques entre le milieu poreux et la paroi à la paroi même, alors que ces résistances sont notamment dues à l'augmentation de la porosité à proximité de la paroi. Le modèle (h−λ) induit donc une surestimation des températures dans la zone en proche paroi et fausse par conséquent la représentation des phénomènes se produisant dans cette zone, notamment l'estimation de la vitesse de réaction. Le problème d'évaluation des échanges thermiques au sein d'un milieu poreux sera abordé dans un paragraphe ultérieur.
4.2.3.1 Expression du terme source de chaleur dans les modèles hétérogène et homogène
Comme pour les équations de bilan de matière, la formulation hétérogène du terme source de l'équation (35) traduit un échange entre la phase fluide et solide représenté par un coefficient d'échange, kt.
| (37) |
La température du catalyseur solide est définie par l'équation de conservation de l'énergie appliquée à l'échelle du grain :
| (38) |
4.2.3.2 Retour sur les équations de fermeture de transfert thermique dans le cas d'un lit de grains
Les échanges thermiques au sein d'un milieu poreux constitué d'un empilement de grains ont été très largement étudiés dans le cadre du modèle évoqué précédemment. Comme son nom l'indique, ce modèle utilise principalement deux paramètres de fermeture : le coefficient d'échange à la paroi, h, et une conductivité thermique équivalente du milieu poreux (gaz+solide), λ. Dans la grande majorité des cas, ce modèle est utilisé dans l'hypothèse d'une porosité constante. Comme illustré dans la Fig. 43, cet unique paramètre représente les échanges par conduction entre les grains de la phase solide et les échanges par convection entre les grains et les échanges interne à la phase fluide, regroupant les échanges par conduction et ceux liés à l'écoulement du fluide dans la structure poreuse. Lorsque la température est plus élevée (>500 °C), les phénomènes de rayonnement sont également à prendre en compte. Ceux-ci ne seront toutefois pas retenus ici. Il est courant de dissocier la conductivité équivalente en plusieurs contributions : la conductivité dite « stagnante », la contribution radiative, n'ayant de réelle importance qu'à haute température, et enfin la contribution liée à l'écoulement du fluide, généralement appelée composante ou contribution dispersive.
| (39) |
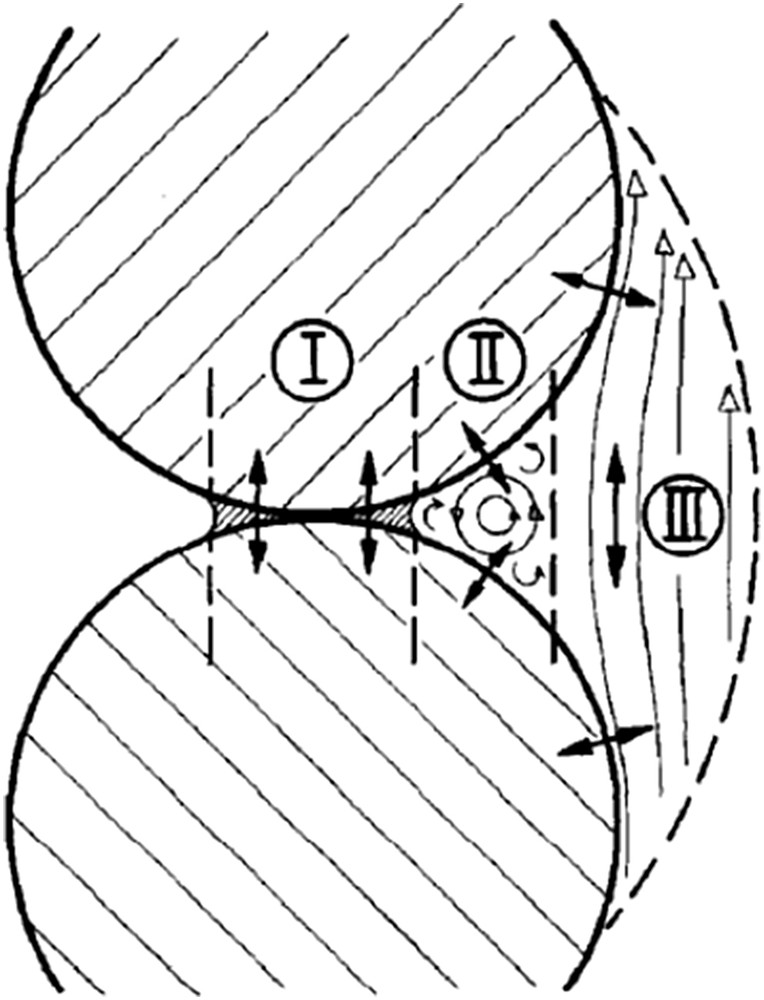
Illustration des mécanismes de transferts de chaleur au sein d'un lit de grains : I, conduction pure entre les grains ; II, échange par agitation mécanique ; III, échange dans la phase fluide [131].
La conductivité stagnante λeq,0 représente les phénomènes participant aux échanges de chaleur en l'absence d'écoulement (vitesse du fluide nulle). Elle est souvent considérée isotrope.
D'un point de vue formel, elle est bornée par les conductivités stagnantes de couches en parallèle ou en série des milieux solide et fluide :
| (40) |
Ces modèles font appel à la conductivité du grain λs, qui, dans le cas d'un grain de catalyseur poreux, est délicate à déterminer, car elle dépend de la structure du catalyseur, de sa composition et des gaz présents dans les pores du catalyseur. La littérature fournit un grand nombre de corrélations permettant de définir la conductivité stagnante équivalente d'un milieu poreux. Ces corrélations sont généralement déterminées en considérant des combinaisons de résistances thermiques à l'échelle du milieu poreux ou d'une cellule représentative, et vérifiées expérimentalement à partir de lits de grains dont la conductivité est connue [132–134]. Ces corrélations font en général appel à la conductivité du grain, et requièrent, pour les plus complexes, la connaissance de paramètres caractéristiques de la géométrie du milieu poreux. La contribution liée à l'écoulement du fluide, ou contribution dispersive, n'est, quant à elle, pas isotrope. Celle-ci est plus élevée dans le sens direct de l'écoulement que dans le sens radial à celui-ci. Dans les corrélations établies, cette contribution dépend souvent linéairement de la vitesse du fluide. Ces corrélations sont généralement exprimées par rapport au nombre de Péclet thermique particulaire de l'écoulement :
| (41) |
Dans le sens orthogonal à l'écoulement, la valeur de k est proche de 0,1. Elle est plus élevée dans le sens de l'écoulement, ou sens axial. Yagi et Kuni [132] proposent, par exemple, de prendre k = 0,11 et 0,75 dans les sens orthogonal et axial, respectivement. Des formulations plus complexes ont été proposées pour la contribution radiale, par exemple la formule de Bauer et Schlünder [129] exprimant cette contribution comme dépendant du ratio diamètre de particule (ou grain) sur diamètre de réacteur, N = DR/Dp :
| (42) |
Les valeurs du coefficient k dépendent toutefois du lit de grain considéré, et en particulier de la forme des grains. De plus, le transfert par conduction axiale est souvent négligeable devant le flux convectif (axial) du fluide, ce qui explique le moindre intérêt qui lui est porté [129].
La détermination du coefficient d'échange à la paroi est également problématique. Il existe en effet de nombreuses données expérimentales et corrélations permettant de représenter les échanges en paroi. Cependant, comme on peut le voir sur la Fig. 44, il n'y a généralement aucun accord concernant les valeurs à faible nombre de Reynolds (<1000), qui comprennent notamment les applications où le fluide est un gaz.
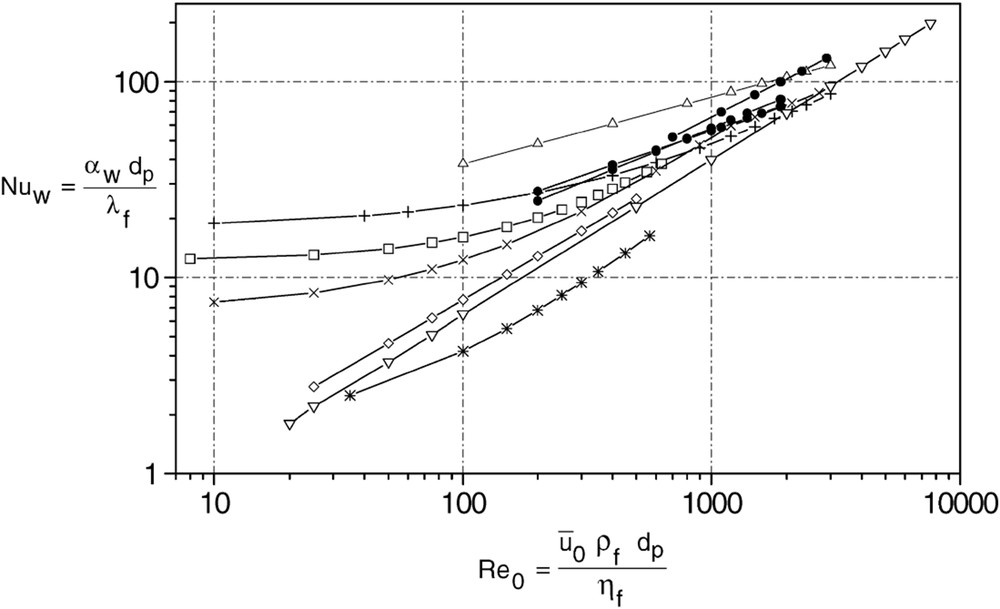
Exemple de données expérimentales et corrélées pour le coefficient d'échange en paroi αw en termes de nombres de Nusselt et de Reynolds pour un lit de grains [130].
Les différences observées sont attribuées à une composante dite conductrice, ou stagnante, de l'échange en paroi, très dépendante du système utilisé [129]. En termes de nombre de Nusselt rapporté à la conductivité du fluide, l'échange en paroi se présente alors comme la somme de deux contributions : une contribution stagnante évoquée précédemment, et une composante liée à l'écoulement, généralement exprimée via les nombres de Reynolds et de Prandtl :
| (43) |
Il est généralement admis que la composante stagnante soit liée à la conductivité stagnante du lit. Bey et Eigenberger [135] proposent, par exemple, une relation linéaire entre ces deux grandeurs, avec un facteur de proportionnalité de 2,4. D'autres corrélations proposent une dépendance linéaire avec la conductivité stagnante du lit corrigée d'un facteur dépendant du ratio : diamètre de grain sur diamètre de réacteur. Les constantes a, m des corrélations existantes dépendent des propriétés du lit et de la forme des grains utilisés. La valeur de a se situe typiquement entre 0,1 et 0,5 et celle de m entre 0,5 et 1. Dans le cas où le fluide est un gaz, la dépendance avec le nombre de Prandtl, n, n'est, quant à elle, que rarement abordée [136]. Les gaz généralement utilisés, lorsqu'il y en a plusieurs, présentent en effet dans la grande majorité des cas des nombres de Prandtl similaires, compris entre 0,6 et 0,7 du fait de leurs natures mono-ou diatomique. Une valeur de 0,33 est généralement utilisée, avec l'argument de la similitude entre transfert thermique et transfert de masse [137].
Le modèle (λr−h) est régulièrement critiqué à cause du « saut » de température qu'il impose à la paroi et de la disparité des données expérimentales concernant le coefficient d'échange à la paroi. Différents auteurs ont alors proposé d'autres façons de représenter les échanges au sein d'un lit de grains, en lien avec la considération d'un profil de porosité. Il est possible de classer ces alternatives en trois groupes. La première alternative consiste à relier directement la conductivité équivalente du lit au profil de porosité. Ainsi, la conductivité thermique (radiale) diminue grandement à proximité de la paroi (Fig. 45) et est responsable de la résistance thermique, répartie dans la zone en proche paroi et non plus à la l'interface lit–paroi. Une condition de continuité de la température est alors appliquée à la paroi [130]. Ce modèle est appelé modèle dispersif.
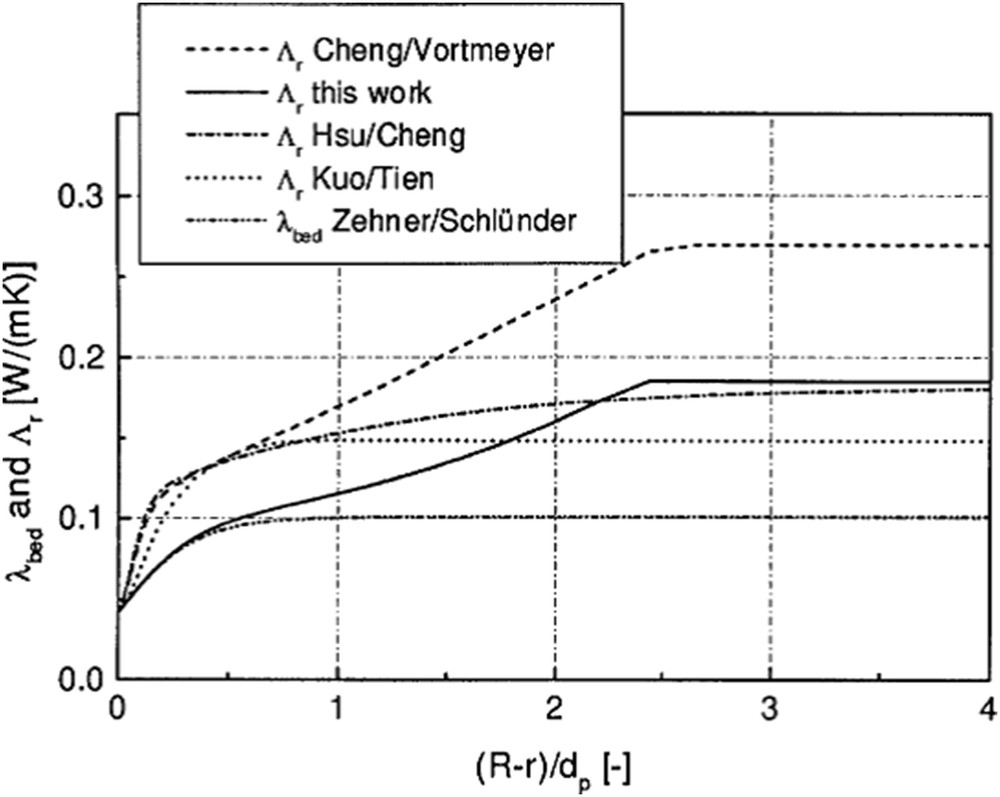
Évolution de la conductivité radiale effective le long du rayon d'un lit de grain, d'après diverses corrélations [130].
Un second type de modèle divise le lit fixe en deux zones : une zone à cœur et une zone en proche paroi. Des coefficients de transferts sont utilisés entre les différentes zones et la paroi. De ce fait, le saut de température à la paroi est divisé en deux sauts, situés à la paroi et à l'interface entre les deux zones. Ce type de modèle constitue ainsi une alternative intermédiaire entre le modèle dispersif et le modèle (λr−h) [110,138]. Enfin, une troisième alternative consiste à calculer le profil de vitesse au sein du lit par un modèle (généralement CFD) séparé, et à utiliser ensuite ce profil pour dériver la variation de la conductivité radiale et d'autres propriétés de transfert. Ce type de modèle itère ainsi entre deux modèles différents pour résoudre les profils de vitesses et de températures au sein du lit [139]. L'utilisation de ces alternatives au modèle (λr−h) nécessite toutefois la connaissance du profil de porosité et de ses conséquences sur la valeur de la conductivité équivalente.
4.2.3.3 Les équations de fermeture de transfert thermique dans le cas spécifique des mousses cellulaires
La conductivité équivalente d'une mousse cellulaire peut s'exprimer et se décomposer de la même manière que pour un lit de grains (équation (39)).
La conductivité stagnante de mousses conductrices s'avère être très bien représentée par la formule de Lemlich [94,140], ne considérant que la conductivité dans le solide, avec un facteur de tortuosité d'un tiers :
| (44) |
La composante dispersive peut également s'exprimer en fonction d'un nombre de Péclet thermique, comme dans le cas d'un lit de grains. Cette composante de la conductivité effective, ainsi que la contribution radiative aux températures considérées (<500 °C), est toutefois négligeable devant la conductivité stagnante dans le cas de mousses très conductrices, comme des mousses en aluminium [94].
Les mousses cellulaires possédant une structure globalement isotrope, le modèle (λr−h) semble tout à fait adapté à la représentation de l'échange en paroi. Le coefficient d'échange peut, comme pour les lits de grains, être représenté via une composante conductive et une composante convective. Encore une fois, du fait de la grande conductivité des mousses cellulaires conductrices, l'échange par conduction est souvent prépondérant, notamment dans les cas où le fluide est un gaz. L'échange entre la mousse et la paroi du réacteur est cependant très dépendant de leur état de surface et de l'ajustement appliqué entre les deux éléments. La méthode de découpe de la mousse peut, par exemple, avoir une grande influence sur l'échange à la paroi, ce qui rend difficile toute prévision [141]. Par exemple, Bianchi et al. [95] ont trouvé que l'échange à la paroi entre des mousses d'aluminium ou de FeCrAlloy était limité par une couche de gaz résiduelle entre la mousse et la paroi. Les échanges en paroi dépendent, de plus, de la méthode de liaison à cette dernière, les mousses pouvant être par exemple brasées pour diminuer cette résistance thermique [141].
4.3 Modèles cinétiques de la réaction de méthanation du dioxyde de carbone
La connaissance des lois décrivant le processus de réaction chimique est essentielle à la modélisation des réacteurs catalytiques. Les phénomènes réactionnels sont généralement regroupés sous la forme d'une seule loi, décrivant les influences de la température, de la pression et de la composition sur les vitesses de réactions. Les modèles cinétiques des réactions sont parfois établis de manière simpliste via l'identification de lois dites « en puissance », mais sont généralement issus de la considération (et donc de la supposition) de mécanismes réactionnels. Afin de regrouper les étapes du mécanisme en une loi unique, l'hypothèse de l'étape cinétiquement déterminante est utilisée. Cette hypothèse suppose qu'une étape est plus lente que les autres et impose la cinétique de réaction, les autres étapes étant alors supposées à l'équilibre. Ces lois reposent généralement sur le formalisme généralisé de Hougen [142] représentant les cinétiques de catalyse hétérogène comme la combinaison de trois termes fondamentaux :
| (45) |
Le facteur cinétique contient la constante cinétique de la réaction cinétiquement déterminante, éventuellement modulée par des constantes d'équilibres d'adsorption. Le terme de potentiel, ou force motrice, représente l'écart entre l'état du système et son état à l'équilibre thermodynamique. Ce terme contient, par conséquent, la constante d'équilibre de la réaction ainsi que les pressions partielles des différents réactifs et produits. Enfin, le terme d'adsorption traduit la compétition d'adsorption sur les sites de la phase active disponibles. La puissance n dépend essentiellement de la nature mono-ou pluri-moléculaire de l'étape déterminante, mais peut varier selon le mécanisme considéré. Ce terme d'adsorption est souvent représenté par la théorie de Langmuir, le modèle cinétique est alors appelé modèle de Langmuir–Hinshelwood. La théorie d'adsorption de Langmuir suppose toutefois une adsorption sur une seule couche à la surface de la phase active du catalyseur. Elle permet de représenter le taux de recouvrement d'une espèce i à la surface de la phase active en utilisant les constantes d'équilibre d'adsorption Kj des différentes espèces j (incluant i) s'adsorbant sur cette même surface :
| (46) |
Cette section est dédiée aux modèles de lois cinétiques permettant de représenter la méthanation du CO2. Peu de modèles ont cependant été établis directement pour la méthanation du CO2 dans la littérature, ce qui nous a conduits à étudier aussi des lois établies pour la réaction de vaporeformage du méthane.
4.3.1 Modèles décrivant la cinétique de la réaction de dioxyde de carbone uniquement
En 1974, Lunde et Kestler ont proposé une loi cinétique pour la réaction de méthanation du CO2 permettant de décrire cette réaction pour un catalyseur à base de ruthénium. Cette loi, décrivant l'influence de la composition par de simples puissances, a été établie à la pression atmosphérique et pour des températures comprises entre 204 et 360 °C (entre 400 et 680 °F) [143]:
| (47) |
D'après leurs expériences, les auteurs ont obtenu une valeur de n de 0,225. La constante cinétique k suit une loi d'Arrhenius avec un facteur pré-exponentiel de 0,1769·1010 h−1 atm−0,125 et une énergie d'activation de 70,5 kJ/mol :
| (48) |
Un autre modèle a été proposé [144] pour un catalyseur également à base de ruthénium. Les expériences ont été réalisées à la pression atmosphérique pour des températures comprises entre 200 et 300 °C. Afin d'établir leur modèle, les auteurs ont considéré 28 mécanismes différents, malheureusement non explicités, discriminés sur la seule base de la concordance avec les résultats expérimentaux. La réaction inverse a également été négligée. Le modèle permettant de mieux représenter les résultats des auteurs suppose l'étape cinétiquement déterminante suivante :
| (49) |
Les études sur les mécanismes de réaction indiquent, cependant, qu'il est peu probable que l'hydrogénation du CO2 puisse se produire en une seule étape élémentaire ; le mécanisme décrit ici paraît, par conséquent, incomplet. La loi cinétique obtenue est la suivante :
| (50) |
Les valeurs des constantes de ce modèle sont données par :
| (51) |
| (52) |
| (53) |
Les unités ne sont toutefois pas réellement explicitées, il est supposé que les différentes énergies sont en kcal/mol, que les constantes d'adsorption sont en atm−1 et que la constante cinétique est en mol/g/h.
Ces deux exemples de modèles cinétiques ne considèrent que la méthanation du CO2, sans considérer d'autres réactions parallèles, comme la réaction de gaz à l'eau inverse (RWGS), entraînant la formation du CO ou la méthanation de celui-ci. La présence du CO ayant été mise en évidence lors de la mise en œuvre de la méthanation du CO2, il peut être nécessaire de considérer ces deux réactions.
4.3.2 Modèle considérant plusieurs réactions : le modèle de Xu et Froment
Aucun modèle cinétique prenant en compte plusieurs réactions dans le cas de la méthanation du CO2 n'a été trouvé dans la littérature. De tels modèles ont cependant été établis dans le cadre du reformage du méthane [145]. Un exemple de modèle souvent repris dans la littérature est le modèle de Xu et Froment [146]. Ce modèle [146] a ainsi été établi avec un catalyseur à base de nickel déposé sur MgAl2O4 à partir d'expériences de reformage de méthane, mais également de méthanation du CO2/réaction de gaz à l'eau inverse. Les expériences de reformage ont été effectuées sous des pressions comprises entre 3 et 15 bar, à des températures comprises entre 500 et 575 °C. Les expériences de méthanation/RWGS ont été quant à elles effectuées entre 3 et 10 bar et à des températures entre 300 et 400 °C. Ces dernières expériences ont toutefois été réalisées avec un ratio H2/CO2 compris entre 1 et 0,5. Enfin, ce modèle cinétique a été établi avec un catalyseur usagé, après 70 heures de fonctionnement, lorsque la vitesse de désactivation du catalyseur est suffisamment lente pour être corrigée par un facteur définit par des expériences de références [146].
Le modèle de Xu et Froment considère ainsi les trois réactions suivantes :
Chacun des mécanismes des réactions précédentes comporte une unique étape déterminante :
- • pour la méthanation du CO, l'étape limitante est l'hydrogénation du CO en CHO en phase adsorbée,
- • l'étape limitante pour la méthanation du CO2 est également la conversion en CHO, avec libération d'un atome d'oxygène en phase adsorbée,
- • celle pour la réaction de water gas shift est l'oxydation du CO en CO2 en phase adsorbée.
Les expressions cinétiques issues de ce mécanisme sont données dans le Tableau 8, formulées dans le sens de la méthanation (et de la RWGS) :
| (54) |
| (55) |
| (56) |
| (57) |
Étapes élémentaires du modèle de Xu et Froment et étapes cinétiquement déterminantes (r.d.s.) : r1, méthanation du CO ; r2, RWGS ; r3, méthanation du CO2 [146].
| (1) | |
| (2) | |
| (3) | |
| (4) | |
| (21) | |
| (22) | |
| (23) r.d.s. ; r1 | |
| (8) r.d.s. ; r2 | |
| (25) r.d.s. ; r3 | |
| (7) | |
| (10) | |
| (1-bis) | |
| (1-bis) |
Il sera noté l'absence du terme d'adsorption du CO2 au dénominateur, les auteurs ayant trouvé ce paramètre négligeable devant les autres termes d'adsorption, ainsi que le terme d'adsorption de l'eau, qui suppose, de manière contestable, la dissociation directe de l'eau en hydrogène.
Les constantes cinétiques déterminées par Xu et Froment [146] sont présentées dans le Tableau 9.
| Paramètre | k1,0 (mol·bar0,5/kg/s) | k2,0 (mol·bar−1/kg/s) | k3,0 (mol·bar0,5/kg/s) | (kJ/mol) | (kJ/mol) | (kJ/mol) |
| Xu et Froment | 1,17·1015 | 5,43·105 | 2,83·1014 | 240,1 | 67,13 | 243,9 |
| Oliveira et al. | 5,79·1012 | 9,33·105 | 1,29·1013 | 217,01 | 68,2 | 215,84 |
Les paramètres sensés représentés les constantes d'adsorption ont été identifiées numériquement par Xu et Froment à partir de leurs expériences. Ces constantes sont définies par les lois d'Arrhenius suivantes :
Le modèle de Xu et Froment a été utilisé par Oliveira et al. [147] dans le cadre du reformage du méthane avec un catalyseur à base de nickel déposé sur alumine. Les auteurs ont ré-identifié les constantes cinétiques du modèle en conservant les valeurs des constantes d'adsorption déterminées par Xu et Froment. Des expériences de reformage de méthane ont pour cela été effectuées à 2 bar avec des températures comprises entre 460 et 620 °C. Les paramètres cinétiques identifiés par Oliveira sont également résumés dans le Tableau 9.
Les énergies d'activation des différentes réactions obtenues dans les deux cas sont relativement proches. Il sera noté la similitude entre les énergies d'activation des réactions de méthanation, ce qui appuie l'idée d'une méthanation du CO2 suivant le même mécanisme que celle du CO. Les constantes pré-exponentielles diffèrent, quant à elles, de plusieurs ordres de grandeur. Ces paramètres dépendent cependant fortement du catalyseur utilisé et notamment de la surface de nickel qu'il présente, liée à la masse de nickel qu'il contient et à sa dispersion. Plus récemment, le modèle de Xu et Froment a été adapté par Zhang et al. [148] dans le cas de la méthanation du CO avec un catalyseur à base de nickel (50% massique). Le modèle de Xu et Froment a cependant été modifié, d'une part, en réduisant la puissance de 2 à 1 au dénominateur afin de représenter les résultats expérimentaux et, d'autre part, en ne considérant que les réactions de méthanation du CO et de gaz à l'eau. Les auteurs ont ainsi cherché à identifier les constantes cinétiques du modèle de Xu et Froment en conservant les constantes d'adsorption obtenues par Xu et Froment. Ce modèle a été déterminé pour des pressions entre 1 et 5 bar et des températures entre 300 et 360 °C. Les auteurs ont toutefois rencontré des difficultés expérimentales en raison de la formation rapide de dépôt de carbone à la surface du catalyseur. Les résultats obtenus sont résumés dans le Tableau 10.
Paramètres cinétiques identifiés par Zhang et al. [148].
| Paramètre | k1,0 (mol bar0,5/kg/s) | k2,0 (mol bar−1/kg/s) | (kJ/mol) | (kJ/mol) |
| Valeur | 4,42·1016 | 2,18·106 | 248 | 62 |
Encore une fois, les énergies d'activation sont très proches de celles obtenues par Xu et Froment. Les facteurs pré-exponentiels sont quant à eux supérieurs, probablement en raison de la forte teneur en nickel du catalyseur employé.
Ce modèle ne considérant pas la méthanation directe du CO2, il n'est pas assuré qu'il soit utilisable pour cette dernière réaction. Pour l'application de la réaction de méthanation du CO2, le problème est en effet de pouvoir discriminer les voies de méthanation, directe ou indirecte, ou de savoir si une des deux est prépondérante par rapport à l'autre.
5 Conclusions
Il ressort de cette étude que, malgré sa découverte il y a plus d'un siècle, la réaction de méthanation du CO2 présente encore de nombreux enjeux dans le cadre récent de son application à un procédé power to gas. Les catalyseurs développés à partir de métaux comme le nickel et déposés sur des supports céramiques ont été étudiés, et leurs efficacités démontrées à de nombreuses reprises pour les réactions de méthanation. Les mécanismes de réaction sur ce genre de catalyseur sont toutefois toujours débattus, même si de nombreuses études ont permis de mieux les définir. Il a ainsi été montré que deux mécanismes de méthanation du CO2 pouvaient coexister : l'un décrivant la décomposition du CO2 en CO, l'autre passant par un intermédiaire carbonate, puis formiate, réservé à des catalyseurs utilisant des supports plus basiques (comme la cérine-zircone). Le mécanisme exact de l'hydrogénation du CO fait également toujours débat. Lors de la mise en œuvre de la méthanation du CO2, ces catalyseurs peuvent être sujets à différents phénomènes de désactivation. Outre l'empoisonnement, qui est généralement traité par l'épuration du gaz en amont des réacteurs catalytiques, les principales causes de désactivation sont le frittage des cristallites métalliques et la formation de dépôts de carbone à la surface du catalyseur, tous deux étant généralement favorisées par des températures élevées. Il apparaît donc que la gestion de la température est primordiale pour obtenir, d'une part, une productivité importante et limiter, d'autre part, la diminution de celle-ci dans le temps. Par ailleurs, les principales applications industrielles de méthanation, essentiellement du CO, ont été développées dans les années 1970–1980 pour la production de SNG à partir de la gazéification du charbon, le gaz entrant du procédé étant alors un syngas, c'est-à-dire un mélange H2/CO/CO2/H2O. Un grand nombre de ces applications a utilisé des réacteurs adiabatiques à lit fixe, simples et robustes, mais nécessitant le recours à des mesures énergivores et coûteuses, ayant pour conséquence de limiter les performances des catalyseurs ou de rendre l'équilibre thermodynamique moins favorable, afin de limiter les températures au sein des réacteurs. Du fait de leur nature adiabatique, plusieurs réacteurs sont nécessaires pour atteindre de fortes conversions. Ces installations sont adaptées au cadre spécifique de la production de SNG à partir du charbon. Elles ne correspondent cependant pas au paradigme du procédé power to gas où la nature du gaz entrant est différente, les tailles d'installations sont plus réduites, les contraintes de coût, de compacité et de flexibilité sont plus importantes. Les réacteurs à lit fluidisé ont également été utilisés pour leur meilleure homogénéité thermique. Ces réacteurs posent toutefois le problème du fait de la gestion de l'attrition des catalyseurs. Le comportement hydrodynamique d'un lit fluidisé entraîne, de plus, une flexibilité très limitée et un accès plus difficile aux très fortes conversions, pourtant essentielles pour une application power to gas. Plus récemment, l'utilisation de réacteurs-échangeurs à lit fixe a montré qu'il était possible de réduire le nombre de réacteurs nécessaires par rapport aux réacteurs adiabatiques tout en conservant les avantages de la forme lit fixe. Les réacteurs-échangeurs sont plus compatibles pour une application power to gas. Ils se heurtent, cependant, aux problèmes de la gestion thermique liés à la réaction et à la désactivation des catalyseurs du fait des faibles performances thermiques de ce type de réacteur. Des mesures visant à réduire l'activité catalytique, comme une alimentation étagée des réactifs utilisée dans le pilote d'AUDI, sont alors toujours nécessaires. Ces mesures ont pour conséquence d'augmenter le volume des réacteurs et d'augmenter les coûts de l'installation. Parmi les solutions émergentes, l'utilisation de réacteurs-échangeurs et de catalyseurs à architectures structurées, comme les réacteurs à lit fixe milli-structurés ou encore les catalyseurs déposés sur des structures monolithiques conductrices, semblent être des approches prometteuses pour la méthanation du CO2. Ces structures doivent cependant encore être optimisées pour répondre aux besoins de la réaction dans le cadre d'une application industrielle du procédé power to gas.
L'étude de la modélisation des réacteurs catalytiques, appliquée à la réaction de méthanation, a permis de mettre en évidence la problématique complexe de la modélisation d'un milieu poreux et celle de la formulation des cinétiques de réaction en catalyse hétérogène. Le problème posé par la modélisation d'un milieu poreux est complexe, car il nécessite la représentation de différents phénomènes physiques couplés, comme le transfert de la masse, de la chaleur et de la quantité de mouvement, et ce à différentes échelles définies au sein de la structure géométrique du milieu poreux. Une méthode accessible et couramment utilisée est la méthode V.E.R., qui consiste à transposer les équations de conservation sur le fluide, présent dans les pores du milieu poreux finement divisé, à une échelle macroscopique représentée par le milieu continu équivalent d'un volume élémentaire représentatif. Cette méthode d'homogénéisation par prise de moyenne volumique est toutefois fortement critiquable dans le cas de réacteurs dont les dimensions sont faibles en raison des contraintes portant sur la taille d'un volume élémentaire représentatif par rapport à l'échelle de la microstructure et celle des canaux réactifs. Le principal inconvénient de cette méthode est la perte d'informations qu'elle entraîne, certains phénomènes de transfert n'étant plus directement résolus, mais intégrés dans des coefficients globaux apparus dans les équations de conservation. La difficulté est alors de déterminer ces coefficients par des corrélations, appelées équations de fermeture, qui sont pour la plupart spécifiques au système utilisé et qui doivent donc être obtenus par l'expérience directe sur les réacteurs utilisés. L'aspect thermique de la réaction de méthanation étant un aspect essentiel, il apparaît alors inévitable de caractériser ces transferts expérimentalement dans les réacteurs utilisés avec le catalyseur utilisé. Nous avons mis en évidence le manque de travaux sur le sujet de la formulation d'une cinétique de méthanation du CO2, applicable dans la gamme de paramètres envisagés dans notre étude. Cette absence de loi générique provient en grande partie du fait que les mécanismes des réactions demeurent toujours mal connus. En particulier, la question de la discrimination de la voie de méthanation du CO2 directe et indirecte par la combinaison de la réaction de gaz à l'eau inverse et de la méthanation du CO est encore posée. Cette interrogation est de plus appuyée par les considérations mécanistiques supposant que la méthanation du CO2 suit la méthanation du CO. Afin d'établir un modèle de simulation de réacteurs-échangeurs suffisamment représentatif pour analyser les comportements et les performances de ces derniers et de les optimiser, il apparaît nécessaire de caractériser expérimentalement les phénomènes et paramètres importants lors de la mise en œuvre de la réaction de méthanation du CO2 en réacteur-échangeur.


