1 Introduction
The lignin-derived phenolic compounds are among the main components in pyrolysis bio-oil. For example, the vapors evolved during torrefaction of red oak contain about 19% phenolics (on a dry basis) [2]. The oxygen functionalities in phenolic compounds, usually in the form of hydroxy–OH or methoxy–OCH3, make them reactive for many different CC bond formation chemistries such as alkylation, hydroxyalkylation, acylation [3–5], and so forth to create longer chain molecules that fit into the fuel pool. However, after the CC bond forming step, these oxygen functionalities still remain on the aromatic ring, and it is necessary to perform hydrodeoxygenation (HDO) chemistry to remove oxygen and create hydrocarbon fuels. This work focuses on the removal of hydroxy–OH functionality, with m-cresol as the model compound, because it is one of the dominant functionalities in biomass-derived compounds.
The HDO reaction of phenolic compounds has been extensively studied and reported in the literature over different metals and bimetallic alloys [6–10], different supports [11–13], or in cooperation with an acidic function [14–21]. Understanding the reaction mechanisms and finding relationships between the observed catalytic behavior and the catalyst structure is of crucial significance for optimizing catalyst design and selection.
In our previous studies, we have shown that the oxophilicity of the metal catalysts, reflecting the metal–O bond strength, is a crucial descriptor of their HDO activity [22]. In a series of studies on the HDO of m-cresol and phenol as the model compounds, we have compared the reactivity and prevalent mechanisms over different metals, including monometallic (Pt, Pd, Ru, Fe, and Ni) and bimetallic catalysts supported on inert SiO2 [1,22–24] or more oxophilic supports [12]. In particular, SiO2 is an inert support with minimum participation in the reaction, which has allowed us to focus on the catalytic behavior of the metals.
In this contribution, honoring Prof. Francois Gault, we analyze the observed trends with the oxophilicity of the metals and present new results on the effect of extent of metal atom coordination, which can be controlled by varying the metal cluster size, which in turn affects oxophilicity, and consequently the HDO activity. Throughout his illustrious career, Prof. Gault called attention to the dramatic changes in selectivity of hydrocarbon conversion (e.g., hydrogenolysis and isomerization) over metal catalysts as the particle size changes. He recognized that the changes commonly observed in product selectivity with varying particle size can be traced to changes in reaction mechanisms, which in turn are related to the number of low-coordination (corner and edge) atoms relative to high-coordination (face or terrace) atoms [25–29]. Here, we are using these concepts to interpret changes in HDO reaction mechanism and selectivity changes for the conversion of phenolics on different metal catalysts.
2 HDO of m-cresol on different types of metal
As depicted in Fig. 1, when m-cresol is converted in the presence of H2 over different metal catalysts, two types of products are typically observed: (1) hydrogenation products (3-methylcyclohexanone and 3-methylcyclohexanol) and (2) HDO products (toluene [TOL], methylcyclohexane, and 3-methylcyclohexene). In principle, TOL could be produced via two different pathways: (1) hydrogenation of m-cresol to 3-methylcyclohexanol, followed by dehydration to 3-methylcyclohexene and further dehydrogenation to TOL, and (2) direct HDO from m-cresol.
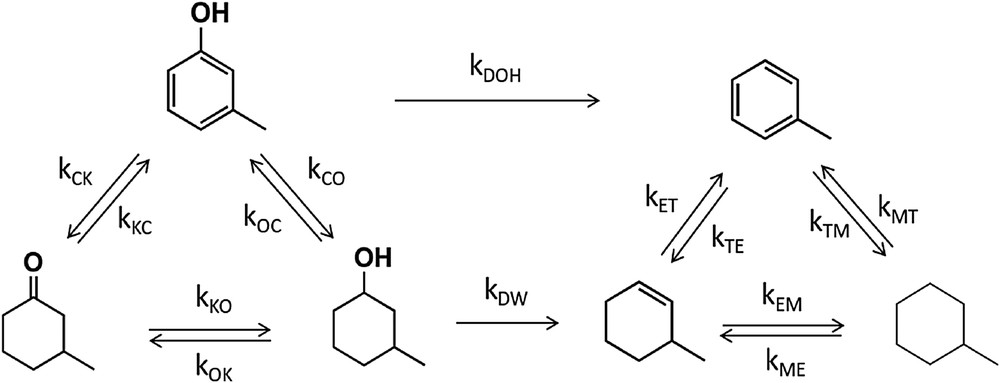
Reaction pathway for HDO of m-cresol (modified with permission from Ref. [1]).
2.1 HDO of m-cresol over Pt catalyst
In a detailed kinetic study conducted with a Pt/SiO2 catalyst[1,30], we showed that pathway (1) only occurs to a very low extent due to the low acidity of the SiO2 support. As shown in Fig. 2, the yield of TOL increases with increasing m-cresol conversion but when 3-methylcyclohexanol or 3-methylcyclohexanone was used as feed, the yield of TOL remains almost zero in all cases, even at high feed conversions, which shows that TOL is not obtained from the alcohol or the saturated ketone.
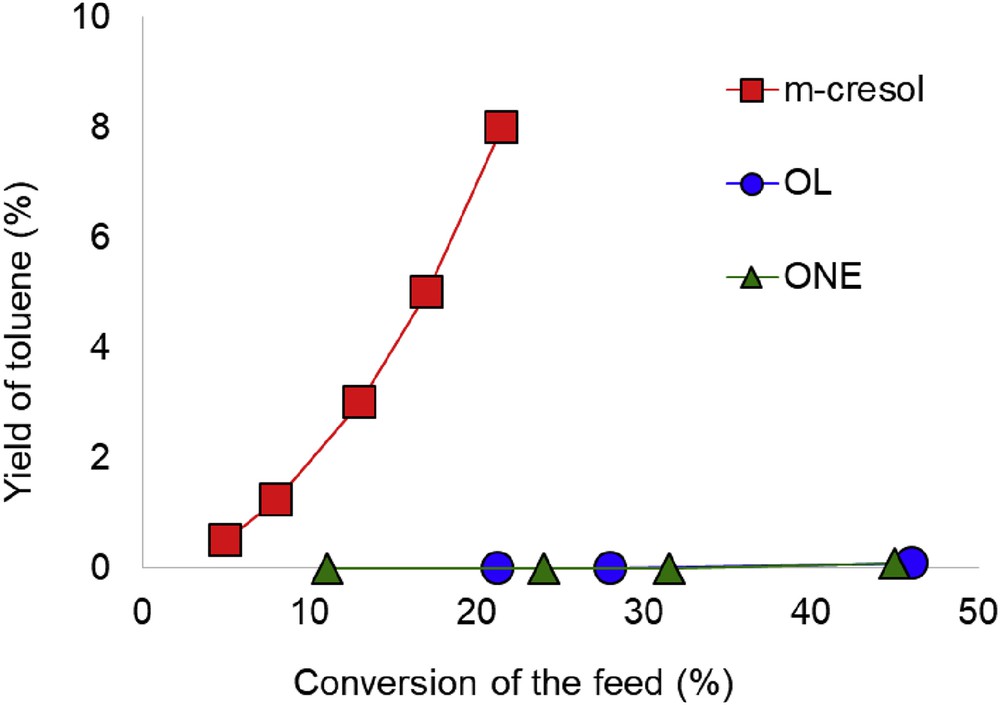
The yield of TOL vs conversion of feed over Pt/SiO2 at 300 °C with different feeds including m-cresol, 3-methylcyclohexanol (OL) and 3-methycyclohexanone (ONE) (modified with permission from Ref. [1]).
It was also clearly demonstrated that TOL was not derived from methylcyclohexene either. In fact, as shown in Table 1, at low conversions over Pt/SiO2, methylcyclohexene results in a TOL/methylcyclohexane ratio of about unity. This ratio gradually increases to its equilibrium value (∼11 at 300 °C) with feed conversion. That is, far from equilibrium, the methylcyclohexene to TOL and methylcyclohexene to methylcyclohexane reactions occur at similar rates, but as conversion increases, the secondary methylcyclohexane to TOL reaction drives the TOL/methylcyclohexane ratio close to the equilibrium of 11. This was indeed the trend observed when the feed was either 3-methylcyclohexanol or 3-methylcyclohexanone over the Pt/SiO2 catalyst.
The yield of TOL and methylcyclohexane (MCANE) when 3-methylcyclohexene was fed over Pt/SiO2 at 300 °C (modified with permission from Ref. [1]).
| Conversion of 3-methylcyclohexene (%) | Yield (%) | Ratio TOL/MCANE | |
| TOL | MCANE | ||
| 13.3 | 1.7 | 1.9 | 0.89 |
| 18.9 | 4.7 | 3.9 | 1.2 |
As shown in Fig. 3, when 3-methylcyclohexanol or 3-methylcyclohexanone was fed over the Pt/SiO2 catalyst, the TOL/methylcyclohexane ratio was near unity at low feed conversion and only increased to near 10–11 as the feed conversion increased. This is reasonable because 3-methylcyclohexanol was slowly dehydrated to methylcyclohexene, followed by simultaneous hydrogenation to methylcyclohexane and dehydrogenation to TOL. However, a drastically different pattern was observed when m-cresol was used as the feed. In this case, even at the lowest feed conversions, the TOL/methylcyclohexane ratio was much greater than the equilibrium value of 11. Clearly, this trend indicates that TOL is not formed from any of the hydrogenated intermediates, but rather directly from m-cresol, whereas methylcyclohexane is mostly produced from secondary hydrogenation of TOL. It should be noticed that this may not be the case when Pt is supported on more acidic supports, in which the acid-catalyzed dehydration of 3-methylcyclohexanol become significant [31].

The ratio of TOL to methylcyclohexane (MCANE) vs conversion of different kinds of feed including m-cresol, 3-methylcyclohexanone (ONE) and 3-methylcyclohexanol (OL) over Pt/SiO2 at 300 °C (modified with permission from Ref. [30]). Dashed lines simply illustrate the opposite trends for approaching equilibrium.
The mechanism of m-cresol conversion to TOL is rather puzzling because a direct CO bond cleavage may not be possible on Pt due to the low metal–oxygen bond strength, which results in a high activation energy for direct deoxygenation (DDO). Therefore, a different reaction pathway must be considered to explain the production of TOL as an observed primary product.
2.2 Mechanism of hydroxyOH removal from m-cresol
As illustrated in the reaction scheme of Fig. 4, we have proposed that the direct conversion of m-cresol to TOL can alternatively happen via two different mechanisms, DDO and tautomerization (TAU) [22]. In the DDO mechanism, the CaromaticO bond would undergo direct cleavage to TOL and water, whereas in the TAU mechanism, the keto-enol isomer of m-cresol would undergo hydrogenation at the CO to an intermediate alcohol followed by dehydration to TOL. The nature of the metal catalyst determines which one is the more plausible mechanism.
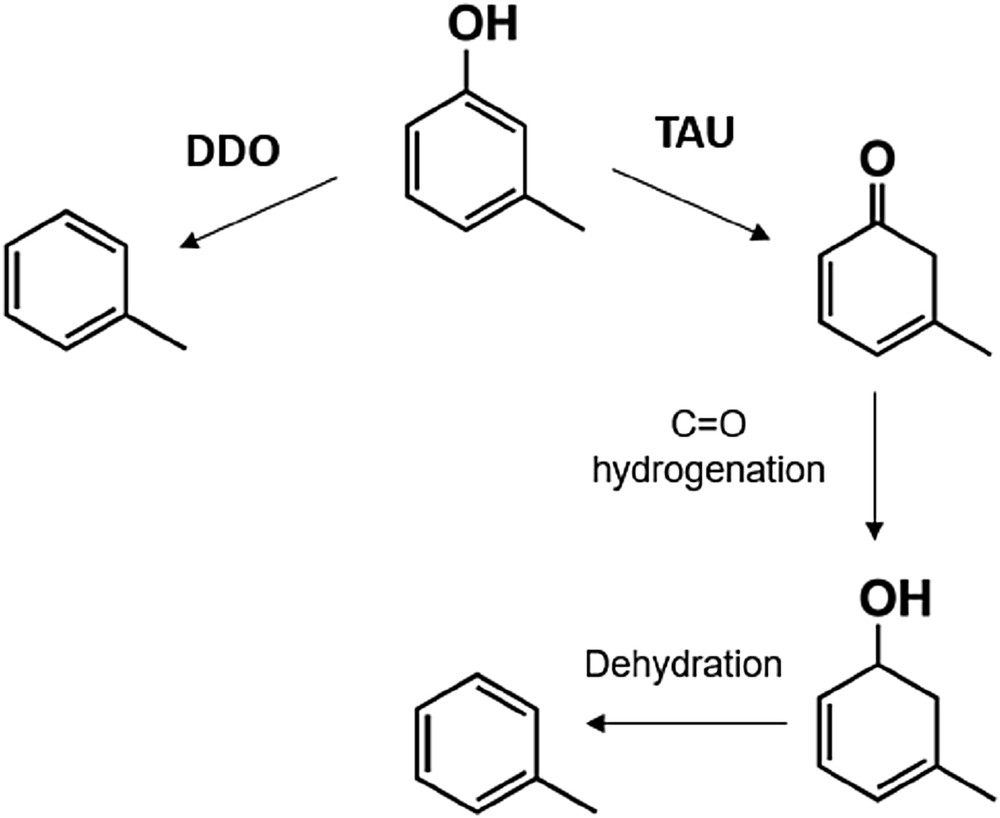
HDO mechanism for the conversion of m-cresol to TOL, DDO, and TAU.
Our previous study using density functional theory (DFT) calculations has shown that, in the case of Pt(111), the energy barrier for the DDO pathway is exceedingly high (242 kJ/mol). Therefore, on such a surface, the HDO has to proceed via a different mechanism. In fact, the DFT calculations show that the proposed TAU pathway is plausible, with a significantly lower energy barrier (203 kJ/mol) and the rate limiting step is determined by the final dehydration of the cyclic diene alcohol intermediate. Although dehydration is not particularly favorable over Pt, this path is energetically favored compared to the direct CO bond cleavage [22].
As shown in Fig. 5, the DFT calculated energy barriers for the DDO of m-cresol correlate very well with the oxophilicity of the metal catalysts. That is, the metal–O bond strength (oxophilicity) increases in the order Pt < Pd < Rh < Ru < Fe. When plotted in the same graph, the calculated energy barriers for the DDO of m-cresol decrease linearly from Pt to Fe. As a result, although over Pt, the TAU pathway is more favorable than the DDO pathway, the opposite is true on more oxophilic metals such as Rh, Ru, or Fe.
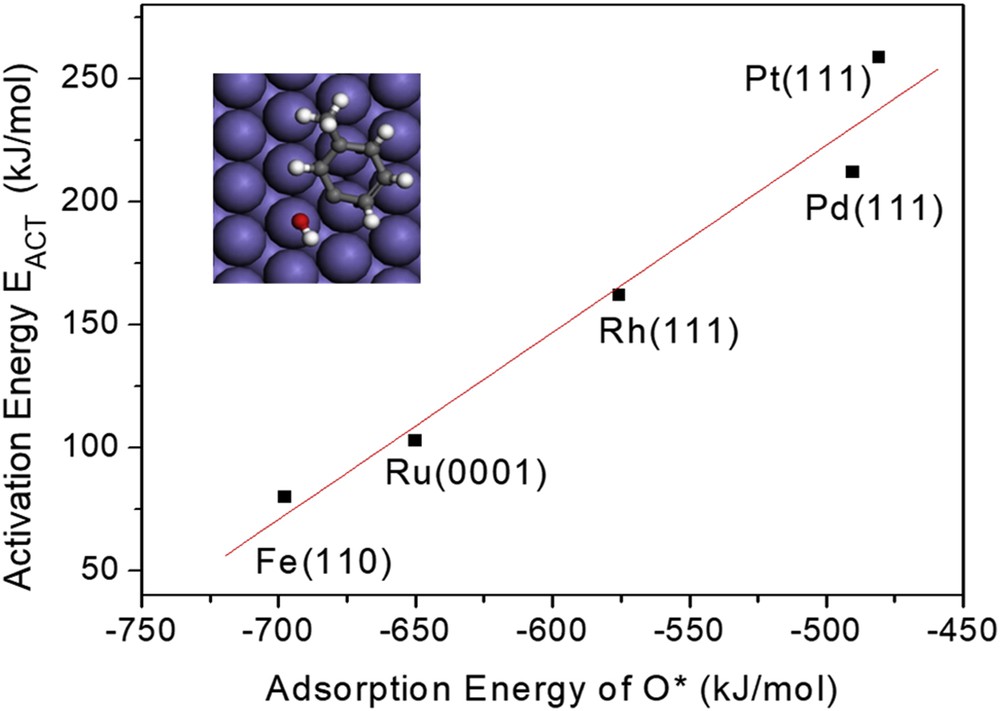
Correlation between activation energy for DDO of m-cresol and the adsorption energy of O* over different metals. Modified with permission from Ref. [22].
3 Relationship between metal atom coordination and oxophilicity
Oxophilicity, as measured by the MO bond strength, is a direct function of the position of the d-band center [32]. As the d-band center is closer to the Fermi level, the antibonding orbital of the hybridization between metal and oxygen is further away from the Fermi level and has a low electron occupancy. Therefore, the MO bond becomes stronger and the metal is more oxophilic. The d-band center gets closer to the Fermi level as one moves upward and to the left in the periodic table. To further illustrate this trend, as shown in Fig. 6, the adsorption energy of O* increases as the d-band center is closer to the Fermi energy (0 eV). Theoretical and experimental studies have shown that the d-band center also depends on the extent of metal atom coordination. That is, surface defects such as steps, edges, and kinks with smaller coordination are more free atom-like and have sharper d-bands. Thus, to maintain the same occupancy of d-state electrons, the d-band center shifts closer to the Fermi level. This shift does not occur to such a large extent for terrace atoms with high coordination and broader d-bands [33–36]. Therefore, we can expect that the HDO activity of metal should be strongly influenced not only by the metal type, but also by the atomic coordination. Lower coordination sites are more dominant on small metal clusters, whereas the high coordination sites are more dominant on large metal clusters.
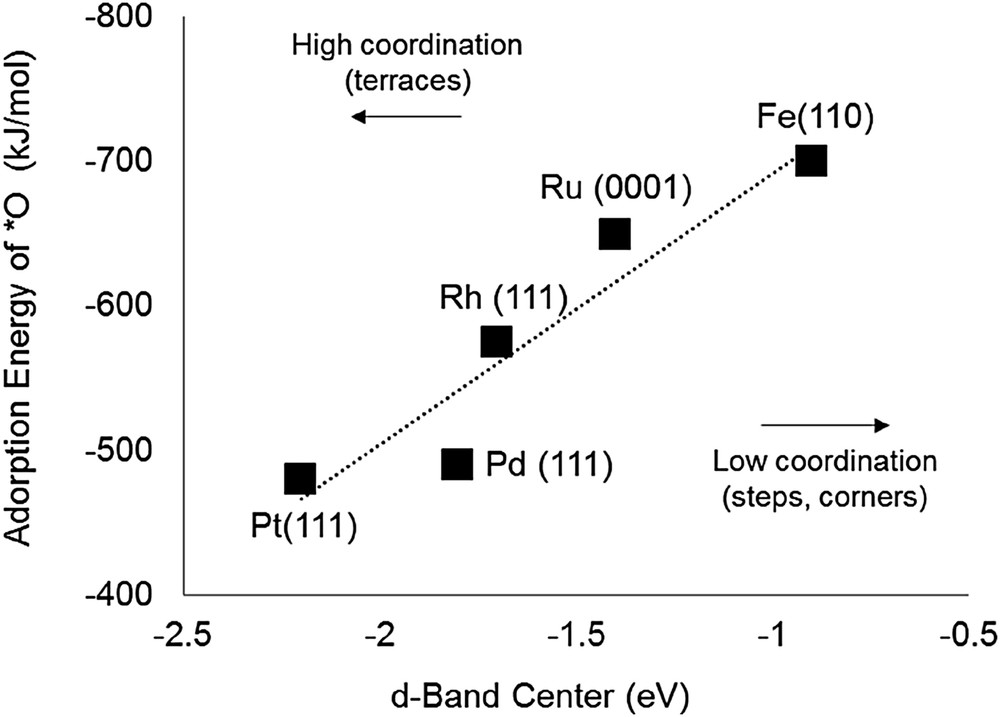
Correlation between adsorption energy of O* (kJ/mol) and d-band center (eV).
To further explore this concept, the HDO of m-cresol was investigated on two Rh catalysts with varying particle sizes to compare the resulting product distributions and overall catalytic behavior. The metal Rh was chosen because it has an intermediate oxophilicity (bulk d-band center = −1.7 eV, MO bond = −575 kJ/mol), which is between those of Pt and Ru and may thus evidence the particle size effects more clearly. On the former, the MO bond strength is too weak to catalyze DDO and on the latter it may be too strong to show variations between low- and high-coordination sites.
4 Characterization of Rh/SiO2 catalysts of different particle sizes
Two Rh/SiO2 catalysts were synthesized with varying metal loadings (2.5 and 7 wt %) and treated at different reduction temperatures to obtain different ranges of particle sizes and surface defects. The two catalysts were characterized by HRTEM (high resolution transmission electron microscopy) and diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) analysis of adsorbed CO after in situ reduction. As shown in Fig. 7, HRTEM results of the two catalysts clearly reflects the different ranges of metal cluster sizes and shapes. The high-temperature treated 7 wt % Rh/SiO2 catalyst contains bigger and better-defined metal particles compared with the low-temperature treated 2.5 wt % Rh/SiO2 catalyst. A histogram indicating the different average particle sizes (4 vs 2 nm) is included in Fig. 8.
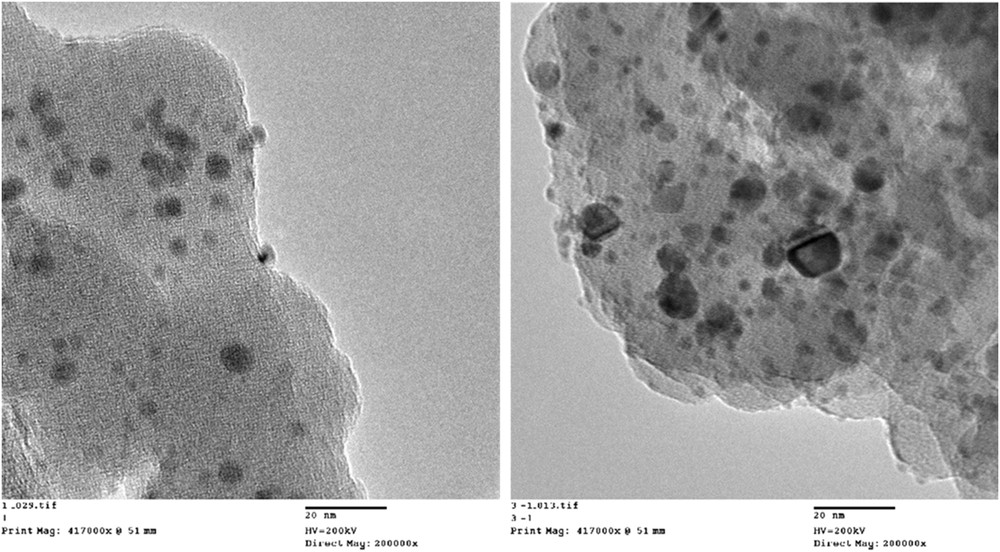
HRTEM of 2.5 wt % Rh/SiO2 (left) and 7 wt % Rh/SiO2 (right) catalysts.
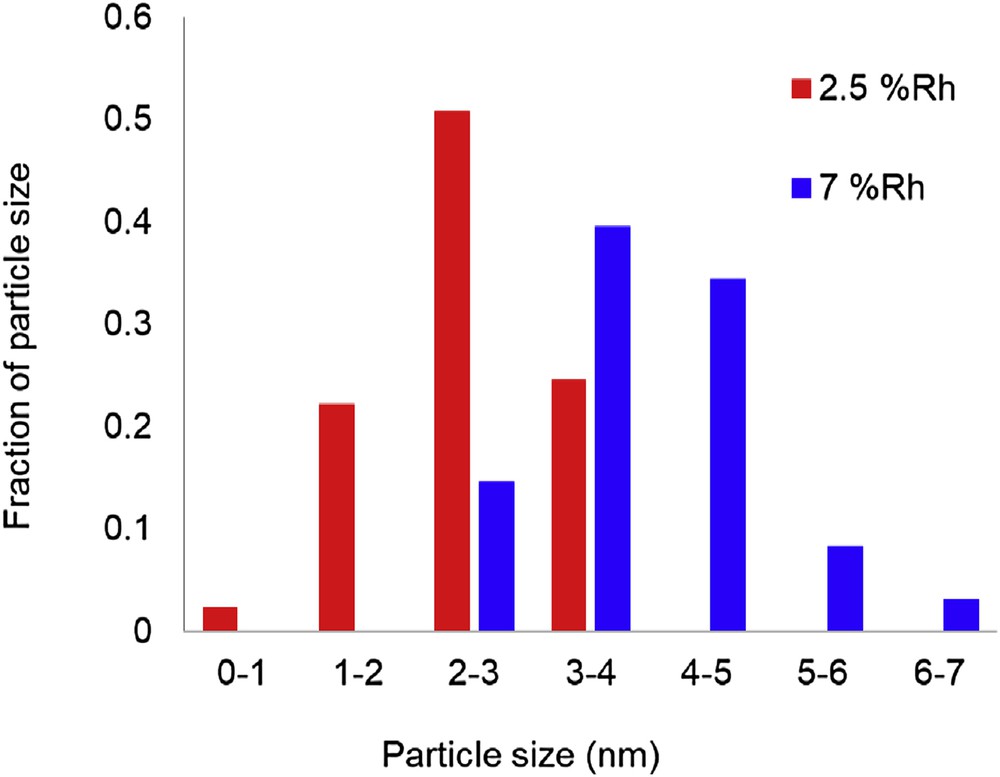
Particle size distribution 2.5 wt % Rh/SiO2 and 7 wt % Rh/SiO2 catalysts.
These observations were further corroborated by DRIFT analysis of adsorbed CO (see Fig. 9). This technique is particularly suited to characterize Rh catalysts of varying coordination numbers and particle sizes. It is well known that CO can adsorb on Rh via three different adsorption modes: linear (L), gem (G), and bridge (B). In the L mode (2050–2070 cm−1), a single CO molecule adsorbs on a top single metal site. Generally, the frequency of this band shifts to lower values as the surface coverage increases. In the G mode, two CO molecules adsorb on a single metal site, generating a doublet of vibrational modes, corresponding to the concerted symmetric and asymmetric (2030 and 2100 cm−1) vibrational modes. When CO molecules adsorb on small metal particles, the repulsion forces among adsorbed CO molecules can be strong enough to disrupt the metal cluster [37]. This phenomenon could happen when the metal-support interaction is weak, which is our case because SiO2 was used as an inert support. The resulting single metal atom can accommodate two CO molecules, giving rise to the G vibrational modes. This doublet is a fingerprint for the presence of small, defective Rh clusters in a high state of dispersion over the support [38–40]. Finally, the B mode corresponds to one CO molecule adsorbed on an ensemble of metal sites (1800–1900 cm−1) [41]. Although the G and L modes are usually rather sharp bands, the B mode is significantly broader, because CO can adsorb on metal site multiple of varying number (2, 3, or 4), which results in a broad band including a range of frequencies.
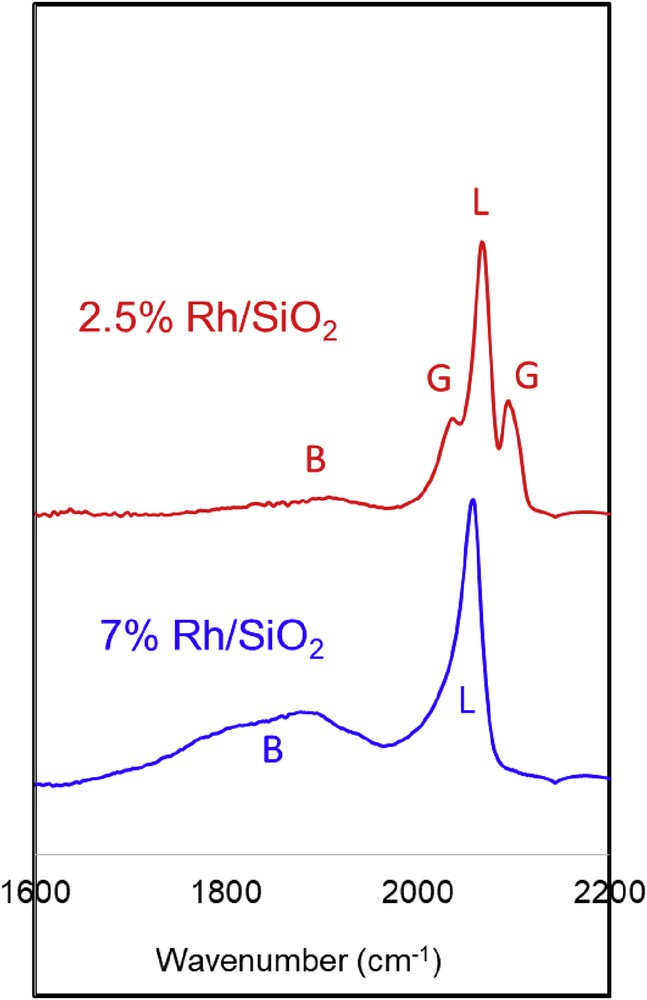
DRIFTS of CO adsorption more than 2.5 wt % Rh/SiO2 and 7 wt % Rh/SiO2 catalysts.
Significant differences in the infrared spectra are clearly evident in Fig. 9. The low-temperature treated 2.5 wt % Rh/SiO2 catalyst, with the smaller metal particles, exhibits features that are consistent with a high density of low-coordination surface sites. In addition to the L CO band, this catalyst (TEM ∼2 nm) shows intense G dicarbonyl bands and a much smaller B band than the 7 wt % Rh catalyst (TEM ∼4 nm), which shows a dominant B band, and complete absence of the G dicarbonyl bands. Also, the shift to lower frequencies observed on the L band for this catalyst is consistent with a higher extent of adsorbate–adsorbate interaction, also typical of flat planes and generally associated with dipole–dipole interactions [42].
That is, the TEM results and DRIFT profiles unequivocally demonstrate that the 7 wt % Rh/SiO2 catalyst contains a higher density of flat plane terraces than the 2.5 wt % Rh/SiO2 catalyst, which in turn contains a higher proportion of small metal clusters with more steps and edges. The 2.5 wt % Rh/SiO2 catalyst with more steps and edges will have the d-band center closer to the Fermi level, which makes it more oxophilic, whereas the 7 wt % Rh/SiO2 catalyst would be less oxophilic [43].
5 Catalytic behavior of Rh with different particle size
To precisely monitor the change in activity of the two different surfaces (i.e., 2.5 and 7 wt % Rh), starting from the pristine surface to one partially covered by poisons such as carbonaceous fragments or oxygen species, catalytic measurements were conducted in a micropulse reactor. In this device, the catalyst after in situ reduction was kept at the reaction temperature (285 °C in this study) under pure H2 stream all the time, whereas a small and controlled amount of feed was periodically injected into the catalyst bed. This micropulse reactor system allows us to precisely monitor the effects of the initial stages of catalyst deactivation and approach to steady-state conditions starting with the pristine catalyst. This reactor is particularly valuable for observing activity–structure relationships, minimizing the secondary effects that carbonaceous deposits may have on the activity and selectivity of the catalyst, which is not possible in a conventional steady-state continuous flow reactor. Moreover, the study of the behavior of pristine catalysts can be more directly related to DFT calculations, which typically simulate the interaction of the reactants with a pristine metal surface.
In this case, the two catalysts (2.5 and 7 wt % Rh/SiO2) were tested for their catalytic activity for the HDO of m-cresol, keeping the overall m-cresol conversion at ∼30% and constant m-cresol partial pressure in the feed. The turnover number (TON) of each product was normalized by the number of exposed Rh metal atoms, calculated based on the particle size from TEM with the assumption of a hemispherical particle shape. Fig. 10 shows the variation in normalized TON for each product as a function of the pulse number. It is observed that the TON to HDO (TOL) and hydrogenation (OL and ONE) products is higher on the 2.5 wt % Rh than on the 7 wt % Rh, which means that the small particle size is more active for HDO and hydrogenation of m-cresol. On the other hand, the TON to cracking products C2C6 is similar for both cases. It should be noticed that the cracking products (lighter than C6) were not observed over Pt catalyst at the same reaction conditions. In contrast, over more oxophilic metals such as Rh and Ru a significant amount of cracking products was observed.
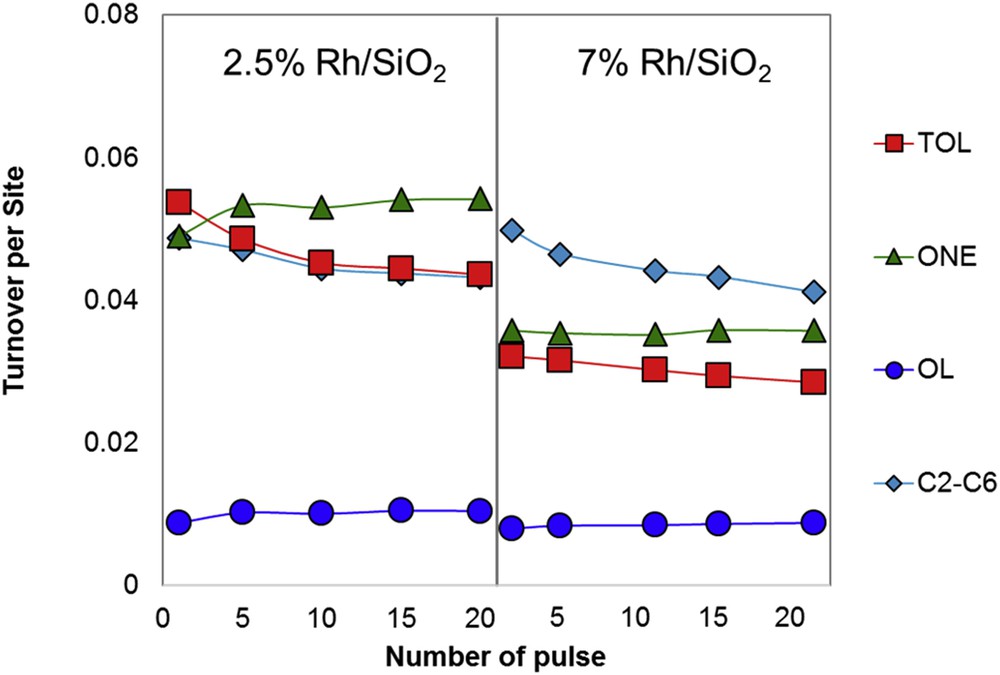
The turnover frequency from m-cresol to different products including TOL, 3-methylcyclohexanone (ONE), 3-methylcyclohexanol (OL), and cracking products (C2–C6) at increasing number of pulses of 2.5 and 7.5 wt % Rh/SiO2 at 285 °C.
Interestingly, in the case of 2.5 wt % Rh/SiO2 catalyst, the rate of formation of TOL in the first pulse was higher than that of 3-methylcyclohexanone (ONE) (0.054 vs 0.049), but TOL quickly dropped whereas ONE increased. As a result, at the 20th pulse, the TON of TOL became smaller than that of ONE (0.043 vs 0.054). This trend may indicate that very active HDO sites are initially present on the small Rh particles, readily converting m-cresol to TOL, but they are quickly deactivated, allowing hydrogenation to ONE and OL become dominant.
In contrast, in the case of the 7 wt % Rh/SiO2 catalyst, TON of TOL is lower than that on 2.5 wt % Rh catalyst (0.032 vs 0.054) even during the first pulse, but TOL does not drop much in the subsequent pulses, that is, TOL only dropped from 0.032 in the first pulse to 0.028 in the 20th pulse. This behavior indicates that the high-coordination terrace sites (typical of large particles) in 7 wt % Rh catalyst are less active for HDO, but they retain their activity more effectively.
The common trend observed on both large and small Rh particles is that as the catalyst deactivates, the yield to HDO product decreases whereas that for the hydrogenation product increases. Micropulse reactor is proven in this study to be a very useful tool to monitor the deactivation and has helped us to follow changes in activity and selectivity as some of the most active sites become deactivated.
6 DFT calculations of Rh surface with varying surface coordination number
To model the behavior of a flat terrace and a defective surface, DFT calculations were conducted over a Rh(111) terrace site and a Rh(533) step site, respectively. These calculations have allowed us to understand how the different sites influence the HDO of m-cresol and how they deactivate. First, the binding energy of atomic oxygen was calculated over the two surfaces. As shown in Table 2, the strength of the O bonding was significantly higher on the stepped Rh(533) surface (−610 kJ/mol) than on the Rh(111) flat surface (−575 kJ/mol), which substantiates the initial expectation that the step site is more oxophilic than the terrace site.
Summary of the adsorption energies of atomic oxygen and carbon, and the energy barriers and reaction energies for the hydrogenation of OH* and carbon species CHx* on Rh(111) and Rh(533) in kJ/mol.
| Rh(111) | Rh(533) | |||
| Eads | Eads | |||
| O* | −575 | −610 | ||
| C* | −699 | −766 | ||
| EACT | ERXN | EACT | ERXN | |
| OH* + H* → H2O* | 68 | −16 | 127 | 42 |
| C* + H* → CH* | 67 | −30 | 90 | 11 |
| CH* + H* → CH2* | 62 | 58 | 113 | 42 |
| CH2* + H* → CH3* | 43 | 9 | 50 | 22 |
| CH3* + H* → CH4 | 53 | −8 | 57 | 6 |
The removal of hydroxyOH of m-cresol over Rh catalyst was proven to happen via DDO, which is similar to the reaction observed on Ru, rather than the TAU pathway predicted for Pt. That is, the energy barrier for DDO over Rh(111) is 164 kJ/mol, whereas the energy barrier for TAU is exceedingly high of 289 kJ/mol, the same trend that we calculated for Ru(0001) [22].
Therefore, the DDO reaction was modeled over the two surfaces Rh(111) and Rh(533). The structures of reactant, transition state, and product are compared in Fig. 11. It can be seen that, over the two metal surfaces, the CO bond elongates from around 1.4 Å in the reactant to the transition state (2.09 Å for the Rh(111) and 2.15 Å for the Rh(533)). Although the structure of the transition states is similar on the two surfaces, the energetics is very different. For the Rh(111) terrace site, the energy barrier and reaction energy for the CO scission of m-cresol were calculated to be 164 and 90 kJ/mol, respectively. These values are significantly higher than the corresponding values for Rh(533) step site, which were calculated as 122 and 10 kJ/mol, respectively. The less endothermic CO cleavage reaction over the more oxophilic Rh(533) surface is consistent with the trends of the energy barrier versus oxophilicity of different metals that we reported earlier [22]. This result is in good agreement with the experimental results, which clearly show that the catalyst with the smaller Rh particles is more active.
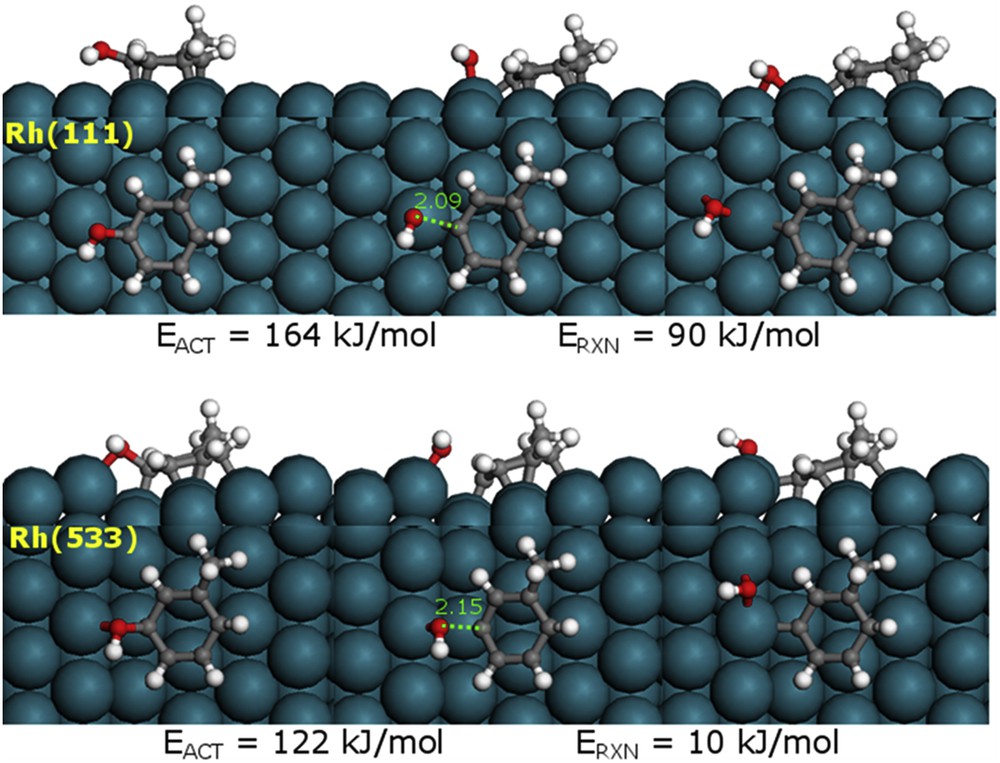
DFT calculated reactant, transition state, and product structures for the deoxygenation of m-cresol on Rh(111) and Rh(533).
To rationalize the observed deactivation behavior displayed by the two different catalysts as a function of the number of subsequent pulses, we conducted additional DFT calculations. We speculate that upon deoxygenation of m-cresol, the surface OH* formed as a fragment of the DDO reaction needs to be removed via hydrogenation and formation of water. The energy requirement for this “site cleaning” will be a measure of the propensity of a given site to catalyst deactivation. As shown in Fig. 12, the energy barrier for the hydrogenation of OH* to form water on the Rh(533) step site is calculated to be 127 kJ/mol, which is much higher than the energy barrier required over the Rh(111) terrace site (68 kJ/mol). Consistently, the reaction energy for the site cleaning is more endothermic for the step site (42 kJ/mol) than for the terrace site (−16 kJ/mol). It is then clear that the oxophilicity of the surface site influences the m-cresol deoxygenation and OH* hydrogenation reactions in the opposite direction. The more oxophilic is the site and the stronger it binds to oxygen, the more active it is for the DDO reaction. However, the hydrogenation reaction requires the weakening of the metal–oxygen bond to reconstitute the clean active site. Obviously, this step is disfavored on the more oxophilic site. That is, the more difficult removal of the OH* from the Rh(533) step site reflects a higher tendency for site blockage.
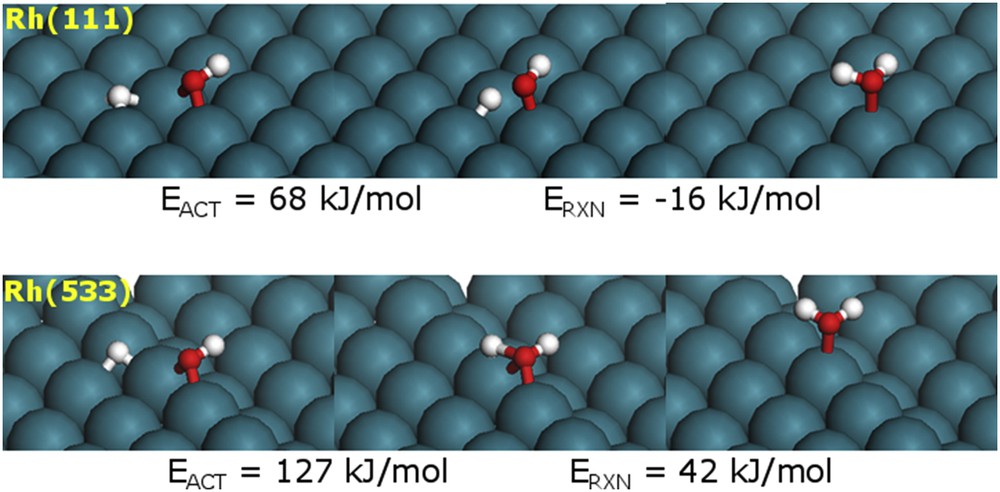
DFT calculated reactant, transition state, and product structures for the hydrogenation of OH* on Rh(111) and Rh(533).
In addition, because CC cracking occurs to a significant extent during the HDO of m-cresol over the Rh catalysts, carbon species could also be formed on the metal surfaces, participating in site blocking and consequent deactivation. Therefore, we have also calculated the hydrogenation of different carbon species CHx (x = 1–3) on the two Rh surfaces. The calculated energetics are summarized in Table 2. We can see that similar to case of OH*, the hydrogenation of carbon species CHx is more difficult on the Rh(533) step site with higher energy barrier and more endothermic reaction energies than on the Rh(111) terrace site. This is expected, and in correspondence with the stronger metal-carbon bonding at the Rh(533) site (−766 kJ/mol) compared to the Rh(111) (−699 kJ/mol).
On the basis of this analysis, it can be concluded that the step and other low-coordination sites, which are more dominant on small metal particles, are initially more active for the DDO reaction of m-cresol because of its higher oxophilicity. However, the stronger binding of oxygen and carbon species at these step sites also inhibits their subsequent removal to keep the low-coordination site available, which leads to deactivation. This conclusion is supported by experimental observations, which demonstrates that the 2.5 wt % Rh/SiO2 catalyst with smaller metal particles is more active and selective in the HDO of m-cresol. However, it deactivates faster than the 7% Rh/SiO2 catalyst.
7 Conclusions
Metal particle size strongly affects HDO activity of rhodium catalysts. Small Rh particles with low-coordination sites are more active than large particles with high-coordination sites for HDO of m-cresol to TOL, but also get more easily deactivated. The experimental results are confirmed by DFT calculations, which show that the energy barrier for direct CO bond cleavage is lower on Rh(533) step sites than on Rh(111) terrace sites. Furthermore, the energy barrier required to remove the adsorbed O* or C* is higher on Rh(533); therefore, it is harder to clean the step sites and the deactivation is more pronounced.
Aligned with previous study, the metal oxophilicity is proven to be a good descriptor for the corresponding metal HDO activity. We can control the metal oxophilicity by tailoring d-band center by either changing the type of metal or the coordination of the metal atoms. This is important in the design and selection of metal catalysts for HDO of phenolic compounds.
8 Materials and methods
8.1 Catalyst preparation
Two Rh/SiO2 samples with different metal particle sizes were prepared by incipient wetness impregnation of SiO2 (Hi-sil 290), used as the support, with an aqueous solution of rhodium(III) nitrate, purchased from Sigma–Aldrich (10 wt % Rh in >5 wt % HNO3). The metal loading and treatment conditions were manipulated to control the particle sizes of these catalysts. After impregnation, the low-loading catalyst (2.5 wt % Rh/SiO2) was heated under H2 at 200 °C for 2 h, whereas the high-loading catalyst (7 wt % Rh/SiO2) was heated under N2 at 550 °C for 2 h, and then for additional 12 h at 550 °C under H2.
8.2 Catalysts characterization
Samples were characterized by TEM and DRIFTS. TEM images were obtained on a JEOL 2000 field emission system operated at 200 kV. For this analysis, the prereduced catalysts were dispersed in ethanol and sonicated with a horn sonicator (Cole–Parmer), operating at 25% amplitude for 10 min before deposition onto holey carbon–coated copper grids. DRIFTS of adsorbed CO was performed on a Perkin–Elmer Spectrum 100 FTIR spectrometer, equipped with an MCT (mercury cadmium telluride) detector. Experiments were conducted in a diffuse reflectance cell from Harrick Scientific, type HVC-DR2 with CaF2 windows that allowed us to perform in situ thermal pretreatments. For each infrared spectrum, taken at a resolution of 4 cm−1, 256 scans were added. Before each spectrum, the catalyst was reduced in situ in a flow of H2 for 1 h at 300 °C, cooled under He flow, and purged in He at room temperature for 30 min. The background was recorded at this time. Then, the catalyst was exposed to a flow of 5% CO in He for 30 min at room temperature and purged in He for 30 min, before obtaining the scans, to remove the contributions from gas phase and weakly adsorbed CO.
8.3 Catalytic measurements
In a typical experiment, a small amount of catalyst (∼5–10 mg) was packed in the middle of a 20-cm glass tube reactor and re-reduced in situ under continuous flow of H2 at 400 °C for 1 h. Subsequently, the temperature was lowered to the reaction temperature (285 °C), keeping the catalyst bed under H2 flow during the entire time of the experiment. When the temperature was stabilized, a 50 L pulse was injected into the H2 carrier gas from a sample loop filled with controlled partial pressure of m-cresol vapor diluted in N2 by a separate line. The carrier gas drives the feed from the sample loop over the catalyst bed, introducing a known amount of m-cresol (1.3 μmol) in each pulse.
8.4 DFT calculations
We have compared the experimental results with DFT calculations performed with methods implemented in the Vienna ab initio Simulation Package [44], using the PBE (Perdew, Burke and Ernzerhof) functional for the exchange correlation energy within the generalized gradient approximation [45]. The DFT-D3 method was used to account for van der Waals interactions [46]. The projector augmented wave method was used to describe the electron–ion interactions [47]. The cutoff energy of 400 eV was applied for the plane-wave basis set to represent valence electrons.
The 4 × 4 Rh(111) surface and the Rh(533) surface with four metal layers and 15 Å of vacuum separating the slabs in the z-direction were used to model the Rh terrace and step sites. The top two metal layers were allowed to relax during the calculations, and the bottom two layers were held fixed to their initial bulk position. The electronic energies were converged within 10−6 eV. The geometric structures for all reactants, intermediates, and products were optimized until the forces on each atom were less than 0.01 eV/Å. A 3 × 3 × 1 k-point mesh was used to sample the first Brillouin zone [48]. Transition state searches were performed using the dimer method [49], with the initial guesses for the transition state structure and the reaction trajectory obtained through the nudged elastic band method [50].


