Selectivity effects related to the diversity of active sites operating on nanostructured multifunctional catalysts

Yahia Alhamed; Krassimira Kumbilieva; Abdulraheem Al-Zahrani; Mohmmad Daous; Lachezar Petrov

doi:10.1016/j.crci.2017.08.005

Selectivity effects related to the diversity of active sites operating on nanostructured multifunctional catalysts

Yahia Alhamed ^1,² ; Krassimira Kumbilieva ³ ; Abdulraheem Al-Zahrani ^1,² ; Mohmmad Daous ^1,² ; Lachezar Petrov ^1,²

¹ SABIC Chair of Catalysis, King Abdulaziz University, PO Box 80204, Jeddah 21589, Saudi Arabia
² Chemical and Materials Engineering Department, King Abdulaziz University, PO Box 80204, Jeddah 21589, Saudi Arabia
³ Institute of Catalysis, Bulgarian Academy of Sciences, Acad. G. Bonchev Street, Block 11, Sofia 1113, Bulgaria

Comptes Rendus. Chimie, Volume 21 (2018) no. 3-4, pp. 369-381.

Résumé

The goal of the present study was to gain a better understanding of the selectivity of processes over multifunctional catalysts exhibiting diversity of operating active sites. The concept is that the concurrent performance of different types of active sites may provoke effects on the process selectivity comparable to the effects resulting from the kinetic regularities and activation energies of the occurring reactions. Accordingly, in the kinetic model the authors introduce specific parameters reflecting the contribution of distinct types of active sites, facilitating different reaction routes. Reasons are adduced how suchlike parameters serve to account the impact of various reaction routes occurring on different types of sites. The suggested approach links the deactivation-caused selectivity changes to dissimilarities in the vulnerability of different types of active sites. This work relates the probabilities for action of different types of sites to the size of active-phase islands. Various reaction mechanism patterns are modeled to examine relevant selectivity effects.

Métadonnées

Reçu le : 2017-04-18
Accepté le : 2017-08-29
Publié le : 2017-10-08

DOI : 10.1016/j.crci.2017.08.005

Mots clés : Multifunctional catalysts, Selectivity effects, Nanostructured active phase, Kinetic models, Structure sensitivity

Affiliations des auteurs :

Yahia Alhamed ^{1, 2} ; Krassimira Kumbilieva ³ ; Abdulraheem Al-Zahrani ^{1, 2} ; Mohmmad Daous ^{1, 2} ; Lachezar Petrov ^{1, 2}

@article{CRCHIM_2018__21_3-4_369_0,
     author = {Yahia Alhamed and Krassimira Kumbilieva and Abdulraheem Al-Zahrani and Mohmmad Daous and Lachezar Petrov},
     title = {Selectivity effects related to the diversity of active sites operating on nanostructured multifunctional catalysts},
     journal = {Comptes Rendus. Chimie},
     pages = {369--381},
     publisher = {Elsevier},
     volume = {21},
     number = {3-4},
     year = {2018},
     doi = {10.1016/j.crci.2017.08.005},
     language = {en},
}

TY  - JOUR
AU  - Yahia Alhamed
AU  - Krassimira Kumbilieva
AU  - Abdulraheem Al-Zahrani
AU  - Mohmmad Daous
AU  - Lachezar Petrov
TI  - Selectivity effects related to the diversity of active sites operating on nanostructured multifunctional catalysts
JO  - Comptes Rendus. Chimie
PY  - 2018
SP  - 369
EP  - 381
VL  - 21
IS  - 3-4
PB  - Elsevier
DO  - 10.1016/j.crci.2017.08.005
LA  - en
ID  - CRCHIM_2018__21_3-4_369_0
ER  -

%0 Journal Article
%A Yahia Alhamed
%A Krassimira Kumbilieva
%A Abdulraheem Al-Zahrani
%A Mohmmad Daous
%A Lachezar Petrov
%T Selectivity effects related to the diversity of active sites operating on nanostructured multifunctional catalysts
%J Comptes Rendus. Chimie
%D 2018
%P 369-381
%V 21
%N 3-4
%I Elsevier
%R 10.1016/j.crci.2017.08.005
%G en
%F CRCHIM_2018__21_3-4_369_0

Yahia Alhamed; Krassimira Kumbilieva; Abdulraheem Al-Zahrani; Mohmmad Daous; Lachezar Petrov. Selectivity effects related to the diversity of active sites operating on nanostructured multifunctional catalysts. Comptes Rendus. Chimie, Volume 21 (2018) no. 3-4, pp. 369-381. doi : 10.1016/j.crci.2017.08.005. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2017.08.005/

Version originale du texte intégral

1 Introduction

The authors dedicate this study to the series of pioneer works of Gault and colleagues concerning the correlation between the diversity of the active sites operating and the varieties of reaction mechanisms observed on some catalyst surfaces (see, e.g., Refs. [1–9]). The concepts developed by Gault and colleagues with account of the Ledoux classification [10] maintain the idea that specific groups of reaction mechanisms are associated with distinct types of active sites. These concepts have withstood for more than three decades the test of time and new findings and are relevant to the present state of knowledge.

It is well recognized nowadays by lots of distinguished researchers (see, e.g., Refs. [11–16]) that active sites differing in coordination, nature, configuration, location, and physicochemical and adsorption properties may participate in the operation of multifunctional catalysts. The differences may influence the catalytic properties and thus selectivity to various reaction routes. At the same time, usually the regularities describing the reaction rates along the different routes are by tacit consent derived by applying the concept of ideal adsorbed layer. Practically, it is acknowledged that such essential simplifications of this concept as homogeneity of the adsorption properties of the catalyst surface, equivalence of active sites, negligibility of electronic effects, absence of lateral interactions are not precise in many cases of heterogeneous catalytic processes. Nonetheless, the model is routinely applied, because the kinetic problems to be solved become much more difficult if any of its simplifications is removed. On the other hand, in certain circumstances it is of importance both theoretically and for practical purposes some of the effects, which are neglected by its limitations, are to be taken into account in the process description. The approaches addressed to move beyond the ideal adsorbed layer frames are scarce and seek for the possibility of removing only one or two of its simplifications, for the sake of solubility of the resulting set of equations and lucidity in the result interpretation. The choice of the simplifications to be removed naturally depends on the concrete catalytic system and the problems brought into focus.

The problems linked to the participation of active sites differing in coordination, configuration, adsorption, and catalytic properties in the performance of multifunctional catalysts gain in actuality in view of the wide application of such catalysts in reforming, dehydrogenation, hydrodesulfurization, hydrodenitrogenation (HDN), and other industrial processes. Adsorption nonuniformity of the catalyst surface may provoke effects, which can hardly be explained within the frames of ideal adsorbed layer. Actually, various experimental data are in good agreement with kinetic models assuming the contribution of active sites of unequal adsorption activity. Such an approach applied for modeling the catalytic combustion of p-xylene over Pd catalysts gave us the opportunity of elucidating the regularities following from the experimental data and of better understanding the peculiarities of the catalyst deactivation including its reversibility under the influence of the reactant atmosphere [17]. Another essential point of concern is the mode of adsorption, which can be realized on active sites of different configuration. Thus, it is believed for the case of hydrotreating processes that depending on the configuration of the adsorbed form (e.g., vertical or planar, via heteroatom or via benzoic ring, etc.), various routes of the reaction network may be facilitated [13,18–26]. Pertinently the mode of adsorption may condition specific selectivity effects.

The dispersion of the active phase of supported catalysts in the form of nanosized islands conditions diversity in the properties of active sites depending on their location, coordination, and structure. Consequently, the populations of internal and interfacial active sites, appreciably differing in coordination, become comparable. It is reasonable to consider the diversities in the coordination and behavior of internal, edge, corner [3–5,8,9], and valley anion vacancies [18]. This is particularly significant for processes the reaction network of which involves structure-insensitive reactions (facilitated by a single active metal atom [27–31]) and structure-sensitive routes facilitated by catalytic clusters—ensembles of adjacent active atoms constructing multicentered adsorption sites [18–23,27–40]. The finite number of active metal surface atoms comprised within the active-phase islands may restrain the population of such active sites. Occurrence of structure-sensitive reactions may thus be predetermined by the sizes of the structures containing the active component. The consequences following from the structure sensitivity or insensitivity of the concurrent routes exercise reciprocal effects on the process selectivity, but these effects are hardly reflected in the functions applied to predict the selectivity. On this account, appropriate models are necessary to reflect the specificity of complex reaction systems. Various models have been suggested to relate the catalyst action with the properties of internal and interfacial active sites with due understanding that edge active sites exhibit unique activity and free energy characteristics [3,5,8,9,41,42]. The models developed by Gault and colleagues take their rightful place in this field. Exploring the behavior of several processes on nonuniform catalysts, Murzin [43–45] adduced factual arguments about the influence of the active-phase nanostructures on the reaction kinetics. Until now, however, kinetic analysis of processes realized with the participation of different types of active sites is far from sufficient.

The aim of this study was to gain a better understanding of some linked aspects of the selectivity of complex processes occurring on supported multifunctional catalysts. The approach suggested is associated with the necessity to consider (1) the nanostructure character of the active phase and (2) the participation of active sites differing in coordination, configuration, adsorption, and catalytic properties in the performance of multifunctional heterogeneous catalysts. To avoid additional complexity of the mathematic solutions at the present level of the approach, we skip from consideration of the electronic effects and lateral interactions.

2 Approach

In Refs. [17,47–51], we suggested an approach providing a way to consider the participation of several types of active sites in the operation of heterogeneous catalysts. For avoiding contradiction with the Langmuir–Hinshelwood kinetics, this approach assumes that in case n types of active sites participate in the catalytic performance, the catalyst surface can be modeled as consisting of n coexisting ideal adsorbed layers, each of which can be specified by own intrinsic characteristics. The function of current overall catalyst activity a(t) can be presented as a vector sum of the individual activity functions $(a_{j})$ associated with the action of the particular active site types:

a (t) = \sum_{j = 1}^{n} a_{j} (t)

(1)

Furthermore, we consider the fact that the active phase dispersed on the carrier often constitutes nanosized fragmentations comprising a finite number of active metal surface atoms. To avoid misunderstanding in the further, so far as these fragmentations are called by different authors “particles”, “clusters”, “islands”, and so forth, it is worth itemizing some of the notions and terms used in this study. We shall designate the aforementioned fragmentations as “active-phase islands”. The term of “catalytic cluster” specifies an ensemble of several (viz. M in number) proximal active surface atoms properly located to facilitate a structure-sensitive reaction [32–34].

In Ref. [46], we developed an approach accounting the population of catalytic clusters within the active-phase nanostructures and explored the relation of the size of active-phase islands with the probabilities for action of multisite active centers facilitating structure-sensitive reactions. The goal of this study was to extend the approach suggested in Ref. [46] in view of revealing resources for a better understanding and more adequate modeling of the selectivity of complex processes facilitated by multifunctional catalysts.

In association with the selectivity problems, which are under concern in this study, our approach makes the following allowance. Contrary to processes over uniform catalytic surfaces for which selectivity is principally determined by the ratio of the reaction rates represented as functions of the kinetic regularities and the activation energies of the proceeding reactions, the selectivity of processes occurring over multifunctional catalysts may along with that be a function of the impact of the different types of active sites operating. Such effects may enhance under conditions of catalyst deactivation, especially if the deactivating agent affects in a different way and extent the population of the distinct types of sites. It is to the point to recall the arguments adduced by Gault and colleagues [3–5,8,9] that modifications of the metal surface and poisoning [5] may change the relative amounts of distinct types of sites and accordingly the process mechanism and selectivity—a conclusion supported by the experimental data reported in these works. To consider the aforementioned specificity of reactions over multifunctional catalysts, we have suggested [48–51] the selectivity description to reflect the current activity $(a_{j})$ toward the jth reaction route as follows:

S_{D} = \frac{k_{D}^{0} \exp (- E_{D} / R T) f_{D} (P_{1}, P_{2}, \dots, P_{q}, T) (a_{D})}{\sum_{n} {k_{j}^{0} \exp (- E_{j} / R T) f_{j} (P_{1}, P_{2}, \dots, P_{q}, T) (a_{j})}}

(2)

The finite number of surface atoms of the active metal contained within a nanostructured active-phase island is a factor giving rise to additional problems concerning the reaction kinetics and selectivity (see Refs. [1,7–9]), especially when some of the reactions are structure sensitive. As these reactions are facilitative by multicentered catalytic clusters, there appears the question about the population of proper catalytic clusters within the small-sized active-phase islands and the evolution of the probabilities for their existence in the course of accompanying coke formation reactions. In Ref. [46], we adduced reasons based on calculus analysis that much before coke deposits block the whole of active sites contained within the active-phase island, the coke species may either terminate the action of partially coke-covered cluster configurations or reduce the capability of certain active metal atoms to construct multicentered active configurations. Thus coke species may terminate the chances for existence of multisite active centers facilitating structure-sensitive reactions, whereas single sites, which have been constituents of partially blocked cluster configurations, may continue their catalytic action by facilitating structure-insensitive reactions. On this account, related selectivity effects may be expected. In this study, we shall further develop this topic.

3 Model considerations

The model deals with processes occurring on supported multifunctional catalysts, the active phase of which is dispersed on the carrier in the form of nanosized islands. Three types of sites are envisaged to operate: (1) single active metal atoms located inside the islands (designated further as Z-type sites); (2) active sites located on the interface active phase/support (designated as Y-type sites); and (3) catalytic clusters involving a certain number (M) of neighboring active metal atoms in a proper configuration (designated as X-type sites). Catalytic clusters involving different number of single surface atoms are classified as different types of active sites. Actually, the Z-type sites are the same distinguished by Gault as A sites; the Y-type sites coincide to a great extent with the B-type sites specified in Refs. [3,8,9] with the difference that we have integrated as Y-type the edge and corner atoms, by reason of the necessity to consider as a third (X-type) group the multisite active ensembles promoting structure-sensitive reactions. Accordingly, we define the variables $N_{Z}$ , $N_{Y}$ , and $N_{X}$ , which designate the actual number of correspondent sites per active-phase island. The approach assumes that the active sites of different types facilitate different reaction steps that are determining for different reaction routes. Consequently, the availability of sites of a particular type is a factor influencing the selectivity.

The variables relevant to the fresh catalyst will be marked by 0 superscripts. N⁰ designates the number of active surface atoms comprised within an active-phase island. By geometric reasons, the initial number $N_{Z}^{0}$ of Z-type sites can be assumed proportional to the island area; the initial number $N_{Y}^{0}$ of Y-type sites can in turn be assumed proportional to the active-island perimeter.

The use of such approach in our work [47] proved fruitful adequately to describe and interpret the peculiarities observed in the performance of isobutane dehydrogenation over promoted and unpromoted Pt catalysts. The relations following from the postulated model considering the participation of the aforementioned three types of active sites coincided with the regularities established from experimental data. Beyond that, its assumptions served to explain important appearing peculiarities of the investigated catalytic systems, such as the experimentally observed stepwise character of the deactivation kinetics and promoter-provoked effects. This gives the reason to expect that such an approach may be helpful in exploring the peculiarities of similar systems that overflow the restrictions of ideal adsorbed layer.

When modeling the active site decrease in the course of coking, we assume that coke precursors formed inside active-phase islands realize fast migration to the island boundaries with possible overlap onto the support. It is useful to highlight in this regard that interaction with hydrogen from the gas phase or surface collisions with adsorbed hydrogen forms may discontinue the process of coke formation from the precursors. Accordingly, in Ref. [47] we have modeled such a development by incorporating in the regularity for coke formation a distinct term accounting for the impact of steps terminating the coke formation pathway. More detailed information on this point can be found in the original study [47]. To reflect the arguments advanced by some researchers [52–54] that the overlap of coke may cause a coke tolerance effect, we introduce the stepwise function $f_{th} (N_{c})$ :

f_{th} (N_{c}) = 0 for N_{c} < N_{c}^{crit}

(3a)

f_{th} (N_{c}) = 1 for N_{c} \geq N_{c}^{crit}

(3b)

where

N_{c}^{crit}

denotes the critical number of coke-covered active sites below which the coke tolerance effect can be expected. Under the assumption that the number

(N_{c})

of surface sites blocked by coke or tightly adsorbed species is the key deactivation-responsible factor, the decrease in single active sites can be considered to be proportional to the increase in

N_{c}

- d N_{Z} = k_{Z} f_{th} (N_{c}) d N_{c}

(4)

- d N_{Y} = k_{Y} f_{th} (N_{c}) d N_{c}

(5)

In Ref. [46], we reported arguments that the potential number $N_{X}$ of catalytic clusters constituted by (M) active metal surface atoms depends on the concrete value of (M), on the number $N$ of single sites within the active-phase island, and on the probability $(μ_{M})$ that M active metal atoms are properly located:

N_{X} \propto \frac{1}{M} (μ_{M}) N

(6)

When modeling the coke-caused changes in the population of active catalytic clusters, it is important to take into account the potential alterations of the $μ_{M}$ term, as the probability $μ_{M}$ may estimably change on increasing the number of blocked sites:

- d N_{X} = k_{X} \frac{1}{M} {μ_{M} \frac{d N}{d N_{c}} + N \frac{d μ_{M}}{d N_{c}}} d N_{c}

(7)

The relation (7) actually describes the modification of the catalyst activity for structure-sensitive reactions taking place via complex multisite surface intermediates. The formation of these intermediates is related to the probability

μ_{M}

for availability of the necessary (M) sites in convenient configuration. When the change in this probability in the course of coking

(\partial μ_{M} / \partial N_{c})

is not negligible, this may result in coincident effects on the selectivity.

When modeling the coke-caused loss of active sites, we presume that coke build takes place by successive integration of surface forms adsorbed on catalytic clusters (X-type sites).

We hold that it is reasonable to include into the selectivity description particular parameters reflecting the contribution of the distinct types of sites to the various reaction routes of reactions proceeding on multifunctional catalysts. Thus, if we assume that the catalytic performance is realized through the contribution of three types of active sites (e.g., Z, Y, and X types) and that one of these site types facilitates the reaction route resulting in the target product D, according to Eq. (2) the selectivity $S_{D}$ is described by use of the expression as follows:

S_{D} = \frac{k_{D}^{0} \exp (- E_{act}^{(D)} / R T) f_{D} (P_{1}, P_{2}, \dots, P_{q}, T) (a_{D})}{\sum k_{j Z}^{0} \exp (- E_{j}^{(Z)} / R T) f_{j}^{Z} (P_{q}, T) (a_{Z}) + \sum k_{j Y}^{0} \exp (- E_{j}^{(Y)} / R T) f_{j}^{Y} (P_{q}, T) (a_{Y}) + \sum k_{j X}^{0} \exp (- E_{j}^{(X)} / R T) f_{j}^{X} (P_{q}, T) (a_{X})}

(8)

Here,

E_{act}^{(D)}

stands for the activation energy of the target reaction;

E_{j}^{(Z)}

E_{j}^{(Y)}

, and

E_{j}^{(X)}

denote the activation energies of the reactions facilitated, respectively, by the active sites of Z, Y, or X type;

a_{Z}

a_{Y}

, and

a_{X}

stand for the corresponding activity functions. By

f_{j}^{Z} (P_{q}, T)

f_{j}^{Y} (P_{q}, T)

f_{j}^{X} (P_{q}, T)

, we denote the kinetic expressions determining the resulting reaction rate along the jth route considered as a sum of the rates in forward and backward direction, in case of reversibility. The variables

(P_{1}, P_{2}, \dots, P_{q})

stand for the current partial pressures of the reactants. Each of these concentrations appears as a function of the proceeding interactions, regardless of parallel or consecutive to each other, and for this reason the overall regularity Eq. (8) reflects the intrinsic process selectivity irrespective of the particular mechanistic peculiarities. The “D” index in the numerator matches with “Z”, “Y”, or “X” subscript, depending on the target reaction mechanism. Each of the “individual activity” functions

a_{z}

a_{Y}

, and

a_{x}

may be considered proportional to the current fraction of active sites of the corresponding type:

a_{Z} \propto N_{Z} / N_{Z}^{0}, a_{Y} \propto N_{Y} / N_{Y}^{0}, a_{X} \propto N_{X} / N_{X}^{0}

(9)

When estimating the number $N_{X}$ of acting catalytic clusters, it is of importance to consider the impact of the probability function $μ_{M}$ . The key point is that the probability $μ_{M}$ may decline in different modes under the action of coke growth and thus cause different effects on the selectivity for the structure-insensitive and structure-sensitive reactions.

We find it reasonable to put to discussion the following idea. When the different routes of a complex reaction network are facilitated by different types of active sites (viz. internal sites, interface sites, and catalytic clusters), specific parameters reflecting the contribution of the distinct types of sites are to be included in the kinetic model. The introduction of such parameters may turn instrumental for considering the additional factors influencing the selectivity of such systems. It is appropriate at this point to note the assumption of Gault and colleagues [3–5,8,9] that the selectivity of heterogeneous catalytic processes may to a great extent depend on the structure of the catalyst surface and the relevant availability of distinct types of sites promoting different mechanisms. We believe that introducing the parameters defined in the following paragraph appears a contribution to the mathematical description of this concept.

Preliminarily let us designate suchlike parameters by $ξ_{k}$ . Concerning the model developed in this study, three distinct parameters of that sort can be specified—viz. $ξ_{z}$ , $ξ_{Y}$ , and $ξ_{X}$ . We assume that these parameters reflect the probability of realizing the reaction performance, respectively, via the Z, Y, or X types of sites. As a first approximation, it can be assumed that the parameters $ξ_{z}$ , $ξ_{Y}$ , and $ξ_{X}$ are proportional to the ratio between the number of the sites of relevant type and the total number $N_{act}$ of all active sites available on a particular active-phase island:

ξ_{Z} \propto N_{Z} / N_{act}, ξ_{Y} \propto N_{Y} / N_{act}, ξ_{X} \propto N_{X} / N_{act}

(10)

With consideration of these parameters, the selectivity relation (8) takes the form:

S_{D} = \frac{k_{D}^{0} \exp (- E_{act}^{(D)} / R T) f_{D} (P_{1}, P_{2}, \dots, P_{q}, T) (a_{D} ξ_{D})}{\sum k_{j Z}^{0} \exp (- E_{j}^{(Z)} / R T) f_{j}^{Z} (P_{q}, T) (a_{Z} ξ_{Z}) + \sum k_{j Y}^{0} \exp (- E_{j}^{(Y)} / R T) f_{j}^{Y} (P_{q}, T) (a_{Y} ξ_{Y}) + \sum k_{j X}^{0} \exp (- E_{j}^{(X)} / R T) f_{j}^{X} (P_{q}, T) (a_{X} ξ_{X})}

(11)

In the further treatment, we shall put to analysis also the case, when the reaction network includes two structure-sensitive reactions facilitated by catalytic clusters of different structure (constituted by two or six active surface atoms, by way of example). In that case, it appears appropriate to apply the following selectivity dependency:

S_{D} = \frac{k_{D}^{0} \exp (- E_{act}^{(D)} / R T) f_{D} (P_{1}, P_{2}, \dots, P_{q}, T) (a_{D} ξ_{D})}{k_{Z}^{0} \exp (- E_{act}^{(Z)} / R T) f {}_{Z}{(P_{q}, T)} (a_{Z} ξ_{Z}) + k_{Y}^{0} \exp (- E_{act}^{(Y)} / R T) f {}_{Y}{(P_{q}, T)} (a_{Y} ξ_{Y}) + k_{X 2}^{0} \exp (- E_{act}^{(X 2)} / R T) f {}_{X 2}{(P_{q}, T)} (a_{X 2} ξ_{X 2}) + k_{X 6}^{0} \exp (- E_{act}^{(X 6)} / R T) f {}_{X 6}{(P_{q}, T)} (a_{X 6} ξ_{X 6})}

(12)

The algorithms developed, by use of which we have simulated the proceeding of different reactions over various catalyst patterns, apply some of the principles and considerations of the probability calculus in view of the expedience to associate the catalyst activity for structure-sensitive reactions with the chances for availability of appropriate catalytic clusters.

When deriving the pattern set of models, the following parameters characterizing a given catalytic system have been considered:

• The number (M) of single active sites constituent of a catalytic cluster facilitating a structure-sensitive reaction. By way of example, the cases of M = 2, M = 3, M = 4, and M = 6 are considered.
• The catalyst surface lattice. We shall inspect {111} and {100} facets, which are often considered as typical for the surfaces of supported catalysts. In sober fact, the most active catalyst surfaces are stepped, the facets of the steps being characterized by various crystallographic lattices. We include in the further analysis only {111} and {100} facets for the sake of simplicity in manifesting the suggested approach. In case of necessity to analyze other concrete lattice facets or their combinations, the approach may be applied with appropriate arithmetic modifications concerning the geometric features of the concrete lattice.
• The average number (b) of single active atoms comprised within the edge of an active-phase island. The initial number $N^{0}$ of active metal atoms contained within the island depends on the value of b and on the geometry of the crystallographic lattice.

4 Results and discussion

4.1 Sites of distinct types and selectivity parameters on the fresh catalyst

Naturally, the fractions of internal and interface sites depend on the lattice, geometrics of the island (assumed to be hexagonal for the case of {111} lattice and quadratic at {100} lattice), distance between the active metal surface atoms, and on their number (b) per island edge.

In the case of {100} lattice, the active-phase islands were modeled as flat textures of quadratic form. If we denote by b the number of active metal atoms incorporated within an edge, the number of interfacial single sites will be $N_{Y}^{0} = 4 b$ , four of which are specified as corner sites, the remaining ( $N_{Y}^{0} - 4$ ) as edge sites:

N_{Y}^{0} = 4 b = N_{corner} + N_{edge}, N_{corner} = 4, N_{edge} = 4 b - 4

(13)

The potential initial number $N_{Z}^{0}$ of internal single sites can be estimated from the relation

N_{Z}^{0} = N^{0} - N_{Y}^{0} = β_{conv} (b^{2} - 4 b)

(14)

The coefficient

β_{conv}

accounts for the influence of the convexity of the catalyst grains. For the sake of simplicity of our calculations, we assume that

β_{conv} = 1

In conformity with Eq. (6), we can estimate the potential number of X-type active sites on the fresh catalyst dispersed on {100} lattice as follows:

N_{X}^{0} \propto \frac{1}{M} (μ_{M}^{0}) N^{0} = \frac{1}{M} (μ_{M}^{0}) b^{2}

(15)

The simulation performed on this basis served to assess the potential number of catalytic clusters constructed by two (M = 2), three (M = 3), four (M = 4), or six (M = 6) neighboring active metal atoms, at values of b equal to 10, 16, 24, and 32.

As consistent with Eq. (10), we get about the initial values of the selectivity parameters:

ξ_{Y}^{0} = N_{Y}^{0} / N_{act}^{0} = 4 b / b^{2} = 4 / b

(16a)

ξ_{Z}^{0} = N_{Z}^{0} / N^{0} = (b^{2} - 4 b) / b^{2} = 1 - 4 / b

(16b)

The selectivity parameters inherent in the cases of reactions facilitated by X-type active sites follow more complex dependencies related to the actual value of the probability parameter $μ_{M}$ .

ξ_{X}^{0} = N_{X}^{0} / N_{act}^{0} \propto \frac{1}{M} μ_{M}^{0} (λ_{Z} ξ_{Z}^{0} + λ_{Y} ξ_{Y}^{0})

(16c)

The coefficients λ_Z and λ_Y account for the participation of internal and interfacial sites in the configuration of catalytic clusters. Their values may be a helpful tool to account for the impact of terrace and edge surface atoms in the cluster configurations.

Concerning the case of hexagonal lattice {111}, the active-phase islands were modeled as flat normal hexagons, each edge of which comprises (b) surface atoms of the active metal. Accordingly, the potential initial number of interfacial single sites $N_{Y}^{0}$ and that of internal single active sites $N_{Z}^{0}$ is assessed as follows:

N_{Y}^{0} = 6 b = N_{corner} + N_{edge}, N_{corner} = 6, N_{edge} = 6 b - 6

(17a)

N_{Z}^{0} = N^{0} - N_{Y}^{0} = (1.5 \sqrt{3} b^{2} - 6 b)

(17b)

The potential initial values of the selectivity parameters $ξ_{Y}^{0}$ , $ξ_{Z}^{0}$ , and $ξ_{X}^{0}$ can be estimated as follows:

ξ_{Y}^{0} = N_{Y}^{0} / N_{act}^{0} = 6 b / (1.5 \sqrt{3}) b^{2} = (4 / \sqrt{3}) / b \approx 2.3094 / b

(18a)

ξ_{Z}^{0} = N_{Z}^{0} / N_{act}^{0} = {(1.5 \sqrt{3}) b^{2} - 6 b} / (1.5 \sqrt{3}) b^{2} = 1 - (6 / 1.5 \sqrt{3}) / b \approx 1 - 2.3094 / b

(18b)

ξ_{X}^{0} = N_{X}^{0} / N_{act}^{0} \propto \frac{1}{M} μ_{M}^{0} (γ_{Z} ξ_{Z}^{0} + γ_{Y} ξ_{Y}^{-})

(18c)

The simulation calculations performed in concern of X-type sites considered catalytic clusters constituted by two (M = 2), three (M = 3), four (M = 4), and six (M = 6) contiguous surface atoms, for values of b equal to 6, 10, 15, and 20.

4.2 Size of active-phase islands and impact of distinct types of sites

It follows from Eqs. (16a) and (18a) that smaller sizes of the active-phase islands presuppose a higher contribution of interface (Y-type) active sites. This is of importance in view of their key role in facilitating certain reactions [3,5,8,9,55–65]. Specifically, it is well acknowledged (see e.g. [15,18,21,22]) that the coordinately unsaturated anion vacancies which are clue participants in the hydrotreating action of sulfide catalysts are preferentially located at the crystallite edges. One or several edge vacancies are instrumental for the adsorption conducing catalytic performance. In this connection, it is relevant to the subject to examine how the impact of the distinct types of sites is related to the size of the active-phase islands. Tables 1–4 show the estimated distribution of active sites and kinds of site comprised within active-phase islands depending on the facets, island dimensions, and the active metal nature. The island edge length was assumed equal to the sum of the distances between the neighboring constituent active atoms. As a first approximation, these distances can be set equal to the sum of the atomic-orbital radii of the active surface atoms. The value of the number L of active-phase islands per square centimeter was assessed as the ratio of the number of active metal atoms per square centimeter (assumed to be on the order of 10¹⁵) to the particular $N^{0}$ value. As a case in point we have assessed the previously noted characteristics relative to exemplary alumina-supported catalysts such as sulfide Mo/Al₂O₃ whose promoted forms are efficient in hydrodesulfurization and HDN processes and Pt/Al₂O₃ catalysts widely applied in many dehydrogenation, hydrogenolysis, isomerization, refining, and other catalytic processes.

Table 1

b	Edge length (nm)	Island area (nm²)	$Y_{0}$	$Z_{0}$	$Y_{0} + Z_{0}$	$\frac{Y_{0}}{Z_{0}}$	L (islands/cm²)	Internal sites per cm²	Interface sites per cm²	Fraction of island area (%)	Coke-free zone width $r_{width}^{0}$ (nm)	$\frac{r_{width}^{0}}{r_{island}}$
6	1.56	6.36	36	57	93	0.63	1.07 × 10¹³	0.62 × 10¹⁵	0.38 × 10¹⁵	68.05	0.76	0.486
10	2.82	20.62	60	200	260	0.3	0.38 × 10¹³	0.77 × 10¹⁵	0.23 × 10¹⁵	79.29	1.21	0.430
15	4.38	49.89	90	500	590	0.18	0.17 × 10¹³	0.85 × 10¹⁵	0.15 × 10¹⁵	85.41	1.83	0.418
20	5.95	91.89	120	923	1043	0.13	0.10 × 10¹³	0.88 × 10¹⁵	0.12 × 10¹⁵	88.43	2.32	0.3909

Table 2

b	Edge length (nm)	Island area (nm²)	$Y_{0}$	$Z_{0}$	$Y_{0} + Z_{0}$	$\frac{Y_{0}}{Z_{0}}$	L (islands/cm²)	Internal sites per cm²	Interface sites per cm²	Fraction of island area (%)	Coke-free zone width $r_{width}^{0}$ (nm)	$\frac{r_{width}^{0}}{r_{island}}$
10	2.82	7.94	40	60	100	0.67	1.0 × 10¹³	0.60 × 10¹⁵	0.40 × 10¹⁵	79.36	0.86	0.6141
16	4.70	22.04	64	192	256	0.33	0.39 × 10¹³	0.75 × 10¹⁵	0.25 × 10¹⁵	86.10	1.35	0.5746
24	7.20	51.82	96	480	576	0.20	0.17 × 10¹³	0.83 × 10¹⁵	0.17 × 10¹⁵	89.97	1.99	0.5543
32	9.70	94.15	128	882	1010	0.14	0.10 × 10¹³	0.88 × 10¹⁵	0.12 × 10¹⁵	91.94	2.64	0.5443

Table 3

b	Edge length (nm)	Island area (nm²)	$Y_{0}$	$Z_{0}$	$Y_{0} + Z_{0}$	$\frac{Y_{0}}{Z_{0}}$	L (islands/cm²)	Internal sites per cm²	Interface sites per cm²	Fraction of island area (%)	Coke-free zone width $r_{width}^{0}$ (nm)	$\frac{r_{width}^{0}}{r_{island}}$
6	1.22	3.90	36	57	93	0.63	1.07 × 10¹³	0.62 × 10¹⁵	0.38 × 10¹⁵	41.70	0.89	0.7272
10	2.20	12.63	60	200	260	0.30	0.38 × 10¹³	0.77 × 10¹⁵	0.23 × 10¹⁵	48.58	1.42	0.6435
15	3.43	30.56	90	500	590	0.18	0.17 × 10¹³	0.85 × 10¹⁵	0.15 × 10¹⁵	52.28	2.08	0.6072
20	4.66	56.30	120	923	1043	0.13	0.10 × 10¹³	0.88 × 10¹⁵	0.12 × 10¹⁵	54.18	2.75	0.590

Table 4

b	Edge length (nm)	Island area (nm²)	$Y_{0}$	$Z_{0}$	$Y_{0} + Z_{0}$	$\frac{Y_{0}}{Z_{0}}$	L (islands/cm²)	Internal sites per cm²	Interface sites per cm²	Fraction of island area (%)	Coke-free zone width $r_{width}^{0}$ (nm)	$\frac{r_{width}^{0}}{r_{island}}$
10	2.20	4.86	40	60	100	0.67	1.0 × 10¹³	0.60 × 10¹⁵	0.40 × 10¹⁵	48.62	0.995	0.903
16	3.68	13.51	64	192	256	0.33	0.39 × 10¹³	0.75 × 10¹⁵	0.25 × 10¹⁵	52.75	1.558	0.847
24	5.64	31.75	96	480	576	0.20	0.17 × 10¹³	0.83 × 10¹⁵	0.17 × 10¹⁵	55.13	2.309	0.820
32	7.60	57.68	128	882	1010	0.14	0.10 × 10¹³	0.88 × 10¹⁵	0.12 × 10¹⁵	56.33	3.060	0.806

The assessments contained in the right two columns have relevance to the potential “coke-free” zone surrounding the active-phase islands under the event of coke formation and will be interpreted in more detail in the next section.

4.3 Coke-free zone and coke tolerance effects

According to the hypothesis supported by some researchers, in the initial phases of the process, the crystallites of the dispersed active metal (which we define as active-phase islands) are actually surrounded by a so-called “annular cleared”, that is, coke-free zone [53] or a zone of reduced carbon content [54]. It is believed that such a zone is maintained because of the hydrogenation activity of the peripheral active sites. Within this framework, our model deals with the assumption that in the initial phase of coking, before the critical amount of coke deposit ( $C_{crit}$ ) is attained, coke precursors arise on catalytic clusters (X-type sites), migrate aptly to the periphery, and may either undergo rehydrogenation facilitated by highly active interfacial sites or overlap onto the support, causing the formation of a coke layer enclosing the active-phase borders. If chances are for partial breaking the process of coke build through rehydrogenation of coke precursors or under any other influence of the operation conditions, such a feasibility has to be considered by a special term in the deactivation description. The concrete forms of these dependencies are specific for each particular system. During this phase, the number of active sites remains practically unchanged, and the so-called coke tolerance effect is the reasonable consequence. Richardson et al. [53] suggested a relation linking the dimensions of the annular zone with the size and density of active-phase islands, and with the actual coke loading $C_{actual}$ . Expressed in the terms applied in the present study, this relation takes the form

C_{actual} = C_{crit} (1 - L π (r_{zone}^{2} - r_{island}^{2}))

(19)

where

L

denotes the number of active-phase islands per unit catalyst surface;

r_{island}

is the efficient radius of an active-phase island;

r_{zone}

is the distance between its conventional center and the surrounding coke layer. Within this framework, let us note by

r_{zone}^{0}

the width of the annular zone surrounding the active-phase island in the start of the process, at

C_{actual} \to 0

r_{width}^{0} = r_{zone}^{0} - r_{island}

(20)

(1 - L π (r_{zone}^{2} - r_{island}^{2})) = 0

(21a)

By use of this relation, we can assess the initial value of the initial distance

r_{zone}^{0}

as follows:

r_{zone}^{0} = \sqrt{r_{island}^{2} + 1 / π L}

(21b)

Accordingly, we come to estimate the initial width of the annular zone (

r_{width}^{0} = r_{zone}^{0} - r_{island}

) as

r_{width}^{0} = \sqrt{r_{island}^{2} + 1 / π L} - r_{island}

(22)

It follows from Eqs. (21b) and (22) that higher density (

L

) of active-phase islands would result in smaller width of the initial annular zone. The initial values of

r_{width}^{0}

assessed from relation (22) with regard to active-phase islands of structure and lattice facets referred previously are listed in Tables 1–4. These estimations indicate as well that larger dimensions of the active-phase islands would make for larger potential width and area of the initial coke-free zone, but at the same time, presuppose smaller relative difference between the width of the coke-free belt and the size of the active-phase island (viz. the (

r_{width}^{0} / r_{island}

) ratio).

In obedience to Eq. (19), in the course of coke build the value of $r_{zone}$ follows the dependence:

r_{zone} = \sqrt{r_{island}^{2} + \frac{C_{crit} - C_{actual}}{π L C_{crit}}}

(23)

Naturally, $r_{zone}$ and $r_{width}$ will be of maximal value in the beginning whereas $C_{actual} \to 0$ and will decrease on increasing of $C_{actual}$ in the course of coke formation. It follows from Eqs. (19) and (23) that under the condition ( $C_{crit} \geq C_{actual} \geq 0$ ) in the presence of coke, the actual width of the annular zone can be estimated as

r_{width} = \sqrt{r_{island}^{2} + \frac{C_{crit} - C_{actual}}{π L C_{crit}}} - r_{island}

(24)

By using these relations, we can estimate the expected shrink of the annular zone in the course of coke build. Extending the hypothesis stated in Ref. [53], it can be speculated that during this period of the process, regardless of “shrinking” the width of the coke-free zone, the coke tolerance effect will be still in action. The stepwise function $f_{th} (N_{c})$ introduced in Eq. (3) actually provides that the number of active sites will remain constant until the coke deposits attain the critical amount. Naturally, the width of the coke-free zone $r_{width}$ will reach zero, and the annular zone will be abolished when the deposited coke amount $C_{actual}$ attains the critical value ( $C_{crit}$ ). The expected logical effect is a start of the coke-caused catalyst deactivation, as frequently observed.

4.4 Coke-caused changes in the activity of diverse types of sites

At modeling the blockage-caused loss of active sites when poisoning or coke formation is realized inside the active-phase island. We represent the changes on the catalyst surface in terms of finite differences to account for the stepwise character of coke build:

- Δ N_{Z} = k {}_{Z} Δ N_{c} {at N_{c} > N_{c}^{crit}}

(25a)

- Δ N_{Y} = k {}_{Y} Δ N_{c} {at N_{c} > N_{c}^{crit}}

(25b)

The scheme of simulating the coke-caused alteration of the catalyst activity for structure-sensitive reactions considers the actual values of the probability factor $μ_{M}$ and its changes reasoned by coke build:

- Δ N_{X} = k_{X} \frac{1}{M} {μ_{M} \frac{Δ N}{Δ N_{c}} + N \frac{Δ μ_{M}}{Δ N_{c}}} Δ N_{c} {at N_{c} > N_{c}^{crit}}

(25c)

The curves plotted in Fig. 1 show patterns of simulation results calculated based on Eq. (25c) and illustrate the coke-caused drop of the probability function $μ_{M}$ specifying the actual chances for occurrence of six-, three-, and two-centered catalytic clusters (viz. M = 6, M = 3, and M = 2).

Fig. 1
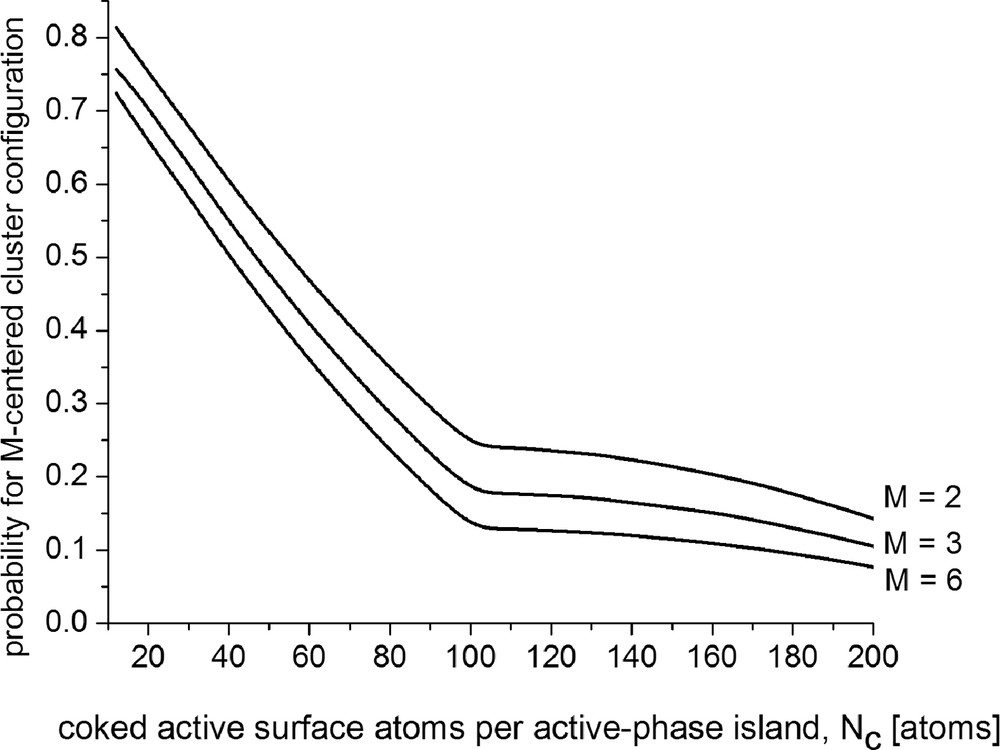
Coke-caused decrease in the probabilities for formation of catalytic clusters configured by M properly located active metal surface atoms on crystals having {111} face lattice.

As can be judged from these plots, the probabilities for occurrence of catalytic clusters appreciably decrease in the first stages of coking, more pronouncedly for catalytic clusters containing larger number of surface atoms. These results are in support of our understanding that the efficiency of a multiple site may be terminated even if one of its constituents is affected. Furthermore, our previous probabilistic calculus analysis [46] has shown that the active metal surface atoms, which are adjacent to blocked sites, are of reduced capability to construct cluster configurations. These effects are more pronounced for clusters containing larger number of constituents. Effectively, this may bring to surface reconstruction of the active-phase island resulting in reducing or terminating the action of multicentered active sites. The remainder of unblocked constituents of the deactivated catalytic clusters may continue in turn their action either facilitating structure-insensitive interactions or as constituents of smaller catalytic clusters. Consequently, relative increase in the population of single active sites and/or the population of smaller catalytic clusters may be expected.

The important inference from these results is that the process selectivity may be estimably modified in the course of coke building, to the damage of structure-sensitive pathways. It can be expected that coke formation also will be retarded because it is a structure-sensitive reaction.

Next, it is important to pay attention to some effects following from deteriorating or shielding the action of interfacial sites at abolishing the annular zone. As the coke formations reach the borders of an active-phase island, first the interfacial sites become vulnerable. The consequences are essential for the selectivity of processes for which interfacial sites play a key role. As recognized, the reaction networks of many hydrotreatment processes on supported sulfide catalysts involve routes requiring multicentered adsorption realized through the interaction of polyaromatic molecules with anion vacancies located predominantly at the island edges and corners. The surface intermediates formed may give rise to either hydrogenation or hydrogenolysis routes, depending on the mode of the adsorption realized. The vertical (perpendicular to the basal catalyst planes, “end-on”) form of adsorption is associated with the valley-shaped sites comprising one edge anion vacancy and one or more adjacent basal-plane vacancies [21]. The parallel (flatwise, “side-on”) adsorption is considered [18,66] to proceed on complex active sites involving several edge vacancies. Hence, it appears that the availability of properly located edge vacancies is of key importance for the mode of adsorption and thus selectivity. According to the hypothesis of Perot [22], in case some of the vacancies constituting a given configuration come out of action, this will either bring to a breakdown of the center complex or the latter will be transformed into a complex comprising a smaller number of properly located sites. Hence, the disruption of interfacial anion vacancies may reduce the amount of center complexes appropriate for flatwise adsorption or transform them into valley-shaped anion sites, which will result in increasing the impact of vertically adsorbed intermediates. Our results reported in the next section focus on some potential consequences.

4.5 Related selectivity effects

The results obtained for the probabilistic forecast of the actual number of the active sites of diverse types served to estimate the selectivity parameters $ξ_{z}$ , $ξ_{Y}$ , and $ξ_{X}$ as functions of $N_{Z}$ , $N_{Y}$ , and $N_{X}$ as specified by Eq. (10).

The solid curves in Fig. 2 show the prognosticated variation in the selectivity parameter $ξ_{X}$ for structure-sensitive reactions facilitated by six-, four-, three-, and two-centered ensembles (viz. M = 6, M = 4, M = 3, and M = 2) on {111} facets in the course of progressing coking of active sites. We substantiated in Section 2 the correctness of incorporating suchlike parameters in the equations assessing the selectivity of processes involving structure-sensitive routes (see Eqs. (10–12)). The dashed curves on the plots show the selectivity parameters corresponding to the concurrent structure-insensitive reaction.

Fig. 2
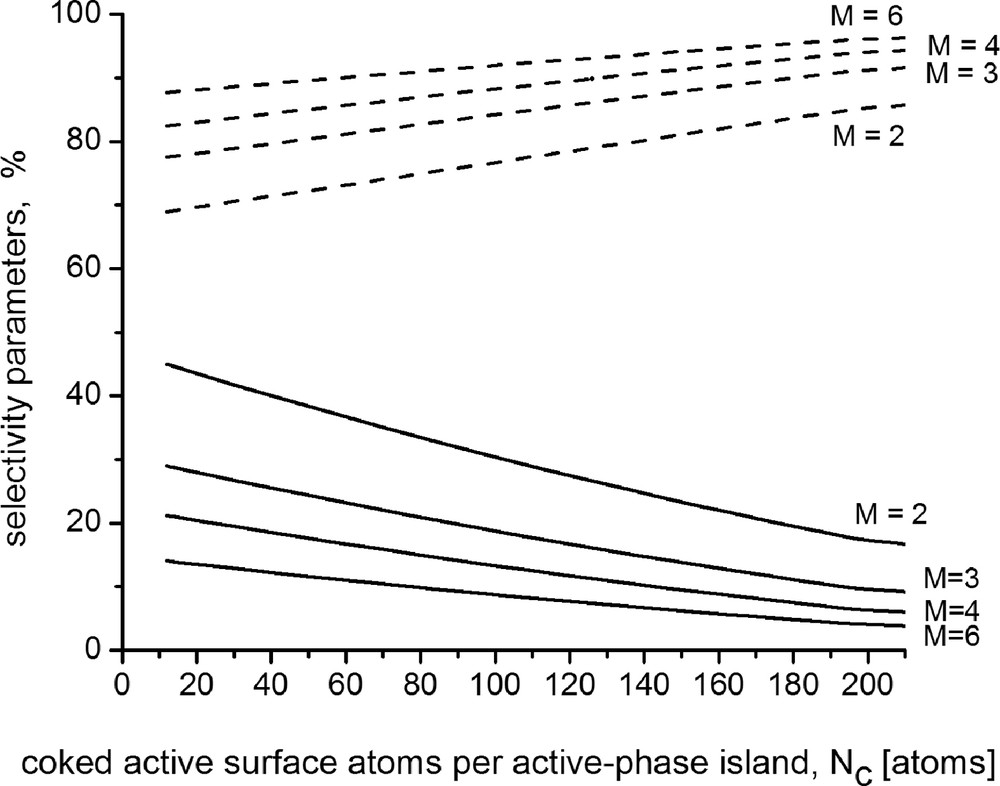
Simulated patterns of coke-caused changes of the $ξ_{k}$ parameters influencing the selectivity: (- - -) - toward structure-insensitive reactions; (—) – toward structure-sensitive reactions facilitated by catalytic clusters configured by M properly located active metal atoms for the case of the {111} lattice.

These results indicate that when structure-insensitive and structure-sensitive reactions occur concurrently on catalysts with dispersed active phase, the selectivity toward structure-sensitive reactions determined by use of relation (11) would be lower than that determined on the grounds of the reaction conditions over indiscrete active-phase structure. Actually, the physical sense of this relation is associated with the fact that the nanosized structure of the active-phase islands induces restrictions for the chances of occurrence of the catalytic clusters facilitating the performance of structure-sensitive reactions. The effect gains in magnitude in the course of coke build, in accordance with the drop of the population of proper catalytic clusters. Naturally, the selectivity parameters relevant to the structure-insensitive reactions increase correspondingly.

The simulation results indicate that the selectivity parameter values may be estimably lower at larger number of the constituents configuring the catalytic clusters. Consequently, it is possible to expect, by virtue of steric reasons, different selectivity patterns in the case of complex processes involving more than one structure-sensitive reaction, which are facilitated by catalytic clusters configured by different number of active metal surface atoms. Hence, if a given process involves structure-sensitive routes, which are facilitated by catalytic clusters including different number of active metal surface atoms, the selectivity may come influenced by steric factors. These results manifest the role of the steric restrictions for availability of complex active sites on nanostructured catalysts and the associated influence on the selectivity functions.

The development of the structure-sensitive pathways may depend on the mode of feasible adsorption configurations. By way of example, let us consider a catalytic process occurring on a multifunctional catalyst, the active phase of which is dispersed on the support as nanosized islands. Let us consider two basic routes of the process: a route proceeding via two-centered surface intermediates (noted by the index of two relevant variables) and a route proceeding via six-centered surface intermediates (noted by the index of six relevant variables). Such a scheme corresponds, for instance, to the reaction network of HDN of quinoline (Q) at thermodynamic equilibrium with 1.4-tetrahydroquinoline (TQ-14) on supported sulfide catalysts, which is frequently explored as a conventional model system. It is well known (see, e.g., Refs. [16,18–25]) that the hydrogenation and CN bond scission paths in the network of this process occur on different types of active sites: anion vacancies associated with the exposed metal cations, which appear naturally located on the edges and corners of the active-phase crystallites, and Brønsted acid sites donating proton, more readily to the heteroring because of its higher electronic density [22]. It is widely recognized that the hydrogenation of the aromatic rings takes place via planar adsorption requiring six properly located anion vacancies [18,38,39]. Within the frames of our model, we present these ensembles as six-centered catalytic clusters, which involve six properly configured interfacial sites. Besides, vertical adsorption of the reacting molecule can be realized in the so-called valley-shaped sites, involving one edge vacancy and one or more adjacent basal-plane sites, which may favor direct NC(sp²) bond cleavage [16,18]. We present this configuration as a two-centered catalytic cluster. The commonly supposed adsorption configurations of TQ-14 are (1) the vertical form involving a doublet bond between the lone electron pair of the N heteroatom with a valley-shaped site on the catalyst surface, and (2) the flatwise form occurring via planar adsorption of the aromatic ring through its π-electrons [16,21,24]. Thus TQ-14 may either form a two-centered intermediate vertically adsorbed through the lone electronic pair of the N atom (path “2” proceeding with rate r₂) or undergo flatwise adsorption requiring interaction of the electron cloud of the aromatic ring with six properly configured edge sites (path “6” proceeding with rate r₆). Route 2 is more beneficial, because it requires lower hydrogen consumption, and the products are of higher octane number, but route 6, although sterically hindered, is predominant inasmuch as the sp² bonding between the N and the aromatic-type C atom of the heteroring is stronger than the aliphatic-type sp³ CH bonding. According to data of Refs. [36,67,68], the ratio (r₆/r₂) varies from 10.4 to 1.65 at 350 °C and from 4.44 to 1.4 at 375 °C.

Provided the process is realized on catalysts of nanosized active-phase structure, the selectivity description should take into account, along with the participation of several types of active sites, the chances $ξ_{X 2}$ and $ξ_{X 6}$ for availability and contribution, respectively, of two-centered and six-centered catalytic clusters. These chances determine the values of the ( $a_{2} ξ_{X 2}$ ) and ( $a_{6} ξ_{X 6}$ ) factums (see Eq. (6)). Thus we get

S_{2} = \frac{r_{2}}{r_{2} + r_{6}} = \frac{r_{2}^{0} (P_{j}, T) a_{2} ξ_{X 2}}{r_{2}^{0} (P_{j}, T) a_{2} ξ_{X 2} + r_{6}^{0} (P_{j}, T) a_{6} ξ_{X 6}} = \frac{1}{1 + {\frac{r_{6}^{0} (P_{j}, T)}{r_{2}^{0} (P_{j}, T)}} {\frac{a_{6} ξ_{X 6}}{a_{2} ξ_{X 2}}}}

(26)

S_{6} = \frac{r_{6}}{r_{2} + r_{6}} = \frac{r_{6}^{0} (P_{j}, T) a_{6} ξ_{X 6}}{r_{2}^{0} (P_{j}, T) a_{2} ξ_{X 2} + r_{6}^{0} (P_{j}, T) a_{6} ξ_{X 6}} = \frac{1}{1 + {\frac{r_{2}^{0} (P_{j}, T)}{r_{6}^{0} (P_{j}, T)}} {\frac{a_{2} ξ_{X 2}}{a_{6} ξ_{X 6}}}}

(27)

We can assume that under conditions of catalyst deactivation, both the initial rates $r_{2}^{0}$ and $r_{6}^{0}$ (and consequently their ratio) remain unchanged, because they appear as functions of concentrations and temperature. Conversely, the terms $(a_{2} ξ_{X 2})$ and $(a_{6} ξ_{X 6})$ depend on the probability functions for availability of two-site or six-site ensembles on the active-phase islands comprising finite number of active metal atoms. The physical sense of this statement is that $(a_{2} ξ_{X 2})$ and $(a_{6} ξ_{X 6})$ actually depend on the surface structure of the active-phase islands, and therefore, may change in the course of surface reconstruction induced by increasing the number N_c of coke-blocked metal atoms. In the general case the ( $a_{2} ξ_{X 2}$ ) and ( $a_{6} ξ_{X 6}$ ) terms will evolve in different modes in the course of coke formation. Naturally, in the case of nanostructured active phase, the changes which ( $a_{2} ξ_{X 2}$ ) and ( $a_{6} ξ_{X 6}$ ) undergo depend on the efficient size of the active-phase islands and on the fraction of coked sites. Accordingly, induced selectivity changes may be expected.

The plots in Figs. 3 and 4 show the changes in the model selectivity functions S₂ and S₆ (corresponding, respectively, to the routes 2 and 6 designated subsequently) calculated in accordance with Eqs. (26) and (27) under the assumption that $r_{6}^{0} = 2 r_{2}^{0}$ (Fig. 3) or $r_{6}^{0} = 1.5 r_{2}^{0}$ (Fig. 4). The assumed relations are near to some of the data relations (see, e.g. Refs. [36,67,68]) in concern of the reactions conversion of TQ-14 into OPA (ortho-propyl aniline) and hydrogenation of TQ-14 to DHQ (decahydroquinoline):

TQ-14 → OPA (route 2 proceeding at rate r₂ with selectivity S₂)
TQ-14 → DHQ (route 6 proceeding at rate r₆ with selectivity S₆)

Fig. 3
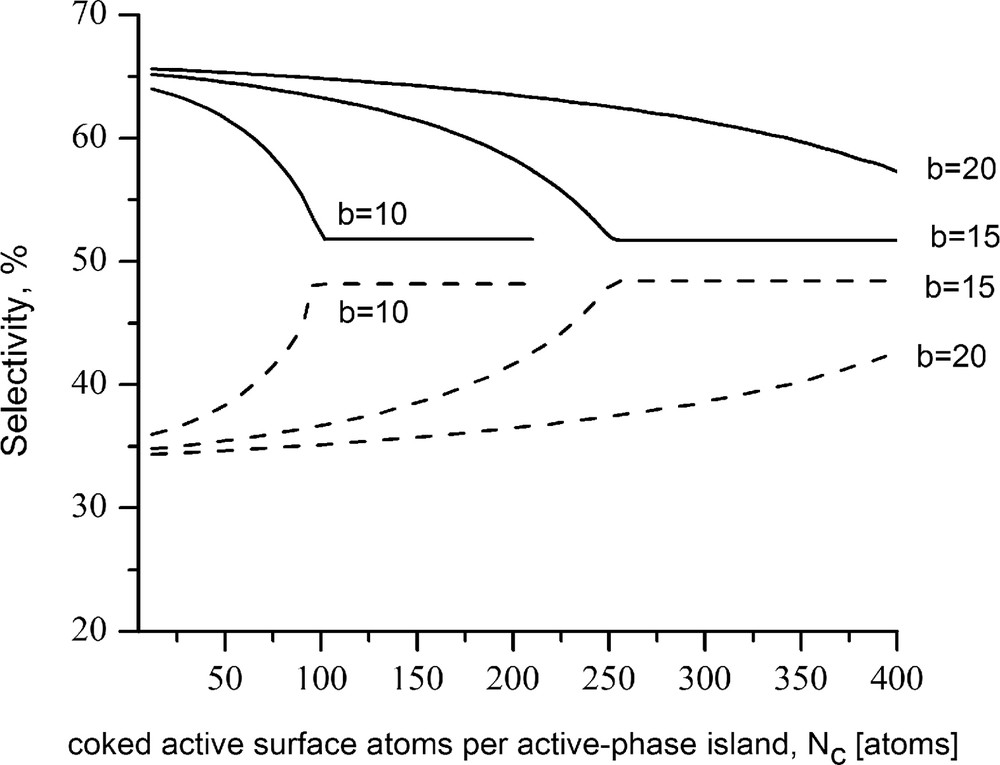
Changes in the selectivity of complex process involving concurrent routes facilitated by two-centered (dashed lines) and six-centered (solid lines) catalytic clusters; b is the number of surface atoms of the active metal constituting an edge of active-phase island. The initial rate of the sextet-catalyzed reaction is assumed to be twofold higher than the initial rate of the doublet-catalyzed reaction.

Fig. 4
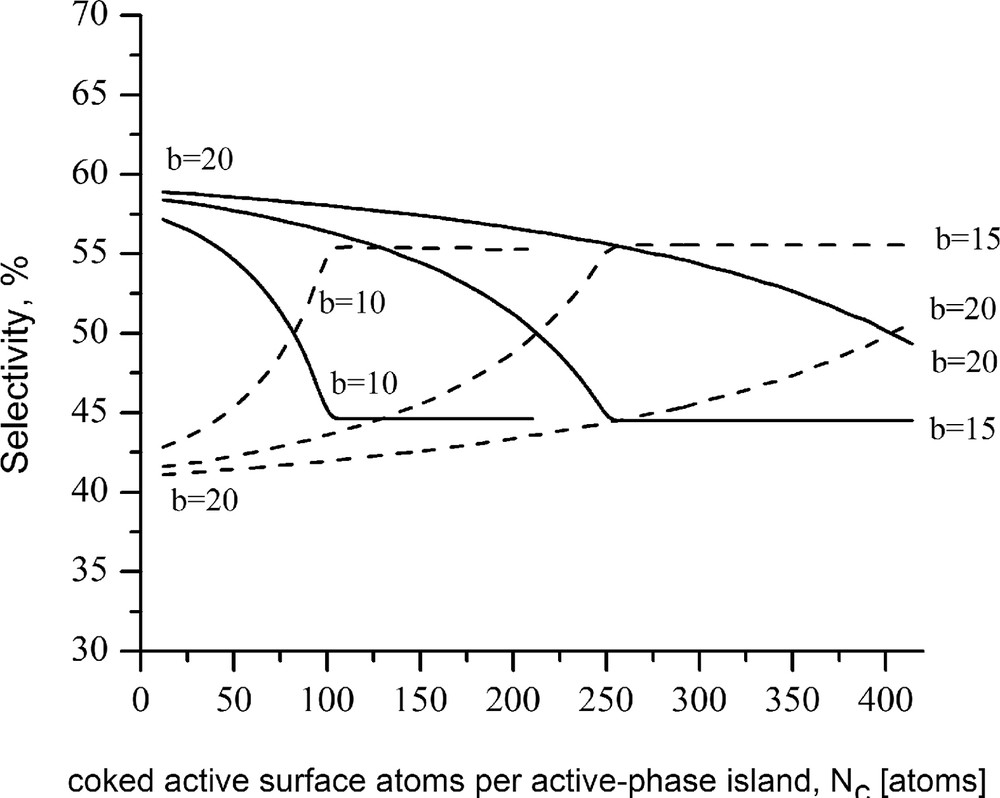
Changes in the selectivity of complex process involving concurrent routes facilitated by two-centered (dashed lines) and six-centered (solid lines) catalytic clusters; b is the number of surface atoms of the active metal constituting an edge of active-phase island. The initial rate of the sextet-catalyzed reaction is assumed to be 1.5-fold higher than the initial rate of the doublet-catalyzed reaction.

It is to be recalled that the flatwise adsorption requires complex sites involving several edge vacancies [18,66], whereas the vertical adsorption generally requires one edge anion in combination with adjacent basal-plane vacancies [21]. Hence, the active ensembles, which enable the adsorption resulting in six-centered intermediates, are much more vulnerable to the action of coking. The blockage of any constituent may deactivate the whole complex. In the event of nanostructured active phase presupposing finite number of the edge sites, the aforementioned disruptions may appreciably hamper the associated reaction routes. At the same time, part of the remaining unblocked constituents of the eliminated sextet complexes may reconstruct into doublet catalytic clusters giving rise to vertical adsorption. This may bring change in the overall selectivity.

The calculations were performed under the following assumptions: (1) the coke precursors arise from surface intermediates strongly adsorbed on six-centered catalytic clusters; (2) {111} crystallographic lattice; (3) the active-phase islands are of hexagonal shape, each edge of which comprises 10, 15, or 20 single peripheral sites. As can be seen from the plots, initially the selectivity toward the more rapid reaction proceeding via six-centered flatwise adsorbed intermediates is higher. In the course of coke formation, because of drop of the probability for flatwise adsorption, the selectivity toward the reaction requiring horizontally adsorbed surface intermediate (case in point the hydrogenation {TQ-14 → DHQ} route) may appreciably decrease. At the same time, chances are that some of the vacancies formerly constituting the deteriorated six-centered configurations will be engaged in additional valley-shaped sites [22], thus increasing the selectivity for the reaction realized via vertically adsorbed surface intermediates (e.g., the hydrogenolysis route {TQ-14 → OPA}). Such a speculation is in accord with the aforementioned concept stated in Ref. [22], inasmuch as route 6 {TQ-14 → DHQ} proceeds via planar adsorption of the aromatic ring of TQ-14 onto an ensemble of several edge sites, whereas route 2 proceeds through bonding of the free electron pair of the TQ-14 heterocycle with a valley-shaped site, requiring a smaller number of edge vacancies.

Taking into consideration the assumption that the coke precursors arise on the account of flatly adsorbed multicentered surface intermediates, it follows that coke formation will have the retarding effect on its own rate. It is thus natural for a process to come to a point at which the rate of coke building will become negligible. In that case, the rates of the different reaction routes may turn stationary and accordingly the resulting selectivity will remain constant. These considerations are in accord with the apparent shape of the simulated selectivity curves. As is seen, initially the selectivity toward the route facilitated by six-centered configurations falls down; in contrast, the selectivity for the route requiring two-centered adsorption forms increases. When the number of coked sites attains a given threshold value, supposedly coinciding with the coke amount causing break of the coke-formation rate, the selectivity curves level off. Naturally, the resultant steady levels of the particular selectivity curves depend on a variety of factors, including the initial values of the selectivity functions.

Case in point appears the steady levels of the selectivity curves shown in Figs. 3 and 4. As mentioned previously, the simulated selectivity curves in Fig. 3 are attributed to the initial condition $r_{6}^{0} = 2 r_{2}^{0}$ , whereas those in Fig. 4 are attributed to the case $r_{6}^{0} = 1.5 r_{2}^{0}$ . The latter case demonstrates the possibility of the induced surface–structure changes resulting from the reconstruction of the rest of unblocked sites to bring a shift in the overall process selectivity in favor of a route initially with inferior rate.

The interpretation of these results indicates about a beneficial potentiality. When the process is carried out on catalysts with dispersed active phase, the coke build may result in lowering the selectivity for reactions facilitated by larger catalytic clusters against reciprocal increase in the selectivity for the reaction facilitated by smaller ensembles. Moreover, under certain conditions, these effects may bring about a shift in the process selectivity. In the exemplary case considered, such a shift would be beneficial, because it would result in raising the impact of the more profitable hydrogenolysis route {TQ-14 → OPA}. As the case may be, an advantageous shift in the selectivity pattern may be achieved as well by appropriate active-phase dispersion. It is appropriate to recall that the aforementioned results have been obtained by introducing in the selectivity functions the specific parameters $ξ_{k}$ ( $ξ_{X 2}$ and $ξ_{X 6}$ in the instant case), which account for the chances for different modes of adsorption responsible for facilitating different reaction routes. This is of special importance for heterogeneous catalysts with nanostructured active phase because of the finite number of active surface atoms, which may contribute to one or another key form of adsorption.

These developments manifest feasible still not explored additional resources for improving the process selectivity through a proper design of the active-phase dispersion over the support of multifunctional catalysts. Appropriate sizes of the active-phase islands may turn out instrumental for improving the selectivity toward the more beneficial reaction route.

In that regard, it is appropriate to note that some of the last Gault's works [7–9] deal with similar matter. On exploring the mechanism of isomerization, hydrogenolysis, and reforming reactions of hydrocarbons over alumina-supported Pt catalysts, the occurrence of “selective” and “nonselective” mechanisms has been specified and their impact linked to the sizes of the active metal crystallites. In Refs. [8,9] convincing evidence was reported, based on investigating the reaction performance over six Pt catalysts with mean crystallite size varying in the range 1–20 nm, that the selective mechanism occurs on crystallites larger than 2.5 nm.

5 Conclusions

Following the adduced arguments that the selectivity of processes occurring over multifunctional catalysts may substantially depend on the input of the different types of active sites facilitating different reaction routes, we suggest to include in the selectivity description of such processes specific parameters reflecting the contribution of the distinct types of active site. The introduction of such parameters is especially important when nanostructured catalyst surface is concerned, as far steric factors may influence the efficiency of complex active sites facilitating structure-sensitive routes. Accordingly, we introduce specific parameters designated to account for the share of internal sites, interface sites, and catalytic clusters in the catalytic performance. The simulation results imply that, when the active phase is dispersed as nanosized islands on the catalyst surface, the selectivity toward structure-sensitive reactions would be lower than that determined by the reaction conditions over catalysts of indiscrete active-phase structure. More pronounced sterically induced influence on the selectivity is to be expected at larger number of the multisite constituents. Assessments grounded on the developed model link the dimensions of the active-phase islands to (1) the selectivity toward structure-sensitive reactions; (2) the feasible orientation of adsorbed surface intermediates, which may be determinative for different reaction routes and hence selectivity of complex processes; (3) the initial width of the potential coke-free zones implementing coke tolerance stages. The effects gain in magnitude in the course of coke build, because the drop of the population of proper catalytic clusters may reduce the process selectivity toward structure-sensitive pathways. In view of the foregoing, incorporation of the suggested parameters appears instrumental for considering the additional factors influencing the selectivity of processes over multifunctional catalysts. Specifically, it may turn helpful to estimate the active-phase dispersion optimal for selectivity. This study manifests feasible still not explored additional resources for improving the process selectivity through proper design of the active-phase dispersion over the support of multifunctional catalysts.

Acknowledgments

This work was supported by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under grant no. D-135-989-1435. The authors, therefore, gratefully acknowledge the DSR technical and financial support.

Bibliographie

[1] C. Corrolleur; D. Tomanova; F.G. Gault J. Catal., 24 (1972), p. 401

[2] R. Touroude; F.G. Gault J. Catal., 32 (1974), p. 294

[3] M.J. Ledoux; F.G. Gault; A. Bouchy; G. Roussy J. Chem. Soc. Faraday Trans. 1, 74 (1978), p. 2652

[4] M.J. Ledoux; G.F. Gault J. Catal., 60 (1979), p. 15

[5] M.J. Ledoux; F.G. Gault; A. Bouchy; G. Roussy J. Chem. Soc. Faraday Trans. 1, 76 (1980), p. 1547

[6] V. Mintsa; R. Toroude; F.G. Gault J. Catal., 66 (1980), p. 412

[7] H.C. de Jongste; V. Ponec; F.G. Gault J. Catal., 63 (1980), p. 395

[8] V. Amir-Ebrahimi; F.G. Gault J. Chem. Soc. Faraday Trans. 1, 76 (1980), p. 1735

[9] V. Amir-Ebrahimi; F.G. Gault J. Chem. Soc. Faraday Trans. 1, 77 (1981), p. 1813

[10] M.J. Ledoux Nouv. J. Chim., 2 (1978), p. 9

[11] S.H. Yang; C.N. Satterfield J. Catal., 8 (1983), p. 168

[12] G.C. Bond Z. Phys. Chem. Neue Folge, 144 (1985), p. 21

[13] E. Furimsky Oil Gas Sci. Technol., 44 (1989), p. 337

[14] N. Topsøe; H. Topsøe; K. Massoth J. Catal., 119 (1989), p. 252

[15] U.S. Ozkan; L. Zhang; S. Ni; E. Moctezumo J. Catal., 148 (1994), p. 184

[16] H. Topsǿe; B.S. Clausen; F.E. Massoth Hydrotreating Catalysis, Springer, Berlin, Heidelberg, 1996

[17] K. Kumbilieva; N.A. Gaidai; A.V. Dryahlov; N.V. Nekrasov; L. Petrov; A.L. Lapidus Catal. Commun., 10 (2009), p. 1034

[18] J. Shabtai; N. Nag; F.E. Massoth Proceedings 9th International Congress on Catalysis, Calgary (M. Philips; M. Ternan, eds.), 1988, p. 1

[19] F. Gioia; V. Lee Ind. Eng. Chem. Proc. Des. Dev., 25 (1986), p. 918

[20] N. Jian; R. Prins Ind. Eng. Chem. Res., 37 (1988), p. 834

[21] T. Ho Catal. Rev. Sci. Eng., 30 (1988), p. 117

[22] G. Perot Catal. Today, 10 (1991), p. 447

[23] S. Kim; F. Massoth Ind. Eng. Chem. Res., 32 (2000), p. 1705

[24] C. Moreau; P. Geneste Theoretical Aspects of Heterogeneous Catalysis, Van Nostrand Reinhold, NY, 1990

[25] M. Jian; F. Kapteijn; R. Prins J. Catal., 168 (1997), p. 491

[26] H. Backman; D.K. Neyestanaki; D.Y. Murzin J. Catal., 233 (2005), p. 109

[27] P. Biloen; J.N. Helle; W.M.H. Sachtler J. Catal., 58 (1979), p. 95

[28] E.H.V. Broekhoven; J.W.F.M. Schoonhoven; V. Ponec Surf. Sci., 156 (1985), p. 899

[29] R.D. Cortright; J.A. Dumesic J. Catal., 148 (1994), p. 771

[30] F.H. Ribeiro; A.L. Bonivardi; C. Kim; G.A. Somorjai J. Catal., 150 (1994), p. 186

[31] M. Boudart Adv. Catal., 20 (1969), p. 153

[32] J.H. Sinfelt J. Catal., 29 (1973), p. 308

[33] J.H. Sinfelt Acc. Chem. Res., 10 (1977), p. 15

[34] A.A. Slinkin Kinet. Katal., 22 (1981), p. 71

[35] L. Bendarova; C.E. Lyman; E. Rytter; A. Holmen J. Catal., 211 (2002), p. 335

[36] C. Satterfield; J. Cochetto Ind. Eng. Chem. Proc. Des. Dev., 20 (1981), p. 53

[37] R. Laine Catal. Rev. Sci. Eng., 25 (1983), p. 459

[38] M. Girgis; B. Gates Ind. Eng. Chem. Res., 30 (1991), p. 2021

[39] E.E. Furimsky; F.E. Massoth Catal. Today, 52 (1999), p. 381

[40] R. Prins Adv. Catal., 46 (2001), p. 399

[41] G.A. Somorjai Catal. Today, 12 (1992), p. 343

[42] L. Yang; A.E. DePristo J. Catal., 148 (1994), p. 575

[43] D.Y. Murzin Chem. Eng. Sci., 64 (2009), p. 1046

[44] D.Y. Murzin J. Mol. Catal. A: Chem., 315 (2010), p. 226

[45] D.Y. Murzin J. Catal., 276 (2010), p. 85

[46] Y. Alhamed; K. Kumbilieva; A. AlZahrani; L. Petrov Chem. Eng. Sci., 105 (2014), p. 77

[47] K. Kumbilieva; N.A. Gaidai; N.V. Nekrasov; L. Petrov; A.L. Lapidus Chem. Eng. J., 120 (2006), p. 25

[48] K. Kumbilieva; L. Petrov Chin. J. Catal., 32 (2011), p. 51

[49] K. Kumbilieva; L. Petrov; Y. Alhamed; A. AlZahrani Chin. J. Catal., 32 (2011), p. 387

[50] K. Kumbilieva; L. Petrov Kinetic Aspects of Catalyst Deactivation, Marin Drinov Academic Publishing House, Sofia, Bulgaria, 2011

[51] K. Kumbilieva; L. Petrov Catal. Ind., 4 (2012), p. 39

[52] M.R. Gray; A.R. Ayasse; E.W. Chan; M. Veljkovic Energy Fuels, 9 (1995), p. 500

[53] S. Richardson; H. Nagaishi; M.R. Gray Ind. Eng. Chem. Res., 35 (1996), p. 3940

[54] F. Diez; B. Gates; J. Miller; D. Sojkowski; S. Kuhes Ind. Eng. Chem. Res., 29 (1999), p. 1015

[55] M. Haruta; S. Tsobota; T. Kobayashi; H. Kageyama; M.J. Genet; B. Delmon J. Catal., 144 (1993), p. 175

[56] D. Cunningham; W. Vogel; H. Kageyama; S. Tsubota; M. Haruta J. Catal., 177 (1998), p. 1

[57] G.C. Bond; D.T. Tompson Catal. Rev. Sci. Eng., 41 (1999), p. 319

[58] G.C. Bond; D.T. Tompson Gold Bull., 33 (2000), p. 41

[59] K. Ruth; M. Hayes; R. Burch; S. Tsubota; M. Haruta Appl. Catal. B, 24 (2000), p. L133

[60] A. Wolf; F. Schuth Appl. Catal. A, 226 (2002), p. 1

[61] M.B. Cortie; E. Lingen Mater. Forum, 26 (2002), p. 1

[62] J. Guzman; B. Gates J. Phys. Chem. B, 106 (2002), p. 7659

[63] R. Davis Science, 301 (2003), p. 926

[64] M. Cargnello; V.T. Doan-Nguyen; T.R. Gordon; R.E. Diaz; E.A. Stach; R.J. Gorte; P. Fornasiero; C.B. Murray Science, 341 (2013), p. 771

[65] Q. Fu; W.X. Li; Y.X. Yao; H.Y. Liu; H.Y. Su; D. Ma; X.K. Gu; L.M. Chen; Z. Wang; H. Zhang; B. Wang; X.H. Bao Science, 328 (2010), p. 1141

[66] E. Furimsky Ind. Eng. Chem. Proc. Des. Dev., 17 (1978), p. 329

[67] C. Satterfield; M. Modell; R. Hites; C. Declerck Ind. Eng. Chem. Proc. Des. Dev., 17 (1978), p. 141

[68] C. Satterfield; M. Smith Ind. Eng. Chem. Proc. Des. Dev., 25 (1986), p. 942

Commentaires - Politique

Ces articles pourraient vous intéresser

Transformation of m-xylene over an USHY zeolite: Deactivation and regeneration

Aicha Benamar; Zohra Bechket; Youcef Boucheffa; ...

C. R. Chim (2009)

Insight in the mechanism of deactivation of a Pt/mordenite (MOR) catalyst during the isomerization of n-pentane

Christophe Lenoir; Friedemann Rohr; Michael Stöcker; ...

C. R. Chim (2005)

Effect of phosphorus on the performance of IM-5 for the alkylation of toluene with methanol into p-xylene

Cui Wang; Yaquan Wang; Hengbao Chen; ...

C. R. Chim (2019)