1 Introduction
The so-called spin-crossover (SCO) phenomenon corresponds to the spin-state switching in metal ions [1], which can be induced by temperature, pressure and light or other external fields [2]. The associated change in the electronic state between low-spin (LS) and high-spin (HS) states of the metal is related to the population of antibonding orbitals. This is responsible for the elongation of the bonds between the metal and the ligand (Fe–L). This structural change represents the main reaction coordinate of the process [3]. At the macroscopic scale in the solid state, the transformation of crystals translates up to macroscopic volume expansion, due to the elastic interactions between its constituent molecules. The spin-state switching driven by temperature is mainly related to the higher entropy in the HS state, which includes both electronic and vibrational terms [4]. In addition to temperature, pressure can be used to drive transformation as it favours the LS state of lower volume [3]. Light, which can modify the electronic distribution, can also be used for switching the spin state, because of the important electronic–structural coupling in SCO systems, resulting in an efficient trapping of the photoinduced spin state [5]. Because of the intimate coupling between the electronic state and the molecular structure, additional structural changes may involve symmetry breaking at the intramolecular or intermolecular levels [3]. The connection between the electronic and the structural degrees of freedom is therefore central for understanding and controlling SCO. In this article, we review some acquired basic knowledge and recent progress in the field when investigating SCO phenomena by various structural approaches such as microscopy (TEM [Transmission Electron Microscopy], STEM [Scanning Transmission Electron Microscopy], AFM [Atomic Force Microscopy] and optical), diffraction (PXRD [Powder X-Ray Diffraction], SCXRD [Single Crystal X-Ray Diffraction ], ND [Neutron Diffraction] and ED [Electron Diffraction]) or, in some cases, absorption (XANES [X-ray absorption near-edge spectroscopy] and EXAFS [Extended X-Ray Absorption Fine Structure]). These views provide an understanding of the process from microscopic to macroscopic scales under different stimuli (T, P, hν,…) and over different time scales from ultrafast molecular photoswitching (100 fs), elastic lattice expansion (ns), laser heating (μs) or phase nucleation or relaxation (ms–s).
2 From microscopic to macroscopic
2.1 Structural analysis and methods
2.1.1 Real space imaging with microscopy
The SCO phenomenon in materials is associated with colour and optical density changes due to different optical absorption bands between LS and HS states, resulting from coupled electronic–structural reorganization [7]. In connection with magnetic studies, colour change constitutes the easiest observation of SCO phenomenon in crystals at thermal equilibrium and more interestingly under light excitation, as initially reported from optical spectra [8] and optical microscopy [9]. Since 2008 more detailed experimental observations of the nucleation and growth mechanism were reported in individual single crystals, with a spatial resolution approaching ∼1 μm. Fig. 1 shows typical images of the nucleation and growth process presented in a recent work during the thermally induced spin transition [10], from which the propagation speed of the interface was obtained (12–16 μm/s). In addition, a colorimetric method can be used to decouple the contributions of structural and electronic transformations involved in the spin-state switching, both for thermo- and photoinduced spin transitions [11].
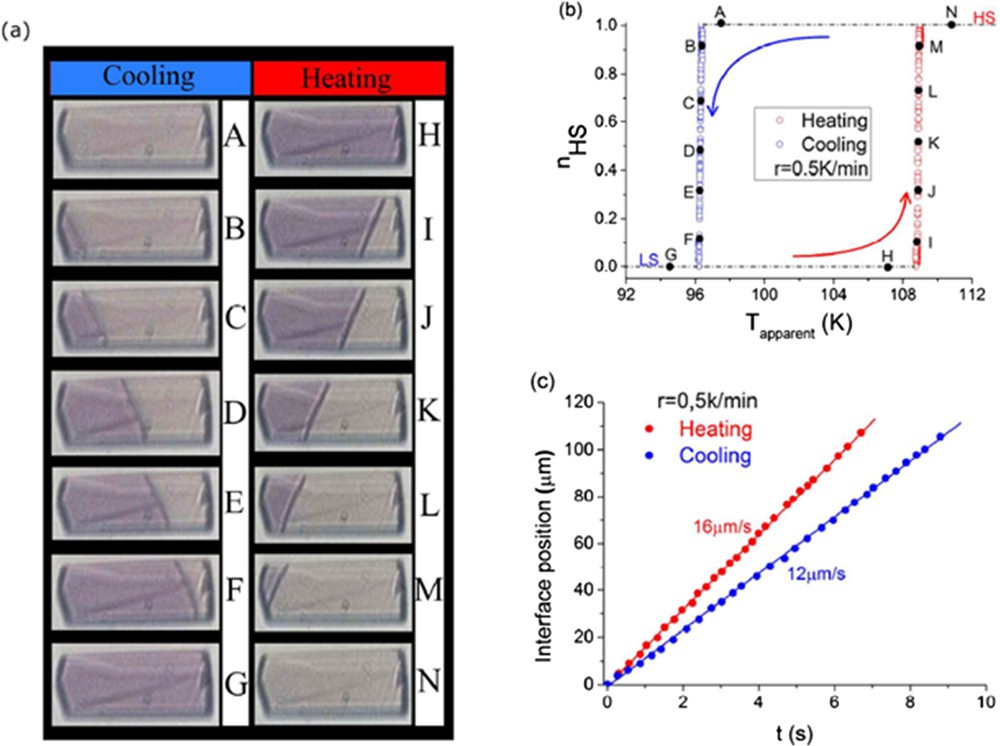
(a) Typical observation by optical microscopy of the nucleation phenomenon in an SCO single crystal during the thermally induced spin transition. (b) Corresponding thermal dependence of the HS fraction. (c) Temporal evolution of the HS–LS interface position. Reprinted with permission from [10]. Copyright 2017 American Chemical Society.
By applying this technique in many materials (see [12] and references therein for recent results), some common trends or more sample-specific features related to macroscopic SCO in crystals were extracted. In these experiments, the ∼10 ms temporal resolution is limited by the camera. Although this is too slow to observe the dynamics of macroscopic transformations induced by a laser pulse, optical microscopy can reveal the fast and important volume change related to the macroscopic change [13]. It should also be emphasized that when the colour contrast is not so pronounced, making optical microscopy observation difficult, Raman imaging [14] can then allow the spatial mapping of changes due to SCO in crystals.
These “light” observation techniques, performed with conventional microscopes, have a limited spatial resolution and cannot provide details of the transformation of nanocrystals or nanoparticles. Then other methods with higher spatial resolution and higher sensitivity come into play to reveal global structural changes related to spin-state changes. These include scanning probe microscopy methods (AFM and SNOM [ Near-field Scanning Optical Microscopy ]) [15]. In addition to the observation of SCO at the atomic scale, a fine control of the LS–HS phase boundary motion was achieved with the AFM tip.
Electron microscopy was also used to observe the SCO phenomena of single nanocrystals, in the time-resolved mode [16]. This technique allows visualization of the macroscopic structural dynamics of single nano-objects in both real and reciprocal spaces. The techniques mentioned above, mainly probing macroscopic changes, cannot provide intramolecular details of the SCO, which requires sub-angstrom resolution. For that, diffraction, scattering or X-ray spectroscopic techniques are required.
2.1.2 Reciprocal space analysis by X-ray, neutron and electron diffraction techniques
Diffraction techniques of X-rays, neutrons and electrons represent a fundamental tool for investigating structural aspects during the transformation of materials with sub-angstrom resolution [17]. In SCO materials, this allows for watching intra- and intermolecular reorganizations coupled with the change in the spin state. A wealth of information can be extracted from diffraction patterns by following the positions of diffraction peaks, their intensities and their shapes [3]. Diffraction comes from constructive interferences of the waves (X-ray, neutron or electron) scattered by the constituting atoms in crystals. Because of their 3D periodic lattice the intensity is scattered along vectors , defined by the variation in the wave vector between incident and diffracted beams . The scattered intensity therefore concentrates on the nodes of the reciprocal space on different . The reciprocal lattice is then defined by vectors, which are related to the direct lattice of the crystal, defined by the unit cell (, , , , , and so forth). This condition for the Bragg scattering gives rise to sharp peaks in the diffraction pattern around the different nodes of the reciprocal lattice, corresponding to integer values of the (hkl) coordinates. The amplitude of the wave scattered on the Bragg peak, by all the atoms of a unit cell, reaches
Note that in practice the relation is I(hkl) = κ|F(hkl)|2, where κ reflects different experimental aspects going, for instance, from the polarization of the X-ray beam to the Lorentz factor but also integrating various aspects of the sample itself, from the absorption coefficient to the surface roughness of the crystal. Information about the distribution of atoms within the unit cell is then distributed within the structure factors of various nodes of the reciprocal lattice. The spatial distribution of atoms or of electron density ρ(x, y, z) and its symmetry in the real space (space group) translates into the reciprocal space. For example, in the case of a mirror symmetry perpendicular to the crystalline axis in the crystal structure, any spatial density ρ follows this symmetry ρ(x, y, z) = ρ(x, −y, z). This gives the relationship between different structure factors F(hkl) = F(h − k·l). The symmetry operators of the space group, which relate the different symmetry-equivalent atomic positions in the unit cell, translate in the symmetry equivalence of the intensities of Bragg peaks with different (hkl). In addition, nonprimitive unit cells or nonsymmorphic symmetry operators (screw axes or glide planes) induce systematic extinctions: some specific combination of (hkl) gives zero diffracted intensity. Information about the crystalline symmetry is therefore also contained in the intensity of the diffracted intensity in the reciprocal space.
Solving and refining a structure consist first of finding the real lattice from the observed reciprocal lattice and then the space group and the atomic positions within the unit cell, from the intensities of the Bragg peaks. Structural refinement from single crystals or powder data is now possible with many software packages. Crystallography performed by X-ray, neutron or electron scattering is a powerful approach for investigating SCO phenomena that take advantage of spectacular recent technological leaps [18]. Various sample environments allow us now to perform crystallography studies of SCO induced by temperature, pressure, light irradiation or external fields [3,19]. Cryostats can be used down to a few Kelvin, pressure cells can be used up to hundreds of gigapascals, and light irradiation is easy with a cryostream. X-ray diffraction is performed in many laboratories on single crystals down to ≈10 μm or on powders in different forms. Synchrotron sources offer much higher flux and also tunable X-ray wavelengths. X-ray diffraction is, however, less sensitive to light elements such as H. Neutron diffraction requires usually larger crystals but is sensitive to H atoms, and large sample environment can be used (cryostat, gas pressure cell, and so forth) for combining diffraction and magnetic inelastic neutron scattering, for example, [20]. Electron diffraction can also be used and is generally more suited to study very small (nanoscale) crystals [21].
2.2 Structural probe of SCO at various physical scales
Structural analyses using the above methods allow us first to describe the consequences of the spin-state modifications on the structural properties at all the physical scales, from the metal environment (Å) to the crystal packing (nm), the coherent domains (nm–μm) and the particles or single crystal (nm–cm) scales (Fig. 2). Since the early stages of SCO investigation, the structural properties were thoroughly investigated, generating fascination and a substantial literature including many review articles [22]. The structural modifications accompanying the SCO at the level of the metal polyhedron are always spectacular, although very similar from one compound to another. These modifications are very well characterized nowadays either experimentally by diffraction techniques [22] or theoretically [23]. For instance in the case of the FeN6 coordination sphere, the volume of the metal polyhedron increases by about 25% from LS to HS. The volume expansion results from the increase in the metal–ligand bond lengths and the deformation of the polyhedron. The amplitude of the latter suffers, however, a large variation from one compound to another. Being only related to the spin state, the expansion of the metal coordination sphere is perfectly reversible. At upper physical cases, the situation is much more complicated. The consequence of the polyhedron expansion/reduction at the molecular and crystal packing scales appears in contrast very dissimilar from one compound to another and therefore is also affected differently at the micrometric scale. The diversity of behaviours encountered, almost each case appearing specific, explains that structural analyses are undoubtedly crucial approaches to describe any new SCO compound or any novel design of a known SCO material. The structural consequences of SCO are dependent on both the stimulus used for switching and the sample form itself. In some cases, different crystal packing adjustments have been observed when the spin-state switching is induced by light irradiation, pressure or thermal effects [3,24], whereas in other cases pressure and temperature induced similar structural switching [3,25]. In addition to this intricate situation, it is clearly known that a crystalline powder can react differently to spin-state modifications than its single-crystal form notably because of the strain on the micrometric powder grains [26].
Schematic view of the SCO consequences on the structural properties at different physical scales of the material (left) including a reminder of the relevant experimental techniques for the structural analysis (right). Crosses mean the corresponding method suits perfectly the physical scale whereas question marks with numbers indicate that it is restricted to peculiar cases or narrow fields as explained: (1) powder diffraction can lead to fully reliable structural determination only in very rare cases, (2) electron diffraction may give information on the surface composition, (3) when one (nano)particle only contains one coherent domain then microscopies that give data on the particle morphology also inform on coherent domains, (4) in the case of contrasted colours between HS and LS, for example, optical microscopy also gives information on the spin state at this scale. Figure freely adapted from [23d].
Metal–ligand bond lengths are a straightforward probe to structurally characterize the spin state. The contrast between HS and LS for FeN lengths (∼0.2 Å), for instance, is strong enough to highlight partial SCO and to obtain the HS–LS ratio within a sample through diffraction techniques, as illustrated by many examples [22,26]. Note, however, that depending on the nature of the ligand there can be significant discrepancies between the metal–ligand length modifications. Apart from these bond lengths, some tools have also been defined to describe the distortion of the polyhedron.
Among them, the distortion parameter Σ [22g,27] is now routinely and widely used to probe the spin state in crystals [22f,28–37]. Other parameters are also in use to finely probe the spin state from the coordination sphere geometry, such as, for example, the trigonal twist Θ parameters [22f,22g,28–38], the length-distortion ζ parameter [4] and the polyhedron volume, Vp [22d,22f,22g,27,36,39,40]. All these structural tools (see Table 1) demonstrate that the metal surrounding is always more regular and smaller in LS than in HS, allowing an easy identification of the spin state from structural data. At the molecular scale, the use of the average root-mean-square deviation (RMSD) gives a basic comparison of the molecular shape in the HS and LS states.
Probing the spin state from the structural analysis. Proposition of selected parameters that should be looked for a quick and straightforward structural description of the spin state for the different physical scales. The example is taken for the SCO molecular compound [Fe(PM-AzA)2(NCS)2] known to exhibit an SCO at 190 K.
| FeN6 polyhedron | HS at 290 K | LS at 110 K |
| <FeN> (Å) | 2.154(2) | 1.960(1) |
| The angle distortion, Σ (°) | 82(1) | 46(1) |
| The trigonal distortion, Θ (°) | 214 | 298 |
| The length distortion, ζ (Å) | 0.41(2) | 0.09(1) |
| The polyhedron volume, Vp (Å3) | 13.0(3) | 10.0(2) |
| Molecular scale | ||
| Superposition of HS (green) and LS (blue) complexes Maximum RMSD = 0.441 Average RMSD = 0.202 | ||
| Unit cell changes from HS to LS (%) | ||
| Total (SCO + thermal): Δa; Δb; Δc and ΔV | −0.76; −1.48; −2.34 and −4.52 | |
| SCO only (corrected): Δa; Δb; Δc and ΔV | −0.51; +1.09; −2.32 and −1.59 | |
| Crystal packing | ||
| Intermolecular interactions shown by di vs de (Å) fingerprints | ||
| Crystal density | 1.322 | 1.383 |
| Coherent domain | ||
| Relative mosaicity | 1.0 | 1.3 |
Describing the unit cell modifications due to SCO looks straightforwardly achievable using diffraction techniques (X-ray or neutron). When cautiously performed, variable temperature diffraction (single crystals, powder) is indeed a powerful approach that provides an accurate view of the unit cell modifications, very often showing a strong anisotropy in SCO compounds, and can even afford thermal expansion parameters [41]. Variable pressure and coupled pressure–temperature experiments are rare and still cutting edge in crystallography, but they always provide new insights into SCO, revealing unexpected phase diagrams, explaining unusual behaviours and allowing calculation of fundamental values such as the bulk modulus [3,24,25]. Elsewhere, in the context of the structural analysis of SCO materials, isostructural compounds showing no SCO are sometimes investigated in parallel to decorrelate the effects due to SCO from those due to the thermodynamic changes [27,31,41]. It is then mandatory to compare unit cell modifications obtained with the same protocol. For instance, the unit cell volume modification shown within a temperature range is the sum of the SCO and the pure thermal effects, the latter can even sometimes mask the pure switch effects.
The packing modifications induced by SCO may sometimes be arduous to describe due to the number of intermolecular distances to be taken into account. In addition, each compound or at least each family of compounds deserves a specific description because the impact of SCO on the crystal packing appears very different if not unique from one compound to another. Some structural analysis tools may be used to facilitate this aspect. Among them, the Hirshfeld surface approach through fingerprint representations provides a new tool to summarize the intermolecular interactions that could be used to easily locate the intermolecular interactions that deserve to be scrutinized in more details [40,42,43]. Interesting propositions to empirically summarize the amount and diversity of intermolecular interactions in the crystal packing of SCO compounds into a simple data have been proposed and should be more systematically used [22d,22k]. The basic and initial structural description of an SCO compound should contain at least the above structural parameters; an example provided in Table 1 clearly shows how the HS and LS may be probed by distinct structural parameters at various physical scales. Note that, thanks to modern crystallography, this description of the HS–LS structural properties is accessible not only to variable temperature conditions, as taken in this example, but also under high pressure (HP) and light irradiation conditions [3]. Furthermore, pioneering diffraction methods also allow actual time-scaling investigations [13,44] and structural analysis at upper physical scales (coherent domains, nanoparticles, crystal) that necessitate the combination of diffraction and microscopy methods. Both aspects refer to the current challenges in the field of SCO materials, as detailed in Section 3.
2.3 Structural view of the SCO mechanism and symmetry breaking
The relative stability of the LS and HS states in SCO materials is balanced by the competition between the electron pairing energy, the energy splitting between the t2g and eg orbitals, which is modified by the structural reorganization, and the entropy increase from LS to HS states [4]. At thermal equilibrium, most of the SCO systems undergo a single-step spin-state switching. We should emphasize that the associated structural distortions listed above are usually totally symmetric (do not involve a change in symmetry). Indeed, the polyhedron surrounding the metal may be close to an octahedron but does not have true octahedral symmetry in any phase: the structural change often corresponds to a relative distortion between LS and HS structures. In addition to this intramolecular view of the process, the (elastic) interactions between the molecules in the crystal can drive a more or less cooperative spin-state switching. Weakly interacting systems exhibit a crossover regime for the change in the spin state. This is often called gradual conversion because of the gradual evolution of the population of HS and LS states. Systems with strong interactions exhibit a first-order phase transition (often called discontinuous or abrupt), with a discontinuous change in the population of HS and LS states. The molecular volume change is responsible for elastic interactions between molecules in crystals, and these depend on the molecular reorganization and on molecular packing. Therefore, if the nature of the molecule is important (ligand field, entropy, and so forth), its coupling with the environment in the crystal is another important parameter.
The role of intermolecular coupling is revealed when comparing the response of polymorphs made of the same molecule, especially when macroscopic volume and intermolecular (bond lengths or angles) modifications accompanying the spin-state conversion occur without symmetry change. This is the case for [Fe-(PM-BIA)2(NCS)2]: the orthorhombic crystal (BIA I) undergoes a first-order phase transition with discontinuous volume change, whereas the monoclinic crystal (BIA II) undergoes a crossover (Fig. 3).
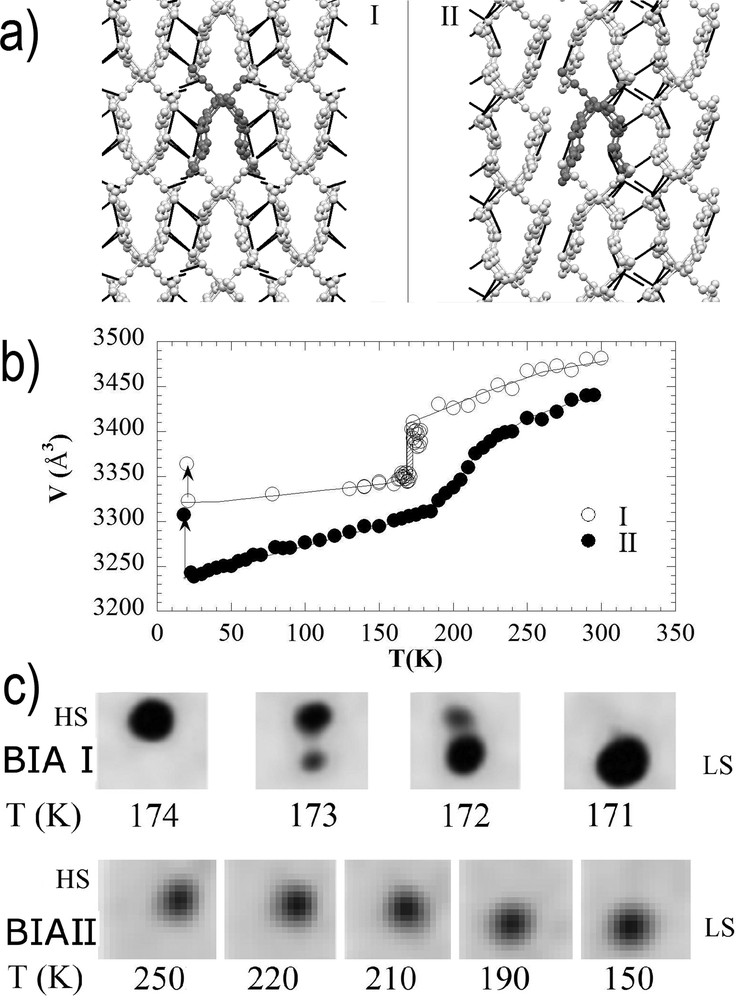
a) Packing of the molecules in the BIA I and BIA II polymorphs, with different intermolecular contacts. (b) Volume change characteristic of a first-order transition (I) or crossover (II). (c) Bragg peak shape and position evolution during the thermal HS to LS switching for BIA I and BIA II. Adapted from [4].
The growth of long-range domains of HS and LS phases was observed inside the thermal hysteresis of BIA I, through the coexistence of the HS and LS Bragg peaks [4]. This phase separation process is commonly observed in many first-order phase transitions, including SCO materials. The gradual thermal conversion of BIA II is associated with a gradual shift in the Bragg peak in the reciprocal space (Fig. 3). The very different molecular packing between the two polymorphs results in stronger interactions in the case of BIA I than BIA II, responsible for the change in the thermal conversion regime from cooperative to crossover. Strong similarities were also observed from the cooperative point of view between behaviours at thermal equilibrium (phase transition in BIA I vs crossover in BIA II) and those under light irradiation: self-amplified (BIA I) versus quasilinear (BIA II) phototransformation, sigmoidal and phase separation relaxation process (BIA I) versus exponential and homogeneous one (BIA II).
Another example is the case of the monoclinic and orthorhombic polymorphs of [(TPA)Fe(III)(TCC)]PF6 [45]. Both exhibit thermal crossover at very similar temperatures. Contrary to BIA I and BIA II, which have different molecular interactions, the [(TPA)Fe(III)(TCC)]PF6 polymorphs consist of similar cation layers alternating with PF6 anion layers. The layers are just packed differently in the two polymorphs. The fact that the most important interactions are intralayer explains the similar thermal crossover in these polymorphs.
There are also few SCO crystals, which exhibit symmetry breaking at thermal equilibrium or in the photoinduced state [22j,46]. The symmetry breaking may involve a change in the lattice due to molecular packing change (e.g., from orthorhombic to monoclinic), molecular distortion due to ordering of ligand bonds, ligand bending and/or tilting of molecules on the lattice, motions of counter ions or solvent molecules. Such intermolecular order is often associated with the appearance of new Bragg peaks due to the symmetry change for the nonsymmorphic space group or change in the periodicity. The symmetry breaking can be coupled with the change in the spin state, but it can also occur at a different temperature. One famous example is the [Fe(ptz)6](BF4)2 complex, for which the spin conversion and the structural order–disorder phase transition from to are in fact two distinct phenomena [47]. Another example is the [FeH2L2−Me](ClO4)2, for which a ligand ordering occurs below the SCO temperature [6]. LIESST (Light-Induced Excited Spin-State Trapping) can also be associated with symmetry breaking, as revealed by photocrystallography experiments. There are few examples of materials for which the crystal structure of the metastable photoinduced HS state differs from the one of the thermal equilibrium HS state observed at high temperature (HT). For example, in the case of [FeH2L2−Me][XF6]2, with XP or As [48,49], the cations are located on a twofold axis in the HS state at HT. At low temperature (LT), the photoinduced HS state corresponds to a different crystal structure and the twofold axis is lost on some molecules, resulting in tripling of the unit cell, which can only be probed by diffraction techniques. At LT, a low symmetry HS state can be favoured compared to a high-symmetry HS state because of entropy gain [50]. SCO materials have various competing false ground states and some of them can only be reached under nonequilibrium conditions by light irradiation. This is one of the important aspects of the research developed in the emerging field of photoinduced phase transitions and for SCO materials, in particular, and diffraction techniques are important to study symmetry changes related to the appearance of functionality. Elsewhere, note that rare evidence of HS → LS transitions induced by heating, a kind of reverse spin transition, was observed in some Co(II) complexes and are probably related to phase transitions [51].
2.4 Multistep phase transitions
In addition to single-step SCO, different types of two-step thermally induced SCO between completely HS HT and LS LT phases have been reported, with an intermediate (INT) phase associated with a partial conversion from HS to LS states. Four types of two-step transitions were reported so far as summarized in Fig. 4. Type 1 corresponds to materials exhibiting molecular multistability, such as binuclear systems. The coupled bistability of the two switchable intramolecular sites corresponds to three molecular states (LS–LS, LS–HS or HS–HS), balanced by temperature. The two steps correspond to two crossover regimes from LS–LS to LS–HS and from LS–HS to HS–HS and on the step there is no order of the HS–LS or LS–HS molecular state [52]. Type 2 corresponds to materials for which the asymmetric unit cell of the crystal comprises two molecular sites (A and B), which are not equivalent by symmetry. The molecular sites on the different sublattices A and B have different structures and therefore different ligand fields and each site undergoes its SCO at its own temperature, resulting in a global two-step SCO of the crystal [53].
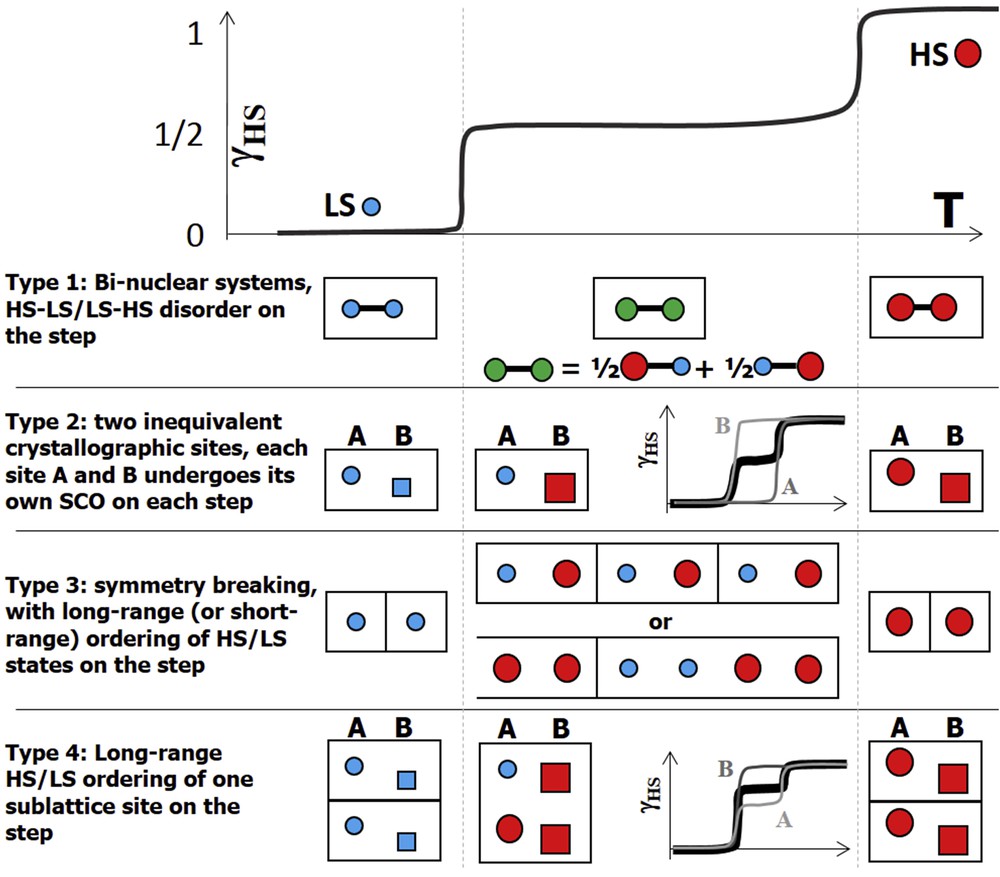
The four different types of two-step SCO.
Type 3 corresponds to mononuclear complexes, where the INT phase results from symmetry breaking and a long-range ordering of the spin state (HS–LS) as reported in several Fe(II) [48,49,53–55], Fe(III) [56], Co(II) [57] and Mn(III) [58] complexes. This is often associated with the appearence of new Bragg peaks due to the change of periodicity. Short-range HS/LS order may also exist before the occurence of long-range order, giving rise to diffuse scattering. Type 4 corresponds to a mixing of types 2 and 3, where one sublattice undergoes a two-step SCO and the other one a single step coupled with the one of the other sites [59]. The elastic coupling between molecules mediated by the lattice is at the origin of mechanical frustration, generating stepwise conversions of the fraction of HS molecules [54].
2.5 Established structure–property relationships
The previous sections describe how SCO modifies the structural features of a compound, at any physical scale. Conversely, it is well established that the structural characteristics of the atomic architecture strongly influence the SCO features such as temperatures (T1/2, T(LIESST)), abruptness, hysteresis width, rate of conversion and even the occurrence of the SCO itself [22]. As a result, establishing structure–function relationships appears a major aspect of the SCO field. The task proves difficult because any parameter acting on atomic positions potentially acts on the SCO features and candidate parameters are numerous. For example, the SCO hysteresis width is extremely dependent on supramolecular connections. The cooperativity between the SCO metal centres that correspond to the abruptness and hysteresis width of the transition is directly linked to the efficiency of the communication pathways between these centres through intermolecular interactions. Consequently, any parameter affecting the crystal packing strongly modifies the cooperativity. The long-range elastic energy cost, due to the formation of an interface between HS and LS phases of different lattice parameters, is also an important aspect of the process. Although well-defined orientations of the interface should coincide to a minimization of its energy cost (Fig. 1), this is difficult to analyze due to the multiscale aspect of elastic interactions.
Structural analyses have clearly demonstrated how deeply SCO depends on aspects like polymorphism [22,29,31,45,60] as well as the presence of anions [22f,61], solvents [36,62] and guest molecules [63] that contribute to crystal cohesion through hydrogen bonding, aromatic π–π or van der Waals interactions. Variations in the nature of the ligands present are also known to strongly impact SCO characteristics [64]. The literature is full of examples for which, starting from the same molecular substance, the SCO features are finely or drastically tuned from temperature(s) to cooperativity and occurrence by playing on the above aspects. The optimistic perspective is that it really makes possible to design SCO materials with expected properties (large hysteresis, full conversion and room temperature SCO) by a skilful crystal-engineering approach. In practice, this seems a hard challenge due to the abundance of possibilities offered by molecular crystal packing. In addition, thermodynamic parameters must also be accounted for in this design process. The application of pressure and the modification of temperature often induce phase transitions in molecular materials, leading to intricate (P, T) phase diagrams resulting from the synergy between SCO and pure structural transformations [3,22g,24]. In some unusual but beautiful cases, SCO may even generate the coexistence of different INT structural phases in the single crystal [65]. Besides, solvent or guest molecules may be expelled from or absorbed within the crystal packing due to the (P, T) modifications [32,63,66a,b], which then complicates even more the overall structure–function panorama. On the other hand, this is part of the beauty of SCO systems because it leads to materials sensitive to their environment and able to detect the presence of small molecules. Because of this complexity, proposing definitive conclusions with universal value as regards to the structure–property relationships in SCO materials seem to be out of reach until now. However, when focussing specifically on a family of compounds for which it is approximately possible to edit one parameter at a time, structure–property relationships may be evidenced. Although the number of studies is innumerable, the harvest of practical learning is relatively weak, but results converge. To date, it has been clearly demonstrated that the strength, nature, direction and number of intermolecular interactions account for the temperature and abruptness of the thermal SCO, whereas the photoinduced SCO is more likely predominantly linked to the distortion of the metal coordination sphere [22f,22g,38,40]: the larger is the distortion of the metal coordination sphere at SCO the higher is T(LIESST). Extreme distortions of the metal coordination sphere lead to the highest known T(LIESST), and vice versa.
To guide the design of SCO materials on the basis of these structural features, it may be useful to define general tools to compare compounds but also to identify classes of crystal packings. For instance, structural tools to estimate the cooperativity of crystal packings have been proposed [22k] and, in parallel, attempts to classify SCO compounds as a function of their crystal packing have been made, notably thanks to the investigation of polymorphism [22i]. When focussing on a series of compounds, it is sometimes possible to extract a simple structural parameter that can be used to make predictions, as recently demonstrated for the occurrence of SCO anticipated from the length of an interatomic distance in a specific family of mononuclear compounds [67a,b]. Yet the structure–property relationships is far to be fully elucidate in SCO materials.
2.6 Time scaling of photoinduced spin-state switching
More or less sophisticated techniques can be used to perform time-resolved structural studies, depending on the required time resolution. Conventional techniques allow investigating structural changes on the time scale of seconds or minutes, induced by temperature or laser irradiation [24a,52,55d,66a,b]. Techniques with much shorter time resolution are based on pump–probe methods, in which a laser flash drives a photoswitching process and a probe pulse (X-ray or electrons) visualizes the excited structure after laser excitation [67a,b,68]. Over the past 15 years, tremendous advances in ultrafast X-ray and electron science, with complementary spectroscopy, scattering, and diffraction techniques, made possible the investigation of ultrafast processes [69,70]. These ultrafast techniques can deliver in the time domain new insight into the dynamics of molecular systems, solutions, solids and biosystems.
Time resolution is limited by the duration of the probe pulse, as optical laser pulses reach easily the 10 fs range. Conventional X-ray sources can be equipped with a chopper but the time resolution is then in the microsecond–millisecond range. Large-scale facilities provide more intense and shorter X-ray pulses. Synchrotrons can generate 100 ps X-ray pulses that can be shortened to 100 fs using the slicing technique [69]. X-ray free electron lasers (X-FELs) can generate more intense X-ray pulses of few femtoseconds' duration [71]. New electron sources can also generate electron pulses in the 100 fs range [21].
LIESST was discovered in SCO crystals more than 30 years ago [5,8] induced by weak cw light excitation. It is more recently that the response of SCO materials to pulsed laser irradiation was investigated. Nanosecond laser excitation was used to induce permanent switching inside the thermal hysteresis or to induce transient spin-state switching outside [13,72,73], but dynamical processes are limited by the relatively long pulse duration.
The use of femtosecond lasers to excite SCO crystals and the use of ultrafast complementary techniques (optical spectroscopy and X-ray) revealed the complex out-of-equilibrium dynamics associated with three main steps (Fig. 5) [74,75]. In step 1, the light pulse locally photoswitches an initial fraction of molecules from LS to HS states within ∼200 fs. The associated molecular structural reorganization, related to the Fe–L bond elongation, was probed by ultrafast X-ray and electron diffraction [21,75]. In step 2, the internal lattice pressure due to HS molecular swelling and lattice heating induces lattice expansion on the nanosecond time scale. As the HS state is then favoured on account of its higher molecular volume, an additional switching towards the HS state occurs, increasing the HS fraction up during this so-called elastic step (2). The laser heating drives a “thermal” step (3). Here again, structural studies sensitive to intra- and intermolecular reorganizations play a key role for understanding the dynamical transformation of these materials and the basic mechanism behind photoinduced phenomena.
Schematic out-of-equilibrium dynamics in SCO crystals. The laser pulse locally switches molecules from LS (blue) to HS (red) states (less than 1 ps, step 1). The molecular swelling and lattice heating induce lattice expansion driving cooperative elastic switching (≈nanosecond time window, step 2). The lattice heating warms up the materials, allowing for thermal population of the HS state (≈μs, step 3). Reprinted with permission from [74b]. Copyright 2017 The Royal Society of Chemistry.
It is important to emphasize that during the initial photoswitching process at the molecular level, the lattice has no time to expand. This occurs only on the 100 ps–ns time scale, when a mechanical equilibrium is reached within the crystal, because the photoswitched molecules of higher volume exert an internal pressure on the lattice. This drives a self-amplified molecular transformation, reminiscent of a feedback mechanism intrinsic to active media. For SCO solids, the more the volume expands, the more molecules switch, and thus the more the volume expands. Hence, the elastically driven response, resulting from the simultaneous absorption of many photons, is greater than the sum over individual responses of the constituent molecules. This is a direct manifestation of the cooperative effects induced by a light pulse, where a single photon can transform more than seven molecules [74,75].
van der Veen et al. [16] used time-resolved electron microscopy and diffraction to visualize in real and reciprocal space the structural dynamics at the level of a single nanocrystal. The experiment was performed on the Fe(pyrazine)Pt(CN)4 SCO material, with a limited time resolution (7 ns). Anisotropic thermal expansion on the 200 ns time scale was observed at the level of a single particle. This was attributed to a temperature jump induced by laser excitation, but it may result from the negative pressure induced by the photoswitching.
3 Recent results, perspectives and challenges
3.1 Challenging crystal structure determinations of SCO compounds
X-ray crystallography is the leading technique for structural analyses of materials. It is fascinating to see how this science is currently undergoing a development corresponding to a technological leap that affects all aspects from X sources to detection and analysis methods [18]. Consequently, innovative investigations become accessible, including those targeting dynamics as detailed in Section 3.3 but also, simply, the determination of crystal structures previously considered not reachable. First, it is now often possible to solve and refine the atomic positions from intensity data sets collected on laboratory machines using very small crystals (few micrometres) or powders; yet, the latter is still challenging for low-symmetry molecular architectures. In the field of SCO, for example, this has opened the determination of the crystal structures of 1D polymeric iron compounds based on the triazole ligand. This family of materials has been known for decades to be among the most promising SCO materials for application [2,76], but it is only recently that the first crystal structures were solved either on powder or small single crystals [35,77]. Progress in X-ray crystallography allows challenging SCO in the context of very large unit cells [78], charging density approaches [79], problematic twinnings [47], and aperiodicity [55j]. Sequential movies based on structural determination all along the spin-state modification make it possible to fully picture the SCO, far beyond the simple determinations of the crystal structures above and below the transition [41]. In parallel, one of the current tasks in difficult crystal structure determinations concerns HP. SCO on molecular compounds generally occurs at pressure in the range of 0–20 kbar. The first structural analyses of SCO compounds under HP were performed a long time ago [25] but are still uncommon although not rare [3,22g, 42]. The scrutiny of SCO crystal structures under HP requires further methodological developments to combine HP, LT and light-irradiation experiments; neutron diffraction being notably more appropriate to this kind of combination [19]. The interest in these combinations has been highlighted by magnetic measurements [80] and by preliminary structural analyses [81], performed in combined conditions. A rapid growth of HP structural data for SCO compounds, including powder or single crystal, can be predicted and is desirable to seriously address fundamental questions relative, for example, to the structure–property relationships under HP and the determination of phase diagrams. In this regard, it is clear that one of the most daunting challenges is the exploration of charge density under HP, which is a pioneering task in crystallography [82]. In all cases, difficult crystal structure determinations should be solved on the basis of the whole panel of structural techniques including electron microscopy, in particular, when the diffraction volume of the sample is small, such as in nanoparticles [83], or when the sample has a limited crystalline order, as for SCO liquid crystals [84].
3.2 Microstructures in SCO materials
As demonstrated in Section 2, the SCO features are closely linked to the atomic architecture, namely, the crystal structure of the compound, but it is also strongly dependent on the upper physical-scale properties of the material. The morphology of the crystal, for instance, plays a clear role in the spreading of the spin-conversion at the scale of the crystal itself. This is well illustrated by recent optical microscopy studies that allow a deep insight into the phase transition mechanisms at the macroscopic scale [14,85]. This approach is particularly efficient for investigating light-induced SCO mechanisms in crystals [86] but is limited to relatively large samples of few tenths of micrometres. When the SCO material is made of smallest particles, down to nanoparticles, the scrutiny of the morphology–property relationship must be done by other techniques. As a general matter of fact, it is well established that the properties of nanocrystalline materials are shape dependent [87]. The relation between the size and morphology of SCO particles has started to be explored in the case of the 1D coordination iron polymers based on triazole using electron microscopy [16,88]. First, these studies, which are still in progress, show the richness of the SCO behaviours. The absolute values and the distribution range of the sizes as well as the morphology of the nanoparticles affect the SCO features. For instance, the role of nanoparticle size on the hysteresis width is clearly established but the corresponding amplitude, limits and mechanism are still debated on the basis of electron microscopy observations and theoretical considerations [89]. In addition, it has been clearly demonstrated that the synthesis protocol influences the final size of the nanoparticles with a clear impact on the SCO temperature [16,88,90]. In this context, AFM approaches are also currently under development to elucidate the role of the surface of the particles on the SCO features as well on the functionalization of the particles [91]. Another physical scale, however, has to be taken into account. Nanoparticles or powder grains with a particle size in micrometres, are built by a mosaic of coherent domains, that is, the volume truly containing a unique periodic atomic assembly. When the coherent domains are large the sample is a single crystal, but if the coherent domains are very small (<1 μm) then it is a crystalline powder. A particle may contain from one to millions of coherent domains, this number largely governing the so-called crystal quality of the sample. The Bragg peak shapes in X-ray diffraction experiments, notably powder X-ray diffraction, gives access to the size and morphologies of the coherent domains [92]. The microstructure corresponds to the structural information at this physical scale. The microstructure can be determined from the shape of the diffraction peak. This is a well-known and routinely used aspect in metallurgy but is quite new in the field of molecular materials where methods have to be adapted. Crystallographic studies at the physical scale of the coherent domain size are still very rare in the SCO field, although microstructure features are often argued to be a potential key point to understand SCO anomalies and the influence of crystal quality on SCO features is well known and was first demonstrated some time ago [93]. Preliminary results in the SCO field have shown that in some cases the size of the coherent domains is probably a more relevant parameter than the size of the particle to account for the SCO features [94]. In other cases, comparison between electron microscopy and powder diffraction data clearly indicates that the crystal defects (crystal quality) more than the crystallite size are responsible for the higher cooperativity [95].
Microstructure determination can also be used to link crystal packing to the particle scale (Fig. 6). One of the more crucial questions that can be addressed with the above techniques concerns the mechanical fatiguability upon SCO cycles. Ageing of the SCO compounds has been observed and is often linked to solvation or oxidation [96] but investigation of the fatiguability is, strangely, a very rare approach. Preliminary investigations based on X-ray diffraction [97] or AFM [91] have confirmed that, in some cases, a relatively low number of SCO cycles may strongly alter the structural properties of the sample. In such cases, a degradation of the atomic architecture is observed reducing the coherent domain size. Elsewhere, microstructure becomes a key point when dealing with functionalized SCO nanoparticles such as hybrid nanocomposites for instance. The interplay between the SCO nanoparticles and its environment, either a gel or a core–shell system, triggers the features of the conversion. X-ray characterization is then of crucial importance, although difficult to undertake and difficult to interpret, to determine how microstructure influences the conversion properties. Pioneering microstructure studies of encapsulated SCO nanoparticles notably based on X-ray studies completed by theoretical considerations have already depicted a large diversity of situations showing the complexity of the interaction between nanoparticles and their environment at the microstructural scale. Dramatic effects of microstructure in the case of an SCO compound [98] and of the parent charge-transfer–induced spin transition materials [99] were clearly demonstrated. The impact on the SCO features is not clearly established so far but, in any case, systematic and large-scale investigations of microstructure relationships are surely one of the current challenges in the SCO field. To this aim, innovative methods such as, for instance, pair distribution functions [100] or X-ray ptychography [101] are very promising for accessing an accurate multiscale structural description of nanosized samples. The latter is an X-ray imaging that gives a high-resolution 3D view of the microstructure including strains in nanoparticles. The Pair Distribution Function (PDF) analysis can be determined from the total scattering data, using laboratory or synchrotron X-ray or neutron diffraction. The PDF allows getting microstructural and atomic architecture information from the same experiment—therefore the same sample—in the case of bad crystallinity, that is, from nanometre-sized coherent domains to even “amorphous” particles. It allows us, for example, to confirm that the crystal structure determined for micrometric crystals remains the same for nanoparticles [77b]. Clearly, challenging the knowledge of the microstructure scale is achievable but will require the combination of many approaches.
View of the [Fe(Htrz)2(trz)](BF4) 1D SCO polymer (a) in powder form as seen with human eye, (b) in nanoparticles form as seen by electron microscopy, (c) at the scale of coherent domains that are described (thanks to the shape of Bragg peaks in powder X-ray diffraction experiments) and (d) at the atomic architecture scale as determined from the Bragg peak intensities. The structural investigation of the different physical scales allows us to show that the axis of the chains correspond to the long axis of domains and particles. Adapted from [90c,90d] and [96].
3.3 Complex ordering phenomena
During the last few years, the stepwise transitions of types 3 and 4, related to long-range order, were described in more detail, based on advanced structural analysis developed in the frame of the Landau theory of phase transition [54,55]. The long-range spatially periodic structures of LS and HS states on the step result from the competition between ferroelastic and antiferroelastic coupling, also described in the frame of the ANNNI (anisotropic next-nearest-neighbour interaction) model [54]. The long-range HS–LS ordered structures form the so-called spin-state concentration waves (SSCWs, Fig. 7) [54,102]. This spatial modulation of the HS fraction γHS on the different molecular sites in position r of the lattice is simply described by the modulation of the HS population of the molecular sites: γHS(r) = γHS + (η/2) × cos(Qc·r).
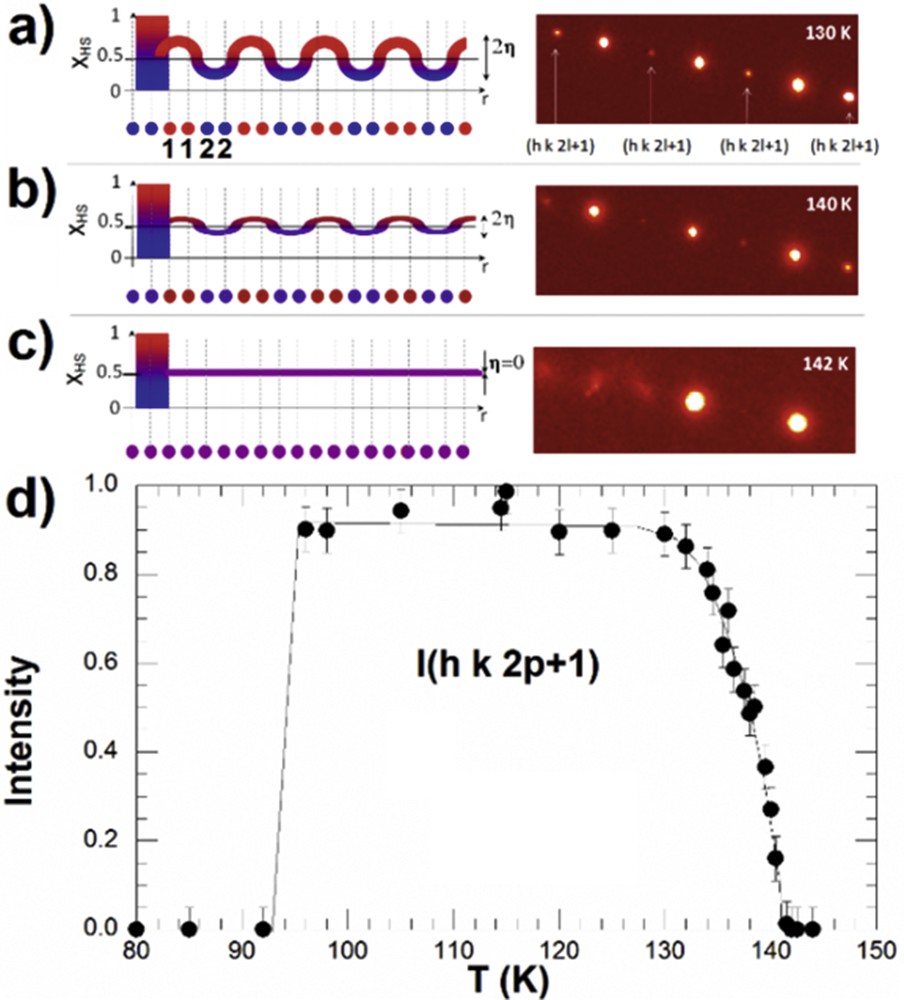
a) SSCW among molecular sites 1 and 2 schematically represented by γHS(r)= γHS + η × cos(Qc·r) on the plateau where γHS ≈ 0.5. The periodicity of the modulation is 2c, where c is the distance between sites 1 and 2, which are symmetry equivalent at HT in the high-symmetry phase. The SSCW gives rise to diffracted intensity at Qc indicated by arrows (right). Below 135 K, the order is maximum with a strong diffracted intensity at Qc. (b) At 140 K, η ≈ 0.125. (c) Above 142 K, η = 0. (d) Temperature dependence of the diffracted intensity at Qc, characterizing the formation of the SSCW. Adapted from [102].
For two-step SCO, in the high-symmetry phases, the molecular sites are equivalent and with the same HS population (in the LS phase γHS(r) = 0 and in the HS phase γHS(r) = 1). When the SSCW forms on the step and the HS and LS molecules alternate (e.g., along the crystalline axis, Fig. 7), the doubling of the unit cell in the real space induces the appearance of new Bragg peaks (at ) into the reciprocal space. In the INT phase, the average HS fraction is γHS = 0.5 and the order parameter η measures the amplitude of the wave, that is, the difference in the HS population on sites 1 (HS) and 2 (LS). X-ray and neutron diffraction can reveal the formation of an SSCW through the spatial modulation of <FeN> bond length between crystalline sites in r.
There are more and more examples of systems undergoing multistep SCO (with more than two steps). The steps correspond often to a partial and fractional conversion of the average molecular state towards the HS state, where long-range ordered HS–LS structures form. It is very recently that the analogy with the Devil's staircase concept was established [103], allowing for a simple, but meaningful description, of the structure of the steps in terms of the SSCW. The SSCW on each step is characterized through the value of the order parameters γHS (average HS fraction), η (amplitude of the order) and Q (modulation wave vector breaking symmetry).
Different spatial modulations of HS (+) and LS (−) states are shown in Fig. 8, where Q is locked onto a rational number n/m. There are infinite steps between any two steps, as there are infinite rational numbers lying between any two rational numbers. This is the reason why such a stepped sequence of phases is called the Devil's staircase.
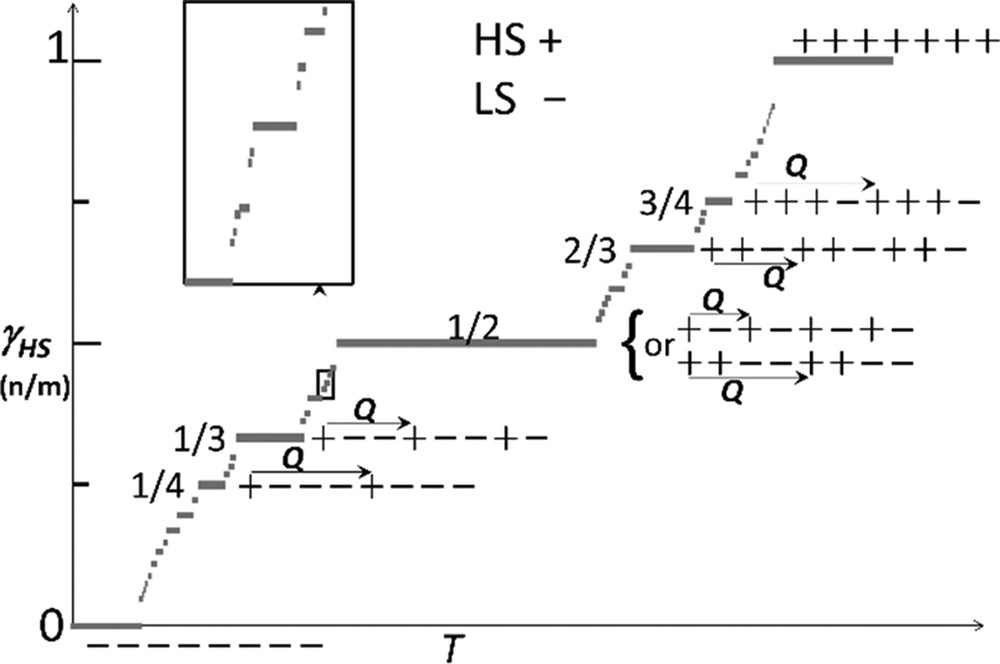
Devil's staircase for SCO materials, the steps with T correspond to fractions γHS = n/m of HS (+) molecules forming a periodic sequence with LS (−) molecules along the modulation vector Q. Structure of the simplest (thick segments) steps are represented. Adapted from [103].
The relative stability of the steps is governed by interactions and temperature. The formation of such long-range structures modulated by Q is revealed by diffraction techniques through the appearance of new Bragg peaks in the reciprocal space [48,49,54,103]. This modulation of the structure modifies the periodicity in the real space. The sequence of HS and LS molecules (e.g., identified by their FeN bond length) can then be found by solving the structure in the supercell defined by Q.
Devil's staircase–type phase transitions were theoretically constructed on the ANNNI model extension of the Ising model. The step γHS = 1/2 is the most likely to be observed [104], and both the HS–LS–HS–LS and the HS–HS–LS–LS sequences were reported in different SCO materials, as well as other steps at γHS = 1/3 (LS–LS–HS) or γHS = 2/3 (HS–HS–LS) corresponding to a unit cell tripling, as well as at ¼ and ¾ ([3,48–58,103] and references therein).
In addition to the commensurate structures shown in Fig. 8, the ANNNI model is known to form incommensurate structures, where the modulation vector Q is incommensurate with the lattice. This feature is characterized by the appearance of satellite reflections in the reciprocal space, which cannot be indexed with the three basis vectors of the reciprocal lattice. A fourth vector qi is required for indexing the satellite peaks. The structure is therefore no longer 3D periodic, but incommensurately modulated with respect to the initial (a, b, c). Such structures can be refined in dimension higher than three and the main feature is again an SSCW with a period incommensurate with the one of the lattice. Four-dimensional structure in SCO materials were, for example, refined in the P(α,β,γ)0 and P211(0βγ) super space groups [55j,103]. Atomic coordinates are then described by their positions in the average 3D unit cell and the modulation functions of these coordinates along the fourth dimension coordinate x4.
In addition to these long-range periodic orders (in 3D or higher dimension), for which new Bragg peaks appear due to the new periodicity, short-range HS–LS orders were also reported by X-ray diffuse scattering. The diffuse scattering signal is spread out within reciprocal and its shape depends on the spatial extension of the local order over different cells. Local 1D HS–LS order is associated with diffuse planes perpendicular to the stack, whereas diffuse ellipsoids correspond to local 3D order [105,106].
3.4 Ultrafast studies of LIESST
The photoresponse of an SSCW to femtosecond light excitation was investigated by time-resolved X-ray diffraction and time-resolved optical spectroscopy [102]. The typical time scale for a molecular system to explore different HS–LS configurations and to reach thermal equilibrium, erasing the SSCW, is in the 100 μs range, whereas the SSCW reforms within 15 ms. This is characterized by the disappearance and reappearance of the Bragg peaks associated with the spin-state order.
The most impressive and recent ultrafast structural results concern the real-time studies of the electronic and structural dynamics behind LIESST, on the times cale of elementary molecular motion. Understanding the elementary processes allowing the structural trapping of the electronic excited state is challenging because the changes in electronic and nuclear configurations impact each other and cannot be treated independently. In addition, the required time resolution of such experiments must be of 100 fs or shorter. By combining femtosecond optical spectroscopy and XANES, detailed understanding of structural trapping during LIESST was provided in different FeN6 SCO materials [71,107]. During LIESST, as already mentioned, the main structural change is the FeN bond elongation. The latter combined with electronic reorganization is responsible for significant XANES changes between LS and HS states.
Extremely short X-ray pulses of the Linac Coherent Light Source (LCLS) X-FEL at Stanford University were used to study LIESST dynamics in Fe(bpy)32+ [71]. The femtosecond transient XANES changes ΔI(t)/Ioff after photoexcitation measured at different X-ray energies revealed ultrafast reorganizations (Fig. 9). In the pre-edge region (7113.5 eV), X-ray absorption is lower in the HS state than in the LS state as eg states are occupied. At 7164 eV, the XANES change is predominantly sensitive to molecular structure change. XANES changes show signatures of the metal-to-ligand charge-transfer state (MLCT) around t = 0 fs and damped oscillations, with 126 cm−1 frequency in the HS state due to the activation of the breathing mode. This corresponds to the in-phase stretching of the six FeN bonds with almost rigid ligands [71,107]. XANES studies revealed an important dephasing of the structural dynamics in the MLCT state and coexisting coherent and incoherent structural dynamics accompanying LIESST (Fig. 10). The structural trapping of the photoinduced state in the HS potential is then associated with the activation of the HS breathing mode, whereas its fast damping avoids reversion towards the LS state. These results explain the high quantum efficiency of LIESST. Additional studies confirmed this point and show that INTs shorter than MLCT allow enhancement of the structural coherence in the HS potential [108].
(a) Time scans XANES change at different X-ray energies revealing 126 cm−1 oscillations. Red lines correspond to the global fit using the MLCT lifetime τMLCT = 120 fs, 265 fs oscillation period and 320 fs damping and 1.6 ps vibrational cooling. Orange lines represent the MLCT contributions. (b) Fit for 7121.5 eV (top panel), showing the individual contributions of MLCT and oscillating HS contributions. The model disentangles the electronic kinetic (MLCT and HS population, mid panel) from the structural dynamics given by the time evolution of the FeN distance r (bottom panel). The exponential growth of the HS population from the MLCT INT state leads to an average coherent oscillating trajectory (dark blue). Reprinted with permission from [71].
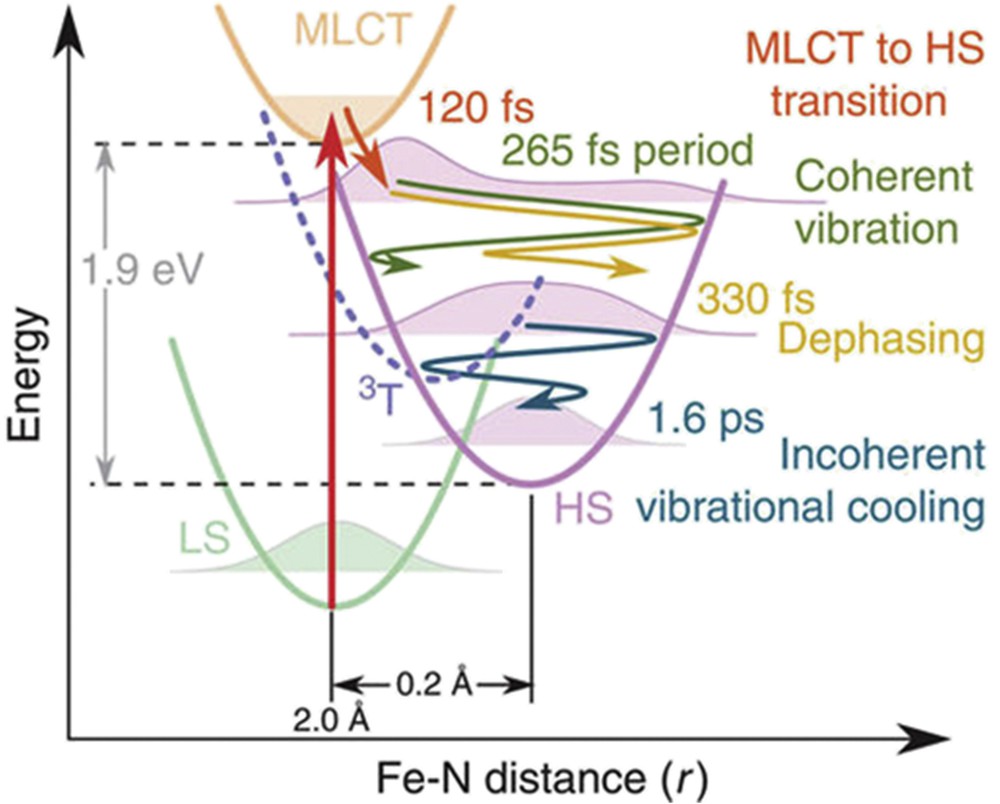
(a) Structural trapping during LIESST from LS to HS states along the FeN distance reaction coordinate r. The photoexcited MLCT decays towards the HS state within 120 fs. r expands and coherently oscillates around the HS equilibrium structure. The wave packet disperses within 330 fs and vibrationally cools in the HS potential within 1.6 ps. Reprinted with permission from [71].
Femtosecond X-ray scattering experiment at the LCLS X-FEL was also performed on photoexcited [CoII(terpy)2]. The scattering data revealed similar structural breathing of the CoN bond length arising from the displacive excitation of a vibrational mode dominated by the symmetrical stretch of all six CoN bonds.
Femtosecond electron diffraction was also used on single crystal to study LIESST dynamics in [Fe(PM-AZA)2(NCS)2] [21], for probing the molecular motions and tracking the ultrafast structural changes within the crystal lattice in comparison to the thermal SCO behaviour [41]. For analyzing the formation of a photoinduced structure, found to be similar to the thermally induced HS state, the time-dependent changes in the intensity of the Bragg reflections were monitored. The global structural reorganization within the unit cell occurs within 2.3 ps, involving FeN bond-length distribution narrowing during intramolecular vibrational cooling. Three independent dynamical groups of the structure were used to model the structural dynamics upon photoinduced SCO, because of the limited number of Bragg peaks measured.
These recent years have witnessed tremendous development of ultrafast structural science with new data acquisition schemes at synchrotrons (slicing, high repetition rate scheme) and the advent of X-FELs [70]. In addition to diffraction, scattering and XANES, these ultrafast X-ray sources have broadened the range of methods, complementary to structural ones, for investigating molecular transformations. The combination of femtosecond resolution X-ray spectroscopies and scattering will be important as it allows simultaneous probing of the electronic and structural dynamics, from the interatomic bond to the global reorganization all along the sample, which is of great importance to go deeper in the analysis of LIESST.
4 Conclusions
This brief overview highlights the important role of structural analyses in the understanding of the spin-state switching of molecular materials. Crystallography allows for precise observation of molecular structures, down to electronic density, and offers a harvest of information at any physical scales in almost all external conditions. In addition to the molecular view of the process, multiscale aspects in space and time are of great importance to understand how materials respond to external stimuli, because of the interaction between molecules mediated by the lattice. The transformation spans from the reorganization of the ion coordination sphere (down to the sub-angstrom length and femtosecond time scales) to the global reorganization of the crystal (up to the centimetre length and second time scales). It is therefore important to combine different types of structural studies, which can provide detailed understanding of symmetry and/or symmetry change, and to combine them with theory to construct relevant models or reveal unusual reorganizations. Because of the paramount impact of structure–property relationships, structural studies are essential for better understanding, controlling and hopefully designing SCO materials.
Acknowledgements
E.C. would like to thank his collaborators H. Cailleau, M. Buron, M. Lorenc, M. Cammarata, R. Bertoni, H. Lemke, S. Koshihara, M. Wulff, K. Moffat, R. Henning and T. Graber in the field of ultrafast X-ray science. He would also like to thank the Institut Universitaire de France, Rennes Métropole, Région Bretagne (CREATE 4146), ANR (ANR-13-BS04-0002) and Europe (FEDER) for constant support. P.G. thanks all ICMCB members of the “molécules et matériaux commutables” group and of the X-ray diffraction centre for the daily fruitful interactions, the Aquitaine Region, the CNRS and the University of Bordeaux for their support. The authors also thank Malcolm Halcrow for the careful reading of this manuscript.