1 Introduction
One of the most important tasks in spin crossover (SCO) research is the physical characterization of transition metal–based molecular systems in their different spin states. The variation in the spin is accompanied by the variation in most microscopic and macroscopic properties, including the electron density of states, magnetic moment, metal–ligand bond lengths, vibrational properties, magnetization, unit cell volume, and so forth. This makes SCO observable by a great many characterization techniques. To study thermal-, pressure-, and light-induced spin-state transitions, appropriate techniques need to be selected to monitor the evolution of the different spin states as a function of the external stimulus. In steady-state experiments usually the dependence of the molar fraction of the high spin (HS) molecules is of interest; however, in ultrafast pump–probe studies intermediate spin states may also be observed in addition to the low spin (LS) and the HS states. In solids, cooperative interactions modify the molecular behavior and may lead to less gradual and more abrupt spin transitions, with possible hysteresis, or even steps. Physical studies need to be conducted to unveil such features, allowing us to understand the mechanism of the spin transitions and the nature of the cooperative interactions. Such a spectroscopic approach not only leads to a better understanding of the SCO process itself but also sets the ground for future applications of SCO materials in, for example, spintronic devices. In this section, we review the applications of vibrational, optical, Mössbauer, nuclear magnetic resonance (NMR), and X-ray spectroscopy techniques in SCO research. This contribution is meant as an overview of the field without going into too much detail and wherever possible we give references to more detailed reviews in the field.
2 Vibrational spectroscopy
A broader review on the application of vibrational spectroscopy to SCO phenomena was published in 2012 [1]. The role of molecular vibrations was also discussed in an exhaustive review by Tuchagues et al. [2] The essential phenomenon followed by this type of spectroscopy is the shift in molecular vibrational frequencies upon switching of the spin state. Typically, the metal–ligand bonds are elongated upon population of the state of higher multiplicity, because of populating of the antibonding eg orbitals of the SCO complex. The result is that the force constants of the metal–ligand vibrations, particularly those having stretching character, decrease, leading to a shift in the corresponding vibrational bands toward lower frequencies. This effect is particularly pronounced for d [6] Fe(II) systems, where all six Fe–ligand bonds undergo an elongation of approximately 0.2 Å (for N-ligands) leading to a shift of up to 200 cm−1 on LS to HS conversion. For octahedral Mn(III) [3,4] and Co(II) [5,6] systems the elongation concerns either two or four of the six metal–ligand bonds, and hence in this case the corresponding changes in the vibrational pattern upon spin switching are less pronounced. For the square-planar (LS)–tetrahedral (HS) isomerism in Co(II), on the other hand, all four metal–ligand bonds are elongated by 0.12–0.15 Å and the infrared (IR) bands shift from the 400–480 cm−1 region to 330–390 cm−1 on LS to HS interconversion [7]. Apart from the metal–ligand stretching vibrations that appear in the far IR area, there are also internal vibrations of the small ligands, typically cyanide and thiocyanate that may be used as spin-state marker bands (vide infra).
2.1 Infrared spectroscopy
With IR spectroscopy solutions and solid samples can be measured, using the transmission, reflection, or attenuated total internal reflection (ATR) techniques. To observe spin marker bands arising from the metal–ligand stretching vibrations, it is necessary to record the spectra in the far IR region (<400 cm−1), which is normally not accessible with conventional IR spectrometers. The earliest results on SCO complexes of Fe(II) revealed a change in the vibrational pattern upon spin switching for Fe(phen)2(NCS)2 (NCS: isothiocyanate) [8] and Fe(III) tris-dithiocarbamate [9], showing that an IR band shifts from 235 to 393.0 and 374.7 cm−1 accompanies the SCO upon LS to HS for the former. In the recent literature, the IR spectra are more often reported in the more readily available 2000–2200 cm−1 range, revealing vibrational band changes of NCS− and CN− ligand modes themselves upon spin transition. A very interesting result has been reported for the Cs[Fe{Cr(CN)6}] complex [10]. Depending on the temperature the bands due to both N and CFe-bonded cyanide were observed for both HS and LS Fe(II). The IR spectra in this region also give a quick and efficient way of monitoring the light-induced excited spin state trapping (LIESST) effect [11].
Apart from “static” experiments, time-dependent IR spectroscopy may give unique information on the dynamics of SCO systems. In a typical experiment, an LS complex solution is excited with an ultrashort laser pulse, and the photoinduced changes are recorded as a function of time [12]. Changes in the IR spectrum can thus be observed with subpicosecond resolution, yielding information on the short-time dynamics of different relaxation processes [13].
2.2 Raman spectroscopy
The availability of Raman and micro-Raman spectrometers makes this technique a versatile method to characterize SCO materials. The advantage compared with IR spectroscopy is that the far-IR region is immediately accessible. Another one is that the need for sample grinding and/or pelletizing for IR transmission studies is avoided in Raman spectroscopy, which can use tiny amounts of samples of basically any form without virtually any sample preparation. However, the relation between the observed spectral changes upon LS–HS switching and the band shifts of the metal–ligand stretching vibrations is less straightforward than in the case of IR and nuclear inelastic scattering (NIS) (vide infra) spectra. The reason is that normally SCO materials do not show exclusively classical nonresonant Raman scattering with a rather low-probability or resonant Raman scattering with some bands having enhanced intensity. Typically, some degree of “preresonance effect” is always present, depending on the wavelength of the exciting laser radiation. In addition, the ultraviolet–visible (UV–vis) absorption pattern changes upon LS–HS transition, the observed characteristic Raman bands (spin marker bands) may not be easily related to metal–ligand stretching modes. A good example is [Fe(ptz)6](BF4)2 for which the LS spin marker bands lie at 300 and 995 cm−1 and disappear upon switching to the HS state [14]. The latter shows a spin marker band at 284 cm−1 only.
Still, the availability of the spin marker bands in the Raman spectra allows the versatile use of Raman spectroscopy in investigations of the SCO systems [1] including the characterization of micro- and nanostructures. Here, we would like to mention the application of Raman microscopy to observe LS and HS domains in a single crystal [15]. Again the vibrations of the coordinated NCS– ligands were monitored. It should also be mentioned that ultrafast time-dependent Raman spectroscopy may give information on the photochemically induced relaxation processes [16].
The advantages as well as the experimental problems and limitations of IR and Raman spectroscopy when applied to SCO materials have been reviewed recently [1]. Here, we would like to draw the attention of the reader to the problem related to the applied laser power when performing Raman experiments. Evidently, too high power (necessary to obtain the intense spectrum quickly) leads to increase in the sample temperature and hence to an apparent shift in the spin transition curve to lower temperatures or even to complete switching of the spin state, particularly when working at temperatures within the hysteresis loop [17]. It is, however, less known that this problem could also occur with the use of Fourier transform infrared spectroscopy, for which a 50–60 K beam-induced sample heating has been recently reported [18].
2.3 Nuclear inelastic scattering (nuclear resonance vibrational spectroscopy)
NIS, also known as nuclear resonance vibrational spectroscopy, is a synchrotron radiation–based technique detecting only those vibrations with nonzero amplitude of the Mössbauer resonant nuclei. Otherwise, there are no other optical selection rules. The basics of this method and its application to SCO systems can be found in, for example, two review articles [19,20].
NIS can be used to observe vibrational modes from a few to ca. 1000 cm−1, with a typical resolution of 8 cm−1 at contemporary third-generation synchrotron sources. Similarly to Mössbauer spectroscopy, measurements on solid samples including oriented single crystals, thin films, nanoparticles, and frozen solutions are possible. In the case of iron-containing molecules the enrichment with 57Fe is usually necessary. Since the first NIS study of the SCO system [Fe(tpa)(NCS)2] [21], NIS has proven to be a very powerful tool to characterize SCO materials [1,19,20,22,23]. Revealing only vibrations involving iron atoms—but all of these, with the exception of the fully symmetric Ag modes in mononuclear complexes—NIS provides a plethora of information on the change in vibrational pattern upon spin transition, often yielding spectra that are simpler to interpret than Raman or IR ones. Typically the change from the HS to the LS Fe(II) state results in the disappearance of several bands clustered at ca. 200–250 cm−1 and the appearance of a better resolved spectral pattern in the area of 350–500 cm−1. Moreover, apart from revealing the molecular vibrations NIS also offers the possibility to access vibrational modes having very low frequencies less than 100 cm−1. From the experimental data the partial density of vibrational states (pDOS) of the iron centers can be obtained. Contrary to Raman and IR spectroscopies, which probe only the modes in the center of the Brillouin zone, NIS probes other than k = 0 modes, as well. In turn from the pDOS it is rather straightforward getting information about thermodynamical parameters (like, e.g., Debye temperature, sound velocity, and mean force constants) relevant to the spin transition [24]. As an example Fig. 1 depicts the pDOS obtained by NIS and corresponding Raman patterns of [Fe(pyrazine)]{Pt(CN)4} nanoparticles [24].
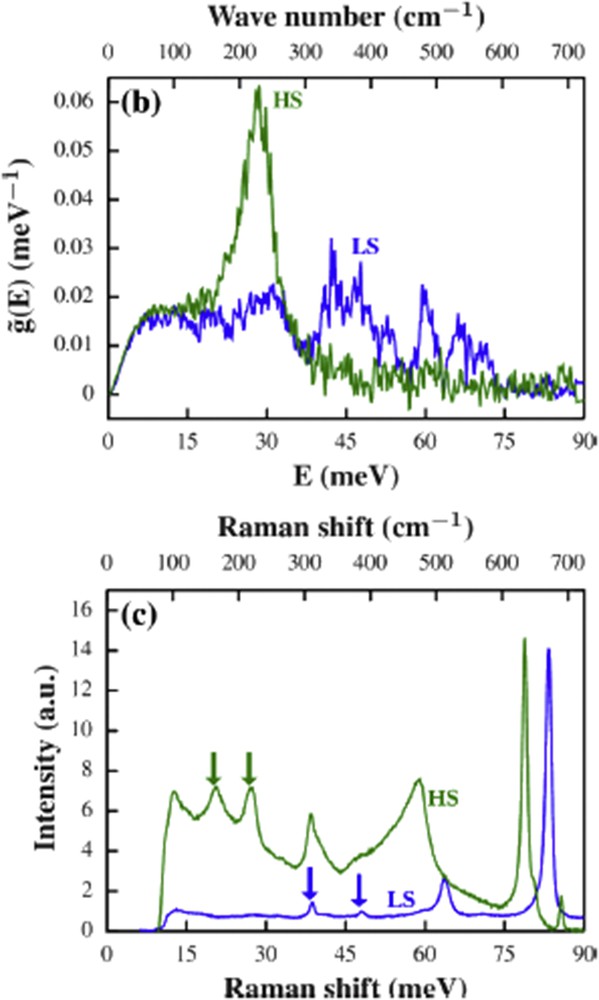
pDOS of [Fe(pyrazine)]{Pt(CN)4} nanoparticles in the HS (green) and the LS (blue) state (a) and the corresponding Raman spectra (b) [24].
2.4 Density functional theory calculations and vibrational entropy
The interpretation of the vibrational band patterns obtained by any of the aforementioned methods can be supported by quantum chemistry calculations. Density functional theory (DFT) is very reliable in predicting both the molecular geometry and the frequencies of the molecular vibrational modes [25,26]. With current DFT methods it is possible to calculate all vibrations of a given molecule with an accuracy of 20–30 cm−1 [1]. Therefore, it is usually possible to assign experimentally observed spin-state marker bands to specific vibrational modes. Both IR spectra and pDOS derived from NIS are in principle well reproduced with DFT methods. The same holds for the vibrational frequencies observed in Raman spectra. However, the calculation of Raman intensities is a much more complicated issue (cf. Ref. [1] and references therein). Apart from frequencies, the important parameters that could be derived from DFT normal coordinates analysis are the zero-point correction and total vibrational energy, as well as the vibrational contribution to the entropy. The latter is also available on the basis of the experimental data [2,27]. Typically, DFT calculations are performed for isolated molecules in vacuum, leading to obvious neglecting/inaccuracy of soft vibrations that significantly contribute to the entropy. The solid-state calculations that have recently been shown to predict the energetics of the spin transition very effectively [28] are still far from being a standard procedure, despite the evident success for small molecules [29]. First, the computational time is quite long, even for simple geometry optimization. Second, it is even longer for vibrational calculations and its accuracy is limited, particularly for the soft transitions, cf. the results obtained for Fe[(phen)2(NCS)2] complex [30]. In our opinion, this sort of method will become more mature in the near future, completed with the approaches based on molecular dynamics [26] that were recently shown to elucidate the partial density of states in SCO systems [31]. Nevertheless, we want to emphasize that the most powerful method of bands assignment is still the classical isotope substitution, as demonstrated in the classical article by Takemoto and Hutchinson [32].
3 Optical spectroscopy
The LS–HS transition is related to the change in the electronic ground state and as such causes the change in spectral properties observed with optical spectroscopy. Although it is hardly a rule, SCO systems quite often show a change in color upon spin transition, which makes them interesting materials for temperature, pressure, and solvent sensors [33]. Within terms of ligand-field theory the spin switching corresponds to a shift along the 10Dq/B axis of the Tanabe–Sugano diagram. On the other hand, the maxima of absorption bands correspond to vertical transitions in these diagrams [34]. What actually changes is the ligand-field strength that decreases with elongation of the metal–ligand bonds upon the LS–HS transition [34]. The 10DqLS/10DqHS value is equal to (rHS/rLS)n, where r denotes the corresponding metal–ligand bond length and n = 5–6, so in a typical case of Fe(II) (rHS =2.2 Å, rHL =2.0 Å) 10DqLS amounts to 1.75 of 10DqHS. Both fundamental values, 10Dq and B (that barely changes on spin transition), could be derived from optical absorption spectra of single crystals. Hauser [34,35] elucidated these for the classical system [Fe(ptz)6](BF4)2, obtaining the values of 10DqLS, 10DqHS, and B to be 19,410, 11,800, and 740 cm−1, respectively.
Similarly to vibrational spectroscopy, optical spectroscopy may be used to follow the SCO processes in solution, in the solid state using transmission and/or reflection techniques, in thin films, and in nanoparticles. Being a fast method, it is commonly used to follow the fast and ultrafast photoinduced relaxation processes in SCO complexes [12] following the approach introduced by McGarvey and co-workers [36]. Apart from solution studies the corresponding HS–LS relaxation can be measured in single crystals. Spectacular results have been presented few years ago by Krivokapic et al. [37] They showed that the intersystem crossing rate of the photoinduced (reverse LIESST) LS state (relaxing back to a HS ground state) is extremely dependent on temperature, varying by 14 orders of magnitude between 40 and 225 K for dilute [FexZn1−x(bbtr)3](ClO4)2, x = 0.02 (bbtr = 1,4-di(1,2,3-triazol-1-yl)butane). For the powder sample the time-resolved reflectivity was measured for [Fe(NH2-trz)3](Br)2∙3H2O following the laser excitation [38].
The emerging field of luminescent SCO materials [39] brings about the use of emission spectroscopy. In a typical experiment the SCO complex modified with a fluorescent moiety (organic or f-electron metal) is irradiated by light and the fluorescence as a function of temperature (and hence spin state of the crossover center) is measured.
Introducing chirality (or a chiral center) to SCO complexes/materials allows the use of circular dichroism (CD) spectroscopy. Although examples of such results are rather scarce, it is worth to mention the results of Guralskiy et al. [40] who demonstrated a memory effect of the chiro-optical properties associated with the hysteresis of the spin transition.
Generally speaking, the ability of standard DFT methods predicting the electronic spectra does not match the quality of calculating the geometry and vibrational frequency. Yet time-dependent DFT, being a standard procedure to date, is offered by common quantum chemistry software. Time-dependent DFT is mature enough to provide a reasonable estimate of the electronic structure and the UV–vis spectra of SCO complexes [25,41–43]. For more precise calculations ab initio methods are advocated [25].
4 NMR and Mössbauer spectroscopy
4.1 NMR spectroscopy
NMR spectra of complexes showing spin switching in solution are necessarily the ones of the paramagnetic molecules and as such differ significantly from a typical NMR pattern of diamagnetic molecules. The chemical 1H shifts can be up to 1 order of magnitude larger, and typically no spin–spin couplings can be observed. Typically the HS–LS solution interconversion rates are fast on the NMR time scale, the exception being some Ni(II) complexes, revealing the square-planar–tetrahedral equilibria [44]. Therefore, typically the averaged spectra are observed unless the temperature corresponds to molar fraction of LS to be 1 or 0. Still, the complexes revealing spin equilibria were one of the first measured as the technique of paramagnetic NMR developed. It is 51 years ago when Evertett and Holm characterized the planar (LS)–tetrahedral (HS) Co(II) and Ni (II) four-coordinate complexes [45], determining the thermodynamic parameters of their interconversion by means of measuring the magnetic susceptibility in solution using the Evans method [46]. Later the octahedral Fe(III) dithiocarbamate SCO system has been characterized [47]. Since that time the essential results derived from NMR spectra for spin switching in solution remain the same: magnetic susceptibility obtained by the Evans or the more modern ideal solution model [48] and the declination of the temperature dependence of the isotropic shifts from Curie-behavior as a criterion for spin equilibria in solution. Quite recently Hogue et al. [49] proposed the improved method of measuring the magnetic susceptibility with NMR based on the analysis of the spectra of SCO systems and their diamagnetic zinc analogue. All of these possibilities are convincingly presented in Ref. [50], the illustrative results of which are shown in Fig. 2. A very new result for kinetically robust Fe(II) complexes has been presented, showing for the first time that the thermodynamics and kinetics for SCO can be deduced by using variable temperature 1H NMR spectroscopy [51]. Examples of the applications of two-dimensional (2D) NMR techniques are given in Ref. [52].
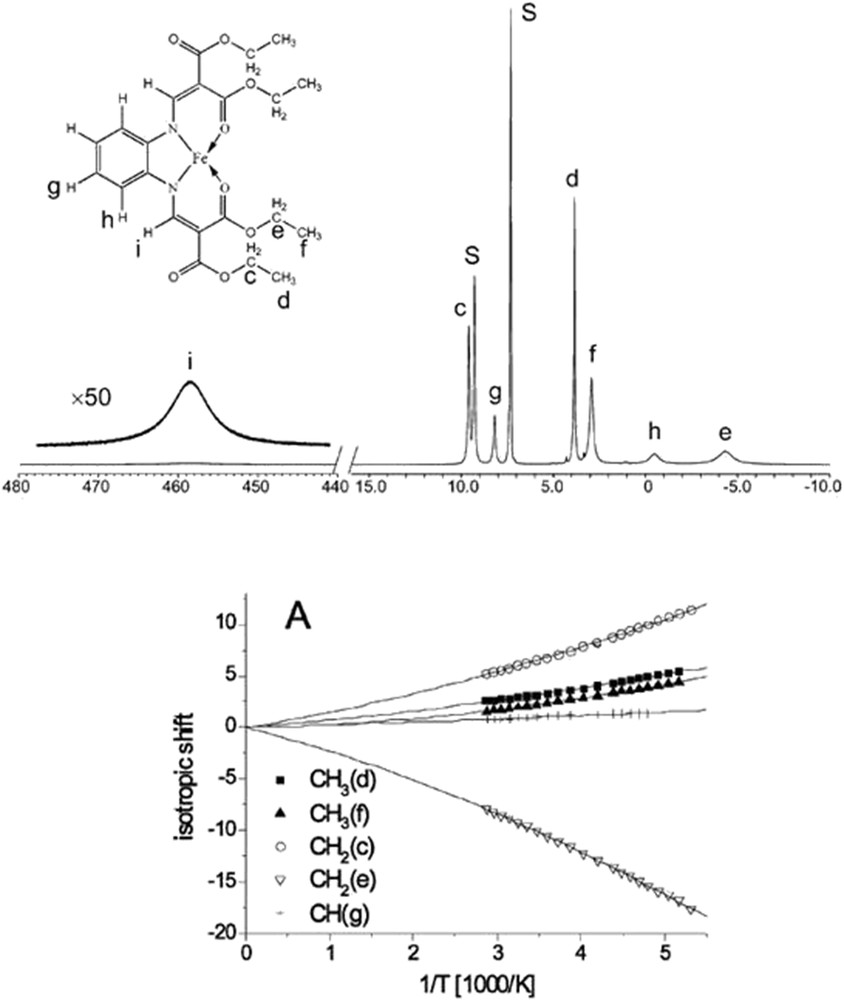
1H NMR spectrum of [FeL1(OEt/COOEt)(py)2] in a pyridine at 55 °C. The signal assignment is given at the left. S denotes the solvent pyridine (top) and the isotropic shift of signals of selected protons (bottom). Reprinted with permission from Ref. [50].
4.2 Mössbauer spectroscopy
Although NIS is based on events where during a nuclear resonant absorption process vibrations are created or annihilated due to the recoil of the absorbing nucleus, recoil-free events (when the solid takes up the momentum of the γ-quantum) are registered when collecting Mössbauer spectra. With this method, it is possible to obtain the magnitude and the asymmetry of the electron density as well as the magnetic field at the corresponding Mössbauer nuclei. The application of 57Fe Mössbauer spectroscopy to SCO research was pioneered by Gütlich and has been one of the most powerful quantitative probes of the spin state because of its sensitivity to the distribution of the 3d electrons in iron compounds. The variation upon LS to HS transition in the electron density and the oxidation state of the iron ions is reflected in a change of the isomer shift. Changes in the asymmetry of the electron cloud can be detected by variations in the quadrupole splitting. One should keep in mind although that the differences in the Lamb–Mössbauer factor for the different spin states have to be taken into account for a quantitative phase analysis.
Until recently energy-domain Mössbauer spectroscopy depends on radioactive sources emitting noncoherent γ-radiation. However, since the mid-1990s, synchrotron-based energy-domain Mössbauer spectroscopy has become available [53,54], enabling the utilization of the many superior properties of synchrotron radiation to laboratory sources, such as polarization, microsize focus, higher brilliance, and so forth.
The basics of conventional Mössbauer spectroscopy are described extensively in reviews including Refs. [55–57]. Therefore, we only focus here on the synchrotron equivalent of this technique, which is termed as nuclear forward scattering (NFS).
4.3 Nuclear forward scattering
NFS is a spectroscopic technique in which the coherent nuclear re-emission of radiation in the forward direction is measured after excitation of the Mössbauer transitions by synchrotron radiation [58]. The result of the NFS measurement is a spectrum showing the time dependence of the intensity of the re-emitted radiation within the time window of the synchrotron pulse interval (typically a few tens to a few hundreds of nanoseconds). The superposition of the quanta emitted coherently from the different hyperfine-split nuclear levels leads to quantum beats in the temporal evolution of the decay. Therefore, the so obtained time pattern contains information on the hyperfine interactions that can be derived with the appropriate scripts [59]. For a typical SCO Fe(II) system the HS state spectrum due to the high quadrupole splitting of the HS iron exhibits a high frequency “beating” pattern, which is absent for the LS state because the quadrupole splitting of LS iron is approximately zero [60]. As an example temperature-dependent NFS spectra of a Fe(II) SCO system are shown in Fig. 3. Applications of NFS for the study of SCO complexes were reviewed exhaustively by Paulsen et al. [19] Owing to the high-brilliance of synchrotron radiation this technique could also be used for very small objects like nanostructures [61] or thin and ultrathin films [62]. Also, the application of NFS to study the SCO behavior of microstructures of polymeric 1D Fe(II) chains based on aminotriazole ligand has been shown [63].
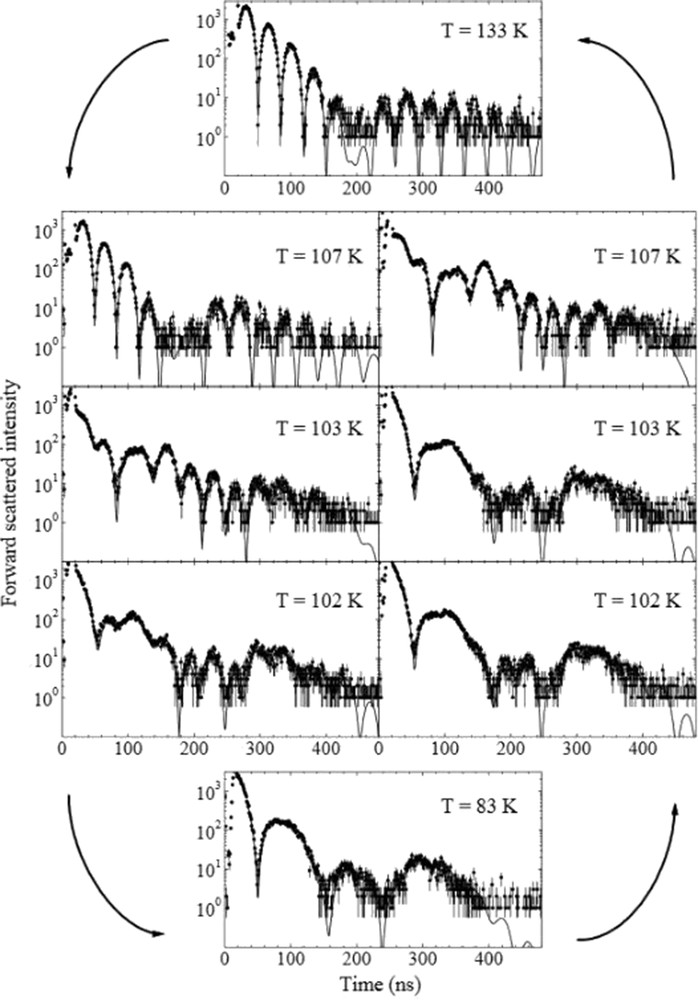
Time evolution of the NFS intensity for [Fe(tpa)(NCS)2] at various temperatures (reprinted with permission from Ref. [60]) The solid lines are results of simulations. Note the hysteretic behavior of the complex. The spectrum taken at 133 K shows a typical pattern for HS Fe(II), illustrating the fact that the higher the quadrupole splitting the higher the frequency of the observed quantum beats.
The theoretical modeling of Mössbauer parameters became relatively accurate with DFT, often reaching quantitative levels of prediction. Most functionals can easily reproduce the isomer shift using core-polarized or real Slater-type basis sets. Strategies to calculate accurate quadrupole splittings have also been developed [64–67].
5 X-ray spectroscopy
X-ray spectroscopy encompasses a range of techniques where spectroscopic information is gained from a process in which a core hole is created by an X-ray photon. Such techniques can provide unique insight into the electronic and molecular structure, often combined with element-, spin-, orbital-, and orientational sensitivity [68–70]. For SCO systems, the unambiguous identification of the spin and oxidation states often calls for X-ray spectroscopy techniques, in particular, in the case of heteronuclear systems or charge transfer systems (e.g., Prussian-Blue analogues).
For transition metal complexes, the absorbing atom is typically the metal center, but in principle the donor atom of the ligand can also be probed.
X-ray photon energies are classified as soft (<1 keV), tender (1–5 keV), and hard (>5 keV). The softer energy usually implies smaller natural line widths [71] and also smaller penetration depths. The hard X-ray–based techniques probe the bulk properties of the matter and are even compatible with sample environments needed for extreme conditions because of the large penetration power [72]. Most of these techniques have low cross-sections; therefore, they are usually performed with intense monochromatic beams at large-scale X-ray infrastructures, typically synchrotron radiation facilities.
The most common of these techniques—X-ray absorption spectroscopy (XAS) with its variants X-ray absorption near edge structure (XANES, but the name near-edge X-ray absorption fine structure is also used for soft X-rays) and extended X-ray absorption fine structure (EXAFS)—have proven their utility in determining the unoccupied electron states and the local structure around the absorbing atom, respectively [73–77]. X-ray emission spectroscopy (XES) and resonant inelastic X-ray scattering (RIXS) are very powerful in elucidating the electron structure, providing information on the electron energies, local geometry, spin, and charge states [68,78–85]. Further techniques based on the inelastic scattering of X-rays [86,87] are seldom used in spin-state studies and will not be covered in this review. X-ray photoemission spectroscopy, which provides invaluable information on the occupied electron states, is beyond the scope of this article, albeit it is more and more often used to study SCO films [88,89].
In addition to steady-state measurements, these tools can also deliver information complementary to ultrafast laser spectroscopies when implemented in a pump–probe experiment with laser excitation (pump) followed by an X-ray probe pulse at chosen time delays between them [90–93].
In what follows, we very briefly introduce some aspects of X-ray spectroscopy by directing the reader to a few articles that used such techniques to follow spin-state variations. Later, we will list up selected recent applications, in particular studies that present some novel aspects.
5.1 X-ray absorption spectroscopy
X-ray absorption is the most conventional X-ray spectroscopy technique. During the X-ray absorption process, a core electron is excited into unoccupied bound states or to the continuum. It is usually implemented by scanning the X-ray energy through an absorption edge, recording the transmitted X-ray intensity. Secondary processes can also be used for detection, measuring the (total or partial) fluorescence or electron yield upon the core hole creation. The spectra are dominated by dipole transitions; however, the 2 orders of magnitude weaker quadrupole transitions can also be very informative [77,94,95]. The absorption cross-sections can also reveal information about the characteristic directions of the local magnetic moments or the inhomogeneous charge distribution in oriented samples, from the anisotropy that depends on the principal axes in the sample and the respective directions of the orientation and polarization of the X-ray beam [73]. The most important of these are X-ray magnetic CD, which is often used to image the magnetic domain structure or to determine the spin and the total angular momentum, and X-ray linear dichroism, which can be used as a “search light” to explore the spatial orientation of the unoccupied orbitals [96].
To illustrate the applications of XAS, we take the [Fe(phen)2(NCS)2] archetype SCO system as an example, where XANES for both L2,3 and the K was performed on the iron by Briois et al. [97], well below and above the SCO temperature. The L2,3-edge is due to 3d ← 2p transitions, thus it is directly sensitive to the populations of the Fe 3d orbitals, making it an excellent probe of the spin state, and it has indeed been used to resolve spin-state–related problems [98–100]. The lifetime broadening of the Fe 2p orbitals is 0.37 eV [71], which allows us to resolve the fine structure of the spectra. The L-edge spectra can also be rather accurately modeled with ligand-field multiplet calculations, which allowed the extraction of the relevant ligand-field parameters for [Fe(phen)2(NCS)2] [97]. However, the 700 eV X-rays are easily absorbed before reaching the probed atoms (only 33% passes through 1 mm air), which might often lead to experimental challenges related to vacuum, sample surface, and sample environment.
With X-ray energy of 7.1 keV at the iron K-edge, the requirements on the sample environment are more relaxed (85% of the radiation is transmitted in 10 cm air). The main K-edge stems from the excitation of the 1s electron to 4p and higher p-type orbitals; therefore, even in the XANES region it mostly reflects the consequences of the changes in the molecular structure, as it has been convincingly shown for [Fe(phen)2(NCS)2] [97]. The EXAFS region reflects the energy-dependent interference of the photoelectron that is scattered back from the atoms around the iron, thus it is sensitive to the atomic number, the coordination number, and the distance of the coordination shells, making it a sensitive probe of the local atomic structure. Indeed, for [Fe(phen)2(NCS)2] and other SCO complexes it was shown that the increase in the metal–ligand bond lengths upon population of the antibonding eg∗ orbitals can be quantified with confidence [101]. This direct structural determination does not require samples with long-range order, not even solid phase. In the so-called pre-edge region small peaks arise from 3d ← 1s quadrupole transitions in an octahedral environment; lowering the symmetry gives rise to p–d mixing, which lends intensity to these features. The pre-edge region is again directly sensitive to the 3d populations, thus to the spin state; however, the small intensity and the enhanced lifetime broadening (∼1.3 eV for Fe 1s) [71] makes it poorly resolved [94].
5.2 X-ray emission spectroscopy
The sensitivity of XES to the spin state has long been known [102]; however, it was rarely used to follow spin-state transitions [103]. The first of such experiments were motivated by high-pressure research [104–106]. The main X-ray emission lines are made up of radiative transitions when electrons from a higher core orbital fill deeper core holes created in an ionization process. The spin-state sensitivity arises from the final state of this emission process, in which a remaining unpaired core hole electron engages in exchange interaction with the unpaired 3d electrons. The fine structure of the spectrum is resolved with a crystal spectrometer.
The spectral variations in the Fe 1s XES spectra upon spin-state transitions are illustrated again in the example of [Fe(phen)2(NCS)2] in Fig. 4, replotted using data from Ref. [79]. The spin–orbit split Kα spectrum (1s ← 2p3/2, 1s ← 2p1/2) shows only an apparent increase in the line broadening at the transition, because the relevant 2p–3d exchange interaction is small in this case, around 1–2 eV [68,79,107]. Nevertheless, the spectral differences are large, and therefore at experiments with very low count rates the Kα spectra can be the first choice to probe the spin state [91,107,108]. Because of the large spatial overlap of the 3p and 3d electrons, the 3p–3d exchange is relatively large (∼15 eV for Fe(II)), the corresponding exchange splitting in the Kβ spectra (1s ← 3p) results in the appearance of a low-energy satellite to the main line, Kβ′, whose intensity is correlated with the atomic spin density [102,107,109]. As the spectra is easier to interpret because of their richer structure, this spectral line is often preferred to the Kα.
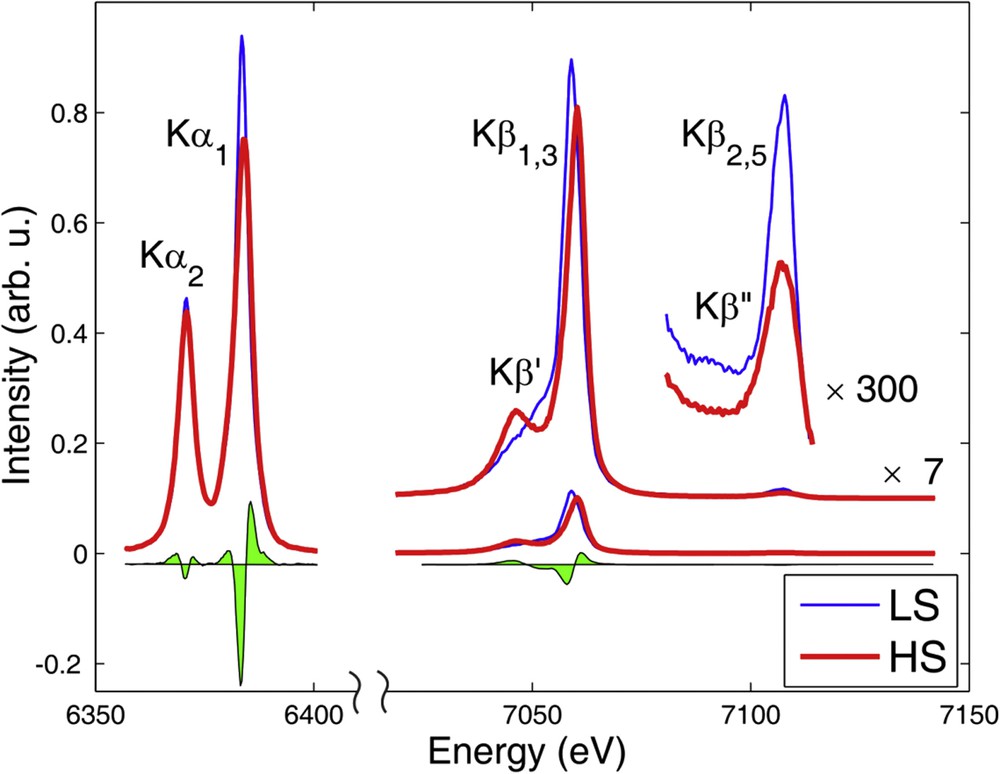
Full Fe 1s XES of [Fe(phen)2(NCS)2] in the HS and LS state, the green filled area shows their spectral difference. Adapted with permission from Ref. [79].
With probability 2–3 orders of magnitude smaller than the main emission lines, the core hole can also be filled by a valence electron. The X-rays emitted in this transition give rise to the so-called valence-to-core XES (vtc-XES) spectrum. The final states of this process are practically the same as those of the photoemission process, thus the resulting spectral information is rather similar. This also implies that high chemical sensitivity can be achieved with vtc-XES. Furthermore, the spectral features are not only characteristic for the metal, but also show high sensitivity to the nature of the ligand [81,110–116]. What makes it a particularly powerful probe is that the theory-based understanding and assignment of the spectral lines are well developed and rather reliable. The one-electron description provides a good framework for the interpretation of the vtc-XES spectra; thus, with a good quality calculation of the ground state occupied electron density of states and the transition probabilities the spectrum can be reproduced rather satisfactorily, and the molecular orbitals relevant to the transitions can be identified [81,111,113]. Unlike the core-to-core transitions, vtc-XES is not sensitive to the spin moment, but is largely influenced by the nature and the strengths of the chemical bonds. Fig. 4 shows an intensity drop in this region for the HS state. Actually, the spectral regions Kβ2,5 and Kβ″ stem from transitions from molecular orbitals that involve the N 2p and N 2s atomic orbitals of the ligands, respectively [110]. The disappearance of the Kβ″ feature and the decreased Kβ2,5 intensity is thus easily explained by the decrease in the overlap of the Fe 1s orbital with the ligand orbitals because of the elongated FeN bond lengths.
5.3 Other techniques based on inelastic X-ray scattering
Combining X-ray absorption and X-ray emission leads to resonant XES (RXES). In such an experiment, we explore the intensity of the emitted X-rays over a 2D plane spanned by the incident X-ray energy and the energy transferred to the system (the latter being the difference between the energies of the incident and the emitted X-rays). This is particularly useful to better reveal the usually weak, overlapping, and smeared X-ray absorption pre-edges. However, one often takes only special 1D cross-sections of the full RXES plane. One of them is the constant emission energy scan, when the energy of the incident X-rays is scanned, instead of taking the full emission spectrum the XES spectrometer is used as a detector with a very narrow energy bandwidth, and only the intensity at a single selected emission energy is recorded through a crystal spectrometer. Using the spectrometer in this mode will result in an absorption spectrum that has the core hole lifetime-broadening partly removed [117]. This technique, when detected at a main emission peak, is called high-energy resolution fluorescence detected (HERFD) XAS, and it allows us to record a spectrum with better energy resolution and improved signal-to-noise ratio [68,118,119]. Practically, HERFD, a constant emission energy scan, produces a diagonal cross-section of the RXES plane. It is important to keep in mind for the correct interpretation that HERFD-XANES might show an apparently richer structure than the actual XANES if different RXES final states, which belong to some of the resonances, produce apparent extra peak(s) in the spectrum [119,120]. HERFD can also be performed to obtain spectra that belong to different final states by selecting the appropriate different emission energies. It is well known that the final states of the main Kβ1,3 emission peak and its low-energy Kβ′ satellite stem from different multiplicities, which allows us to distinguish “spin up” and “spin down” excitations. Therefore, when the majority and minority spin density is different, the HERFD-XAS measured through these two spin-sensitive channels will be markedly different [119,121–123]. Another interesting cross-section of the RXES plane is taken at constant incident energies, which means recording the XES spectrum at a single selected incident energy. When the incident energy is tuned to the excitonic pre-edges, it helps to unveil the final states of the RXES process, which are similar to the final states of the corresponding soft X-ray absorption edges [68]. However, taking the XES with the incident energy not far below the absorption resonances gives rise to another technique, called high-energy resolution off-resonant spectroscopy for X-ray absorption [124]. This constant incident energy cross-section of the RXES plane practically uses the lifetime-broadening tails of the absorption lines, and it allows us to reconstruct the XANES spectrum from this special XES using the Kramers–Heisenberg formula, which describes the cross-section for the RXES process [124–126]. This technique is best performed with the dispersive von Hámos spectrometers, which do not require scanning, and it is particularly useful for X-ray free electron laser (XFEL) experiments, where the incident energy cannot be changed rapidly [127].
Finally, if we take the aforementioned setup, a monochromator on a powerful X-ray source producing an intense monochromatic beam with tunable energy and a spectrometer equipped with an appropriate analyzer crystal that resolves the energy of the photons leaving the sample, and construct it in a way so that the spectrometer can be rotated around the sample, then we are left with a triple-axis spectrometer, which allows us to take spectra while controlling both the energy transfer (with the monochromator and analyzer) and the momentum transfer (via the scattering angle chosen by the spectrometer) to the sample. This can still be used choosing the incident energy at around an absorption edge, in which case it is called RIXS [69,70], or it can also be performed at energies far from the core transitions. In the latter, we lose the element specificity, and it can be considered as a photon energy loss spectroscopy technique, which is called non-RIXS [86]. Non-RIXS can determine the dynamical structure factor, resolving collective excitations (phonons, plasmons) as well as local valence [128,129] or core excitations. The latter is often called X-ray Raman scattering, and it allows us to measure soft X-ray absorption cross-sections with hard X-rays [86,130–132]. Nyrow et al. have already applied X-ray Raman scattering to follow the pressure-induced HS to LS spin-state transition of Fe(II) in FeS through a diamond anvil cell, scattering 19.4 keV X-rays to record the variation in the spectra at 50–80 eV energy transfer that corresponds to the iron M2,3-edge [133].
6 Recent applications
In the following sections the results obtained in the past 7 years are briefly surveyed, without making any attempt at completeness.
6.1 IR and Raman spectroscopy
Seifried et al. [134] presented the mid infrared (MIR) and far infrared (FIR) spectra for propargyl-tetrazole complexes of Fe(II) (Fe(L)6X2, X = ClO4−, BF4−). The LS state of the tetrafluoroborate salt reveals a broad marker band centered at 467 cm−1, whereas the HS marker band occurs at 267 cm−1. Gerasimova et al. [135] performed an in-depth DFT analysis of normal vibrations for the trinuclear Fe(II) complex of the 4-propyl-1,2,4-triazole ligand, assigning the observed MIR bands to particular modes in different spin states. Polarized Raman scattering studies of powder and single crystals of polymeric 1D [Fe(NH2trz)3](X)2∙nH2O were performed and the DFT normal coordinate analysis for the model trimeric system was presented [136]. Durand et al. [137] studied the temperature-dependent MIR behavior of a SCO silica nanocomposite based on the classical 1D chain [Fe(trzH)2(trz)](BF4)2 complex. Photoswitching of this material under continuous laser irradiation in a Raman scattering experiment was also investigated [17]. Its microcrystals embedded in a bacterial cellulose biofilm were characterized with temperature-dependent Raman spectroscopy [138]. Similarly, Raman spectroscopy was used to characterize its composite upon dispersion in a PMMA matrix [139] and photothermal plasmonic effects in SiO2–gold nanocomposites [140]. MIR and Raman spectroscopy were used to characterize the cellulose–SCO particle composite papers with reverse printing performance, based on the aforementioned and analogous systems [141]. The 1D chain system containing the 4-N-alanylo–substiuted triazoles was studied using temperature-dependent Raman and IR spectroscopies, revealing IR marker bands in the 840–920 cm−1 region, whereas DFT calculations yielded the assignment of the observed bands [142]. Microrod particles of the related [Fe(Htrz)3](CF3SO3)2 have been characterized with temperature-dependent Raman spectroscopy [143]. SCO behavior of arrays of gold nanoparticles covered with [Fe(AcSBPP)2](ClO4)2, (AcSBPP = (S)-(4-{[2,6-(dipyrazol-1-yl)pyrid-4-yl]ethynyl}phenyl)ethanethioate) was studied by means of Raman spectroscopy supported by DFT calculations [144]. Temperature-dependent IR (2000–2200 cm−1) and Raman spectra were measured to characterize the fluorescent SCO [Fe(L)2(NCS)2] and [Fe(L)2(NCSe)2] complexes (L = naphthyl derivative of pyridyltriazole). Similarly, Raman bands due to thiocyanate CN stretch were used to monitor the temperature-dependent behavior of lipophically substituted [Fe(II)(padpt)2(SCN)2] and [Fe(II) (hpdpt)2(SCN)2] [145,146]. Matar et al. [147] published the far IR spectra and DFT frequency calculations for another classical SCO complex [Fe(PM-BiA)2(NCS)2]. Naggert et al. [148] used MIR and temperature-dependent Raman spectroscopy to characterize the thin films deposited from the gas phase of a sublimable Fe(II) complex based on the dipyrazolylborate ligand. The thin films of the related Fe(HB(triazolyl)3)2 complex were characterized with Raman spectroscopy [149]. Gros et al. [150] used ATR Fourier transform infrared to characterize the layered structure of a heterostructure containing an SCO Fe(II) Hoffman-like complex and Prussian-Blue analogue. Rupp et al. [151] investigated the ultrafast SCO in Co(II) semiquinonate radical complex using picosecond time-resolved solid-state ATR spectra and femtosecond time-resolved MIR spectra in MeCN solution. Temperature-dependent Raman studies of single crystals of a nonanuclear Fe(II)/Fe(III) SCO complex have been performed to elucidated the spin and oxidation states [152]. ATR spectra were also used to characterize [Fe(pyrazine){Ag(CN)2}2] and its solvate [153] and Fe(HB(pyrazolyl)3)2 in closed nanoconfinement of an NH2-MIL-101(Al) MOFmetal–organic framework [154]. Temperature- and pressure-dependent Raman measurements were performed for the [Fe(H4L)2](ClO4)2·H2O·2(CH3)2CO complex (H4L = 2,6-bis(5-(2-hydroxyphenyl)pyrazol-3-yl)pyridine) under a variety of conditions [155]. A similar approach was used for [FeL12](ClO4)2 (L1 = 2,6-bis{3-methylpyrazol-1-yl}-pyrazine) [156]. Resonance Raman studies revealed the reversible switching between HS and LS states of myoglobin heme FeONO/2-nitrovinyl species [157]. Raman spectroscopy supported by DFT calculations was used to explain the effects of coherent structural vibrations observed in femtosecond studies of spin switching dynamics in [Fe(III)(3-MeO-SalEen)2]PF6 [158]. The solvatochromic spin-state switching in an SCO compound based on a Fe(II) complex and the simultaneous change in spectroscopic properties for selective multimodal sensing of methanol and ethanol was followed with Raman spectroscopy [159]. The same system was shown to reveal different structures with different SCO properties, depending on the surface it was deposited on. Micro-Raman spectrometry, allowing measurement with a spatial resolution less than 1.5 μm was used in this study [160]. An usual SCO behavior was found in a tetrahedral Fe(II) complex with P3X coordination, the IR spectra revealing that the ν(NP) band at 1207 cm−1 is a spin marker band of the HS isomer [161].
6.2 Nuclear inelastic scattering
Li et al. [162] reported the SCO behavior of five-coordinate cyano-(tetraphenylporphyrinato)iron(II), [Fe(TPP)(CN)]−, using oriented single crystal inelastic scattering and DFT calculations. It was shown that the availability of the entire iron vibrational spectrum allows the complete correlation of the modes between the two spin states. In a previously mentioned study [24], NIS was measured for nanoparticles of the SCO Hoffman-type complex [Fe(pyz){Pt(CN)4}] showing the spin marker bands and yielding the lattice dynamic parameters. The [Ni(CN)4] analogue of the aforementioned complex has been also investigated along the same line with molecular dynamics simulation of the DOS and pDOS [31]. A combined Raman and NIS study of [Fe(H2B(pz)2)2(phen)] (pz = pyrazolyl, phen = 1,10-phenanthroline) again yielded the Debye temperature, sound velocity, and the Young modulus for HS and LS isomers. NIS experiments confirmed the gradual spin transition behavior of a 2 × 2 grid Fe(II) complex [163]. Two luminescent Fe(II) SCO complexes, a trinuclear FePt2 [164] and a dinuclear Fe2 one [165], were also characterized by temperature-dependent NIS. The pDOS was calculated with DFT, yielding the normal vibrations of these molecules. A similar investigation has been performed for a dinuclear Fe(II) system displaying an LS–HS to HS–HS spin transition [166]. NIS experiments on [57Fe(atrz)3(CH3SO3)2] and a corresponding compound with Fe(II) partially replaced by Zn(II) yielded significant differences in the pDOS of the LS centers. DFT calculations imply that this effect was related to the fact that an LS Fe(II) center feels structural changes of its neighbors when the latter undergo spin changes from HS to LS and vice versa. The triazole analogue of the aforementioned 1D chain, Fe(trzH)2(trz−) (BF4)2, was also studied along the same lines [167].
6.3 Optical spectroscopy
Only the less standard use of UV–vis spectroscopy will be mentioned here. Fast and ultrafast time-dependent UV–vis spectroscopy was used together with X-ray–based methods to characterize the photoinduced kinetics in the classic [Fe(phen)2(NCS)2] [168]. Using transient absorption spectroscopy with a time resolution of less than 60 fs in the UV range and less than 40 fs in the visible range, it was recently possible to show that the HS quintet state in [Fe(bipy)3]+2 in solution is populated in less than 50 fs after the laser pulse excitation of the singlet ground state [169]. Solid-state femtosecond transient absorption study of the same system showed that the lifetime of the HS state is much shorter (100 ps) than in solution [170]. The optical spectra of thin films of SCO systems have been measured [148]. Gels containing the 1D polymeric aminotriazole complexes of Fe(II) were characterized by UV spectroscopy [171], as well as the cellulose–SCO particle composite paper material [141] and PMMA dispersions of [Fe(trzH)2(trz−)](BF4)2 obtained as reflectance spectra [139]. Thermal evolution of the diffuse absorbance spectra following the thermally induced SCO and the LIESST effect was studied for the Hoffman-type complexes [172]. A similar approach was applied to novel 2D SCO framework materials [173]. Synergetic SCO and fluorescence in 1D hybrid Fe(II) complexes based on aminotriazole derivative ligands were also studied [174]. Fluorescence in heterobimetallic systems, namely, in a trinuclear FePt2 complex [164] and in Tb-nanocomposites containing a 1D triazole polymeric complex of Fe(II) [175] was investigated. Correlations between SCO and fluorescence in a dinuclear compound of Fe(II) [176] as well as photoluminenscence of a mononuclear Fe(II) SCO complex were reported [177]. Also, the fluorescence properties of the previously mentioned [146] Fe(pyridyltriazole)2(NC(S/Se))2 were investigated. A bis(2,6-bis(1H-pyrazol-3-yl)pyridine)iron(II) SCO complex was characterized with UV spectroscopy in solution and as composite materials encapsulated in a zeolite matrix [178]. The unusual SCO effect in a tetrahedral Fe(II) complex was also monitored with UV–vis spectroscopy [161]. Last but not least, the use of CD spectroscopy to SCO materials should be mentioned [40,179,180].
6.4 NMR spectroscopy
Both kinetic and thermodynamic parameters of the SCO process were determined by 1H NMR [51]. pH- and T-dependent 1H NMR spectra of [Fe(bipy)3]Cl2 in D2O were obtained, indicative of a proton-driven coordination-induced spin-state switch [178]. NMR was also used to establish the stability of a dinuclear SCO Fe(II) supramolecular helicate in solution [181]. Non-Curie behavior and magnetic susceptibility measurements in solution revealed the spin switching of Fe(III) porphyrin pyridine N-oxide derivative diadducts [182]. The same approach was used for the aforementioned SCO behavior in a tetrahedral Fe(II) complex [161]. An NMR study of the LS to HS transformation of a Fe(II)4 cage has been performed [183]. The solution behavior of a series of iron(II) complexes of 2,6-bis(oxazolinyl)pyridine was studied, yielding the thermodynamical parameters of spin switching [184]. A broad variety of NMR techniques including the EvansQ method, the ideal solution model, and 2D NMR techniques were applied to characterize the octanuclear metallosupramolecular cage of Fe(II) [185]. Magnetic susceptibility measurements in solution revealed the spin switching of a novel Fe(II) complex of thiazolylimine base hexadentate ligand [186]. NMR studies revealed that iron complexes derived from 6-diaminotriazyl-2,20-bipyridines display SCO behavior, and hydrogen bonding–controlled self-assembly with a suitable barbiturate partner can modulate the crossover from mixed LS and HS to HS [187]. The potential utility of paramagnetic transition metal complexes as chemical shift 19F magnetic resonance thermometers was shown [188]. The potential utility of SCO iron(II) complexes as temperature-responsive paramagnetic chemical exchange saturation transfer contrast agents in magnetic resonance imaging thermometry was discussed [189]. Two theoretical articles on calculations of paramagnetic shifts in SCO complexes [190] and SCO host–guest systems were published [191]. Finally, to the best of our knowledge, there is only one example of the application of solid-state NMR to an SCO system to date: a solid-state 2H NMR spectroscopy study of the polymeric SCO compound {Fe(pyrazine)[Pt(CN)4]} shows that the switching of the rotation of a molecular fragment—the pyrazine ligand—occurs in association with the change in spin state [192].
6.5 Mössbauer spectroscopy
Many SCO systems had been thoroughly characterized by Mössbauer spectroscopy in the past decades [56], here we focus only on a few selected recent results.
New monomolecular SCO complexes like [Fe(3ditz)3](BF4)2 (3ditz =1,3-bis(tetrazol-1-yl)propane), which features an abrupt and almost complete spin transition at T½= 159 K [193], halogen-substituted salicylaldehyde-based Fe(III) gradual SCOs [194], and ferric aroylhydrazone SCO molecules [195] have been characterized by Mössbauer spectroscopy. Schmitz et al. [196] studied the effect of a coordinated π-radical ligand and found that the reduction of the strong π-acceptor ligand is accompanied by a decrease in the ligand-field strength. Among other spectroscopic tools, low temperature in-field Mössbauer studies provided major contribution to the characterization of two different crystalline forms of a heterotrinuclear [Pt2Fe] complex, only one of which shows SCO properties [23,164,197].
Following the first observations of the SCO effect in organometallic polymers (see the review of Gütlich et al. [198]), the pursuit for novel ways to manipulate the spin state of the core iron ion(s) continues. A triazole-bridged iron(II) polymeric chain system, [Fe(II)(R-trz)3]X2.xH2O (where trz is triazole and X is the anion), was found to exhibit the SCO phenomenon with thermal hysteresis around room temperature [199]. It was shown that the SCO hysteresis depends not only on the organometallic chain but also on the type and chain length of the organic counter ions. Moreover, new types of Fe(3,5-lutidine)2Ni(CN)4·2[(H2O)(3,5-lutidine)] and Fe(3-Clpy)2Pd(CN)4 (py = pyridine) 3D coordination polymer frameworks have also been characterized as SCO systems with at least 90% spin conversion rates [200].
6.6 X-ray spectroscopy
X-ray spectroscopy techniques (XAS, X-ray magnetic CD, X-ray photoemission spectroscopy, etc.) proved to be extremely useful for the investigation of SCO molecules deposited on surfaces including both thick films and submonolayer deposits. Moreover, they also became efficient element-selective ultrafast probes in time-resolved experiments, opening new opportunities for femtochemistry.
X-ray absorption remained the most widely used tool to study spin-state transitions; thus, for this established technique we only selected a few applications that go beyond routine characterization. Starting with soft XAS, using the Co L2,3-edge, Poneti et al. [201] proved that temperature- and light-induced valence tautomerism can occur even in a monolayer form, and the effect reproduces closely the one observed in the crystalline phase. This finding may help to transfer molecular properties to the nanometer scale, enabling new hybrid molecular-based architectures for novel technologies. Warner et al. [202] examined isolated Fe(II) complexes on a gold surface with Fe L2,3 XAS and concluded that the temperature- and light-induced SCO properties are conserved for a submonolayer of the [Fe(H2B(pz)2)2(2,2′-bipy)] complex evaporated onto a Au(111) surface. Many molecules in the submonolayer system remain pinned in one of the two spin states, however. They concluded that although the results demonstrated that temperature- and light-induced SCO was possible for isolated molecules on surfaces, interactions with the surface might play a key role in determining when this could occur. Gruber et al. [203] made a further step in this direction studying the archetype SCO complex [Fe(phen)2(NCS)2] on several different metallic surfaces and found pronounced differences in the SCO behavior depending on the strength of the interaction of the molecules with the substrates. Molecules in direct contact with the surfaces were found in either HS or LS states, but could not be switched between the two, because of the strong chemisorption that determined the spin state of the molecules through the adsorption geometry. Upon reducing the interaction with the surface, the SCO behavior was restored and the molecules could be switched between the two states [203]. Previous work revealed that at low temperatures irradiation with X-rays can lead to a spin-state transition, similar to light [204,205]. Davesne et al. [206] studied the dynamics of such a process, the soft X-ray induced excited spin-state trapping effect of [Fe(phen)2(NCS)2] using soft XAS at a range of temperatures, different exposures, and in comparision with another Fe(II) complex that showed rather different cooperativity. In addition to studying the metal center, it is also interesting to examine the ligands directly at a spin-state transition. van Kuiken et al. [207] has studied the photoexcited HS state of [Fe(bipy)3]2+ (in aqueous solution) at the N K-edge (399 eV). This complementary technique revealed that in the HS state the electron density increases on the N atom, whereas the Fe eg* orbitals are more delocalized than in the LS state. Although these observations were expected from the molecular orbital description of the LS and HS states, one should keep in mind that this technique can provide a more concise picture of the variations in the electronic structure.
From the applications of hard XAS, again we can only mention a few. Magnetic field–induced SCO was studied in [Mn(III)(taa)] (H3taa = tris(1-(2-azolyl)-2-azabuten-4-yl)amine) by XANES, in pulsed high magnetic fields up to 37 T and temperatures down to 17 K. The spectra showed significant variations related to the SCO from the LS to the HS state. The observed field-induced spin-state transition was attributed to the local microscopic transition at the single-molecule level [208]. Fe K-edge XANES was used to investigate the characteristics of temperature-induced SCO in metallosupramolecular polyelectrolyte amphiphile complexes containing FeN6 octahedra, attached to two or six amphiphilic molecules. The changes in the XANES profiles during SCO revealed that the spin-state transition is caused by a structural phase transition in the (amphiphilic) matrix, in contrast to the typical SCO behavior [209]. Finally, we report on the work of van Kuiken and Khalil [210], who simulated Fe K-edge XANES spectra using DFT-based modeling to analyze the line shape changes that should occur when studying the electronic structure variations in Fe(II) SCO complexes.
In addition to XAS, the most often used X-ray spectroscopy technique for transition metal complexes, XES is also getting applied in SCO research due to its spin-state sensitivity. Mebs et al. used Fe Kβ XES (besides hard XAS) on [Fe(phen)2(NCS)2] and [Fe(dedtc)3], (dedtc = N,N′-diethyldithiocarbamate) to follow the temperature-dependent spin-state variations in these systems of rather different cooperativity. A better understanding of the cooperativity was also the main motivation for a study of the 2D manganese(II) honeycomb lattices, where pressure-dependent S = [5]/2 to S = ½ SCO was observed with Mn Kβ XES [211]. Co Kβ (and L2,3 XAS) spectra were used for the characterization of the spin state in cobalt bis(o-dioxolene) valence tautomers, which confirmed LS Co(III) state in the low-temperature phase and HS Co(II) in the high-temperature phase [212]. Finally, we mention a study on an iron-porphyrin–based metal–organic framework, where Fe Kβ XES and K-edge XAS measurements revealed the local coordination geometry, oxidation, and spin-state changes experienced by the Fe sites upon reaction with piperidine, an axially coordinating reducing agent [213].
Although the application of XES and RXES remains scarce for steady-state SCO studies, these techniques are used more and more often as probes in time-resolved studies, to monitor the time variation in the spin momentum and the population of the different states [93,214,215]. As these experiments are at the forefront of modern X-ray research, we will briefly cover them, too. Also, their intense research presents many recent examples of the applications of the techniques, which could also be used in static SCO studies. The capabilities of X-ray probes can be appreciated from an exhaustive study made on the nanosecond-lived quintet state of [Fe(terpy)2)]2+ in aqueous solution, which presents the detailed characterization of the structure and electronic structure of this HS state [216]. The molecular structure was determined with high accuracy by EXAFS and X-ray scattering, whereas the unoccupied electron structure was revealed with XANES and RXES, both supported by theoretical modeling. Although XES was also used for the determination of the spin-state population in this study, these efforts were completed by another work in which the full Fe 1s XES was recorded simultaneously, including the vtc-XES (with its theoretical description) [217]. Results from some of these techniques are briefly summarized in Fig. 5.
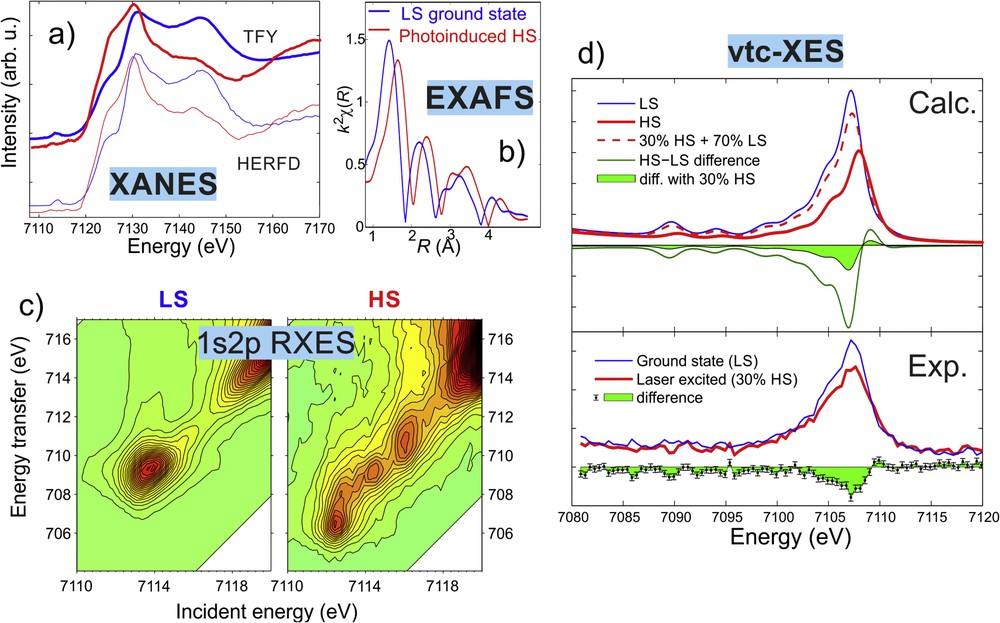
X-ray spectra of the aqueous solution of [Fe(terpy)2]2+ in the LS ground state and in its photoexcited HS state (whose spectra have been reconstructed from the laser-excited transients and the ground state). (a) Fe 1s K-edge XANES recorded with HERFD and total fluorescence yield (TFY) detection. (b) Fitted EXAFS spectra of the two states. (c) 1s2p RXES spectra over the pre-edge region. (d) Calculated and measured vtc-XES spectra. Adapted with permission from Ref. [216,217].
These tools, combined with the ultrashort pulses of XFELs, offer the possibility of probing the dynamics of spin-state changes with femtosecond time resolution, resulting in a dynamic expansion of ultrafast studies. As the working horse of such time-resolved studies, [Fe(bipy)3]2+, has been studied with femtosecond-resolved X-ray absorption [218,219], emission [220], and scattering [221]. Such studies can explore not only the evolution of the populations of the different states, but also intricate details of the relaxation including locations of intersystem crossings of the potential energy surfaces and coherent nuclear wave packet dynamics. These will be reviewed in part in another article of this special issue [Light-Induced Spin Crossover - solution and solid state processes, Guillaume Chastanet, Maciej Lorenc, Roman Bertoni, Cédric Desplanches (MS no. CRCHIMIE-D-17-00607)].
6.7 Emerging laboratory-scale XAS and XES
Low intensity X-ray sources and inefficient spectrometers prevented high-resolution X-ray spectroscopies to spread into local laboratories, thus for long synchrotron radiation sources were thought to be inevitable to perform such measurements. However, the routine application of these techniques is hindered by the complicated and slow access to synchrotron radiation facilities.
In recent years instrumental developments revolutionized the field of these spectroscopic methods by extending the range of applicable X-ray sources to much lower brilliances. Because of the progress in monochromatization, detection technology, and sources, the development of efficient tabletop instruments became a reality. New, economic, easily operated laboratory high-energy resolution Johann [222] and von Hámos [223,224] type X-ray spectrometers have been realized, delivering synchrotron grade signal-to-noise measurements for both XAS and XES in reasonable acquisition times (few hours) for high concentration samples. These new instruments are not direct competitors to synchrotrons but they can be used routinely at universities or research institutes, and they can also greatly help researchers to prepare for synchrotron or XFEL experiments. In a completely different approach, laboratory-scale time-resolved X-ray absorption and emission studies seem to be within reach via using femtosecond laser-driven liquid jet plasma sources and modern microcalorimetric detection, which records photons more effectively because of the large solid angle covered. The working principle and feasibility have already been demonstrated [225,226], and intense development work is currently being carried out. Even spin-state studies have been tried with this technique [227,228].
7 Outlook and perspectives
There is a general trend of turning SCO complexes into SCO materials, often hybrid and microstructurized ones. There is also a parallel development of the spectroscopic techniques that offer, on the one hand, new possibilities of observation of fast and ultrafast processes and, on the other hand, the possibility to measure the areas of micrometer (Raman microscopes) to tens of micrometer size with synchrotron techniques (cf. Ref. [229]). The latter provide further possibilities to map the microstructures with spectroscopic techniques. The development of synchrotron Mössbauer spectroscopy [230] that gives the possibility to measure the spectra of very small specimen could surely be useful for research in the area of SCO materials. Synchrotron-based techniques having small probe volumes are practically all appropriate for imaging—this is well known for magnetic CD, but this can apply to most of the X-ray techniques mentioned, even the most unusual ones, such as inelastic X-ray scattering, which offers exciting opportunities to create profiles of very special characteristics [231]. The aforementioned application of time-resolved IR ATR spectroscopy and further ultrafast UV–vis experiments on single crystals seems to be the new perspective of comparing the dynamical processes in solid to that observed in solution. One may expect more frequent use of solid-state NMR and its application to the dynamics in solution, also using the 2D techniques. A promising approach seems to be the use of time-domain terahertz spectroscopy, which to the best of our knowledge was used only once to investigate SCO materials [232]. With the emerging new spectrometers that allow relatively fast and convenient measurements in the home laboratories, the simplest yet powerful X-ray spectroscopy techniques (XAS and XES) are expected to become widespread, replacing the long wait for beamtimes at synchrotron radiation facilities for routine cases. Finally, even more frequent and effective applications of quantum chemistry calculations to support the spectroscopic results are anticipated. Although in most cases DFT provides reasonably accurate theoretical support with current developments in wave function–based methods, it is likely that such ab initio calculations will appear to be soon affordable for transition metal complexes, providing a more accurate and reliable routine description of the properties and spectra of these systems [233,234].
Acknowledgments
The authors acknowledge financial support from the "Lendület" (Momentum) Program of the Hungarian Academy of Sciences (LP2013-59), the Government of Hungary, and the European Regional Development Fund under grant VEKOP-2.3.2-16-2017-00015, and the National Research, Development, and Innovation Fund (NKFIH FK 124460). J.A.W. and V.S. acknowledge the support of the German Research Foundation (DFG) through SFB/TRR173 Spin+X and SFB/TRR88 3MET.


