1 Introduction
The spin-crossover (SCO) phenomenon is a change in the electronic configuration of molecular complexes induced by external stimuli. This change is associated with changes in ligand field strength, molecular structure, volume, magnetic susceptibility, and color, which drastically modify the physical properties of each electronic spin state. Among the different stimuli used, temperature and light are probably the most commonly used. Although the temperature can basically be viewed as a source of energy that allows electrons to be promoted from the t2g orbitals to eg within ground states, light can act in different ways. Owing to wavelength tunability, specific transitions (d–d, metal to ligand charge transfer [MLCT], ligand to metal charge transfer [LMCT], ligand to ligand charge transfer, etc.) can be selected. In that sense, when photon energy matches ligand absorption bands that can induce ligand conformation changes (photoisomerization or cyclization), the ligand field can be tuned and consequently the global SCO behavior. This is typically the case of the ligand-driven light-induced spin change (LD-LISC) and the light-driven coordination-induced spin-state switching (LD-CISSS) phenomena. When the wavelength is set on the metallic d–d bands or metal–ligand charge transfer transitions, some transient excited states can be populated leading to the photoinduced spin-state switching. This is the case of the widely studied light-induced excited spin-state trapping (LIESST) effect. Finally, there is a third action of light related to the energy deposited onto the material. Depending on the number of photons, a strong heating may occur, leading to photothermal effects that allow the occurrence of SCO transition. Apart from these three main ways of photoswitching an electronic configuration, one can also mention electron transfer (ET) and valence tautomerism, as well as phosphorescence implying states of different spin configurations.
The interest in using light resides in it being selective, affording the reversibility of the light-induced spin-state switching. Moreover, it operates on an ultrafast time scale because the photoswitching can be achieved within less than one picosecond. The combination of a fast and selective tool with fast optical readout of the spin state paves the way for the ultrafast data manipulation.
This article aims at reviewing these different light-triggered processes (Scheme 1) by describing the different light-induced effects. Moreover, the lifetime of the photoinduced state will also be discussed, particularly regarding the LIESST process and the dynamics involved. This latter phenomenon will be described both at different sizes and time scales to evidence the molecular and macroscopic collective behaviors. Most of the investigations were performed so far focus on iron(II) complexes, which will be at the core of this review. Therefore, this review is not exhaustive and it covers only representative and selected examples discussed at different levels of details.
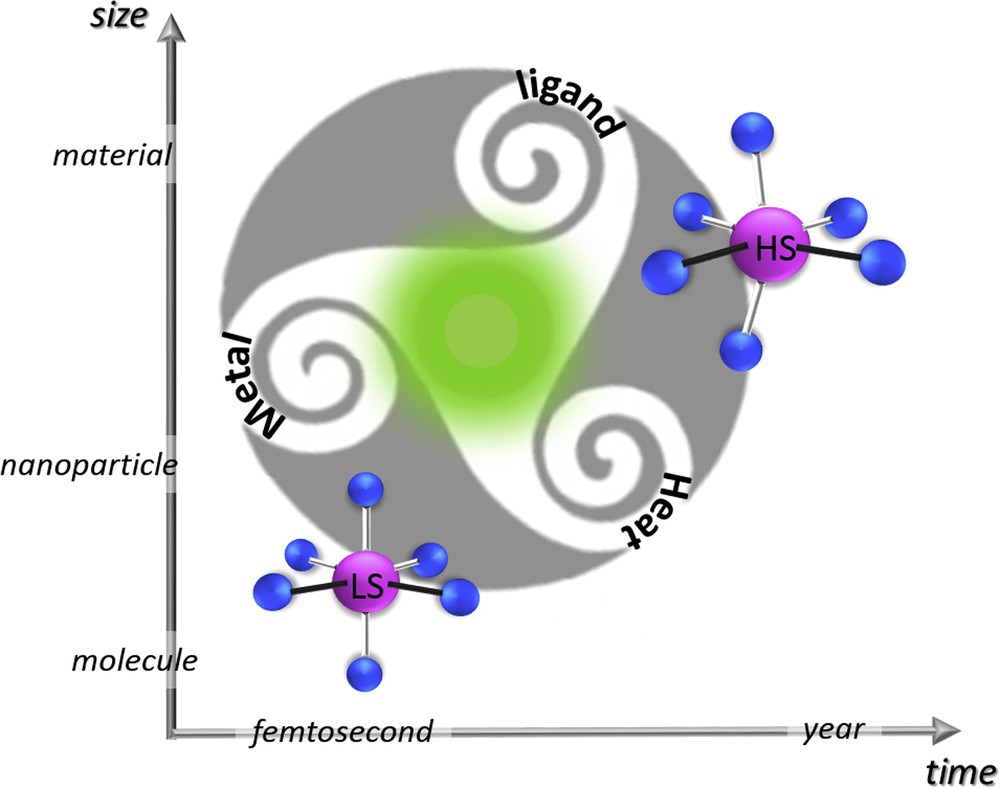
Outlook of the review.
2 Light-induced SCO—an overview
2.1 Ligand-driven light-induced spin change
The LD-LISC process is based on a spin-state triggering of the metal ion through a photochemical reaction of the ligands. It requires that the ligand field produced by the two stable photoisomers on the metal center be different. This is typically the case of cis–trans photoisomerization or photocyclization whose electronic density on the coordination site is affected by the electronic delocalization on the ligand that strongly depends on its geometry. Such systems can operate at room temperature, in a reversible way, between two stable or long-lived isomeric forms with different optical, magnetic, and chemical properties.
The principle of LD-LISC is depicted in Scheme 2. A prerequisite for this effect to be observed is the different magnetic behaviors in temperature exhibited by the photoisomers PIA and PIB. Several situations may be expected depending on the thermal behavior of each photoisomer. With the hypothesis that PIA exhibits a weaker ligand field than PIB, (1) a totally high-spin (HS) PIA can be transformed into an SCO PIB form (Scheme 2, case a); (2) an SCO PIA can be switched into another SCO PIB with a higher switching temperature (Scheme 2, case b); and (3) an SCO PIA can be switched into a totally low-spin (LS) PIB form (Scheme 2, case c). In each case, there is a temperature range where ligand photoexcitation results in a spin-state switching. Complexes with photoactive ligands have been developed to operate at room temperature.
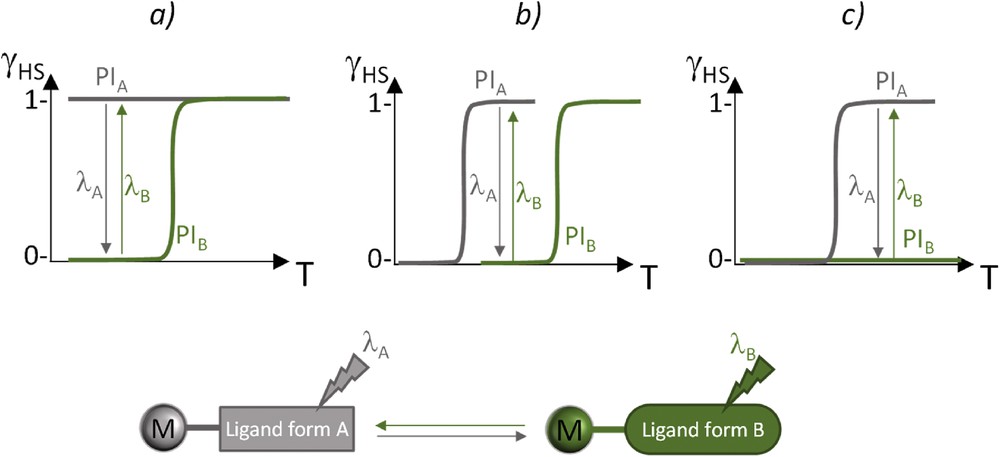
Relative HS fraction behavior of PIA and PIB complexes (a–c) favoring the observation of the LD-LISC effect and scheme of principle of the LD-LISC effect at the molecular scale. Adapted from Ref. [1].
The first photochemical process selected by Boillot, Zarembowitch et al. [1] to promote the LD-LISC effect was the cis–trans photoisomerization of ligand [2]. The main advantages of this approach are the lifetime of the photoproducts of years [2] and a purely molecular process. For example, the 4-styrylpyridine (stpy) molecule exhibits a planar (trans) to nonplanar (cis) conformation change upon selective light irradiation (Fig. 1a). Used as ligand, the trans conformation exhibiting a higher electronic delocalization should induce a stronger ligand field than the cis isomer. In the [Fe(NCS)2(stpy)4] complex case (Fig. 1b) [3], it was shown that (1) both isomers can be separately isolated and structurally characterized, (2) the trans isomer exhibits an SCO at 108 K whereas the cis form remains HS. This corresponds to the first case in Scheme 2 with PIA corresponding to the cis form and PIB to the trans-form, respectively. Due to the low T1/2 value (108 K), very weak photoisomerization quantum yields were observed because sufficient thermal motion is required to favor structural reorganization. To increase the SCO temperature, several substituents were used instead of the NCS−, such as NCBPh3− or NCBH3− [4]. In both [Fe(NCBPh3)2(stpy)4] and [Fe(NCBH3)2(stpy)4] complexes, the cis isomers remain HS whereas the trans isomers undergo a thermal SCO around 190 K. At this stage, the concept was valid with plenty of room for improvement. Indeed, the phenomenon was observed far below room temperature and the photoconversion yield reached 67% (without mention of the photoexcitation time). Finally, this effect was also observed for complexes dispersed in an organic polymeric media [4,5].
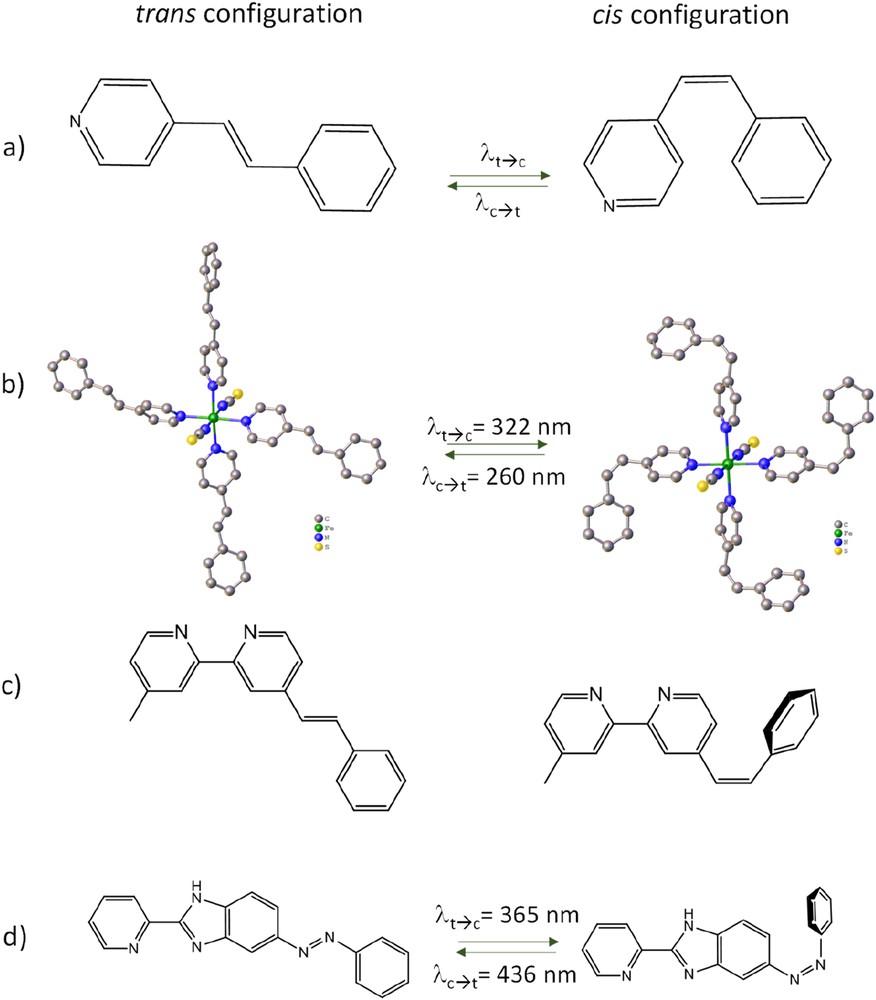
Representation of the different cis and trans isomers used for the LD-LISC effect. (a) 4-Styrylpyridine (stpy) ligand; (b) [Fe(NCS)2(stpy)4] complexes; (c) 4-methyl-4′-styryl-2,2′-bipyridine ligands (msbpy); (d) phenyl(2-pyridin-2-yl-3H-benzoimidazol-5-yl)diazene ligand.
A first development was to tune the ligand field of the styrylpyridine-based family by introducing substituents [3]. In all cases, the cis complexes were HS whereas the trans complexes exhibit an SCO, with T1/2 ranging from 155 to 200 K. In this family of compounds, the ligand field was not strong enough to shift the thermal SCO around room temperature.
To increase the ligand field, a second approach was followed using polydentate ligands. Using a bipyridine-based ligand (msbpy = 4-methyl-4′-styryl-2,2′-bipyridine, Fig. 1c), a derivate of the SCO [Fe(bpy)2(NCS)2] complex was obtained and a gradual SCO centered at 263 K was observed [6]. The photoinduced SCO was reported in solution (acetonitrile) at room temperature (293 K), following from the trans → cis photoreaction. Light irradiation at 334 nm induced a partial LS → HS photoswitching at room temperature without achieving reversibility. The main difficulty encountered with the stilbene derivatives is the close proximity of the cis → trans and trans → cis absorption bands (separated by 60 nm). By using an azo-type ligand, in which 2-(2′-pyridyl)benzimidazole (pybim) and photoisomerizable azobenzene are connected in a π-conjugated fashion (Fig. 1d), a more pronounced separation can be achieved (90 nm). Therefore, a reversible photoswitching was recorded on phenyl(2-pyridin-2-yl-3H-benzoimidazol-5-yl)diazene in solution [7] albeit with a weak spin state conversion (∼5%).
Regarding the photoisomerization process, the LD-LISC occurs in solution or for molecules dispersed in polymeric media. It is mainly because of the strong structural reorganization upon photoisomerization. Very few examples in the solid state were reported using several hours of irradiation time with small photoconversion yield [8]. Therefore, a third approach arose using photoactive ligands with less structural reorganizations, such as photocyclizable molecules. Prototypal example of such a system is the diarylethene switching unit based on a reversible opening/closing of chemical bonds upon selective irradiation (UV light for the open → close transformation and visible light for the close → open transformation, Fig. 2a). Upon cyclization, the electronic delocalization on the molecule increases leading to a stronger ligand field that should favor the LS state. The advantage of this system lies in the chemistry richness to functionalize the diarylethenes, the high thermal stability of both photoisomers, and the reversibility evidenced in the solid state [9].
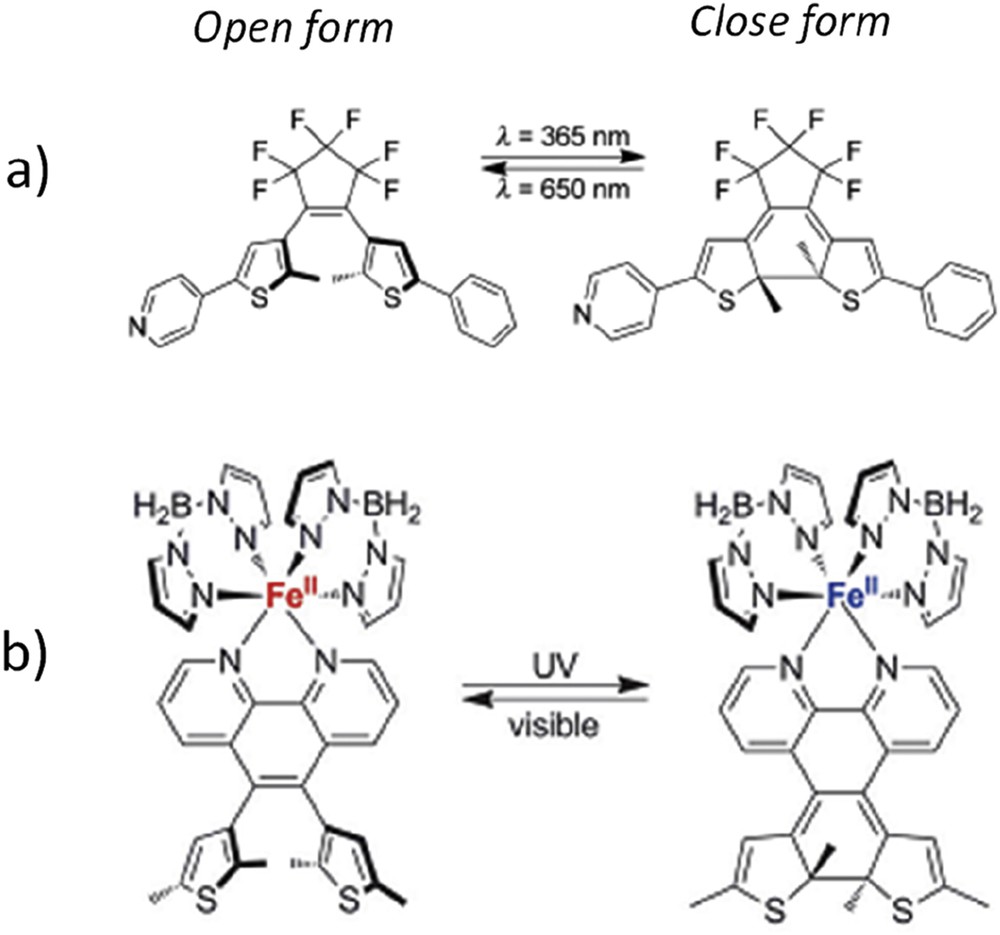
(a) Prototype of diarylethene photocyclizable monodentate ligands and (b) SCO complex with bidentate photocyclizable ligands.
The first attempts to achieve LD-LISC on SCO iron(II) complexes with diarylethene-pyridine–based monodentate ligands were made by Senechal-David et al. [10] and Garcia et al. [11]. The results have evidenced photoswitching at room temperature in the solid state. However, there are some unclarified behaviors of these compounds including a possible ET. Going to bidentate bipyridine-based ligands, Nihei et al. [12] and Khusniyarov and co-workers [13] succeeded to perform irreversible and reversible spin-state photoswitching at room temperature, both in solution and in solid state (Fig. 2b). Almost 30–40% of photoconversion was achieved with 1 h of irradiation [13].
Globally, the use of bidentate-based ligands substituted by either photoisomerizable or photocyclizable unit led to room temperature photoswitching of iron(II) spin state. To achieve an efficient LD-LISC in the solid state at room temperature, the use of photocyclizable functions seems to afford the best promising results, with room for improvement such as photoswitching irradiation time and yield.
2.2 Light-driven coordination-induced spin-state switching
Generally, the electronic ground state of a metal complex is determined by its coordination sphere (geometry, coordination number, distortion, ligand field, etc.). Usually, SCO complexes are based on d4–d7 metal centers and upon the change in the spin state, the geometry of the coordination sphere changes but its coordination number does not, albeit few counterexamples were reported [14]. However, in these examples it is unclear if the SCO induces a coordinance change or the change in coordinance induces the SCO. In the case of Ni(II) ion, square planar species are LS whereas square pyramidal and octahedral species are HS (Fig. 3). In a square planar geometry, the d orbitals are split into four energy levels and the eight valence electrons of the Ni(II) occupy three levels leading to S = 0 ground state. In a square pyramidal geometry, the four energy levels are slightly reorganized leading to the occupation of the five orbitals inducing S = 1 ground state. Finally, in an octahedral geometry, the t2g level is completely filled whereas the eg level is half filled, leading to an S = 1 spin state. Therefore, the addition of one or two coordinating ligands to a square planar Ni(II) complex would switch the spin state from diamagnetic to paramagnetic.
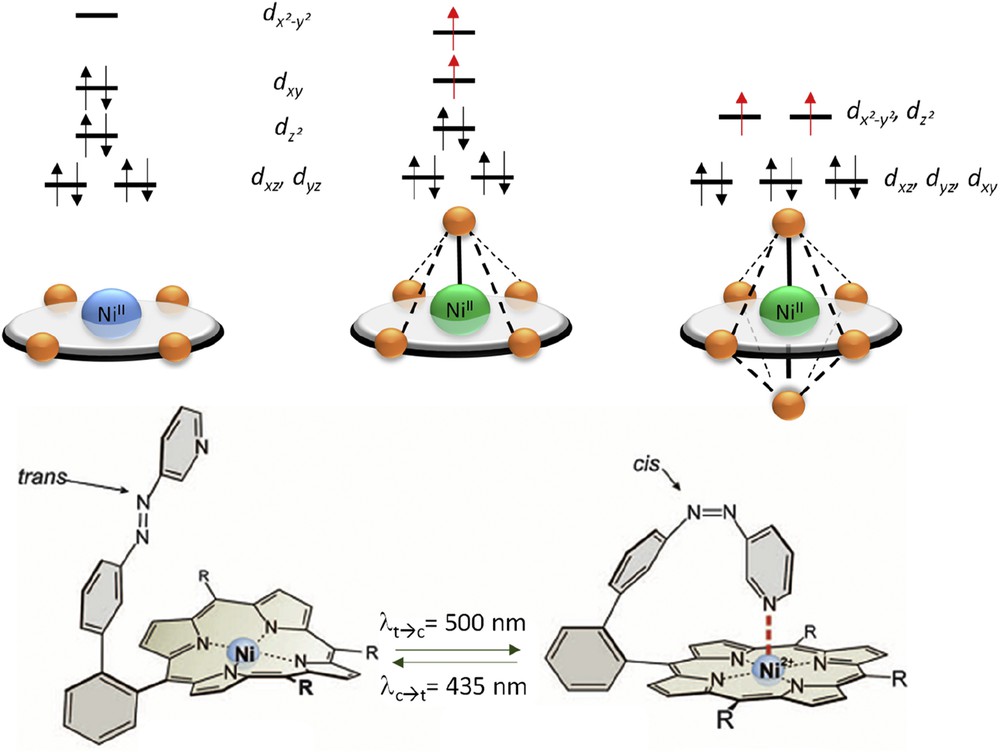
(Top) Electronic configuration of Ni(II) as a function of the coordination sphere geometry; (bottom) example of azobenzene-functionalized porphyrin ligand for LD-CISSS process. Adapted from Ref. [17a].
This approach has been widely studied by Herges and co-workers [15] and is highly investigated for MRI contrast agents [16]. The additional ligand can be either provided by the liquid medium or by a photoreaction of the coordinating ligand. This latter approach is related to the LD-LISC. Indeed, the spin-state switching of the metal ion arises from a photoreaction occurring in the ligand in both cases. Instead of a ligand field change in the LD-LISC process, the LD-CISSS causes ligand coordination/dissociation at the metal ion that strongly affects the ligand field and the orbital occupation. To achieve such an effect, a four-coordinate square planar [Ni(FTPP)] (FTPP = tetrakis(pentafluorophenyl)porphyrinato(2-)) was used with Ni(II) ion placed in the center of a porphyrin ring (Fig. 3). In solution, upon addition of the trans form of a photoisomerizable ligand functionalized by pyridine-coordinating units, like in LD-LISC process, the Ni(II) coordination geometry was increased from four to five or six [17]. It induced a spin-state switching from 0 to 1. Upon irradiation of the solution in the UV, the trans → cis transformation induces a photodissociation of the pyridine moiety and the Ni(II) recovers its original square planar geometry and the corresponding diamagnetic state. Depending on the photoisomerizable ligand used (functionalized azobenzene-type ligands), the process could reach up to 68% of photoconversion at room temperature.
This concept has been extended by functionalizing the porphyrin ring with the photoisomerizable ligand bearing the pyridine coordination unit (Fig. 3). Although in the trans conformation this pyridine function is not coordinated to the metallic site in a square planar geometry, the cis form obtained by light irradiation in the UV induces a structural rearrangement favoring the coordination of the pendant pyridine to the Ni(II) site. In the resulting square-pyramid geometry, the Ni(II) is in the S = 1 spin state whereas it was in the S = 0 state in the square planar geometry [18]. The reversible cis → trans photoisomerization of the azo-group triggered a reversible HS → LS transition at the Ni(II) center in solution at room temperature. By improving the chemistry, especially the bonding of the azo-group to the porphyrin ring, a spin-state photoconversion of 85% could be reached. Moreover, both photoisomers are remarkably stable upon time (year) and photocycling (10,000 cycles). It has incited the study of such systems for MRI contrast agents [16].
2.3 Photoinduced phase transition induced by photothermal effect
One way to induce the SCO phenomenon is to deliver thermal energy to the system. This can be achieved with a thermal bath, the common way of investigating thermal SCO behaviors. A related approach is to use intense light irradiation to heat the sample. Indeed, short laser pulses are highly energetic and can deposit a huge amount of energy on the sample in a very short time. This principle is used, for instance, in laser ablation, 3D laser printing, and for magneto-optical storage [19]. Applied to SCO materials, the principle is based on laser-induced heating of the LS state to trigger the population of the HS state and induce the SCO. Such technique has been applied both in SCO (gradual conversion) and first-order (abrupt) transitions. Gradual conversion allows us to characterize the dynamics of the SCO and access thermodynamical parameters of the transition.
In 1973, Beattie et al. [20] reported the first study in solution using the Raman laser temperature jump technique. The energy of the laser pulse was used to heat a solvent within the pulse duration. A study on the [Fe(HB(pz)3)2] complex in dichloromethane and methanol (HB(pz)3 = hydro-tris-pyrozolylborate) reported a relaxation time of 32 ns at 298 K. Extending this technique to other complexes and solvents allowed us to conclude that the relaxation rate is almost solvent independent. It indicates that this process is mainly an intramolecular process [21]. Also by performing this experiment at different temperatures, it is possible to determine the enthalpy and entropy terms of the spin equilibrium.
The relaxation rate at room temperature for the compounds studied ranges from 30 to 120 ns. The studies have demonstrated that in solution, the HS ↔ LS spin equilibrium is weakly “spin forbidden”, and the activation energy mainly arises from structural reorganizations of the coordination sphere. Indeed, in the HS state, two electrons occupy eg* orbitals with an antibonding character weakening the metal–ligand bond strength. As a consequence, at the molecular level the metal–ligand bond length is larger in the HS state and the HS molecules bigger than in the LS state. Moreover, this volume change in the coordination sphere is not symmetric, and the HS state is more distorted than the LS state [22].
The first study in solid state on a pure SCO system was reported by Freysz et al. [23] with the goal of an efficient LS → HS photoconversion leading to a long-lived HS state. For this purpose, the cooperative material [Fe(PM-BiA)2(NCS)2] (PM-BiA = N-2′-pyridylmethylene-4-aminobiphenyl) that exhibits a 5 K hysteresis width centered at 170 K was selected. Optical reflectivity was used to monitor the evolution of the material both in temperature and in time domain. A single laser pulse of 8 ns at 532 nm with a fluence of 14 mJ/cm2 was applied to the sample. When the temperature is set at the center of the hysteresis, the laser pulse induced a quantitative LS → HS irreversible photoswitching due to the stable character of the HS state in the hysteresis. This irreversible switching process is of great interest for optical data treatment. The main requirement to reach this target being a hysteresis centered at room temperature. An experiment was performed later on the three-dimensional (3D) [Fe(pz){Pt(CN)4}] material (pz = pyrazine) that undergoes a spin transition centered at 295 K associated with a 25 K large hysteresis [24]. Using 532 nm laser pulses with fluence of 250 mJ/cm2, a quantitative reversible photoswitching was reported and is still debated [25].
This phenomenon has been observed on other SCO systems [26] and the suggested process to explain the LS → HS single laser pulse switching is the heating effect [24d,26]. The temperature jump associated with the laser pulse drives the materials along the heating branch of the hysteresis curve. After thermalization toward the initial temperature, the system follows the cooling branch of the hysteresis and the HS state is then trapped. This approach is very similar to the Raman laser temperature jump technique [20] but there are two main differences. Indeed, in solution experiments no hysteresis is expected and the switching leads to an out-of-equilibrium state, although the presence of the hysteresis curve in cooperative materials allows an ultrafast photoswitching between two stable states. Also in solution, the irradiation is selected to induce heating of the solvent, whereas in the solid state, the irradiation is chosen to excite directly the iron(II) center. Nevertheless, SCO particles dispersed in an organic polymer can also be photoswitched by irradiation within the absorption bands of the polymeric matrix, as if it was a solvent [27]. This latter process is used in infrared (IR) detection cards [27b].
Let us mention a recent strategy to reduce the irradiation energy needed to induce this photoswitching. SCO nanoparticles of the [Fe(trz)(Htrz)2](BF4)2 1D polymer (Htrz = 1,2,4-triazole) have been decorated by gold nanospheres. These gold nanospheres due to their surface plasmon resonance act as a local heater when photoexcited [28] and trigger thermal switching of the SCO nanoparticles. It has been demonstrated that the energy needed to induce the photoswitching of such materials can be reduced by a factor 4 using such a hybrid approach [29]. This method is hereby promising from the perspective of room temperature photoswitching.
2.4 Light-induced excited spin-state trapping
When the photon energy is tuned in resonance with absorption bands of the metal complex, it can induce the electronic spin-state switching of the system. For example, transition from LS singlet state to HS quintet state involves intermediate excited states as the ΔS = 2 spin change is highly forbidden. The photophysical processes have been investigated by different techniques to evidence the mechanism at play and the transient electronic states involved. In 1982, McGarvey and Lawthers [30] used the laser flash photolysis to probe in solution the dynamics of the spin equilibrium. This technique uses lasers with wavelength centered on d–d or MLCT absorption bands of the complexes. Technological advances of laser-based techniques have ultimately led to studies showing that the photoconversion mechanism [31] occurs at ultrafast time scale.
In 1984, Decurtins et al. [32] investigated the LS → HS photoswitching in the solid state. Studying [Fe(ptz)6](BF4)2 (ptz = 1-propyltetrazole) crystals by absorption spectroscopy, irradiation in the absorption band of the LS state (514 nm) induced the population of the HS state. This phenomenon is named LIESST to describe the fact that light allowed the population of an excited metastable state with long lifetime. This phenomenon has been observed at low temperatures (below 50 K) in the region where the photoinduced HS state lifetime is long enough to allow steady-state characterizations through optical and X-ray techniques. Two years later, an irradiation at 820 nm into the absorption band of the photoexcited HS state has evidenced the population of the LS ground state, proving the reversibility of the LIESST process, later referred to as reverse LIESST [33]. This discovery has led to numerous investigations to evidence the mechanism of photoswitching from the molecule to the material scale, the different time scales of the intersystem crossing (ISC), and the lifetime of the final photoinduced state. These investigations will be discussed in the following sections.
2.5 Spin crossover and electron transfer
Another class of photoswitchable molecular materials relying on the SCO phenomenon is based on intramolecular ET. In these molecules, the presence of electron donor and acceptor moieties promotes a reversible transfer of one electron between the two sites through temperature change and/or photoexcitation at low temperature. In addition, this ET can be associated with an SCO process. As for SCO materials, the modification of the electronic configuration by light irradiation allows magneto-optical bistability. Different donor/acceptor couples have been considered in molecular compounds, such as radicals or complexes, implying an ET between an organic moiety (radical/ligand) [34] and a metal center or between two metal ions [35]. Basically, when one electron is transferred from one metal to another (or an organic ligand–valence tautomerism), the oxidation state of the metal changes. This change is associated with an electronic reorganization leading to an SCO. A topical question related to these systems is whether the charge transfer triggers the spin-state switching or if it is the other way around [36]. Although several reviews have been dedicated to these systems [35,37], they fall out of the scope of this article.
3 LIESST photoswitching
The LIESST photoswitching has been widely studied since its discovery in 1984, either in diluted samples to unravel the spin transition of noninteracting molecules or in bulk solid samples to explore collective character of the light-induced spin-state switching. This broad topic has been largely discussed in terms of the energy diagram shown in Fig. 4b, depicting the potential energy surface (PES) of an SCO material, based on detailed optical absorption spectroscopy studies (Fig. 4a). These studies have evidenced the different optical fingerprints of the LS and HS states (Fig. 4a). The LIESST effect is based on the specific absorption of the LS state around 514 nm corresponding to the 1A1 → 1T1 transition (green curve in Fig. 4a) whereas the reverse LIESST uses the HS state absorption around 830 nm corresponding to the 5T2 → 5E transition (red curve in Fig. 4a). As already mentioned, the LS to HS photoswitching should involve a cascade between excited states with at least two ISCs of ΔS = 1 each (e.g., Fe(II) systems). One expects the presence of an intermediate short-lived triplet state on the way from the singlet LS state to the quintet HS state. Extremely short lifetime of the intermediate states has motivated a number of high time resolution experiments granting access to those transients, as well as to the kinetics of population of the 5T2 metastable/final state. Here, we only discuss the results obtained using optical spectroscopies, whereas X-ray spectroscopic techniques are discussed in another review [22b].
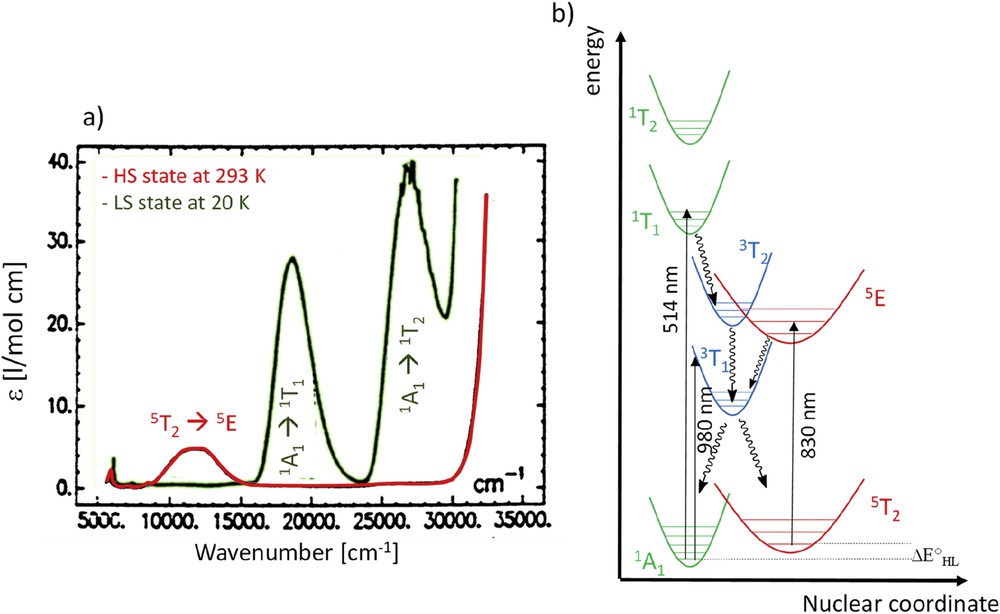
(a) Single-crystal optical spectra of the [Fe(ptz)6](BF4)2 compound at 293 and 20 K. Adapted from Ref. [65]. (b) Energy diagram depicting vibrational potential wells and their spectroscopic assignment. The straight lines represent the irradiation, whereas the wavy lines stand for nonradiative relaxations.
3.1 Solution studies
Before the spectacular advances of ultrafast pump–probe techniques, the early work with flash photolysis on the photoinduced transfer in dilute systems already provided significant insights into the dynamics of molecules in solutions [30]. Those investigations of photoinduced effects (the Nobel Prize in Chemistry 1967, M. Eigen, R. Norrish, G. Porter) began well before the discovery of LIESST. However, the achievable resolution at that time would only allow one to observe the relaxation of the final excited state 5T2 toward the ground state 1A1. In the late 1980s, the emergence of pulsed lasers with picosecond duration was a major step forward helping evidence the existence of a very short-lived charge transfer state (metal to ligand in this case) during the spin-state photoswitching, as observed by Winkler et al. [38]. Major breakthroughs came with the availability of tabletop femtosecond laser sources and the birth of femtochemistry in the 1990s (the Nobel Prize in Chemistry 1999, A. Zewail). It has rendered possible the observation of elementary process involved in the LIESST mechanism, and it became feasible to look into details of the nature and the lifetime of the transient excited states before reaching the HS potential [39] (Fig. 5).
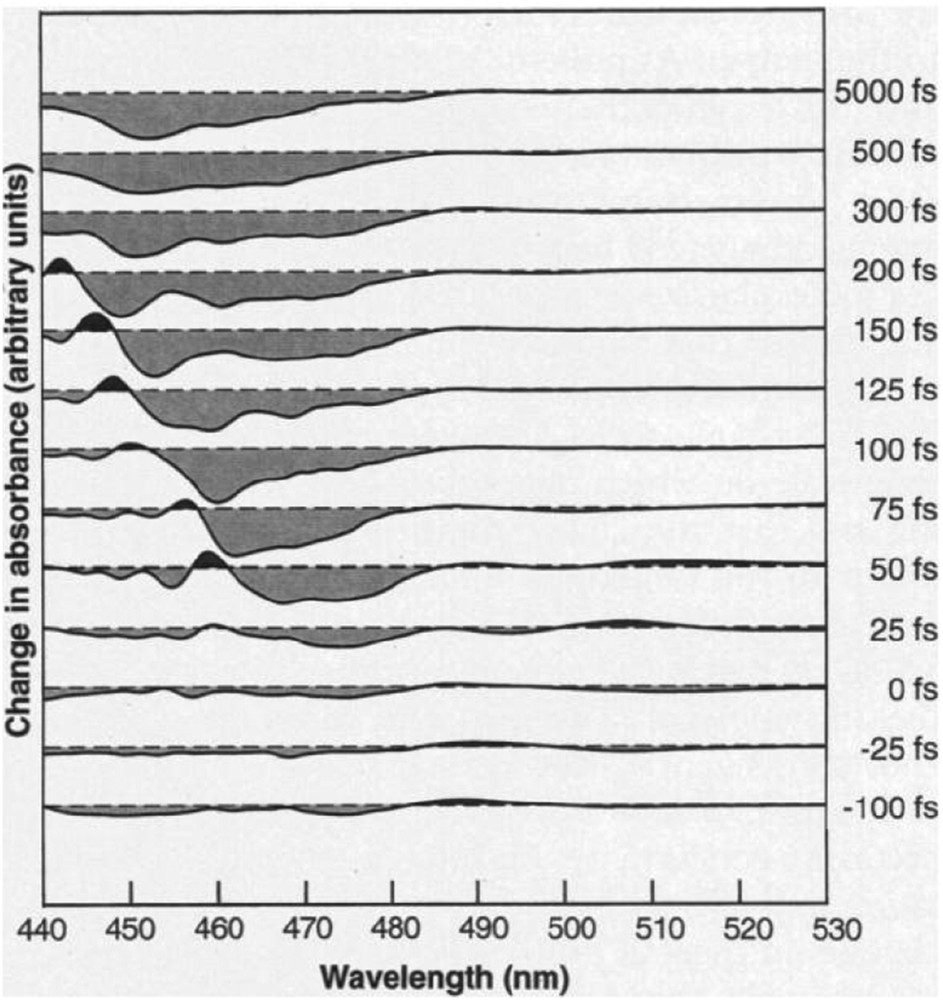
Transient absorbance changes after femtosecond excitation in [Ru(bpy)3](PF6)2. The early changes reveal a transient excited state with lifetime of around 300 fs. Adapted from Ref. [39].
Despite numerous similarities, the LIESST and photoinduced spin-state switching in diluted systems are not exactly the same phenomena. The initial mechanism triggering the switch of molecules is independent of whether they are organized in crystalline lattice or diluted. However, LIESST requires a metastable state with long lifetime only attainable in a solid. The complete cycle of photoinduced spin-state transition at the molecular level was for long a challenging task, eventually realized with laboratory-based laser sources [40].
In the following section, we briefly introduce the most common way to investigate ultrafast phenomena in diluted and bulk systems, namely the laser pump–probe spectroscopy. It is based on the use of two ultrashort laser pulses referred to as pump and probe. The pump is a high-intensity (strong fluence) pulse that will set the system in an electronically strongly excited state. The probe pulse (weak fluence) will monitor the evolution of the system in the time domain after the initial photoexcitation. In this short review, we will not consider higher-order spectroscopies, such as 2D-IR, second harmonic generation (SHG), or optical Kerr effect, but only linear spectroscopy probing the excited state absorption and the ground state bleaching. The first one results in an increase in absorption due to population of new transient species, and the second one is related to the depopulation of the ground state resulting in a decrease in absorption.
The LIESST effect is triggered by an optical excitation resulting in a vertical transition in the PES (Fig. 4). As the first samples studied show octahedral symmetry around the metallic center, the classical Oh space group is often used to characterize the nature of the involved electronic states during the process. Hereafter, this terminology will be used when discussing excited states and orbital symmetry in the general case. The very first step of the spin-state photoswitching is a d–d transition, MLCT, or LMCT, depending on the wavelength used and the oxidation state of the metallic center (Fe(II) and Fe(III) in case of iron). Ultrashort laser pulse leads to an instantaneous population of this charge transfer state via a Franck–Condon process (vertical transition on the PES). It was theoretically predicted that this initial step will be followed by one or several ISCs before reaching the HS potential surface (Fig. 4). In the 1990s, it was already reported that such cascading ISC was occurring on the sub-picosecond time scale, but observation of steps involved in such a phenomenon was hindered by insufficient time resolution [38,39]. In addition, on the basis of the steady-state experiments, the efficiency of such a process was postulated to be close to unity (see Section 3.2.1). The structure of the HS state being different from that of the LS, mainly by the length of bonding connecting metal to its ligand, several vibrational modes sensitive to such structural changes are activated during the photoswitching process and push the system to settle in the HS potential.
However, the driving force launching the electronic wave packet in the HS potential is still under debate. A recent theoretical work predicted that the activation and very efficient damping of a key vibrational mode acting on the main reaction coordinate (metal–ligand bond length) is the main factor behind the efficiency and the speed of the spin-state trapping [41]. It implies that the initial excited state couples very strongly to a single vibrational mode in the very short of time resulting in a coherent and deterministic dynamics over the PES. It also explains why the structural dynamics preclude recurrence of the initial LS state, as the efficient energy dissipation upon curve crossing traps the system in the HS potential. The first glimpse of vibrational coherence during the spin-state switching was reported by Consani et al. [42], who observed vibrational coherence after the photoexcitation in a Fe(II) complex. The vibrational mode of about 130 cm−1, lower than the FeN stretching mode around 280 cm−1, was proposed at that time as the driver of the structural distortion. In addition, impulsive Raman scattering on LS modes was excluded as the coherent modulation is only observed in the transient excited state absorption and not in the ground state bleaching. This slow frequency was attributed to ligand motions such as bending modes of benzene or NFeN with a damping time of around 1.1 ps, implying that the ISC and arrival in the HS potential is faster than the period of the vibrational mode, thereby rendering the observation of coherent wave packet possible.
More elaborate optical studies such as time-resolved fluorescence and time-resolved Raman scattering can be used to study the ultrafast spin-state photoswitching in dilute phases. The use of time-resolved Raman scattering is a judicious choice because HS and LS species have distinct vibrational frequency modes. Indeed, the antibonding character of the eg orbitals populated in the HS configuration leads to a red shift of vibrational frequency when switching from LS to HS states. By monitoring the Raman shift, it is possible to record the arrival of the molecules in the HS potential after femtosecond excitation. Time-resolved Raman scattering experiment performed by McCusker and co-workers allowed such observation, a spin-state switching occurring in 190 ± 50 fs in the case of [Fe(tren(py)3)]2+ (tris(2-pyridylmethyliminoethyl)-amine) [43]. Therefore, the cascade of ISC phenomena occurs on the sub-picosecond time scale with transient excited states with lifetimes shorter than elementary vibrational excitation. It strongly suggests that the Born–Oppenheimer approximation is no longer valid as both atomic structure and electronic state evolve in parallel in the time domain [44].
Although the above processes yield an almost unity quantum efficiency, a small fraction of photoexcited molecules undergo radiative recombination allowing for time-resolved fluorescence measurements. As a consequence, it is possible to monitor the intermediate state through a defined emission band. On the basis of the results obtained for Ru and Fe materials, the lifetime of the initial 1MLCT state was determined in the range of 15 ± 10 fs [45]. The lifetime of a second charge transfer state, possibly 3MLCT, the last transient state preceding the HS state, was postulated to be on the order of 130 fs (Fig. 6) [40,46]. With an impressive array of experimental techniques and a formidable amount of experimental and theoretical articles, the study of spin-state photoswitching is an invariably active field of research, continually stimulating debates about the nature of the transients or the structural dynamics accompanying the photoinduced spin-state switching.
(a) Time-resolved fluorescence of [Fe(bpy)3]2+ after photoexcitation in resonance with the CT band. Clear fingerprints of the 1MLCT state are observed. (b) Schematic photocycle of the [Fe(bpy)3]2+ compound. Adapted from Ref. [40].
To summarize the so far acknowledged picture defining the molecular-scale dynamics of diluted systems, three main processes are observed. An instantaneous charge transfer state (MLCT or LMCT) obeying Franck–Condon principle is first generated, and then followed by an ultrafast ISC potentially involving transient excited states toward the HS potential. Finally, the vibrationally excited HS molecules relax to the bottom of their potential well. The LS ground state is recovered within 1 ns in most of the cases (Fig. 6).
3.2 Solid state
3.2.1 Photoconversion efficiency
Few studies dealt with the quantum yield of the LIESST effect. Detailed investigations were performed on the [Fe(ptz)6](BF4)2 and [Fe(pic)3]Cl2, EtOH (pic = 2-picolylamine) [47]. Overall, it was shown that the quantum efficiency for the light-induced population of the metastable HS state at low temperature (10 K) is close to unity. Moreover, it does not depend on the irradiation intensity and is almost temperature independent. The presence of the transient triplet state implies a branching ratio between triplet → singlet and triplet → quintet states of 1 for 4. Because of cooperative effects, the quantum efficiency at the macroscopic scale might depend on the LS/HS fraction, leading to nonlinear responsiveness to laser excitation. This remarkable feature of SCO materials will be discussed later. In the solid state, upon laser excitation, the decrease in the population of the ground state induces a decrease in the absorption coefficient of the material. This bleaching effect can strongly affect the penetration of light inside the material and its absorption, leading to nonlinear behaviors [48]. In such cases, the photoexcitation term depends on the converted fraction.
3.2.2 Photoconversion pathways in the solid state
The main differences between spin-state switching in diluted systems and solid state are the environment of switched molecules and the lifetime of the metastable state. To investigate the photoswitching dynamics in the solid state using a pump–probe technique, the lifetime of the metastable state thereby the the repetition rate of the experiment have to be such that the material recovers the ground state between consecutive laser shots.
Femtosecond spin-state switching in the solid state has proven to be technically challenging because of the crystalline nature of the medium. For macroscopic bulk samples, an additional difficulty arises from a small penetration depth of the laser compared to the size of the crystal resulting in very small converted HS fraction, and difficult to measure [48,49]. Recently, this difficulty has been remedied with synthesis of nanocrystalline samples where the penetration depth of the laser at the given wavelength is on the order of the nanocrystal length itself. It ensures homogeneous excitation and much higher conversion of HS molecules than in single crystals. In addition, the overall decrease in optical density of such samples provides with the opportunity to perform thorough analysis in a broad spectral range.
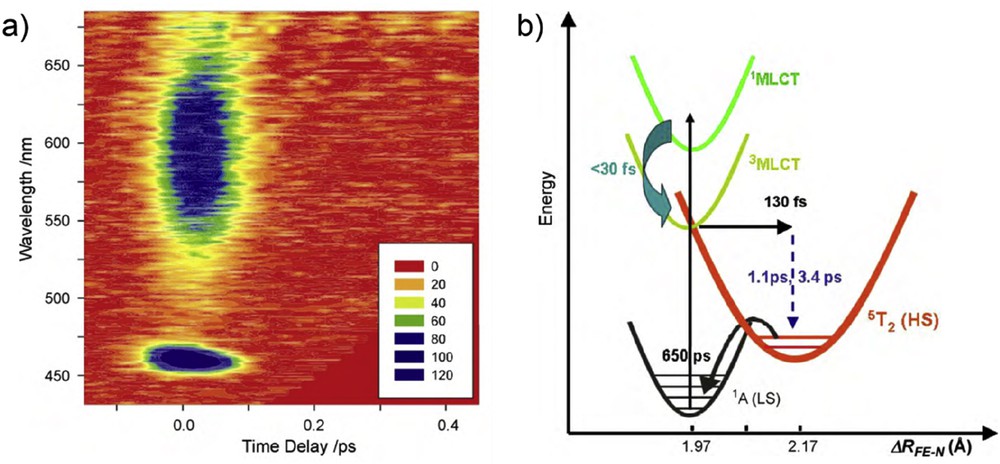
Results on the Fe(III) compound [Fe(3-MeO-SalEen)2]PF6 (H-3-MeO-SalEen being the condensation product of 3-methoxy-substituted salicylaldehyde and N-ethyl-ethylenediamine) have evidenced the femtosecond spin-state switching within 1 ps (τ1 in Fig. 7) [50]. By using femtosecond transient absorption visible spectroscopy it was possible to evidence the presence of intermediate states with an upper lifetime of 200 ± 20 fs (τ2 in Fig. 7). Interestingly, the near-IR part of the spectrum revealed slower kinetics and narrowing of the absorption bands. This is a stamp of vibrational cooling, and in the case of SCO indicates the presence of vibrationally hot HS molecules relaxing to the bottom of the HS potential. As these experiments were performed in the visible range, it was not possible to probe the complete cooling process. This shortcoming can in principle be remedied with mid-IR spectroscopy, directly resonant with vibrational levels of lower energy. Time-resolved mid-IR experiments performed in solution yielded time constants for vibrational cooling exceeding 30 ps [51]. IR spectroscopy has its own challenges, essentially related to the entanglement of spectral content carrying both the electronic and vibrational contributions. Hence, it contains more information but the analysis is not straightforward and applying such a technique to the crystalline material requires a fair amount of benchmarking with Fourier transform IR spectroscopy and density functional density (DFT) [52].
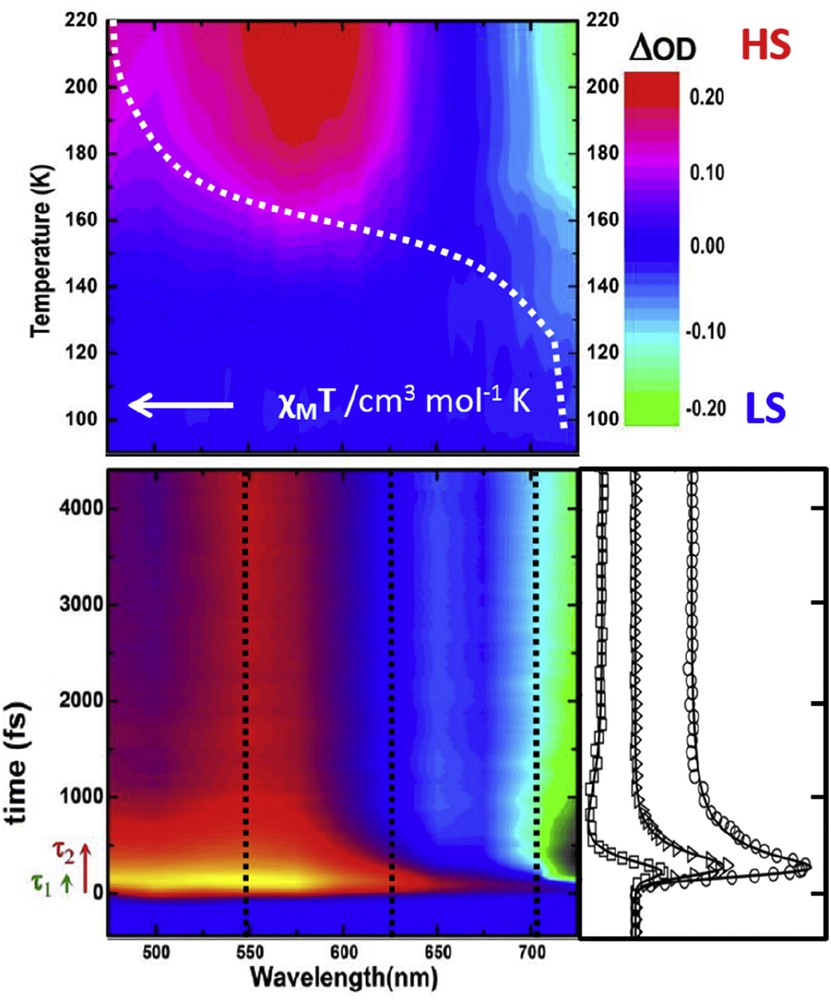
Thermal (top) and photoinduced change (bottom) of optical density after a femtosecond excitation in nanocrystals of [Fe(3-MeO-SalEen)2]PF6. The kinetic traces reveal the HS spectral fingerprints in the time domain within 1 ps. Adapted from Ref. [50].
Solid-state materials offer advantages too, for example, when addressing the question of the initial photoswitching mechanism, the crystal provides a well-defined orientation of molecules in a 3D lattice. It allows for polarization-dependent studies and hence the insights into the relation between electronic transitions and the symmetries of structural modes coupled with these transitions. Indeed, solid-state studies have also caught signatures of coherent structural dynamics during the spin-state photoswitching [53]. The ultrafast photoswitching of single crystals of [Fe(phen)2(NCS)2] triggers the oscillatory component in the optical response after a femtosecond excitation of the MLCT state (Fig. 8). This oscillatory component was transformed in the frequency domain into several modes with frequencies in the 33–130 cm−1 range (1–4 THz). By comparing these values with those reported in the literature, it was possible to assign the two highest frequencies. The mode at 130 cm−1 is the totally symmetric breathing mode corresponding to an in-phase modulation of the FeN bonding. The second mode around 80 cm−1 is the bending mode corresponding to torsion of the Fe-coordinating ligand. More interestingly, the bending mode seems delayed and builds up to the maximum amplitude at around 1 ps. This suggests a sequence of events, whereby the breathing mode is activated instantaneously, and after a short lapse the energy is transferred from the breathing mode to the bending mode. Hence, the transformation pathway connecting the initial photoexcited state to the final state involves several key reaction coordinates including breathing and bending of the molecule. These results show the need to replace the classical single coordinate picture used so far with a more complex multidimensional energy surface.
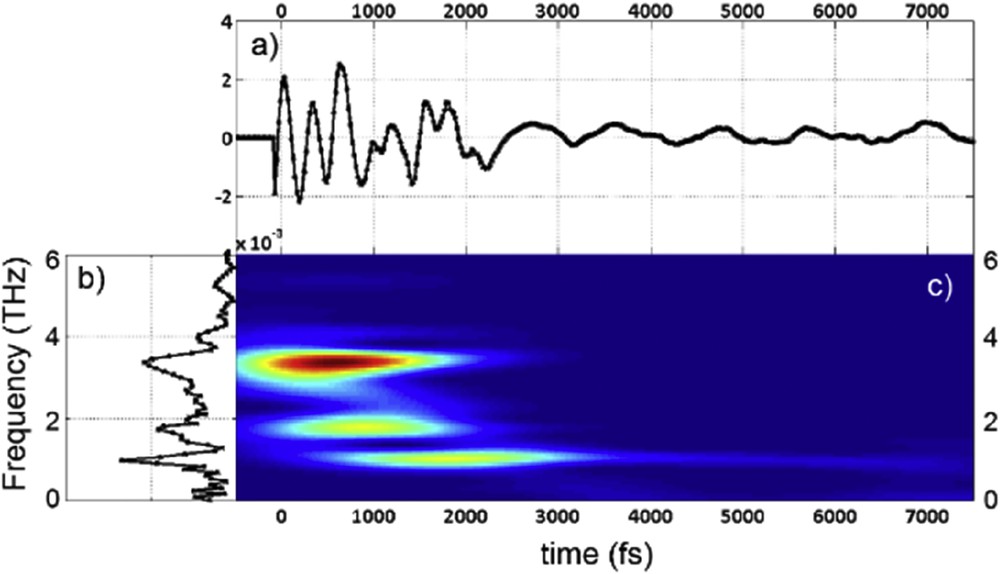
(a) Residual transient optical changes after femtosecond excitation in [Fe(Phen)2(NCS)2]. The transformation kinetic traces are removed for keeping the oscillating components. (b) Time-dependent Fourier transform of the corresponding dynamics in frequency domain, revealing the sequential activation of several phonon modes.
Coherent dynamics was also observed in several iron-based materials with modes in the range 30–100 cm−1, most likely revealing the breathing mode and lattice phonon modes [54]. Let us very briefly discuss the latter. Typically, the energy difference between the HS and LS potential is around ∼100 meV. This and the fact the photon energy of the pump laser is greater than 1 eV imply that most of the initial energy imparted on the system has to dissipate. Eventually, the conversion of electronic energy into vibrations will end with the activation of lattice phonon modes of low frequency (large wavelength), the latest to occur in a sequence of structural dynamics events observed with femtosecond optical spectroscopy [54]. This complex local dynamics represents the first stage of an out-of-equilibrium dynamics occurring at the local molecular level. In the case of the quantum efficiency reaching unity, one photon will switch one molecule. Overall, the observed dynamics during the initial stage are similar to the ones in diluted systems and such a trend was reported for different materials [55].
With ultrafast spectroscopy, the reverse LIESST process can also be investigated in the solid state. It consists in a reverse conversion from HS to LS, for example, 5T2 to 1A1 reported for [Fe(ptz)6](BF4)2 compound (Fig. 9) [33]. The proposed mechanism is the following [44]: the HS state is optically excited to a metal center state 5E conserving the spin multiplicity ΔS = 0. This electronic state is populated within the laser pulse duration and will quickly relax via ISC to a ligand field state 3T1 with a change in spin multiplicity ΔS = 1. The time constant for this first process was found to be 1.1 ps, indicating slower dynamics than that reported for the forward LIESST (LS–HS). From there, the system undergoes another ISC with another change in spin multiplicity ΔS = 1, with a time constant of 39 ps to finally reach the 1A1 LS ground state (Fig. 9). The lifetime of the lowest energy ligand field state (39 ps) suggests that the system is vibrationally relaxed when arriving in the LS potential that constitutes a striking difference with the LIESST case. This study has revealed the path followed by the system after d–d excitation and allowed determination of the transient states lifetime.
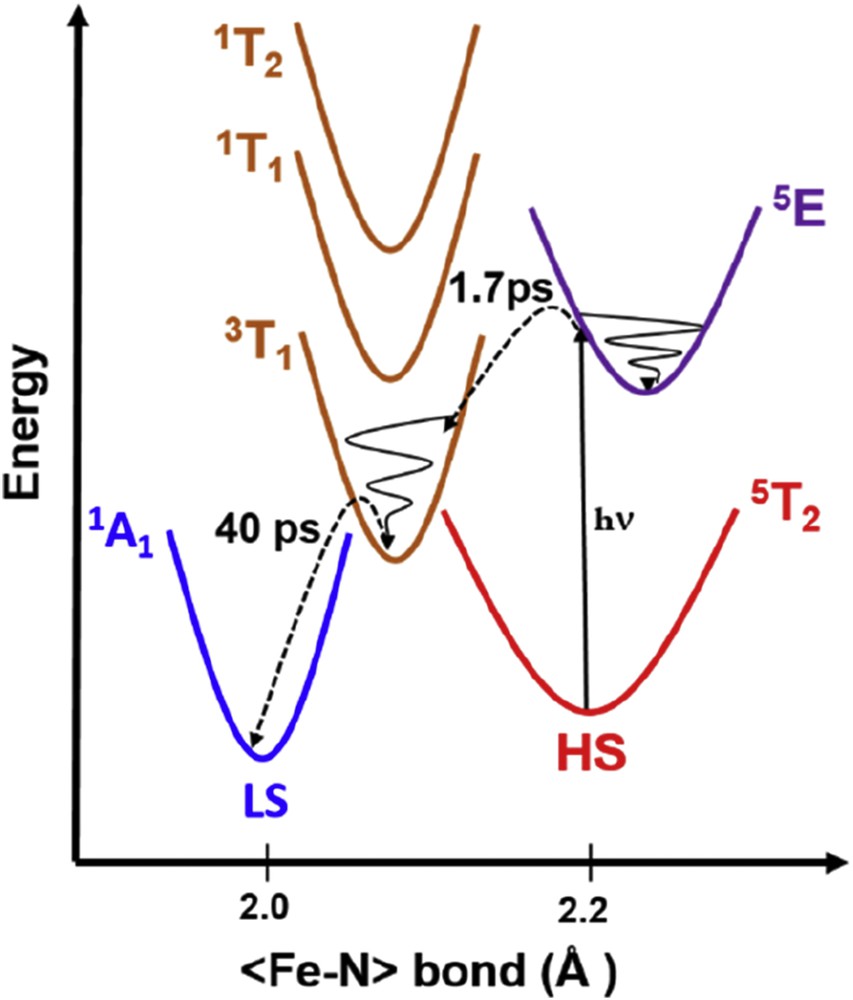
Schematic PES during reverse LIESST with lifetimes of transient excited states. Adapted from Ref. [44].
3.2.3 Multiscale dynamics
When an SCO material is impacted by an ultrashort laser pulse, it triggers a complex out-of-equilibrium dynamics involving different degrees of freedom (electronic, molecular structure, and lattice) launching the system onto a complex trajectory on PES. Indeed, each degree of freedom has a different response to such excitation and will act on different length and time scale starting from the local molecular process and extending to the material scale through propagative dynamics. To capture such complex dynamics, typically spanning many decades in time, a suitable optical setup is required to cover the complete range of dynamics from femtosecond to millisecond [56].
Out-of-equilibrium dynamics can be divided into three distinct steps, excluding the relaxation part that will be discussed in detail hereafter. At the femtosecond time scale, the laser pulse locally switches the molecules to the HS state, as previously explained. This is a local and linear process, whereby one photon switches one molecule, resulting in a one-to-one ratio between the number of absorbed photons and the number of switched molecules. The fraction of HS molecules switched in the initially LS lattice can be determined with optical spectroscopy (Fig. 10). Typical value of this HS fraction is a few percent and is manifested with a plateau in the time domain (phase 1). The newly formed HS molecules of larger volume generate stress within the LS state lattice of smaller structural parameters. In addition, a significant amount of energy imparted by the laser on molecules dissipates through lattice heating. These two concomitant features induce an internal pressure inside the crystal that is going to relax through macroscopic dilation. This deformation is mediated by acoustic phonons of long-range interaction and long period. The relevant time of this mechanism is the so-called “acoustic time scale”, determined by the length scale (i.e., the crystal thickness) and the speed of sound in the material. This lattice expansion favors the switching of additional molecules toward the HS state as shown in Fig. 10 when a second increase in HS fraction is observable around tens of nanoseconds (phase 2). It corresponds well to the crystal thickness (50 μm) over the speed of sound (∼2 km/s). This suggests propagative mechanism over the macroscopic scale of the crystal. Once the stress is relaxed, the material is still strongly out of equilibrium because the energy imparted by the laser pulse converts to heat and increases the average crystal temperature. In case of bulk single crystals, the penetration depth of light pulse can be smaller than the crystal thickness, thus leading to inhomogeneous excitation and consequently a gradient of temperature along the crystal thickness. The thermal equilibration of the lattice then occurs by heat diffusion following this gradient. The time scale of heat diffusion through a typical bulk crystal of tens of micrometers takes microseconds, which is similar in duration to the thermal equilibration of populations residing in HS and LS states (phase 3). The latter is driven by Arrhenius-like process, whereby energy barriers are overcome at a local molecular scale. Diffusion can precede thermal population on much smaller size than the bulk crystal. It was demonstrated on nanomaterials, whose lattice thermalized on the nanosecond time scale, whereas the thermal population invariably set in microseconds in the studied cases [57]. In case of a large single crystal showing gradual transition, this thermal process yields conversion of HS fraction as high as ∼15%. Finally, the material will relax to the LS ground state by equilibration with the surrounding thermal bath, typically a cryogenic gas stream. This last process sets the limit for experiments in the solid state, as the ground state has to be recovered between two consecutive excitation pulses [58].
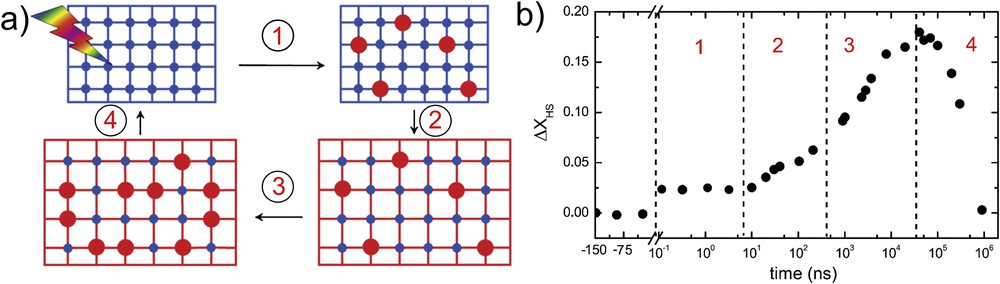
(a) Scheme of the out-of-equilibrium dynamics and (b) evolution of the transient HS fraction after a femtosecond excitation. Adapted from Ref. [59].
The investigation of such complex phenomena spanning 10 decades in time strongly benefits from a multiprobe approach sensitive to different degrees of freedom. For instance, combining time-resolved optical spectroscopy probing the electronic state, with X-ray diffraction probing the atomic structure, permits tackling such intertwined dynamics of both the electronic process and structural dynamics [59].
An interesting feature is the propagative nature of the elastic step, as the stress has to relax throughout the crystal. It was first reported in an experiment performed on single crystals of different thickness, with a ratio of 3 between them. The increase in the relevant length (the thickness) causes a prolonged crystal expansion over this axis with the expected factor 3. This expansion was concomitant with the second increase in HS fraction proving the direct relationship between the expansion and the increase in HS fraction. The validity of this picture can be questioned as the size of the sample shrinks to the nanoscale. Addressing such question is possible, thanks to the capability to synthesize crystals of exactly the same compound but in different sizes and shapes, thus allowing us to cover the size dependence of the phenomenon from micrometer to nanometer [60]. This investigation was performed on crystals of three different sizes: single crystals (∼300 × 200 × 15 μm3); microcrystals (∼7.5 × 0.64 × 0.21 μm3); and nanocrystals (∼950 × 270 × 35 nm3), respectively. The microcrystals and nanocrystals were dispersed in a polyvinylpyrrolidone matrix. The obtained results clearly demonstrated that only the elastic step is affected by the sample size. The elastic step shifts down to 200 ps in the case of smaller samples when compared to 20 ns in the case of large single crystals [61]. This reduction by two orders of magnitude scales well with size of these two samples. On the other hand, the intrinsic dynamics of phases 1 and 3 (the spin-state photoswitching and the thermal population of the HS state) are not affected. However, in the case of the nanocrystals, the surrounding environment composed of a polymeric matrix is a very efficient energy dissipation channel. It results in a reduction, or even complete suppression, of the last step of thermal nature. All these results emphasize that the size and the local environment play a role in the complex out-of-equilibrium dynamics of SCO materials.
3.2.4 Cooperativity: from linear to nonlinear regime
A crucial point where the solid state and dilute systems differ is the emergence of feedback mechanisms from the lattice. In the case of negative feedback, a more efficient and quicker recovery from the photoexcited state to the ground state will be favored. For SCO materials, it means that the lifetime of HS metastable molecules will be shorter than in the diluted system [55]. The inverse scenario is possible too, whereby a positive feedback leads to stabilization and even amplification of the newly formed photoinduced phase. Indeed, such features have been recently reported in nanocrystalline materials, where one photon absorbed switches ∼5 molecules on the acoustic time scale. It was observed through the increase in HS fraction from 6% at picosecond time scale to 27.5% at nanosecond time scale (Fig. 11) [61]. The latter illustrates the nature of SCO materials, in which the behavior of the ensemble cannot be understood in terms of a sum over individual elements. Indeed, in a diluted system the interaction with one photon will only switch one molecule, so the observation of several switched molecules per photon in a solid can be regarded as overcoming the unity quantum yield limit. To observe the above-mentioned amplification a threshold condition has to be met. As can be seen in Fig. 11, in the case of low light intensity only a relaxation of the HS fraction is observed. However, amplification is observed in the high excitation density case, thus suggesting the presence of a threshold value for the emergence of the cooperativity. A simple scheme allows us to explain this mechanism. If the fraction of HS molecules is low, the pressure exerted by the LS lattice is strong, which restores the previous equilibrium. The HS molecules of larger volume than the LS molecules are confined in a lattice with LS state parameters. If the fraction of switched HS molecules is sufficiently large, the overall pressure that these molecules exert on the lattice is enough to trigger volume dilation as the internal stress is released. This expansion occurring at the acoustic time scale allows more room for molecules to switch to the HS phase. Then the newly formed HS molecules cause again volume dilation and hence the feedback process leading to the elastically driven cooperativity. The exact origin of the internal pressure is not yet clear, as two concomitant processes occur. The switching of HS molecules induces a mechanical stress on the lattice, due to bonding elongation, but at the same time the excess energy imparted by the photons causes accumulation of internal pressure as the volume of the crystal remains constant during the dissipation of excess energy (a few tens of picoseconds).
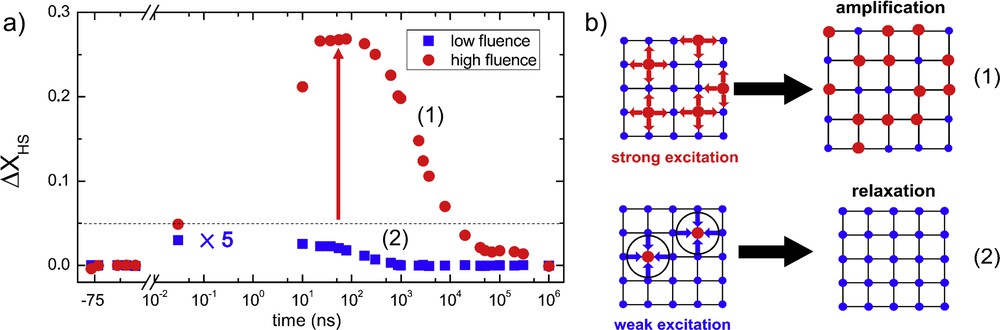
(a) Out-of-equilibrium dynamics of nanocrystals. The large self-amplification in the high fluence case in black exemplifies the notion of elastic switching. (b) Schematic representation of the threshold mechanism. Adapted from Ref. [61].
More insights into this intriguing phenomenon were obtained, thanks to the use of a newly developed mechanoelastical model, based on the Monte Carlo method [62]. In the latter, the crystal is simulated by a spring-and-ball model in which molecules are represented by rigid spheres bound to the neighboring molecules (spheres) via springs in a 2D grid. The state of the molecules is checked in a stochastic way with probability for a given molecule to switch from LS to HS and vice versa. By resolving the mechanical equation of motions, while allowing the molecules to switch between HS and LS states and consequently strain the springs of neighboring molecules, the whole system is followed out of its mechanical equilibrium. The model is first tried to reproduce the basic phenomena of materials, such as first-order transition and hysteresis. It reproduces very closely the experimental observation of elastically driven self-amplification [61], including the appearance of a threshold value. Simulations also suggest a clustering of HS molecules toward the edge of the crystals, and the influence of parameters such as the homogeneity of the excitation or the lattice rigidity.
4 Relaxation of the photoinduced state
4.1 Theoretical description
On the basis of the PES diagram (Fig. 4b), the photoinduced HS state, owing to its metastable character, will relax back to the LS ground state. In 1980, Buhks et al. [63] have theoretically described this relaxation as a nonadiabatic multiphonon process. As it involves two vibrational potential wells, molecular vibrations and phonons are crucial in this process, driven in the first approach by the separation between two potential wells (Fig. 12a). This theoretical approach [63] and experimental results [64,65] evidenced that this relaxation strongly deviates from a simple Arrhenius law because at low temperature the relaxation process is temperature independent while a thermally activated process occurs at elevated temperature [66].
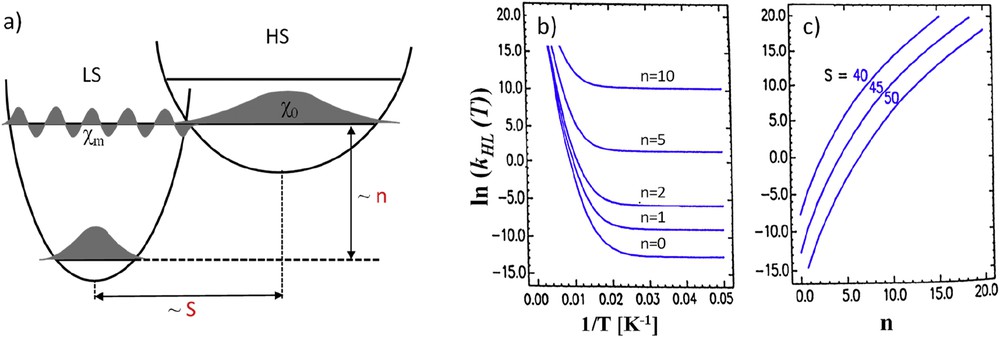
(a) Scheme of the LS and HS potential wells with example of vibrational wavefunction. (b) Evolution of the calculated ln kHL(T) as function of 1/T with S = 45 at various reduced energy n values. (c) Calculated tunneling rate at T → 0 as a function of the n parameter at various S values. Adapted from Ref. [65].
In this approach, the relaxation rate is given by Eq. 1 in which βHL is the electronic coupling matrix element provided by second-order spin–orbit coupling (∼150 cm−1), ℏω is the vibrational frequency of the metal–ligand breathing mode (∼250 cm−1), and f its strength. Finally, Fn(T) is the thermally averaged Franck–Condon factor given by Eq. 2. This Franck–Condon factor accounts for the thermal population of all m vibrational levels of the HS state. Using the LS state as reference, the energy of a vibrational state can be estimated as m′ = m + n, where n is the reduced energy gap equal to . For T → 0, Fn(T → 0) simplifies as shown in Eq. 3. In this equation, S is the Huang–Rhys factor S = ½fΔQ2/ℏω with ΔQ = ΔrHL accounting for the variation in the bond length during the HS to LS transition. This S factor is typically on the order of 45 for iron(II) compounds.
| (1) |
| (2) |
| (3) |
From this set of equations, a temperature-independent relaxation rate at low temperature can be determined (Fig. 12a and b). In addition, the relaxation rate at T → 0 K increases exponentially with increasing n values. In other terms, the higher the zero point energy difference the faster the relaxation. Because at low temperature this energy difference is related to the transition temperature T1/2, compounds with high transition temperature will exhibit the metastable HS state with short lifetimes at low temperature. This behavior is known as the “inverse energy gap law”. Moreover, this kHL(T → 0) relaxation rate decreases with increasing S values (Fig. 12c). It means that the larger the metal–ligand bond length changes, the slower the relaxation. In summary, long metastable state lifetime will be favored by low T1/2 and strong structural reorganization. This first trend has driven many researches to increase the structural changes in SCO materials.
After the discovery of the LIESST effect, most of the studies conducted on the lifetime of the photoinduced state have been done with UV–vis absorption and reflectivity, or IR and Raman spectroscopies, allowing easier sample preparation but a more limited range of time scales (from hours down to few minutes).
4.2 In solution
The relaxation kinetics have been studied in solution essentially in the family of iron(II)–polypyridyl complexes using spectroscopic methods such as laser temperature jump [20,21], ultrasonic method [67], and laser flash photolysis [30,39,64,68]. Although laser temperature jump and ultrasonic techniques mainly probe the SCO thermodynamics, laser flash photolysis was used similarly to the LIESST effect. It allows transient population of the HS metastable state and the probing of its lifetime in solution, around room temperature. The recorded lifetimes are consequently very short (∼tens of nanoseconds). Much longer long lifetimes (∼milliseconds) were recently reported [68] showing that the relaxation is not only governed by simple single coordinate configuration model, Fig. 4 (see Section 4.3.4).
In solution, the relaxation is expected to follow first-order kinetic law, obeying the Arrhenius thermal activation of the relaxation (Eqs. 4 and 5, where nHS is the HS fraction). However, in solution the molecular conformation could differ from that in the solid state. Therefore, the isothermal relaxation features could deviate from this simple law, with multiexponential relaxations. Moreover, quantum tunneling has not been observed because the studies have been conducted at temperature high enough to prevent solvent freezing.
| (4) |
| (5) |
4.3 In solid state
4.3.1 Methods used to measure the lifetime of the metastable state
In solid state, molecules are arranged in a long-range order. As a consequence, internal pressure effects due to the volume change will impact the SCO transition, as for the photoswitching process. Two methods can be used to record the lifetime of the photoinduced state. One way is the detailed analysis of the relaxation kinetics at different temperatures to extract the activation energy parameters, similar to studies in solution. The other way is to follow the lifetime of the metastable state by measuring the “relaxation temperature” called T(LIESST).
In 1986, Herber et al. [69] used variable-temperature Fourier transform IR spectroscopy to follow the thermal evolution of the metastable HS state. This study is based on the observation of sufficiently different IR fingerprints of the HS and LS states of [Fe(phen)2(NCS)2] [70] allowing us to identify the state under light irradiation. This is typical of cyanide-based complexes for which the metal–ligand bond strength is modulated by the spin state, leading to a shift in the νCN vibration (∼2100 cm−1). On the basis of this, the authors defined a temperature T2 above which the light-induced phenomenon is no longer observable with the technique used. They attempted to correlate this value with the thermal spin transition temperature T1, but this comparison was only done on the basis of six iron(II) SCO materials leading to inaccurate results. It may be explained by the fact that the IR probe laser of the spectrophotometer could induce the LIESST effect.
The idea of recording the relaxation temperature above which the metastable HS state is erased was followed by Létard and co-workers [71,72]. Fig. 13 presents a typical measurement performed on the mononuclear SCO complex, [Fe(dpp)2(NCS)2] (dpp = dipyrido[3,2-a:2′,3′-c]phenazine), using an SQUID magnetometer [71]. The magnetic response is expressed as the χMT product (χM stands for the molecular magnetic susceptibility and T the temperature). Light irradiation is applied to the material at 10 K in the diamagnetic LS state to induce the population of the paramagnetic HS state resulting in an increase in the magnetic signal. The irradiation is stopped when photosaturation is reached. Afterward, the temperature is slowly increased at a rate of 0.3 K/min while the magnetic behavior is recorded. Typically, the magnetic response of the light-induced HS state remains almost constant up to 40–50 K. A slight increase in χMT is observed between ca. 10 and 20 K and can be attributed to zero-field splitting of the HS state in a nonideal octahedral environment. Up to 40–50 K, the relaxation process is governed by the quantum tunneling regime through the energy barrier. Such an effect is negligible with regard to the experimental time scale. Above this region, the relaxation process becomes thermally activated and the efficient relaxation induces a decrease in the χMT product that recovers its original value. The T(LIESST) is determined by the minimum of the ∂χMT/∂T curve (inset of Fig. 13).
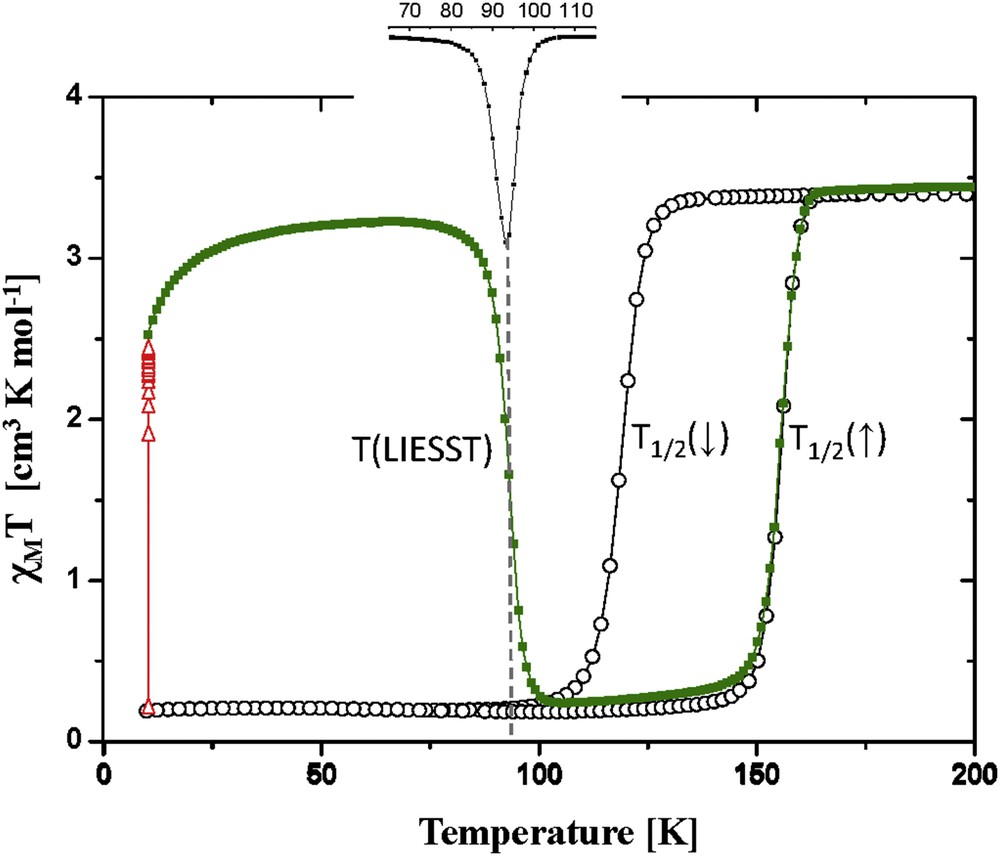
T(LIESST) experiment recorded for the mononuclear [Fe(dpp)2(NCS)2] complex [73] with (○) the temperature dependence of χMT recorded in the cooling and warming modes without irradiation, () the change recorded during 1 h of irradiation at 10 K, and () the behavior recorded during the warming mode (0.3 K/min) when the light irradiation was switched off. The inset reports the ∂χMT/∂T curve.
Caution is required when recording the T(LIESST) of different materials. Indeed, the very same procedure has to be followed irrespective of the technique used, in particular the same heating rate. Several studies have shown how crucial the latter point is [72e,g,73]. It has to be pointed out that T(LIESST) is not a critical temperature (because it depends on the temperature scan rate). Indeed, this temperature scans both the tunneling and thermal activated regions of the relaxation leading to a strong dependence on the time scale of the technique used. Laser flash photolysis, ultrafast X-ray diffraction, and spectroscopy can detect the photoinduced LIESST state far above the T(LIESST). It is therefore an empirical method used for fast testing and comparison of samples. In that sense it has provided several insights and trends to obtain long-lived metastable states.
4.3.2 Noncooperative materials
Noncooperative materials were initially investigated to minimize the effects of the elastic strains taking place during the transition. It has allowed the study of relaxation at low temperatures in conditions close to solution phases. Several conclusions have been drawn from this molecular behavior. First, the relaxation kinetics follow a first-order law described by Eqs. 4 and 5 [74]. It emphasizes the fact that “isolated” molecules were probed in these weakly interactive materials. Second, the quantum tunneling region was investigated and brought experimental evidences to the theoretical nonadiabatic multiphonon description [65,75]. Third, in some cases, a deviation from the first-order kinetics was observed and described as a distribution of activation energy. This distribution causes relaxation to take on the shape of stretched exponential that has been ascribed to material inhomogeneity.
A brief remark on how these noncooperative materials are obtained should be added. Most of the compounds are solid solutions of iron(II) SCO units dispersed in an isostructural network built on a non-SCO ion such as [FexM1−x(ptz)6](BF4)2 (with M = Zn, Mn, Cd, Ni, and Co) [65]. Hauser et al. have shown that the tunneling rate kHL(T → 0) strongly depends on the non-SCO ion while the thermally activated region is almost unaffected. It demonstrates that, even in noncooperative materials, the internal pressure plays an important role on the lifetime of the metastable state. In general, the bigger the non-SCO ion, the longer the lifetime. The inert host network exerts an internal pressure on the iron(II) proportional to its ionic radius. As a consequence, big host ions such as manganese or cadmium will stabilize the HS state. This has been widely demonstrated on the thermal SCO and is reflected on the lifetime of the metastable state [73,76]. This observation evidenced the influence of the network on the relaxation kinetics. Another approach consisted in inserting SCO complexes into the polymeric matrix [77] leading to similar observations, with deviation from simple exponential decay.
4.3.3 Cooperative materials
Because cooperativity in SCO materials arises from the presence of ferroelastic-like interactions [78], internal pressure plays a crucial role on the photoinduced state lifetime demonstrated in 1985 [79]. From optical studies, Hauser et al. [80] have observed that the relaxation kinetic feature is sigmoidal, due to a self-acceleration process coming from cooperative behaviors. Solid solutions with an increasing amount of iron(II) or polymorphs may exhibit either cooperative or noncooperative relaxation features (Fig. 14a and b). In the self-accelerated case, the relaxation is slower than the ones following first-order kinetics at short time scale but tends to be faster at longer time scale. It is the consequence of the variation in the internal pressure inside the material during the SCO transition (Fig. 14c). After complete photoconversion, when the first HS molecules switch back to the LS ground state, they shrink in a matrix made of HS molecules. The pressure exerted by this matrix on the LS molecules is weak inducing a slow relaxation rate. When the amount of LS molecules increases, the matrix becomes more and more constrained. Consequently, the internal pressure exerted on the remaining HS molecules increases due to cooperative interactions. The stressed HS molecules experience a reduction in the energy barrier, speeding up the relaxation process. This self-acceleration process because of a change in the energy barrier along the HS → LS relaxation was translated in Eqs. 6 and 7, where the relaxation rate depends on the HS fraction:
| (6) |
| (7) |
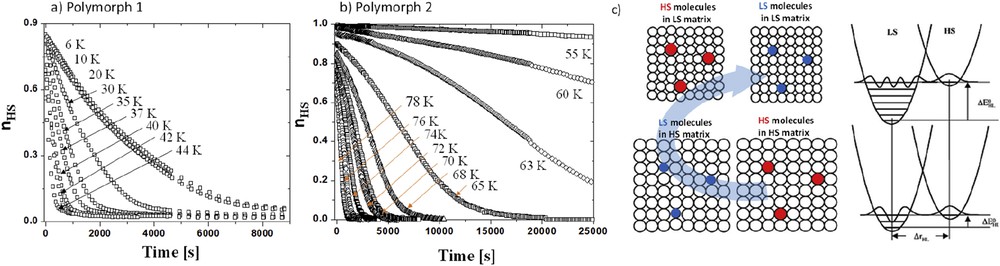
Relaxation kinetics of polymorphs 1 (a) and 2 (b) of the [Fe(PM-BiA)2(NCS)2] compounds [72e]. (c) View of the internal pressure effect due to cooperative interaction along the HS → LS relaxation. Adapted from Ref. [66].
Cooperativity plays a crucial role on the relaxation kinetics leading to self-acceleration and nonlinear behavior. However, changes in cooperativity weakly affect the relaxation rate or the T(LIESST) [66,70]. In real cases, cooperativity comes together with other structural effects that could strongly affect the photoinduced HS state lifetime.
4.3.4 Influent parameters
Since 1984, many studies have been undertaken giving important clues on ways to tune the lifetime of the photoinduced state. There are two levels at which chemistry can act: the molecule and the surrounding network.
The inverse energy gap law has given some useful trends to favor long-lived photoinduced HS states. The higher the transition temperature, the faster the relaxation. The transition temperature T1/2 reflects the required thermal energy to induce the LS → HS switching and therefore primarily depends on the ligand field strength. However, because it is a thermodynamic parameter equal to ΔH/ΔS, it depends also on the global entropy of the material and many parameters may affect this value. The network also plays a key role regarding the lifetime of the metastable state. For instance, in solid solutions the size of the host network strongly tunes the quantum tunneling relaxation rate [65]. Hence, cadmium and manganese of larger size than the iron in its HS state stabilize the HS state by exerting a ‘‘negative” internal pressure. It leads to an important decrease in T1/2 and an increase in the T(LIESST) value. Zinc and cobalt, with a similar ionic radius to iron HS state, induce no change in T(LIESST) but shift T1/2 toward lower temperatures. Finally, nickel with an almost intermediate ionic radius between iron HS and iron LS generates a slight decrease in T(LIESST) and T1/2 with increasing doping level [81].
From the molecular point of view, the nonadiabatic multiphonon theory has evidenced that the greater the metal–ligand bond length variation, the weaker the overlap between the potential wells, and by consequence the slower the relaxation. However, studies using phosphorus ligand–based complexes that present larger ΔrHL variations [82] have shown some photoswitching effects without any clear improvement compared to nitrogen-based ligands [83]. The use of the T(LIESST) measurement has brought important insights gathering the [T(LIESST), T1/2] values of more than 50 compounds [72]. In agreement with the inverse energy gap law, T(LIESST) was found to linearly follow T1/2 as T(LIESST) = T0 – 0.3T1/2. The lowest T0 values were found in complexes based on monodentate ligands, whereas the highest values correspond to pentadentate macrocyclic ligands. At a given transition temperature T1/2, the T(LIESST) increases as a function of the denticity of the ligand and the stiffness of the coordination sphere. However, the most promising parameter that would favor long-lived metastable states is the distortion of the coordination sphere. It implies that the single configurational coordinate (Fig. 4) is no more valid, as we already mentioned in Sections 3.2.2 and 4.3.4, because of the nonisotropic bond length variation [22,84]. From structure–property relationships, it appeared that T(LIESST) increased with the distortion of the coordination sphere [85]. In Fig. 15, the effect of distortion on the energy barrier is sketched, showing that for a given bond length variation, the increase in a distortion parameter increases the height of the energy barrier [66,68,86].
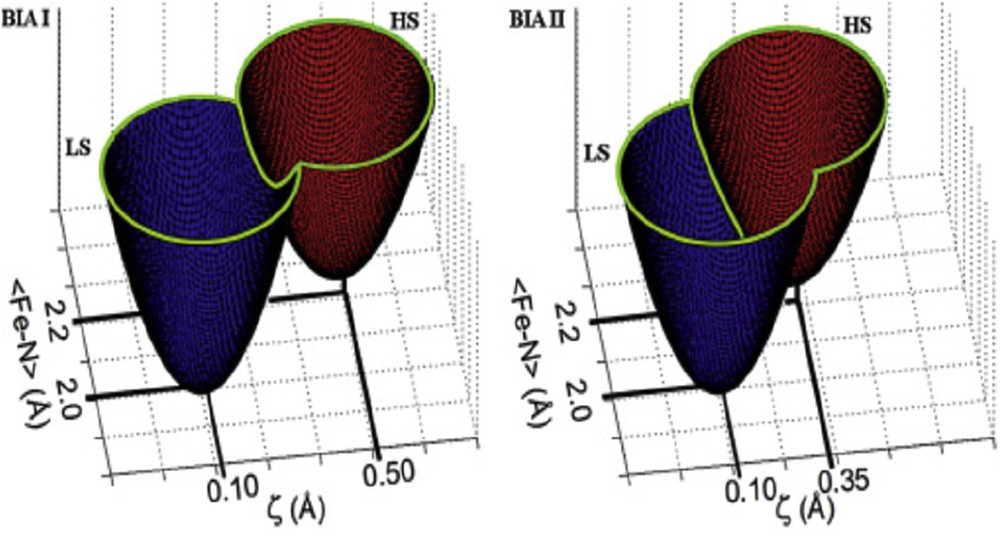
Sketch of the LS (blue) and HS (red) potential wells of polymorphs I (a) and II (b) of the [Fe(PM-BiA)2(NCS)2] compounds as a function of the FeN bond length and the distortion parameter [86a].
The lifetime of the metastable HS state depends on the inner coordination sphere geometry. The molecular packing acts as a perturbation that can modulate this lifetime in agreement with the inverse energy gap law.
5 Conclusion and outlook
Light-induced spin-state switching involves different physical processes depending on whether the ligands or the metal ions are excited. This review has covered most of the light-induced effects. Some of them were not presented such as light-induced thermal hysteresis [71,87], light-induced optical hysteresis [87a,88], and light-induced pressure hysteresis [89]. These effects are all based on the equilibrium between the population of the HS state by light, at various intensities, and its relaxation favored by the temperature or the pressure.
Thanks to a wealth of research, all excitation and relaxation pathways with corresponding mechanisms are well understood, from molecular (femtosecond) to macroscopic (nanoseconds to days) scale [59,90]. The combination of high-resolution techniques both spatially and temporally will benefit other developments of fast and efficient photoswitching at the nanometer scale. This will be particularly useful in the design of photoswitchable devices in which light is used to trigger the electrical [91] or mechanical [92] properties. Indeed, SCO molecules are increasingly implemented in nanodevices of molecular electronics [93].
Regarding the development of long-lived photoswitched states, three promising results are highly encouraging. The first one is the efficient LD-LISC effect in the solid state [13]. The use of photocyclizable units instead of photoisomerizable ones lowers the structural reorganization thus favoringthe cyclability of the process. The development of such weakly fatigable systems is of importance for their further integration in switching devices. The second strategy that appears promising is the photothermal effect inside a hysteresis loop centered at room temperature [23–29]. It offers a robust way of photoswitching that deserves more investigations to make it clearly reversible andwith larger hysteresis. The third promising result lies in the reversibility of the LIESST process. Indeed, this bidirectional process can be applied on materials blocked in their HS state. This has been recently demonstrated in paramagnetic networks [94] in which the long-lived HS state is switched into a long-lived LS state. It is particularly interesting to note that this photoswitching involves hidden hysteresis loops, for example, revealed using the light-induced thermal hysteresis approach [94d]. Because this hysteresis occurs below ∼100 K up to now, efforts have to be devoted to the increase in temperature toward ambient conditions. One interesting way to follow could be the elastic frustration of the network that was shown to inhibit totally or partially the SCO [95]. Moreover, the elastic frustration is responsible for symmetry breaking (cf. review from Guionneau and Collet, this issue) and the occurrence of multistability [88,96].
Challenges are therefore numerous and the good understanding of the light-induced SCO mechanisms will help in the design of fast, reversible, and energetically viable photoswitching at room temperature.
Acknowledgments
G.C. and C.D. thank the “molecules et matériaux commutables” group for the daily fruitful interactions, the Aquitaine Region, the CNRS, the University of Bordeaux, and the ANR for their support. M.L. and R.B. thank the colleagues from “Matériaux et Lumière” of IPR and all co-workers for a long-standing and prolific collaboration on SCO photoswitching in the solid state. We also express our gratitude to Région Bretagne, Rennes Metropole, CNRS, Univérsité de Rennes 1, and ANR for a sustained support. The authors thank the French network “magnétisme et commutation moléculaires” for the exchanges and the collaborative framework it affords.


