Thermodynamical aspects of the spin crossover phenomenon

William Nicolazzi; Azzedine Bousseksou

doi:10.1016/j.crci.2018.10.003

Account/Revue

Thermodynamical aspects of the spin crossover phenomenon
[Aspects thermodynamiques du phénomène de conversion de spin]

William Nicolazzi ¹ ; Azzedine Bousseksou ¹

¹ LCC, CNRS and University of Toulouse (UPS, INPT), 31077 Toulouse, France

Comptes Rendus. Chimie, Volume 21 (2018) no. 12, pp. 1060-1074.

Résumés

Anglais
Français

Fundamental aspects of spin crossover (SCO) mechanisms are reviewed through considerations of ligand/crystal field theory, thermodynamics, and modeling of the thermoinduced spin transition in the solid state based on macroscopic–mesoscopic approaches . In particular, we highlight success of thermodynamic models in the simulation of first-order spin transitions with hysteretic behaviors (bistability) and multistep conversions. Bistability properties originate from elastic interactions, the so-called cooperativity between SCO molecules in the crystal packing. Although physical and chemical properties and thermodynamical quantities of noninteracting SCO compounds can be readily injected in macroscopic models, taking cooperativity into account remains problematic. The relationship between phenomenological numerical parameters and experimentally accessible quantities can only be most of the time indirectly established. Recent extensions of these thermodynamical models to grasp SCO properties at the nanoscale and combinations with ab initio numerical methods show that macroscopic models still constitute useful theoretical tools to investigate SCO phenomena. The necessity to further probe the thermomechanical properties of SCO materials is also emphasized.

Dans cette revue, les aspects fondamentaux des mécanismes de conversion de spin sont abordés au travers de divers formalismes théoriques bien connus en physique et chimie de la matière condensée, tels que la théorie du champ de ligand/cristallin, la thermodynamique des mélanges binaires et les modèles macroscopiques–mesoscopiques associés pour simuler la transition de spin thermo-induite. En particulier, nous rapportons les différents succès des modèles thermodynamiques dans la simulation de transitions de spin du premier ordre présentant des phénomènes d'hystérésis (bistabilité) et des transitions en plusieurs étapes. L'existence du phénomène de bistabilité est directement reliée aux mécanismes d'interaction élastique entre les molécules à conversion de spin appelés « cooperativité ». Alors que les propriétés physiques et chimiques ainsi que les quantités thermodynamiques des composés à conversion de spin isolés peuvent être facilement injectées dans des modèles macroscopiques, la prise en compte de la coopérativité reste compliquée à réaliser. La relation entre les paramètres numériques phénoménologiques et les quantités accessibles expérimentalement ne peut être, la plupart du temps, établie que de manière indirecte. Des extensions récentes de ces modèles thermodynamiques destinées à mieux comprendre les propriétés de la conversion de spin à l'échelle nanométrique combinées à des méthodes numériques ab initio montrent que les modèles thermodynamiques constituent toujours un outil théorique utile pour étudier la transition de spin. La nécessité d’étudier davantage les propriétés statiques et de transport thermomécaniques de cette classe de matériaux bistables est également soulignée.

Métadonnées

Reçu le : 2018-07-02
Accepté le : 2018-10-15
Publié le : 2018-11-12

DOI : 10.1016/j.crci.2018.10.003

Keywords: Spin crossover, Thermodynamics, Cooperative effects, Phase transitions
Mot clés : Conversion de spin, Thermodynamique, Effets coopératifs, Transition de phase

Affiliations des auteurs :

William Nicolazzi ¹ ; Azzedine Bousseksou ¹

¹ LCC, CNRS and University of Toulouse (UPS, INPT), 31077 Toulouse, France

@article{CRCHIM_2018__21_12_1060_0,
     author = {William Nicolazzi and Azzedine Bousseksou},
     title = {Thermodynamical aspects of the spin crossover phenomenon},
     journal = {Comptes Rendus. Chimie},
     pages = {1060--1074},
     publisher = {Elsevier},
     volume = {21},
     number = {12},
     year = {2018},
     doi = {10.1016/j.crci.2018.10.003},
     language = {en},
}

TY  - JOUR
AU  - William Nicolazzi
AU  - Azzedine Bousseksou
TI  - Thermodynamical aspects of the spin crossover phenomenon
JO  - Comptes Rendus. Chimie
PY  - 2018
SP  - 1060
EP  - 1074
VL  - 21
IS  - 12
PB  - Elsevier
DO  - 10.1016/j.crci.2018.10.003
LA  - en
ID  - CRCHIM_2018__21_12_1060_0
ER  -

%0 Journal Article
%A William Nicolazzi
%A Azzedine Bousseksou
%T Thermodynamical aspects of the spin crossover phenomenon
%J Comptes Rendus. Chimie
%D 2018
%P 1060-1074
%V 21
%N 12
%I Elsevier
%R 10.1016/j.crci.2018.10.003
%G en
%F CRCHIM_2018__21_12_1060_0

William Nicolazzi; Azzedine Bousseksou. Thermodynamical aspects of the spin crossover phenomenon. Comptes Rendus. Chimie, Volume 21 (2018) no. 12, pp. 1060-1074. doi : 10.1016/j.crci.2018.10.003. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2018.10.003/

Version originale du texte intégral

1 Introduction

Spin crossover (SCO) compounds are switchable molecules capable of reversible switching from a low-spin (LS) electronic state to a high-spin (HS) electronic state [1–11]. This spin state change can be induced by various external stimuli such as temperature [11], pressure [12], light irradiation [13–17], magnetic [18] and electric field [19], guest molecules [20–22], and so forth. From a thermodynamic point of view, the switching from the low-spin (LS) to the high-spin (HS) vibronic state originates from a competition between enthalpy, which tends to favor the lower energy fundamental state at low temperatures, and the entropy, which favors the most disordered thermodynamic phase at high temperatures. In the solid state, SCO materials can exhibit a first-order transition involving the existence of a latent heat and hysteretic behaviors can also be observed [23,24]. Abrupt spin transition and bistability phenomenon occurs when intermolecular interactions between SCO compounds are strong enough. Intermolecular interactions have an elastic origin, mainly because of the difference in volume, shape, and elasticity between the HS and LS phases [25–27]. Indeed, a HS molecule surrounded by LS molecules generates a local elastic strain field, and an elastic stress builds up in the whole crystal [28–31]. The elastic collective behaviors can be viewed as a combination of both short- and long-range interactions, usually called cooperativity [25]. The strong complexity of interaction mechanisms coupled with molecular properties very sensitive to controllable small energetic inputs gives rise to a large diversity of experimentally observed phenomena, which is perfectly illustrated by the different possible thermoinduced SCO curves recorded in these materials (Fig. 1).

Fig. 1
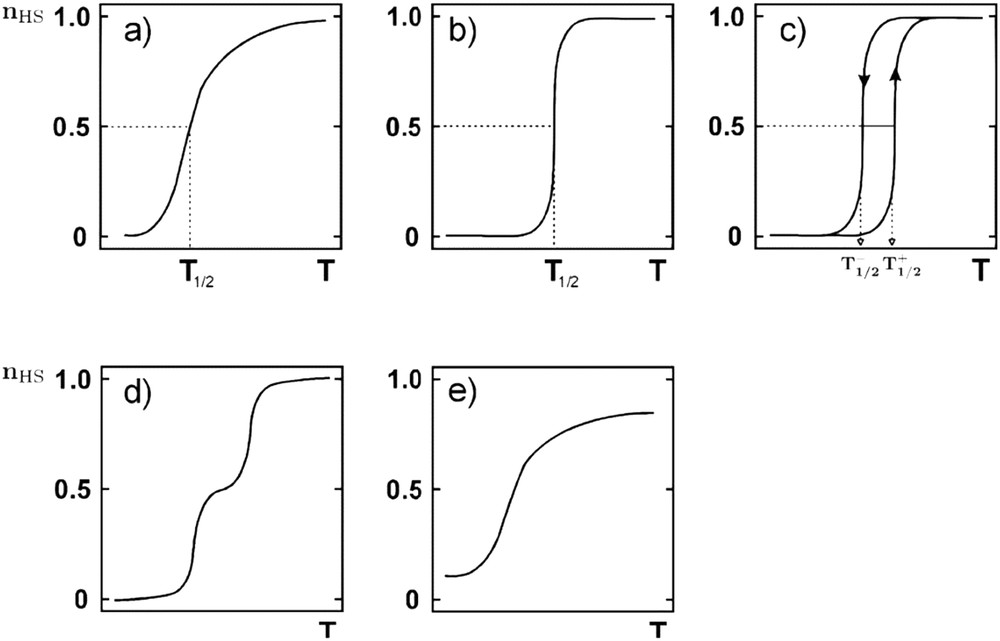
Schematic representation of the main thermoinduced SCO curves. The spin state change is followed by the thermal evolution of the fraction of molecules in the HS state, the so-called HS fraction (n_HS). (a) Gradual spin conversion, (b) abrupt spin transition, (c) abrupt spin transition with hysteresis loop, (d) two-step transition, and (e) incomplete spin conversion (from Ref. [11]).

To these behaviors are added the different nonequilibrium processes as photoexcitation [16], kinetic relaxations from metastable states [32–36], dynamical equilibrium [37,38], ultrafast experiments [39–43], and so forth.

Because of the drastic modifications in physical properties of the SCO materials upon an SCO (magnetic, optical, electric, structural, vibrational, elastic, etc.), static, quasi-static, and nonequilibrium spin state changes can be monitored by various experimental techniques (magnetic, optical measurements, vibrational spectroscopies, Mössbauer techniques, etc.) [8,11]. In parallel to these intense experimental investigations, the modeling of SCO phenomena has been developed early. Initially, theoretical studies have mainly focused on the reproduction of spin conversion curves and the understanding of the different accessible experimental data. To this aim, macroscopic thermodynamic models have been introduced, in which the available physical quantities from calorimetric, crystallographic and spectroscopic measurements are injected, in addition to more phenomenological model parameters. At the same time, models based on statistical physics' considerations (Hamiltonian approaches), usually called microscopic models, have been proposed with the aim to give a description of SCO phenomenon at the chemical bonds and at molecular level (for an overview of microscopic models see also Refs. [44,45]). This class of model allows analyzing the spin conversions beyond the mean field or Bragg–Williams approximation, considering spatial fluctuations and correlations [46–50].

Historically, the first simple use of microscopic approaches for SCO systems has been initiated on the basis of discrete multilevel fictitious spin models [51]. Starting from a four-level fictitious spin model [52], a degenerated two-level Ising model has been developed in the 1990s, in which intermolecular interactions between Ising spins are described by phenomenological exchange-like coupling [53]. The so-called Ising-like model allows retrieving one-step/two-step thermal conversions and the main different results obtained from macroscopic models [53,54]. This later approach gave a microscopic origin to SCO phenomena, by specifying the possible ordering processes originated from the observed macroscopic curves (modulated structures, quenching, etc.).

The prediction of the SCO curves of a particular material from only a simple consideration of the molecular structure remains nowadays impossible. Indeed, the SCO phenomenon is still a complex problem: a small chemical modification of the SCO compound leads usually to strong modifications of the thermal switching behavior and structural properties affecting cooperative mechanisms and so on. The polymorphism of SCO materials, shown in Fig. 2, highlights this limited power of prediction of both macroscopic and microscopic models.

Fig. 2
An example of experimental thermal evolution of magnetic susceptibility measured in three polymorphs of the same complex [FeL_Br (dca)₂], where L_Br is N,N′-bis [(5-bromo-2-pyridyl)methyl] ethane-1,2-diamine and dca is dicyanamide [55]. α form exhibits abrupt spin transition with hysteresis, β form a two-step spin transition, and γ form does not present an SCO.

During the past few decades, a particular interest fell on the detailed analysis of the different spatial and temporal steps of the spin state change [56]. The different observations, in the case of abrupt SCO, show that the first-order character of the spin transition in highly cooperative materials gives rise to heterogeneous phase transformation, whereas homogeneous phase transformations are observed in weakly cooperative or diluted systems (Fig. 3).

Fig. 3
Schematic representation of the transition mechanisms and associated thermal spin transition curves in three characteristic SCO systems having different degrees of cooperativity: (a) in solution (no cooperativity, gradual conversion); (b) in a solid exhibiting a weakly cooperative spin conversion (intermediate cooperativity, more abrupt transition); and (c) in a solid exhibiting a first-order spin transition (high cooperativity, abrupt transition with thermal hysteresis loop). LS and HS molecules are depicted by blue and red circles, respectively [56].

Microscopic models seem to be more suitable to grasp nucleation and domain growth mechanism. Therefore, the Ising exchange-like coupling has been substituted by a more realistic description of elastic interactions and by a better modeling of electron–phonon coupling, including lattice distortions [57]. Strongly inspired by the study of Bari and Sivardière [58] and a mesoscopic approach of Spiering and Willenbacher [26,27], atom–phonon [59] and spin–phonon (mechanoelastic [60] electroelastic [61], anharmonic [62] spin–phonon) models have emerged in the beginning of the 21st century (see also Ref. [45] and references therein). Different aspects and mechanisms of spatiotemporal dynamics have been successfully explained by such class of models (for an overview see also Ref. [56] and references therein).

However, quantitative analysis and predictions of the spatiotemporal behaviors of particular SCO compound are nowadays not achieved. The knowledge of elastic, mechanical (bulk, Young and shear moduli, Poisson ratio, etc.), and thermal transport properties (thermal conductivity, convection transfer coefficient, etc.) remains scarce [63–68], and it is still difficult to relate such macroscopic quantities to parameters of microscopic models [69].

A similar limitation is encountered in another hot topic of the SCO phenomenon: size reduction effects [70–77]. An important question concerns the becoming of phase stability, bistability and the major macroscopic observed properties after size reduction, at the nanoscale, and the consequence of the predominance of surface physical properties on the spin transition.

In this review, different thermodynamic aspects of the SCO phenomenon are reviewed. First, basic considerations of crystal field theory and thermodynamics are recalled. Then, the different thermodynamic models including cooperativity through phenomenological terms, simulation of electron–phonon coupling, or continuum mechanics approach are reported, and their respective results concerning the simulation of spin transition curves are discussed. Finally, recent developments of thermodynamic models coupled with ab initio calculations for the simulation of two-step transitions are presented. Finally, recent nonextensive thermodynamic approaches, taking surface/interface contributions in SCO nanoparticles into account, are evoked.

2 Thermodynamic aspects

2.1 Crystal field theory

The understanding of the SCO phenomenon starts with the study of the required electronic properties for a molecule to be switchable. In a first step, the molecular energy spectrum has to be determined. However, the complicated electronic structure of a SCO molecule prevents to obtain analytical solutions from Schrödinger's equation. In the past few decades, first principle and quantum chemical calculations adapted for SCO molecules have been intensively developed and success in the simulation of molecular vibrational properties has been realized [78]. However, the systematic prediction of the ground state and the precise estimation of the ground energy level remain a challenge. Therefore, it becomes essential to use more simplified approaches. In this sense, crystal field theory is very convenient to qualitatively describe the SCO electronic structure and spin conversion phenomenon [79]. In this context, ligands are considered as punctual electric charges interacting with the metallic cation. The octahedral symmetry leads to a partial degeneracy splitting of the 3d energy level of the metallic cation. For example, for the Fe(II) cation, the five 3d orbitals are degenerated in the absence of the ligands. When this cation is placed in an octahedral field formed by six ligands, electrons of the cations are submitted to repulsive forces and the occupation of d orbitals is governed by electrostatic energy minimization. The 3d energy level splits into two levels: a lower energy level t_2g, containing the three degenerated orbitals d_xy, d_xz, d_yz, and a higher energy level e_g formed by the two orbitals d_z² and d_x²_-y². The energy difference between these two levels can be expressed in terms of ligand field force or crystal field splitting being 10 Dq, where Dq corresponds to a semiempirical parameter related to the crystal force field. The energies of the t_2g and e_g levels can be divided into two contributions: a spherical part whose only effect is to shift the electronic levels of the free ion and another contribution related to the lowering of the symmetry leading to the degeneracy partial splitting (Fig. 4).

Fig. 4
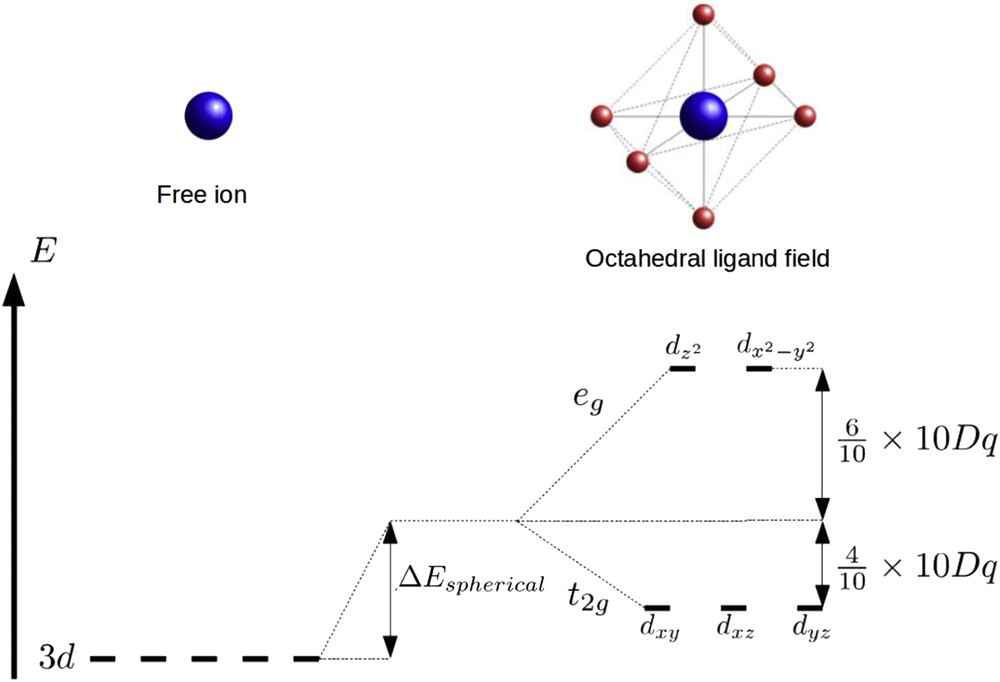
Schematic representation of the partial degeneracy splitting of 3d orbitals due the presence of the octahedral ligand field.

At the molecular scale, two main effects compete: on one hand, electrons tend to occupy d orbitals according to Hund's rule due to the exchange coupling. On the other hand, electrons tend to fill the t_2g level, which is the lowest energy level. The consequence of these antagonist effects is the existence of two possible ground states according to the strength of the ligand field that is strongly spin state dependent in comparison with the electron pairing energy Π, which is almost insensitive to the spin state. In the case of a weak ligand field, electrons mainly occupy t_2g orbitals and the total spin momentum takes a minimal value (S = 0 for Fe(II)), corresponding to the LS state (¹A_1g term symbol). On the contrary, when the ligand field is strong in comparison with the electron pairing energy, electrons occupy a maximum number of orbitals, in agreement with Hund's rule, and the spin momentum value is maximal (S = 2 for Fe(II)) corresponding to the HS state (⁵T_2g term symbol). When the ligand field force is of the same order of magnitude of electron pairing energy, any small external perturbation is able to switch the molecule from one to the other spin state in a reversible manner.

This phenomenon is called spin crossover, spin equilibrium, or spin conversion and commonly spin transition. The range of ligand field values for which an SCO can be observed is narrow as it can deduced from the Tanabe Sugano's diagram (Fig. 5). A first direct “consequence” of this electronic configuration change upon LS to HS conversion is an increase in metal–ligand distances, around 10%, corresponding to an increase in the octahedron volume of about 25%. This variation suggests important differences in terms of vibration modes as inferred from IR and Raman spectroscopy measurements (Fig. 6). For example, in a FeN₆ octahedron_, stretching vibrational modes ν_(FeN) are greater in the LS state than in the HS state with typical ratio ν^LS_FeN/ν^ΗS_FeN ranging from 1.1 to 1.9 [81].

Fig. 5
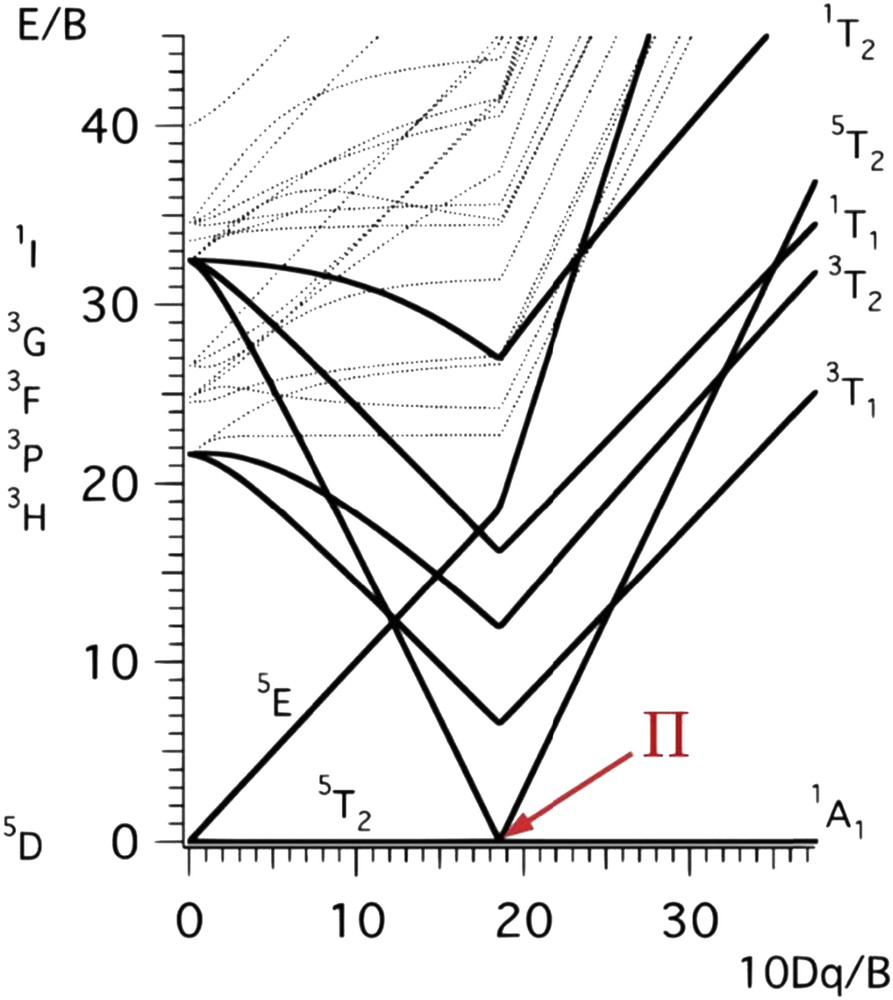
Tanabe Sugano's diagram giving the energy levels of the electronic state as a function of the ligand field energy for a metallic ion of electronic configuration d⁶ embedded in a octahedral ligand field (Racah parameter B: electronic repulsion [80].

Fig. 6
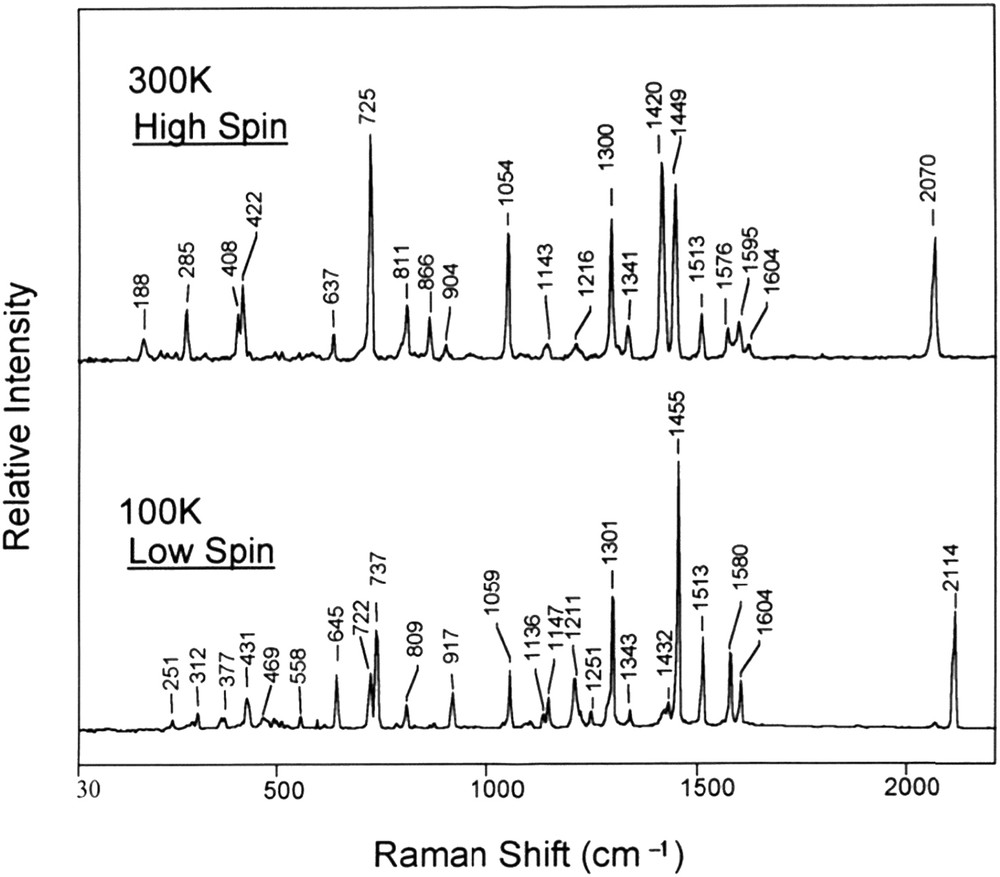
Raman spectra of Fe (phen)₂(NCS)₂ in the HS state (300 K) and LS state (100 K) [81]. In the range <600 cm⁻¹ where the entropy values are maximized, the average of vibrational modes are ν_av,HS = 298 cm⁻¹ and ν_av,LS = 393 cm⁻¹ in the HS and LS states, respectively, leading to a ratio ν_av,HS/ν_av,LS ∼1.3.

A thermoinduced spin conversion is possible when the difference between the zero-point energies of the two spin states has the same order of magnitude as the thermal energy, that ΔE = E^HS₀ − E^LS₀ ≈ k_BT. In SCO compounds, the zero-point energy corresponds to the sum of electronic and vibrational contributions. Except for few rare SCO compounds [82–86], the lowest zero-point energy is the LS state and thus the ground state is the LS state at zero temperature (Fig. 7). However, at high temperature, the HS state becomes the thermodynamic stable state. This change is due to the entropic contributions, which are more important in the HS state than in the LS state. Indeed, the entropy difference has two origins: electronic origins due to a higher spin multiplicity (and to a lesser extent to the orbital momentum, vide infra) in the HS state and especially a vibrational origin due to weaker vibrational frequencies [80]. It is commonly accepted that the SCO can be seen as an entropy-driven phase conversion.

Fig. 7
Schematic representation of a configurational diagram in the case of an Iron(II) complex. The two spin states are represented by a harmonic potential double well in the adiabatic approximation (T = 0).

2.2 Thermodynamic aspects of the spin conversion

When SCO molecules interact with an external environment, the spin conversion phenomenon can be understood by axiomatic thermodynamic aspects. In a first step, a set of N noninteracting (isolated) SCO molecules in contact with a thermal bath T is considered with a possible control of the external pressure P, the so-called isothermal and isobaric ensemble (N,P,T). At constant pressure, the spin conversion can be viewed as a thermal equilibrium between two phases. The relevant state function for such experimental conditions corresponds to Gibbs energy G = H − TS, where H and S stand for the enthalpy and the entropy of the system, respectively. Thermodynamic properties of the system are described by the Gibbs energy difference between the HS and LS phases:

Δ G = Δ H - T Δ S

(1)

where ΔH = H_HS − H_LS is the enthalpy variation [87] and ΔS = S_HS − S_LS is the entropy variation of the system. We can define the equilibrium temperature T_1/2 for which there are the same proportions of HS and LS molecules corresponding to ΔG = 0:

T_{1 / 2} = \frac{Δ H}{Δ S}

(2)

From Eq. 2, when T < T_1/2 the enthalpic term is dominant and the LS state is favored, whereas for T > T_1/2, the entropic term becomes dominant and the HS state is favored, justifying hence the terminology “entropy-driven phase conversion”.

Let us consider the different contributions to enthalpy and entropy variations. ΔH can be subdivided into two parts: a temperature-independent electronic part ΔH_el and a vibrational part ΔH_vib. In a similar manner, ΔS can be arbitrarily divided into different contributions to the statistical disorder:

Δ S = Δ S_{el} + Δ S_{vib} + Δ S_{trans} + Δ S_{rot}

(3)

The two last terms ΔS_trans and ΔS_rot correspond, respectively, to the entropy variation due to translation and rotation, respectively, and are neglected most of the time in the solid state. The first term ΔS_el = ΔS_orb + ΔS_spin is the electronic entropy variation and originates from the difference in terms of degeneracy (orbital and spin momenta) between the HS and the LS electronic states:

Δ S_{orb} = R ln (\frac{2 L_{HS} + 1}{2 L_{LS} + 1})

(4.1)

and

Δ S_{spin} = R ln (\frac{2 S_{HS} + 1}{2 S_{LS} + 1})

(4.2)

where R is the perfect gas constant. L_i and S_i (i = HS, LS) are, respectively, the total orbital and total spin momenta of the spin state i. In the ideal situation of a SCO Fe(II) complex with a perfect octahedral symmetry, we have ΔS_spin=R ln (5) = 13.38 J mol⁻¹ K⁻¹ and ΔS_orb = R ln (3) = 9.13 J mol⁻¹ K⁻¹ (for the real cases, the local symmetry of the iron(II) is usually lower, the orbital momentum is “blocked” to L = 0 and the orbital contribution to the entropy change is usually neglected). In such case ΔS_el = ΔS_spin > 0.

Electronic entropy favors the HS state and is temperature independent. The second term ΔS_vib is the vibrational entropy variation. In the case of isolated molecules, ΔS_vib is only dependent on the variation of intramolecular modes between the HS and LS states. In the solid states, the contribution related to intermolecular vibrations has to be added, even if this contribution is often considered as less important than the intramolecular part (in fact intramolecular and intermolecular vibrations are coupled and it is difficult to distinguish their respective contributions). Vibrational entropy can be expressed as follows (a more detailed analysis is described in Ref. [82]):

S_{vib} (T) = R \sum_{λ} (- ln [1 - e^{- h ν_{λ} / k_{B} T}] + \frac{h ν_{λ}}{k_{B} T} \frac{1}{exp (h ν_{λ} / k_{B} T)})

(5)

where the sum ∑_λ runs over all vibration modes. A convenient hypothesis is the low frequency approximation (hν < < k_BT), in which case Eq. 5 becomes

S_{vib} = - R \sum_{λ} ln (\frac{h ν_{λ}}{k_{B} T})

(6)

Then, the vibrational entropy variation can be deduced as

Δ S_{vib} = S_{vib}^{HS} - S_{vib}^{LS} = R \sum_{λ = 1}^{15} ln (ν_{λ}^{LS} / ν_{λ}^{HS}) = 15 R \ln (〈 ν^{L S} 〉 / 〈 ν^{H S} 〉)

(7)

Considering a perfect octahedron (λ = 15 molecular vibrational modes) and taking 〈ν^LS〉/〈ν^HS〉 = 1.3 (Fig. 6), we obtain ΔS_vib ≈ 32.7 J mol⁻¹ K⁻¹ in agreement with the experimental measurements [81].

This result allows us to draw two important conclusions. First, vibrational entropy is higher in the HS state and then this latter is favored at high temperatures. Then, the variation in vibrational entropy shows the important role of vibrations in the SCO phenomena. More generally the entropy variation ΔS ranges from 40 to 80 J mol⁻¹ K⁻¹ in comparison with ΔS_el = 13.38 J mol⁻¹ K⁻¹. It is important to note that all of these thermodynamic quantities can be extracted from calorimetric measurements [88–90] (Fig. 8), whereas vibrational properties can be assessed with Raman and infrared spectroscopies [81,91,92].

Fig. 8
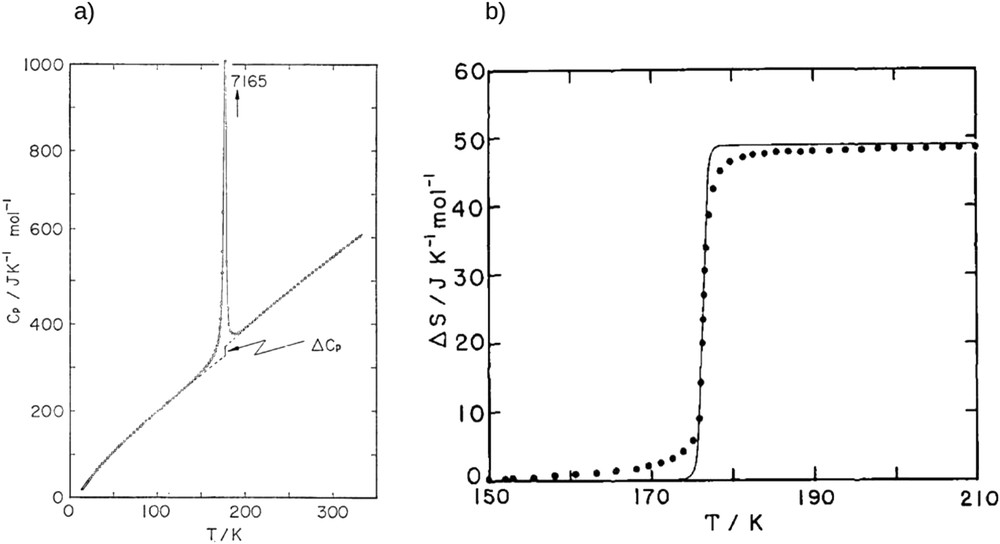
(a) Temperature dependence of the heat capacity of Fe(Phen)₂(NCS)₂ crystal. ΔC_p corresponds to the discontinuity associated with the spin transition. (b) Temperature dependence of entropy variation of the same compound (full black circles). Straight line corresponds to a fit using the so-called domain model [88] (vide infra).

The mixing entropy S_mix has not been discussed yet. Considering N noninteracting molecules, among them N_HS are in the HS state, and we can define the HS fraction n_HS = N_HS/N, which is abusively called the order parameter of the spin transition. We can express the Gibbs energy of an SCO system as

G = n_{HS} G_{HS} + (1 - n_{HS}) G_{LS} - T S_{mix}

(8)

The mixing entropy corresponds to a loss of statistical information for the system related to the large number of possibilities to distribute N_HS molecules in the HS state among N molecules. In the thermodynamic limit, mixing entropy can be written as

S_{mix} = - k_{B} N [n_{HS} ln (n_{HS}) + (1 - n_{HS}) ln (1 - n_{HS})]

(9)

The equilibrium condition corresponds to

{(\frac{\partial G}{\partial n_{HS}})}_{T, P} = 0

(10)

It is then possible to follow the thermal evolution of the HS fraction (Fig. 9):

T = \frac{Δ H}{R ln (\frac{1 - n_{HS}}{n_{HS}}) + Δ S}

(11)

Fig. 9
Thermal evolution of the HS fraction n_HS (blue line) in the case of noninteracting SCO molecules. The equilibrium temperature T_1/2, where n_HS = 0.5 is indicated with a red dashed line.

In the case of noninteracting SCO molecules, a gradual spin conversion can only be observed from the LS to the HS state by increasing the temperature. The occurrence of abrupt first-order transition with bistability phenomena is directly related to the emission or absorption of a latent heat whose existence is completely governed by interactions between SCO compounds. In contrast to the basic thermodynamic approaches describing the SCO phenomenon of isolated molecules, taking into account the complex interaction mechanism between SCO molecules needs most of the time the introduction of phenomenological parameters whose links with measurable experimentally quantities are not trivial at all. These parameters imply drastic simplifications of collective behavior mechanisms in the solid state. In the next section, a brief summary of several macroscopic/thermodynamic models simulating interacting SCO compounds is presented.

3 Macroscopic/thermodynamic models

3.1 Collective behaviors or cooperativity

The thermodynamic approach introduced in the previous section is only valid for diluted systems as solutions (solid or liquid). Interactions between molecules can no more be neglected in bulk solid materials. The increase in the octahedron volume upon LS to HS switching is around 25%. In parallel, vibrational modes are higher in frequency in the LS state. It means a higher bonding energy (and also a higher stiffness) in the LS state than in the HS state. In the crystal packing, the change in structural properties of a molecule upon a spin state change has an important impact not only on its immediate environment but also affects the whole lattice (long-range interactions). The switching from LS (respectively HS) molecule to HS (respectively LS) state implies important local strains because of the expansion (respectively the contraction) of the molecular volume. The HS (respectively LS) molecule is submitted to a compressive (respectively tensile) stress exerted by the neighboring molecules, which tend to switch back the molecule to its initial state. These elastic mechanisms induce collective effects, which lead, if they are strong enough, to first-order transition, that is, discontinuities of first derivatives of Gibbs energy (entropy, volume, and also HS fraction). Spin state change induces modifications in volume of the whole material (V_HS–V_LS/V_LS ≈ 13%) [93] and of the bulk modulus B (B_LS − B_HS/B_HS ≈ 30%) [94]. From the first basic point of view, these two ingredients play an important role in the magnitude and range of the interactions. In the SCO field, all of these intermolecular interaction mechanisms are usually called cooperativity. It is important to understand that the response of the lattice to the switching of a molecule is not local. The spin state change of one or several molecules generates elastic distortions, which spread in the whole crystal and give rise to a global response of the lattice, sometimes called image pressure. This image pressure is a complicated and inseparable combination of short- and long-range interactions. The complexity degree in the modeling of cooperative aspects in SCO materials is obviously dependent on the kind of experimental observations to simulate (spin transition curves, nonequilibrium process, nucleation and domain growth processes, mechanical properties, etc.). Macroscopic/thermodynamical models are an excellent first step in the simulation of SCO curves and nonequilibrium kinetic curves (macroscopic master equations). In this review, we limit the description of macroscopic models to equilibrium spin transition curves. The microscopic models are addressed in other dedicated articles within this special issue [44,45].

3.2 Slichter and Drickamer models and “domain” model

In 1972, Slichter and Drickamer [95] have introduced a first thermodynamic model based on regular solid solution theory. Starting from Gibbs energy given by Eq. 8, they added a nonlinear phenomenological term Γn_HS (1 − n_HS), which takes into account intermolecular interactions. By analogy with magnetism, it can be seen as a second-order Taylor's expansion as a function of the HS fraction n_HS:

G = α + β n_{HS} + γ n_{HS}^{2} - T S_{mix}

(12.1)

G = α + (β + γ) n_{HS} - γ n_{HS} (1 - n_{HS}) - T S_{mix}

(12.2)

G = G_{LS} + (G_{HS} - G_{LS}) n_{HS} + Γ n_{HS} (1 - n_{HS}) - T S_{mix}

(12.3)

G = n_{HS} G_{HS} + (1 - n_{HS}) G_{LS} + Γ n_{HS} (1 - n_{HS}) - T S_{mix}

(12.4)

The interaction parameter Γ is directly related to the force of intermolecular interactions in the crystal (cooperativity). In the initial model, Slichter and Drickamer have proposed that Γ parameter should be temperature and pressure dependent because of the importance of vibration and mechanical properties in SCO systems. However, the knowledge of temperature and pressure dependence of this phenomenological term is difficult, and despite some links with microscopic spin–phonon models have been established [69], Γ is most of the time kept constant. As previously, the extrema of Gibbs energy (which are no more unique) are given by Eq. 10 [95].

T = \frac{Δ H + Γ (1 - 2 n_{HS})}{R ln (\frac{1 - n_{HS}}{n_{HS}}) + Δ S}

(13)

In this model, the transition temperature T_1/2 = ΔH/ΔS remains unchanged.

It is important to note that in some cases, three values of HS fraction can give the same temperature. This is the signature of the existence of stable, metastable, and unstable states. To verify the stability of the extrema, it is interesting to inspect the sign of the second derivative of Gibbs energy around the equilibrium temperature (i.e., n_HS = 1/2):

{(\frac{\partial^{2} G}{\partial n_{HS}^{2}})}_{T, P, n_{HS} = 0.5} = - 2 Γ + 4 R T_{1 / 2}

(14)

From Eq. 14, three situations can occur (see Fig. 10). If Γ < 2RT_1/2 (weak interactions), then the second derivative is positive and the state n_HS = 1/2 is a minimum point of Gibbs energy. The spin state change is gradual (spin conversion). If Γ > 2RT_1/2 (strong interactions), the second derivative is negative and n_HS = 1/2 is a maximum of Gibbs energy. The transition is abrupt (first-order phase transition) with the presence of a hysteresis loop. There are also two transition temperatures corresponding to minima of Gibbs energy: T_1/2⁺ (warming process) and T_1/2⁻ (cooling process) corresponding to the limit of the metastability and whose average is approximately the equilibrium temperature. For example, during a warming process, when T < T_1/2⁻ the material is in the stable LS phase. By increasing the temperature until T_1/2⁻ < T < T_1/2, a metastable HS phase appears, separated from the stable LS phase by an unstable state. For T = T_1/2, the HS and LS phases are both stable. In the range T_1/2 <T <T_1/2⁺, the LS phase becomes metastable and the more stable phase is the HS one. However, the system remains in the metastable LS phase due to the presence of the energy barrier generated by the unstable state. For T > T_1/2⁺, the energy barrier disappears and the system switches from the LS to the HS phase. The behavior of the SCO materials is similar in the cooling mode. If Γ = 2RT_1/2 the second derivative is null, which corresponds to an inflexion point. The SCO is abrupt without hysteresis. This situation corresponds to the critical point of the phase diagram related to the critical temperature T_C = T_1/2 = Γ/2R, which gives the limit conditions of the two previous cases.

Fig. 10
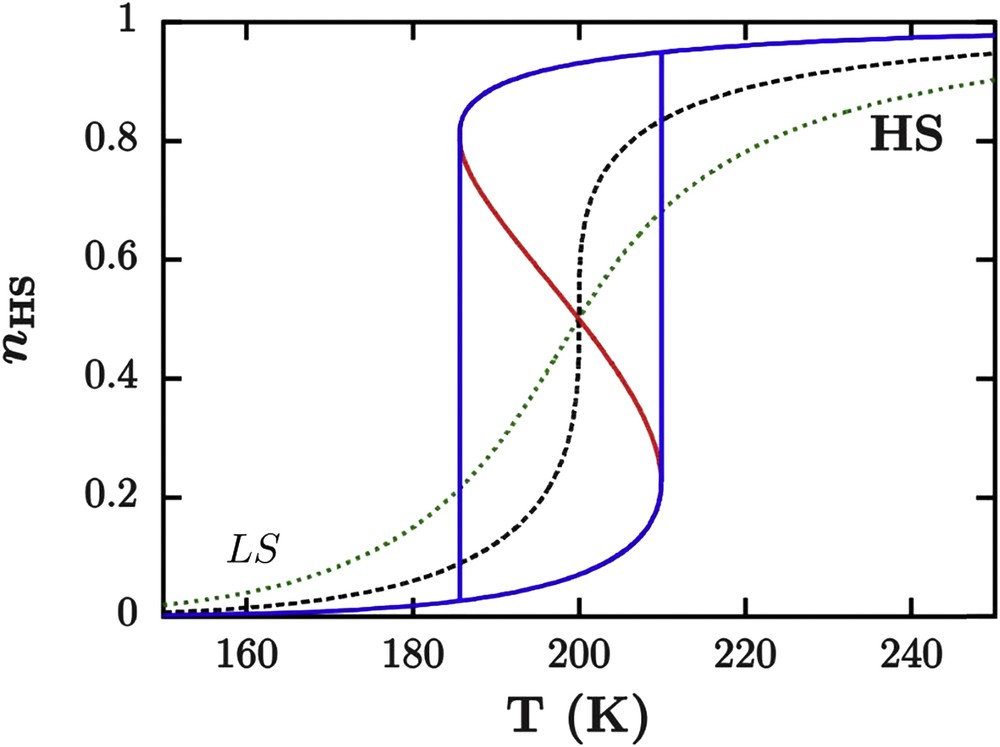
Simulation of thermoinduced spin transition with the Slichter and Drickamer model for different interaction strengths. Variations in enthalpy and entropy are, respectively, ΔH = 12,000 J mol⁻¹ and ΔS = 60 J mol⁻¹ K⁻¹. Three different values of Γ have been chosen to illustrate three different situations: the spin conversion (gradual, green dotted line) 2RT_1/2 > Γ = 2000 J mol⁻¹, the abrupt transition (black dashed line) 2RT_1/2 = Γ = 3324 J mol⁻¹, and the first-order transition with hysteresis phenomenon (blue full line) 2RT_1/2 < Γ = 5000 J mol⁻¹. The red curve represents the instable states of the transition (local maxima of Gibbs energy).

The increase in Γ tends to amplify the abrupt character of SCO until the occurrence of a first-order transition. In classical terms, the transition is called first-order phase transition because the first derivative of the free energy F is discontinuous (the discontinuity corresponds to the generated entropy term: S = −(δF/δT)_v). The Slichter and Drickamer model does not take into account the interface energy between the HS and LS phases. This supposes a homogeneous spin conversion without domain formation. Indeed, the expression of the mixing entropy assumes that a molecule can be equivalently distributed at any part of the lattice: this is the mean field approximation. First-order phase transitions are usually accompanied by heterogeneous phase transformation related to the spatiotemporal dynamics governed by a nucleation and domain growth mechanism [30]. Spin transition phenomenon belongs to this class of phase transformations. Indeed heterogeneous phase separation has been indirectly observed by X-ray diffraction measurements [96,97] due to the structural differences between the HS and LS phases and has been directly highlighted using optical microscopy techniques for a decade [56].

Early in the 1970s, the existence of spin like-domains, that is, adjacent molecules in the same spin state, has been speculated by Sorai and Seki [88]. To take into account this finding, they considered that the system is divided in N_D clusters of similar shape in which molecules have the same spin state. There is no interaction between domains. Thus, the mixing entropy does not describe the distribution of molecules in the material any more, but rather the arrangement of domains. The Gibbs energy of the so-called “domain model” can be expressed as

G = n_{HS} G_{HS} + (1 - n_{HS}) G_{LS} + n_{D} R T [n_{HS} ln (n_{HS}) + (1 - n_{HS}) ln (1 - n_{HS})]

(15)

where n_D is the number of domains per mole.

This model is able to reproduce spin conversions and abrupt spin transitions in the limit of large clusters (highly cooperative materials) without the possibility to simulate hysteretic behaviors (Fig. 11). Next, Purcell and Edwards [98] have modified the interaction parameter Γ of the Slichter and Drickamer model to make it dependent on the number and the spin state of pairs of molecules:

G_{inter} = g_{HS - HS} I_{HS - HS} + g_{HS - LS} I_{HS - LS} + g_{LS - LS} I_{LS - LS}

(16)

where I_i-j is the i-j pair number and g_i-j represents interaction Gibbs energy between molecule pairs i-j. This thermodynamic model has been able to improve the fit of the spin transition curves obtained by magnetic measurements for the Fe (phen)₂X₂ (X=NCS⁻, NCSe⁻, and NCBH₃⁻) SCO compound family.

Fig. 11
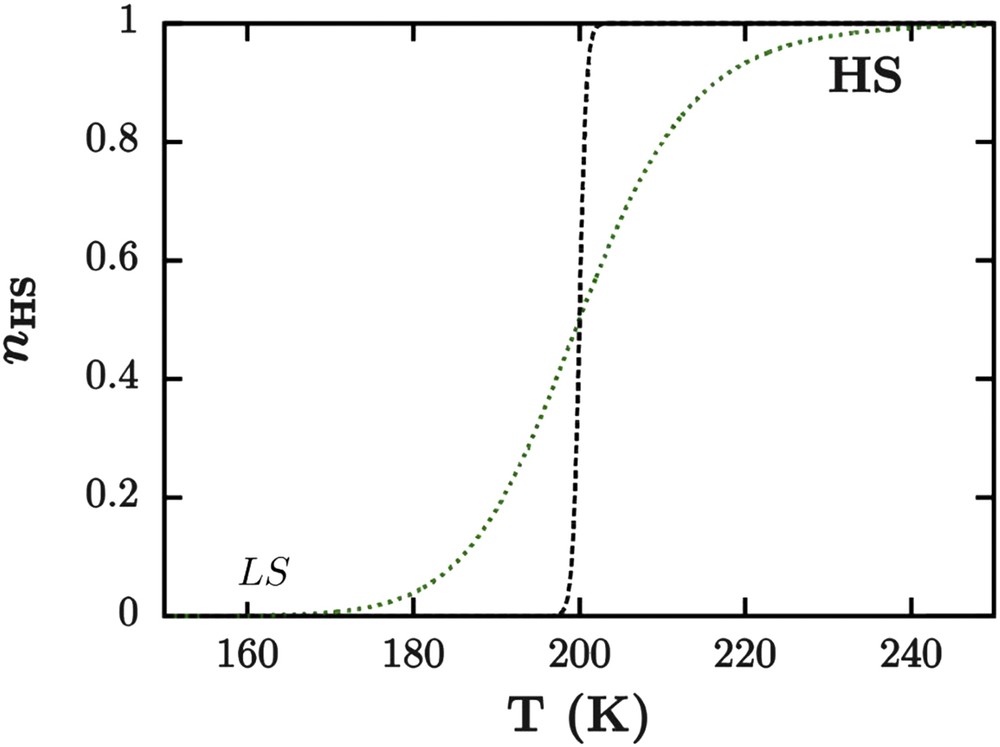
Spin transition curves simulated with domain model for n_D = 0.015 mol⁻¹ (green dotted line) and n_D = 0.25 mol⁻¹ (black dashed line). Other values of model parameters (entropy and enthalpy variations) are the same as Fig. 10.

3.3 Incomplete, multistep transitions, and macroscopic spin–phonon models

In SCO materials, other spin transition curves, different from simple spin conversions or abrupt transitions can be experimentally observed. Indeed, the elastic origin of intermolecular interactions and the strong electron–lattice interplay are able to give rise to richer phase diagrams. Incomplete transitions have been observed with the occurrence of residual HS fractions at low temperature and/or residual LS fractions at high temperature. Incomplete transitions have various origins like quenched effects (kinetic), a HS ground state at zero temperature [82–86], presence of microstructures, size reduction effects (surface effects) [99,100], or nonequivalent metallic sites in the crystal packing, and so forth. For this latter case, two-step transitions have also been observed: each metallic site having different transition temperatures [101,102]. The existence of multistep spin transitions has other possible origins. This phenomenon has been first detected in polynuclear SCO systems [66,103]. The switching of one of the two metallic centers generates elastic distortions within the molecule, preventing the switching of the other metallic centers. In mononuclear SCO compounds, the presence of multistep transitions has been interpreted as a competition between short- and long-range interactions, which favor modulated ("chessboard") structures such as a regular alternance of HS–LS molecules in the crystal. To account for these experimental observations, the description of the interaction parameter contained in the domain and the Slichter and Drickamer models has been refined. For example, Cantin et al. [104] consider new ingredients as intra- and interdomain interactions and domain size effects. This thermodynamic model predicts the occurrence of HS thermally metastable and stable states at low temperature, and thus the possible existence of incomplete (Fig. 12a)) and irreversible LS to HS (Fig. 12b) transitions.

Fig. 12
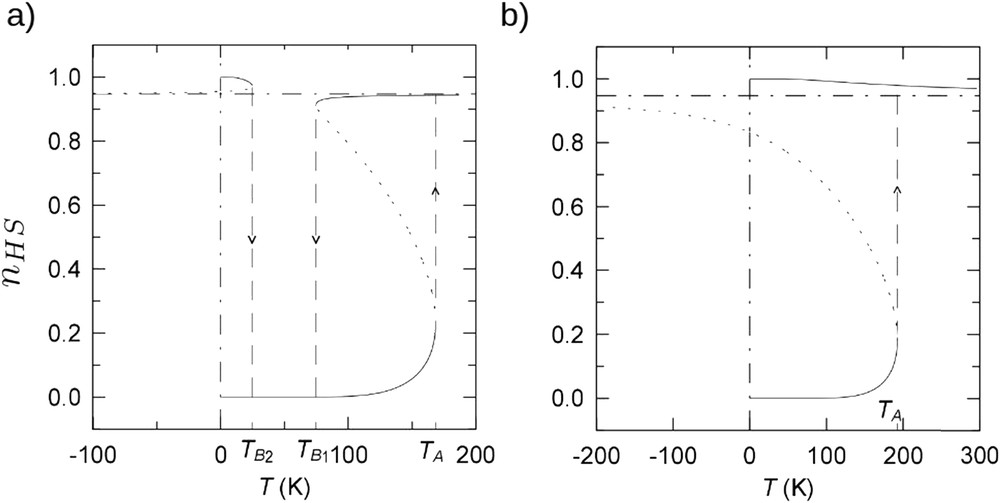
Thermal evolution of the HS fraction modeled with a thermodynamic model taking into account intra- and interdomain interactions and domain size distribution [104]. (a) Simulation of metastable HS state at low temperature. (b) Modeling of irreversible LS to HS transition.

The previously introduced thermodynamic model is able to reproduce the main features of the experimentally observed spin transition. However, the main drawback of this model is the absence of a more realistic description of the elastic intermolecular interactions and electron–lattice coupling. In this context, Zimmermann and König [105] developed an elastic model solved in the framework of the Bragg–Williams approximation—equivalent to a mean field treatment of the Slichter and Drickamer model—in which lattice vibrations have been taken into account through the Debye temperatures of the HS and LS phases. This approach allows us to establish strong relations with thermodynamic models and gives an elastic origin to the cooperativity. It is important to note that in parallel to the thermodynamic models, microscopic models based on statistical physics approaches have been developed, which are out of the scope of this present review. Although the Slichter and Drickamer model and the mean field Ising-like model are completely equivalent, as shown by Bousseksou and co-workers [53,54], the Zimmerman and König model is isomorph to spin–phonon, mechanoelastic, or electroelastic microscopic models (discussed within the present special issue [45]) in the framework of Debye's model and Bragg–Williams approximation. The addition of phonon contribution improves the fitting of experimental data (Fig. 13a)) [105]. Then, Koudriavtsev [106] has developed a similar approach to the Zimmermann and König model for the description of electron–phonon coupling. The spin state dependence of vibration modes between neighboring molecule pairs coupled with specific spatial correlation conditions (called occupational conditional probability) is able to fit two-step transition curves (Fig. 13b).

Fig. 13
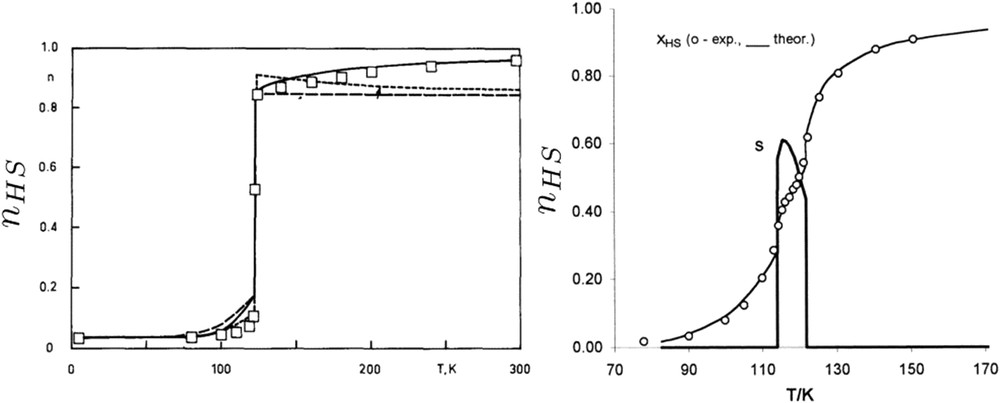
(a) Temperature dependence of the HS fraction for the compound [Fe (4,7-(CH₃)₂-phen)₂(NCS)₂)] (open squares). The dashed curves represent results of a calculation within the electronic SCO model including the electrostatic interaction between HS ions. The solid curve gives results obtained by the model including the contribution by phonons [105]. (b) Two-step spin transition fitted by the Koudriavtsev approach [106]. The quantity s is directly related to the fraction of HS–LS molecule pairs.

It is worth mentioning at this stage that two-step crossover has also been grasped using the Landau–Devonshire theory in which spin transitions can be viewed as an isostructural transition with a totally symmetric order parameter [107]. To reproduce the long-range ordering of different spin states, a model is developed in which the spin transition is coupled with a structural transformation through an order parameter, which “measures” the symmetry breaking. However, this latter approach is very similar to the well-known mean field Ising-like model for two-step SCO [53] with two interacting sublattices and the elastic nature of interactions is not explicitly taken into account. Of course, the symmetry breaking (from magnetism point of view) has also been predicted by the Ising-like model for a binuclear system in the symmetrical case (identical ferro-like interaction with neighbors of both binuclear centers) [54].

3.4 “Mesoscopic” elastic model

In the Zimmermann and König model and the Koudriatsev approach, intermolecular interactions are considered through lattice vibrations and vibronic coupling. An alternative description of the cooperative mechanism in SCO solids is a mesoscopic model based on continuum mechanics. Starting from the theory of Eshelby [108], Ohnishi and Sugano [109] have developed an elastic model taking into account overall lattice deformations and local deformations attributed to the change in metal–ligand distances during the spin state change. Thereafter, Spiering and co-workers explicitly considered the interaction term by expressing the Gibbs energy of a set of SCO molecules distributed in a host matrix with the aim to identify the different terms. Gibbs energy is given by Refs. [26,110]:

G = n_{HS} (G_{HS} - G_{LS}) - T S_{mix} + x ξ n_{HS} - x γ n_{HS}^{2}

(17)

where xξ is the energy shift due to the matrix and xγ represents an interaction constant. These two parameters depend on x (0 < x < 1), the fraction of SCO molecules in the lattice. The lattice is assumed to be an isotropic homogeneous medium characterized by a bulk modulus B and a Poisson ratio σ. In this lattice, HS and LS molecules as well as the host matrix are approximated by a hard sphere whose respective volumes are v_HS, v_LS, and v_m, whereas the volume of the unit cell in the lattice is v₀. Deformation energy related to a molecule of volume v_α can be expressed as

e_{α} = \frac{1}{2} B (γ_{0} - 1) \frac{{(v_{α} - v_{0})}^{2}}{v_{0}} - \frac{1}{2} B γ_{0} (γ_{0} - 1) \frac{{(v_{α} - v_{0})}^{2}}{V}

(18)

where V is the total volume of the lattice and γ₀ (0 < γ₀ < 3) is Eshelby's constant. This latter represents the consequence of a local volume change (v_α − v₀) on the overall volume change of the lattice γ₀ (v_α − v₀). The first term in Eq. 18 represents the local lattice deformation induced by the molecule, whereas the second term that vanishes when V → ∞ represents the response of the crystal due to the presence of surfaces, called image pressure. This pressure originates from the change in volume of the whole crystal, which is more important than the initial change in local volume. Considering the total elastic energy, it is also possible to identify the phenomenological terms of Eq. 17 [26].

γ (x) = \frac{x}{2} B γ_{0} (1 - γ_{0}) \frac{{(v_{HS} - v_{LS})}^{2}}{v_{m}}

(19a)

ξ (x) = \frac{x}{2} B γ_{0} (1 - γ_{0}) \frac{(v_{HS} - v_{LS}) (v_{m} - v_{LS})}{v_{m}}

(19b)

These relations show that the interaction constant γ is only dependent on the difference in the volume between the two spin states and on the bulk modulus. An increase in these two ingredients leads to a more cooperative materials. Eq. 17 can be rewritten as [26,110]

G = n_{HS} (G_{HS} - G_{LS}) - T S_{mix} + (ξ - γ) x n_{HS} + x γ n_{HS} (1 - n_{HS})

(20a)

G = n_{HS} (G_{HS} - G_{LS}) - T S_{mix} + Z x n_{HS} + x Γ n_{HS} (1 - n_{HS})

(20b)

where the interaction term is Γn_HS (1 − n_HS). It is interesting to mention that the constant Z takes into account internal pressures exerted by SCO molecules and also the elastic response of the whole lattice. As function of the unit cell volume of the host matrix, the term Zxn_HS favors the HS or the LS state. A direct consequence of these effects is the modification of the equilibrium temperature (this term is linear in n_HS). This model has been improved by considering elastic dipoles rather than hard spheres [27]. This model is only valid for small ratio of SCO molecules in the host matrix. In the opposite case, the bulk modulus of SCO molecules has to be considered [110].

4 Recent extensions and prospects

As mentioned previously, the main drawback of most thermodynamic models lies in the need to introduce phenomenological interaction parameters. Describing the collective behavior between SCO compounds by means of elastic approaches already corresponds to a modeling of electronic reorganizations within the solids induced by the spin state change. In the past decade, macroscopic models based on numerical predictions using ab initio calculations have been developed and can be seen as another vision of cooperative aspects, which complements the common description of interaction mechanisms by elastic-driven cooperativity [111–113]. This method assumes that the Γ parameter of the Slichter and Drickamer model can be divided into two contributions: weak bond contacts (van der Walls interactions) $Γ_{vdW}$ and polarization effects $Γ_{pol}$ due to charge redistributions upon ligand fields, geometry reorganizations, and lattice expansion. $Γ_{pol}$ parameter corresponds to a modulation of the electrostatic contributions generated by the crystal environment (Madelung fields). The authors show that interactions through weak bond contacts are not sufficient to explain the existence of hysteretic behaviors in some SCO materials. In this study, the growth of hysteresis loop is controlled by electrostatic contributions (fluctuations of Madelung fields).

In another context, thermodynamic models have evolved with the aim to investigate the very important question concerning the SCO phenomena at the nanoscale. Switchable properties are generally strongly affected by size reduction effects resulting in a change in both phase stability (transition temperatures, completeness of the transition, etc.) and cooperativity mechanisms (first-order character of the spin transition and bistability properties) [99,100,114–121]. In SCO systems, reducing the size usually leads to a downshift in the transition temperature, the occurrence of residual HS or/and LS fraction, respectively, at low and high temperatures. Hysteretic behavior and also bistability can disappear or survive by approaching the nanometer scale according to the SCO nanomaterials. Intriguingly, a nonmonotonic size evolution of the hysteresis loop has been observed: a shrinking of the hysteresis loop with the size reduction followed by a reappearance of bistability phenomenon in ultrasmall nanoparticles (ca. 2 nm) [100].

It is well known that size reduction does not only imply a decrease in the quantity of matter but also an increase in the surface-to-volume ratio. Similar thermodynamic behaviors and physical properties are observed in nano-objects with the same surface-to-volume ratio, whatever their respective volumes. At the nanometric scale, surface/interface chemical and physical properties can no more be ignored. From a thermodynamic point of view, taking into account surface properties can be achieved by introducing the concept of surface energy density as it has been proposed by Gibbs in the end of the 19th century [122]. Then, in the 1970s, Hill [123] has extended the idea of surface energy to “small systems”, developing a new thermodynamic formalism called “nanothermodynamics”. In the SCO field, a spin state–dependent energy density has been included in a Slichter and Drickamer approach adapted for the modeling of core–shell nanoparticles [124]. The phase stability in SCO nanoparticles has been demonstrated to be completely governed by the difference in terms of surface energies between the HS and LS phases, which constitute the driving force of the spin transition at the nanoscale. First, estimations of the difference between a HS and LS surface leads to $Δ σ = 0.1 J {mol}^{- 2}$ [124]. According to this result, a HS surface usually has an energy cost lower than a LS surface. This may explain the important downshift in the transition temperature and the spin state of surface molecules, which seems to be fixed in the HS state. To go further, an interfacial elastic energy density and an interfacial stress of a core–shell SCO nanoparticle have been expressed as a function of the Young moduli and Poisson's ratios of the hybrid system in the framework of a continuum mechanics approach [125]. According to the structural misfit and differences in the mechanical properties between an inactive core and a SCO shell, this interfacial elastic energy density favors either the HS (tensile stress) or the LS (compressive stress) state. It results, respectively, in a downshift or an upshift of the transition temperature, giving the perspective of the control of phase stability in SCO nano-objects. The main advantage of such approaches is the possibility to inject experimentally accessible mechanical properties of core–shell systems. However, the total surface energy can be divided into many contributions: chemical, elastic, disorder... so forth, whose effects are strongly intricated. Nevertheless, the experimental measure of the total surface energy in both spin states is still lacking and its knowledge seems to be of paramount importance for deeper theoretical investigations of size effects and especially surface effects on phase transition in SCO nano-objects.

The preservation of bistability phenomena through the presence of hysteretic behavior in SCO nanoparticles seems to be counterintuitive if analogies are established with the size evolution of other phase transitions, like melting process or ferromagnetism [73,126]. However, the elastic origin of collective behaviors in SCO systems constitutes an important difference with the other examples: elastic properties may be size dependent. Mössbauer spectroscopy measurements have shown a drastic increase in the Debye temperature with the size reduction in Prussian-Blue analogue [124] and SCO coordination nanoparticles [100]. This increase in the Debye temperature means stiffening—at least in appearance—of the nanoparticle by approaching the nanoscale, which may be explained by the existence of a compressive stress exerted by the external environment. This experimental finding has been injected in the nanothermodynamic version of the Slichter and Drickamer model, considering the linear dependence of the phenomenological interaction parameters Γ with the bulk modulus ( $B \sim θ_{D}^{2}$ ) [110] established in the framework of the mesoscopic elastic model (Section 3.4). This combination experiments–thermodynamic model allows us to give a possible explanation of the existence of bistability phenomena in ultrasmall SCO nanoparticles.

Most of these thermodynamic approaches emphasize the primary role of structural and elastic properties for the understanding of cooperative mechanisms in SCO materials. If investigations of crystallographic properties are routine and X-ray diffraction experiments are common characterization techniques to probe of mechanical/elastic properties remains scarce and experimental techniques, which allow a systematic determination of such properties, are still lacking. It would be important to further probe elastic and vibrational properties of SCO materials and nanomaterials to constitute a database of elastic moduli of molecular materials and coordination networks. Various techniques have been proposed to this aim: Brillouin spectroscopy [64], X-ray diffraction under pressure [71], near-field microscopy techniques (atomic force microscopy) [72,127], Mössbauer spectroscopy [66], and so forth. In particular, nuclear inelastic scattering measurements [128] have been performed to probe lattice dynamics of SCO powder [68] and nanoparticles [129,130] in both spin states. Nuclear inelastic scattering techniques permit accessing to the density of vibrational states from which the Debye sound velocity and different thermodynamical quantities can be extracted. More recently, the integration of SCO materials into microelectromechanical systems (MEMS) devices [131,132], for the conception of microactuator able to convert heat, into motion constitutes an original possibility to measure mechanical properties of SCO thin films [133,134]. All of these new techniques combined with the old ones will undoubtedly make it possible to complete the lack of characterization of the mechanical properties of SCO materials. The access to a database listing the thermal and mechanical properties of SCO materials may succeed in the prediction of the effects of the different physical ingredients on the observed equilibrium properties [135]. However, the thermodynamic aspects of nonequilibrium kinetic processes or spatiotemporal dynamics (nucleation and domain growth mechanisms) need the knowledge of thermomechanical properties of SCO solids of which we currently have only orders of magnitude. In particular, the spatiotemporal evolution of the spin transition seems to be very sensitive to heat exchange with the external environment [136] and the experimental determinations of the thermal conductivity, the heat and the radiative transfer coefficients become unavoidable for the building of a thermomechanical model in the framework of the local equilibrium approximations.

5 Conclusions

SCO is a phenomenon that involves two electronic states (HS and LS) close in energy and in a thermodynamical equilibrium. The thermodynamic approach for the phenomenological description of the measured properties is therefore crucial and has accompanied all of the experimental observations made since the discovery of the phenomenon. Many models called microscopic models going beyond the phenomenological descriptions made on the molecular or supramolecular SCO compounds including the kinetics and spatiotemporal aspects have been proposed. A point of convergence between the thermodynamical and microscopic approaches certainly lies in the analysis of objects of reduced size (nano-objects) going even to the single molecule or an assembly of molecules. This analysis can be called nanothermodynamics where the notion of surface energy, the ratio of the core to the shell in core–shell nano-objects, the stiffness of the chemical bonds, the matrix surrounding the molecule, and so forth, become crucial parameters to consider to go deeper into the understanding and the control of the SCO phenomenon.

Acknowledgments

This work was supported by the European Commission through the SPINSWITCH project (H2020-MSCA-RISE-2016, Grant Agreement No. 734322).

Bibliographie

[1] E. König Coord. Chem. Rev., 3 (1968), p. 471

[2] H.A. Goodwin Coord. Chem. Rev., 18 (1976), p. 293

[3] P. Gütlich Structure and Bonding (M.J. Clarke; J.B. Goodenough; P. Hemmerich; J.A. Ibers; C.K. Jörgensen; J.B. Neilands; D. Reinen; R. Weiss; R.J.P. Williams, eds.), Springer, Berlin, Heidelberg, 1981, pp. 83-195

[4] E. König; G. Ritter; S.K. Kulshreshtha Chem. Rev., 85 (1985), p. 219

[5] H. Toftlund Coord. Chem. Rev., 94 (1989), p. 67

[6] J.A. Real; A.B. Gaspar; V. Niel; M.C. Muñoz Coord. Chem. Rev., 236 (2003), p. 121

[7] J.A. Real; A.B. Gaspar; M.C. Muñoz Dalton Trans. (2005), p. 2062

[8] P. Gütlich; H.A. Goodwin Spin Crossover in Transition Metal Compounds I-III, Springer, Berlin, Heidelberg, 2004

[9] A. Bousseksou; G. Molnar; L. Salmon; W. Nicolazzi Chem. Soc. Rev., 40 (2011), pp. 3313-3335

[10] M.A. Halcrow Spin-crossover Materials: Properties and Applications, John, Wiley & Sons, Chichester, UK, 2013

[11] P. Gütlich; A.B. Gaspar; Y. Garcia Beilstein J. Org. Chem., 9 (2013), pp. 342-391

[12] V. Ksenofontov; G. Levchenko; H. Spiering; P. Gütlich; J.-F. Létard; Y. Bouhedja; O. Kahn Chem. Phys. Lett., 294 (1998), p. 545

[13] J.J. McGravey; I. Lawthers J. Chem. Soc., Chem. Commun. (1982), p. 906

[14] I. Lawthers; J.J. McGarvey J. Am. Chem. Soc., 106 (1984), p. 4280e-4282e

[15] J.K. McCusker; K.N. Walda; R.C. Dunn; J.D. Simon; D. Magde; D.N. Hendrickson J. Am. Chem. Soc., 114 (1992), p. 6919

[16] S. Decurtins; P. Gütlich; C.P. Köhler; H. Spiering; A. Hauser Chem. Phys. Lett., 105 (1984), p. 1

[17] S. Bedoui; M. Lopes; W. Nicolazzi; S. Bonnet; S. Zheng; G. Molnár; A. Bousseksou Phys. Rev. Lett., 109 (2012), p. 135702

[18] S. Bonhommeau; G. Molnár; M. Goiran; K. Boukheddaden; A. Bousseksou Phys. Rev. B, 74 (2006), p. 064424

[19] C. Lefter; R. Tan; J. Dugay; S. Tricard; G. Molnár; L. Salmon; J. Carrey; W. Nicolazzi; A. Rotaru; A. Bousseksou Chem. Phys. Lett., 644 (2016), pp. 138-141

[20] G.J. Halder; C.J. Kepert; B. Moubaraki; K.S. Murray; J.D. Cashion Science, 298 (2002), p. 1762

[21] S. Cobo; G. Molnár; J.A. Real; A. Bousseksou Angew. Chem., Int. Ed., 45 (2006), p. 5786

[22] M. Ohba; K. Yoneda; G. Agustí; M.C. Muñoz; A.B. Gaspar; J.A. Real; M. Yamasaki; H. Ando; Y. Nakao; S. Sakaki; S. Kitagawa Angew. Chem., 121 (2009), p. 4861

[23] W.A. Baker; H.M. Bobonich Inorg. Chem., 3 (1964), pp. 1184-1188

[24] E. König; K. Madeja Inorg. Chem., 6 (1967), pp. 48-55

[25] H. Spiering Top. Curr. Chem., 235 (2004), p. 171

[26] N. Willenbacher; H. Spiering J. Phys. Chem., 21 (1988), p. 1423

[27] H. Spiering; N. Willenbacher J. Phys. Condens. Matter, 1 (1989), p. 10089

[28] W. Nicolazzi; J. Pavlik; S. Bédoui; G. Molnár; A. Bousseksou Eur. Phys. J. Spec. Top., 222 (2013), pp. 1137-1159

[29] A. Slimani; K. Boukheddaden; F. Varret; H. Oubouchou; M. Nishino; S. Miyashita Phys. Rev. B, 87 (2013), p. 014111

[30] A. Slimani; K. Boukheddaden; F. Varret; M. Nishino; S. Miyashita J. Chem. Phys., 139 (2013), p. 194706

[31] A. Slimani; K. Boukheddaden; K. Yamashita Phys. Rev. B, 92 (2015), p. 014111

[32] J.F. Létard; G. Chastanet; O. Nguyen; S. Marcen; M. Marchivie; P. Guionneau; D. Chasseau et; P. Gütlich Monatsh. Chem., 134 (2003), pp. 165-182

[33] A. Hauser Top. Curr. Chem., 234 (2004), pp. 155-198

[34] A. Hauser Chem. Phys. Lett., 192 (1992), pp. 65-70

[35] J. Degert; N. Lascoux; S. Montant; S. Létard; E. Freysz; G. Chastanet; J.-F. Létard Chem. Phys. Lett., 415 (2005), pp. 206-210

[36] H. Watanabe; H. Hirori; G. Molnár; A. Bousseksou; K. Tanaka Phys. Rev. B, 79 (2009), p. 180405

[37] J.F. Létard; P. Guionneau; L. Rabardel; J.A.K. Howard; A.E. Goeta; D. Chasseau et; O. Kahn Inorg. Chem., 37 (1998), p. 4432

[38] A. Désaix; O. Roubeau; J. Jeftic; J.G. Haasnot; K. Boukheddaden; E. Codjovi; J. Linares; M. Noquis et; F. Varret Eur. Phys. J. B, 6 (1998), p. 183

[39] M. Lorenc; J. Hébert; N. Moisan; E. Trzop; M. Servol; M. Buron-Le Cointe; H. Cailleau; M.L. Boillot; E. Pontecorvo; M. Wulff; S. Koshihara; E. Collet Phys Rev. Let., 103 (2009), p. 028301

[40] M. Lorenc; C. Balde; W. Kaszub; A. Tissot; N. Moisan; M. Servol; M. Buron-Le Cointe; H. Cailleau; P. Chasle; P. Czarnecki; M.L. Boillot; E. Collet Phys. Rev. B Condens. Matter, 85 (2012), pp. 1-8

[41] R. Bertoni; M. Lorenc; A. Tissot; M. Servol; M.L. Boillot; E. Collet Angew. Chem. Int. Ed., 51 (2012), pp. 7485-7489

[42] E. Collet; M. Lorenc; M. Cammarata; L. Guérin; M. Servol; A. Tissot; M.-L. Boillot; H. Cailleau; M. Buron-Le Cointe Chem. Eur J., 18 (2012), pp. 2051-2055

[43] R. Bertoni; M. Lorenc; H. Cailleau; A. Tissot; J. Laisney; M.-L. Boillot; L. Stoleriu; A. Stancu; C. Enachescu; E. Collet Nat. Mater., 15 (2016), p. 606

[44] J. Pavlik and J. Linares, C. R. Chimie 21 (2018) 1170–1178.

[45] C. Enachescu and W. Nicolazzi, C. R. Chimie 21 (2018) 1179–1195.

[46] J. Linares; H. Spiering; V. Varret Eur. Phys. J. B, 10 (1999), p. 271

[47] I. Shteto; K. Boukheddaden; F. Varret Phys. Rev. E, 60 (1999), p. 5139

[48] K. Boukheddaden; J. Linares; H. Spiering; F. Varret Eur. Phys. J. B, 15 (2000), pp. 317-326

[49] B. Hôo; K. Boukheddaden; F. Varret Eur. Phys. J. B, 17 (2000), pp. 449-457

[50] F. Varret; K. Boukheddaden; E. Codjovi; C. Enachescu; J. Linares Top. Curr. Chem., 234 (2004), pp. 199-229

[51] J. Wajnflasz Phys. Status Solidi, 40 (1970), p. 537

[52] J. Wajnflasz et; R. Pick J. Phys. IV. France, 32 (1971), p. C1

[53] A. Bousseksou; J. Nasser; J. Linares; K. Boukheddaden; F. Varret J. Phys. I France, 2 (1992), p. 1381

[54] A. Bousseksou; F. Varret; J. Nasser J. Phys. I France, 3 (1993), p. 1463

[55] H. Hang; B. Fei; X. Qin Chen; M. Liang Tong; I.A. Gural'skiy; X. Bao J. Math. Chem. C, 6 (2018), p. 3352

[56] K. Ridier; G. Molnár; L. Salmon; W. Nicolazzi; A. Bousseksou Solid State Sci., 74 A1 (2017), p. A22

[57] J.A. Nasser Eur. Phys. J. B, 21 (2001), pp. 3-10

[58] R.A. Bari; J. Sivardière Phys. Rev. B, 5 (1972), p. 4466

[59] M. Nishino; K. Boukheddaden; Y. Konishi; S. Miyashita Phys. Rev. Lett., 98 (2007), p. 247203

[60] C. Enachescu; L. Stoleriu; A. Stancu; A. Hauser Phys. Rev. Lett., 102 (2009), p. 257204

[61] Y. Konishi; H. Tokoro; M. Nishino; S. Miyashita Phys. Rev. Lett., 100 (2008), p. 067206

[62] W. Nicolazzi; S. Pillet; C. Lecomte Phys. Rev. B, 78 (2008), p. 174401

[63] J. Jung; H. Spiering; Z. Yuban; P. Gütlich Hyperfine Interact., 95 (1995), pp. 107-128

[64] J. Jung; F. Bruchhauser; R. Feile; H. Spiering; P. Gütlich Z. Phys., 100 (1996), p. 517

[65] Z. Yu; G. Schmitt; S. Hofmann; H. Spiering; Y.F. Hsia; P. Gütlich Hyperfine Interact., 93 (1994), p. 1459

[66] J.-A. Real; H. Bolvin; A. Bousseksou; A. Dworkin; O. Kahn; F. Varret; J. Zarembowitch J. Am. Chem. Soc., 114 (1992), p. 4650

[67] H.J. Shepherd; T. Palamarciuc; P. Rosa; P. Guionneau; G. Molnár; J.-F. Létard; A. Bousseksou Angew. Chem., Int. Ed., 51 (2012), p. 3910

[68] G. Félix; M. Mikolasek; H. Peng; W. Nicolazzi; G. Molnár; A.I. Chumakov; L. Salmon; A. Bousseksou Phys. Rev. B, 91 (2015), p. 024422

[69] C. Enachescu; A. Hauser Phys. Chem. Chem. Phys., 18 (2016), p. 20591

[70] A. Bousseksou; G. Molnár; L. Salmon; W. Nicolazzi Chem. Soc. Rev., 40 (2011), p. 3313

[71] H.J. Shepherd; G. Molnár; W. Nicolazzi; L. Salmon; A. Bousseksou Eur. J. Inorg. Chem. (2013), p. 653

[72] G. Molnár; L. Salmon; W. Nicolazzi; F. Terki; A. Bousseksou J. Mater. Chem. C., 2 (2014), p. 1360

[73] M. Mikolasek; G. Félix; W. Nicolazzi; G. Molnár; L. Salmon; A. Bousseksou New J. Chem., 38 (2014), p. 1834

[74] G. Molnár; S. Rat; L. Salmon; W. Nicolazzi; A. Bousseksou Adv. Mater., 30 (2018), p. 17003862

[75] M. Cavallini Phys. Chem. Chem. Phys., 14 (2012), p. 11867

[76] K. Senthil Kumar; M. Ruben Coord. Chem. Rev., 346 (2017), p. 176

[77] P.N. Martinho; C. Rajnak; M. Ruben Spin-crossover Materials (M.A. Halcrow, ed.), John Wiley & Sons Ltd, Chichester, UK, 2013, pp. 375-404

[78] H. Paulsen; A.X. Trautwein Top. Curr. Chem., 235 (2004), pp. 197-219

[79] A. Hauser Top. Curr. Chem., 233 (2007), pp. 49-58

[80] S. Sugano; Y. Tanabe; H. Kamimura, Multiplets of Transition-metal Ions in Crystals, vol. 33, Academic Press, New York, 1970

[81] A. Bousseksou; J.J. McGarvey; F. Varret; J.A. Real; J.-P. Tuchagues; A.C. Dennis; M.L. Boillot Chem. Phys. Lett., 318 (2000), pp. 409-416

[82] A. Bousseksou; H. Constant-Machado; F. Varret J. Phys., 5 (1995), p. 14

[83] A. Bousseksou; M. Verelst; H. Constant-Machado; G. Lemercier; J.P. Tuchagues; F. Varret Inorg. Chem., 35 (1996), p. 110

[84] A. Bousseksou; L. Salmon; F. Varret; J.P. Tuchagues Chem. Phys. Lett., 282 (1998), p. 209

[85] N. Moliner; M. Muñoz; S. Létard; L. Salmon; J.P. Tuchagues; A. Bousseksou; J.A. Real Inorg. Chem., 41 (2002), p. 6997

[86] L. Salmon; B. Donnadieu; A. Bousseksou; J.-P. Tuchagues Comptes Rendus Acad. Sci. Ser. IIC Chem., 2 (1999), pp. 305-309

[87] L.F. Lindoy; S.E. Livingstone Coord. Chem. Rev., 2 (1967), pp. 173-193

[88] M. Sorai; S. Seki J. Phys. Chem. Solid., 35 (1974), pp. 555-570

[89] S.K. Kulshreshtha; R.M. Iyer Chem. Phys. Lett., 108 (1984), pp. 501-504

[90] S.K. Kulshreshtha; R.M. Iyer; E. König; G. Ritter Chem. Phys. Lett., 110 (1984), pp. 201-204

[91] N. Moliner; L. Salmon; L. Capes; M.C. Muñoz; J.-F. Létard; A. Bousseksou; J.-P. Tuchagues; J.J. McGarvey; A.C. Dennis; M. Castro; R. Burriel; J.A. Real J. Phys. Chem. B, 106 (2002), pp. 4276-4283

[92] G. Molnár; V. Niel; A.B. Gaspar; J.-A. Real; A. Zwick; A. Bousseksou; J.J. McGarvey J. Phys. Chem. B., 106 (2002), pp. 9701-9707

[93] P. Guionneau Dalton Trans., 43 (2014), p. 382

[94] E.M. Hernández; C.M. Quintero; O. Kraieva; C. Thibault; C. Bergaud; L. Salmon; G. Molnár; A. Bousseksou Adv. Mater., 26 (2014), pp. 2889-2893

[95] C.P. Slichter; H.G. Drickamer J. Chem. Phys., 56 (1972), pp. 2142-2160

[96] S. Pillet; J. Hubsch; C. Lecomte Eur. Phys. J. B., 38 (2004), p. 541

[97] S. Pillet; V. Legrand; M. Souhassou; C. Lecomte Phys. Rev. B., 74 (2006), p. 140101

[98] K.F. Purcell; M.P. Edwards Inorg. Chem., 23 (1984), pp. 2620-2625

[99] F. Volatron; L. Catala; E. Rivière; A. Gloter; O. Stéphan; T. Mallah Inorg. Chem., 47 (2008), p. 6584

[100] H. Peng; S. Tricard; G. Félix; G. Molnár; W. Nicolazzi; L. Salmon; A. Bousseksou Angew. Chem., Int. Ed., 53 (2014), p. 10894

[101] H. Köppen; E.W. Müller; C.P. Köhler; H. Spiering; E. Meissner et; P. Gütlich Chem. Phys. Lett., 91 (1982), p. 348

[102] V. Petrouleas; J.-P. Tuchagues Chem. Phys. Lett., 137 (1987), p. 21

[103] G.S. Matouzenko; J.-F. Létard; S. Lecocq; A. Bousseksou; L. Capes; L. Salmon; M. Perrin; O. Kahn; A. Collet Eur. J. Inorg. Chem. (2001), pp. 2935-2945

[104] C. Cantin; J. Kliava; A. Marbeuf; D. Mikaïlitchenko Eur. Phys. J. B, 12 (1999), pp. 525-540

[105] R. Zimmermann; E. König J. Phys. Chem. Solid., 38 (1977), pp. 779-788

[106] A.B. Koudriavtsev Chem. Phys., 241 (1999), p. 109

[107] D. Chernyshov; H.-B. Bürgi; M. Hostettler; K.W. Törnroos Phys. Rev. B., 70 (2004), p. 094116

[108] J.D. Eshelby Solid State Phys. (1956), pp. 79-144

[109] S. Ohnishi; S. Sugano J. Phys. C Solid State Phys., 14 (1981), p. 39

[110] H. Spiering; K. Boukheddaden; J. Linares; F. Varret Phys. Rev. B., 70 (2004), p. 184106

[111] M. Kepenekian; B. Le Guennic; V. Robert J. Am. Chem., 131 (2009), p. 11498

[112] M. Kepenekian; B. Le Guennic; V. Robert Phys. Rev. B., 79 (2009), p. 094428

[113] M. Kepenekian; J. Sánchez Costa; B. Le Guennic; P. Maldivi; S. Bonnet; J. Reedijk; P. Gamez; V. Robert Inorg. Chem., 49 (2010), pp. 11057-11061

[114] I. Boldog; A.B. Gaspar; V. Martínez; P. Pardo-Ibañez; V. Ksenofontov; A. Bhattacharjee; P. Gütlich; J.A. Real Angew. Chem., 47 (2008), p. 6433

[115] T. Forestier; A. Kaiba; S. Pechev; D. Denux; P. Guionneau; C. Etrillard; N. Daro; E. Freysz; J.-F. Létard Chem. Eur. J., 15 (2009), p. 6122

[116] A. Rotaru; F. Varret; A. Gindulescu; J. Linares; A. Stancu; J.F. Létard; T. Forestier; C. Etrillard Eur. Phys. J. B, 84 (2011), p. 439

[117] J. Galán-Mascarόs; E. Coronado; A. Forment-Aliaga; M. Monrabal-Capilla; E. Pinilla-Cienfuegos; M. Ceolin Inorg. Chem., 49 (2010), p. 5706

[118] A. Tokarev; L. Salmon; Y. Guari; W. Nicolazzi; G. Molnár; A. Bousseksou Chem. Commun., 46 (2010), pp. 8011-8013

[119] L. Larionova; L. Salmon; Y. Guari; A. Tokarev; K. Molvinger; G. Molnár; A. Bousseksou Angew. Chem., 47 (2008), p. 8236

[120] I.A. Guralskiy; C.M. Quintero; G. Molnár; I.O. Fritsky; L. Salmon; A. Bousseksou Chem. Eur. J., 18 (2012), p. 9946

[121] Y. Raza; F. Volatron; S. Moldovan; O. Ersen; V. Huc; C. Martini; F. Brisset; A. Gloter; O. Stephan; A. Bousseksou; L. Catala; T. Mallah Chem. Commun., 47 (2011), p. 11501

[122] J.W. Gibbs, Volume vol. 1, Dover, New York (1961), p. 63

[123] T.L. Hill Nano Lett., 1 (2001), pp. 273-275

[124] G. Félix; W. Nicolazzi; L. Salmon; G. Molnár; M. Perrier; G. Maurin; J. Larionova; J. Long; Y. Guari; A. Bousseksou Phys. Rev. Lett., 110 (2013), p. 235701

[125] G. Félix; M. Mikolasek; G. Molnár; W. Nicolazzi; A. Bousseksou Eur. J. Inorg. Chem. (2018), pp. 435-442

[126] C. Bréchignac; P. Houdy; M. Lahmani Nanomaterials and Nanochemistry, Springer, Berlin, 2007

[127] M. Lopes; C.M. Quintero; E.M. Hernández; V. Velázquez; C. Bartual-Murgui; W. Nicolazzi; L. Salmon a; G. Molnár; A. Bousseksou Nanoscale, 5 (2013), pp. 7762-7767

[128] G. Félix; M. Mikolasek; H.J. Shepherd; J. Long; J. Larionova; Y. Guari; J.-P. Itié; A.I. Chumakov; W. Nicolazzi; G. Molnár; A. Bousseksou Eur. J. Inorg. Chem. (2018), pp. 443-448

[129] S. Rat; M. Mikolasek; J.S. Costá; A.I. Chumakov; W. Nicolazzi; G. Molnár; L. Salmon; A. Bousseksou Chem. Phys. Lett., 653 (2016), p. 131

[130] M. Mikolasek; G. Félix; H. Peng; S. Rat; F. Terki; A.I. Chumakov; L. Salmon; G. Molnár; W. Nicolazzi; A. Bousseksou Phys. Rev. B., 96 (2017), p. 035426

[131] H.J. Shepherd; I.A. Gural'skiy; C.M. Quintero; S. Tricard; L. Salmon; G. Molnar; A. Bousseksou Nat. Commun., 4 (2013), p. 3607

[132] I.A. Gural'skiy; C.M. Quintero; J.S. Costa; P. Demont; G. Molnar; L. Salmon; H.J. Shepherd; A. Bousseksou J. Mater. Chem. C., 2 (2014), p. 2949

[133] M.D. Manrique-Juarez; S. Rat; L. Mazenq; F. Mathieu; I. Séguy; T. Leïchlé; L. Nicu; L. Salmon; G. Molnár; A. Bousseksou 2017 19th International Conference on Solid-state Sensors, Actuators and Microsystems (TRANSDUCERS, 2017, pp. 1300-1303

[134] M.D. Manrique-Juarez; S. Rat; F. Mathieu; D. Saya; I. Séguy; T. Leichlé; L. Nicu; L. Salmon; G. Molnar; A. Bousseksou Appl. Phys. Lett., 109 (2016), p. 061903

[135] M. Mikolasek; M.D. Manrique-Juarez; H.J. Shepherd; K. Ridier; S. Rat; V. Shalabaeva; A.- C Bas; I.E. Collings; F. Mathieu; J. Cacheux; T. Leichle; L. Nicu; W. Nicolazzi; L. Salmon; G. Molnár; A. Bousseksou J. Am. Chem. Soc., 140 (2018), p. 8970

[136] K. Ridier; S. Rat; L. Salmon; W. Nicolazzi; G. Molnár; A. Bousseksou Phys. Chem. Chem. Phys., 20 (2018), pp. 9139-9145

Commentaires - Politique