1 Introduction
Molecular spin-crossover (SCO) complexes are known to be very sensitive to external pressure because of the large difference in volume (ΔVHL = VHS − VLS) between the high-spin (HS) and low-spin (LS) isomers. Although the volume of the coordination octahedron is always modified by virtually the same ratio—ca. 25% for complexes with FeIIN6 coordination core—the unit cell volume modification that reflects the macroscopic change strongly varies from one complex to the other [1]. This is in part a result of anisotropic structural response of these materials that are often of low symmetry, although the difference in volume is always noteworthy (several percent). Hence, for relatively small applied pressures (i.e. a few hundred bars) the work term, pΔV, of the Gibbs' free energy is already significant. For this reason, pressure tuning the spin state of SCO compounds has been a valuable experimental tool since the early stages of SCO research and continues to attract significant attention from researchers.
High-pressure spectroscopic studies of Drickamer and colleagues and Ferraro and colleagues [2–20] in the 1960–1970 have already addressed the SCO phenomenon using Mössbauer, ultraviolet–visible (UV–vis) and infrared (IR) spectroscopies associated with either piston–cylinder or anvil-type pressure cells. High-pressure investigations (primarily using Mössbauer spectroscopic detection) were then taken up in the 1980s by various study groups [21–41]. There was a renaissance of interest in the effect of pressure on SCO compounds during the 1990s [42–77], involving studies using either clamp-type and helium gas cells coupled with magnetic susceptibility [26] and optical [49,60] detection methods or diamond anvil cells (DACs) in conjunction with X-ray spectroscopic [61,64,66,70] or X-ray diffraction (XRD) [68,78] techniques. These and also some more recent studies that we will discuss have led to a range of experimental observations on several dozens of SCO compounds. Besides the exploration of the p–T phase diagram, numerous investigations were also conducted to elucidate pressure effects on spin-state relaxation phenomena as well [28,33,36,38,41,52,57,58,63].
In a first approximation one can describe the pressure effects on SCO systems by expressing the HS–LS energy gap as ΔEHL(p) = ΔEHL(p = 0) + pΔVHL. The pressure dependence of the spin transition temperature (Tc) is given then by the Clausius–Clapeyron equation:
| (1) |
On the whole, pressure effects also remain less investigated as compared to thermal- and light-induced spin-state changes, mainly because of experimental difficulties of working under hydrostatic pressure and variable temperature at the same time. In addition, the experimental high-pressure setups are, in most cases, homemade and the associated know-how for their use remains to some extent confidential for their rather specialized features. Much of the technical literature concerning high-pressure experimental methods relates to research at pressures well in excess of the relatively modest pressure range typically encountered in SCO research. For these reasons, the primary aim of the present review is to assess the experimental aspects of high-pressure SCO research, which will be then illustrated by selected examples.
Although we restrict the scope of this contribution to the effects of in situ, externally applied pressure, it is important that readers be aware of the conceptually related area of research into the effect of the so-called internal pressure in SCO systems. Doping an SCO material with metal ions of a different ionic radius exerts an internal pressure on the lattice (either positive or negative depending on the size of the guest ions with respect to the host) and produces a concomitant shift in T1/2, that can be enhanced or negated through the application of external pressure [55,81].
2 Experimental methods
Molecular-based SCO compounds are relatively soft, and as such they are particularly sensitive to shear stress caused by the presence of nonhydrostatic environments [82]. SCO materials are notoriously sensitive to the presence of lattice defects, so the possibility of inducing these by nonhydrostatic pressure must be assessed in any high-pressure experiment. As such, it is important to consider carefully the experimental methods used to generate high pressure during investigations of these systems.
2.1 High-pressure generation
Techniques for the generation of high pressures for individual experiments are dictated both by the pressure range of interest for the material and the experimental technique used [83]. The pressure range of interest for molecular-based SCO materials ranges from atmospheric to ca. 5 GPa, and thus the discussion presented here is limited to this relatively “low” high-pressure regime. It should, however, be noted that pressures up to the megabar (1 GPa = 10 kbar = 0.01 Mbar) range can be achieved experimentally, and although these extreme pressure ranges are far in excess of those of interest for most molecular SCO studies, they are successfully exploited by geophysicists in the study of spin-transition processes occurring in minerals within the temperature and pressure ranges relevant to the Earth's interior [84,85]. In this section, we will introduce the most commonly used methods for generating high pressure that have been used in the study of SCO materials. It is not intended to be an exhaustive review, but rather designed to serve as a tutorial for newcomers to the experimental study of SCO materials at high pressure.
As a general concern for all kinds of pressure cells, the choice of hydrostatic pressure transmitting medium may be dictated by the pressure and temperature range of interest, the transparency to the characterization technique, ease of loading and chemical solubility/reactivity with regards to the sample. It should also be noted that the sensitivity of many SCO materials to the presence of certain guest molecules may well be another important factor in the choice of pressure transmitting medium. Typical media include silicone oils, a mixture of methanol/ethanol, helium gas, liquid helium or other condensed gases [86,87]. In some cases, the relatively soft polycrystalline SCO complexes were even successfully compressed without any additional pressure transmitting medium [88].
Another common problem is the determination of pressure inside the cells. (N.B. The particular case of pressure determination with piston–cylinder cells and capillary-fed “low-pressure” cells is discussed separately in Sections 2.1.2 and 2.1.3, respectively.) Whenever optical access is available to the sample chamber the pressure inside the cell is most commonly determined by measuring the position of the R1 fluorescence line of a small ruby chip or sphere located inside the sample chamber [89], as shown in Fig. 1, which shifts with applied pressure according to Eq. 2 [90]:
| (2) |
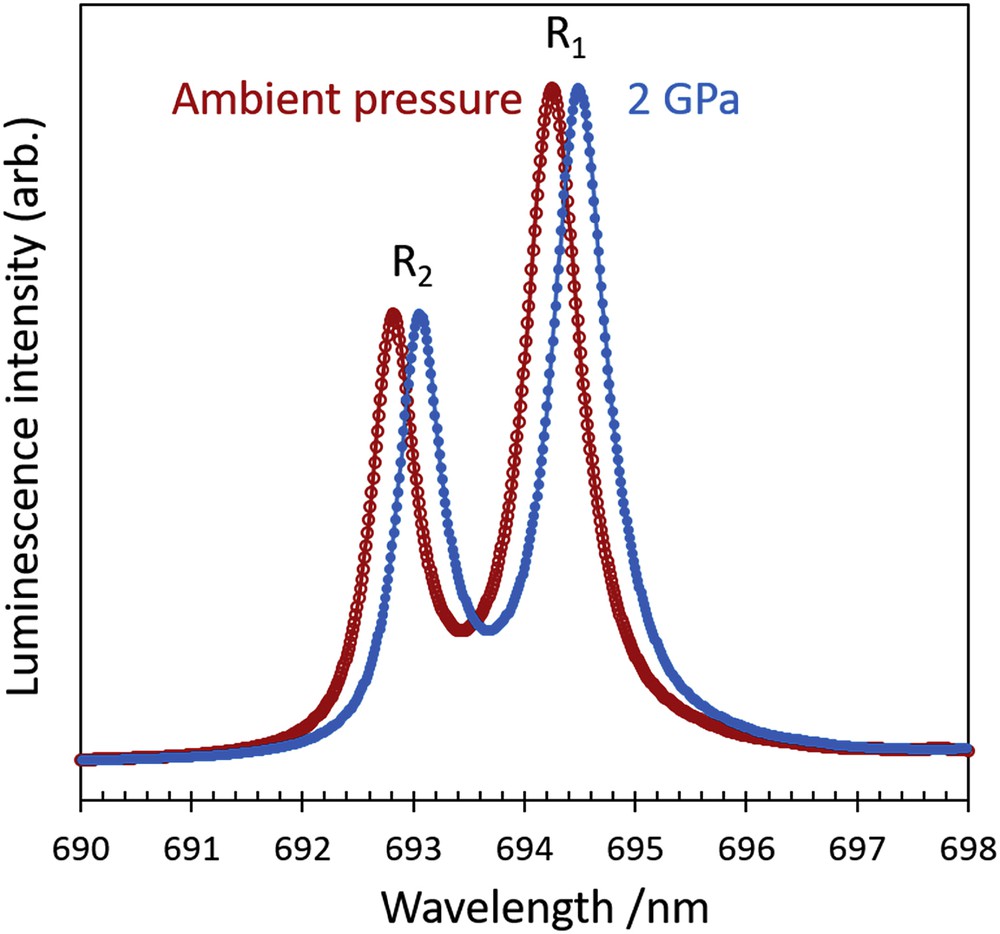
Illustration of the shift in position of the R1 fluorescence line of ruby on increasing pressure from ambient pressure to 2 GPa at room temperature.
Reproducible phase transitions of some materials can also be used as a pressure gauge. Of particular relevance to the SCO field is the pressure dependence of the superconducting transition of Sn or Pb, which is commonly used to infer the applied pressure in magnetometry experiments, as illustrated in Fig. 2. In this case, a small piece of high purity metal is placed inside the cell and the precise transition temperature is recorded. The pressure (up to 5 GPa) is determined according to the following analytical expressions, as presented in Ref. [92]:
| (3) |
| (4) |
| (5) |

Illustration of the shift in temperature of the superconducting transition of Pb on the application of pressure from ambient to 0.73 GPa.
The typical accuracy of these various pressure gauges is rarely better than approximately 0.05 GPa and depends strongly on the instrumental resolution as well as on various other experimental conditions—most crucially on the investigated pressure and temperature ranges. This level of accuracy remains an important concern for the SCO research where the applied pressure frequently remains less than 1 GPa. In this context the use of electrical gauges may be particularly advantageous. In particular, four-wire resistance measurements using tiny Manganin wires can provide very precise pressure readings (better than 0.01 GPa). In addition, the pressure dependence of the Manganin resistance is only very weakly temperature dependent.
Temperature variations not only complicate pressure calibrations, but also problems of hydrostaticity may substantially increase at low temperatures. It is thus useful to note that with some care most pressure gauges allow for detecting the loss of hydrostaticity. To this aim one can either measure the pressure gradient across the cell using several gauges (e.g., ruby chips) or analyse peculiar changes in the behaviour of the gauge. For example, the decreasing sharpness of the Pb superconducting transition or the broadening of the ruby lines is symptomatic of shear stresses.
Before going into further details a word of CAUTION is necessary here. Potential danger from high-pressure apparatus must be always carefully evaluated—even when using certified commercial equipment—and appropriate safety measures must be taken. Perhaps surprising at first sight, but the most dangerous equipment is often moderate—low-pressure vessels. Indeed, the danger is not linked to the magnitude of the applied pressure but to the potential energy stored during compression. Key factors are the volume and the compressibility of the pressurized medium. For example, DACs with their tiny sample chambers can be largely considered safe even in the megabar range, whereas large-volume helium gas cells can be extremely dangerous at just a few bar of pressure. The danger is further enhanced if the energy of the compression is entirely transmitted to small parts (e.g., leads, windows), which can be propelled with high velocity. Best practice rules include (1) careful preliminary testing of the equipment before routine use, (2) always working below ca. 90% of the highest tested pressure value, (3) changing pressure and/or temperature smoothly, (4) using shielding and (5) depressurizing the cell immediately after taking the measurements [93].
2.1.1 Anvil cells
Anvil cells, most commonly DACs, have been used in scientific research for more than 50 years; having been continually modified and adapted to the specifications of a great range of characterization and synthetic techniques, they still represent a relatively simple and safe way to obtain pressure up to the megabar range in the home laboratory [83]. Early iterations of the DAC comprised two opposing diamonds (supported by backing plates) between which a sample was compressed in a uniaxial manner. The use of gaskets in the DAC (shown schematically in Fig. 3) allows for relatively hydrostatic environments by providing a chamber for the sample, which is filled with a hydrostatic medium that transmits pressure throughout the chamber. Perhaps the most significant influence on the actual pressure range attainable is the size of the smallest diamond face, or culet, with smaller culets able to produce significantly higher pressures [83]. The culet size, of course, also affects the size of the sample that may be studied in a DAC, with the largest samples often being no more than ≈300 μm in any one dimension and usually much smaller than this. It should be noted that for single crystal samples, the size must also be limited in the axial direction to avoid contact with both diamonds simultaneously, which would result in pressure gradients across the sample and, in the case of molecular materials, likely destruction of the crystal.

DACs: (a) schematic gasketed DAC, (b) exploded view of a Merrill–Bassett DAC as presented in Ref. [96]. Reproduced with permission from the International Union of Crystallography. Illustration of a DAC used in (c) transmission and (d) transverse geometry.
The diamonds are supported by seats and/or backing plates and pressure is generated by driving the diamonds together, deforming the gasket to reduce the volume of the sample chamber. Perhaps the simplest design for DACs is the Merrill–Bassett DAC [94], shown schematically in Fig. 3b, in which pressure is increased manually by tightening screws in the cell body. Its simple design allows it to be relatively compact, enabling it to be easily incorporated into a variety of different experimental setups. This is vital in the field of SCO, where a combination of several experimental techniques (structural, spectroscopic, etc.) under the exact same conditions is often required to elucidate complex pressure effects. For example, a combination of high-pressure single-crystal XRD and Raman spectroscopy using the same DAC allowed for the rationalization of complex pressure-induced SCO behaviour that differs significantly from the thermal behaviour in a dinuclear Fe(II) complex [80]. Another common design of the DAC uses an inflatable gas membrane to apply pressure [95]. This latter method of pressure generation allows for finer control over the pressure at the sample via an external controller and also allows for more controlled release of pressure if measurements as a function of decreasing pressure are of interest. This opens the possibility to study piezohysteresis loops of SCO materials, which may be difficult to investigate using screw-driven DACs. It should, however, be noted that membrane-driven cells tend to be more complicated, more expensive and bulkier than screw-driven cells.
The simplicity and adaptability of the DAC design coupled with the fact that the diamonds (depending upon the type and level of impurities) are to a greater or lesser extent transparent to many types of radiation, have resulted in their use for a multitude of experimental techniques. The most relevant of these to the field of molecular SCO materials include XRD and neutron diffraction, X-ray spectroscopy, Mössbauer spectroscopy, Raman, FTIR, UV–vis and other optical spectroscopies. Two modes of use may be considered for the anvil cells: the probe radiation reaches the sample through the anvils, which act as windows (either in transmission or reflection geometry), or the probe passes through the gasket to the sample—transverse geometry, as illustrated in Fig. 3c and d. In general, transmission or reflection is the most commonly used DAC geometry when considering all experimental techniques, although some early examples of high-pressure diffraction experiments used DACs in transverse geometry [76,97,98]. In that case a beryllium gasket provides the X-ray transparent sample chamber, as shown schematically in Fig. 3d. The limiting factor to this design is the toxicity of the Be gasket material. The dangers associated with machining beryllium have largely resulted in its elimination from use as a gasket material, and thus transmission geometry cells becoming much more widely used. Other materials have been suggested as a replacement for Be [99], but none have yet found application in the study of molecular SCO materials. In transmission (or reflection) geometry, the choice of material for the gasket is rather freer as it does not need to be transparent to the probe radiation. Many different metals have been used, with the commonest being stainless steel and rhenium. The choice is largely dictated by the pressure range of interest, with harder metals being required for the highest pressures. Gaskets can also be preindented before making the hole for the sample chamber, which will considerably increase the pressure range achievable due to work-hardening the active region of the gasket and providing massive support [100]. For molecular-based SCO materials the pressure range of interest tends to be less than 5 GPa, and thus stainless steel, used without preindenting is often sufficient. The advantage here is the possibility to drill gasket holes using standard—if small—drilling equipment without the need for accurate placement of the hole within the preindent. Such accurate placement can be done using a spark eroder coupled with a microscope and x–y translation stage [101]. Generally the diameter of the hole that forms the sample chamber should be no more than 50% of the width of the culets, should be circular and strictly perpendicular to the plane of the gasket sheet to avoid pressure gradients. The gasket hole should also be well centred on the diamond culet. Imperfect or poorly centred gasket holes can lead to a blowout of the sample chamber, loss of the sample and even destruction of the diamonds.
DACs built from nonmagnetic materials have recently been adapted to fit within the confines of a superconducting quantum interference device (SQUID) magnetometer [102,103], increasing the potential pressure range available to magnetic studies beyond that offered by a piston–cylinder cell (vide infra) by an order of magnitude. It also allows the possibility of incorporating light irradiation into the high-pressure experiment through the diamond windows, allowing observation of pressure-induced photomagnetic effects on SCO materials [104]. It is possible to use anvils other than diamond in these cells to reduce the cost of the equipment. Cubic zirconia, sapphire and moissanite anvils are commercially available, and can be used for a range of experiments provided they are translucent to the probe radiation and are suitable for the pressure range of interest. It may also be worth mentioning that toroidal anvil [105] and multianvil [106] devices may provide an interesting, yet unexplored, scope for SCO research with considerable advantages in terms of larger sample volumes and more precise control of temperature and pressure fields.
2.1.2 Piston–cylinder-type systems
Probably the most straightforward way to generate pressure is the use of piston-cylinder–type systems, in which the cylinder acts as a pressure chamber and the piston is used to compress the medium. In particular, these systems allow for accurate pressure determination on a force-per-area basis, provide hydrostatic conditions and large sample volumes. Despite the inherent opacity of the materials used to construct pistons and cylinders, windows for various probe radiations and electrical feedthroughs can be easily implemented. The latter are generally not used in the study of SCO materials, although they are required when calibrating the applied pressure. In general piston–cylinder cells can be used up to 1–4 GPa, but the maximum pressure achievable is dependent largely on the size of the cell and the material from which the cell is constructed [107,108]. A key limiting factor is the yield strength of the cylinder, which can be improved by different methods—the most popular being the autofrettage [93].
In the SCO field, clamped piston–cylinder cells are used preferentially in combination with magnetic and optical measurements. In this configuration, after applying a pressure with a press, the cell is clamped by locknut(s) to keep the piston(s) in the desired position even after removing the cell from the press. These (relatively) small autonomous cells are particularly popular because they can be easily combined with cryostats, magnetometers and other equipment [26,82,109]. Although several designs, both home built and commercially available, have been used in the study of SCO materials, the principle upon which they work is similar. In general, the sample is placed in a Teflon capsule along with a pressure transmitting oil and, in some cases, with a Pb or Sn pressure gauge (vide infra). The sample capsule is placed inside the cell body and pressed by the pistons as shown in the cross-section in Fig. 4. After clamping the cell, it is placed usually in a cryogenic flow and temperature cycles are carried out for a given pressure. Then, this operation is repeated while progressively increasing the pressure.
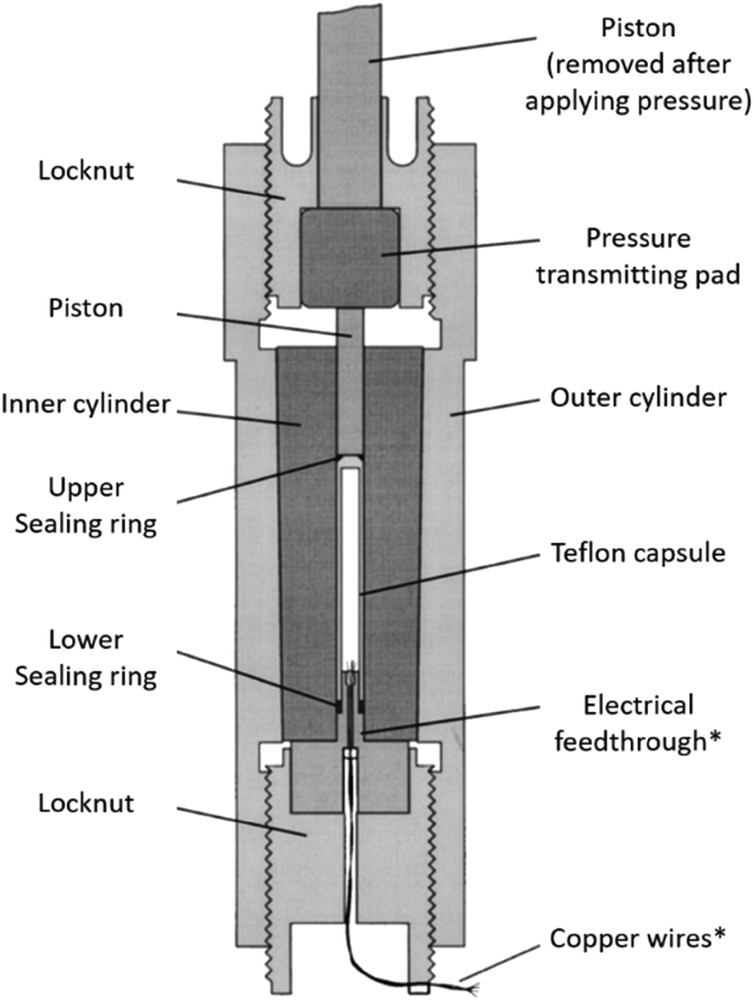
Cross-section of a typical clamp-type piston–cylinder pressure cell. Components marked * may only be used during pressure calibration. Reprinted with permission from Ref. [108], AIP Publishing.
2.1.3 Capillary-fed hydrostatic cells
Although DACs and clamp-type cells will no doubt remain popular for the ease of their use and their compact, autonomous construction, an important concern for SCO research is that they can potentially present difficulty when investigating isothermal pressure cycles (e.g., piezohysteresis effects). In addition, they are not readily designed for working at relatively low pressures (<1 GPa) nor do they allow for a fine control of the pressure (partly for the lack of appropriate pressure gauges). Perhaps even more importantly, they exhibit an inevitable drop of pressure upon cooling. The freezing of the pressure transmitting oil may also lead to less hydrostatic conditions. Most of these drawbacks can be alleviated to some extent by gas loading and improved design (e.g., in membrane-driven DACs), but this inevitably brings in bulkier and much more complex instrumentation.
To overcome the limitations of DACs and clamp-type cells one can also use a helium gas compressor or a liquid pump connected by a capillary to the pressure cell, an example of which is shown in Fig. 5a. The pressure limit of these systems is usually limited by the capillary to a few kilobars (<1 GPa), the pressure generators are often rather complex and the potential danger of compressed gases is significant, yet they have allowed the investigation of unique features of the SCO phenomenon. A key advantage of this approach is that truly hydrostatic conditions can be maintained down to very low temperatures (using He gas). In addition, one can increase/decrease both temperature and pressure in very small increments (frequently <0.005 GPa and <1 K) in a facile manner, which provides a unique means to explore the P,T-phase diagram. This high precision is partly attributable to high precision valves and mechanical gauges (e.g., the Bourdon tube gauge), which can be used in conjunction with these cells. The relatively modest pressure range is not a real drawback for SCO research. On the contrary, such low pressures are very difficult to achieve using a DAC or a clamp cell, and therefore these systems allow an important region of the structural phase diagram to be investigated. Last but not least, contrary to the previously mentioned static pressure generators, these capillary systems combined with automatic valves can also allow for dynamic (e.g., pulses) pressure generation as well [110].

(a) Schematic of a capillary-fed hydrostatic cell, (b) temperature dependence of the electrical conductivity of [Fe(Htrz)2(trz)](BF4) at various applied pressures, (c) pressure dependence of the electrical conductivity of [Fe(Htrz)2(trz)](BF4) at various temperatures, and (d) the phase diagram in P,T coordinates showing an excellent agreement between variable temperature and variable pressure experiments. Reprinted with permission from Refs. [111,112]. Copyright 2003 American Chemical Society.
Capillary-fed low-pressure cells have been used with UV–vis spectroscopy (either in transmission or reflection mode), Mössbauer spectroscopy, Raman spectroscopy and dielectric measurements to investigate SCO compounds [25,49,60,111,112]. The first observation of a piezohysteresis effect used such a cell to investigate the SCO behaviour of the molecular [Fe(btr)2(NCS)2]·H2O complex using optical reflectivity [77]. A simple pressure cell that uses a quartz capillary filled with nitrogen gas or water to generate pressures up to ca. 1 kbar in fine increments [113] was used to follow the structural evolution of an SCO material via single-crystal XRD [114,115]. This type of cell has advantages in that the pressures attained are close to those a material may be exposed to in real-world situations, and fine resolution of this important low-pressure region is more accessible than with virtually any other technique.
A subsequent investigation used a cell driven by hydraulic oil pressure transmitting medium to investigate the SCO in a series of three-dimensional (3D) coordination polymers using Raman spectroscopy [111]. Not only was it possible to observe a memory effect using a perturbation other than temperature, but the authors also used a theoretical analysis of their results to support their suggestion that piezohysteresis effects should be observed in many SCO materials. The importance of piezohysteresis loops has recently been highlighted for the ubiquitous [Fe(Htrz)2(trz)](BF4) complex, which shows a pronounced pressure-induced increase in conductivity, as well as a significant piezoresistive effect during SCO, as shown in Fig. 4b–d [112]. These properties combined with piezohysteresis suggest that these materials may have a wealth of exciting possibilities in pressure sensing and piezoelectric applications.
2.2 Detection methods
In Section 2.2.3, we discuss the different physical and spectroscopic methods used in conjunction with high-pressure cells in the SCO field. For its recently growing importance as a readily available—although still highly specialized—laboratory technique with a key impact on the SCO field we discuss separately crystallographic techniques under pressure in Section 2.2.1. Because magnetic susceptibility measurements remain a standard in the SCO field, we dedicate Section 2.2.2 to high-pressure magnetic methods. On the other hand, only a relatively brief account is given on the various other methods (Raman, FTIR, UV–vis, Mössbauer and X-ray spectroscopies).
2.2.1 XRD and neutron diffraction
There are relatively few high-pressure structural studies of molecular SCO materials in the literature as highlighted by a recent review [116] perhaps as a result of the relative complexities of the diffraction experiment at high pressure when compared with ambient conditions or low temperature measurements. The relatively low-pressure range of interest for molecular SCO materials means reasonably large single crystals can be investigated at high pressure inside DACs. As a consequence, standard diffraction equipment found in modern laboratories is suitable for high-pressure single-crystal diffraction experiments. However, in contrast to ambient pressure single crystal XRD experiments, experiments at high pressure require extensive user input and are still not considered routine. However, in recent years many diffractometer manufacturers include high-pressure hardware options and specific software routines that can make high-pressure data collection less challenging than even a few years ago.
Things which must be considered include the presence of additional Bragg reflections in the diffraction pattern from diamonds (and possibly ruby), angular-dependent variation in transmission of X-rays through diamond, shadowing of the detector by the body of the DAC and the reduced access to reciprocal space due to the restricted opening angle of the DAC [117,118]. The vast majority of molecular crystalline materials (including SCO systems) have relatively low symmetry, most commonly crystallizing in triclinic, monoclinic or orthorhombic space groups [119]. This means that single crystal diffraction experiments of such materials at high pressure are often incomplete and/or have low redundancy, as a result of the restricted access to reciprocal space imposed by the body of the cell [118]. This problem has in the past been mitigated by using an X-ray translucent berylium gasket and a transverse DAC geometry [120], shown schematically in Fig. 3d. Rotation of the cell about the axis of the diamonds through 360° makes it possible to sample a much larger portion of reciprocal space than in transmission geometry. If the crystal is carefully oriented within the cell, a virtually complete unique data set can be expected for monoclinic systems. This geometry was used in the first high-pressure XRD study of molecular SCO materials Fe(phen)2(NCS)2 and Fe(btz)2(NCS)2 [68] as well as in the study of SCO in the [MnII(pyrol)3tren] [78]. As described previously, the dangers associated with machining beryllium have largely resulted in cells of transmission geometry becoming much more widely used in XRD. Problems with low completeness in transmission geometry can be to some extent ameliorated by using more than one crystal in the sample chamber (each with different orientations) [121] or using short wavelength X-rays, for example, at a synchrotron source. Modern transmission geometry DACs specifically designed for XRD work have opening angles of up to 100°, thanks to careful design of the diamond anvils and backing plates [96]. Although complete data sets for monoclinic systems often still prove illusive, sufficient data can be collected to reliably investigate structural changes that occur on SCO, as confirmed by several complimentary experimental techniques [79]. For the lowest symmetry triclinic systems, it is often not possible to obtain anything more detailed than unit cell parameters as a function of pressure. Although less information is gained in this case, unit cell parameters can still prove very informative for obtaining the volumic and axial compressibilities and thus rationalizing elastic interactions and anisotropic lattice distortions.
The limitation of the sample size and the restricted angular aperture means that synchrotron radiation is almost always necessary to observe diffraction from powder samples inside DACs, where high-flux short-wavelength X-ray beams are available. However, with the increasing availability of Ag and Mo microfocus X-ray sources it may well be the case that high-pressure powder studies become accessible outside of central facilities in the next few years.
Another challenge in high-pressure structural studies of SCO materials is the combination of high pressure and variable temperature experimental environments. The vital importance of structural studies in rationalizing SCO behaviour is clear; however, the difficulties associated with mounting a traditional DAC inside a cryostat on a goniometer have so-far limited such studies to central facilities [79]. Recent developments in the production of miniature DACs that can be mounted on an in-house diffractometer and are small enough to be cooled by standard open-flow cryocooling devices present exciting opportunities [122], and it is hoped that such devices will accelerate research in this area.
The inherent low-flux of neutron sources, combined with the relatively low neutron scattering efficiency of materials, requires that larger sample volumes be used during neutron diffraction experiments. In the study of SCO materials this has been achieved using a TiZr clamp cell for high-pressure neutron powder diffraction experiments [123,124].
2.2.2 Magnetic measurements
High-pressure cells designed for use inside an SQUID magnetometer are limited in their design by the restrictions of the sample space and must, of course, be constructed from suitable materials. Both commercial and homemade clamp cells designed for magnetometry measurements have traditionally been constructed from beryllium bronze (CuBe) because of its high strength, good thermal conductivity and diamagnetic nature. It may be heat treated for increased strength, but it presents some potential dangers associated with toxic dust generated during machining of beryllium alloys. Beyond these considerations as to construction material, a pressure cell designed for use in a commercial SQUID magnetometer must also have a narrow diameter (typically 9 mm or less) to fit within the bore of the sample chamber and should be approximately symmetrical laterally over several centimeters, to aid with peak fitting and sample centring. The additional weight of the cell as compared to standard (ambient pressure) measurements makes thoroughly securing it to the sample transport rod particularly important.
Pressure is applied using a hydraulic press via a piston that is removed after applying the desired pressure. To achieve a specific pressure at the sample, it is necessary to calibrate the pressure applied at the hydraulic press with that obtained in the cell using a four-wire measurement first using a Manganin resistance gauge [93]. The pressure inside the cell is determined at very low temperatures by measuring the temperature of the superconducting transition of a small piece of high purity Pb, In or Sn metal placed with the sample inside the sample capsule, as illustrated in Fig. 2. This calibration is done usually at very low temperature scan rates and by applying only a weak AC field due to the sensitivity of the superconducting transition to magnetic fields. It is also important to note that pressure will inevitably vary as a function of temperature due to thermal contraction of the cell and the pressure transmitting oil. The pressure drop between room temperature and liquid helium temperature can be as high as 0.1–0.2 GPa.
The high-pressure SQUID magnetometry experiment may be complicated by the large diamagnetic contribution of the cell body, Teflon capsule and pressure transmitting oil. As a possible consequence, in the course of the temperature scan the magnetization may change between positive and negative values resulting to unacceptably poor fit for values close to zero magnetization. Adding a known quantity of a stable paramagnetic substance may resolve this issue. It is also sometimes unavoidable in a high-pressure experiment that the sample mass is not accurately known. As such, calculating accurate values of χMT can be difficult; calculation of χMT may require the use of a series of calibration measurements in the absence of sample, and/or the application of a series of assumptions. Such assumptions may include that χMT of the sample in, for example, the HS state is equal to that observed in the HS state at ambient pressure, that diamagnetic contribution is constant at all temperatures and that χMT of the sample is constant at temperatures well away from the SCO. It is important that the validity of any such assumptions is evaluated in each case before application. Because the first report of high-pressure magnetic susceptibility measurements of SCO solutions [12] and solids [26], there have been numerous studies of SCO materials under pressure using SQUID magnetometry, which will be largely covered in Section 3. There are also some reports of DACs that have been optimized for use in SQUID magnetometers [103]. As discussed previously, they have the potential to reach significantly higher pressures than clamp-type cells, but the small sample volume required by these cells has so far limited their application to the field of molecular SCO. They do, however, present interesting possibilities for the incorporation of light irradiation, pressure and temperature within a single experiment.
2.2.3 Other detection methods
Because the SCO phenomenon is accompanied by the change in various material properties (electronic, structural, vibrational, magnetic, optical, electrical, etc.) it is not surprising that a large variety of detection methods have been used for its investigation under high pressures. Here, we briefly review the most important ones.
High-pressure Raman spectroscopy of SCO materials was first reported using the hydrostatic cell presented in Fig. 5a [111], and has since been used several times as a straightforward means to follow the HS → LS transition as a function of pressure using characteristic marker bands for each state [79,80,115,125–127], an example of which is shown in Fig. 6. Specific marker of the two spin states can be first identified during a separate variable temperature experiment. Besides following the spin-state changes, in certain compounds Raman spectroscopy allowed one to detect the occurrence of simultaneous pressure-induced structural changes [111] and also to estimate the pressure-induced modification of the vibrational entropy as inferred from the frequency shifts [88]. Raman spectroscopy has the advantage that it can operate at long working distances from the sample, allowing for the relatively bulky sample environment of a pressure cell. It can be used to probe small sample volumes often encountered in pressure cells, and the Raman spectrometer can be used to measure the pressure via the ruby fluorescence technique in situ. It can also be used to carry out complementary optical absorption measurements. Importantly, Raman spectroscopy can be used to study single crystals, powders, thin films or solutions with virtually no sample preparation. Using reflection geometry, the only requirements for pressure cells used in Raman studies are that they have one window that is transparent to the wavelengths relevant to the experiment. Examples might include diamond, sapphire and quartz, although the use of DACs is perhaps the most common and convenient. When diamond is used as the window materials, the type of diamond needs to be selected carefully because of different fluorescence responses between type I and type II diamonds [128]. It is also interesting to note that laser-induced heating of the sample is reduced to a large extent in the high-pressure cell (vs ambient air) because of the improved heat dissipation provided by the pressure transmitting medium. This feature is obviously very advantageous in investigating SCO compounds.
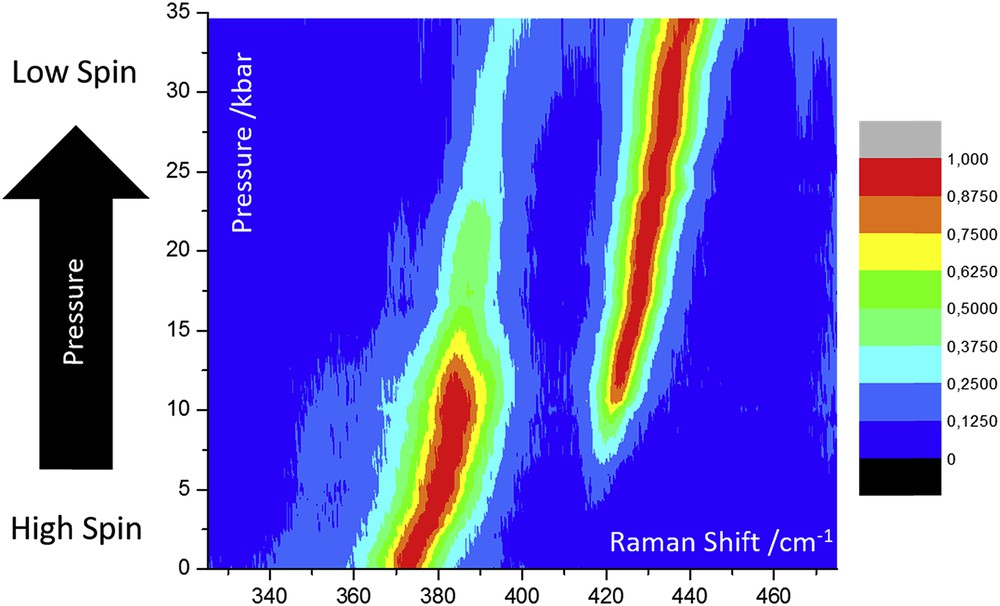
Normalized Raman intensities of characteristic marker peaks of a molecular SCO material at 370 (HS) and 420 cm−1 (LS) as a function of pressure. Adapted from Ref. [80].
Despite very early applications of the DAC in high-pressure IR spectroscopy [83], the technique is complicated by the necessity for more expensive nitrogen-free diamonds, the small sample size, and requires specialized focussing optics to obtain a suitable signal-to-noise ratio [129]. Although specific modifications to the DAC have been proposed to facilitate IR measurements [129] and FTIR microscopes have been also significantly improved recently, it is still not a routine experiment. Although several high-pressure IR spectroscopic studies of SCO materials using a DAC have been reported in the 1970–1980 [3,4,13–17,19,20,32], by now this technique has been largely replaced by high-pressure Raman spectroscopy, giving access to similar information about the sample, while providing ease of use, no sample preparation and a larger selection of possible pressure transmitting fluids. Indeed, because the pressure transmitting medium should not interfere with the spectrum of the sample, in the far-IR Nujol is often used, but the relatively low hydrostatic limit of Nujol limits the investigated pressure range to less than 1.5 GPa [32].
A significant number of high-pressure 57Fe Mössbauer spectroscopic investigations of SCO materials were reported and reviewed several years ago [82]. The key interest of this technique is that it usually allows for a simple yet accurate quantification of the HS fraction as a function of pressure and temperature in iron complexes. In general, either clamp-type or capillary-fed cells were used, incorporating windows that are transparent to γ radiation, most commonly boron carbide [25,130]. (N.B. Beryllium is a more suitable window material, but it is scarcely used because of its previously mentioned toxicity.) Pressure transmitting media include inert gasses and oils. In general, studies consist of variable temperature investigations at high pressure, and as such represent one of the few early examples of combining more than one external stimulus to control the spin state in these materials. One significant limitation of this technique is the relatively small sample volume often encountered in high-pressure cells. This fact combined with the relatively small Fe content and low Lamb–Mössbauer factor of typical SCO samples as well as with the restricted γ-ray transmission of the windows makes isotope enrichment of the samples with 57Fe to give a suitable signal-to-noise ratio inevitable [82]. For this reason, high-pressure Mössbauer spectroscopy has been sparingly used in the study of molecular SCO materials in recent years. Sample volume is even more restricted in diamond anvil–type cells used in conjunction with Mössbauer spectroscopy. In this case, not only isotope enrichment, but also high specific-activity, “point” sources have been used [23]. However, these sources imply increasing linewidths and increasing price. DACs can be advantageously used in combination with synchrotron radiation sources. Notably, nuclear inelastic scattering experiments at pressures up to 2.6 GPa have been performed for two powder samples of molecular SCO complexes [131]. The pressure cell was based on a DAC design, but was adapted to the requirements of the technique by incorporating photodiode detectors close to the sample chamber to detect nuclear fluorescence signals. The study enabled the determination of the partial vibrational density of states for the complexes as a function of pressure for the first time, revealing similar changes to those occurring as a function of temperature.
Synchrotron X-ray spectroscopy techniques, such as X-ray absorption near edge structure (XANES), extended X-ray absorption fine structure, X-ray emission, X-ray magnetic circular dichroism, and so forth, are particularly well suited for the investigation of SCO complexes under pressure as they allow one to probe the spin state quantitatively in small sample volumes with elemental sensitivity. Indeed, the first high-pressure XANES study of SCO complexes investigated the phenomenon in both Co2+ [70] and Fe2+ [66] complexes using a DAC. Interestingly, in both cases, the authors reported significant shifts in the pressure required to switch between HS and LS states on repeated cycling. This effect was subsequently attributed to the reduction in the number of defects in the lattice on pressure cycling. Similar effects are commonly observed on thermal SCO, and so perhaps it should not be surprising that observations should also be made with pressure. That this effect has not been observed more frequently on pressure cycling is perhaps just a result of the rarity of experiments that repeatedly cycle the same sample with pressure. Subsequent XANES studies allowed us, not only to establish the HS fraction versus pressure curves, but also to follow the main structural changes using X-ray absorption fine structure [43,61]. As a final note on synchrotron X-ray experiments it may be worth noting that the intense focused X-ray beam may lead to the degradation of relatively fragile SCO complexes and therefore the sample integrity must be always carefully controlled. (N. B. The same concern applies to laser Raman spectroscopy.)
High-pressure optical (UV–vis–NIR) absorption measurements on single crystals and solutions as well as reflectivity measurements on powder samples represent simple and efficient means to probe the SCO phenomenon through the piezochromic properties of SCO complexes. In particular, quantitative optical absorption measurements on crystals can be carried out using a cheap optical microscope and an appropriate bandpass filter. Optical spectroscopy has been used since the onset of SCO research [10,11,16,49,59,132] in conjunction with DACs, piston–cylinder and capillary-fed cells as well. Optical spectroscopy is particularly well suited for time-resolved measurements. For instance, McGarvey et al. [33] used pulsed-laser photoperturbation technique together with a capillary-fed cell to determine both the reaction and activation volumes of various SCO complexes in solution. Solid samples were also investigated by Wang et al. [57] using pump–probe optical spectroscopy in combination with DAC, and an impressive eight orders of magnitude acceleration of the low-temperature tunnelling process could be evidenced for an external pressure of 2 GPa. We expect that recent ultrafast (fs) optical spectroscopy experiments on SCO samples will be also complemented by measurements under pressure in the near future.
3 Pressure effect studies on Fe(II) SCO or paramagnetic coordination compounds
As described Section 1, the effect of pressure on SCO compounds is to stabilize the LS state due to its smaller ionic radius (ca. 0.2 Å smaller in LS than HS state for Fe(II) complexes). The change in volume provides the driving energy in pressure-induced phase transitions [(∂G/∂p)T = V]. For most of the SCO complexes investigated, the transition/equilibrium temperature (usually denoted T1/2) of the SCO is shifted upwards with increasing pressures, and the hysteresis width and steepness (cooperativity) of the SCO decrease and vanish at a critical pressure [82]. However, there are a significant number of examples of SCO compounds where the shape of the SCO curve remains essentially unaltered across a reasonable range of pressure, the hysteresis increases/decreases or nonlinear behaviour of the Tc(p) versus p plot is exhibited [47,50,54,133–135]. In rare cases, stabilization of the HS state under pressure has also been reported [134]. From a phenomenological viewpoint, these different behaviours seem to depend on the change in the elastic energy of the material (compressibility) and the intermolecular interactions in the crystal under pressure [136]. Structural features including hydrogen bonding, π–π stacking or metallophilic interactions will be affected differently by pressure and are not distributed isotropically throughout the material. As such the structural changes induced by the application of pressure may be highly anisotropic, affecting the total volume change during the HS ↔ LS transition [116]. Theoretical progress in understanding such unexpected pressure effects requires systematic investigations on single-crystal structure determination under applied pressure to rationalize the origin of unusual pressure-induced SCO behaviour on a case-by-case basis [68,79,80,98,116,123,127].
3.1 Compounds undergoing continuous thermal SCO
For a continuous—or gradual—thermal spin conversions without hysteresis, most materials behave as predicted by the Clausius–Clapeyron equation as described in Section 1. In general, application of hydrostatic pressure results in stabilization of the LS state and a concomitant shift in the transition temperature upwards. Examples of such behaviour are presented in Table 1 [22,53,137–143], along with the change in their T1/2 values as a function of pressure. The compound [Fe(H2B(pz)2)2(bipy)] [134] is a representative example of such type of pressure-induced behaviour, as shown in Fig. 7, along with χMT versus T curves (χM is the molar magnetic susceptibility and T the temperature) at different hydrostatic pressures. At atmospheric pressure, T1/2 is 160 K and the transition is complete within 70 K. Between 0.2 and 0.5 GPa the spin transition experiences a shift to higher temperature and its character becomes more continuous. Indeed, under pressure the SCO becomes more gradual, occurring over a range of more than 150 K at 0.5 GPa. The variation in T1/2 is linear as a function of pressure: 210 K (0.26 GPa), 233 K (0.4 GPa) and 255 K (0.5 GPa). The slope of the line in the T1/2 versus P plot, dT1/2/dP = 187.5 K GPa−1 is comparable with the values observed for several mononuclear compounds whose magnetic properties under pressure have been investigated (Table 1). These molecular complexes with continuous SCO behaviour, the coordination polymers [Fe(3py-im)2(NCS)2]·7H2O [142] and [Fe(dpms)2(NCS)2] [143] also show typical pressure-dependent magnetic properties.
Values of dT1/2/dP for Fe(II) mononuclear coordination complexes exhibiting continuous thermal spin conversion.
| Compound | dT1/2/dP (K GPa−1) |
| [Fe(pmea)2(NCS)2] [140] | 146 |
| [Fe(pic)3]Cl2·EtOH [22] | 150 |
| [Fe(PM-AzA)2(NCS)2] [53] | 160 |
| [Fe(dpa)2(NCS)2] [138] | 176 |
| [Fe(abpt)2(NCS)2] polymorph I [139] | 176 |
| [Fe(stpy)4(NCBH3)2]trans [141] | 186.3 |
| [Fe(H2B(pz)2)2(bipy)] [134] | 187.5 |
| [Fe(phen)2(NCS)2] polymorph II [137] | 220 |
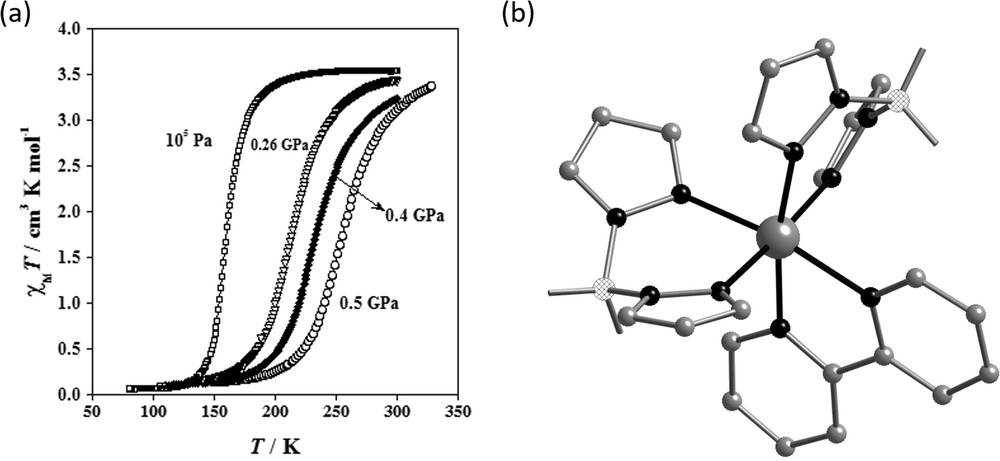
(a) Magnetic properties under hydrostatic pressure in the form of χMT vs T and (b) illustration of the molecular structure of the complex [Fe(H2B(pz)2)2(bipy)]. Reproduced with permission from Ref. [134].
3.2 Compounds with abrupt thermal spin transition accompanied with hysteresis
Again, many compounds with abrupt spin transitions at ambient pressure also show typical pressure-induced SCO behaviour. [Fe(2-pic-ND2)3]Cl2·EtOD [144] and [Fe(bt)2(NCS)2] [67] are typical examples, where the transition temperature increases and the hysteresis and the slope of the transition curve diminish as pressure increases. The hysteresis vanishes at a critical pressure, and at even higher pressures the transition transforms to the gradual type. More unusual behaviour has been displayed by the complex [Fe(phy)2](BF4)2, which shows an increase in the width of the hysteresis loop under pressure, as depicted in Fig. 8. In addition, a nonlinear response of T1/2 as a function of pressure has been reported. This singular behaviour was explained using the mean field theory by introducing the dependence of the bulk modulus (K) under pressure [50]. However, to date there is no single crystal diffraction data at high pressure to further probe this unexpected behaviour.

Plot of γHS vs T, HS molar fraction vs temperature, at different pressures for [Fe(phy)2](BF4)2. Reprinted with permission from Ref. [50]. Copyright 1999 Elsevier.
A series of mononuclear complexes of general formula [Fe(PM-L)2(NCS)2] (where PM-L ligands represent a series of 2-pyridylmethylene-4-anilino derivatives) were studied under pressure [53] and revealed a variety of different behaviours, including increasing width of hysteresis in [Fe(PM-BIA)2(NCS)2]. Subsequent high-pressure reflectivity [145] and neutron diffraction structural studies [124] allowed the complex interplay between polymorphism, phase transitions and SCO effects to be assessed in detail. Other unusual effects seen in this class of compounds include irreversible increases in hysteresis width after pressure is released in [Fe(PM-PEA)2(NCS)2] [53]. Although detailed structural investigation of this material as a function of pressure was prevented by reduction in crystal quality [114], a phase transition under pressure was clearly demonstrated. Such pressure-induced irreversible modification may well represent an interesting method for tuning properties of SCO materials, and as such, the importance of measuring the properties of the material under ambient conditions after depressurization is clearly highlighted.
A study of the compound [Fe(dpp)2(NCS)2]·py (dpp = dipyrido[3,2-a:2′3′-c]phenazine and py = pyridine) highlights clearly the importance of high-pressure structural studies in understanding unusual pressure-induced behaviour and even sheds light on the mechanism of the thermal transition responsible for the highly cooperative thermal SCO behaviour. At ambient pressure it displays a very cooperative spin transition with a 40 K hysteresis width, accompanied by an isostructural crystallographic phase transition. High-pressure structural studies revealed a highly anisotropic scissor-like distortion of the molecule (Fig. 9) coupled with physical intercalation of the large dpp ligands as the origin of the highly cooperative interactions observed [127]. The mechanism is also responsible for exotic mechanical behaviour including negative thermal expansion and negative linear contraction. The ability of the lattice to accommodate the opposing change in shape of the molecule during the spin transition is what governs whether the HS–LS transition can occur. This is essentially an elastic property of the lattice; as the volume of the HS cell contracts by 2% on cooling from 275 to 150 K, the lattice can accommodate the change in shape required for SCO to occur. The same contraction, but with a much greater magnitude (15%), occurs on pressurization up to 0.18 GPa and the lattice is no longer capable of accommodating the change in geometry. The HS–LS transition is thus suppressed, but eventually under the application of further pressure a spin transition occurs to a structurally distinct LS state.
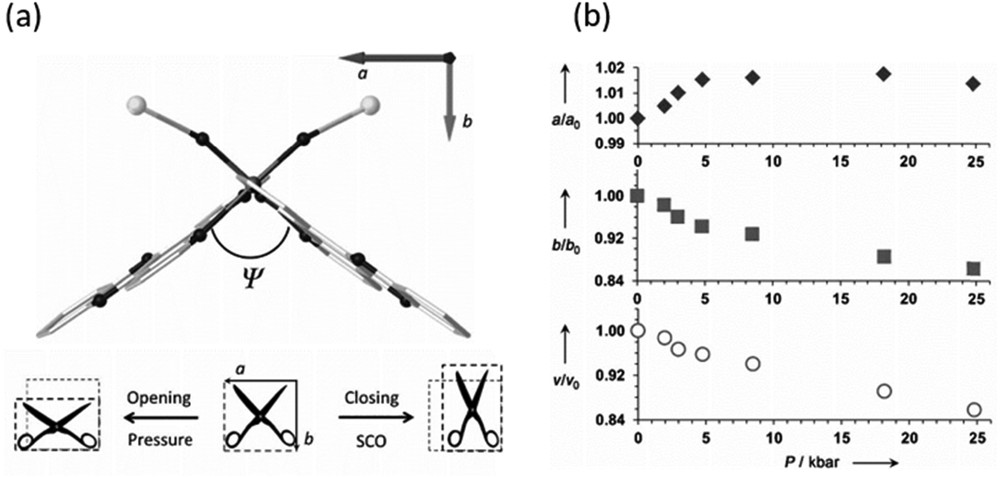
(a) Structure of the molecule [Fe(dpp)2(NCS)2]·py in the ab plane denoting the relative orientation to the unit cell axes. The Ψ angle quantifies at the molecular level the “scissor-like opening–closing” mechanism that induces or inhibits the SCO process. The a and b axes change as a consequence of the opening (HS) or closing (SCO) mechanism. (b) Variation in the a and b axes together with the cell volume as a function of pressure derived from single-crystal diffraction studies. Reproduced with permission from Ref. [127].
In addition to molecular complexes, several coordination complexes have also shown interesting behaviour under pressure. For example, the 3D coordination complex {Fe(pmd)(H2O)[Ag(CN)2]2}·H2O [133] shows pressure-tunable thermal bistability and piezochromic bistability at room temperature. Fig. 10 shows the polymeric structure, the χMT versus T curves at different pressures and the pressure dependence of the HS molar fraction at room temperature. In the crystal, there are two different iron(II) pseudo-octahedral sites, [FeN6] and [FeN4O2]. The equatorial positions of both sites are occupied by the nitrogen atoms belonging to the [Ag(CN)2]− anions, whereas the axial positions are occupied by pmd ligands and water molecules, respectively. The [Ag(CN)2]− ligands act as bridges connecting both sites defining an infinite 3D open framework. Three identical nets interpenetrate to fill the empty spaces. As evidenced by the χMT versus T plot pressure allows one to place the hysteresis loop at will in a large range of temperatures without losing its well-defined square shape. At 300 K, the electronic spectrum in the visible region acquired at different pressures demonstrates that the compound undergoes a complete pressure-induced SCO accompanied by reproducible piezohysteresis loop of 0.2 GPa. The transition pressure values corresponding to half-conversion are ≈ 0.71 GPa and ≈ 0.52 GPa.

(a) Picture of the 3D network and (b) perspective view of the three interlocked networks of {Fe(pmd)(H2O)[Ag(CN)2]2}·H2O. (c) χMT vs T curves at different pressures for {Fe(pmd)(H2O)[Ag(CN)2]2}·H2O: 105 Pa and 0.10, 0.12, 0.15, 0.18, and 0.34 GPa. (d) Pressure dependence of the HS molar fraction, γHS, of the SCO iron(II) ions at 300 K deduced from the visible spectra. Reproduced with permission from Ref. [133].
Other Fe(II) 2D coordination polymers investigated include {Fe(3-F-py)2[M(CN)4]} [132,135] (M(II) = Ni, Pd and Pt), {Fe(3-Cl-py)2[Pd(CN)4]} [146] and {Fe(phpy)2[Ni(CN)4]} [147]. The main structural difference among the 2D polymers based on 3-X-pyridine ligands and that based on the ligand 4-phenylpyridine is the distance between the {Fe[M(CN)4]}∞ layers imposed by the organic ligand and the strength of the π–π contacts. Table 2 gathers characteristic transition pressures derived from spectroscopic experiments in the visible region at 298 K carried out for these complexes. The compound {Fe(phpy)2[Ni(CN)4]} presents the largest intersheet distance and the largest Δpc observed (0.3 GPa). Presumably, compound {Fe(phpy)2[Ni(CN)4]} acts as a better pressure absorber than the previously mentioned 3D and 2D cyanide-based SCO polymers. Recently, a theoretical study has demonstrated that the changes in the elastic and inelastic forces in the crystal as a function of pressure or temperature determine the behaviour of the spin transition in these polymers [132,148].
Characteristic transition pressures derived from visible spectroscopic experiments at 298 K for several cyanide-based Fe(II) SCO coordination polymers.
| Compound | (GPa) | (GPa) | (GPa) | Δpc (GPa) |
| {Fe(pmd)(H2O)[Ag(CN)2]2}·H2O [22] | 0.71 | 0.52 | 0.615 | 0.2 |
| {Fe(3-F-py)2[Ni(CN)4]} [53,140] | 0.38 | 0.29 | 0.33 | 0.1 |
| {Fe(3-F-py)2[Pd(CN)4]} [53,140] | 0.39 | 0.27 | 0.33 | 0.11 |
| {Fe(3-F-py)2[Pt(CN)4]} [53,140] | 0.34 | 0.27 | 0.30 | 0.07 |
| {Fe(3-Cl-py)2[Pd(CN)4]} [141] | 0.65 | 0.57 | 0.61 | 0.08 |
| {Fe(phpy)2[Ni(CN)4]} [142] | 1.6 | 1.3 | 1.45 | 0.3 |
3.3 Compounds with multistepped spin transitions
Multistepped spin transitions are those spin transitions with two or more discernible steps (gradual or abrupt) separated by plateaus or discontinuities along the γHS (T) curve (γHS = HS molar fraction). A two-step spin transition was first observed in the mononuclear compound [Fe(2-pic)3]Cl2·EtOH [22]. Later on the same phenomenology was reported for dinuclear coordination complexes [149,150] and for a series of Fe(II) polymeric species [151–153]. Recently, three- and four-step spin transitions have been reported for both polynuclear [154,155] and polymeric Fe(II) compounds [156]. Examples of multistepped SCO in Fe(III) coordination compounds are scarce [157]. Detailed variable-temperature crystal structure analysis in conjunction with magnetic, calorimetric and spectroscopic studies revealed that the short- and long-range elastic interactions in the crystal lattice are responsible for the energetic stabilization of the [⋯HS–LS⋯] “chessboard” structures. Thus, step-like SCO behaviour can arise as a consequence of the elastic forces in the crystal [158–165]. Alternatively, multistepped spin transition can also be observed when two or more chemically or crystallographically nonequivalent iron centres are present either in the crystal lattice or in a cluster. In such a case, each iron centre undergoes spin transition at different temperature, resulting in a stepwise spin transition [135,166]. Pressure provides a unique tool to probe elastic interactions in the solid state, and as such have been used to examine complexes showing stepped SCO behaviour.
Dinuclear complexes based on the 2,2′-bipyrimidine (bpm) bridge ligand, {[Fe(bpm)(NCSe)2]2bpm} and {[Fe(bt)(NCX)2]2bpm} (X: S, Se and bt: 2,2′-bithiazoline), show one-step [HS–HS] ↔ [HS–LS] and two-step [HS–HS] ↔ [HS–LS] ↔ [LS–LS] spin transitions, at atmospheric pressures, respectively. Fig. 11 shows the magnetic properties under applied hydrostatic pressures in the form of χMT versus T [73]. At 0.45 GPa, {[Fe(bpm)(NCSe)2]2bpm} undergoes less steep [HS–HS] ↔ [HS–LS] conversion and the transition temperature is shifted upwards. As pressure increases the SCO curve transforms into a two-step curve, which is complete at 1.03 GPa. The plateau between the steps smears out and diminishes as the pressure increases. The magnetic behaviour of {[Fe(bpm)(NCSe)2]2bpm} under pressure resembles that of the dinuclear complex {[Fe(bt)(NCX)2]2bpm} at atmospheric pressure. For compound {[Fe(bt)(NCSe)2]2bpm}, the spin transition is displaced 50 K at relatively low pressures (0.37 GPa) [73].
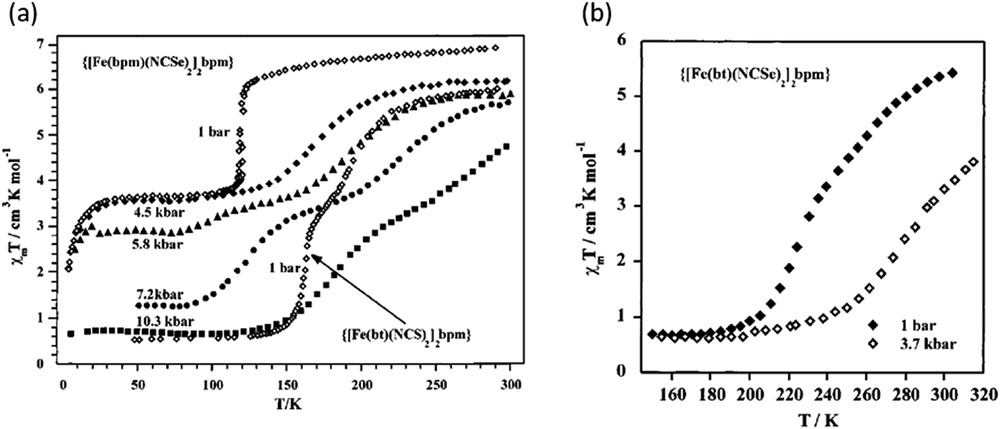
(a) Temperature dependence of χMT for {[Fe(bt)(NCS)2]2bpm} at atmospheric pressure and for {[Fe(bpm)(NCSe)2]2bpm} under applied hydrostatic pressure. (b) Temperature dependence of χMT for {[Fe(bt)(NCSe)2]2bpm} under applied hydrostatic pressure. Reprinted with permission from Ref. [73]. Copyright 2001 American Chemical Society.
In contrast to the magnetic behaviour of bpm-based dinuclear complexes under pressure, the dinuclear complex [Fe2(PMAT)2](BF4)4·DMF shows only one step [HS–HS] ↔ [HS–LS] spin transition up to 1.03 GPa [167]. The steepness of the transition observed at 10−4 GPa disappears gradually as pressure increases. The inhibition of the spin conversion in the second iron centre of the dinuclear unit seems to be related to the steric constraints imposed by the bridge ligand.
Another dinuclear complex undergoing a steep one-step spin transition at 10−4 GPa is [Fe(bpp)(NCS)2}2(4,4′-bipy)]·2MeOH (bpp = 2,6-bis(pyrazol-3-yl)pyridine and 4,4′-bipy = 4,4′-bipyridine) [80]. In this compound it has not been possible to elucidate if the one-step spin transition observed at 10−4 GPa corresponds to [HS–LS] molecules or a random distribution of 50% [HS–HS] and [LS–LS] dinuclear units in the crystal lattice. Raman and structural studies under pressure revealed a total and gradual conversion to the LS state in the interval of pressures comprised between 0.7 and 2.0 GPa.
The mononuclear compound [Fe(tpa)(NCS)2] (tpa: tris(2-pyridylmethyl)amine) exhibits one-step spin transition at atmospheric pressure. Single-crystal to single-crystal transformation occurs upon exposure of the complex to methanol vapours resulting in a new compound, {[Fe(tpa)(NCS)2]·[Fe(tpa)(NCS)2·CH3OH]}. The new complex contains two distinct Fe(II) crystallographic sites one of which features strong hydrogen bonding interactions with methanol molecules in the solid state. It shows a continuous two-step spin conversion and the [HS–LS] state has been crystallographically resolved: (Fe1(HS)Fe2(LS)). Application of pressure minimizes the differences in the crystal field strength of the iron(II) sites. Indeed, the two-step transition transforms into a one-step transition with a considerable amount of Fe(II) molecules in the LS state at room temperature. At pressures as high as 1 GPa the complex is in the LS state. In contrast, the one-step spin transition of the pristine compound converts to a two-step transition under pressure. As pressure increases the characteristic temperatures are shifted to higher temperatures [168].
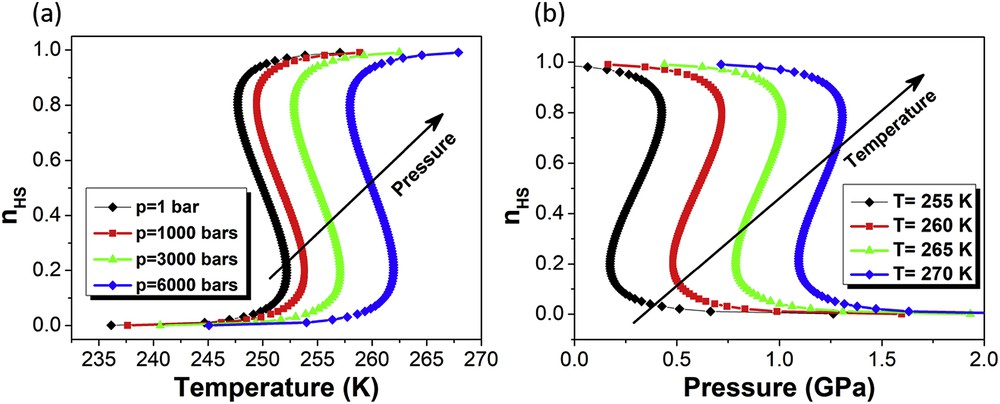
The complex [Fe(mtz)6](BF4)2 (mtz = methyltetrazole) possesses two distinct Fe(II) crystallographic sites. The crystal field strength at one of the iron sites is stronger and undergoes one-step spin transition at low temperature (75 K). Low pressures (0.14 GPa) shift the transition temperature up to 100 K, and the application of 0.57 GPa results in SCO being induced at the other Fe(II) site. At 0.81 GPa the spin transition is continuous, complete and is centred at around 180 K, as shown in Fig. 12 [82]. Similar observations were reported also on the compound Fe(3-methylpyridine)2[Ni(CN)4] [169].
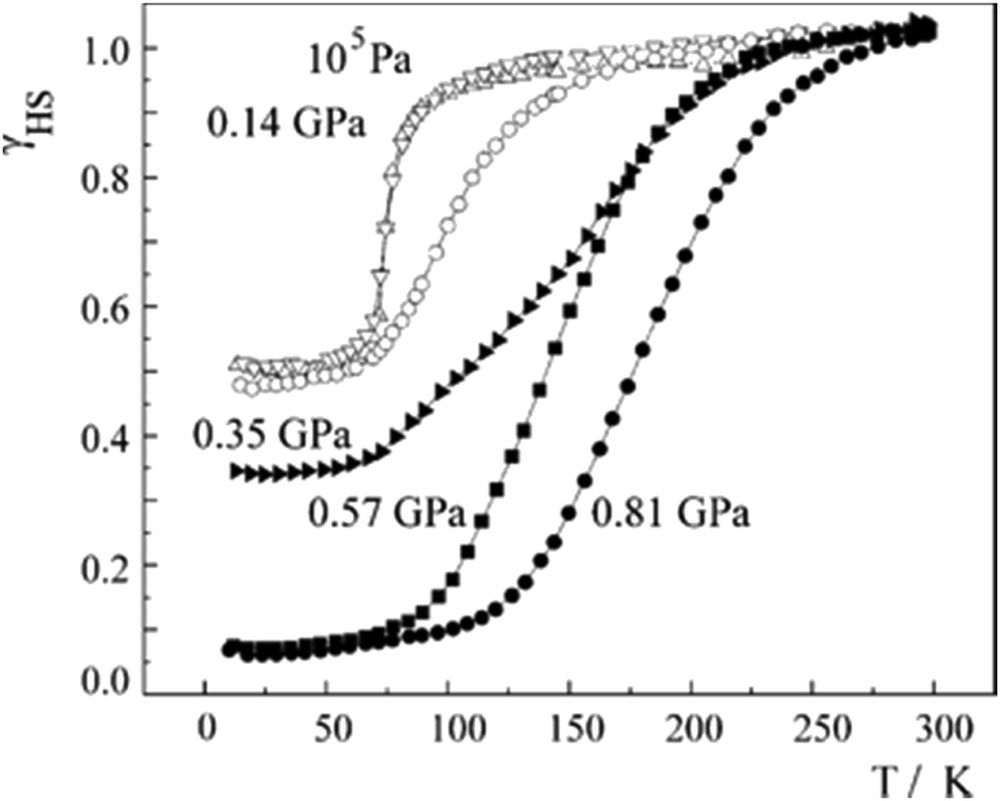
HS fraction as a function of the temperature at distinct hydrostatic pressures for complex [Fe(mtz)6](BF4)2. Reprinted with permission from Ref. [82]. Copyright 2005 Elsevier.
An anion order–disorder transition has been proved to be the driving force for the two-step thermal spin transition in the mononuclear compound [Fe(L)2](ClO4)2 (L = 2,6-bis{3-methylpyrazol-1-yl}-pyrazine). The first step of the spin transition curve is abrupt, concomitant with an isostructural phase transition provoked by the cessation of dynamic anion disorder on lowering the temperature. The second step is more continuous. High-pressure single-crystal XRD and Raman spectroscopy studies performed up to 2 GPa have revealed a similar mechanism for the pressure-induced SCO [126].
The mononuclear compounds [Fe(bapbpy)(NCS)2] (bapbpy = 6,6′-bis(amino-2-pyridyl)-2,2′-bipyridine) [79] and [Fe(5-NO2-sal-N(1,4,7,10))] [82] exhibit a two-step spin transition accompanied with hysteresis at atmospheric pressure. Application of pressure discloses a very particular behaviour of the two-step transition curve: parallel shift to higher temperature and increase in the hysteresis width as pressure increases, as shown in Fig. 13. Detailed structural analysis in the case of [Fe(bapbpy)(NCS)2] revealed that the same series of phase transitions occur both on cooling and on application of pressure, and variable temperature and pressure XRD experiments allowed the structural phase diagram to be experimentally plotted for the first time [79].

(a) Magnetic properties under hydrostatic pressure for [Fe(bapbpy)(NCS)2]. Reprinted with permission from Ref. [79]. Copyright 2011 American Physical Society. (b) Magnetic properties under hydrostatic pressure for [Fe(5-NO2-sal-N (1,4,7,10))]. Reprinted with permission from Ref. [82]. Copyright 2005 Elsevier.
The 2D square grid-type porous coordination polymer [Fe(bdpt)2]·guest (Hbdpt = 3-(5-bromo-2-pyridyl)-5-(4-pyridyl)-1,2,4-triazole, guest = EtOH and MeOH) shows a two-step spin transition accompanied by a re-entrant crystallographic phase transition [100% HS (P21/n) ↔ [50% HS–50% LS] (P-1) ↔ 100% LS (P21/n)]. In Fig. 14 the magnetic properties at different hydrostatic pressures of the guest-free framework and those of the frameworks loaded with ethanol and methanol are shown [152]. At 10−4 GPa the highest transition temperature of the two-step process is observed for the guest-free framework and the lowest for the framework loaded with EtOH. Interestingly, for pressures less than 0.5 GPa the second step of the spin transition is shifted to lower temperatures and the hysteresis width increases for all compounds. In contrast, the first step is shifted to higher temperatures and the displacement is approximately 70 K at 0.72 GPa for the MeOH-loaded framework. The hysteresis width also increases for the first step, being 2 K for all compounds at the highest pressure applied (0.7–0.8 GPa). Both thermal- and pressure-induced SCO in the guest-loaded frameworks are influenced by the steric effects imposed by the guest molecules, which provoke the stabilization of the HS state and hence displacement of the Tc (second step) to lower temperatures. For the guest-free framework the stabilization of the intermediate state [50% HS–50% LS] (P-1) occurs on lowering the temperature or increasing the pressure.
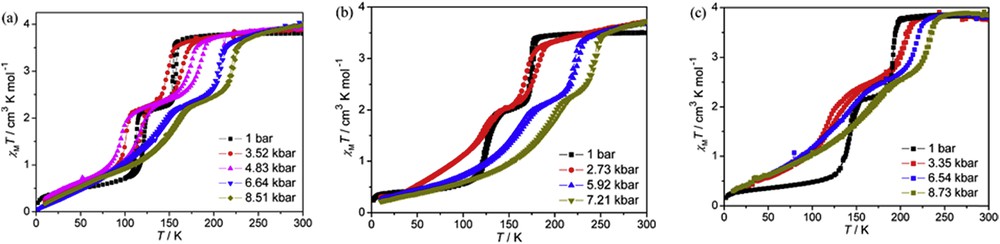
χMT vs T plots at different hydrostatic pressures for [Fe(bdpt)2]·G: (a) G = EtOH, (b) G = MeOH and (c) guest-free framework. Reprinted with permission from Ref. [152]. Copyright 2012 American Chemical Society.
3.4 Paramagnetic compounds
The effect of hydrostatic pressure on the paramagnetic, ferromagnetic or antiferromagnetic behaviour of several Fe(II) coordination complexes has been studied. For example, a complete thermal spin transition in the interval of pressures from 0.5 to 1 GPa has been reported for the mononuclear complexes [Fe(abpt)2(NCS)2] polymorph B [139] and [Fe(stpy)4(NCBH3)2]cis [141], which are paramagnetic (i.e. not SCO active) under atmospheric pressure (Fig. 15). These studies corroborate the expected modification of the ligand field strength and the stabilization of the LS state under the application of external hydrostatic pressure. The induced thermal spin transitions are continuous and the equilibrium temperatures are displaced to higher temperature as pressure increases. For compound [Fe(abpt)2(NCS)2] polymorph B, T1/2 at the highest pressure investigated (1.05 GPa) is 179 K whereas it is 175 K for complex [Fe(stpy)4(NCBH3)2]cis at 0.7 GPa. Both compounds show a linear dependence of T1/2 with pressure.

(a) Thermal variation of the molar magnetic susceptibility, χMT, for [Fe(abpt)2(NCS)2] polymorph B at different hydrostatic pressures. Reprinted with permission from Springer Nature [139]. (b) Thermal variation of the molar magnetic susceptibility, χMT, for [Fe(stpy)4(NCBH3)2]cis at different hydrostatic pressures. Reprinted with permission from Ref. [141]. Copyright 2011 Elsevier.
Other remarkable studies of paramagnetic complexes under pressure concern the dinuclear {[Fe(bpm)(NCS)2]2bpm} and the 1D [Fe(bpm)(NCS)2]n compounds based on the 2,2′-bipyrimidine bridge ligand [73]. Coexistence of antiferromagnetically coupled [HS–HS] pairs and spin transition has been proved for the dinuclear complex under the application of pressure. At 0.63 GPa, nearly 50% of the [HS–HS] pairs transform into the [HS–LS] pairs (Fig. 16). Further increase in pressure until 0.89 GPa provokes the total conversion of the [HS–HS] pairs to the magnetically uncoupled [HS–LS] pairs. The magnetic behaviour of the 1D [Fe(bpm)(NCS)2]n complex is very similar to that of the dinuclear ones with the difference that the spin transition, [⋯HS–HS⋯] ↔ [⋯LS–HS⋯], takes place at higher pressures (1.18 GPa).

(a) Temperature dependence of χMT for {[Fe(bpm)(NCS)2]2bpm} at different hydrostatic pressures. Reprinted with permission from Ref. [73]. Copyright 2001 American Chemical Society. (b) Temperature dependence of χMT for [FePd(CN)4(thiome)2]·2H2O at different hydrostatic pressures. Reprinted with permission from Ref. [170]. Copyright 2016 American Chemical Society.
As far as the study of paramagnetic 2D polymers under pressure is concerned the porous Hoffman-like polymer [FePd(CN)4(thiome)2]·2H2O [thiome = 4-[(E)-2-(5-methyl-2-thienyl)vinyl]-1,2,4-triazole] represents an interesting example [170]. Steric effects hinder the spin transition when water molecules are located within the layered structure. However, at 0.68 GPa, a two-step spin transition is observed in the interval of temperatures of 300–100 K (Fig. 16). The first step is more abrupt and occurs within 30 K whereas the second one is more continuous but accompanied by hysteresis. This result suggests that the layers distort to accommodate the volume change in the structure on going from the HS to the LS state. Moreover, the application of pressure strengthens the intermolecular interactions leading to a cooperative spin transition as that observed for the guest-free compound [FePd(CN)4(thiome)2].
The 3D cyanide-based framework {[Fe(pyrazole)4]2[Nb(CN)8]·4H2O}n presents a diamond-like structure with the iron and niobium ions connected through CN bridging ligands [104]. At ambient pressure, the compound exhibits a ferromagnetic behaviour with a Curie temperature of 9.4 K as a result of the antiferromagnetic coupling between neighbouring Fe(II) (HS, S = 2) and Nb(IV) (S = 1/2) metal centres. The magnetic behaviour of the complex changes dramatically because of the pressure-induced spin transition at the iron(II) centres, which is almost complete at 1.0 GPa (Fig. 17). As pressure increases χT gradually decreases denoting the presence of a percentage of Fe(II) ions in the diamagnetic LS state. At 0.5 GPa the magnetic order switches from ferrimagnetic to antiferromagnetic. For pressures greater than 1.0 GPa, with all of the Fe(II) centres in the LS state, the magnetic order disappears and the compound exhibits a paramagnetic behaviour arising from the niobium ions.
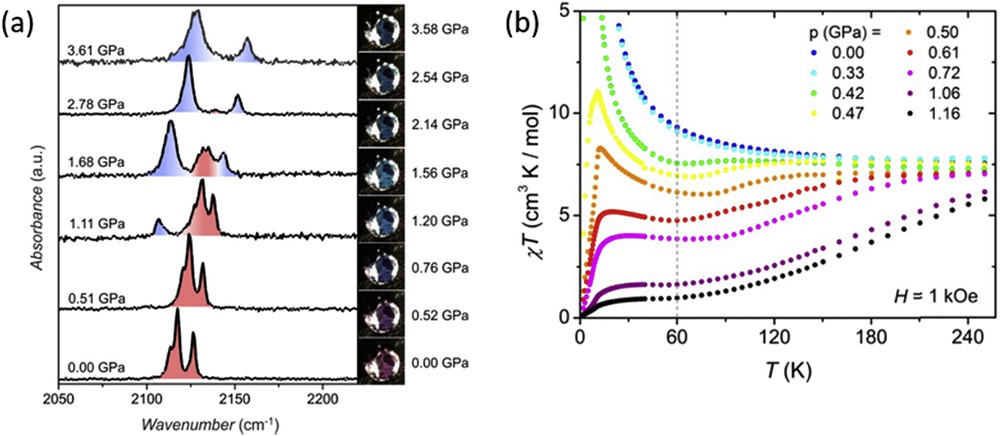
(a) Raman spectra of compound {[Fe(pyrazole)4]2[Nb(CN)8]·4H2O}n under pressure at room temperature. The photographs acquired at different pressures evidence the piezochromic effect of the compound (HS, pink-violet; LS, blue). (b) Magnetic properties in the form of χMT vs T at different pressures. Reprinted with permission from Ref. [104] (https://pubs.acs.org/doi/abs/10.1021/jacs.5b04303).
4 Pressure effect studies on Cr(II), Mn(III), and Fe(III) coordination compounds
The number of complexes of reported Cr(II) and Mn(III) undergoing SCO is very small, whereas more examples have been reported for Co(II) and Fe(III) ions [171]. In the following are described a few studies of the pressure effect on the spin transition properties of these metal complexes.
A thermal spin transition in a Cr(II) compound was firstly reported for [CrI2(depe)2] (depe: 1,2-bis(diethylphosphino)ethane) [172]. The sharp spin transition between the 3T1g (S = 1) and 5Eg (S = 2) electronic states taking place at T1/2 = 169 K at ambient pressure is displaced progressively to higher temperatures as pressure increases (Fig. 18a) [137]. Under pressure the transition becomes more continuous and at 0.8 GPa the compound is in the LS state at room temperature. The dependence of T1/2 with pressure is linear for pressures greater than 0.3 GPa when the CrP bond lengths are noticeably altered by pressure. At relatively low pressures the large iodine ions compress and the CrP distances remain unaltered.
(a) HS fraction vs temperature, γHS vs T, for compound [CrI2(depe)2] at different hydrostatic pressures. Reprinted with permission from Ref. [137]. Copyright 2004 American Chemical Society. (b) Temperature dependence of χMT for [Fe(sal2-trien)][Ni(dmit)2] at different pressures. Reprinted with permission from Ref. [173]. Copyright 2008 Elsevier.
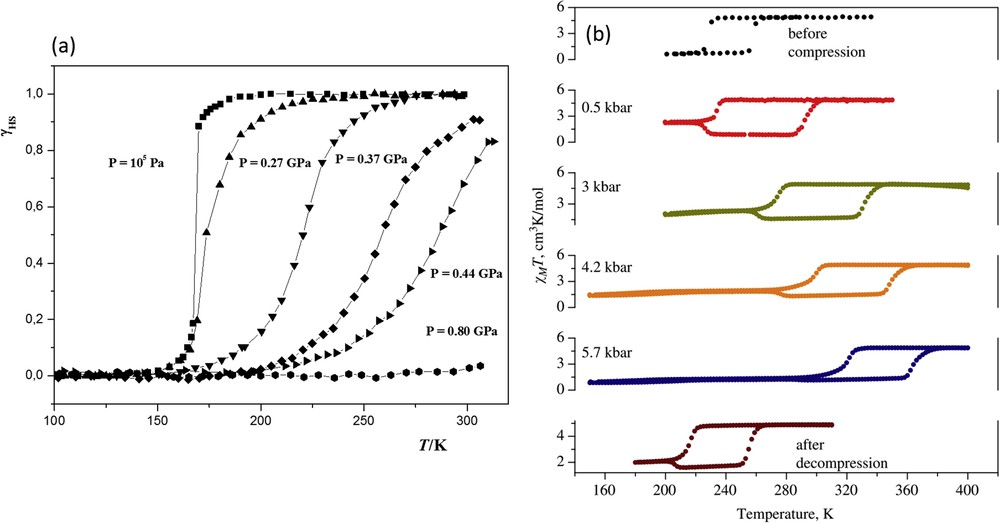
The compound [Fe(sal2-trien)][Ni(dmit)2] exhibits one of the most cooperative spin transitions reported for a Fe(III) SCO compound. It undergoes a spin transition between the S = 5/2 and S = 1/2 spin states around 245 K accompanied by a large hysteresis loop of 30 K. Pressure effect studies reveal that at pressures as low as 0.05 GPa the hysteresis loop becomes wider (60 K) and only half of the Fe(III) centres switch to the LS state [173]. Further increase in pressure up to 0.7 GPa displace the transition temperature upwards but the hysteresis width and the percentage of Fe(III) molecules in the LS state remain unaltered. After releasing the pressure, the spin transition previously observed at 10−4 GPa is not recovered suggesting that the compound experienced and irreversible structural phase transition under pressure.
The [(TPA)Fe(TCC)](SbF6) complex [TPA = tris(2-pyridylmethyl)amine and TCC2− = 3,4,5,6-tetrachlorocatecholate dianion] exhibits an incomplete S = 1/2 ↔ S = 5/2 thermal SCO process centred at 250 K at ambient pressure [174]. In contrast, a complete transition to the S = 1/2 state is induced at relatively small pressures (0.45 GPa) at room temperature as Raman experiments demonstrate (Fig. 19). The spin state conversion is gradual with P1/2 = 0.16–0.17 GPa. The crystal structure of the complex has been studied under pressure as well. In Fig. 19a are depicted the evolution of the unit cell parameters as a function of pressure. At less than 0.4 GPa the decrease in the volume of the unit cell (ca. 8%) as well as in the a, b and c parameters as pressure increases denotes the expected contraction of the crystal lattice as a result of the SCO process. For higher pressures the compression of the LS unit cell volume becomes smoother. The compression of the cell is markedly pronounced in the ac plane where the complex cations [(TPA)Fe(TCC)]+ are located. Indeed, pressure enhances the hydrogen bonding interactions between the complex cations. The cations and anions stack along the b direction and its mutual compression results in a contraction of the b axis (15% at 2 GPa).
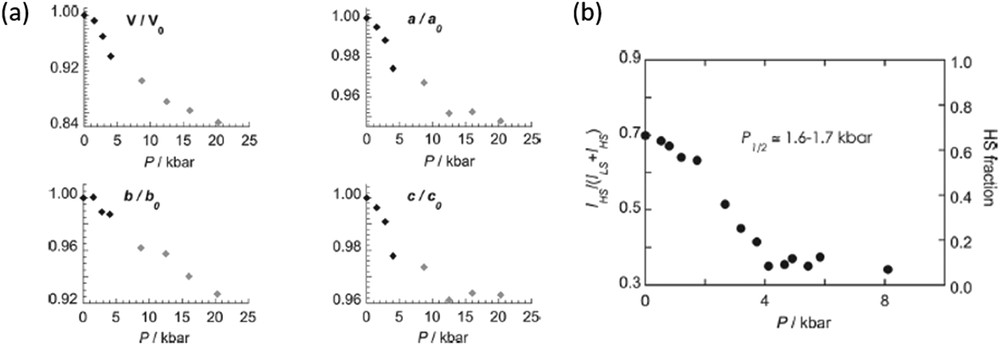
a) Pressure dependence of the unit cell parameters of a single crystal of [(TPA)Fe(TCC)](SbF6) at 293 K. (b) HS fraction as a function of applied pressures at 293 K for complex [(TPA)Fe(TCC)](SbF6) derived from the Raman spectra. Reproduced with permission from Ref. [174].
The porphyrin Fe(III) complex [Fe(PPIX)OH] has been investigated under pressure using Mössbauer spectroscopy [175]. Like observed for other porphyrin compounds an S = 5/2 HS to S = 5/2, 3/2 admixed spin state transition of the Fe(III) site takes place at pressures greater than 2.2 GPa. Pressure induces the ligand movement towards the iron centre and movement of the Fe ion towards the porphyrin plane, which leads to the electronic transition.
The [Mn(pyrol)3tren] complex exhibits a very abrupt spin transition from the HS (5E) to LS state (3T1) at low temperature (44 K). The crystal structure studies performed at room temperature evidenced that the complex remains the HS state at 1.00 GPa. The crystal structure of the HS state under pressure is very similar to that of the complex in the LS state. The differences are the metal-to-ligand bond distances and the intermolecular contacts, which are slightly shorter under pressure. These studies clearly demonstrated that the spin transition in the complex is not connected to the internal pressure in the crystal. Most likely the spin transition is connected to the dynamic Jahn–Teller effect on the Mn(III) ion [78].
5 Theoretical aspects
To better understand the pressure influence on SCO complexes several types of models have been proposed, including thermodynamic [6,27,136,176], Ising-like [111,165,177,178] or mechanoelastic models [179–183]. Because the Ising-like and mechanoelastic models are described in more detail in other articles of this special issue, herein we will only discuss the thermodynamic approach. It should be noted that thermodynamic and Ising-like models are completely equivalent in the mean-field approach [184].
The first model that describes the pressure effect on molecular SCO complexes was proposed in 1972 by Slichter and Drickamer [6], starting from thermodynamic considerations. This model represented the starting point for many macroscopic models attempting to describe the origin of the interactions (atom–phonon coupling, elastic energy, etc.). It is based on the theory of regular solutions assuming a mixture of both HS and LS species with their Gibbs free energy GHS and GLS, respectively. Thus, the free energy for the mixture of the interacting centres is expressed as
| (6) |
| (7) |
| (8) |

Thermal variations of the HS molar fraction for four selected values of the intermolecular interaction constant Γ = 200, 400, 600 and 800 J. The following values have been used for the enthalpy and entropy variations: ΔH = 15 kJ mol−1, ΔS = 70 kJ mol−1.
The pressure effect has been taken into account expressing the variation of the free energy as
| (9) |
The first term represents the contribution from the free energy difference at zero pressure, the second term is because the two species have different volumes and the third term corresponds to the fact that the two species have different bulk moduli.
The effect of pressure on the temperature-induced spin transition and the temperature on the pressure-induced spin transition calculated in the framework of Slichter and Drickamer model is reported in Fig. 21.
(a) Thermal variations of the HS molar fraction for various external pressures. (b) The pressure-induced spin transition, simulated for various temperature values. The following values have been used for the enthalpy and entropy variations: ΔH = 15 kJ mol−1, ΔS = 70 kJ mol−1 and ΔV = 10 Å3.
Thus, the model proposed by Slichter and Drickamer can successfully describe the typical behaviour of the SCO complexes, that is, the shift in the characteristic transition temperatures towards higher temperatures, as shown in Fig. 20, and a decrease in the hysteresis width with increasing pressure, as shown in Fig. 21. However, it cannot explain some of the more unusual behaviours (discussed in Section 3) such as increasing width of hysteresis. In this context, Ksenofontov et al. [50] have extended the mean-field approximation approach to indirect couplings of pressure to the order parameter by taking into account the pressure dependence of the bulk modulus of the complex within elasticity theory. By taking into account the lattice elastic energy, the Gibbs free energy can be written as
| (10) |
| (11) |
Spiering et al. set up the complete free energy of the whole system, such that the HS fraction and the volume and anisotropic deformations are freely varying parameters [136,176]. In the model proposed by Spiering et al. the spin transition centres are modelled as point defects and the crystal as an elastic, isotropic and homogeneous medium, of spherical shape with only two elastic constants, the bulk modulus B and the Poisson ratio .
The elastic energy (eα) of the sphere, which has the volume vα (α = HS, LS), placed in an elastic medium that provides a volume v0 for its molecules can be written as follows:
| (12) |
The first term represents the energy that appears due to the difference in volume of the crystal, and the second term is correcting the surface effect of the crystal.
Thus, the total elastic energy for N sites, randomly distributed in an isotropic homogeneous elastic medium is given by the following relation:
| (13) |
The phonon free energy is approximated by the Debye model with a Debye temperature Θ dependent on volume by the Grüneisen approximation:
| (14) |
The Grüneisen constant describes the change in the Debye frequency due to the anharmonicity of the lattice, as illustrated in Fig. 22 [136].

The effect of lattice anharmonicity simulated for an SCO system with a 10 K hysteresis width under an applied pressure up to 4 kbar. With increasing anharmonicity (γG from harmonic (−2/3) to 2.5) pressure favours hysteresis. At γG = 1.8 the width of the hysteresis is almost independent of pressure. At higher anharmonicity, γG = 2.5, an increase in the hysteresis width with increasing pressure is observed. Reproduced with permission from Ref. [136]. Copyright 2004 American Physical Society.
A new approach was proposed by Levchenko et al. [148] who used a microscopic model to analyse the behaviour under pressure of molecular SCO complexes by taking into account the contribution of phonons to the changes in spin state. In the framework of this model, the authors have shown that different experimental behaviours of temperature- and pressure-induced spin transitions are determined by different variations of the inelastic and elastic energies under pressure, and the vibrational component of the free energy drives the spin transition equally with the electronic part. In other words, the (p,T) phase diagram will depend on the nature of the external stimuli. The model takes into account the pressure and temperature influence on the spin state, considering a symmetric deformation of the complexes and elastic medium.
The pressure effect on the spin state switching has been also investigated by the first-order reversal curve (FORC) diagram method. The FORC diagram method provides detailed information from within the major hysteresis loop, which enables determination of the distribution of switching temperatures and interaction fields for all of the “particles” that contribute to the hysteresis loop [185]. The measurement of an FORC begins with the saturation of the sample in HS (LS) state. The temperature is then ramped down (up) to a reversal temperature Ta. The FORC consists of a measurement of the HS fraction as the temperature is then increased from Ta back up (down) to saturation. The HS fraction at Tb on the FORC with reversal point Ta is denoted by (see Fig. 23).

Definition of a thermal FORC in warming/cooling mode.
The temperatures steps are chosen such that Ta and Tb are regularly spaced, which means that can be plotted on a regular grid. The FORC distribution is defined as the mixed second derivative and plotted in rotated coordinates from switching temperature to bias-coercivity .
The FORC distribution is determined at each point by fitting a mixed second-order polynomial of the form to a local moving grid. In this case the value of –a6 provides the mixed second derivative of the fitted surface, and it can be assigned to the centre of the grid as a representation of the density of the FORC distribution at that point. The FORC diagrams can be interpreted in terms of distributions of the physical parameters: energy gap, Δ, and interaction parameter, J.
Rotaru et al. [186] have analysed the thermal behaviour of the spin transition complexes [FexZn1−x(btr)2(NCS)2]·H2O (for x = 0.6 and x = 1) by diffuse reflectivity measurements, under constant pressure in the range of 1–1600 bars obtained with a gas pressure cell. In their study an increase in both Δ and J with increasing pressure has been observed, as shown in Fig. 24.

The pressure dependence of the average values of electronic gap (left) and interaction parameter J (right). Reprinted with permission from Ref. [186]. Copyright 2011 American Physical Society.
It was also shown that, for the pure compound, the J–Δ distributions remain uncorrelated in the whole pressure range, which confirms that these distributions originate from independent mechanisms. An unexpected feature concerning the correlation parameter in the diluted compound, that is, a large decrease induced by pressure has been observed, as shown in Fig. 25. In terms of composition distributions it means that, the like-spin domain size is increased by the applied pressure. These data have been interpreted by assuming that the pure compound has single-domain behaviour and the diluted one, multiple-domain behaviour, in agreement with the expectations derived from the optical microscopy.
The pressure effect on the standard deviations and correlation parameters. Reprinted with permission from Ref. [186]. Copyright 2011 American Physical Society.
6 Summary and perspectives
We have described the major techniques so far used to probe the SCO phenomenon at high pressure. Our aim was to shed some light on equipment, experiments, materials and theoretical approaches for high-pressure research that together advance our fundamental understanding of SCO. We hope that by charting how high-pressure SCO research has developed since its earliest days we can provide newcomers to the field with the tools required to push the boundaries yet further. Here we summarize what we believe to be some of the most important and promising areas for the future development of high-pressure SCO research.
We have shown how important high-pressure structural studies can be in rationalizing unusual SCO behaviour on a case-by-case basis, and highlighted the importance of multiple complimentary techniques to rationalize behaviour. However, examples of such studies using multiple techniques are still exceptionally scarce. More studies on a wide range of samples, each in the exact same environment are required to unambiguously assess more general correlations between the structure of a material and its SCO properties. As the number of such studies increases it is important that their reliability and repeatability are ensured through careful attention to hydrostatic conditions within the pressure cell. Occasionally somewhat ignored in experimental sections in the literature, the pressure transmitting medium and method of applying pressure must be carefully considered in advance of the experiment and fully reported.
Despite the importance of hydrostatic conditions to high-pressure experiments it is also interesting to consider the possibility of deliberate application of nonhydrostatic forces to SCO materials. To the best of our knowledge, no systematic studies aiming to quantify the effect of nonhydrostatic conditions on oriented SCO materials have yet been published. However in real-world applications, SCO materials are more likely to encounter nonhydrostatic stress during manufacturing and use. Such investigations could also reveal important insights on the role of anisotropy, which is often encountered in the structure and mechanical properties of ordered SCO solids [187]. Experimental methods for achieving this must be able to clearly control and quantify the direction and magnitude of the applied anisotropic force. Thus nanoindentation studies of localized pressure on well-oriented samples may well allow such detailed analysis, and we look forward to results in this area.
The importance of elastic interactions for SCO processes is clear, and yet very few experimental determinations of the elastic properties of SCO materials exist to date. High-pressure studies present interesting opportunities to investigate lattice dynamics (compressibility, anharmonicity, etc.) and structure under pressure to rationalize cooperativity [136] and to evaluate potential applications in mechanical actuators [188]. The extension of this approach towards SCO nanomaterials, which are of vivid interest currently [189], may also allow us to probe interactions between nano-objects as well as with their environment (matrix effects).
Under pressure, the dynamic and mechanical properties of the lattice that influence the phase transition are significantly altered from ambient conditions and thus domain formation and propagation events must also be very different. High pressure thus allows for the fine-tuning of inter- and intra-molecular interactions, permitting systematic investigation of their effect on the elastic stiffness of the lattice and hence on the observed switching behaviour. Spatiotemporal studies of SCO materials under pressure could prove fascinating, allowing the development of more advanced theoretical approaches and possibly even the design of novel materials with improved cooperativity. Time-resolved studies of SCO materials at ambient pressure are described in detail elsewhere in this issue. Performing time-resolved photoinduced switching experiments at high pressure rather than low temperature would allow the investigation of the effect of elastic properties on these dynamic processes, something that has remained conspicuously uncharted for phase transition materials at short time scales. We highlighted the importance and complexities associated with obtaining hydrostatic conditions even in isothermal high-pressure experiments. The difficulties are compounded as temperature varies and have the potential to vary significantly during laser pulses. Quantifying the effect of these stimuli on the hydrostaticity of the sample environment may well present experimental challenges, but would again be of fundamental importance to the interpretation of results in this area.
All of these experimental developments promise to supply increasingly reliable and numerous high-pressure investigations of SCO materials that can both inspire and respond to the development of improved theoretical models. In particular, we anticipate that with increasing access to high-pressure structures, ab initio and molecular dynamics calculations will gain in importance in rationalizing the behaviour of SCO materials under pressure.
Acknowledgements
This work was partially funded by the European Commission through the SPINSWITCH project (H2020-MSCA-RISE-2016, Grant Agreement No. 734322). A.R. acknowledges the CNFIS for CNFIS-FDI-2018-058 project. A.B.G. acknowledges the Spanish Ministerio de Economía y Competitividad (MINECO) grant number CTQ2016-78341-P and FEDER funds and Unidad de Excelencia María de Maeztu MDM-2015-0538, Generalitat Valenciana (PROMETEO/2016/147).


