1 Introduction
Fluorination is one of the most effective methods to modify and control physicochemical properties of carbon materials [1–3]. Numerous studies have been mainly devoted to fluorination of graphite or graphitized carbons and to the characterization of the fluorinated compounds, which have found important practical applications, as electrode materials for primary lithium batteries or solid lubricants [4–7]. The nature of the interaction between fluorine and carbon atoms can be varied considerably and modulated as a result of the fluorination route, the morphological and structural types of the carbon precursor [8–11]. Indeed, because of the versatility of the CF bonding and the distribution of fluorine atoms within the carbon network, the physicochemical properties of carbonaceous materials are drastically changed and controlled. In the case of fluorine adsorption on the surface of carbonaceous materials, these interactions are very weak. On the contrary, a covalent, semi-ionic or ionic character can be obtained according to the fluorination condition and nature of the starting carbonaceous material [12–14]. A significant advance concerns fluorinated carbon nanofibres (CNFs) regarding their excellent electrochemical and tribological properties have been shown [15,16].
To decrease wear and loss due to increasing severity of lubrication conditions in engines, new strategies of lubrication consist of introducing either solid nanoparticles of tribo-active phases or precursors of tribo-active phases into the lubricant base [17]. Different studies have shown that fluorinated carbonaceous nanomaterials (carbon blacks, CNFs and carbon nanodiscs) exhibit good tribological properties and can act as excellent precursors of tribo-active phase for lubrication [7,18,19]. The present work focuses on CNFs and their fluorinated analogues (F-CNFs). They are similar to multi-walled carbon nanotubes (MWCNTs) with ill-defined core and a larger diameter. The method of fluorination using F2 (direct fluorination) at an optimal reaction temperature close to 465 °C leads to a high fluorination content F/C of 0.85.
Tribological properties of fluorinated CNFs have been evaluated according to the fluorine content and show that CF0.85 are excellent candidates for lubrication. Indeed, the friction coefficient about 0.080 ± 0.001 is lower than that of nonfluorinated CNFs and also lower than the most popular solid lubricants, that is, graphite . Moreover, the thermal stability of CF0.85 is extended up to 480 °C due to homogenous distribution of the fluorinated parts in the whole volume of nanofibres [20]. The comparison of various samples clearly underlined that the tubular nanostructuring of both the raw carbon and the fluorinated part plays a key role for the stability of fluorinated CNFs. Good thermal and chemical stabilities are then achieved. According to their excellent properties, fluorinated CNFs can be expected to serve as structural reinforcement for lightweight composite systems with the further promise of multifuntionality. However, specifically in polymer composites, the mechanical properties depend on the ability to transfer load from the matrix to the nanotubes [21,22].
In the case of fluorinated nanolubricants, they must be integrated either into an organic media or into a composite to be sprayed onto a mechanical component. Nevertheless, commonly used organic solvents can modulate their properties. Dispersion state, friction properties and damage of the CF0.85 can be modified in the presence of an organic solvent as a function of time. Mickelson et al. [23] have shown that fluorinated single-walled carbon nanotubes (F-SWCNTs) were well dispersed in alcohol solvents to give long-living metastable dispersion. Hansen solubility parameters have been useful in explaining the dispersion state and to determine which solubility parameter is the most influential [24–26]. Nomède-Martyr et al. [27] have shown that fluorinated CNFs (CF0.85) have a higher dispersion state than the nonfluorinated CNFs in ethanol, isopropanol, dimethylformamide (DMF), dimethyl sulfoxide (DMSO), N-methylpyrrolidone, chloroform and 1,2-dichlorobezene. The best result has been obtained in N-methylpyrrolidone for a dispersion limit value of 570 mg/L, whereas 310 mg/L was the maximum for CNFs. Then fluorination appears as an efficient functionalization method to increase the dispersion limit of such dispersible nano-objects. The presence of fluorine atoms on the surface of carbonaceous nanomaterials increased the hydrogen bonding with CNFs and consequently the three Hansen parameters became all important to estimate the dispersion state in organic solvents.
The main objective of this study was to estimate the time dependence of fluorinated and nonfluorinated CNF concentration in different organic solvents. The nanofibres have been dispersed without surfactant or additive with an ultrasonic probe in ethanol, DMF, DMSO and chloroform. UV–visible spectroscopy has been used to determine the percentage of nanofibres in dispersion after a first sonication and after an ageing of 4 months of the dispersions. Hildrebrand and Hansen parameters of solvents were used to evaluate the stability of the mixtures and to understand modifications of surface properties of the nanofibres in dispersion. The fluorinated CNFs were then dried to study changes in their physicochemical properties after a long ageing into the different solvents. It has been reported that sonication cannot only exfoliate the nanotube bundles but also induce defects and even scission of the tubes [28]. The tribological properties of these fluorinated nanofibres have been compared with initial CF0.85 powder. Then, the damage of the CF0.85 was monitored by Raman spectroscopy. The increase in the defect (or D) band compared with the corresponding graphitic (or G) band intensity was considered as an indication of the damage to the nanofibres [29,30].
2 Experimental section
2.1 Materials
High purity (>90%) CNFs, 2–20 μm in length and 150 ± 30 nm in average diameter, were supplied by courtesy of the MER Corporation (Tucson, Arizona). They were obtained by chemical vapour deposition and treated at 1800 °C in an argon atmosphere to enhance their graphitization degree. The graphitization post-treatment insures high crystallinity of the nanofibres with coherence length along the c axis, Lc, of 11.8 nm owing to the Scherrer equation applied to the (002) diffraction peak and along the a axis, La, of 23 nm owing to Raman analysis [20,31].
Direct fluorination was carried out with pure fluorine gas flow in a passivated (with NiF2) Monel reactor. The selected fluorine content of CF0.85 was obtained at a fluorination temperature, TF, of 465 °C with constant duration of 3 h and F2 flux. The gas flux was about 10 mL/min. The fluorine content “x” (i.e., the F/C molar ratio) of fluorinated nanocarbons was first determined by gravimetry upon fluorination (weight uptake) and confirmed by quantitative 19F NMR measurements. The main peaks at 110 ppm/CFCl3 and 83 ppm/TMS in 13C and 19F NMR spectra, respectively, were characteristics of covalent CF bonds as in high temperature graphite fluorides with (CF)n and (C2F)n structural types [32–34]. The F/C ratio was equal to 0.85 and the sample was then named CF0.85. Details on the synthesis and direct fluorination mechanism have been already published elsewhere [35]. All organic solvents were purchased from Aldrich and have been chosen according to their Hansen parameters. Table 1 summarizes Hildebrand solubility and Hansen parameters of the solvents used. These solvents have been chosen according to their Hansen solubility parameters and their chemical properties: protic polar (ethanol), polar aprotic (DMF and DMSO) and nonpolar (chloroform). According to the Hansen and Hildebrand solubility analysis, the maximum dispersibility level is obtained when the distance in the Hansen space from the solvent to the material is smallest. In this article, we will consider CNF solubility parameters identical to SWCNTs: δD/cnt ∼ 17.8 MPA½, δp/cnt ∼ 7.5 MPA½, δH/cnt ∼ 7.6 MPA½ and the CNF Hildebrand parameter is set about 21 MPa½ [26,36].
Hansen parameters of the different organic solvents used.
| Solvent | Dispersion forces δD (MPa1/2) | Permanent dipole forces δP (MPa1/2) | Hydrogen bonding δH (MPa1/2) | Hildebrand solubility parameters |
| Ethanol | 15.8 | 8.8 | 19.4 | 26.5 |
| DMF | 17.4 | 13.7 | 11.3 | 24.8 |
| DMSO | 18.4 | 16.4 | 10.2 | 26.7 |
| Chloroform | 17.8 | 3.1 | 5.7 | 19 |
2.2 Dispersion
Different mixtures of fluorinated and nonfluorinated CNFs have been prepared at approximately 100 mg/L, thanks to sonication of 30 min using an ultrasonic probe (20 kHz with power of 375 W). All the dispersions were analyzed using a UV–visible spectrometer immediately after the sonication.
Different analyses have been carried out to evaluate the ageing effect on the physicochemical properties of both types of CNFs.
After the decantation period of 2 h, to determine the percentage of nanofibres in the suspended state, the dispersion has been investigated by UV–visible spectroscopy. Residues of the fluorinated CNFs (powder located at the bottom of the container) have then been collected and definitively removed before the ageing period. The supernatants were then studied after ageing for 4 months. To simulate a simple use of the mixture after a long period of storage, they have been then shaken manually for 1 min. UV–visible spectra were recorded just after shaking. To estimate the evolution of the percentage of nanofibres in dispersion according to the time, several analyses have been realized by UV–visible spectrometry up to 330 min. The starting concentrations of aged samples have been calculated (subtracting the weight of residues collected after 2 h). At the end of the experiments, the physicochemical properties of the fluorinated CNFs are examined by Raman spectroscopy and tribological tests.
2.3 Methods
UV–visible absorption (Thermo Electron Corporation Evolution 500) measurements have been carried out within a survey ranging from 190 to 650 nm. For all the samples, absorbance measurements were taken at 500 nm to compare with data on SWCNTs. In the case of SWCNTs, 500 nm is used because the interband transitions, as for SWCNTs [37], are not included at this wavenumber. Peak intensities were directly extracted from the measured absorption spectrum.
Raman spectra were recorded at room temperature using a Jobin Yvon T64000 with a charge-coupled device multichannel detector. The excitation source was a 514.5 nm argon laser line. The laser power was tuned at 100 mW.
Tribological properties were investigated using an alternative ball-on-plane tribometer consisting of an AISI 52100 steel ball rubbing against an AISI 316-L steel plane on which the tested material is deposited by a burnishing method. It consists in the deposition of a few milligrams of the powdery fluorocarbon material on a plane. Then a second plane is used to apply manually by crushing the powder on the surfaces leading to the formation of an adherent film of 1–2 μm thickness. Balls were used as delivered, whereas planes are polished to improve the adherence of the tribofilm. A normal load of 10 N was applied leading to a contact diameter of 160 μm (according to the Hertz theory) and a mean contact pressure of 0.5 GPa. The sliding speed was 5 mm/s.
3 Results and discussion
An estimation of the relative content of nonfluorinated CNFs and CF0.85 in different organic solvents was evaluated by UV–visible spectroscopy. The mixtures were prepared by an ultrasonic probe without surfactant. First, initial dispersions at a concentration around 100 mg/L were analyzed after sonication. During a decantation period of 2 h, no agitation has been applied to the dispersions. According to the initial concentration, the percentage of nanofibres in liquid was estimated taking into account the adsorption intensity at 500 nm. Residues of the CF0.85 sample (powder located at the bottom of the container) were then collected and definitively removed before ageing period. In a second part, 4 months after initial sonication, the dispersions were manually shaken for 1 min. It is important to note that after the ageing period of 4 months, the concentration of the dispersions and the percentage of nanofibres in suspension are calculated according to the residue removed in the first part.
Table 2 summarizes the estimated relative content of CNFs and CF0.85 in liquid 2 h after sonication and after the ageing period of 4 months (2 h after manual shaking). The first observation that can be made is the significant influence of the ageing period on the dispersibility. Indeed, in the case of ethanol, DMF and DMSO, an important increase of about 20% and more is observed, in the case of chloroform the effect is not significant, and all in all no negative impact is observed. Finally, the estimated percentage increased to 90% after the ageing period. Before the ageing period not only amorphous carbons but also impurities are in suspensions and are generally not well stabilized in suspensions. Conversely, after ageing these compounds are removed leading to an improvement in the suspension stabilities. Another point is the possible debundling or exfoliation of CNFs in suspension, which can influence the dispersibility of CNFs. The kinetics of this phenomenon should be more important before ageing and for pristine CNFs than for CF0.85. This point will be discussed more in detail later in this article. In addition, a global positive effect of fluorination can be noted. Overall, this observation is in good agreement with the results of Mickelson et al. [38] who have found a better dispersibility of fluorinated SWCNTs in alcohol solvents than with pristine nanotubes.
Estimated percentage of CNFs in liquid immediately after sonication and after an ageing of 4 months.
| Solvent | Estimated relative content in liquid | |||
| 2 h after sonication | 2 h after the ageing of 4 months | |||
| CNFs | CF0.85 | CNFs | CF0.85 | |
| Ethanol | 72 | 91 | 94 | 96 |
| DMF | 77 | 65 | 96 | 94 |
| DMSO | 55 | 43 | 87 | 98 |
| Chloroform | 75 | 82 | 74 | 87 |
To interpret the changes in CNF and CF0.85 dispersibilities in organic liquids, the percentages of nanofibres as a function of the Hildrebrand parameter and the three Hansen parameters of the used organic solvents were plotted (Figs. 1 and 2). The total vaporization energy of a given solvent consists of several individual contributions. These arise from (atomic) dispersion forces (δD), (molecular) permanent dipole–permanent dipole forces (δP) and (molecular) hydrogen bonding (δH). Three-dimensional Hansen solubility parameters give a numerical estimation of the different interactions and provide a clearer idea of the dominant component of the total cohesive energy of a solvent and therefore the physical origin of the interaction. The relationship between the Hildebrand solubility parameters (δ) and three-dimensional Hansen solubility parameters is shown in Eq. 1:
| (1) |
| (2) |

Evolution of the percentage of fluorinated CNFs (red circles) and nonfluorinated CNFs (black squares) as a function of the Hildebrand parameter of the organic solvent used 2 h directly after sonication (a) and after an ageing period of 4 months (b).
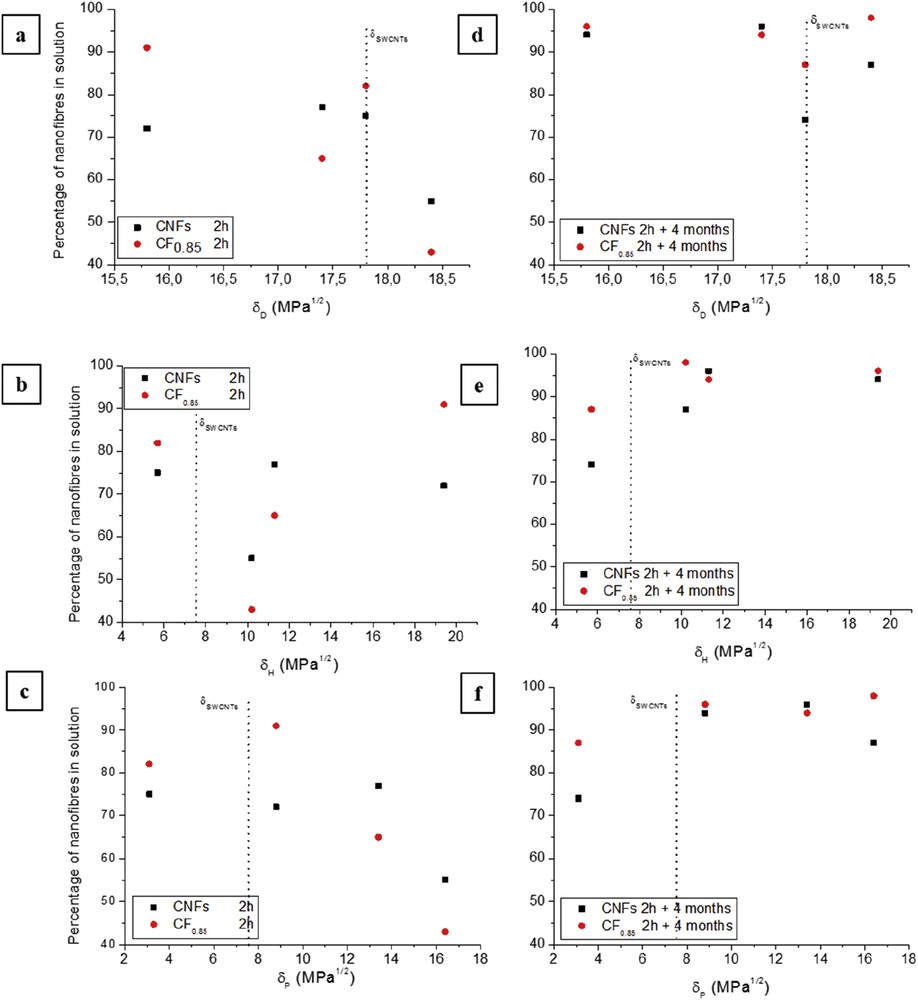
Plots of the percentage of CNFs and CF0.85 in a solvent as a function of the three Hansen parameters at 2 h immediately after sonication (a–c) and after the ageing time (d–f).
Fig. 1 shows the evolution of the percentage of CNFs and CF0.85 according to the Hildebrand parameter of the organic solvents used. First of all, we note a different behaviour of the pristine and fluorinated nanofibres after the ageing period, mainly for raw CNFs, which is in good agreement with previous discussion. Nevertheless, no clear correlation is seen between dispersibility of pristine and fluorinated CNFs and the Hildebrand parameter. Indeed, before ageing, a large dispersion of values of the percentage of pristine nanofibres in dispersion is seen for the same Hildebrand parameter value: ∼55% for pristine CNFs in DMSO characterized by , whereas for the same value of the Hildebrand parameter the percentage of CNFs is ∼72% in ethanol. In the same way, the solvent with the Hildebrand parameter, the closest to the CNF one, is chloroform (δ = 19 MPa1/2 vs δ ∼ 21 MPa1/2 for CNTs), in this solvent the percentage of CNTs is only about 75%. Similar type of conclusions can be drawn with fluorinated nanofibres. After the ageing period, no direct relationship can be deduced: there was more than 90% of CF0.85 in suspension whatever was the organic solvent used, and the lowest percentage of dispersed pristine CNFs is obtained in the case of chloroform, which is the solvent with the closest Hildebrand parameter with CNFs. Then, the dispersibility has to be tested with the Hansen criterion: solvent and nanoparticles must have similar Hansen parameters.
Fig. 2 displays the estimated percentage of CNFs and CF0.85 in liquid measured 2 h after sonication (a–c) and 2 h after the ageing period (d–f) as a function of the three Hansen solubility parameters. No clear correlations can be established between the percentage of nanofibres suspended in a solvent and the Hansen parameters, as with the Hildebrand parameter, either before ageing or after. Whatever the δH, δD or δP Hansen parameters, an important dispersion of values is seen before ageing not only in pristine CNFs but also in CF0.85, unlike after ageing. It is worth noting that dispersion of values is lower in the case of fluorinated nanofibres. The behavioural differences between before ageing and after are probably because of a transient state (in the solution when not aged) before equilibrium (after ageing). The initial and the final states can differ by a difference in the aggregation state in suspensions. Therefore further discussions have to be carried out only for aged suspensions.
In the literature, the plots of concentration dispersions as a function of Hildebrand and Hansen solubility parameters show a major dispersion of values, especially for the δP and δH parameters. Here, it is difficult to conclude with only four values; therefore in the rest of this article, the suspensions of pristine CNFs and CF0.85 in the organic solvents will be discussed through their temporal stabilities.
After having shown the positive impact of ageing on the stability of CNF suspensions, the beneficial effect of fluorination on the stability of aged dispersions is reported in Fig. 3. To evaluate the stability of CNFs and CF0.85 in organic solvents, the evolution of the normalized molar concentration was plotted as a function of the time after 4 months of ageing. Absorbance was measured at 500 nm. For solutions with all organic solvents, the absorbance evolution differed between fluorinated and nonfluorinated CNFs.

Evolution of the molar concentration of CNFs (a) and CF0.85 (b) in ethanol (c), DMSO (d), DMF (e) and chloroform (f) according to the time, after the ageing period of 4 months.
The global effect of fluorination is seen in Fig. 3a and b. It is clearly seen that the estimated percentage of CF0.85 in liquid is higher than those of CNFs. Note also that before fluorination an important gap of stability according to the solvent is seen, but after fluorination, in addition to an overall increase in stability, curves are observed in a tighter range. A more detailed behaviour for each solvent is given in Fig. 3c, d, e and f for ethanol, chloroform, DMSO and DMS, respectively. Before fluorination, the most efficient solvents are DMF and ethanol and no significant differences in the stability can be noted between CNFs and CF0.85 in these solvents. Conversely, the effect of fluorination is important in chloroform and DMSO. These qualitative observations are supported by the calculation of the initial rate of sedimentation reported in Table 3. It is worth noting that in DMSO the rate of sedimentation is divided by 4 after fluorination and is divided by 2 in the case of chloroform, whereas no changes are seen for suspensions in ethanol and DMF.
Molar concentration of CNFs and CF0.85 in organic solvents at t = 0 min and at t = 330 min.
| Solvent | Molar concentration of CNFs (mol/L) | Rate of sedimentation (mol/L/min) | Molar concentration of CF0.85 (mol/L) | Rate of sedimentation (mol/L/min) | ||
| T = 0 s | T = 330 min | T = 0 s | T = 330 min | |||
| Ethanol | 1.70 | 1.40 | 4.4 × 10−4 | 2.35 | 2.05 | 4.4 × 10−4 |
| DMF | 1.10 | 1 (at 250 min) | 4.4 × 10−4 | 1.42 | 1.30 (at 250 min) | 4.4 × 10−4 |
| DMSO | 0.72 | 0.52 | 9.1 × 10−4 | 1.40 | 1.25 | 2.1 × 10−4 |
| Chloroform | 0.63 | 0.37 | 2.6 × 10−3 | 0.75 | 0.60 | 1.2 × 10−3 |
Numerous studies have shown good solvation and dispersion of SWCNTs and MWCNTs into the DMF dispersion [39–41]. This work has shown a good solvation ability of SWCNTs in DMF because of high values for the hydrogen bond acceptance basicity and negligible values for hydrogen bond donation parameter. Bahr et al. [37] have shown that the best results to evaluate stability of SWCNTs are obtained for dichlorobenzene and chloroform.
Previously, no direct correlations between Hildebrand parameter or Hansen parameters with CNF and CF0.85 dispersibilities have been deduced. Then, we can discuss the interactions between pristine CNFs and fluorinated ones with solvents, thanks to the formula of the enthalpy of mixing per unit volume of solvent ΔHmix/Vmix:
| (3) |
In this formula, we can see the importance of the volume fraction, which can change a lot with the nanofibre debundling. After the ageing period it can be considered that this parameter will change less than before, which can explain the important dispersion of concentration values before ageing according to the easiness of a solvent for nanofibre debundling. In the case of fluorinated nanofibres CF0.85, the volume fraction can be higher than with pristine CNFs because fluorination leads to the carbon nanotube debundling [42]. Nevertheless, because of the debundling by fluorination, the volume fraction of nanofibres will be more stable than with pristine ones. This can be an element that contributes to the higher temporal stability of fluorinated nanofibres. Another point is the nanoparticle diameter. It is now well known that fluorination not only leads to an increase in the diameter of nanotubes but also for the highest fluorine contents to a partial unzipping of the nanofibres. This latter phenomenon is more pronounced with the use of ultrasound. The unzipping is equivalent to an increase in the curvature radius, which is favourable for the dispersion of nanoparticles. This effect can explain why the dispersibility of fluorinated nanofibres is higher than the pristine ones. Finally, the last parameter is the surface energy of nanofibres. The surface energies of the solvents can be compared with their surface tensions, which are 21.97 mJ/m2 for ethanol, 42.92 mJ/m2 for DMSO, 35.74 mJ/m2 for DMF and 26.67 mJ/m2 for chloroform at 25 °C. The best dispersibility is obtained if (δCNF − δsolvent)2 is low, that is, if the surface energy of CNFs (pristine or fluorinated CNFs) is close to the surface energy of the solvent. Here, there is no influence of the surface energy of the solvents on the dispersibility of CF0.85. Indeed, as seen previously, the curves of stability for each solvent are close to each other. Similarly, in the case of pristine CNFs, no ranking can be made as a function of solvent surface tensions. In conclusion, it seems that the ratio of φ/D between the volume fraction and the particle diameter is the main value to understand the changes observed in the dispersion experiments between pristine CNFs and CF0.85 nanofibres.
To summarize, the ageing is an important benefit for the stability of suspensions, and fluorination appears to be a good mean to increase the nanofibre diameter and to decrease the volume fraction changes, then fluorination is a good mean to improve the stability of nanofibres in a suspension. The averaged length significantly decreased whereas the diameter slightly increased due to the addition of fluorine atoms. These behaviours reinforce the hypothesis of chemical and/or physical interaction between fluorinated CNFs and organic molecules. Despite the weak difference between CNFs and CF0.85 concentration value evolutions, fluorination favours the stability of the solutions with time.
Tribological experiments were carried out to evaluate the effect of ageing on friction properties of CF0.85. Fig. 4 displays the changes in friction coefficients for CF0.85 dried after ageing period in an organic solvent as a function of the cycle number. Results are compared with initial CF0.85 data. It is important to note that no liquid is added at the beginning of the experiments and the powder was dried under air atmosphere. Stable and compact film of nanoparticles was formed on the sliding surfaces without the addition of a volatile solvent, for example, pentane.
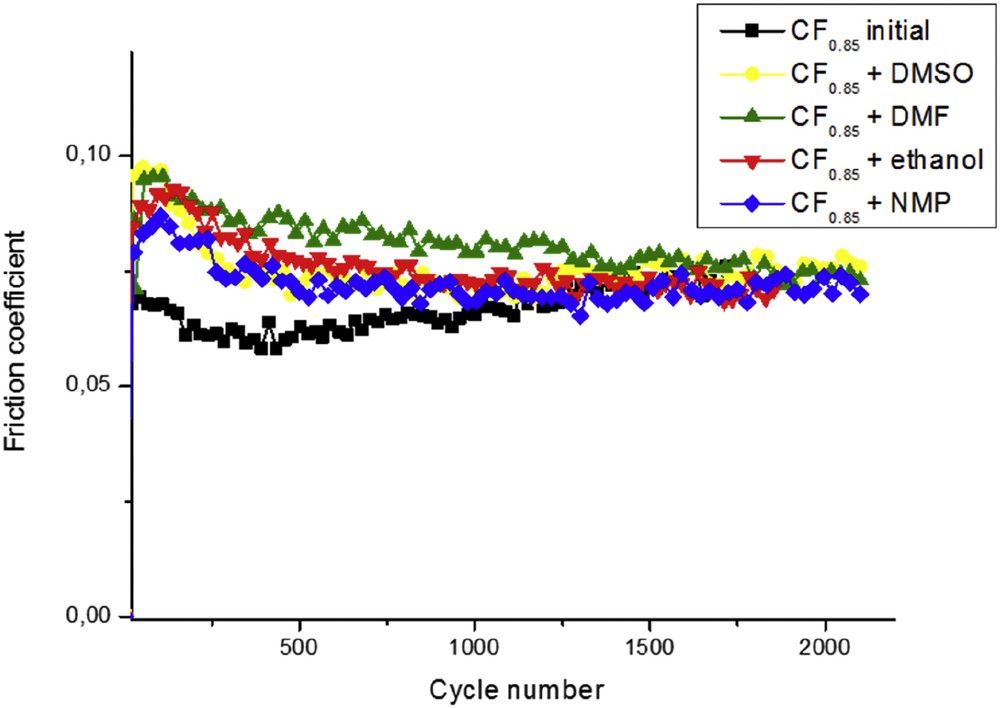
Friction coefficient curves of CF0.85 dried after the ageing period in organic solvents.
All the samples exhibit good intrinsic tribological properties, friction coefficient ranging between 0.07 and 0.09. Whatever the organic solvent used, friction curves remain similar. All started with a quite high friction coefficient and then decreased after a few cycles to stabilize for a long period at . The previous studies evidenced that friction coefficient of CNFs decreased from 0.13 to 0.08 for fluorinated CNFs with F/C = 0.15 and did not change any more when increasing the fluorination rate (F/C in the range of 0.2–0.8) [16]. Their good friction coefficients were attributed to weak interlayer interactions leading to low critical shearing along the sliding direction parallel to the layers.
Friction curve of initial CF0.85 started with a friction coefficient of 0.07 and then decreased up to 0.06 after 300 cycles before to stabilize around 0.07 after 1000 cycles. The value still remained stable until the end of the test evidencing excellent performance of the tribofilm. The induction period corresponding to the first cycles is assigned to an orientation of individual fibre along the sliding direction in the low contact pressure zone. In the case of CF0.85 resulting from ageing, the induction period differed according to the used solvent. The starting friction coefficients were higher than the ones obtained for initial CF0.85. The shortest period is observed for DMSO. The initial value of reached after 300 cycles. When ethanol and DMF were used for the dispersion, the friction coefficients still fluctuated after 500 cycles in the range of and , respectively. Two hypotheses may explain the ageing effect: (1) the physicochemical properties were sufficiently changed to act on the induction period or (2) some solvent molecules were still adsorbed on the carbon surface because of stronger solvent/carbon interactions.
Zisman [42] has shown an evolution of the friction coefficient as a function of the length of the carbonated chain of organic molecules. Another work evidenced that the friction was particularly high with short chains (fewer than eight carbons) [43]. This was ascribed to the large number of dissipative modes in the less ordered short chains. Longer chains, stabilized by van der Waals interaction, formed more compact and rigid layers and then act as an enhanced lubricant. According to this theory, we can assume that an influence of the thickness of adsorbed molecule layers may be expected on tribological properties of CF0.85. However, it is necessary to note that the friction coefficients were stabilized close to the same value whatever was the organic solvent used.
To investigate the structural changes in the fibres upon friction cycling, Raman spectroscopy was used. Fig. 5 displays Raman spectra recorded with CF0.85 dried after ageing in organic solvents before and at the end of tribological tests (around 2000 cycles). On the Raman spectra of graphite, three bands were present, classically assigned to disorder (D band at 1350 cm−1 and D′ band at 1620 cm−1) and to the optical E2g mode of the carbon atoms (G band at 1582 cm−1), respectively. In the case of carbon nanotubes, the G band is composed of several peaks due to the phonon wave vector confinement along the nanotubes, circumferential direction and symmetry-breaking effects associated with carbon nanotube curvature [44].
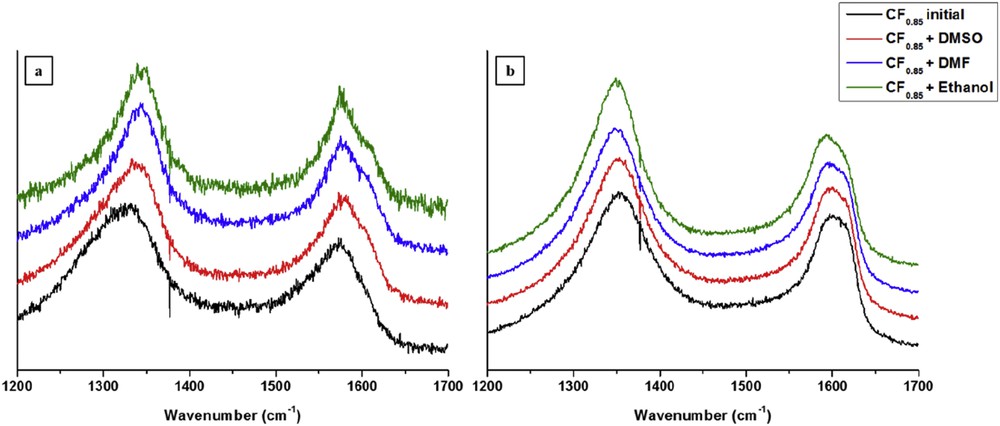
Raman spectra of dried CF0.85 after ageing according to the organic solvent used on the deposited film (a) and on the tribofilm (b).
In the case of initial CF0.85, the high intensity and the shift of the D band towards the low frequency as well as the fact that the D′ band is superimposed with the G band revealed a disordered structure. As a matter of fact, the increase in the D and D′ modes was ascribed to the size reduction of the graphitic domains with increasing fluorination temperature and fluorine content [5,16]. In the case of CF0.85 dried after the ageing in organic solvents, the Raman spectra have similar characteristics whatever was the solvent used. The D band was located at ∼1342 cm−1, the G band at ∼1575 cm−1 and the D′ band at ∼1606 cm−1. After the tribological experiments, no significant differences were observed on the Raman spectra. The physicochemical properties of CF0.85 after ageing in organic solvents are similar to those of initial CF0.85.
4 Conclusions
Little work has been devoted to the interaction of fluorinated carbonaceous nanomaterials with organic solvents especially for long contact time with the solvent. The present work emphasizes on a beneficial effect of the presence of fluorine atoms in the carbon lattice. Differences in solubility between raw and fluorinated CNFs were registered but cannot be fully explained by the Hansen solubility theory. Comparison of Raman spectra before and after ageing of the fluorinated CNFs in liquid showed no significant modifications in their physicochemical properties upon ageing. On the contrary, the tribological properties were changed especially during the induction period. The presence of residual adsorbed solvent molecules at the carbon surface may explain the differences, the interaction being higher after ageing than in the initial state.


