1 Introduction
Synthesis of new materials is one of the central driving forces behind progress in science and technology. Hence, it is well understandable that materials chemists share a dream, the dream of being able to provide in a chemical sense new materials of a desired functionality in a purposeful approach. However, unfortunately even nowadays, discoveries of respective solid materials basically rely on experimental exploration, using empirical and descriptive concepts. Moreover, as illustrated in Scheme 1, in general, there is a distressingly long time lag between discovery of a new solid compound in a chemistry laboratory and the disclosure of its relevance as a material. These two steps used to be taken fully unrelated. Within the descriptive among the heuristic approaches toward solid-state synthesis, one is presuming thermodynamic equilibrium to prevail, that is, exclusively ground states of matter are considered, which in solid-state sciences are commonly documented in the format of phase diagrams. By its stringency, this approach appears to be elegant: all possible equilibrium states of matter in a given system, as characterized by the phase content (defined by phases present, their compositions and concentration) and the respective components' activities, are invariably fixed for given composition, temperature, and pressure. Although mapping phase diagram is an invaluable tool in many areas of materials sciences, in particular for intermetallic alloys, it is merely descriptive and does not furnish any predictive power. More importantly, this view definitely fails in addressing the full wealth of materials capable of existence because it does not include metastable states, which constitute by far the largest share of the total of chemical matter. A second empirical line of actions taken in rationalizing targets for solid-state synthesis uses extrapolation from known crystal structures, while resorting to crystal chemical rules and relationships among the elements, as may be derived from their locations in the periodic table of elements. Such approaches, however, are widely experienced as inefficient because they are not enabling dependable predictions [1]. Contrary to many areas of molecular chemistry, where meaningful goals for synthesis can be routinely established by assembling robust structural building units [2], the overwhelming structural and compositional diversity of extended solids cannot be addressed by applying similar procedures.
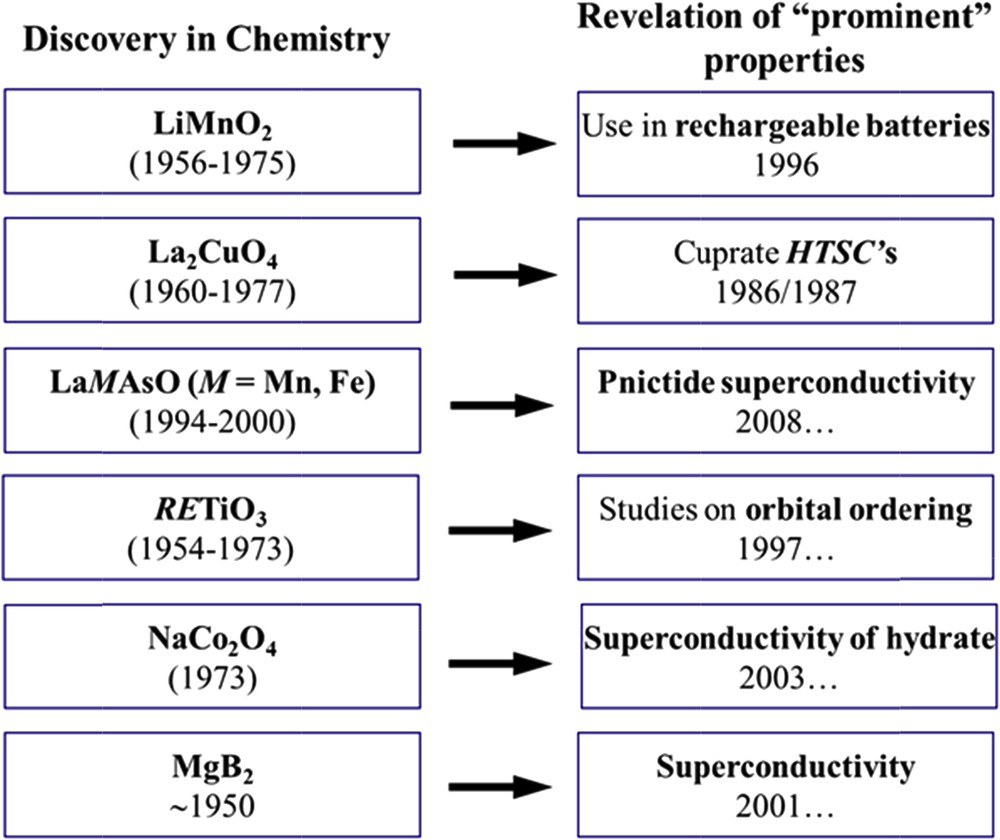
Typical careers of newly synthesized materials, period of discovery in chemistry (left), year of disclosure of prominent functionality (right).
In this account, we trace our efforts made during the past ∼25 years in developing a scheme for rational planning of solid-state synthesis [3–5]. Such an undertaking requires to address two fundamental steps: (1) to identify a target chemical configuration capable of existence, and (2) to provide feasible synthesis routes for accessing such a predicted configuration experimentally. Our approach for achieving the first requirement is based on the “chemical energy landscape” concept [4–6], which moreover is well suited for dealing with the different approaches to solid-state synthesis in a holistic view. Finally, options for translating the predictions into reality will be addressed, comparisons will be drawn to competing approaches toward efficient solid-state synthesis, and possible pitfalls as well as future challenges will be discussed.
2 Chemical energy landscape
2.1 General aspects of energy landscape concepts
Any universally applicable strategy for addressing the first step in synthesis planning, which is to provide candidate structures for synthesis, has to meet the tremendous challenge of completeness, that is, including all chemical configurations capable of existence, the thermodynamically stable and metastable ones. In particular, spotting the latter in a rational way appears to be hardly feasible. However, as can be easily illustrated by existing metastable (at ambient conditions) solid matter like diamond, binary oxides containing silver in oxidation states of 2+ and 3+ [7], or ionic ozonides [8], and many more, this is an indispensable requirement for achieving the self-imposed goal to being able to comprise all possible manifestations of matter. For the reasons given, we start with the world of all conceivable atomic arrangements for N atoms, which is called the configuration space. A point in the configuration space can be represented by a 3N-dimensional vector R = (r1,…, rN). To each such configuration, a distinct potential energy is associated, and the 3N-dimensional hypersurface of the energy over the configuration space is the so-called potential energy landscape. At T = 0 K, p = 0 GPa, and with zero-point vibrations precluded, a continuous hypersurface results. Only those configurations associated with minimum regions on the energy landscape are capable of existence for at least a finite lifetime, and conversely, each stable compound corresponds to a (local) minimum of the energy landscape. For illustration, a three-dimensional (3D) section of the in fact high-dimensional surface of potential energy is displayed in Fig. 1.

Schematic illustration of a 3D section of the potential energy landscape and some chemical configurations associated (central part of picture courtesy of Christoph Delago, University of Vienna).
This way of projecting all chemical configurations capable of existence, that is, all known and not yet known compounds, onto an energy landscape is providing a sound concept for any attempt to analyze chemistry, in particular, to address the issue of synthesis on a universal foundation. As a particular strength of this view, without any exception all manifestations of matter are included on an equal footing, thus artificial trenches are removed, for example, between chemistry of molecular compounds and extended solids. Furthermore, valuable insights into many implications related to chemical synthesis can be extracted without any effort. As mentioned above, in the past the question of whether a targeted solid material would be stable or not was prevailingly evaluated based on thermodynamic considerations. However, corresponding to a local minimum on the hypersurface of potential energy, that is, kinetic stability alone, is sufficient for a certain chemical structure to be experimentally accessible. Because the composition and structure of a stable configuration are predetermined by natural laws, neither its composition nor structure or property can be subject to any kind of arbitrary tuning or shaping by the chemist, and using the term “design of a compound” in the context of developing targets for synthesis is definitely inappropriate [9]. As an even more substantial consequence of this view, chemistry can be approached in a deductive way by deriving the structure of the respective energy landscape from ‘‘first principles” [10].
The chemical energy landscape concept applies universally to all heuristic or inductive approaches to chemical synthesis previously followed, the conceptual and the purely explorative ones, thus allowing for a holistic view of chemistry. Each successful synthesis of a new compound corresponds to the discovery of a new minimum on the respective energy landscape. The underlying rationales of conceiving syntheses continue to be extremely diverse, among others depending on the class of compounds dealt with. The strategies followed most commonly in solid-state chemistry, ranked according to the degree of control provided, are (1) unconditioned experimental exploration (trial-and-error or shake-and-bake), (2) experimental exploration based on analogies and other heuristic concepts, (3) anticipation of structures based on crystal chemical rules, (4) global optimization using nonphysical cost functions, (5) structure prediction by mathematical enumeration and tiling (applicable to systems featuring robust building blocks), (6) global optimization with energy as the only cost function, and (7) global optimization at the ab initio level [11,12].
The robust energy landscape of chemical matter as introduced above is only strictly valid at T = 0 K and with zero-point vibrations suppressed, whereas real chemistry takes place at finite temperatures. However, because the entropic contributions to the standard free enthalpies of formation of solids are small (commonly about 10–15%), moderately raising the temperature would not change the overall minimum structure of an energy landscape of a given chemical system substantially. Thus, the 0 K hypersurface of potential energy is providing valuable indications toward realistic targets for attempts to realize the respective solid materials experimentally. Because any new material that can ever be made is in virtuo present as a (local) minimum in the chemical energy landscape, performing the first step in synthesis planning, that is, anticipating compounds capable of existence, corresponds to the task of exploring this landscape computationally.
2.2 Computational exploration of chemical energy landscapes
Assuming that the Born–Oppenheimer approximation holds, the classical representation of the potential energy landscape under discussion is also obtained in a quantum mechanical treatment. Thus, in principle, the configurations and energies corresponding to the ground and excited states of a chemical system can be calculated by solving the respective Schrödinger equation. However, it is quite obvious that the number of particles to be considered in trying to cover the full compositional and structural diversity exhibited by an ensemble of atoms of realistic size makes such a straightforward approach intractable. Instead, for the exploration of multiminima landscapes, like the chemical energy landscapes, performing random walks guided by physical (e.g., energy based) or nonphysical cost functions have proved to be an efficient strategy. Out of the variety of well-developed algorithms serving this purpose, we have chosen to use the “Metropolis Monte Carlo” variant of “simulated annealing” [4,12–15]. Details of the procedure are displayed in Fig. 2, where in particular the move classes are explicitly addressed. In contrast to the techniques previously used in computational determinations of crystal structures for given compositions and known basis vectors [16], we allow the translational lattices and the compositions to be freely varied. These are indispensable requirements to make sure that the whole landscape under inspection is accessible and the full compositional and structural variability is explored. Achieving the ultimate objectives of the efforts made in predicting (new) compounds that may serve as targets for experimental realizations would even require to perform such searches on respective chemical systems at finite T and p conditions. Furthermore, to attain good accuracy during the total energy calculations to be performed at each step of the global search, it would be desirable to use ab initio calculations. However, such additional demands would dramatically increase the dimensions of the task set. To keep the computational costs bearable, we follow a modular approach [3–6,12,17,18], where the first step is to determine as many of the relevant local minima as possible in the potential energy landscape as a function of atom coordinates and lattice vectors using empirical potentials. The second step involves to locally optimize the candidates at an ab initio level and to order them by energy. Then E (V) curves for every configuration encountered may be computed, which would give first hints toward appropriate p/T conditions to be applied during attempts of synthesis of a respective candidate. Next, these configurations are analyzed with regard to their geometries, and their space group symmetries are determined [19,20]. Subsequently, duplicates are identified and eliminated from the set of candidates, and comparisons with databases containing information about already existing compounds are performed to check whether a configuration identified is new [21]. The final move is to admit finite temperature and pressure, to derive the thermodynamic functions of state, and to construct phase diagrams [17,22,23]. This computational procedure even enables to calculate free enthalpies of the formation for metastable configurations, thus to implement such information in equilibrium phase diagrams [24]. Scheme 2 presents a flowchart of the modular approach discussed.
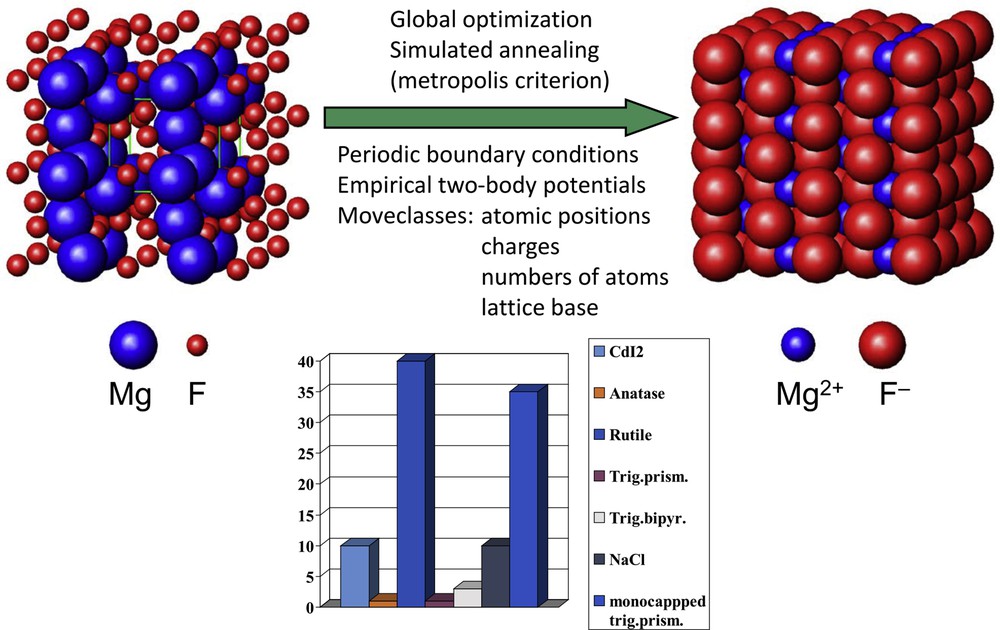
Schematic representation of the procedure followed for global exploration of chemical energy landscapes for the example of Mg/F. (Left) arbitrary start configuration, with basis vectors for the optimization cell and positions of neutral atoms created by a random number generator; (middle) global search algorithm used and move classes admitted; (right) most frequently encountered structure; and (bottom) percentage share of the most frequently encountered structure candidates.
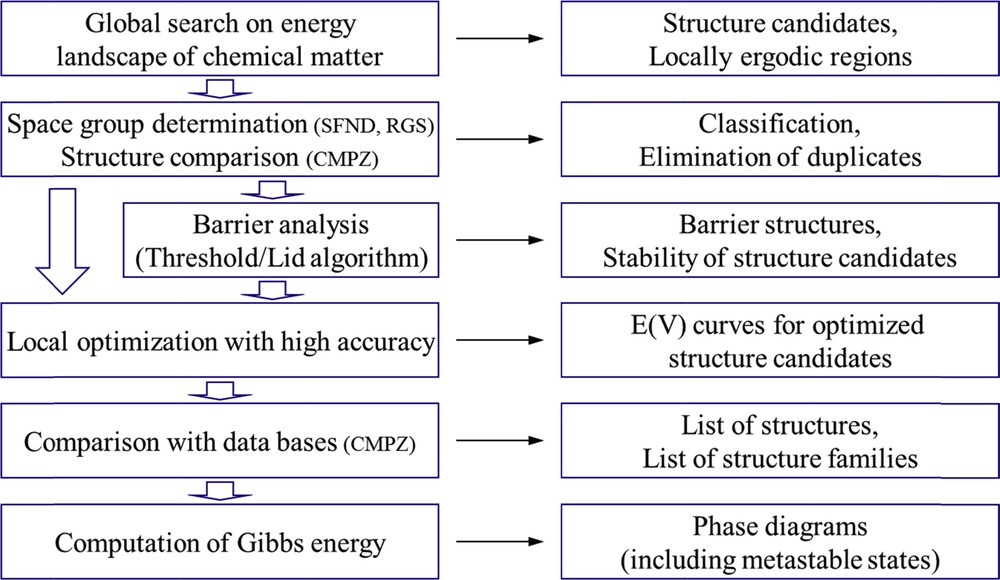
Flowchart for the modular approach toward computational synthesis planning. (Left) sequence of computational procedures; (right) respective output.
The tremendous computational efforts to be made in exploring extended multiminima landscapes have impelled to reduce the size of the task. Although an unrestricted exploration of the configuration space associated with a combination of atoms would be most desirable, it is possible in certain cases to truncate the configuration space to be searched without missing a respective basic goal set. One of the measures taken is to limit the number of atoms admitted per refinement cell to the most frequently encountered formula units per unit cell for known compounds. In another approach, one takes advantage of the fact that for certain combinations of constituting atom types a subset is forming robust building blocks, which in distinguishing from single atoms are called “secondary building units”. These may be kept integral in their equilibrium geometries and used instead of individual atoms. Well-suited entities that can serve this purpose are, for example, complex inorganic anions like CO32− [25] or the still hypothetic orthocarbonate anion, CO44− [26,27]. More recently, it has been impressively demonstrated that such an approach is suited to even generate extremely complex and large configurations representing porous inorganic materials like zeolites and metalorganic frameworks (MOFs). In particular, with the development of the Automated Assembly of Secondary Building Units procedure [27–30] the concept of secondary building units in the prediction of inorganic solids has proven a quite efficient approach to generate new MOF topologies computationally. The key step of the method is the combination of predefined building units and empirical “glueing” rules and in the exploration of their autoassembly in real space through a sequence of simulated annealing steps, using energy as the cost function. It has been proven to apply to bronzes, perovskites [27], or gallophosphates [28], and, for example, to produce new frameworks containing targeted rings or specific cages [29,30]. For an excellent review see Ref. [31].
The field of computational materials prediction by global optimization has been expanding substantially [32–35]. Although the underlying philosophy has remained virtually the same, several technically different approaches have been followed. In the first place, without any significant difference in efficiency, genetic algorithms have been successfully implemented [36,37], besides the very efficient, however, more local ab initio molecular dynamics procedures [38]. More importantly, the bias overweighting structures that benefit particularly from ionic bonding, a consequence of using empirical potentials for the total energy calculations during the search runs, has been overcome by implementing ab initio approaches, based on density functional [37–39] and Hartree–Fock [11,12] theories.
2.3 Structure prediction—some illustrative results
The computational tools developed enable to globally explore energy landscapes of chemical systems for the (local) minima present, which stand for chemical configurations capable of existence.
Alkali metal halides served as an early test case for ionic systems [3,4]. Without recourse to experimental preinformation, for NaCl a large number of local minima was found on the empirical energy landscape. While the global minimum of the landscape corresponded to the known rock salt structure, the structures of most of the energetically competing local minima were identified as typical AB-structure types, ZnS (wurtzite or sphalerite), NiAs, PtS, or CsCl. Most remarkably, one deep-lying local minimum was encountered, which corresponds to a structure featuring commutative substructures for sodium and chlorine with mutual coordination numbers of five [4,40]. This 5–5 structure type was previously unknown and was never anticipated for an ionic AB compound.
To track elusive Na3N, which according to the homology principle should exist in analogy to known Li3N, we searched the Na/N landscape at an empirical energy level. Indeed, several local minima for respective structure candidates were revealed; however, all of them turned out to be metastable with respect to decomposition into the constituting elements. In Fig. 3, the low-energy structure candidates identified are represented as a tree graph [41,42].
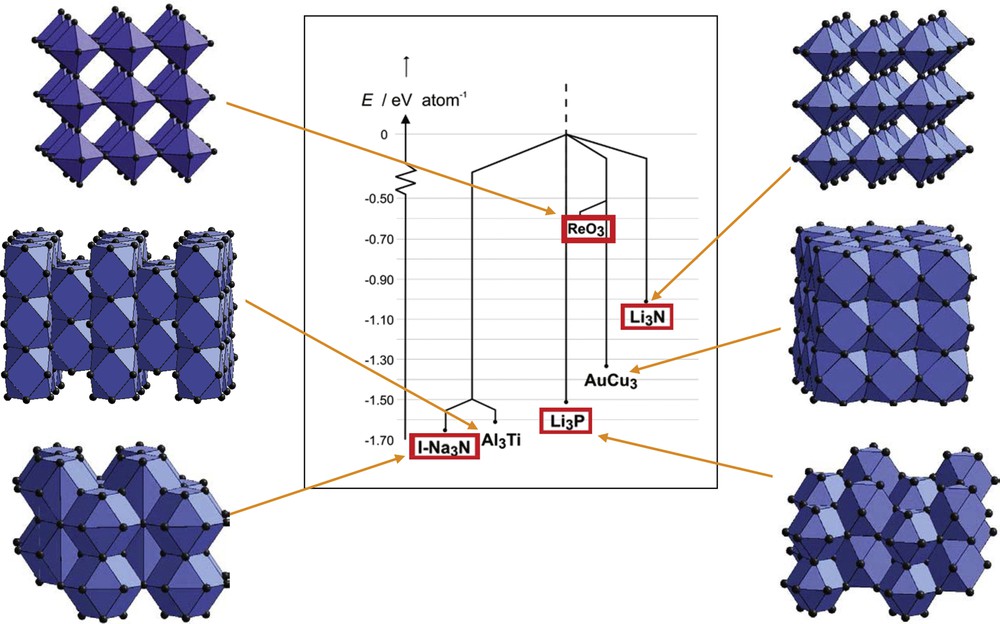
Tree graph of the energy landscape of Na3N at an empirical energy level depicting some of the most relevant local minima. Red boxes mark structure candidates that were experimentally realized many years after their prediction, see Section 3.1 [43–45]. Reprinted with permission from Ref. [39]. Copyright 2011 Wiley-VCH.
The empirical potentials used so far are not suited to address systems in which covalent bonding interactions prevail, and they would evidently fail if applied to homoatomic configurations.
But even for ionic compounds, where good empirical potentials are available, it has been under dispute to what extent the empirical energy landscape deviates from the corresponding ab initio energy landscape [4,46,47]. To assess such objections, simulated annealing was used to search the LiF ab initio energy landscape at standard pressure, where both the Hartree–Fock approximation and density functionals were used to compute the total energy [11]. As a quite satisfying result, the same relevant minima compared with the empirical potential approach were obtained, also including the “exotic” 5–5 structure types. This validated the many landscape explorations based on empirical potentials and at the same time was proving the feasibility of global stochastic explorations on ab initio multiminima energy surfaces.
Boron nitride (BN), a ceramic material that serves diverse applications, was chosen as a crucial test for a predominantly covalently bonded system. This undertaking faces a specific challenge because during the evolution of structures strong covalent bonds need to be broken and formed, which renders convergence for random starting configurations much slower. Global ab initio searches of the BN landscape [48] have retrieved the known layered structure and 3D high-pressure polymorphs of wurtzite and zincblende structure type. In addition, two further layered structures displaying different stacking sequences as compared to the ground state configuration were encountered. Noteworthy, the “random walker” has been able to spot two for BN completely new structure candidates (see Fig. 4). These fascinating and rather stable new polymorphs might represent materials with potentially interesting properties. The E (V) curves as calculated for all known and predicted BN polymorphs [48] indicate that for their synthesis an intricate T/p schedule needs to be followed. In particular, high pressure will have to be applied; however, if a certain threshold in pressure is surpassed, the system would slide into the known high pressure wurtzite and zincblende modifications.
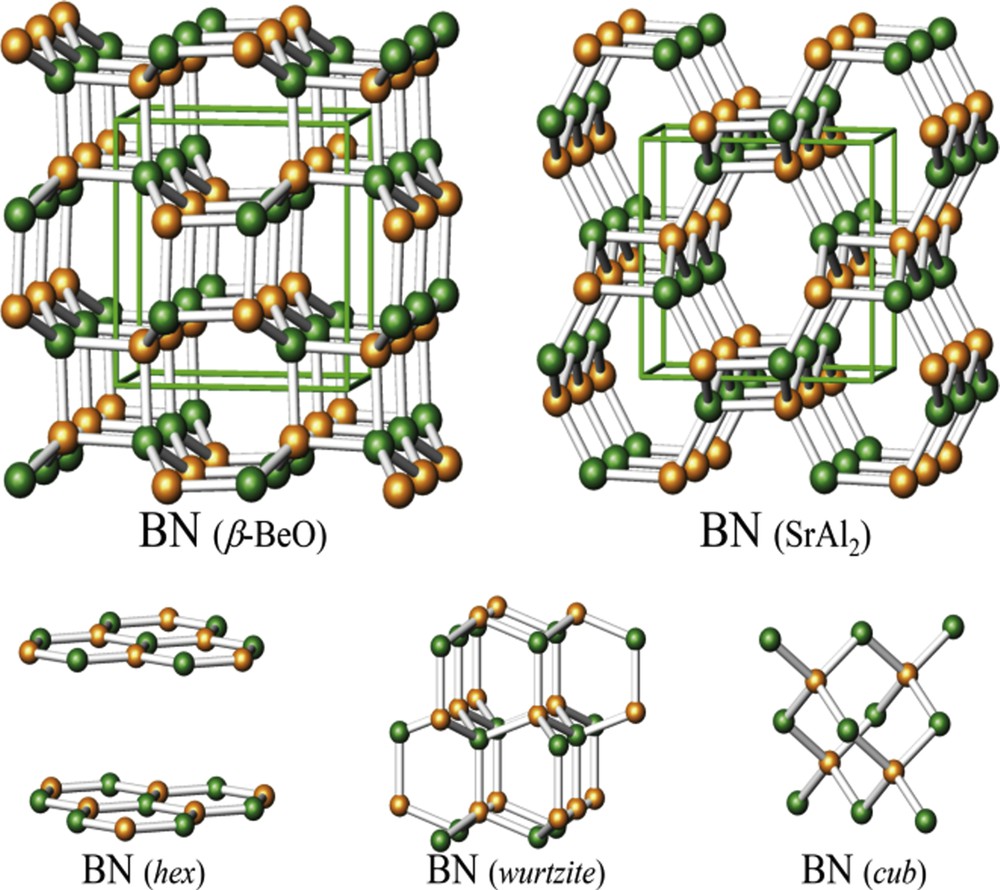
Polymorphs of boron nitride as encountered during global searches on the ab initio landscape: (top) unknown candidates and (bottom) known polymorphs. Reprinted with permission from Ref. [5]. Copyright 2015 Wiley-VCH.
As a specific feature, “lone pair” electron configurations concomitant with covalent bonding induce noticeably crooked first coordination spheres [49]. Such systems might serve as meaningful touchstones to examine whether global optimizations at the ab initio level are suited to produce reasonable structures expressing lone pair dominated topologies without implementing any preinformation. Such kind of investigation has been performed for germanium (II) fluoride [50]. The line of action consisted of a global optimization of the ab initio landscape using simulated annealing with Monte Carlo steps and subsequent highly accurate local optimizations. Because van der Waals interactions were expected to crucially contribute to the total energy, a respective term of correction for such implications [51] was applied. Given this extra intricacy, the results obtained are of impressive dependability (see Fig. 5): the experimentally known facts have been reliably reproduced and definitely meaningful new targets for synthesis have been suggested.
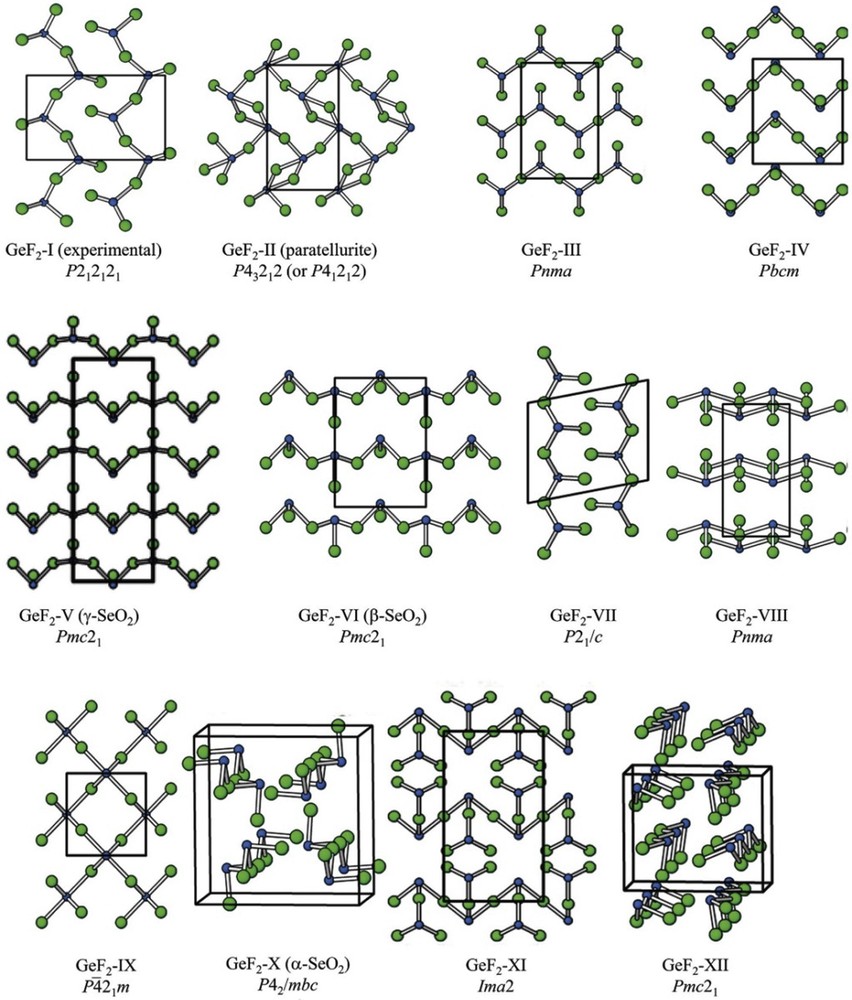
The most stable structure candidates revealed for GeF2 during the global search on the ab initio landscape. Reprinted with permission from Ref. [50]. Copyright 2011 Wiley-VCH.
To sum up, as a highly relevant experience, the approach used for global optimizations of multiminima chemical energy landscapes has been demonstrated to be suited to reveal completely new, in part exotic, compositions and topologies; thus the random walker appears to be in a way “inventive”.
3 Competing approaches to efficient materials synthesis
3.1 Rational approach: experimental realizations of computationally predicted compounds
As a fundamental dialectic requirement in natural sciences theoretical predictions and hypotheses need to be experimentally verified. As a first satisfying confirmation of the validity of our computational approach, for all systems investigated, the previously known structures were retrieved. In validating the computational results, many predicted high-pressure polymorphs have been realized experimentally using conventional large volume or diamond anvil cell high-pressure techniques. Respective unprecedented crystal structures as predicted for the alkaline earth carbides [52] or for alkali metal carbonates [53] were later realized experimentally at the examples of HP-BaC2 [54] and Li2CO3 [55]. Furthermore, the full sequence of pressure-induced phase transitions as predicted for alkali metal sulfides has been fully verified experimentally [56–58]. From the searches on ab initio energy landscapes, one of the predicted structure candidates for GeF2, marked as III in Fig. 5, has been experimentally confirmed and identified as a high temperature polymorph [59].
For addressing compositionally new compounds, our group has carried out experimental verifications of the computational predictions right from the beginning, sometimes in parallel to the theoretical work. With particular focus on the experimental realization of new metastable candidates, we developed a specific procedure (low-temperature atomic beam deposition, LT-ABD) that allows us to perform solid-state reactions at the lowest possible thermal activation [60]. In this approach, atoms are deposited atomically dispersed on a very cold substrate (at liquid nitrogen or liquid helium temperatures) forming an amorphous deposit that is subsequently slowly heated, resulting in the crystallization of product phases at very low temperatures, mostly in a sequence following the Ostwald–Volmer rule. Thus, in a way this setup allows us to simulate experimentally the computational process of “simulated annealing”. The potency of the approach has been demonstrated in several examples, for example, the synthesis of highly metastable wurtzite-type LiBr in an all-solid-state reaction far below ambient temperature [61], fully confirming the predictions. Further exemplifications have been provided by respective studies on the unprecedented metastable polymorphs of LiI [62], LiCl [63], and noteworthy of a LiI/LiBr solid solution [64] in the metastable wurtzite-type structure.
Among the most impressive results of a successful synthesis of a predicted compound is the synthesis of the elusive sodium nitride Na3N in an energetically high-lying structure [43], the ReO3 type, using the LT-ABD method [60]. In particular, the fact that 11 years after the computational discovery of a large number of metastable polymorphs had been reported [41,42], most of them have been realized in the correct sequence of appearance as a function of pressure, see Fig. 3 [43–45]. These results impressively document the strength of the strategy we suggest for running solid-state synthesis in a rational way.
3.2 High-throughput techniques
Traditionally, chemical systems have been screened for the stable solid compounds they host experimentally by “trial-and-error” based on some more or less rational concepts, which also constitute the principal line of action for the inductive approach to chemistry. Although such a way of discovering new materials has been rather successful in disclosing new compounds featuring exciting structures, bonding schemes, or properties, these conditions have always been experienced as uncomfortable for the obvious lack of control and understanding. For improving efficiency along basically the same line of explorative chemistry, one might try to let the chemical systems of interest find their stable configurations on the energy landscape on their own. This is the basic idea underlying the “high-throughput techniques”. Basically, all these techniques have in common a parallel processing of many samples of different compositions. In the recent past, numerous pertinent reviews appeared [65–68]; however, presently interest in this technique appears to wane. In the context of this essay, it is interesting to examine whether high-throughput strategies really meet the challenging requirement of being suited to exhaustively exploring chemical landscapes. Taking superconducting YBa2Cu3O7-x as an example, a rough estimate [6] immediately demonstrates that an intractable number of about 1080 (parallel) experiments would be needed to ensure that one inevitably encounters the target compound as one of the products, assuming the unrestricted configuration space of 86 stable elements was searched. Irrespective of the precision of this estimate, it is obvious that the discovery of new materials cannot rely upon high-throughput techniques alone. Admittedly, the multisample concept of processing many starting material mixtures in parallel has proved its particular strength in optimizing known functional materials, like phosphors [67] or heterogeneous catalysts [68], by applying a fine meshed grid of compositions.
For the purpose of selecting new materials with desired properties straightforwardly, the single-sample concept has been suggested as another new variant of combinatorial chemistry [69–71]. Here, multicomponent mixtures of solids are subjected to solid-state reactions, and the products obtained are directly screened, with respect to a predefined property like ferromagnetism or superconductivity, using this very property for the separation of the functional material from undesired byproducts. However, there are some doubts as to whether the full chemical variability can be explored along such a route because the macroscopic grain sizes and the normally low diffusion coefficients of cations in oxides, for example, will most probably impede all compositions possible in the a respective system to be realized.
4 Challenges and prospects of future approaches to materials discovery
4.1 Flowchart for new materials discovery, present and future
Discovery of a compositionally new inorganic material follows a one-way road. In a first step, (meta)stable solid compounds need to be synthesized, or predicted, and in a subsequent step one is checking the spectrum of properties featured by these very configurations. Unfortunately, there have been irritating proposals ignoring this fact, for example, assuming that starting with the desired properties of a hypothetical material, one should design a chemical compound that possesses these qualities [72,73]. In another case, “cubic” YBiO3 perovskite was predicted to be a topological insulator but actually such a configuration is structurally unstable, whereas its stable structural form is a trivial band insulator [74].
Scheme 3 represents a schematic flowchart for conventional experimental exploration and characterization of new materials (right-hand column) and for a fully computational approach, which might be feasible in not too far a future (left-hand column). Traditionally, the first step, identification of prospective structure candidates, capable of existence and displaying the targeted profile of properties has been done experimentally in an explorative fashion. However, this process is extremely slow and rather aleatory, and most of the important breakthroughs in the past toward new materials were achieved rather unintendedly (see Fig. 1) by chance or by serendipity. The energy landscape concept as developed and implemented [4–6,12–15,17,18] is offering high potential for a significant improvement, because computational searches would considerably speed up the exploration of stable configurations as compared to the experimental procedures, which are particularly slow when all-solid-state reactions are involved. Knowing the composition and structure of a predicted candidate from the computational search would enable screening for its set of properties computationally. The costly experimental synthetic efforts would then be focused on prospective candidates resulting from computational exploration and screening. In this sense, conceptual materials discovery would start by identifying virtual compounds and their structures on the energy landscape, subsequently, the profile of properties will be assured theoretically, and finally those candidates fulfilling the respective expectations will be subjected to the conventional loop of experimental realization and characterization. Of course, the flowchart displayed in Scheme 3 does not need to be followed step by step. Instead, one might take shortcuts and, for example, directly use the raw configurations as obtained from the global search for property screening.
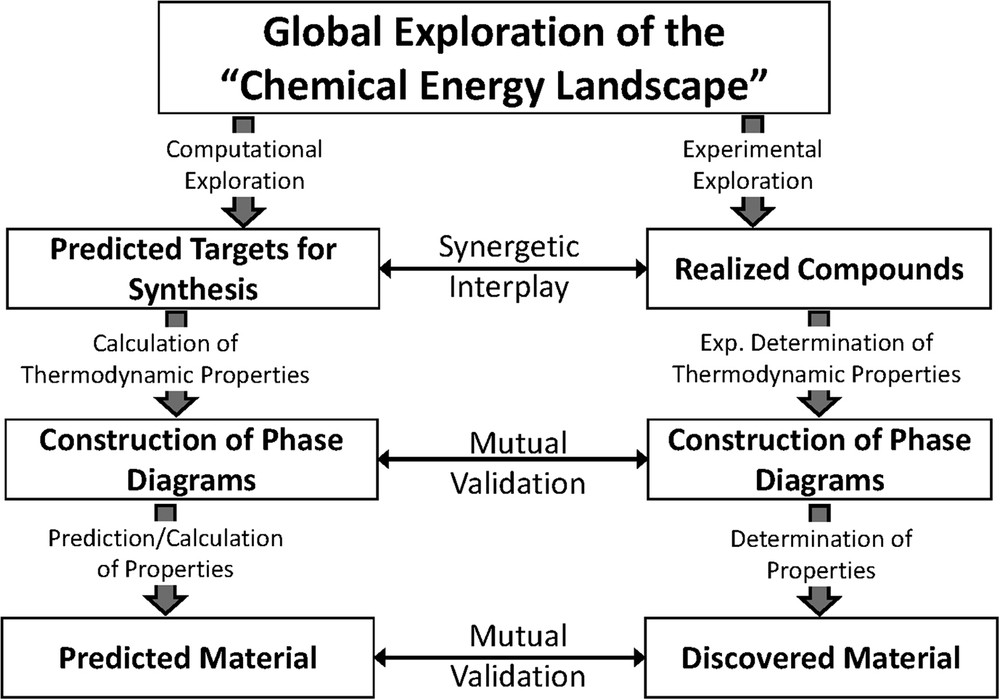
Flowchart for rational materials search. (Left column) present/future computational exploration and (right column) traditional experimental exploration. Vertical arrows indicate synergetic interplay and mutual validations between the approaches.
The action to be taken in addressing the final step mentioned, to determine and assess the potential properties and functionalities offered by a solid material predicted to be capable of existence, has been at the core of theoretical solid-state physics. Regrettably, in certain instances the dependability of the methods available is still unsatisfactory, and one probably would not be able to a priori identify a new superconducting material or to clearly distinguish whether a material is a small band gap semiconductor or a metallic conductor. However, there are examples of celebrated breakthroughs in theory, for example, the fully analytical proof of the existence of counterintuitive magnetic ground states on transition metal honeycomb lattices [75,76] or of particular topological features in band structures, among others giving rise to spectacular surface states [77]. The main focus of this essay is on the first steps of conceptual materials discovery, that is, identifying still unknown solids and assessing their stabilities. Thus, for tracking further progress in properties analyses, we like to refer the reader to the literature reports on addressing computational analyses of properties of, for example, alloys [78], ceramics [79], battery materials [80], and photocatalysts [81].
Admittedly, at present the algorithms in combination with the computing power available are by far not suited to handle chemical systems of realistic sizes as stringently as required for the first parts, the theoretical explorations and property calculations. Aiming at compensating these deficiencies, one would start and exploit some synergetic interplay between computational and experimental techniques (as indicated by horizontal arrows in Scheme 3), which in addition would allow for mutual validations of the findings. In a test case study on the ternary system Li/Cs/Cl, we have shown that such a synergistic interplay of the two approaches is suited to significantly speed up the procedure of establishing the phase diagram of the system investigated. Apparently, for the system studied, at the present state of progress neither computational nor experimental exploration is perfect; however, some of the deficiencies can be compensated by using both techniques in parallel [82].
4.2 Challenges and potential pitfalls of computational materials discovery
In spite of the conceptual advances achieved in computational approaches, there are still definitely critical limitations, standing against applying the procedure to problems to be solved in the technical world. One of such issues is the moderate size of the systems that can be tackled at sufficient accuracy with currently available tools. Trusting in the steadily growing computing power available, many obstacles will be overcome by quantitative progress in the quite demanding numerical computations. However, qualitative progress is indispensable as well, for example, for capturing the probably small share of entropically stabilized configurations, which may not be present as minima on the potential energy landscape, the search at finite temperature, that is, of the free enthalpy landscape, remains as an ultimate objective. There is principle awareness of this issue, and one is able to model entropically stabilized configurations, like glasses [83] or ceramics based on inorganic random networks [84]. However, recent observation that a compound is virtually exclusively stabilized by the configurational entropy of electrons challenges the modular approach presented because this additional, commonly ignored, degree of freedom might cause that such a configuration is not present on the hypersurface of potential energy. Elusive K4O6, the lighter homologue of Rb4O6 and Cs4O6, which are rare manifestations of mixed valency on the oxygen sublattice [85], represents such an example. It has been found that it only exists at elevated temperature and is spontaneously decaying into its constituents KO2 and K2O2 upon cooling below a temperature threshold; the reactions of formation and decay are fully reversible and fast. In terms of equilibrium thermodynamics, this behavior implies that both the enthalpy (ΔHR) and entropy (ΔSR) of a reaction are positive. Thus the reaction does not proceed to the product phase K4O6 unless the term TΔSR, driven by temperature, exceeds ΔHR. Interestingly, for this reaction the only source of a significant gain in entropy is the contribution from configurational entropy of localized electrons (small polarons). Although in the starting mixture for the distribution of charges there is no degree of freedom, in the mixed valent sesquioxide K4O6 one electron has the choice between three structurally equivalent (O2)x− units, giving rise to an entropy gain of ΔS = R ln 3. Thus, K4O6 appears to be exclusively stabilized by configurational entropy of electrons (polarons).
Concerning the challenge of developing new schemes for understanding and predicting functionalities of solid materials, unveiling the Kitaev scenario [75,76] has been experienced as an impressive breakthrough, in particular for the way in which this has been achieved. The model derived is exclusively valid for S = ½ spin states. However, recently the new transition metal oxide AgRuO3 has been reported [86], featuring an open shell, now S = 3/2, transition metal ion on a honeycomb lattice, which apparently displays the same experimental properties as associated with the set of magnetic ground states as envisaged by the Kitaev model. Thus, its frame needs to be amended, or some different explanation has to be developed.
Furthermore, the task of rationally identifying routes of syntheses to the solids predicted, which is posing challenges of an even larger dimension, has not yet been systematically tackled. Although regrettable from a scientific point of view, this latter issue is less disturbing in practice, because a well-skilled and experienced chemist will find ways of synthesis for a material that he firmly trusts to be capable of existence. This is including metastable materials as well, for which an arsenal of “soft chemistry” tools has been made available [87].
5 Concluding remarks
The approach to rational solid-state synthesis as outlined in this account is complete, physically consistent, and its principal feasibility in theory and experiment has been proven. The logical thread appears to be persuasively stringent and is probably anticipating the future approach to efficient new materials discovery. However, the principal viability must not blind us to the fact that tremendous technical obstacles are standing against applying the procedure to large area explorations, to tackle systems of relevance for modern technologies. Respective theoretical and experimental undertakings might be rendered intractable by the “combinatorial explosion”, which constitutes a pertinent feature of chemistry [6]. The number of local minima on the chemical energy landscape, that is, the number of compounds possible is probably enumerative infinite. Obviously, there are ways to escape the dilemma, for example, by restricting the configuration space addressed to the field of interest or by focusing at the low energy and deep minima only. The latter will be tracked down successfully, even when using less accurate codes for total energy calculations, thus saving computational costs. Because a fully rational approach to solid-state synthesis along the road map displayed in Scheme 3 appears to be in principle possible, one might envision that the task of developing new materials might transmute to a kind of engineering. From today's perspective, such an expectation cannot be dependably assessed. The quantitative dimensions to be met are intimidating, and moreover intricate qualities not yet envisaged might emerge. For instance, mixtures subjected to solid-state reactions may show a deterministic chaotic behavior, inasmuch as compositionally identical mixtures move into different local minima, that is, forming different product phases, depending, for example, on memory effects and pretreatment of the reactants, or in general, on the huge space of parameters controlling solid-state reactivity. Such a kind of bifurcation is a characteristic attribute of deterministic chaos, and such implications for solid-state chemistry were analyzed recently [88]. So we may trust, at least for the near future, there will be much room left for serendipity, which is said to favor the prepared mind [89].
Acknowledgments
It is with great pleasure that I gratefully acknowledge the valuable contributions made by several generations of enthusiastic PhD students and postdoctoral researchers as well as of the talented senior scientists Christian Schön and Klaus Doll, see References section.


