1 Introduction
Discrete heterometallic complexes and coordination polymers with oxalate as bridging ligand constitute a very active area of multidisciplinary research envisaging the achievement of functional materials with interesting magnetic properties [1–11]. In these compounds, the anionic networks of general formula [MI/IIMIII(ox)3]2−/− (M = Cr, Fe and ox = oxalate) act as host of templating organic and inorganic cations and also cationic metal complexes, some of them exhibiting magnetic ordering, which is provided by the oxalate framework [12]. In addition to determine their dimensionality (nD with n = 2 or 3), the inserted cation into the oxalate networks allows us to combine the magnetic properties of the oxalate framework with other functions such as chirality [8a–c], magnetochiral dichroism [8d], slow magnetic relaxation [9i], ferroelectricity [11d], second-order optical nonlinearity [13], proton [11b,14] and electrical conductivity [9c,15] and spin crossover [4h,9f,16].
The great number and variety of results obtained in this research field are mainly based on the rational design of polymetallic assemblies through the use of the complex-as-ligand strategy as a synthetic route. Restricting ourselves to the chromium(III) ion, the best example to illustrate the unlimited capacity of this strategy is the [Cr(ox)3]3− building block. Its successful use as metalloligand to afford magnetic heterometallic assemblies is based on the following points: (1) its stability in solution because of the inert character of the chromium(III) complexes towards the exchange of ligands; (2) its negative charge, which makes easier their interaction with metal ions or positively charged metal complexes; (3) the presence of outer carbonyl groups from the three oxalate ligands that can act as donor atoms towards fully solvated metal ions of preformed complexes whose coordination sphere is unsaturated; and (4) the remarkable ability of the oxalate group to mediate magnetic interactions between the paramagnetic centres when adopting a bis-bidentate coordination mode linking them.
The replacement of one of the three oxalate ligands of the [Cr(ox)3]3− building block by a bidentate nitrogen donor leads to the [Cr(AA)(ox)2]− complex with AA = 2,2′-bipyridine (bpy) [17], 4,4′-dimethyl-2,2′-bipyridine (4,4′-dmbipy) [18], 2,2′-bipyrimidine (bpym) [19], 2,2′’-dipyridylamine (dpa) [20], 1,10-phenanthroline (phen) [21], 2-(2′-pyridyl)imidazole (pyim) [22], histamine (hm) [23] and pyridoxamine (pm) [23]. This bis(oxalato)chromate(III) species keeps the advantages of its parent tris(oxalato) one and can also exhibit additional functionalities derived from the nature of the peripheral AA ligand such as π–π stacking interactions (bpy, 4,4′-bpy, bpym, dpa, phen and pyim), hydrogen bonds (dpa, pyim, hm and pm) and even bis-chelation (bpym) [24]. The use of the [Cr(AA)(C2O4)2]− unit as metalloligand towards silver(I), alkaline- and alkaline-earth metal ions has produced heterobimetallic nD compounds (n = 1–3) [17a,b,18,19a,b,20,21a,22b,25–27], whereas discrete oxalate-bridged heteropolymetallic dinuclear [17d,28], trinuclear [17a,b,28c,d,29] and tetranuclear [17b,21c,30] complexes resulted in its interaction with transition metal ions. In addition to the structural variety of this class of heterobimetallic oxalate-containing complexes, two features deserve to be outlined from a magnetic point of view: (1) the rational preparation of moderately anisotropic CrIII2CoII trinuclear species with a high-spin ground state [29c] and (2) the single molecule magnet behaviour [28c,d].
Herein, we report the synthesis, spectroscopic characterization, X-ray structure, variable-temperature magnetic study of the compounds {[Cr(pyim)(ox)2]2Mn}n·2nCH3OH (1) and {[Cr(pyim)(ox)2]2Co(H2O)2}·7.5H2O (2). Molecular orbital and density functional theory (DFT) calculations (1 and 2) and Monte Carlo simulations (1) were used to analyze and discuss the overall ferromagnetic behaviour in both compounds.
2 Results and discussion
2.1 Synthesis and general characterization
The mixed ligand [Cr(pyim)(ox)2]− unit, which was isolated and structurally characterized as tetraphenylphosphonium and tetraphenylarsonium salts in a previous work [22a], appears as an appealing building block in designing heterometallic compounds. The reluctance of the chromium(III) ion towards the ligand exchange, the presence of two peripheral oxalate ligands, which can act as donors towards either fully solvated metal ions of preformed complexes whose coordination sphere is unsaturated, and its overall negative charge make this entity a suitable metalloligand envisaging the construction of tailor-made heterometallic assemblies. Moreover, the presence of the chelating pyim ligand also offers the possibility to induce supramolecular interactions (hydrogen bonds through the NH fragment of its imidazolyl ring and/or π–π stacking), which are relevant in crystal engineering.
As far as we are aware, the potentiality of this building block as a metalloligand has been demonstrated by the structures of only two structurally characterized compounds of formulas [Na(H2O)Cr(pyim)(ox)2]n.2nH2O [27] and {Ba(H2O)3/2[Cr(pyim)(ox)2]2}n.9/2nH2O [22b]. The sodium(I) derivative has a layered structure, which is made up of oxalate-bridged CrIIINaI helical chains with alternative P/M arrangement, their interconnection within each layer being due to the bis-bidentate/monodentate (outer) coordination mode of the oxalate groups of each [Cr(pyim)(ox)2]− unit. The barium(II) salt instead consists of neutral, homochiral double zigzag chains where each chain is formed of diamond-shaped units sharing the barium(II) ion with the other two corners being filled by the chromium(III) ions. Adjacent double chains are related by an inversion centre leading to an achiral structure.
Herein, we show how the use of the [Cr(pyim)(ox)2]− species as a ligand towards the fully solvated manganese(II) (1) and cobalt(II) (2) ions in a 1:2 Cr(III) to M(II) molar ratio in methanol (1) and in a methanol/water mixture (2) as solvents afforded the heterobimetallic double chain {[Cr(pyim)(ox)2]2Mn}n·2nCH3OH (1) and the trinuclear complex {[Cr(pyim)(ox)2]2Co(H2O)2}·7.5H2O (2). The default of the amount the chromium(III) precursor in the synthesis of 1 and 2 slows down the precipitation of the complexes and allows the formation of single crystals of them. Otherwise, polycrystalline powders containing 1 and 2 together with other unidentified byproducts separate in few hours by a reaction of the Cr(III) metalloligand and the M(II) ions in a 2:1 Cr(III) to M(II) molar ratio.
The chemical identity of 1 and 2 was confirmed by elemental (C, H, N) and electron microscopy (Cr, Mn, Co) analyses together with Fourier transform infrared (FTIR) spectroscopy. Analytical and selected spectroscopic data for 1 and 2 are listed in Table 1. The electron microscopy analysis of the metal contents for 1 and 2 confirms the expected 2:1 Cr/M molar ratio [M = Mn (1) and Co (2)].
Analytical and selected infrared data for 1 and 2.
| Compound | νas(CO)b | δas(OCO) | Analysis (%)a | |||
| C | H | N | Cr/M | |||
| 1 | 1708s, 1691s, 1663vs | 813m | 35.99 (36.17) | 2.49 (2.55) | 9.42 (9.50) | 1.97 (2.00) |
| 2 | 1716s, 1681vs | 810m | 29.45 (29.53) | 3.31 (3.38) | 8.55 (8.61) | 1.98 (2.00) |
a Calculated values are given in parentheses.
b Values in cm−1 (KBr disk).
The difference in the νas(CO) absorption bands of 1 and 2 is consistent with the different coordination modes of the oxalate ligand in these compounds [bis-bidentate (1) and bi- and bis-bidentate (2)] [31]. Two strong absorption peaks in the high-frequency region of the infrared spectra of 1 (ca. 3524 and 3398 cm−1) are attributed to the OH stretching frequency of the methanol molecules involved in hydrogen bonds with the pyim ligand. In the case of 2, a broad and intense absorption covering the range 3600–3000 cm−1 is due to the OH stretching frequency of the water molecules, which are involved in an extensive network of hydrogen bonds. The occurrence of three medium intensity peaks at 791, 752 and 703 cm−1 in 1 and 2 (out-of-phase CH bending vibrations of the phenyl ring) can be taken as a diagnostic of the presence of the pyim ligand. A medium intensity peak occurs at 548 cm−1 in the far-infrared region of the spectra of 1 and 2, which is tentatively assigned to ν(Cr–Oox). In addition, weak intensity peaks at 430 (1) and 436 cm−1 (2), which are most likely due to ν(Mn–Oox) and ν(Co–Oox) vibrations, are also observed in this region [31,32]. All of these spectroscopic features of 1 and 2 are confirmed by their crystal structures (see subsequently).
2.2 Description of the structures
2.2.1 {[Cr(pyim)(ox)2]2Mn}n·2nCH3OH (1)
Compound 1 crystallizes in the orthorhombic Pcca space group (Table 2) and its crystal structure consists of [Cr(ox)2(pyim)] units linked through Mn(II) ions to form double chains running along the crystallographic c axis (Fig. 1). These CrIII2MnII2 loops rotate along the chain by 83.87(2)º in a twisted fashion. The chirality of the chromium(III) ions alternates from one loop to the next, leading an achiral chain. This one-dimensional (1D) arrangement resembles that of the compound {Ba(H2O)3/2[Cr(pyim)(ox)2]2}n.9/2nH2O [22b] although homochiral chains occur in the barium(II) derivative.
Crystal data and structure refinement for 1 and 2.
| 1 | 2 | |
| Formula | C26H22N6O18MnCr2 | C48H66N12O51Co2Cr4 |
| Fw | 865.44 | 1952.94 |
| Crystal system | Orthorhombic | Orthorhombic |
| Space group | Pcca | Pnma |
| a (Å) | 20.7645(7) | 9.2845(3) |
| b (Å) | 9.5333(3) | 34.0232(16) |
| c (Å) | 17.4059(5) | 13.7629(5) |
| V (Å3) | 3445.57(19) | 4347.5(3) |
| Z | 4 | 2 |
| μ (mm−1) | 8.830 | 7.817 |
| T (K) | 175.0(1) | 150.0(1) |
| ρcalcd (g cm−3) | 1.668 | 1.463 |
| λ (Å) | 1.54184 | 1.54184 |
| Index ranges | −20 ≤ h ≤ 25 −11 ≤ k ≤ 9 −21 ≤ l ≤ 20 | −11 ≤ h ≤ 11 −40 ≤ k ≤ 41 −10 ≤ l ≤ 16 |
| Indep. reflect. (Rint) | 3543 (0.0340) | 4213 (0.1011) |
| Obs. reflect. [I > 2σ(I)] | 2876 | 3076 |
| Parameters | 248 | 295 |
| Goodness-of-fit | 1.098 | 1.038 |
| R [I > 2σ(I)] | 0.0843 | 0.0827 |
| Rw [I > 2σ(I)] | 0.2444 | 0.2092 |
| R (all data) | 0.0985 | 0.1126 |
| Rw (all data) | 0.2570 | 0.2336 |

A view of a fragment of 1 along with the atom numbering scheme. Thermal ellipsoids are drawn at the 50% probability level.
Intermolecular contacts in the form of parallel displaced π–π interactions between the pyim ligands of adjacent chains occur in 1 (the imidazole ring of a pyim ligand interacts with the pyridyl ring of an adjacent pyim group related by an inversion centre, the values of the centroid to centroid distance and offset angle being 3.4798(1) Å and 22.8(2)º, respectively). Considering this interaction, each chromium(III) ion is connected to another chromium(III) centre of an adjacent chain to build a supramolecular 3D (3,4)-connected [(4 × 102) (42104)]-dmd net (Fig. 2, and Figs. S1 and S2 in the Supplementary material). This 3D net is two-fold interpenetrating net of class Ia with an interpenetration vector of [010] and an internet separation of 9.53 Å. The methanol molecules are located in the vicinity of the pyim ligands, forming a hydrogen bond with the uncoordinated NH group [values of the N(3)⋯O(9) separation, N(3)–H⋯O(9) angle and H···O(9) distance of 2.665(13) Å, 175(1)º and 1.81(2) Å, respectively].
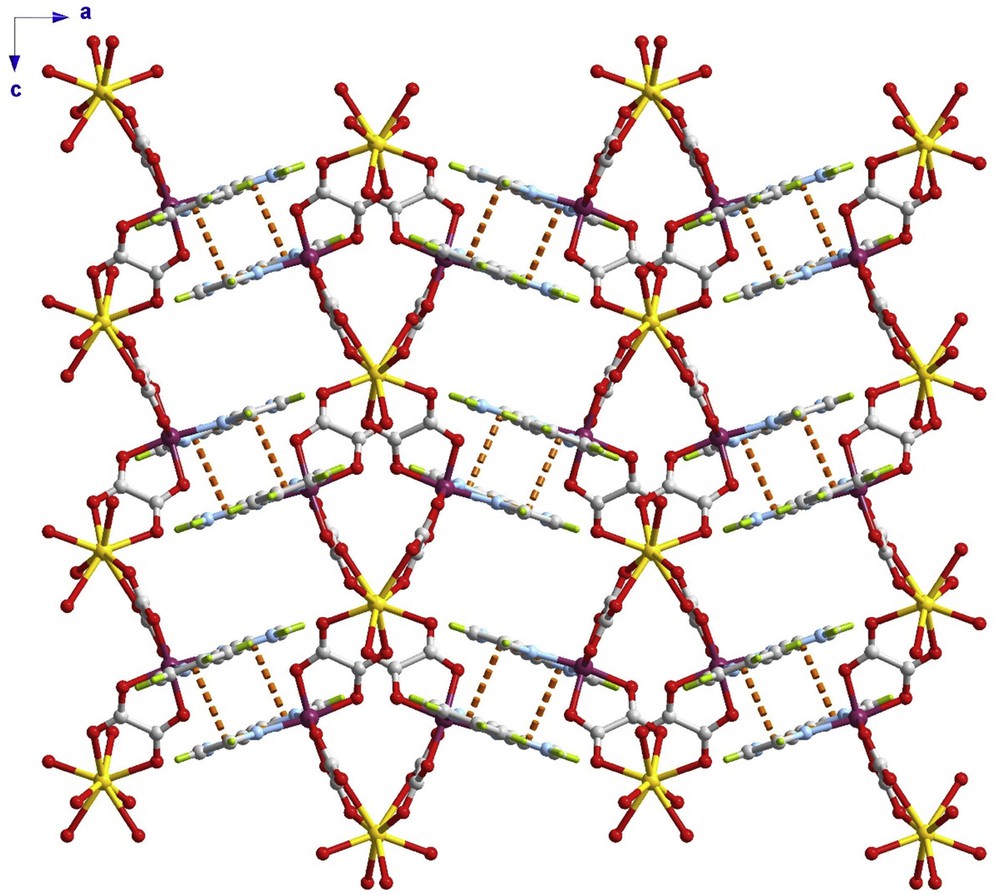
A view of the crystal packing of 1 along the crystallographic b axis. The dashed lines represent the π–π interactions and the solvent molecules are omitted for clarity.
Each chromium(II) ion in 1 exhibits a somewhat distorted octahedral environment, CrN2O4, which is defined by two nitrogen atoms from the chelating pyim molecule and four carboxylate-oxygen atoms from the two bridging oxalate ligands. The reduced values of the angles subtended at the chromium(III) ion by the pyim [80.7(5)º] and oxalate ligands [83.13(18)° and 83.03(18)°] are the main sources for the distortion from the ideal octahedron. The CrN(pyim) [1.962(9) and 2.057(12) Å] and CrO(oxalate) bond lengths [values in the range 1.959(4)–1.974(4) Å] (see Table 3) agree with the corresponding values in the mononuclear complexes XPh4[Cr(pyim)(ox)2]·H2O (X = P and As) and double chain compound {Ba(H2O)3/2[Cr(pyim)(ox)2]2}n.9/2nH2O [values covering the ranges 2.021(7)–2.101(3) (CrN(pyim)) and 1.941(3)–1.977(6) Å (CrO(oxalate))] [22]. The values of the trigonal twist angle (τ) at the Cr(1) atom is 54.8(2)º (τ = 0 and 60° for ideal trigonal prism and octahedron, respectively). This small distortion of the octahedral (Oh) metal environment towards trigonal prismatic (D3h) known as Bailar twist [33], is most likely due to the small value of the bite angle of the chelating pyim ligand. The crystallographically independent Mn(II) ion is eight-coordinate with eight oxygen atoms from four different oxalate groups building a distorted square antiprism whose upper and basal planes are constituted by the O(3)O(4)O(7d)O(8c) and O(3a)O(4a)O(7c)O(8d) sets of atoms, respectively [symmetry code: (a) = −x + 1/2, −y + 1, z; (c) = −x + 1/2, y, z − 1/2; (d) = x, −y + 1, z − 1/2]. The separation between these planes is 2.516(2) Å and the angle between them is 5.98(14))°.
| Cr(1)O(1) | 1.959(4) | O(1)–Cr(1)–O(5) | 91.47(18) | O(2)–Cr(1)–N(2) | 99.3(5) |
| Cr(1)O(2) | 1.974(4) | O(1)–Cr(1)–O(6) | 92.85(19) | O(5)–Cr(1)–O(6) | 83.13(18) |
| Cr(1)O(5) | 1.966(4) | O(1)–Cr(1)–N(1) | 167.4(4) | O(5)–Cr(1)–N(1) | 101.0(4) |
| Cr(1)O(6) | 1.966(4) | O(1)–Cr(1)–N(2) | 86.8(4) | O(5)–Cr(1)–N(2) | 169.2(5) |
| Cr(1)N(1) | 1.962(9) | O(2)–Cr(1)–O(5) | 91.13(18) | O(6)–Cr(1)–N(1) | 87.3(4) |
| Cr(1)N(2) | 2.057(12) | O(2)–Cr(1)–O(6) | 172.86(18) | O(6)–Cr(1)–N(2) | 86.3(5) |
| O(1)–Cr(1)–O(2) | 83.03(18) | O(2)–Cr(1)–N(1) | 98.0(4) | N(1)–Cr(1)–N(2) | 80.7(5) |
| Mn(1)O(3) | 2.359(4) | O(3)–Mn(1)–O(7d) | 124.12(17) | O(4)–Mn(1)–O(8c) | 104.77(17) |
| Mn(1)O(4) | 2.302(5) | O(3)–Mn(1)–O(8c) | 74.67(16) | O(4)–Mn(1)–O(8d) | 89.18(16) |
| Mn(1)–O(3a) | 2.359(4) | O(3)–Mn(1)–O(8d) | 148.08(16) | O(4a)–Mn(1)–O(7c) | 73.09(17) |
| Mn(1)–O(4a) | 2.302(5) | O(3a)–Mn(1)–O(4) | 79.24(17) | O(4a)–Mn(1)–O(7d) | 144.43(17) |
| Mn(1)–O(7c) | 2.552(5) | O(3a)–Mn(1)–O(4a) | 71.41(16) | O(4a)–Mn(1)–O(8c) | 89.18(16) |
| Mn(1)–O(7d) | 2.552(5) | O(3a)–Mn(1)–O(7c) | 124.12(17) | O(4a)–Mn(1)–O(8d) | 104.77(17) |
| Mn(1)–O(8c) | 2.179(4) | O(3a)–Mn(1)–O(7d) | 135.14(17) | O(7c)–Mn(1)–O(7d) | 71.70(16) |
| Mn(1)–O(8d) | 2.179(4) | O(3a)–Mn(1)–O(8c) | 148.08(16) | O(7c)–Mn(1)–O(8c) | 70.37(17) |
| O(3)–Mn(1)–O(4) | 71.41(16) | O(3a)–Mn(1)–O(8d) | 74.67(16) | O(7c)–Mn(1)–O(8d) | 74.45(17) |
| O(3)–Mn(1)–O(3a) | 76.9(3) | O(4)–Mn(1)–O(4a) | 142.3(2) | O(7d)–Mn(1)–O(8c) | 74.45(17) |
| O(3)–Mn(1)–O(4a) | 79.24(17) | O(4)–Mn(1)–O(7c) | 144.43(17) | O(7d)–Mn(1)–O(8d) | 70.37(17) |
| O(3)–Mn(1)–O(7c) | 135.14(17) | O(4)–Mn(1)–O(7d) | 73.09(17) | O(8c)–Mn(1)–O(8d) | 136.2(2) |
a Only one of the disordered pyim ligands has been taken into account.
b Symmetry code: (a) = −x + 1/2, −y + 1, z; (c) = −x + 1/2, y, z − 1/2; (d) = x, −y + 1, z − 1/2.
The two oxalate ligands in 1 are planar and they adopt the bis(bidentate) coordination mode. The average value of the CC bond length is 1.533(9) Å, in agreement with its single bond character. The CO bond distances of the bridging oxalate groups on the side of the chromium(III) ion are somewhat longer [average value 1.278(7) Å] than those at the manganese(II) centre [mean value 1.229(8) Å]. The bidentate pyim ligand is disordered between two positions, one with the imidazolyl on one side and its inverted with the imidazolyl on the other side. The pyim molecule as a whole is quasi-planar, the value of the dihedral angle between the pyridyl and the imidazolyl rings being 2.8(3)º.
The values of the chromium–manganese separation through the two different oxalate groups are 5.5233(14) [Cr(1)⋯Mn(1)] and 5.5735(14) Å [Cr(1)⋯Mn(1b)] [symmetry code: (b) = −x + 1/2, y, z + 1/2]. The interchain supramolecular connection through the π–π stacking of adjacent pyim molecules separates the chromium(II) ions by 7.4669(14) Å [Cr(1)⋯Cr(1e); (e) = −x + 1, −y, −z + 1], but the shortest interchain metal⋯metal distance occurs between the Cr(1) and Cr(1f) atoms [7.1099(14) Å; (f) = −x + 1/2, −y, z].
2.2.2 {[Cr(pyim)(ox)2]2Co(H2O)2}·7.5H2O (2)
Compound 2 crystallizes in the orthorhombic Pnma space group (Table 2), and its structure is made up of discrete linear oxalate-bridged neutral trinuclear entities and crystallization water molecules (Fig. 3). The central cobalt(II) ion sits on a mirror plane with two water molecules in trans-position, and it is linked to two peripheral [Cr(pyim)(ox)2]− entities through bis-bidentate oxalate ligands. This situation resembles that found in the related oxalate-bridged heterotrinuclear CrIII2CoII complex of formula {[Cr(bpy)(ox)2Co(H2O)2}.H2O [17a]. In this case, the two [Cr(bpy)(ox)2]− units coordinate to the trans-[Co(H2O)2]2+ cationic entities in a bidentate manner to give discrete CrIIICoII motifs with a crystallographically imposed Ci molecular symmetry and a collinear arrangement of the metal centres. The linear heterometallic trinuclear units in 2 are connected to the adjacent ones along the crystallographic b axis through a parallel displaced π–π interaction involving the pyim ligands. The imidazolyl ring interacts with the pyridyl ring of the adjacent pyim with an inversion centre between both groups [the values of the centroid to centroid separation and the offset angle are 3.787(2) Å and 28.7(2)º, respectively]. Considering this interaction, the trinuclear units in 2 are arranged in supramolecular chains along the crystallographic b axis, which are linked in turn to the neighbouring chains by hydrogen bonds involving the crystallization water molecules (Fig. 4 and Supplementary Fig. S3).
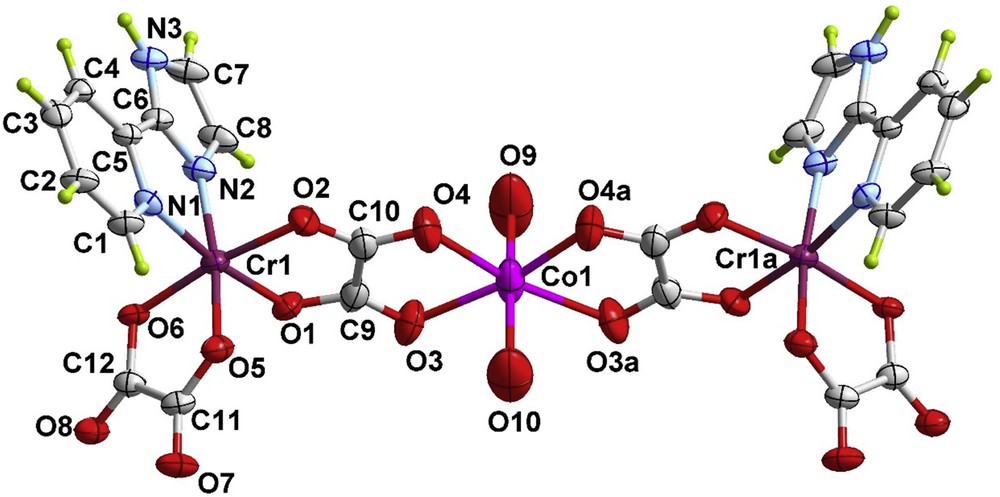
Perspective view of the heterometallic trinuclear unit of 2 along with the numbering scheme. The ellipsoids are drawn at the 50% probability level and the crystallization water molecules are omitted for clarity.

A view of the supramolecular chains of 2 along the [100] direction. The orange dashed lines stand for the π–π contacts between the pyim ligands.
The crystallographically independent chromium(III) ion is six-coordinate with two pyim-nitrogens and four oxygen atoms from two different oxalate groups building a somewhat distorted octahedral environment. The chelate angles at the chromium(III) ion are significantly smaller than those of an ideal octahedron, 79.88(19)º for the pyim and 82.97(17)º and 83.20(18)º for the oxalate groups (see Table 4), values which are similar to those observed in 1. The CrN(pyim) [2.039(5) and 2.073(5) Å] and CrO(oxalate) bond lengths [values in the range 1.953(4)–1.978(4) Å] also agree with those observed in 1. The value of τ at Cr(1) is 51.2(2)º. The six-coordinate cobalt(II) ion lays on a mirror plane with two coordinate water molecules in trans-position and four oxygen atoms from two different oxalate groups building a compressed octahedron. The average Co–O(water) bond length [2.007(13) Å] is significantly smaller than the mean value for the CoO(oxalate) bond distance [2.149(5) Å]. The bite angle of the oxalate groups at Co(1) arise as the main distortion from an ideal octahedron [78.44(19)º for O(3)–Co(1)–O(4)].
Selected bond distances (Å) and angles (degrees) for compound 2.a
| Cr(1)O(1) | 1.978(4) | O(1)–Cr(1)–O(5) | 91.85(18) | O(2)–Cr(1)–N(2) | 92.2(2) |
| Cr(1)O(2) | 1.969(4) | O(1)–Cr(1)–O(6) | 91.59(17) | O(5)–Cr(1)–O(6) | 82.96(17) |
| Cr(1)O(5) | 1.952(4) | O(1)–Cr(1)–N(1) | 171.80(19) | O(5)–Cr(1)–N(1) | 93.90(18) |
| Cr(1)O(6) | 1.964(4) | O(1)–Cr(1)–N(2) | 94.77(19) | O(5)–Cr(1)–N(2) | 172.5(2) |
| Cr(1)N(1) | 2.073(5) | O(2)–Cr(1)–O(5) | 92.02(19) | O(6)–Cr(1)–N(1) | 94.91(18) |
| Cr(1)N(2) | 2.040(5) | O(2)–Cr(1)–O(6) | 172.67(18) | O(6)–Cr(1)–N(2) | 93.37(18) |
| O(1)–Cr(1)–O(2) | 83.21(19) | O(2)–Cr(1)–N(1) | 90.74(19) | N(1)–Cr(1)–N(2) | 79.88(19) |
| Co(1)O(3) | 2.207(5) | O(3)–Co(1)–O(9) | 84.8(3) | O(4)–Co(1)–O(9) | 95.4(4) |
| Co(1)O(4) | 2.091(6) | O(3)–Co(1)–O(10) | 86.9(3) | O(4)–Co(1)–O(10) | 95.4(3) |
| Co(1)O(9) | 2.008(10) | O(3)–Co(1)–O(3a) | 113.6(3) | O(4)–Co(1)–O(4a) | 89.5(3) |
| Co(1)O(10) | 2.005(10) | O(3)–Co(1)–O(4a) | 167.9(2) | O(9)–Co(1)–O(10) | 164.8(6) |
| O(3)–Co(1)–O(4) | 78.44(19) |
a Symmetry code: (a) = x, −y + 2/3, z.
The two crystallographically independent oxalate groups in 2 are planar, and one of them [O(1)O(4)] adopts the bis-bidentate coordination mode and the other one [O(5)O(8)] acts as a bidentate ligand. The average CC bond length in them is 1.534(10) Å, a value similar to that observed in 1 and which is as expected for a single carbon–carbon bond. The values of the CO bonds linked to the cobalt(II) ion in the bis-bidentate oxalate are shorter [mean value of 1.242(8) Å] than those linked to the chromium(III) centre [average bond length 1.269(8) Å], as in 1. The coordinated oxygen atoms in the bidentate oxalate exhibit larger CO bond lengths [average value of 1.291(7) Å] than the uncoordinated ones [mean value of 1.223(7) Å]. The bidentate pyim molecule as a whole is not far from planarity, the value dihedral angle between the pyridyl and the imidazolyl ring being 2.5(2)º.
The value of the chromium(III)–cobalt(II) distance across the bis-bidentate oxalate is 5.3681(11) Å [Cr(1)…Co(1)], whereas the separation between molecules linked through the π–π interaction is 7.7005(14) Å [Cr(1)⋯Cr(1b); symmetry code: (b) = −x, −y + 1, −z + 1]. The shortest contact between the supramolecular chains concerns two cobalt(II) ions being 7.110(3) Å [Co(1)…Co(1c); (c) = x + 1/2, −y + 3/2, −z + 1/2].
2.3 Magnetic properties
The magnetic properties of 1 under the form of the χMT product against T plot [χM is the magnetic susceptibility per CrIII2MnII unit] are shown in Fig. 5. At room temperature, χMT is equal to 8.56 cm3 mol−1 K, a value which is somewhat greater than that expected for a set of one manganese(II) and two chromium(III) ions magnetically isolated (χMT = 4.375 + 2 × 1.875 = 8.125 cm3 mol−1 K with SMn = 5/2, SCr = 3/2 and gMn = gCr = 2.0. Upon cooling, χMT increases to reach a maximum value of 43.3 cm3 mol−1 K at 3.3 K, and then it abruptly decreases to 22.5 cm3 mol−1 K at 1.98 K. This plot is typical of an overall ferromagnetic behaviour, the slight decrease in χMT at very low temperatures being most likely due to weak interchain antiferromagnetic interactions. These features are corroborated by the magnetization per trinuclear unit (M) versus H plot (see Fig. S4). One can see therein how the value of M tends to a saturation value of 11.0 Nβ as expected for a spin state S = 11/2 resulting from the parallel alignment of two spin quadruplets and one spin sextet. No out-of-phase signals were observed in the alternating current (ac) susceptibility measurements.

Thermal dependence of the χMT product for 1: (o) experimental; (−) best-fit curve through Eqs. 1 and 2 (see text).
The lack of a theoretical model to analyze the magnetic data of 1 precludes the determination of the intrachain ferromagnetic interactions between the local quartet [chromium(III)] and sextet [manganese(II)] ions across the bis-bidentate oxalate. Furthermore, the analysis of the experimental magnetic behaviour in systems exhibiting different magnetic exchange couplings, a zero-field splitting (zfs) in one or several of the present metal ions and possible intermolecular interactions turns into a difficult or even a non-manageable task, in particular in ferromagnetic extended systems. Additional data can help to make possible that study. In an attempt to provide extra useful information on this system, DFT calculations were performed on 1. It deserves to be noted that two crystallographically independent bis-bidentate oxalate ligands occur in this compound. So, the coordination of the oxalate is symmetrical enough with long MnO bond lengths but quite close [ca. 2.30 and 2.36 Å for Mn(1)O(4) and Mn(1)O(3), respectively] through a magnetic pathway, whereas this coordination breaks this symmetry with a shorter [ca. 2.18 Å for M(1b)-O(9)] and a longer (2.55 Å for Mn(1b)-O(7)] manganese to oxalate bond lengths across the other intrachain exchange pathway. Consequently, two different magnetic couplings (J1 and J2) coexist along each CrIII2MnII double chain (see Scheme 1).
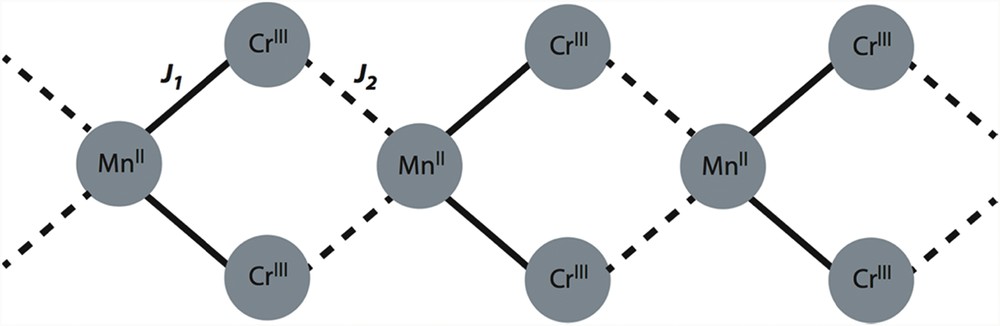
Topology of the spin coupling for each double chain in 1.
However, a detailed inspection of the structure of 1 reveals that the situation is a bit more complicate. In fact, the peripheral N,N′-donor ligand has two different coordinating groups, an imidazolyl ring and a pyridyl ring, and each one can induce a different electronic donation to metal ion, which can influence the magnetic coupling. Curiously, the imidazolyl alternates with pyridyl between neighbouring double chains to occupy the coordination site that is opposite to the longer MnO bond length. Thereby, two different magnetic double chains should be considered in the study. Details about the building of the 1a and 1b models corresponding to these two double chains (see Fig. 6) are given in Section 4. A summary of the some relevant structural parameters for each magnetic coupling and the found theoretical values of the magnetic coupling constants are shown in Table 5. The most significant feature of our theoretical calculations is that all of the calculated magnetic couplings are ferromagnetic in agreement with the experimental observation. Although, there are some differences between two double chains promoted by the different arrangement of the pyridyl and imidazolyl groups, they are small and they can be obviated in the simulations of the magnetic data. More different are the two magnetic coupling constants (J1 and J2) present in a same chain, the somewhat stronger interaction corresponding to the shorter intrachain chromium–manganese separation. Anyway, one first approach considering them equivalent could provide good simulations. As far as the ferromagnetic nature of the interaction between Cr(III) and Mn(II) ions through the oxalate ligand is concerned, it is a well known situation and it is associated with the weakness and strength of the antiferromagnetic t2g–t2g and ferromagnetic t2g–eg contributions, respectively [11a,34].
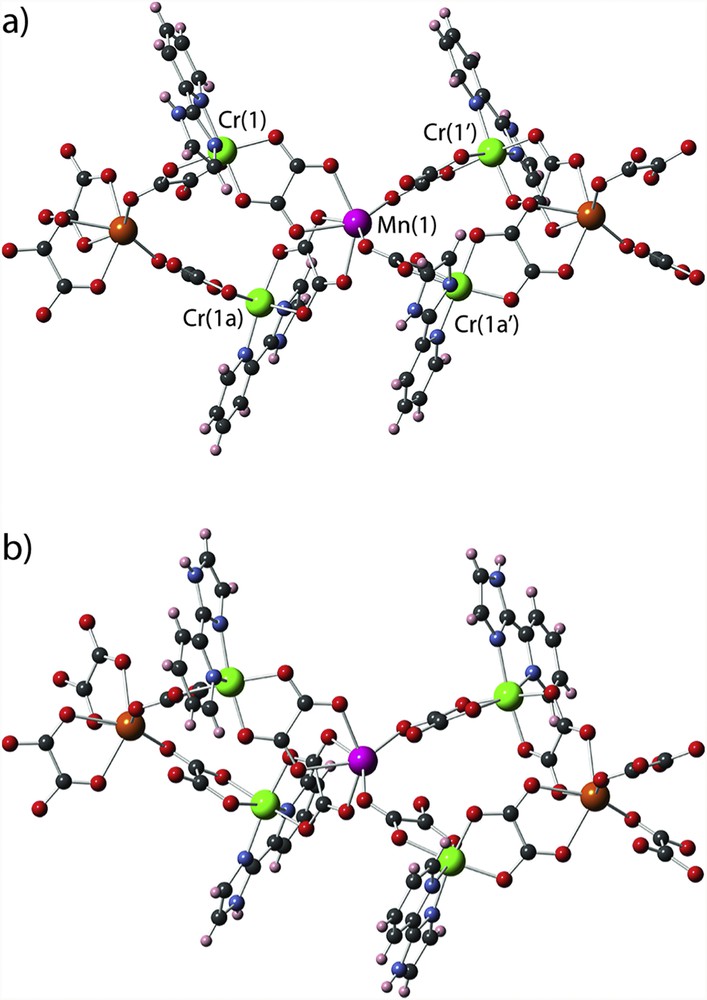
Structural models 1a (a) and 1b (b) used in DFT calculations to evaluate the magnetic coupling constants in 1. Colour code: orange (manganese), green (chromium), blue (nitrogen), red (oxygen), black (carbon) and grey (hydrogen).
Selected magnetostructural data for 1.
| Ji | (Cr⋯Mn) (Å) | d(Mn-O) (Å) | d(CrO) (Å) | J (cm−1) |
| J1 | 5.574 | 2.180/2.552 | 1.966/1.966a | +0.66 |
| J2 | 5.523 | 2.302/2.360 | 1.974/1.959b | +0.96 |
| J1′ | 5.574 | 2.180/2.552 | 1.966/1.966b | +0.58 |
| J2′ | 5.523 | 2.302/2.360 | 1.974/1.959a | +1.19 |
a Bond in trans to the Cr–Nimidazolyl.
b Bond in trans to the Cr–Npyridyl.
The simulation of the magnetic data of a ferromagnetic double chain with intermolecular or dipolar interactions is not an easy task. In this respect, there is no analytical model to study the first component, that is, the CrIII2MnII double chain. For this purpose, the derivation of an analytical law for this starting unit will be our first step. To that effect, the use of a method based on an effective spin Hamiltonian is a good alternative, as some of us have shown in the past [35]. This method, which is based on the exact solution of the individual unities that are a part of the extended system, allows to obtain information about their spin functions and the effective global spin momentum and magnetic coupling, parameters that are used later to be coupled along an extended system. The individual unity used in the simulations with the method based on the effective spin Hamiltonian is shown in Fig. 7.

Scheme of the individual unity used in the simulations with the method based on the effective spin Hamiltonian.
Having this in mind, the system turns into a regular ferromagnetic chain of {CrIII2MnII}2 unities with very large effective spin that can be considered as vectors, that is, as classical spin momenta. Hence, the Fischer law for a chain of classical spins can be used to simulate the magnetic behaviour of 1, considering that the {CrIII2MnII}2 unities show an effective spin (Seff) and that they are coupled through an effective coupling (Jeff), both parameters being temperature dependent. The obtained simulations were compared with those found for us from Quantum Monte Carlo, Classical Monte Carlo (CMC), where the spin momenta are considered as classical momenta that are appropriate for long local S values, and exact solutions for a ring made up of three CrIII2MnII unities (Fig. S5). The approach of the effective Hamiltonian was able to reproduce the results of other methods until where they are suitable and further away. The found analytical law considering an identical g value for Mn(II) and Cr(III) ions and a regular magnetic system, that is, only one magnetic coupling (in K) is given by Eq. 1
| (1) |
| (2) |
The magnetic properties of 2 under the form of the χMT product against T plot [χM is the magnetic susceptibility per CrIII2CoII unit] are shown in Fig. 8. At room temperature, χMT is equal to 6.60 cm3 mol−1 K, a value a which is somewhat greater than that for the sum of two chromium(III) ions (χMT = 2 × 1.875 cm3 mol−1 K with SCr = 3/2 and gCr = 2.0) and one octahedral high-spin cobalt(II) ion with a partially quenched orbital momentum (χMT = 2.48 with SCo = 3/2 and gCo = 2.3). Upon cooling, χMT increases to reach a maximum of 7.43 cm3 mol−1 K at 6.5 K, and then it abruptly decreases to 5.85 cm3 mol−1 K at 1.9 K. This plot is typical of the occurrence of an overall weak ferromagnetic behaviour in 2, the decrease in χMT at the low temperature domain being due to zfs effects and/or weak intermolecular interactions. The maximum of the χMT value is well below the expected one for an S = 9/2 ground state resulting from the intramolecular ferromagnetic coupling between the two spin quartets of the outer chromium(III) ions and the inner high-spin cobalt(II) ion [χMT = (Nβ2g2/3k)S(S + 1) = 12.4 cm3 mol−1 K with g = 2.0]. The M versus H plot per trinuclear unit of 2 in the temperature range 2.0–10 K (see Fig. S6) exhibits a magnetization of 7.30 Nβ at 6 T and 2.0 K, a value which is consistent with that predicted for a parallel alignment between a high-spin Co(II) centre (Seff = 1/2 and g ca. 4.2) [37] and two chromium(III) ions (S = 3/2, gCr = 2.0). No out-of-phase ac signals were observed in the ac susceptibility measurements for 2.

Thermal dependence of the χMT product for 2: (o) experimental; (−) best-fit curve through Eq. 3 (see text).
The analysis of the magnetic susceptibility data of 2 was carried out by full-matrix diagonalization [38] of the spin Hamiltonian for a trinuclear model that takes into account the local axial zfs of the cobalt(II) ion through Eq. 3
| (3) |
The values of the weak intramolecular ferromagnetic coupling between the inner high-spin manganese(II) (1) and cobalt(II) (2) and the outer chromium(III) ions are similar to those observed in other related oxalate-bridged Cr(III)Mn(II) and Cr(III)Co(II) complexes [9a,11a,28c,d,29a,c,34,39]. Aiming at comparing the values of J from both compounds, one has to take into account the number of unpaired electrons (magnetic orbitals) on each pair of interacting paramagnetic centres. So, the experimental J parameter must be decomposed into a sum of individual contributions, Jμν, involving each pair of magnetic orbitals implicated in the exchange process (Eq. 4) [40]
| (4) |
We would like to finish this contribution with an analysis about the fact that the fit of models to the experimental data where ferromagnetic couplings, notable zfs and intermolecular interactions (case of 2) are not evident and sometimes data can be reproduced with several sets of parameters. This occurs because some factors play in opposite directions and also the way that they are correlated increasing or decreasing together. Thus, additional evidence is very useful. Because of this, we decided to perform DFT type calculations on the real structure of 2 in an attempt to evaluate the intramolecular magnetic coupling (see Section 4 for more details). A magnetic interaction of J = +3.5 cm−1 was obtained for 2 through these calculations, its ferromagnetic nature being thus confirmed. Also its magnitude is very close to that obtained by the previous fit of the magnetic data.
DFT calculations of the parameters of the zfs on a GaIII2CoII model built from the experimental geometry of 2 where the CrIII ion was replaced by a diamagnetic GaIII ion were also carried out, the results of which are summarized in Table 6. A positive local D value (DCo = +5.24 cm−1) with a plane of easy magnetization and a moderate rhombicity (E/D = 0.070) were determined through these calculations. Similar calculations on the Cr2IIICoII model for the ferromagnetic ground state (S = 9/2) provide a value of D (D = +0.56 cm−1 and E/D = 0.084) that agrees with the expected value derived from the local DCo calculated through the equation proposed by Bencini and Gatteschi, DS = 9/2 = (2DCr + DCo)/12(DCr being neglected)[41].
Estimated values of D (in cm−1) and the E/D ratio (in parenthesis) for the GaIII2CoII and CrIII2CoII models calculated from the coupled perturbed (CP) and Pederson–Khanna (PK) methods, as well as that based on quasi-restricted orbitals (QROs) applied on the wavefunctions obtained with the Perdew-Burke-Ernzerhof (PBE) functional.
| Model | PK | CP | QRO |
| GaIII2CoII | 5.26 (0.072) | 5.24 (0.070) | 8.33 (0.087) |
| CrIII2CoII | 0.56 (0.084) | 0.56 (0.082) | 0.78 (0.087) |
It is well known that the values of D in octahedral cobalt(II) complexes calculated by the DFT methodology are often much smaller than the real ones, in contrast to what occurs through post-Hartree Fock, complete active space (CAS) and second-order N-electron valence state perturbation theory (NEVPT2) calculations. Unfortunately, these types of calculations are highly limited by the size of the system, that is, by the number of the involved orbitals in the construction of the ground state and the low-lying excited ones. However, it is possible to obtain the values of D and E/D in the GaIII2CoII model. The value found for D through NEVPT2 (D = +67.6 cm−1; see Table 7) is well above that obtained by DFT and very close to the experimental ones in the literature, the positive sign being kept.
Estimated values of D (in cm−1) and the E/D ratio (in parenthesis) for the GaIII2CoII model calculated from a second-order perturbative spin–orbit coupling Hamiltonian applied to the CAS and NEVPT2 wavefunctions.
| Model | CAS | NEVPT2 |
| GaIII2CoII | +91.5 (0.071) | +67.6 (0.021) |
| CrIII2CoIIa | +9.8 | +7.2 |
a D values obtained from the results on the GaIII2CoII model applying the D(CrIII2Co)/D(GaIII2Co) ratio found by DFT methods.
Taking advantage of the relationship between the CrIII2Co and GaIII2Co models found by means of the DFT study, a positive D value about +7.2 cm−1 for the ground state S = 9/2 should be expected. For this calculation, one could use the equation proposed by Bencini and Gatteschi [41], but it does not take into account the contributions from the magnetic interactions to the zfs; moreover, it considers that the tensors of the zfs are collinear. Given that the computational performances have been largely improved nowadays, we have preferred to use the ratio obtained by DFT calculations between the local and global D values for the GaIII2CoII and CrIII2CoII models that take into account all of the effects mentioned previously.
3 Conclusions
Two new heterobimetallic compounds, the double chain of formula {[Cr(pyim)(ox)2]2Mn}n·2nCH3OH (1) and the trinuclear compound {[Cr(pyim)(ox)2]2Co(H2O)2}·7.5H2O (2), were synthesized by the programmed one-step reaction of the [Cr(pyim)(ox)2]− metalloligand towards the fully hydrated manganese(II) (1) and cobalt(II) ions (2). Cryomagnetic studies reveal the occurrence of ferromagnetic interactions between the chromium(III) centre and the manganese(II) (1) and high-spin cobalt(II) (2) ions across the oxalate bridge. Electronic structure calculations based on the DFT were performed for 1 and 2 to substantiate the values of their magnetic interactions in both complexes whose sign and magnitude were substantiated by theoretical calculations. Calculations of the axial zfs parameter D (see Section 4.4) and rhombicity (E/D) of 2 were carried out through different methodologies applied on CrIII2CoII and GaIII2CoII models.
4 Experimental section
4.1 General
All chemicals used were of reagent grade quality. They were purchased from commercial sources and used as received. The pyim molecule and the PPh4[Cr(pyim)(ox)]·H2O complex were prepared by following previously reported procedures [22a,42].
4.2 Preparations
4.2.1 {[Cr(pyim)(ox)2]2Mn}n·2nCH3OH (1)
PPh4[Cr(pyim)(ox)]·H2O (0.25 mmol, 0.19 g) and LiClO4 (0.25 mmol, 0.25 g) were dissolved in 5 cm3 of methanol for a few minutes. The resulting deep purple solution was filtered to remove the PPh4ClO4 salt, which separated as a white solid. [Mn(H2O)6](ClO4)2 (0.5 mmol, 0.13 g) dissolved in 5 cm3 of methanol was placed at the bottom of a test tube and the filtered deep purple solution was layered on the top of the tube. Deep purple parallelepipeds of 1, which were suitable for X-ray diffraction, were grown after a few days of slow diffusion at room temperature. The crystals of 1 were collected by filtration and air-dried. Yield [based on the chromium(III)]: 0.20 g (91%).
4.2.2 {[Cr(pyim)(ox)2]2Co(H2O)2}·7.5H2O (2)
PPh4[Cr(pyim)(ox)]·H2O (0.25 mmol, 0.19 g) and LiClO4 (0.25 mmol, 0.25 g) were dissolved in 5 cm3 of methanol for a few minutes. The resulting deep purple solution was filtered to remove the Ph4ClO4 precipitate. Afterwards [Co(H2O)6](ClO4)2 (0.5 mmol, 0.19 g) dissolved in 20 cm3 of water was added to the previous filtered solution under continuous stirring and allowed to evaporate at room temperature. Deep red parallelepipeds of 2 were grown after a couple of days. They were collected by filtration and air-dried. Yield [based on the chromium(III)]: 0.24 g (95%).
4.3 Physical techniques
FTIR spectra (KBr pellets) were performed with a Nicolet 5700 FTIR instrument (4000–450 cm−1). Elemental analyses (C, H, N) were performed at the Servicio Central de Soporte a la Investigación from the Universitat de València (Spain). A value of 2:1 for the Cr/M [M = Mn (1) and Co (2)] molar ratio was determined through electron probe X-ray microanalysis by using a Philips XL-30 scanning electron microscope from the Central Service for Support to Experimental Research at the University of Valencia. The magnetic susceptibility of polycrystalline samples of 1 and 2 were measured with a Quantum Design SQUID device from 1.9 to 295 K using applied magnetic fields of 0.5 T (T > 30 K) and 250 G (T ≤ 30 K). The measurements of ac magnetic susceptibility were performed at low temperatures in the frequency range 0.1–1400 Hz and under an oscillating magnetic field of ±5 G. Diamagnetic corrections of the constituent atoms were estimated from Pascal's constants [43] and found to be −348 × 10−6 (1) and −428 × 10−6 cm3 mol−1 (2) [per CrIII2MII unit)]. Corrections for the sample holder (a plastic bag) were also applied.
4.4 Computational details
DFT calculations were carried out through the Gaussian 09 package to estimate the magnitude of the magnetic coupling between the magnetic centres [44]. These calculations were performed with the Coulomb-Alternating Method Becke, 3-parameter, Lee-Yang-Parr (CAM-B3LYP) hybrid functional, the quadratic convergence approach and a guess function generated with the fragment tool of the same program [45–47]. Triple-ζ and double-ζ all-electron basis sets proposed by Schäfer et al. were used for the metal and the rest, respectively [48,49]. The magnetic coupling states were obtained from the relative energies of the broken-symmetry singlet spin state from the high-spin state with parallel local spin moments. More details about the use of the broken-symmetry approach to evaluate the magnetic coupling constants can be found in the literature [50–52]. A polarizable continuum model was introduced in the calculations with the parameters corresponding to the acetonitrile [53]. Because compound 1 is a 1D system, we have built a model from the experimental geometry and considering only one fragment that includes one different kind of magnetic exchange couplings that are in gear. To avoid electronic effects from the building of the molecular model, the next neighbour metal centres [Mn(II] ions) and their coordination spheres were also considered, but they were replaced by diamagnetic Zn(II) ions. In fact, despite the intermetallic distances kept constant for different chains in the crystal structure of 1, a subtle structural difference associated with the arrangement of the peripheral ligand allows distinguishing them, being this the cause of the use of two models, 1a and 1b (Fig. 6).
Compound 2 is constituted by two Cr(III) ions connected to a Co(II) ion through an oxalate bridging ligand. The last ion in octahedral surrounding usually exhibits large zfs. Therefore, calculations were carried out with version 4.0 of the ORCA programme [49,54] to figure the values and sign of axial (D) and rhombic (E) components of the zfs tensor. The TZVP basis set proposed by Schäfer et al. [48,49] and the auxiliary TZV/C Coulomb fitting basis set were used in this study [55–57]. The CAS multiconfigurational method and subsequent NEVPT2 allows us to evaluate accurately the components of the zfs on cobalt(II) complexes. However, the evaluation of the CAS wavefunction for the ground state and the necessary excited states is out of our computational capabilities, but it was possible to evaluate the zfs tensor only for the Co(II) ions replacing the Cr(III) ions by the diamagnetic Ga(III) ones. The second-order contributions to zfs were evaluated for five quintets and 30 triplet excited states generated from an active space with four electrons in five d orbitals. The g-tensors for the spin ground state were calculated using multireference configuration interaction wavefunctions with a first-order perturbation theory on the spin-orbit coupling (SOC) matrix [58]. Methods based on the DFT were also used to calculate the components of the zfs tensor on the Ga2Co models. For this purpose, resolution of the identity approximation with the auxiliary TZV/J Coulomb fitting basis sets and the PBE functional were used. The spin–orbit and spin–spin coupling operators were based on the spin-orbit mean field (SOMF) scheme [59]. Coupled perturbed, Pederson–Khanna methods, and that based on quasi-restricted orbitals were used in the calculation of the spin–orbit contribution of the zfs [60]. These methods provide less accurate values of the zfs tensor, but they supply correct trends when results on different systems are compared. On other hand, they are able to evaluate the zfs tensor of long models, in our case on the ground state of the CrIII2CoII model. The ratio between the D values obtained from the PBE functional on the GaIII2CoII and CrIII2CoII models can be applied on NEVPT2 results on the GaIII2CoII model to obtain a more realistic estimation for 2. The magnetic coupling constant was calculated from the energies of the high-spin configuration (S = 9/2, EHS) where all local magnetic moments exhibit an equal alignment and that with the local spin moment on the Co(II) ion opposed to those on the Cr(III) ions (S = 3/2, E1), being EHS–E1 = 12 J.
4.5 X-ray data collection and refinement
Diffraction data on single crystals of 1 and 2 were collected with an Agilent Supernova μ-focus diffractometer at 175.0(1) (1) and 150.00(2) K (2) using Cu radiation (λ = 1.54184 Å). Crystal parameters and refinement results for 1 and 2 are listed in Table 2. The data collection was carried out with ω scans in the 4.26–76.11 (1) and 5.05–70.74° (2) θ ranges. Data were indexed, scaled and integrated using the Agilent CrysalisPro software [61]. The structures of 1 and 2 were solved by direct methods and refined with full-matrix least-squares technique on F2 including all reflections and using the SHELXS-2013 and SHELXL-2013 programs [62] included in the WINGX software package [63]. All non-hydrogen atoms were refined anisotropically. The hydrogen atoms were geometrically positioned and refined using a riding model, except those of the water molecules, which were neither found nor set. The pyim and the solvent ethanol molecules in 1 are disordered between two positions, the site occupancy factor (s.o.f.) were refined giving 0.618(5) for one location and 0.382(5) for the other, and also some restraints were applied to the anisotropic displacements. In the structure of 2, the water molecules of crystallization were disordered and the occupation factors were refined until converge and then fixed. The final geometrical calculations and the graphical manipulations were carried out with DIAMOND program [64]. Selected bond lengths and angles are given in Table 3.
Acknowledgements
Financial support was received from the Spanish Ministerio de Ciencia e Innovación (MCIIN) through Projects CTQ2016-75068P and CTQ2016-75671P and Unidad de Excelencia María de Maetzu MD2015-0538, MAT2014-57465-R and MAT2017-89207-R. F.R.F.P. and J.V. thank the MCIIN for predoctoral grants. C.R.P. is thankful for a visiting professorship at the Universitat de València.
Appendix A Supplementary data
The following are the Supplementary data to this article:
Drawings of the crystal packing of 1 and 2 (Figs. S1–S3), magnetization plots for 1 and 2 (Figs. S4 and S7), simulation of the magnetic behaviour of 1 (Fig. S6) and a table of the calculated spin configurations and their relative energies for a Cr4Mn model of 1 (Table S1). All details concerning the unit cell and structure determination of 1 and 2 were grouped in a data set. The files containing such data (CIF file), except structure factors were deposited with the Cambridge Crystallographic Data Centre as supplementary publication numbers 1524199 and 1524200 for 1 and 2, respectively. Copies of the data can be obtained free of charge on application to CCDC, 12 Union Road, Cambridge CB21EZ, UK (fax: +44 1223 336 033; e-mail: deposit@ccdc.cam.ac.uk).


