1. Introduction
In 1887, the discovery of the photoelectric effect by Hertz [1] gives the basis of the X-ray Photoelectron Spectroscopy (XPS) or electron spectroscopy for chemical analysis (ESCA). The first use of XPS to investigate surface properties was made by Siegbahn in the mid-1960s [2] and led to numerous breakthroughs in physics [3, 4] as well as in nanochemistry later on [5, 6]. Now, XPS spectroscopy has become a relatively simple and increasingly routinary technique for the compositional and chemical state analysis of surfaces [7, 8].
In medicine, XPS spectroscopy brings valuable information in different specialities. On the surface of biomaterials, XPS spectroscopy is able to give an identification and a quantification of possible contaminants [9]. XPS spectroscopy may also describe the covalent attachment of adhesive peptides used to enhance osteoblast adhesion on titanium implants and prostheses [10]. Lastly, it is worth to underline that pathological [11, 12, 13] as well as physiological calcifications and biologically interesting phases [14, 15, 16, 17, 18, 19, 20, 21, 22] have been investigated through XPS spectroscopy to characterize either the very first steps of their pathogenesis [23, 24] or the process of bone formation.
The aim of this publication is to present recent results obtained in the field of biomaterials and pathological calcifications by means of XPS spectroscopy, and to discuss the perspectives of the method. To attain this goal, we will start by a brief (more details can be found in different excellent books or reviews [25, 26, 27, 28, 29]) description on the basic principles of XPS, followed by a presentation of the computational techniques available nowadays for the calculations of theoretical XPS spectra of materials. The second part, namely XPS for the clinician, is dedicated to the medical community. Through different examples, we try to show that XPS is a strong and very useful tool which has a crucial place in medical research.
2. Basic elements of XPS spectroscopy
Like other characterization techniques namely X-ray diffraction or X-ray fluorescence [30, 31, 32, 33], XPS uses X-ray photons as a probe. While X-ray diffraction and X-ray fluorescence involves incident photons of high energy and the detection of photons, XPS spectroscopy uses low-energy (∼1.5 keV) X-rays and is based on the detection of photoelectrons emitted from the sample [6, 7, 8, 9, 10]. It is the measurement of the kinetic energy of these photoelectrons emitted from the surface which yields information on the electronic states of atoms present at the surface.
Ek, the kinetic energy of the emitted photoelectron is given by the Einstein equation: Ek = h𝜈 − EB −𝜑s where EB is the binding energy of an electron in its initial state in the atom, h𝜈 is the energy of the X-ray photon and 𝜑s is the work function of the sample. From the known h𝜈 and the measured Ek, the binding energy of the element EB is obtained. It is worth to notice that in a XPS spectra, a second family of electrons coming from the surface, Auger electrons [7, 34, 35, 36, 37], gives rise to additional peaks. The emission of Auger electrons happens after the photo-absorption and the emission of the photoelectron which created a vacancy. An electron from a higher energy (corresponding to an electronic transition between 2s and 1s state on Figure 1b) releases energy able to expulse an electron (2s on Figure 1b). Such an Auger electron is emitted with a kinetic energy that is independent of the X-ray energy.
Schematic representation related to the different steps of the photoelectron and Auger electrons emission.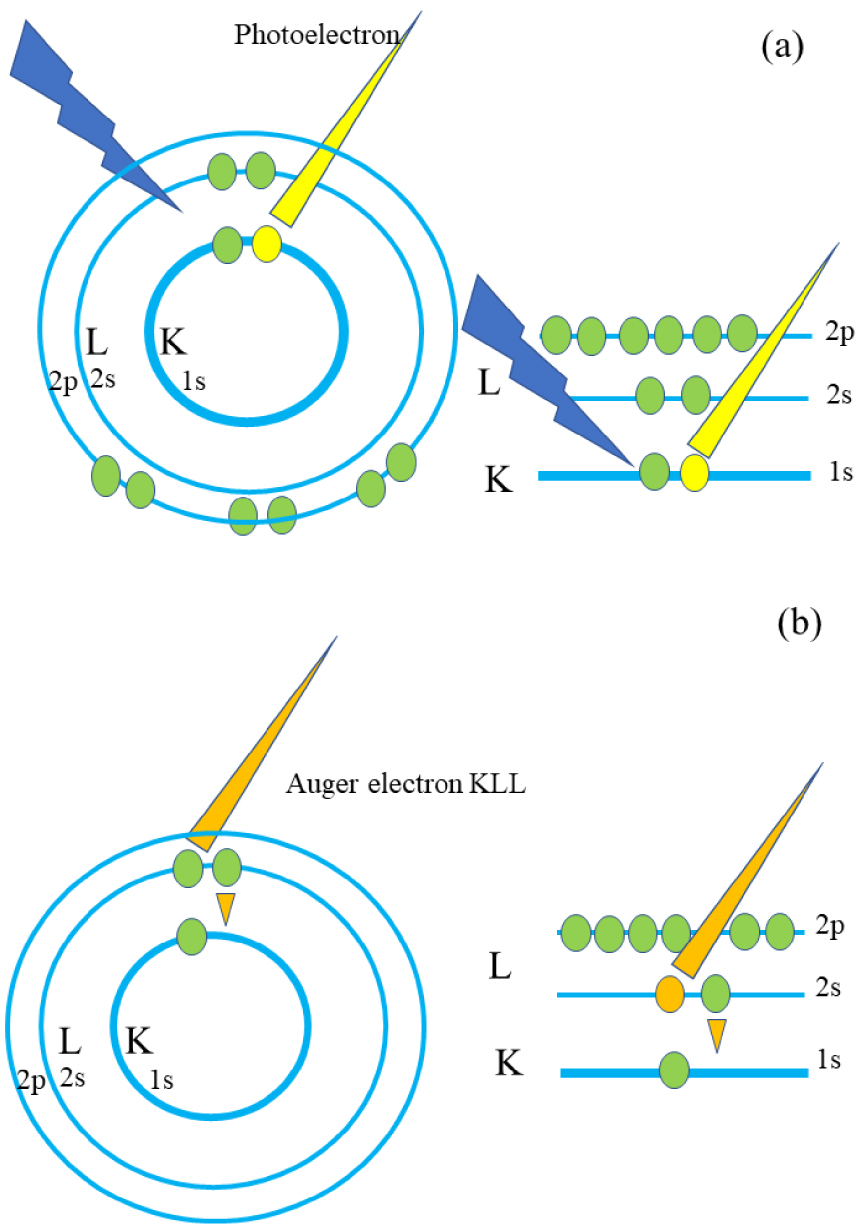
From an experimental point of view, XPS spectroscopy can be considered as in lab experiment. Clinicians have to consider this technique through intimate collaboration with physical chemists in order to discuss the preparation procedure of the sample taking into account working under vacuum and the nature of the surface. Shard [38] have discussed different points that should be considered to obtain reliable and meaningful information from quantitative XPS encompassing the necessity for reference data as well as a consistent and methodical method for the separation of inelastic background from peaks. In a classical XPS experiment (Figure 2), the incident monochromatic photons beam is given by aluminum (h𝜈 = 1486.6 eV) or magnesium (h𝜈 = 1253.6 eV) K𝛼.
(a) Schematic view of the photoelectron spectrometer with a hemispherical electron energy analyzer. (b) By changing the geometry, it is possible to modulate the thickness of the sample which is analyzed.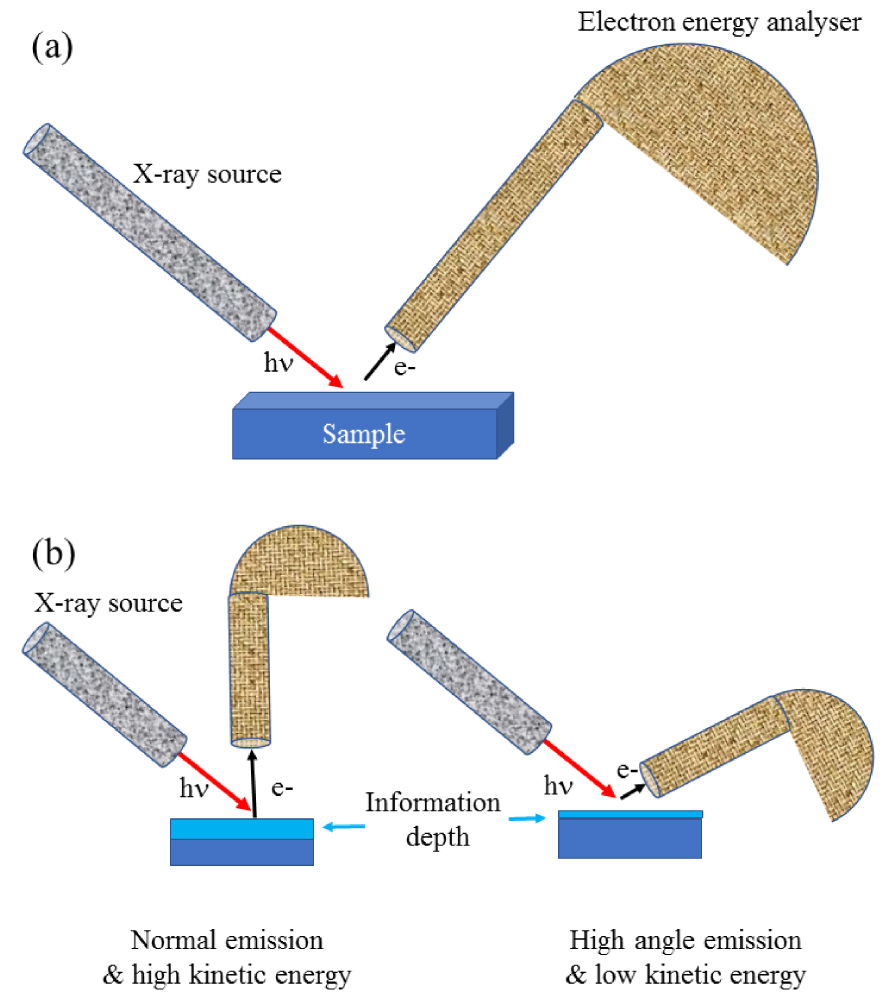
As pointed out by Vohrer et al. [39], experimental developments lead to micro or small spot-XPS systems with near-micron spatial resolution. The analysis of the photoelectron energy implies that the sample is placed in a vacuum chamber, under the best vacuum conditions achievable, typically ∼10−10 torr. Regarding the detection, the binding energies of electrons detected are measured in electron-volts (eV) with an accuracy of ±0.1 eV. The most common type is the electrostatic hemispherical analyzer consisting of two concentric hemispheres [40]. Note that it is possible to modulate the thickness of the sample which is analyzed through a modification of the experimental conditions.
One of the major advantages of XPS spectroscopy comes from the fact that this spectroscopy provides information on almost all the elements in the Periodic Table (except hydrogen and helium). At this point, it is worth to underline that while X-ray fluorescence is limited to the identification and the quantification of elements present in the sample [31, 32, 41, 42], high resolution scans of the XPS peaks can differentiated elements of the same kind but with different states and environments.
Another major advantage comes from the fact that photoelectrons are emitted from the very top surface (1–10 nm) of any solid surface. Such advantage can be easily understood from the following equation which gives the probability, p, that a photoelectron escapes from the sample without losing energy. In this equation, 𝜆e(E) is defined as the photoelectron inelastic mean free path and 𝜃 the angle between the incident beam and the normal of the surface
3. Computational tools for the computation of XPS spectra: first principles calculations
In this paragraph we summarize the fundamental physics behind XPS, illustrated with some theoretical calculations and studies used in the interpretation and prediction of experimental XPS data. After having introduced the theoretical formalism, we provide an overview on the techniques for the computation of theoretical XPS spectra that can provide a full rationalization of XPS experiments on biological materials.
The use of theoretical chemistry computational tools to help in the characterization of biological materials timidly but firmly starting to become the state-of-the-art [43, 44]. Theoretical chemistry which is already omni-present in materials science and which is expected to break open the limits of materials design known up till now will continue to obtain a dominating position thanks to the evolution of the computing power and algorithms. Artificial intelligence, machine learning, neural network calculations etc. are the tools that will enable to solve the complex calculations behind the fundamental laws of physics at the level of the atom and electrons of matter.
Today, we are not yet at this point but this revolution in scientific working protocols is slowly arriving at its aim. The theoretical chemistry-based computations applied on systems of interest by the clinician are still scarce, but some methods can be used already. Especially, on biological mineralisation samples some work has been performed [45, 46, 47, 48].
Typically, structural parameters such as unit cell parameters and atomic coordinates are optimized, but also spectroscopic data (IR and Raman spectra) can be simulated [49, 50]. These simulated data are then a very valuable source of data for comparison with experimental data for the interpretation of the spectra. The models itself provide a molecular picture of the material. Diffraction (X-ray, neutron and electron) patterns are also available thanks to the structural optimisations [51].
However, other spectroscopies, such as XPS are less calculated in general. Some studies are dedicated on the calculation strategies, and/or applied to some specific families of materials. In what follows we would like to give an overview on the methods used in materials modelling science and provide some applications of them, which hopefully will inspire the modelling community to apply XPS on materials of biological interest.
XPS spectroscopy has been widely employed in the field of heterogeneous catalysis since its capability in probing changes in the local bonding environments of atoms at the boundaries between solid surfaces and other media along a reaction process e.g. adsorption and surface reconstruction phenomena [52, 53, 54]. The complexity of the surface chemistry, characterized by a broad spectra of surfaces sites each one with a specific interaction with the substrates and molecules, makes the interpretation of XPS experimental spectra often not straightforward and univocal. Computational approaches able to assign the different components of the XPS spectra to groups of atoms with specific chemical environments are therefore mandatory for the full rationalization of XPS experiments.
The binding energy BE of a given electronic level can be expressed as the energy difference between the initial N electron non-ionized state and the N − 1 electron final ionized state:
The BE can be calculated with different degrees of approximation. When the electronic density is considered frozen, not free to relax in response to the ionization of the system, the BE can be expressed as the negative value of the orbital energy −𝜀i (Koopmans theorem) from which the electron is removed. This is known as Frozen Orbital (FO) approach. In the FO approach the BE is calculated as the difference between the neutral ground state HF (Hartree–Fock) energy and the ionized system HF energy obtained by the HF orbitals of the neutral system.
Absolute BEs cannot be predicted by density functional theory (DFT) calculations since the Koopmans theorem does not hold for Kohn and Sham (KS) orbitals, as recently shown by Pueyo Bellafont et al. [55]. Conversely, DFT calculations in the FO approach have been shown to reflect the experimental trends in Core level binding energy shifts (𝛥BEs) for a series of gas phase molecules [55]. The BEs and 𝛥BEs calculated by the FO approach mainly provide information on the chemical bonding features of the initial neutral ground state (initial state effect), since the relaxation of the electronic orbitals is not taken into account in the final ionized system.
More accurate estimations of the BEs can be obtained by considering the energy difference between the final ionized state and the initial neutral ground state, taking into account the electron density relaxation in response to the electron hole. This approach is known as 𝛥SCF.
The calculations of gas phase molecules BEs based on DFT and HF in the 𝛥SCF scheme, have been shown to reproduce absolute experimental BEs with a good degree of accuracy [56, 57, 58]. However, this could be due to cancellation of errors arising from the neglect of relativistic effects, the poor description of correlation energies and incompleteness of the basis set. In this regard Pueyo Bellafont et al. [59] have directly taken into account relativistic effect in the calculations of 1S core level BEs of N, F, C and B atoms belonging to 68 gas phase molecules with different functional groups. HF and DFT calculations (TPSS functional) in the 𝛥SCF scheme have been performed. The calculated BEs result to be underestimated with respect to the experimental values of 0.11 (HF) and 0.05 eV (TPPS).
An alternative promising method for the computing of gas phase molecules BEs is represented by the GW quasi particle approach [60]. In this approach the HF equations are generalized in terms of Greens functions (G), which poles correspond to the ionization potentials and electronic affinities. In this framework based on ab initio calculations, the ionization potentials and electronic affinities are connected to the dielectric function and self-energy of the system. In the GW method the response of the electron density to the core hole is described by a perturbative approach where the system self-energy is expanded in a Taylor series of the dynamically screened Coulomb interaction (W).
In the past, the GW approach has been successfully applied for the computation of valence electron ionization energies in solid and gas phase molecules. More recently, the use of the GW approach has been also extended to the calculations of core electrons BEs of gas phase molecules [61, 62]. In this regard the work of Goltze et al. [61] applies a partial self-consistent GW scheme for the computation of 1s core level BEs of 68 molecular systems. This work points out how the use of GGA functionals (currently used for the calculation of valence electrons BEs) for the initialization of Green functions and the Coulomb interaction are not enough for an accurate computation of core electrons BEs. By contrast the use of Hybrid functionals with high percentage of exact exchange and the inclusion of relativistic effects provides accurate BEs that agree within 0.3 and 0.2 eV with experiments. The main advantage of the GW methods with respect 𝛥SCF ones lies in the direct computation of ionization potential and electron affinities from the quasi-particle energy of respectively occupied and not occupied electronic levels.
We now move our attention to the methods developed for the computation of BEs and 𝛥BEs of periodic systems. In the last two decades the astonishing increasing in the computational power has led surface science to pass from a cluster to a periodic approach for the modelling of surfaces. In the past, computational works modelling the adsorption process on oxides and metal surfaces by the clusters approach have provided useful information into the nature of the interaction between the adsorbate and the surfaces [63, 64]. However, the small size of the clusters leads to edge effects due to dangling atoms and possible wrong stoichiometry. These issues can be overcome by correctly coordinating the dangling atoms by other atoms, leading, however, to possible new unwanted effects on the computed BE and 𝛥BEs. Periodic systems are used in order to avoid these effects.
This has led to the conceiving of new approaches for the computation of 𝛥BEs of atoms on large periodic surfaces. The difficulties in computing XPS spectra on large periodic models arise from two main reasons:
- The ionization of one core electron in a given surface atom leads to a charged periodic cell. The coulomb repulsion between the periodically repeated infinite unit cells could introduce artefacts in the calculated values core level BEs and 𝛥BEs.
- Generally, Periodic codes (VASP [65, 66, 67, 68, 69], CP2K [70]) are not “full electron”, the core electrons are not explicitly treated. The effect of the atomic core electrons on the valence electron density is modelled by Pseudo Potentials.
In order to overcome such limitations different approaches have been proposed in the literature for the calculation of XPS spectra of periodic models in a 𝛥SCF scheme. In their pioneering work Pehlke and Scheffler et al. [71] calculate core level shift of clean (001) Ga and Si surfaces for excited atoms located at different distance from the surface. The authors generate Hamann–Schluter Chiang pseudo potentials for respectively the neutral and the ionized Si and Ge atoms (with 2p and 3d core holes). The comparison between the excited and the initial ground states revealed a higher screening at the surface with respect to the bulk.
More recently Ljumberg et al. [72] has implemented XPS calculations for periodic and non-periodic systems on the GPAW code, based on DFT and the projector-augmented wave (PAW) method [69, 73]. Interestingly the authors find variations up to 10 eV in the BEs when adopting closed and open shell calculations in the test case of H2O molecule. It follows that the use of spin polarized calculation is necessary for this approach. Curiously, as pointed out in the recent review of Vines et al. [74], negligible differences are instead found between spin and not spin-polarized calculations when adopting the “full electron” cluster approach [64]. The calculation of XPS energies (𝛥BEs) by the PAW approach of CO molecule adsorbed on Ni(100) surface has provided an error of around 2 eV with respect to the experimental value [64].
The implementation of core level 𝛥BEs calculations on periodic systems with PAW based approach and their successful combination with in-situ XPS experiments has led to an increasing number of innovative studies on the characterization of the adsorption and the reactivity of small organic species at metal and metal oxide surfaces. For instance, PAW based approaches have been successfully applied for the computation of XPS energies of: (i) CO molecule adsorbed on Ni(100), Fe(100) and Rh(111) surfaces [72, 75, 76], (ii) sulphur oxidation on Palladium [77, 78], (iii) aspartic acid and methyl Acetoacetate adsorbed on Ni(100) [79, 80] and (iv) small molecular species on copper oxide surfaces [81]. We also highlight the work of Trinh et al. [81], where a synergistic approach of experimental XPS and DFT calculations is proposed in order to determine the Hubbard terms (U term) for adsorbate/intermediate species on transition metal oxide surfaces.
As a drawback, the periodic 𝛥SCF calculations imply the use of approaches in order to prevent the spurious core electron holes’ interaction between the replica of the final system (N − 1 electron), that would lead to Coulomb divergence. The introduction of a uniform background opposite charge [82] and the addition of electrons in the conduction band [76, 83] of the final systems have been the two main approaches adopted to circumvent such problem. However, the addition of fictitious counter charges in the final system can introduce spurious effects in the calculated values of core level BEs and 𝛥BEs [84].
In this regard Ozaki et al. [85] have proposed a new approach based on DFT calculations, where a penalty function is used in order to model the electron core hole and the spurious interaction between the replica is removed using the Coulomb cut-off method. Another interesting methodology is the one of Lischner et al. [86, 87] where absolute core electrons BEs are calculated by DFT-based all-electrons 𝛥SCF calculations. In these works, core-level binding energies for a series of adsorbates on Cu(111) surfaces are computed. In a first step the adsorbate structures are optimized on a periodic slab model of the Cu(111) surface. Then, a cluster of 88 Cu atoms is extracted from the slab and the core BEs are calculated using the all-electron 𝛥SCF. These calculations have led to accurate absolute BEs with a mean unsigned error of 0.08 eV and 0.13 eV for respectively the M06 and PBE functional.
An alternative approach for an accurate prediction of periodic systems 𝛥BEs is represented by the Janak–Slater (JS) transition state method [88, 89]. This approach considers half occupation of the core level (CL) rather than a full core-hole as in other 𝛥SCF approaches. This is done in order to minimize the fictitious repulsion between the replicas. Recent studies have reported the JS to provide 𝛥BEs of gas phase molecules and periodic surfaces [82, 83] in good agreement with experiments, when adopting a PAW description of the atomic cores (implemented on VASP).
Beyond 𝛥SCF approaches, the XPS spectra of periodic systems have also been computed by GW methods [90, 91]. We find of particular interest the work Zhu et al. [90] where an implementation based on crystalline Gaussian Basis set for the computation of core-electrons BEs on periodic systems in the GW scheme, is presented. Also, in this case the use of hybrid functionals with a high percentage of exact exchange results to be mandatory for the computation of accurate core electrons BEs.
The GW method presents the main advantage with respect to the 𝛥SCF approaches to not need considering the final ionized system for the computation of BEs in periodic systems. This avoids possible spurious effects arising from the core-holes interaction between the replicas.
4. XPS for the clinician, some more simple considerations
In this section, we briefly describe some of the studies on the characterization by XPS spectroscopy of materials with biological and medical interest.
The objective is to provide to the reader an idea of which chemical information can be gained by XPS experiments on these materials and which is their impact on application in the fields of medicine and biology.
In particular we focus on the two major elements which play a pivotal role in medicine namely titanium and calcium. Titanium is a material widely used in the medical field for orthopedic prosthesis and implant dentistry [92, 93] while calcium is an element at the core of the research performed on pathological and physiological calcifications as well as bioactive biominerals for orthopedic applications [11, 12, 94, 95, 96].
Different investigations have been dedicated to describing precisely the chemical and physical nature of the TiO2 oxide layer in order to understand why freshly cut titanium seems to be more active in cell adhesion than titanium aged 4 weeks or more [97, 98]. Titanium dioxide may have an amorphous state and eleven polymorphic phases [99]. Thermodynamically, Rutile [100, 101] is the more stable phase, while anatase and brookite are metastable. These two last polymorphs will be transformed into rutile at higher temperature. As underlined by Peng et al. [102], a competition process occurs between the osteoblasts and pathogens introduced during surgery, on the surface of prostheses. Such competition has motivated numerous investigations on this major research subject with different characterization techniques [103, 104].
As underlined in the publication of Roy et al. [105], XPS spectroscopy gives major information on the surface. The authors have considered two commercially available Osteoplant Base™ and Rapid™ titanium dental implants. On Figure 3a, we can see that like XRF spectroscopy, different elements can be identified. More precisely, the XPS spectrum is dominated by photoelectron peaks, corresponding to electrons originating in the 1s orbitals of the C, N, O and F or in the 2s or 2p orbitals of Ti and Al atoms in the sample surface. The intensity of the XPS spectra depends on the concentration of the element present. Moreover, peaks corresponding to the Auger process are visible (CKLL, TiLMM, OKLL…). The third component of a XPS spectrum is related to the background which comes from electrons excited by the X-ray Bremsstrahlung radiation at low binding energy as well as from inelastically scattered photoelectrons at higher binding energy.
(a) The XPS survey spectra obtained for two samples the BASE (red) and RAPID (blue) implants as received. On both surfaces Ti, O, C, Al and F were detectable. (b) High resolution XPS spectrum of the Ti2p core line for RAPID implant. The shape of the 2p doublet was fitted by to five sub-doublets. The doublet with the highest intensity corresponded to TiO2 component. The enlarged region presented the Ti2p3∕2 peaks corresponded to hydrated water Ti–OH, various oxidation states and metallic state of titanium (Roy et al. [105]).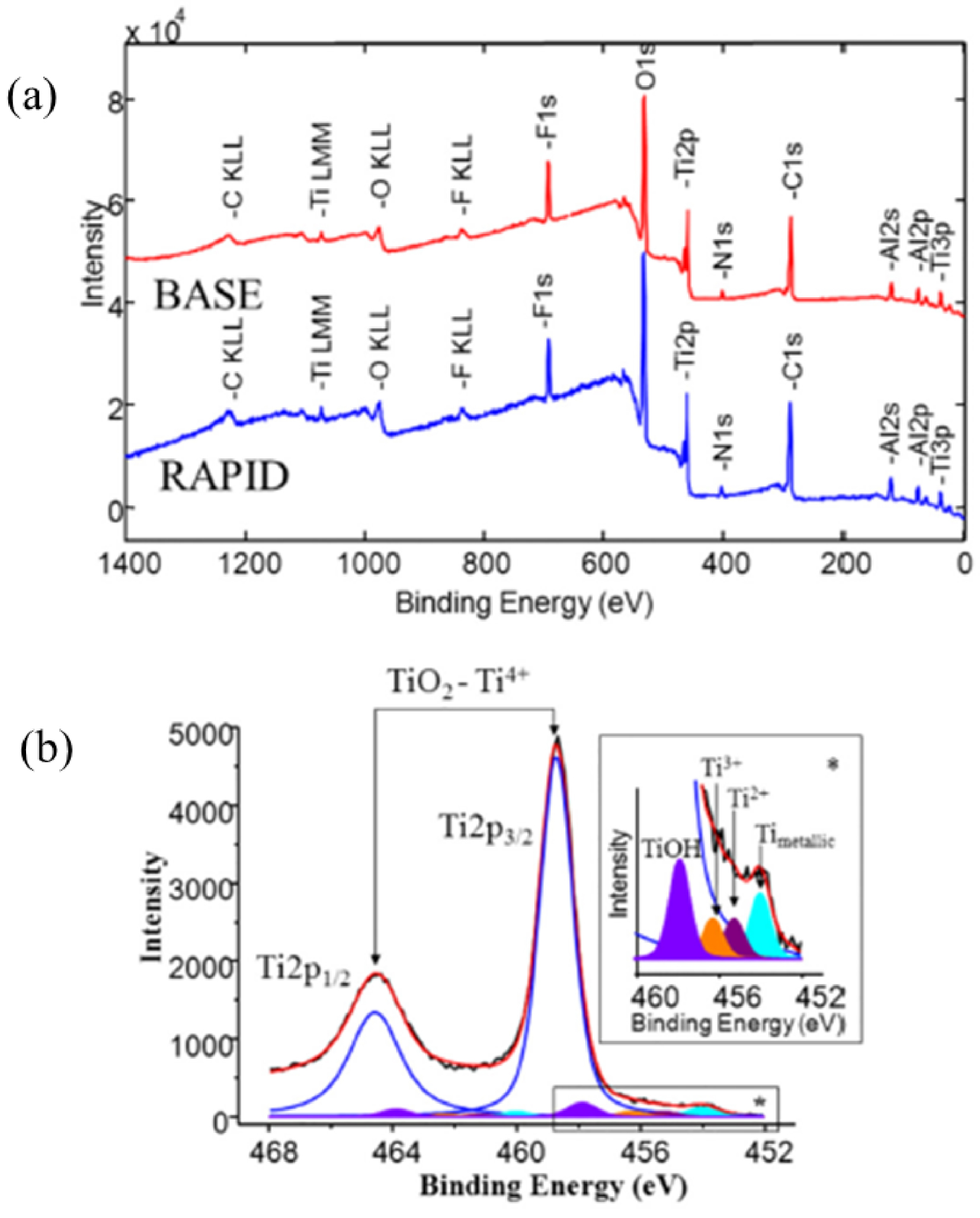
But XPS spectroscopy gives more information. As we can see on Figure 3b, XPS spectroscopy is able through a deconvolution process to distinguish the different oxidation states of Ti namely Ti4+, Ti2+ and Ti0. Basically, the spin–orbit splitting (splitting between Ti2p3∕2 and Ti2p1∕2) is approximately the same for Ti4+, Ti2+ and Ti0). Regarding the chemical shift between Ti0 and Ti4+, the charge withdrawn leads to a 2p orbital relaxation to higher binding energy.
In their study, Roy et al. [105] demonstrate clearly through XPS spectroscopy that UVC irradiation was able to reverse biological ageing of titanium by greatly reducing the amount of carbon contamination present on the implant surface by up to 4 times, while the topography of the surface was not affected.
Note that information can be obtained also through the O2p peak (Figure 4). As reported by Song et al. [106], two large peaks could be measured located at 529.4 and 530.7 eV. These peaks can be assigned to TiO2 and TiOH respectively [107].
XPS core level spectra for O1s of TiO2 samples as prepared and annealed at 450 °C and 700 °C (Song et al. [106]).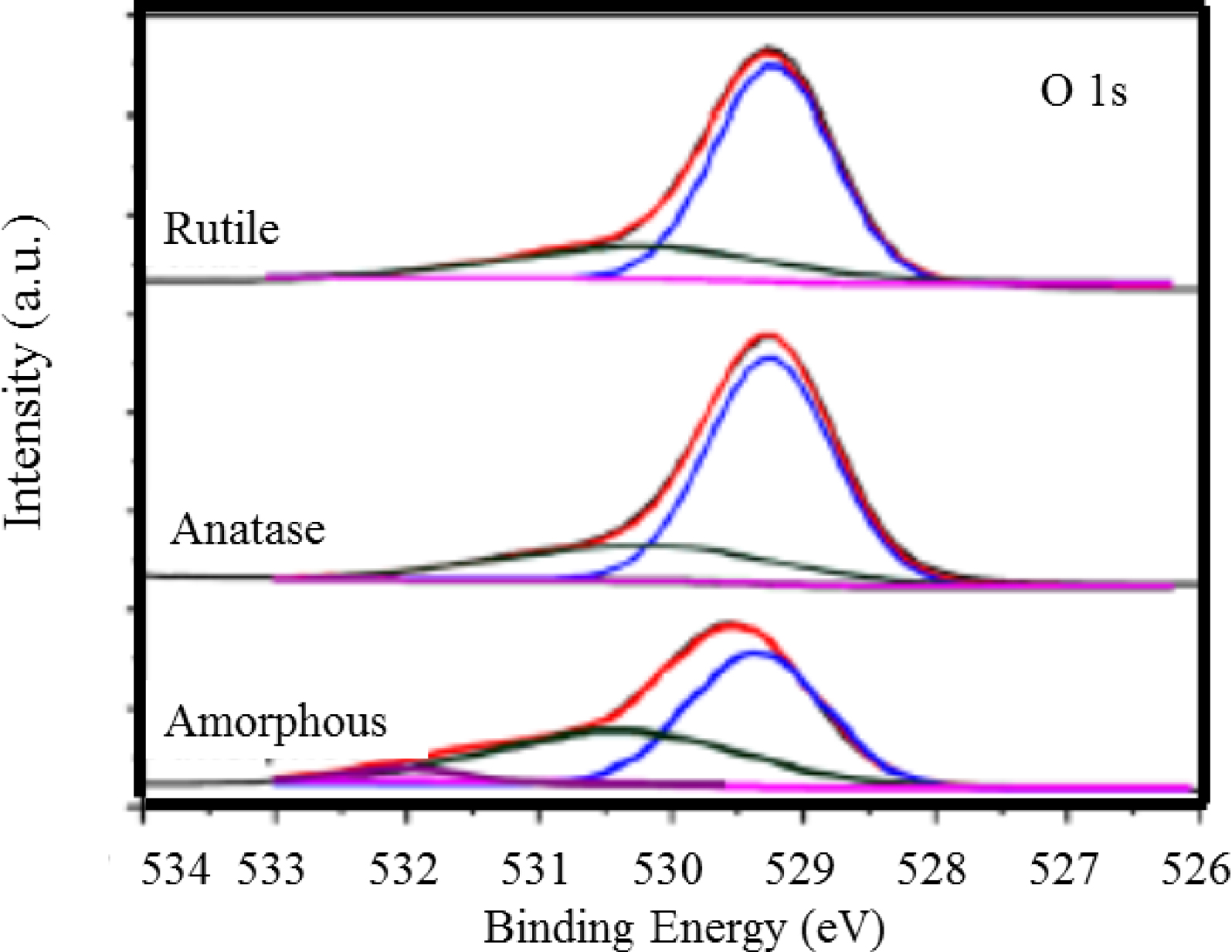
Calcium is another key element in medicine. The chemistry of Calcium orthophosphate is quite complex and encompasses in medicine amorphous and nanocrystals compounds [108, 109, 110]. Demri and Muester [111] have measured the 2p XPS photoemission lines of different compounds containing calcium compounds (Figure 5). The contributions of the Ca2p3∕2 and Ca2p1∕2 can be distinguished for each compound. The position of the most intense Ca2p3∕2 peak is found to be strongly dependent on the local chemical environment of the Ca atom.
Ca2p spectra taken for different compounds (Demri and Muester [111]).
The CaO and CaCO3 peaks are found located around 346.5 eV, while the calcium atoms bounded to phosphate groups are located at about 347 eV. For the compounds characterized by bonds with high ionic character (sulphates, nitrates, etc.), the Ca2p3∕2 peak is found shifted at higher binding energy. Such measurements illustrate the high sensitivity of XPS spectroscopy to the structure and chemical nature of the environment experienced by Ca, an element which plays a major role in medicine.
5. Selected examples related to medicine
Several papers [112, 113] have underlined the different instrumentation and methodology advances that have enhanced the ability to study organic and biological systems through XPS spectroscopy. Among the biological systems and biomaterials which can be investigated through XPS spectroscopy, we can quote bacteria [114, 115], Human cells [116, 117], dental implants [118, 119, 120], intraocular lens [121, 122] or physiological as well as pathological calcifications such as (not only human ones) [123, 124, 125], teeth [126, 127, 128], vascular calcifications [13, 129] or kidney stones [130].
5.1. XPS studies of implants
5.1.1. Multicomponents implants
Regarding their chemical structure, implants may be composed of several elements. Titanium and its alloys are widely used in dental implants and hip-prostheses due to their excellent biocompatibility [131]. The characterization of their surface is clearly of primary importance to understand the relationship between the implant and physiological calcifications namely bones or teeth. For example, using XPS, it is possible to determine quantitatively the surface hydroxyl concentration, which results of the dissociation of a water molecule at the surface, on low specific surface area metal oxides such as TiO2 and Fe2O3 [132, 133]. Similar approach can be performed to characterize the surface of tetragonal stabilized ZrO2 with the addition of 3 mol% Y2O3 dental implants [134]. For such implants which contain several elements, XPS can give the Y/Zr atomic ratio. As underlined by Zinelis et al. [134], a high value of this parameter may indicate yttria segregation. Recently, Su et al. [135] provide a brief summary of state-of-art of surface biofunctionalization on implantable metals by CaP coatings.
With XPS, it is also possible to describe the modifications of the surface induced by a chemical treatment. Takadama et al. [136] show through XPS study that a NaOH and treatments of a Ti–6Al–4V alloy produce an Al and V free amorphous sodium titanate surface layer on the surface. Note that a chemical treatment of the surface may also modify significantly its topology. Kang et al. [119] have observed that the electrochemical oxidation process for Ti implants produces microporous surface (pore size: 0.5–3.0 μm) and modify surface chemistry due to incorporation of anions of the used electrolyte. Regarding commercially pure titanium, Korotin et al. [137] have characterized through XPS such compound before and after chemical treatment (in 1% HF, 1 min and in 40% HF, 1 min). These authors found that acid treatment reduces the content of hydrocarbons increasing the surface energy and biocompatibility (through an increase of the oxygen concentration on the surface) of Ti-implants.
Then, on top of TiO2 surface, zinc oxide nanoparticles can be used as a coating material to inhibit bacterial adhesion and promote osteoblast growth [138]. Recently, Chang et al. [139] have proposed a reliable method by considering the peak shift of Zn2p in XPS to inspect the ZnO matrix, rather than O1s. Finally, coating based on calcium phosphate apatite could significantly improve the biological performances of metallic implants [140, 141]. As underlined by Lu et al. [142] hydroxyapatite is closed to the mineral part of bones and teeth and display a spontaneous interfacial osteointegration when implanted. In their investigation, these authors show that the Ca/P and O/Ca XPS peak ratios provide identification of the CaP phase(s) present in the surface and establish their mole fractions. More precisely, the relative intensity of shake-up satellite II related to O(1s) decreases in the following order: 𝛽-TCP (Tricalcium phosphate) > HAP (Hydroxyapatite) > OCP (Octacalcium phosphate) > DCP (dibasic calcium phosphate) > DCPD (dibasic calcium phosphate dihydrate) > MCP (monobasic calcium Phosphate).
Finally, Combes et al. [143] have investigated the nucleation and growth of dicalcium phosphate dihydrate (CaHPO4⋅2H2O) on titanium powder at 37 °C and pH 5.5. Combining XPS and IR experiments, these authors observed that at the earliest stage of contact with the supersaturated solution, the oxidized titanium surface exhibited an increase of the xylation rate associated with calcium and phosphate uptake. Also, there are direct evidence that the first calcium phosphate layer exhibits the IR characteristics of amorphous calcium phosphate. It is at the end of the induction period that the formation of DCPD crystals was observed.
5.1.2. Toxicity of implants
For such biomaterials, investigations of their surface may be relevant to control their physicochemical structural characteristics and also to assess toxicity problems such as the ones related to the release of TiO2 particles which may also compromise bone-forming cell functions [138]. Recently, Kim et al. [144] have presented a general review of titanium toxicity pointing for example the accumulation of metal debris such as titanium, aluminum, and vanadium found in the bone marrow of some patients or the presence of inflammatory cells around titanium particles in peri-implantitis biopsies.
Oje and Ogwu [145] have underlined the presence of a non-stoichiometric oxide phase. Such conclusion is based on the measurement of the Cr2p3∕2 spectrum which display peaks at binding energy positions of approximately 575.25, 576.40 and 578.46 eV. In line with the publication of Ogwu et al. [146], the peak at approximately 575.25 eV indicates a non-stoichiometric oxide phase between metallic chromium at 574.9 eV and the Cr2O3 peak located at 576.40 eV.
5.2. XPS studies of pathological and physiological calcifications
The deposit of calcium phosphate at the surface of biomedical implants may be a major problem. It is the case for explanted intraocular lens [147], JJ-stents [148, 149] or heart valves [150].
Bian et al. [151] have studied the degradation behaviors and in-vivo biocompatibility of a rare earth- and aluminum-free magnesium-based stent. The XPS data give the elementary composition at the surface through the detection of the contribution coming from Mg, O, Ca, P, C and minor Na. The possible presence of calcium phosphate hydroxyapatite on the surface is based on the measurements of Ca2p peak at 350.90 eV, along with P2p peak at 133.36 eV and O1s peak at 531.17 eV [152]. Simon et al. [121] have combined XPS and Ar+ ion sputtering in order to investigate elemental depth profiles, as the sample can be analyzed layer by layer on the nanometric scale. As noticed by these authors, this is the first investigation on explanted intraocular lenses using XPS depth profiling in order to examine the inside of the opacifying deposits.
Regarding pathological calcifications, XPS offers the opportunity to study the adsorption of molecules or cations at the surface of chemical compounds which have been identified in pathological calcifications. Also, Gourgas et al. [13] used a set of characterization techniques including XPS spectroscopy to understand how pathological calcification is initiated on the vascular extracellular matrix. In their conclusion, the authors show that an interdisciplinary approach combining animal models and materials science can provide insights into the mechanism of vascular calcification in line with previous publications [11, 12]. In their investigation, Gourgas et al. [13] have used XPS spectroscopy to underline the presence of CaP calcifications in on aorta sections. In this work, the authors used XPS to identify mineral phases present in calcified arteries from mouse models. Using XPS, they showed that the amount of calcium phosphate minerals is significantly increasing with time. Also, they observed a significant increase in the average Ca/P ratios overtime which showing the conversion of precursor phases into crystalline apatite phases. Overall, this work shows that mineral deposition in medial arterial calcification starts with precipitation of precursor phases (amorphous calcium phosphate and OCP) and further transformation to hydroxyapatite and carbonated hydroxyapatite.
Finally, XPS spectroscopy offers the opportunity to characterize physiological calcifications such as bones [124] or teeth [108]. The analysis of their surface may give major information regarding the presence of trace elements at their surface [153], the thickness of adsorbed mouth rinse components on dental enamel [154] or the adsorption process of drugs [124]. Zhao et al. [124] have investigated the effects of Sr-incorporation on scaffold physicochemical and mechanical properties, bioactivity, cytotoxicity, and bone formation rate. In the XPS spectra, two major peaks for Sr were measured with binding energies of 269.13 eV (Sr3p3∕2) and 133.52 eV (Sr3d5∕2). The incorporation of Sr increased the Ca element binding energy, with the Ca2p3∕2 peak increasing from 347.08 eV to 348.24 eV.
6. Conclusions
In this short overview we considered the use of XPS characterization methods in the field of clinical sciences. Some elements regarding the theoretical formalism in particular with respect to first principles calculations are given, followed by some practical and experimental information regarding XPS. Two families of mineralization systems are discussed towards their XPS properties: mineralization originating from implants and from physiological pathological origin. Concerning the most studied family of both mentioned some more details are given on multicomponent implants, their toxicity, and their calcifications.
It is a timely work since it was noticed that XPS is becoming of interest in the analysis of biological mineralization applications, and that the experimental methodologies are available. Theoretical quantum chemical-based calculations have been performed so far on different solid systems and on surfaces in particular, but much less on biological mineral systems. However, it is clear that from the works published in the literature the computational methods are ready to be used on biological mineral systems and they are not only restricted to inorganic materials and heterogenous catalysts. In conclusion our message would be that a bright future of XPS is expected in the field of clinical sciences.
Conflicts of interest
Authors have no conflict of interest to declare.
Acknowledgement
FT wishes to acknowledge the VUB for support, among other through a Strategic Research Program awarded to his group.




 CC-BY 4.0
CC-BY 4.0