Parallel-mode EPR spectra of the hexaaqua manganese(II) Ion in tetrahedral symmetry

Margrete Juel Henrichsen; Jesper Bendix; Høgni Weihe

doi:10.5802/crchim.266

Article de recherche

Parallel-mode EPR spectra of the hexaaqua manganese(II) Ion in tetrahedral symmetry
[Spectres RPE en mode parallèle de l’ion hexaaquamanganèse(II) en symétrie tétraédrique]

Margrete Juel Henrichsen ¹ ; Jesper Bendix ¹ ; Høgni Weihe ¹

¹ Department of Chemistry, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen, Denmark

Comptes Rendus. Chimie, Online first (2024), pp. 1-10.

Résumés

Anglais
Français

Parallel-mode X-band EPR spectra of the manganese(II) hexaaqua ion as substitutional impurity in Cs[Mg(H₂O)₆]AsO₄ are presented and interpreted. In this lattice the aqua ion, considering also the disposition of the hydrogen atoms, occupies a crystallographic site with tetrahedral symmetry. This rare situation enables that the line positions as well as the intensities in the parallel-mode EPR spectra can be modelled with a simple three-parameter cubic-symmetry spin Hamiltonian, including the isotropic Zeeman interaction ( $g$ ) pertinent to the $S = 5 / 2$ electronic spin, the isotropic hyperfine interaction ( $A$ ), between the electronic spin and the $I = 5 / 2$ nuclear spin, and the cubic splitting ( $a$ ) of the $S = 5 / 2$ manifold. A simple formalism, based on perturbation theory to grossly account for the observed intensities, is presented. We observe all parallel-mode-allowed hyperfine transitions associated with all fine-structure transitions.

Supplementary Materials:
Supplementary material for this article is supplied as a separate file:

crchim-266-suppl.pdf

Les spectres RPE en bande X et en mode parallèle de l’ion hexaaquamanganèse(II) utilisés comme dopant dans Cs[Mg(H₂O)₆]AsO₄ sont présentés. Dans ce réseau, l’aqua-ion, compte tenu de la disposition des atomes d’hydrogène, occupe un site cristallographique à symétrie tétraédrique. Cette situation rare permet de modéliser les positions des raies ainsi que les intensités des spectres RPE en mode parallèle à l’aide d’un simple hamiltonien de spin à trois paramètres à symétrie cubique, comprenant l’interaction Zeeman isotrope ( $g$ ) relative au spin électronique $S = 5 / 2$ , l’interaction hyperfine isotrope ( $A$ ), entre le spin électronique et le spin nucléaire $I = 5 / 2$ , et le dédoublement cubique ( $a$ ) de l’ensemble $S = 5 / 2$ . Un formalisme simple, basé sur la théorie des perturbations, est présenté pour rendre compte des intensités observées. Nous observons toutes les transitions hyperfines autorisées en mode parallèle, associées à toutes les transitions de structure fine.

Compléments :
Des compléments sont fournis pour cet article dans le fichier séparé :

crchim-266-suppl.pdf

Métadonnées

Reçu le : 2023-05-31
Révisé le : 2023-07-28
Accepté le : 2023-10-12
Première publication : 2024-02-12

DOI : 10.5802/crchim.266

Keywords: Parallel-mode EPR, Manganese(II), Hyperfine interaction, Cubic symmetry, Flip-flop transitions
Mot clés : RPE en mode parallèle, Manganèse(II), Interaction hyperfine, Symétrie cubique, Transitions flip-flop

Affiliations des auteurs :

Margrete Juel Henrichsen ¹ ; Jesper Bendix ¹ ; Høgni Weihe ¹

¹ Department of Chemistry, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen, Denmark

Licence :

CC-BY 4.0

Droits d'auteur : Les auteurs conservent leurs droits

@article{CRCHIM_2024__27_S1_A17_0,
     author = {Margrete Juel Henrichsen and Jesper Bendix and H{\o}gni Weihe},
     title = {Parallel-mode {EPR} spectra of the hexaaqua {manganese(II)} {Ion} in tetrahedral symmetry},
     journal = {Comptes Rendus. Chimie},
     publisher = {Acad\'emie des sciences, Paris},
     year = {2024},
     doi = {10.5802/crchim.266},
     language = {en},
     note = {Online first},
}

TY  - JOUR
AU  - Margrete Juel Henrichsen
AU  - Jesper Bendix
AU  - Høgni Weihe
TI  - Parallel-mode EPR spectra of the hexaaqua manganese(II) Ion in tetrahedral symmetry
JO  - Comptes Rendus. Chimie
PY  - 2024
PB  - Académie des sciences, Paris
N1  - Online first
DO  - 10.5802/crchim.266
LA  - en
ID  - CRCHIM_2024__27_S1_A17_0
ER  -

%0 Journal Article
%A Margrete Juel Henrichsen
%A Jesper Bendix
%A Høgni Weihe
%T Parallel-mode EPR spectra of the hexaaqua manganese(II) Ion in tetrahedral symmetry
%J Comptes Rendus. Chimie
%D 2024
%I Académie des sciences, Paris
%Z Online first
%R 10.5802/crchim.266
%G en
%F CRCHIM_2024__27_S1_A17_0

Margrete Juel Henrichsen; Jesper Bendix; Høgni Weihe. Parallel-mode EPR spectra of the hexaaqua manganese(II) Ion in tetrahedral symmetry. Comptes Rendus. Chimie, Online first (2024), pp. 1-10. doi : 10.5802/crchim.266.

Version originale du texte intégral (Proposez une traduction )

1. Introduction

Parallel-mode EPR (Electron Paramagnetic Resonance) spectra are recorded with the magnetic component of the microwave radiation oscillating parallel to the applied magnetic field, in contrast to the normal perpendicular-mode setting where the magnetic component of the microwave radiation is perpendicular to the applied magnetic field. Different selection rules are associated with these two instrumental settings, and therefore the parallel-mode setting may induce transitions inaccessible by perpendicular mode. The intensity and overall appearance of the parallel-mode spectrum of a given spin system is strongly dependent on the composition of the spin system, and the magnitude of (as well as the ratio between) various parameters in the effective Hamiltonian describing the spin system. These parameters encompass the quantification of Zeeman terms, various anisotropy parameters, exchange coupling constants, and hyperfine coupling constants. Hence, the simple appearance of a parallel-mode spectrum, i.e., the number of lines, may reveal the intensity-giving mechanism.

Parallel-mode EPR spectra have been successfully recorded for a wide variety of both simple and composite spin systems. In the following, not exhaustive list, we group the systems into two classes, namely those exhibiting no resolved hyperfine splittings, and those exhibiting clear hyperfine splittings.

The former class is exemplified by the following works: the parallel-mode setting was used to elucidate the electronic spin-quintet (S = 2) ground state of the iron(II) ion in myoglobin [1]; the ground state S = 4 spin multiplet of the all-ferrous state of the [4Fe–4S] cluster in nitrogenase was characterized by parallel-mode EPR [2]; and several parallel-mode resonances were detected in the ground S = 6 state of a dodecanuclear chromium(III) spin cluster [3].

For the latter class exhibiting clear hyperfine splittings, parallel-mode EPR was applied: to determine the sign and magnitude of the pseudo-axial anisotropy splitting in manganese(III) ions, S = 2,I = 5∕2 (with I being the nuclear-spin quantum number), in superoxide dismutase [4]; to study small splittings arising from the Jahn–Teller distortion in the manganese(III) hexaaqua ion [5]; to observe and resolve the Mn–F superhyperfine interaction in two fluorido complexes of manganese(III), namely ${MnF}_{6}^{3 -}$ and ${Mn(salen)F}_{2}^{-}$ [6]; and to characterize several cobalt(II) complexes with (S,I) = (3∕2,7∕2) [7]. Recently, parallel-mode spectra of Bi as an impurity in silicon were presented and the complementary information obtained from parallel-mode was used to aid the interpretation of the perpendicular-mode spectra of two molecular bismuth radicals with (S,I) = (1∕2,9∕2) [8]. Also recently, a detailed exposition of the parallel-mode EPR spectrum of hydrogen atoms with (S,I) = (1∕2,1∕2) and deuterium atoms with (S,I) = (1∕2,1) trapped in silsesquioxanes was given [9]. We note in passing that understanding this very simple spin system is important for radio astronomy, as the splitting of the 21 cm, 1420.4 MHz, line originating from hydrogen atoms in galaxies might give information about interstellar magnetic fields [10].

For an isolated isotropic spin multiplet with spin quantum number S, the parallel-mode spectrum has no intensity simply because the 2S + 1 projections |S,M⟩ are exact eigenfunctions to the $Ŝ_{z}$ operator (cf. Equation (5) below). Therefore, the parallel-mode intensity observed in the nuclear spin–free spin systems, as, e.g., in refs [1, 2, 3], is induced by the anisotropic terms in the Hamiltonian. Parallel-mode intensities in these spin systems are rather high and can be comparable to the usual perpendicular-mode intensities.

However, for an electronic spin interacting with a nuclear spin, the situation is slightly different as here the hyperfine interaction constitutes an additional intensity-giving mechanism. All the parallel-mode lines in the class of systems exhibiting resolved hyperfine splittings, quoted above, are hyperfine transitions between the two components of an effective non-Kramers [4, 5, 6] or a genuine [7, 8] S = 1∕2 spin system. The parallel-mode spectra of the manganese(III) systems all exhibit 2I + 1 = 6 hyperfine lines connected to only a single fine-structure transition, with I = 5∕2 appropriate for the ⁵⁵Mn nucleus. In these systems, the intensity is induced by a small splitting of a non-Kramers doublet. However, the parallel-mode spectrum of Bi in silicon [8] exhibits 2I = 9 lines, with I = 9∕2 for ²⁰⁹Bi. Likewise, spectrum of hydrogen and deuterium exhibit 2I_H = 1 and 2I_D = 2 lines, respectively, where I_H = 1∕2 and I_D = 1, respectively. In the bismuth, hydrogen, and deuterium spectra, the intensity is induced solely by the hyperfine interaction.

We are not aware of any reports on parallel-mode spectra of an S > 1∕2 spin system exhibiting all the possible allowed fine-structure transitions. Therefore, in this contribution we present parallel- as well as perpendicular-mode spectra of Mn²⁺ in strict tetrahedral symmetry (Figure 1) where all metal centers are magnetically and crystallographically equivalent.

Figure 1.
Illustration of the hexaaqua manganese(II) ion in strict tetrahedral symmetry. Blue: Manganese, Red: Oxygen, White: Hydrogen. The circumscribed tetrahedron whose sides straddle the hydrogen atoms has been drawn to emphasize the T_d lattice-point symmetry of the hexaaqua ion.

This paper is organized as follows. In Section 2 we summarize the experimental details; in Section 3 we present a first-order perturbational treatment of the parallel-mode intensities for a spin system where an electronic spin S is interacting with a nuclear spin I via an isotropic hyperfine interaction. Although the treatment is fairly general, it is aimed at the present spin system, namely Mn²⁺ with S = 5∕2 and I = 5∕2; and in Section 4 we present and discuss single-crystal perpendicular-mode and parallel-mode EPR spectra of manganese(II) hexaaqua ions in perfect tetrahedral symmetry.

2. Experimental

2.1. Synthesis

The synthesis of single crystals of Cs[Mg(H₂O)₆]AsO₄ was performed largely as described in refs. [11, 12], but with some modifications in order to produce large single crystals.

Initially, two solutions were prepared. Solution 1: to 90 ml of water were added 3.92 g of 75% arsenic acid (20.7 mmol) and 2.77 g (20.4 mmol) of sodium acetate trihydrate. Solution 2: to 43 ml of water were added 2.0 ml (30 mmol) of glacial acetic acid, 3.34 g (10.0 mmol) cesium carbonate, and 4.20 g (20.0 mmol) of magnesium acetate tetrahydrate. To solution 2 were finally added 5 mg (0.02 mmol) or 50 mg (0.20 mmol) of manganese(II) acetate tetrahydrate to achieve a doping level of 0.1% or 1%, respectively.

Solution 1 (2 ml) and solution 2 (1 ml) were mixed in a small test tube resulting in a clear solution. The small test tube was placed in a larger test tube containing 4 ml pyridine. The large test tube was stoppered and left for five days. Large octahedrally shaped crystals were separated from a viscous gel by filtration and washed with water. Crystals with edge length up to 1.5 mm could be obtained by this slow vapor diffusion of pyridine into the solution. A microcrystalline powder could be produced by slow addition of ammonia (1 M).

2.2. X-ray crystallography

The identity of the single crystals as well as the microcrystalline powder was verified with single-crystal X-ray diffraction as well as X-ray powder diffraction (see supporting information). The single-crystal X-ray diffraction studies were performed at 100 K on a Bruker D8 VENTURE diffractometer equipped with a Mo K𝛼 high-brilliance I𝜇S radiation source (𝜆 = 0.71073 Å), a multilayer X-ray mirror and a PHOTON 100 CMOS detector, and an Oxford Cryosystems low-temperature device. The instrument was controlled with the APEX3 software package using SAINT [13]. Final cell constants were obtained from least squares fits of several thousand strong reflections. Intensity data were corrected for absorption using intensities of redundant reflections with the program SADABS [14]. Powder X-ray diffraction studies were performed at room temperature on a Bruker D8 advanced equipped with a Cu K𝛼 source (𝜆 = 1.5406 Å).

2.3. EPR spectroscopy

Room-temperature EPR spectra were recorded on a Bruker Elexsys spectrometer equipped with an ER4116DM dual-mode cavity. The crystal was rotated around ⟨110⟩ axis, and hence the magnetic field vector sweeps a plane containing one four-fold (S₄), one two-fold (C₂), and two three-fold (C₃) axes. The power used for perpendicular-mode measurements was 6.325 mW, and for parallel mode 200 mW. Modulation amplitude was in perpendicular-mode 1 G, and for parallel-mode a larger modulation amplitude of 4 G was used due to the low intensity. At room temperature we observed no saturation effects nor multiple quantum transitions [15, 16].

3. Theory

Eigenvalues and eigenvectors pertinent to the EPR spectra of the tetrahedral symmetric manganese(II) hexaaqua ion are obtained by numerical diagonalization of the matrix representation of the spin Hamiltonian [17]

Ĥ = g 𝜇_{B} B \cdot \hat{S} + A \hat{S} \cdot \hat{I} + \frac{a}{6} (Ŝ_{x}^{4} + Ŝ_{y}^{4} + Ŝ_{z}^{4} - \frac{707}{16}),

(1)

which is applicable to our spin system with S = 5∕2 and I = 5∕2. In Equation (1) B,

\hat{S} = (Ŝ_{x}, Ŝ_{y}, Ŝ_{z})

, and

\hat{I} = (Î_{x}, Î_{y}, Î_{z})

are the magnetic field vector, the electron spin operator, and the nuclear spin operator, respectively. g is the electron spin g factor, A is the hyperfine coupling constant, and a quantifies the cubic splitting of the S = 5∕2 manifold into a quartet and a doublet. This splitting is 3a with the quartet higher in energy for a > 0. The linewidths of the spectra presented below did not warrant the inclusion of terms accounting for the nuclear Zeeman effect and nuclear quadrupole splittings.

Fitting of spectral traces of both perpendicular-mode and parallel-mode spectra was performed with a locally developed software as described earlier [18, 19].

To grossly account for the main features, i.e., the number of lines and their intensities in the parallel-mode X-band EPR spectra, we wrote down the first-order corrected wave functions for this system. To do so we chose the z-axis in the direction of the magnetic field and approximated the Hamiltonian as

Ĥ \approx Ĥ^{(0)} + Ĥ^{(1)},

(2)

where

Ĥ^{(0)} = g 𝜇_{B} B Ŝ_{z} + A Ŝ_{z} Î_{z}

and

Ĥ^{(1)} = (A ∕ 2) (Ŝ_{+} Î_{-} + Ŝ_{-} Î_{+})

. In this discussion of the parallel-mode intensities we are ignoring the last term of Equation (1). In the present case with cubic manganese(II), this is fully justified, as the energetic consequence of the a term is very much smaller compared to the hyperfine interaction and the Zeeman term at field values corresponding to resonances at X-band. However, in Section 4 we use the full Hamiltonian Equation (1) to reproduce the experimental spectra. The direct-product functions |M,m⟩ with M and m being electron spin and nuclear spin components, respectively, are eigenfunctions to

Ĥ^{(0)}

. With

Ĥ^{(1)}

as a perturbation we obtain the following expression for the non-normalized first-order corrected wavefunctions

\begin{matrix} | M, m ⟩_{c} = | M, m ⟩ \\ - (\frac{A}{2}) \frac{⟨ M + 1, m - 1 | Ŝ_{+} Î_{-} | M, m ⟩}{E (M + 1, m - 1) - E (M, m)} | M + 1, m - 1 ⟩ \\ - (\frac{A}{2}) \frac{⟨ M - 1, m + 1 | Ŝ_{-} Î_{+} | M, m ⟩}{E (M - 1, m + 1) - E (M, m)} | M - 1, m + 1 ⟩ . \end{matrix}

(3)

At field values corresponding to resonances at X-band, the denominators have absolute values roughly equal to h𝜈. Therefore, we approximate

\begin{matrix} | M, m ⟩_{c} = | M, m ⟩ \\ - (\frac{A}{2 h 𝜈}) ⟨ M + 1, m - 1 | Ŝ_{+} Î_{-} | M, m ⟩ | M + 1, m - 1 ⟩ \\ + (\frac{A}{2 h 𝜈}) ⟨ M - 1, m + 1 | Ŝ_{-} Î_{+} | M, m ⟩ | M - 1, m + 1 ⟩ . \end{matrix}

(4)

The intensity of the transitions in parallel mode is now computed as the squared expectation value of $g Ŝ_{z}$ , as

I (| M, m ⟩_{c} \to | M^{'}, m^{'} ⟩_{c}) = | (⟨ M^{'}, m^{'} |_{c}) g Ŝ_{z} (| M, m ⟩_{c}) |^{2} .

(5)

Inspection of the (2S + 1)(2I + 1) first-order corrected wavefunctions reveals that only (2S)(2I) transitions have non-vanishing parallel-mode intensity in the g ≈ 2 field region. These are those for which M′ = M ± 1 concerted with m′∓ 1. Hence,

\begin{matrix} I (| M, m ⟩_{c} \to | M + 1, m - 1 ⟩_{c}) \\ = {(\frac{g A}{2 h 𝜈})}^{2} [(S - M) (S + M + 1)] [(I + m) (I - m + 1)] . \end{matrix}

(6)

Hence, each 𝛥M = +1 transition consists of 2I hyperfine lines with relative intensity given by the last factor of Equation (6) and a common scaling factor given by the first two factors of Equation (6).

For S > 1∕2 the factor containing S influences the relative intensities of all the possible resonances. The smallest and largest value of this factor is 2S and S(S + 1) + x, respectively, with x = 0 and x = 1∕4 for S being integer and half-integer, respectively. Similarly, the smallest and largest value of the factor containing I is 2I and I(I + 1) + y, respectively, with y = 0 and y = 1∕4 for I being integer and half-integer, respectively. Hence, the ratio of the largest to smallest intensity is

\frac{I (largest)}{I (smallest)} = \frac{[S (S + 1) + x] [I (I + 1) + y]}{(2 S) (2 I)} .

(7)

In the present case with Mn²⁺, (S,I) = (5∕2,5∕2) we have the intensity ratio I(largest)∕I(smallest) = 81∕25.

The intensities for the allowed perpendicular-mode transitions are in stark contrast to those for parallel mode. For perpendicular mode, the intensities are obtained by computing the squared expectation values of $g Ŝ_{x}$ , and the result is

I (| M, m ⟩ \to | M + 1, m ⟩) = {(\frac{g}{2})}^{2} [(S - M) (S + M + 1)] .

(8)

These theoretical perpendicular-mode intensities do not contain the factor (A∕h𝜈)², and unless A is comparable to h𝜈, intensities of parallel-mode spectra are significantly less than those of perpendicular-mode spectra. In the present case with the parameters determined below (see Section 4), this factor is less than 0.001.

4. Results and discussion

In order to identify the crystal orientation, perpendicular-mode spectra were recorded prior to the parallel-mode spectra.

Host	g	a (10⁻⁴ cm⁻¹)	A (10⁻⁴ cm⁻¹)	M–L distance (Å)	Reference
KMgF₃^a	2.000	8.0	−91.2	1.994	[20 ]
Cs[Mg(H₂O)₆]AsO₄^⊥	1.998	8.2	−88.7	2.064	This work
Cs[Mg(H₂O)₆]AsO₄^∥	1.997	8.2	−88.5	2.064	This work
MgO^a	2.000	18.3	−81.4	2.107	[21 , 22 ]
CaO^a	2.001	5.6	−80.8	2.405	[21 ]
SrO^a	2.001	3.0	−78.2	2.562	[21 ]

4.1. Perpendicular-mode EPR

Single-crystal perpendicular-mode spectra of Cs[Mg_0.999Mn_0.001(H₂O)₆]AsO₄ are presented in Figure 2 as a density plot. The spectrum extent on the field axis is roughly 535 G. Forbidden lines of the type |𝛥M| = 1, 𝛥m = ±1 observed in other studies [21, 23] of cubic Mn(II) systems were not visible here. The peak-to-peak linewidths of 7–10 G are significantly broader compared to linewidths in spectra of other cubic manganese(II) systems [21]. A source of the broad lines is the direct dipole–dipole interaction between the electron spin and the 12 protons of the coordinated water molecules. The magnitude of this dipole–dipole interaction can be estimated by using the classical expression for the interaction energy between two magnetic dipoles separated by the distance R. This interaction energy amounts to 1.5 × 10⁻⁴ cm⁻¹ for each proton at a distance R = 2.611 Å from the metal center. For each proton, this interaction energy translates into approximately 1.5 G, and hence is likely the explanation for the rather broad lines. The angular variation of the resonance magnetic field for each line does not exceed 36 G, i.e., about 6% of the full extent of the spectrum. Spectra for three selected orientations of the magnetic field are shown in Figure 3. To determine the parameters of Equation (1), the three spectral traces were simultaneously fitted to theoretical spectra based on Equation (1) [18, 19]. The values obtained for parameters g, a, and A are collected in Table 1. The calculated spectra are virtually identical to the experimental spectra. The energy level diagram in g ≈ 2 field region pertinent to the magnetic field parallel to an S₄ axis is shown in Figure 4. The 30 allowed transitions are indicated with vertical arrows. By comparing Figure 4 with Figure 2 we see that the 5 transitions at approximately 3200 G correspond to 𝛥M = 1 and m = 5∕2, whereas the 5 transitions just below 3700 G correspond to 𝛥M = 1 and m = −5∕2.

Figure 2.
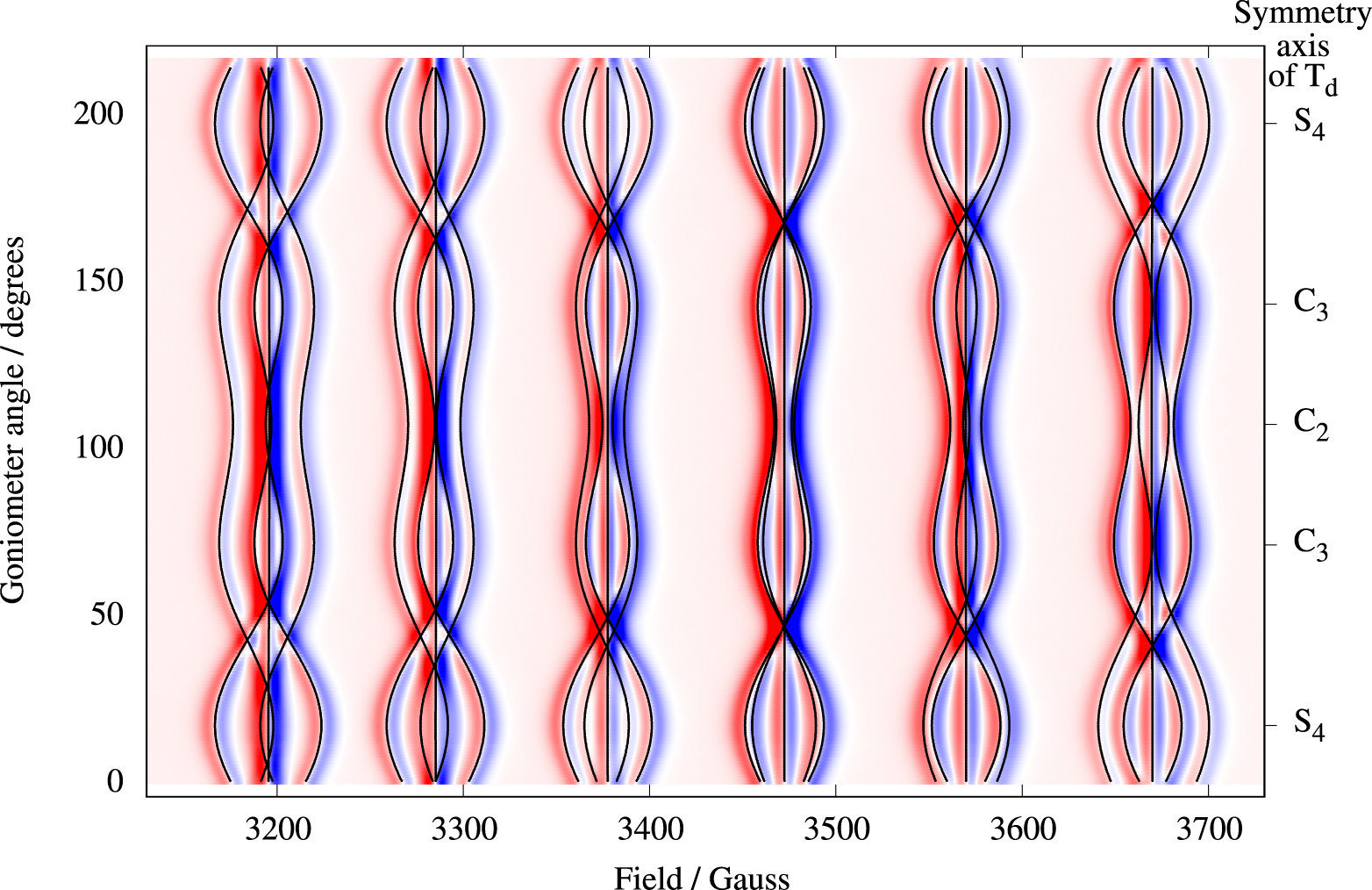
Perpendicular-mode (9.6 GHz) density plot of the angular dependence of the 30 allowed transitions of Mn²⁺(0.1%) in Cs[Mg(H₂O)₆]AsO₄. Red and blue colors represent positive and negative derivative intensities, respectively. The crystal was rotated around a C₂ axis with the magnetic field vector sweeping a plane containing molecular S₄, C₃, and C₂ axes. These special orientations are labelled on the right ordinate axis. The solid black lines are computed resonance magnetic fields based on Equation (1) and the parameters in Table 1.

Figure 3.
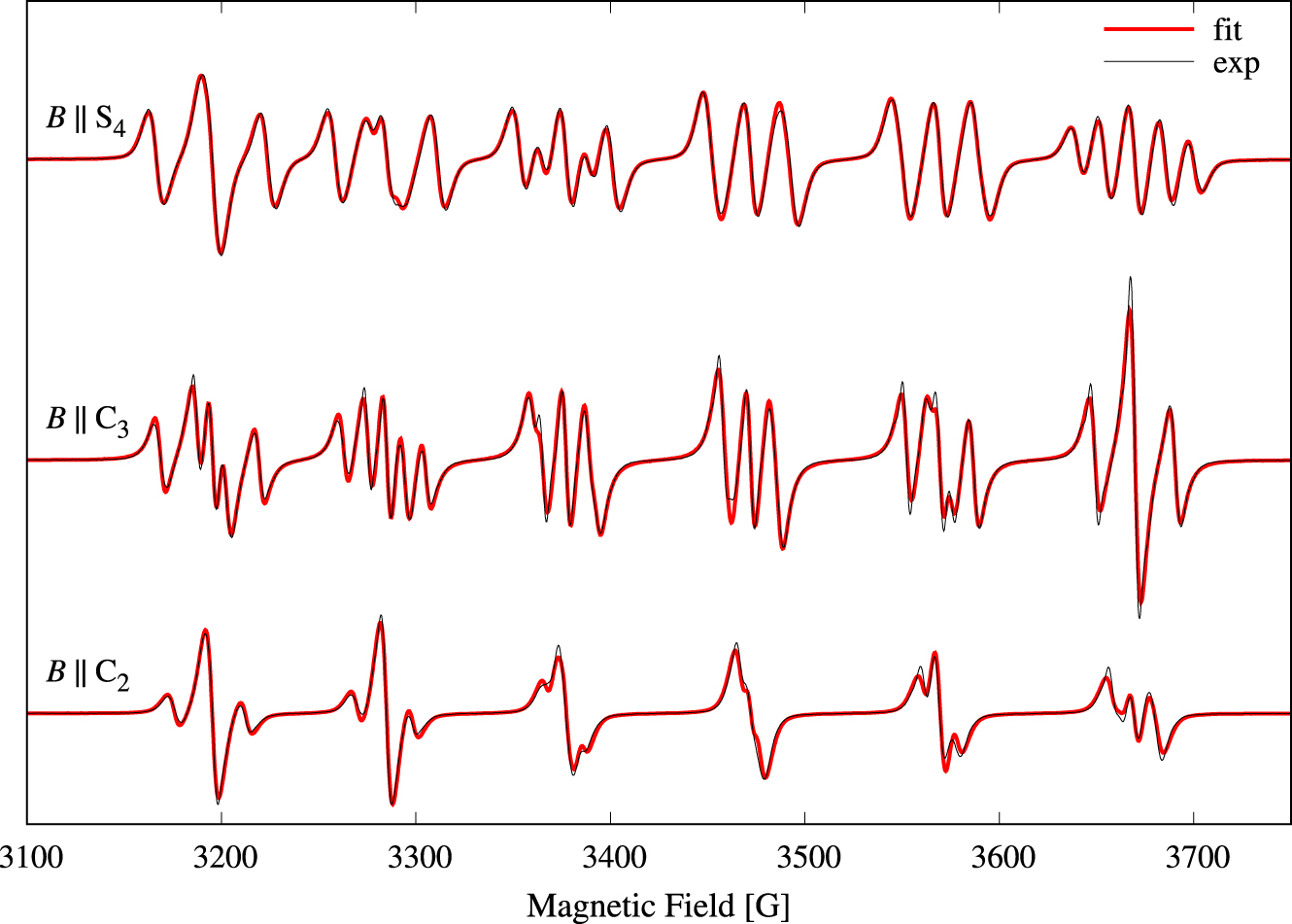
Experimental (solid black traces) perpendicular-mode (9.6 GHz) spectra for three selected magnetic field orientations from Figure 1: B ∥ S₄, B ∥ C₃, and B ∥ C₂. Linewidths of the resonances are in the range 7–10 G. The result of a simultaneous fit of the three perpendicular-mode spectra to Equation (1) is shown with red solid lines.

Figure 4.
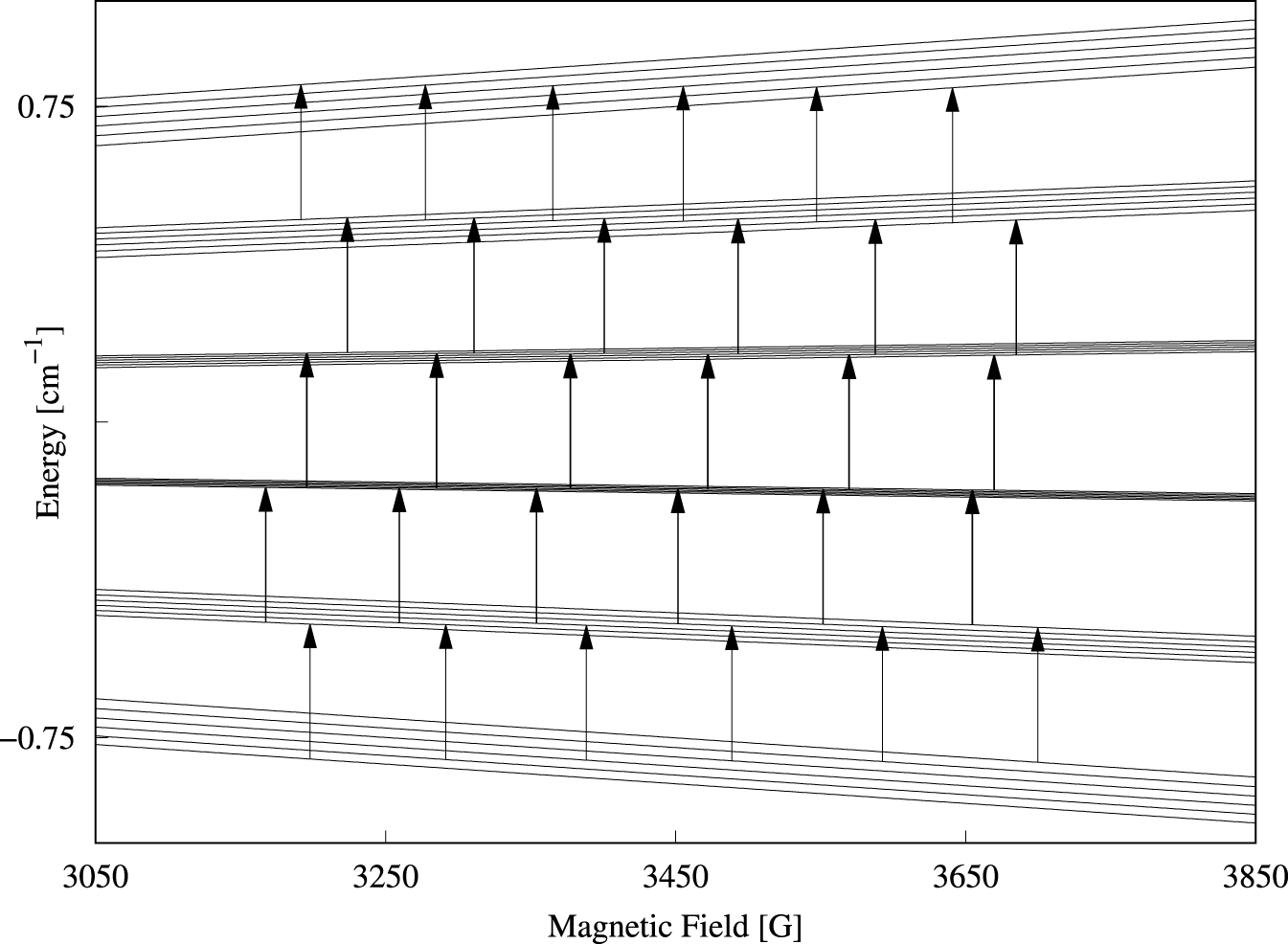
Energy level diagram for B ∥ S₄ in the g ≈ 2 field region obtained by numerical diagonalization of the matrix representation of Equation (1) with the parameters from Table 1. The arrows indicate the allowed perpendicular-mode (9.6 GHz) transitions with 𝛥M = 1 and 𝛥m = 0.

4.2. Parallel-mode EPR

In order to increase the signal-to-noise ratio we recorded the parallel-mode spectra of a crystal containing 1% Mn²⁺. Single-crystal parallel-mode spectra of Cs[Mg_0.99Mn_0.01(H₂O)₆]AsO₄ are presented in Figure 5 as a density plot. The spectrum extent on the field axis is 790 G, i.e., significantly larger compared to Figure 2. The broader lines, 17–26 G, are a result of the higher doping level [24]. The spectra exhibit 9 features centered at roughly 2960, 3044, 3126, 3215, 3303, 3403, 3503, 3608, and 3722 G, and the features are composed of 1, 2, 3, 4, 5, 4, 3, 2, and 1, respectively, separate, partly overlapping or fully overlapping transitions (see also Figure 7). Experimental spectra for three selected orientations of the magnetic field relative to the molecular axes are shown as black traces in Figure 6. Due to the rather large bandwidths combined with the small splittings, only 20 of the 25 possible transitions could be resolved for this high doping level (see the spectrum with B ∥ S₄ in Figure 6). The spectrum with B ∥ C₂, lowest trace in Figure 6, exhibits only 9 lines as a result of overlapping transitions (see also Figure 7). 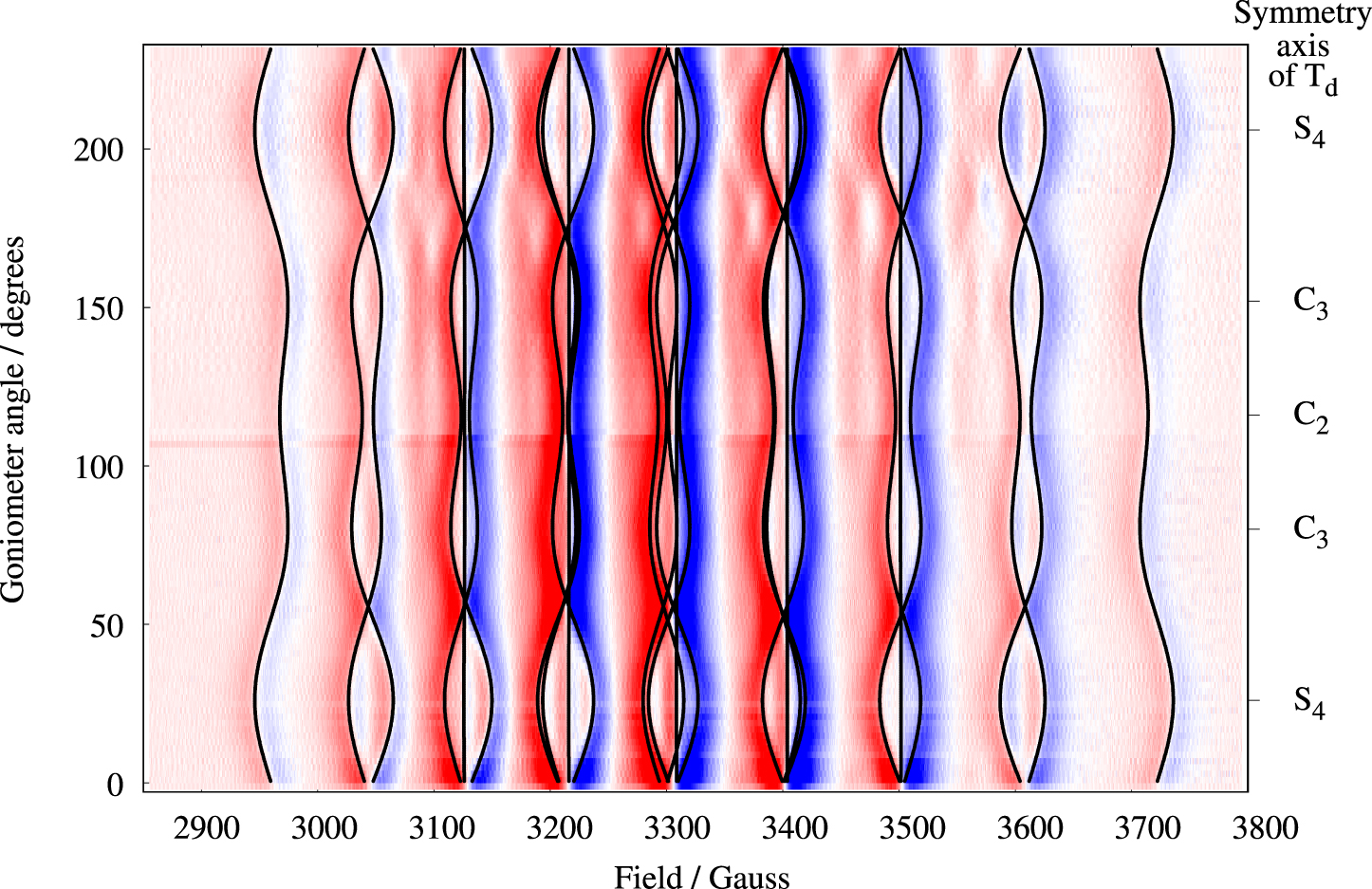The relative intensity of each line can be estimated as $h_{pp} \times w_{pp}^{2}$ , where h_pp and w_pp are the peak-to-peak height and width, respectively. The result is given in the caption of Figure 6. The corresponding theoretical intensities are obtained by vertical additions of the relative intensities in Figure 7. The result is 25, 80, 154, 224, 259, 224, 154, 80, 25. The agreement is fair considering that most of the lines in the lowest trace of Figure 6 are composite and not perfectly overlapping lines.

Figure 5.
Parallel-mode (9.3 GHz) density plot of the angular dependence of the 25 allowed transitions of Mn²⁺(1.0%) in Cs[Mg(H₂O)₆]AsO₄. For each spectra 10 scans were made, due to the low intensity. Color code and crystal orientations as described in caption to Figure 2. The solid black lines are computed resonance magnetic fields based on Equation (1) and the parameters in Table 1.

Figure 6.
Experimental (solid black traces) parallel-mode (9.3 GHz) spectra for three selected magnetic field orientations from Figure 5: B ∥ S₄, B ∥ C₃, and B ∥ C₂. Linewidths of the resonances are in the range 17–26 G. The result of a simultaneous fit of the three parallel-mode spectra to Equation (1) is shown with red solid lines. The presences of a small amount, 0.7‰, of perpendicular-mode in the microwave field is the source of the shoulders marked with a star (*). Relative intensities of the 9 observed lines for B ∥ C₂: 19, 64, 152, 207, 259, 263, 182, 80, 20.

Figure 7.
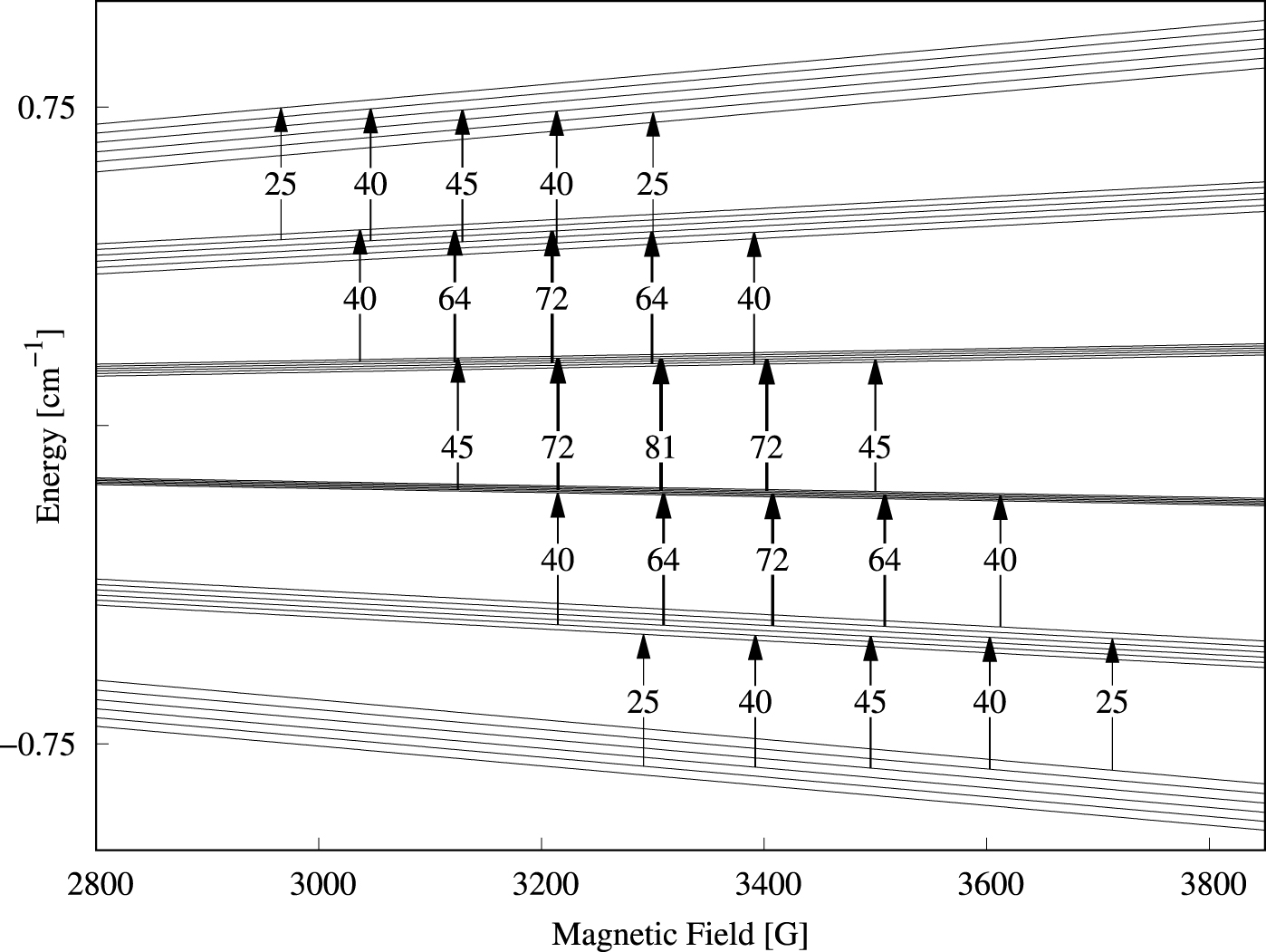
Energy level diagram for B ∥ C₂ in the g ≈ 2 field region obtained as described in the caption to Figure 3. The arrows indicate the allowed parallel-mode (9.3 GHz) transitions with 𝛥M = +1 and 𝛥m = −1. The number attached to each arrow represent the relative intensity obtained from the product of the last two factors of Equation (6).

The three spectral traces were again simultaneously fitted to theoretical spectra based on Equation (1) in order to determine the parameters of Equation (1). The obtained parameters are collected in Table 1. The theoretical spectra are shown with red lines in Figure 6, and the agreement is good. The most noticeable discrepancies are indicated with a “*” in the lowest trace of Figure 6. These weak shoulders result from the presence of 0.7‰ of perpendicular-mode microwave field.

The energy level diagram in the g ≈ 2 field region calculated with the magnetic field parallel to a C₂ axis is shown in Figure 7. The 25 parallel-mode allowed transitions are indicated with vertical arrows.

5. Discussion

The parameter values determined in the two independent fits of the spectra in Figures 3 and 6 are consistent and are collected in Table 1. In the table we have also collected EPR data of manganese(II) ions as a substitutional impurity in other cubic hosts wherein the metal ion is six-coordinated?

The cubic parameter a of the hexaaqua ion is found to be positive in agreement with all results found for eight-, six-, and tetra-coordinated Mn²⁺ in cubic lattices [25].

The isotropic hyperfine coupling constant A for the hexaaqua ion is slightly smaller but comparable in magnitude with the hyperfine coupling constant found for the hexafluorido ion in KMgF₃ (see Table 1). This is in agreement with water and fluoride having similar ligand-to-metal donor properties [26]. The slightly smaller value of A for the aqua ion is also in agreement with the Mn–OH₂ bond being more covalent compared to the Mn–F bond [25]. By the same token, the magnitude of the A parameters for Mn²⁺ in the oxide lattices (see Table 1) are significantly smaller than that for the aqua ion. This indicates that the Mn–O bond is more covalent than the Mn–OH₂ bond despite the fact that the Mn–O bond length is significantly longer than the Mn–OH₂ bond length. Finally we notice that slightly larger and anisotropic hyperfine coupling constants were found for $Mn {(H_{2} O)}_{6}^{2 +}$ as an impurity in hexaaqua zinc hexafluorosilicate and in the ammonium zinc Tutton salt [27].

In summary, we have presented and interpreted parallel-mode EPR spectra of the manganese(II) aqua ion as a substitutional impurity in Cs[Mg(H₂O)₆]AsO₄, wherein the aqua ion occupies a crystallographic site with perfect tetrahedral symmetry. The interpretation agrees with the crystal symmetry by the fact that only a three-parameter cubic model excellently reproduces the experimental spectra. To the best of our knowledge, this is the first report of parallel-mode EPR spectrum of an S > 1∕2 spin system wherein all the allowed fine-structure transitions with associated hyperfine transitions are observed. Expressions based on perturbation theory were derived to account for the relative intensities of the allowed transitions. All the allowed parallel-mode resonances are of the flip-flop type, being zero-quantum coherences [28], i.e., energy but no angular momentum is transferred from the microwave field to the spin system.

Declaration of interests

The authors do not work for, advise, own shares in, or receive funds from any organization that could benefit from this article, and have declared no affiliations other than their research organizations.

Bibliographie

[1] M. P. Hendrich; P. G. Debrunner J. Magn. Reson., 78 (1988), pp. 133-141

[2] S. J. Yoo; H. C. Angove; B. K. Burgess; M. P. Hendrich; E. Münck J. Am. Chem. Soc., 121 (1999), pp. 2534-2545 | DOI

[3] S. Piligkos; D. Collison; V. S. Oganesyan; G. Rajaraman; G. A. Timco; A. J. Thomson; R. E. P. Winpenny; E. J. L. McInnes Phys. Rev. B, 69 (2004), pp. 134424-134428 | DOI

[4] K. A. Campbell; E. Yikilmas; C. V. Grant; W. Gregor; A. F. Miller; R. D. Britt J. Am. Chem Soc., 121 (1999), pp. 4714-4715 | DOI

[5] I. Krivokapic; C. Noble; S. Klitgaard; P. Tregenna-Piggott; H. Weihe; A. L. Barra Angew. Chem. Int. Ed., 44 (2005), pp. 3613-3616 | DOI

[6] Q. Scheifele; T. Birk; J. Bendix; P. L. W. Tregenna-Piggott; H. Weihe Angew. Chem. Int. Ed., 47 (2008), pp. 154-156 | DOI

[7] A. R. Marts; S. M. Greer; D. R. Whitehead; T. M. Woodruff; R. M. Breece; S. W. Shim; S. N. Oseback; E. T. Papish; F. E. Jacobsen; S. M. Cohen; D. L. Tierney Appl. Magn. Reson., 40 (2011), pp. 501-511 | DOI

[8] J. Haak; J. Krüger; N. V. Abrosimov; C. Helling; S. Schultz; G. E. Cutsail Inorg. Chem., 61 (2022), pp. 11173-11181 | DOI

[9] G. Mitrikas; Y. Sanakis; N. Ioannidis Appl. Magn. Reson., 51 (2020), pp. 1451-1466 | DOI

[10] J. A. Weil Concepts Magn. Reson. Part A Bridg. Educ. Res., 28A (2006), pp. 331-336 | DOI

[11] M. Weil Acta Crystallogr. E, 65 (2009), p. i2 | DOI

[12] A. Ferrari; L. Cavalca; M. Nardelli Gazz. Chim. Ital., 85 (1955), pp. 1232-1238

[13] Bruker; Bruker AXS, Inc SAINT, Version 7.68A, Bruker AXS, Madison, WI, 2009

[14] G. Sheldrick Version 2008/2, University of Göttingen, Germany, 2003

[15] S. Bertaina; N. Groll; L. Chen; I. Chiorescu Phys. Rev. B, 84 (2011), 134433 | DOI

[16] P. Sorokin; I. Gelles; W. Smith Phys. Rev., 112 (1958), pp. 1513-1515 | DOI

[17] J. S. Griffith The Theory of Transition Metal Ions, Cambridge University Press, Cambridge, 1961

[18] H. H. Husein; H. Weihe; J. Bendix J. Magn. Res., 207 (2010), pp. 283-286 | DOI

[19] S. Piligkos; I. Laursen; A. Morgenstjerne; H. Weihe Mol. Phys., 105 (2007), pp. 2025-2030 | DOI

[20] S. Ogawa Jpn. J. Appl. Phys., 15 (1960), pp. 1475-1481 | DOI

[21] O. Rubio; P. E. Muñoz; O. J. Boldú; Y. Chen; M. M. Abraham J. Chem. Phys., 70 (1979), pp. 633-638 | DOI

[22] W. Low Phys. Rev., 105 (1957), pp. 793-800 | DOI

[23] S. Smith; P. Auzins; J. Wertz Phys. Rev., 166 (1968), pp. 222-225 | DOI

[24] J. Thorp; A. Skinner J. Magn. Magn. Mater., 69 (1987), pp. 34-42 | DOI

[25] A. Abragam; B. Bleaney Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, England, 1970, pp. 420-440

[26] J. Glerup; O. Mønsted; C. E. Schäffer Inorg. Chem., 15 (1976), pp. 1399-1407 | DOI

[27] B. Bleaney; D. J. E. Ingram Proc. Roy. Soc. A, 205 (1951), pp. 336-356

[28] J. A. Weil; J. R. Bolton Electron Paramagnetic Resonance: Elementary Theory and Practical Applications, John Wiley and Sons, Inc., Hoboken, New Jersey, 2007

Commentaires - Politique

Ces articles pourraient vous intéresser

Branche d’excitation collective du continuum dans les gaz de fermions condensés par paires : étude analytique et lois d’échelle

Yvan Castin; Hadrien Kurkjian

C. R. Phys (2020)

Quantum dynamics in molecular nanomagnets

Wolfgang Wernsdorfer

C. R. Chim (2008)

Effect of diffusional bridging in multicapillary packing

François Parmentier

C. R. Chim (2020)