2.1. Bürgi–Dunitz reaction path and Felkin–Anh rule

In the mid-1970s, Hans-Beat Bürgi and Jack Dunitz proposed to use a structure correlation method, extracted from the Cambridge data base, to obtain information about the molecular potential energy hypersurface which is itself informative about chemical reaction dynamics [5]. The basic assumption is that the observed structures tend to concentrate on the low-lying regions of the potential energy surface. This also implies that the crystalline environment has little influence on the molecular structure. By collecting a series of related species and by looking for correlations between the relevant structural parameters, Bürgi and Dunitz established the pathways for several reactions, namely the nucleophilic substitution, the nucleophilic addition to an aldehyde or a ketone, and the Berry rotation on phosphorus. The same method was later used by Crabtree et al. to propose the pathway for C–H bond activation by an unsaturated metal complex [6]. This input, derived from crystal structures, is very useful although it was only applied to few reactions.

The nucleophilic addition of an amine to a carbonyl group was studied by looking at the relative arrangement of the amino and carbonyl groups in the crystal structures of 14 molecules and by showing the correlation between the N(amino)⋯C(carbonyl) distance and the N⋯C=O angle (Figure 1) [7].

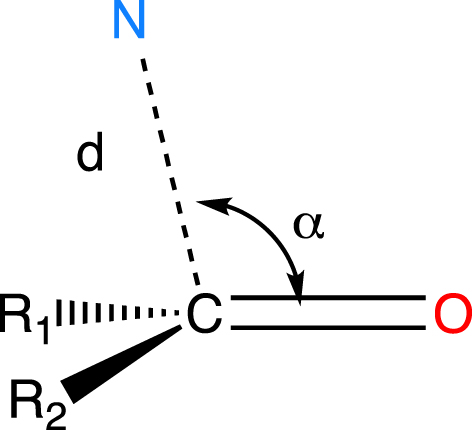
This study suggested that the amino group approaches the carbonyl group from the back of the molecule (𝛼 > 90°). This trajectory was later confirmed by ab initio calculations performed by Lehn and Wipff et al. [8, 9]. The theoretical model was incredibly simple. The nucleophile was an isolated hydride and the substrate was formaldehyde, with all species in the gas phase. Optimization of the whole system using the Hartree–Fock method and a small basis set (the state of the art at the time) for different distances between the hydride and the carbon mirrored the path established by the crystal structures.

This first computational study identified the most important feature of the nucleophilic addition to a carbonyl group, namely that the nucleophile does not add perpendicularly to the C=O bond. This feature was important because it provided information about the short contacts that could occur during the addition. Indeed, this pathway contributed to a more robust interpretation of 1,2-asymmetric induction. The preferred face for the addition of a nucleophile to an aldehyde or a ketone, bearing an 𝛼 chiral carbon (with small S, medium M and large L or polar X substituents), has been a topic of great interest for organic synthesis. Several empirical rules, proposed by Cram, Cornforth, Karabatsos and Felkin, have been used to rationalize the formation of the major diastereoisomer. In these models, the nucleophile preferentially attacked the less hindered face of the carbonyl with a given conformation of the chiral carbon. The problem was that each author had chosen a different conformation resulting in different rules (Figure 2). The purpose of the computational study was to establish which conformation determines the diastereoisomeric preference.

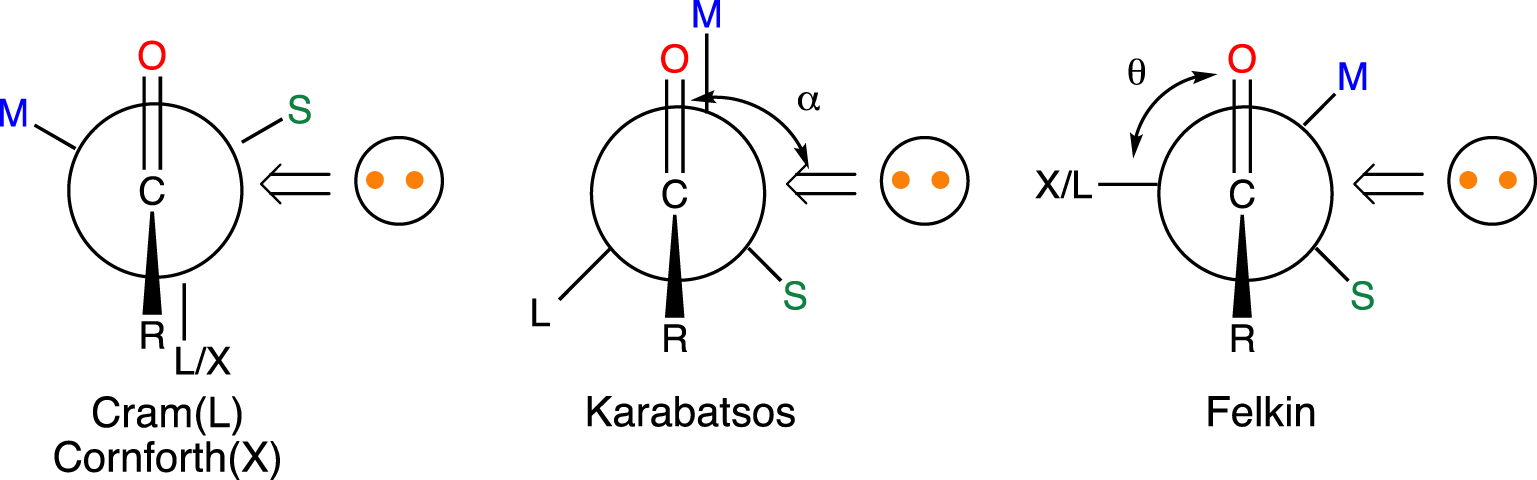
The substrates chosen were Cl(CH₃)HC–CH=O and (CH₃CH₂)(CH₃)HC–CH=O to mimic systems with polar (Cl) or large (CH₂CH₃), small (H), medium (CH₃) and small (H) groups [10]. A naked hydride was positioned at 1.5 Å from the carbon with an optimized H⋯C=O 𝛼 angle (average value around 105°). The Hartree–Fock/STO-3G energies were calculated as a function of the conformation of the chiral carbon described by the 𝜃 dihedral angle, X–C–C–O, (X = Cl or CH₃CH₂) (Figure 2) without further geometry optimization. There was a clear preference for the Felkin model, especially when the 𝛼 angle was greater than 90°. Thus, the nucleophile prefers to add antiperiplanar to the substituent that is either polar (Cl) or the largest (CH₃CH₂) on the face containing the smallest substituent (H).

This conformational preference is rationalized by being associated with the largest interactions between the highest occupied orbital (HOMO) of the nucleophile (the doubly occupied 1s orbital of the hydride) and the lowest unoccupied molecular orbital LUMO π CO ∗ of the carbonyl group (Figure 3). The stabilizing interaction between these two frontier orbitals increases as the energy gap between them decreases and the overlap increases. Thus, lowering the energy of π CO ∗ and increasing the overlap between H⁻ and π CO ∗ is favorable. Interestingly, the energy of the π CO ∗ orbital depends on the conformation of the chiral carbon especially in the case of a polar X group or an atom such as Cl. In fact, the polar C–Cl bond is associated with a low-lying unoccupied σ C–Cl ∗ orbital. When this orbital is parallel to the π CO ∗ orbital (𝜃 = 90° or 270°), the two orbitals overlap and form a low-lying in-phase combination of π CO ∗ and σ C–X ∗ (Figure 3). This interaction between the π and σ orbitals is known as hyperconjugation. The best overlap between the hydride and π CO ∗ is obtained for an obtuse 𝛼 angle to reduce the overlap of the hydride with the oxygen. Some direct overlap of the hydride with σ C–X ∗ could also contribute. This obtuse 𝛼 angle brings the hydride in close proximity to either the S or M group, with a natural preference for the former. This explains why the nucleophile enters antiperiplanar to the X group and on the side containing the smallest group, as suggested by Felkin.

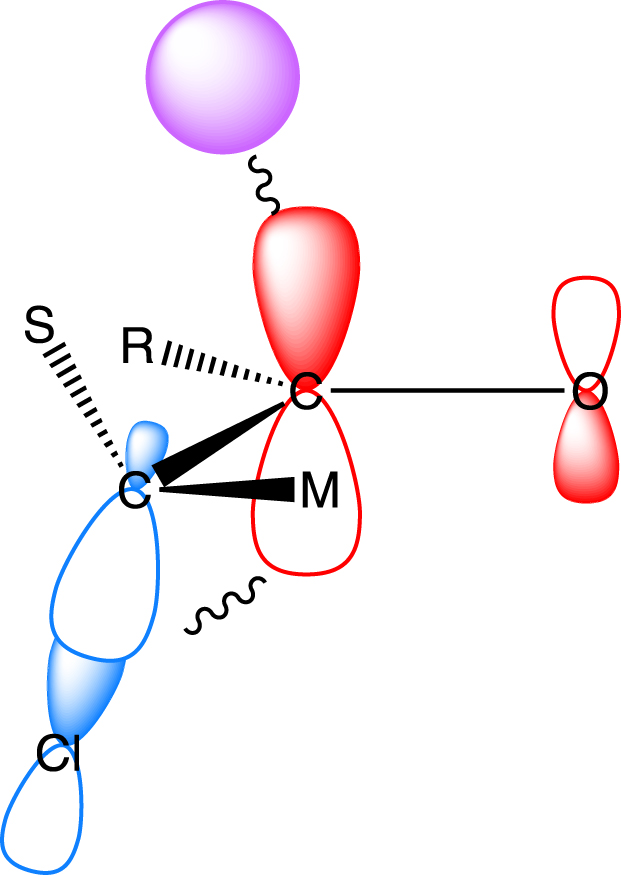
It should be emphasized that the Felkin rule was associated with the best conformation for the nucleophile addition and not with the most stable conformation of the isolated substrate. However, the transition state was not really determined but assumed by following the Bürgi–Dunitz studies. This approach was acceptable until methodological advances made it possible to locate a transition state on a potential energy surface. Naturally, the first studies that included a transition state determination used highly simplified models of the reacting partners. Remarkably, these simplified models were useful and encouraged further studies with better representation of the chemical systems and higher levels of computation.

2.2. The Felkin–Anh and the Cieplak model, the two visions of the antiperiplanarity rule

Interpreting the results in a language that chemists could understand was considered as important by many computational chemists. Explaining the stereoselectivity of the nucleophilic addition to cyclic ketones was particularly challenging. One of the first reviews that attempted to discuss the stereoselectivity of the nucleophilic addition to acyclic and cyclic carbonyls was published by Nguyen Trong Anh, the author’s PhD supervisor [11]. The Felkin–Anh model was not easy to apply. Therefore, an alternative interpretation of the stereoselectivity was presented by Cieplak [12, 13, 14]. This author presented an interpretation in which the bond antiperiplanar to the incoming nucleophile acts as a donor towards the incipient σ C–Nu ∗ empty orbital that is formed when the nucleophile interacts with the carbon of the carbonyl group. The preferred stereoselectivity would be associated with the stronger donor trans to the incoming nucleophile. This was a rather heterodox proposal as it was pointed out by Frenking et al. [15] and by Tomoda [16]. It does not follow the rules of orbital interactions, as established by the frontier orbital theory derived from quantum chemistry [17]. It is also unclear how the C–Nu bond would be formed by the delocalization of electrons into its σ C–Nu ∗ orbital. Although the Cieplak rule has been shown to account for the observed stereoselectivity in some cases [18, 19, 20, 21], it will not appear any longer in the most recent studies because it contradicts basic principles of quantum chemistry. In contrast, the Felkin–Anh rule, which obeys the frontier orbitals theory, gives a qualitative interpretation of how the electron density of the nucleophile is best transferred to the carbonyl substrate and thus contributes to the formation of the incipient bond. It has been used extensively and is still a subject of debate, as illustrated by selected recent literature [22, 23, 24, 25, 26]. A publication, in the 2023 issue of Helvetica Chimica Acta, dedicated to the memory of J. D. Dunitz, used the crystallographic method of Bürgi and Dunitz to rationalize the diastereoselectivity in a peri-naphthalene derivative [27]. However, these antiperiplanarity rules were not sufficient to explain the stereoselectivity of the nucleophilic addition to carbonyl groups and the numerous studies described in the following sections, show the other effects that need to be considered.

2.3. The case of the 1,3-asymmetric induction

The stereoselectivity of 1,3-asymmetric induction was considered in the case of β-ketoester with NaBH₄. The hypothesis in this work was that the transition state is reactant like in non-chelating conditions. Consequently, the preferred conformations of the substrates were considered to determine the selectivity. This proposal gave results in good agreement with experimental data. This is a rare case where the nucleophile was not included in the study [28].

2.4. Energetic aspects of the nucleophilic addition to carbonyl

Ion cyclotron resonance studies and Hartree–Fock calculations for the reaction of alkoxy anions with B₂H₆ provided information on the thermochemical factors that are determining in these reaction pathways [29]. Later, the affinity of the carbonyl groups for anions was calculated with the MP2 method (currently used in the 1990s for organic species) for hydride to XYC=O (X, Y = H, CH₃, NH₂, OH, and F) and selected additional electrophilic compounds (α,β-unsaturated carbonyl, cycloalkanone, heterocarbonyl molecular compounds) with data in good agreement with available experimental data [30]. This study was extended with the calculation of the affinity of various anions Z⁻ (Z = H, CH₃, NH₂, OH, F, CH=CH₂, CH=O, C≡CH, C≡N) for a large variety of carbonyl systems [31].

The interpretation of the obtuse 𝛼 angle for the nucleophilic addition to a carbonyl, currently called the Bürgi–Dunitz angle, has recently been reconsidered and quantified using energy decomposition analysis (EDA) [32] and the activation strain model [33] in the case of the addition of CN⁻ to (CH₃)₂C=O. With the EDA analysis, Bickelhaupt et al. showed that the obtuse bond angle results from the combination of three effects: the Pauli repulsion between the HOMO of the nucleophile and the occupied π orbitals of the substrate, the stabilizing interaction between the HOMO of the nucleophile and the LUMO, π CO ∗, of the substrate and the electrostatic interaction between the nucleophile and the substrate. Combining the strain and the EDA analyses, it was found that the preference for an obtuse 𝛼 angle results from a delicate balance between the strain and the stabilizing energies. The strain energy, associated with the deformation of the different chemical species prevents the 𝛼 angle from becoming too large. In contrast, the stabilizing energy, dominated by the Pauli repulsion, prevents the same angle from getting smaller (i.e. < 90°). These recent studies demonstrate the importance of quantitative analysis tools to determine the relative importance of the attractive and repulsive interactions. This enriches and quantifies the earlier qualitative analyses.

3.1. Early studies with non-cyclic carbonyls

A quantitative computational study of the reaction mechanism requires a reasonable representation of all the reagents and the environment, in particular the solvent, as well as an extensive exploration of the chemical spaces and a proper calculation of the thermodynamics of the chemical systems in solution. These features have been slowly achieved over the years and this section describes, through selected examples, the information that has been gained about the nucleophilic addition to carbonyls and illustrates the improvements in modeling and computation.

Soon after the very first studies, the naked hydride was replaced by more realistic model of the nucleophile. Borohydride was one of them but the cation and the solvent were not yet included. The Hartree–Fock study of the reaction of BH 4 − with formaldehyde showed that the formation of the anionic CH 3 OBH 3 − was thermodynamically favored and led to the localization of a transition state. The reaction was found to be concerted although significantly non-synchronous with the C–H bond being essentially formed while the O⋯B bond was not. The two-step pathway was also identified and found to be at higher energy than the concerted pathway. Both mechanisms were associated with high energy barriers probably due to an overly simplistic modeling of the chemical species which neither included the cation nor the solvent [34]. A related study using B₂H₆ as nucleophile showed that a BH₃ coordinates the oxygen [35]. Calculations showed that the addition of AlH₃ to formaldehyde proceeds via a 4-centered transition state and forms an energetically favorable aluminum methoxide product [36].

A computational model still using a naked hydride was proposed in the 1990s to analyze the face selectivity in the case of sterically unbiased ketones. Using also semi-empirical method (MNDO), the authors were able to consider large molecules like substituted norbornanones and other bicyclic ketones. The experimental selectivity was well reproduced. The authors point out that the geometrical details of the transition state seemed unimportant but the presence of a hydride was necessary in the calculations [37].

3.2. Early studies with cyclic ketones

Considerable efforts have been devoted to the study of the face selectivity for the addition of various nucleophiles to substituted cyclohexanones. These 6-membered ring ketones posed a great computational challenge due to their ring flexibility. The studies were all based on the determination of the reaction pathway by identifying the transition states with different nucleophiles that were modeling as well as possible those used in the experiments. The solvent also began to be included in the computational studies, usually by means of a continuum method, although not yet systematically. This improved the representation of the electrostatic contribution. The studies were aimed at finding the facial preferences and also at understanding, at least in a qualitative way, the various factors that determine these preferences.

The study of the addition of AlH₃ to 5-substituted adamantanones (Figure 4) confirmed the involvement by hyperconjugation of the bond that is antiperiplanar to the incoming nucleophile (the essence of the Felkin–Anh model) and pointed out the importance of torsional effects in the face selectivity [38]. A study of the reduction of substituted 7-norbornanones (Figure 4) using the AM1 method emphasized the importance of determining the transition state and not just looking at the electrostatic properties of the substrate. Using AlH₃ to model the reactivity of NaAlH₄ reproduced the stereoselectivity for a whole series of substituted norbornanones [39].

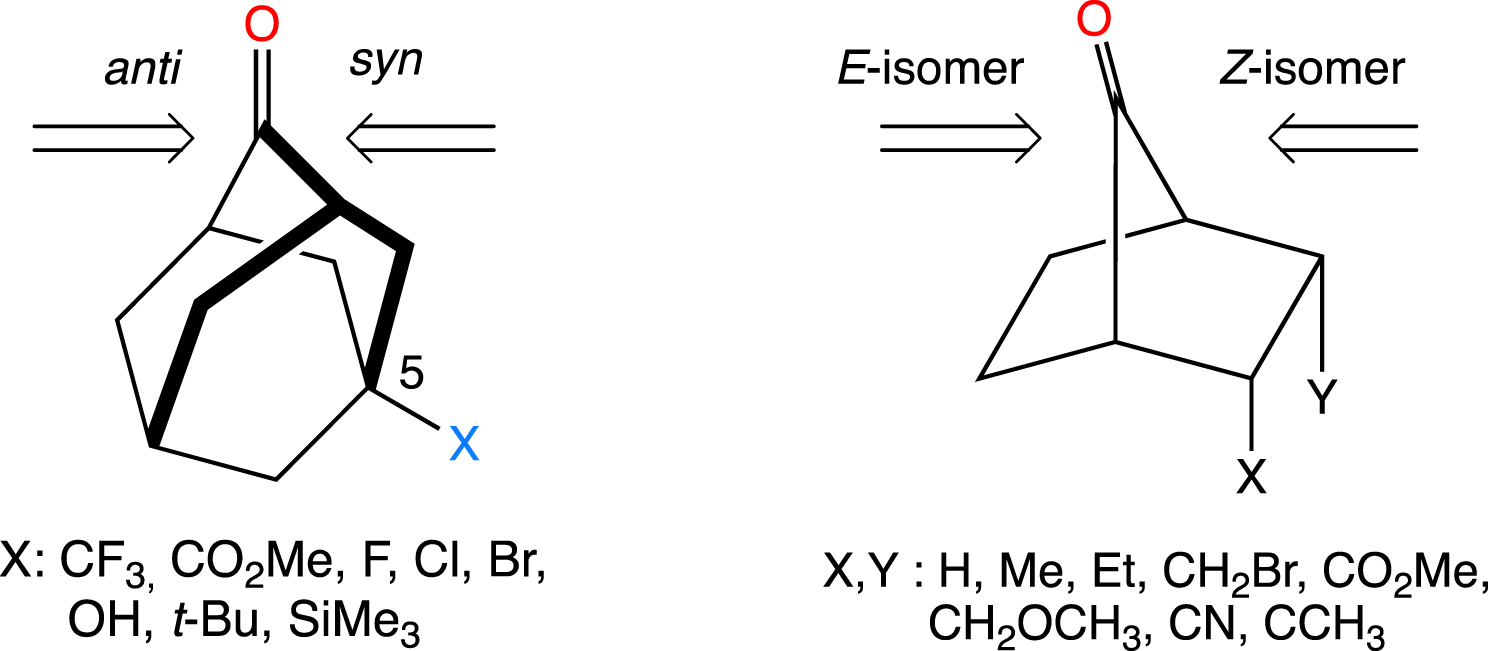
LiH was shown to be associated with a 4-centered transition state and a preference for addition of the hydride to the axial face of the cyclohexanone (Figure 5). This preference, established for a small nucleophile, was related to a distortion of the π CO ∗ orbital, which was more developed toward the axial face. This distortion was shown to be due to the hyperconjugation with the neighboring C–H and C–C orbitals. Large nucleophiles had a preference for the equatorial approach due to steric hindrance on the axial face [15]. Around the same time, the relative importance of torsional strain and electrostatic interactions was studied, with LiH and NaH as nucleophiles and cyclohexanone and related substituted cyclic carbonyl molecules. Some general trends have emerged. Torsional strain at the transition state disfavors the equatorial attack, steric effects often disfavor the axial attack and the electrostatic interactions can dominate when polar substituents are present on the ring. Substituents have stronger effects at the axial site than at the equatorial site [40, 41], and for substituted 7-norbornanones [42]. In 1992, Li and le Noble considered all the rules that have been proposed and favored a rational that mixes the torsional effects, the Felkin–Anh and Cieplak rules in different amounts for each system [43].

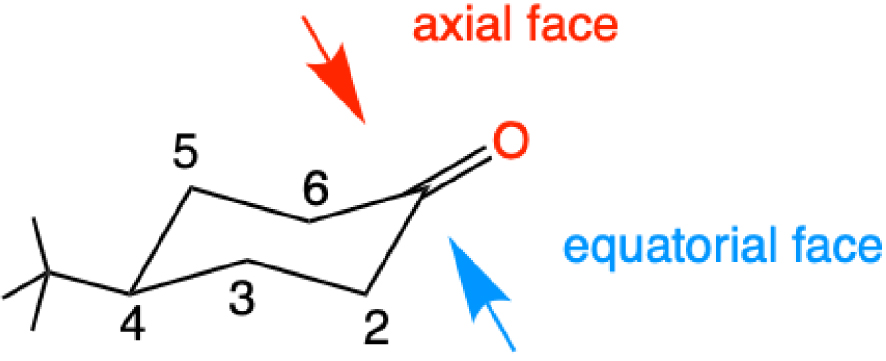
Ion mass spectrometry studies showed that pentacoordinated silicon hydride is also a nucleophile that can add to cyclohexanone and related molecules [44]. This was of interest for the computational studies because gas phase and solution chemistry could be compared. Using SiH 5 − as a simplified model of the experimental pentacoordinated alkoxide silicon hydride, the selectivity of the reduction of several cyclohexanone derivatives was studied using Hartree–Fock and MP2 methods in the gas-phase and the solution [45]. The transition state is dominated by the hydride transfer and very little Si–O bond formation. Axial reduction is preferred for the cyclohexanone but the equatorial reduction is preferred for dithianone, the preferences being similar in the gas phase and in solution. However, for dioxanone, the gas phase favors the equatorial addition and the solution (methanol) favors the axial addition. These computational results were consistent with the observed selectivity of the reactions with NaBH₄, LiAlH₄ and Grignard reagents in solution. They were qualitatively rationalized as coming from a balance between electrostatic interactions which disfavors the axial approach and torsional strain which disfavors the equatorial attack. Further studies with hindered cyclohexanones and various nucleophiles (hydride, methyl, acetylenic Grignard and lithium reagents) were performed. The reaction of CH₃Li or HC≡CLi with non-substituted cyclohexanone was carried out with an ab-initio Hartree–Fock study but the same method could not be applied for hindered cyclohexanones. In this latter case an adapted MM2 force field method was used. This approach led to a good reproduction of the observed selectivity. In this case also, the selectivity resulted from a balance between steric and torsional effects [46]. The intrinsic diastereoselectivity of the reduction of a large series of cyclic ketones by pentacoordinated silicon hydride ions was investigated in the gas phase using the flowing afterglow-triple quadrupole technique [47]. The percent axial reduction was determined by collision-induced dissociation experiments. The trend observed in the condensed phase is consistent with the results observed in the gas phase suggesting that environmental effects are either unimportant or cancel each other out. Consequently, the diastereoselectivity was proposed to be related to the intrinsic nature of the substrate and rationalized as resulting from a competition between steric, torsional and electrostatic effects.

3.3. The relative importance of the effects influencing selectivity

Calculations were clearly able to reproduce the observed stereoselectivity but they were not easy to interpret. The energy difference between the approach to the two faces of the carbonyl group is small (usually less than 1 kcal/mol) and it is a real challenge to identify the driving effect (if there is one) among the several competing interactions. The following factors have been mentioned: (i) the charge transfer of the nucleophile to the substrate also called delocalization or hyperconjugation (i.e. the Felkin–Anh or Cieplak rules), (ii) the electrostatic interaction, (iii) the steric [48] and strain energies, and (iv) the chelation. Another indicator of stereogenicity has been proposed. It is intrinsic to the prochiral substrate and can be derived from its molecular orbitals. The determination of the transition state of the nucleophilic addition can thus be avoided. In a prochiral carbonyl group, the two faces of the π bond are not equivalent. It means that the occupied π orbital as well as the LUMO π CO ∗ have greater extension toward one of the two faces of the carbonyl. Authors have analyzed these distortions focusing on the carbon contribution. These different extensions result from the mixing of the 2p and 2s carbon orbitals (Figure 6). An earlier version of this indicator was used to justify the Cram rule [49]. This dissymmetry in the occupied or empty orbitals has been considered by Klein in particular for 5- and 6-membered ring ketones [50, 51]. An elaborate quantitative evaluation of the expansion of the LUMO π CO ∗ orbital was developed by Tomoda [16].

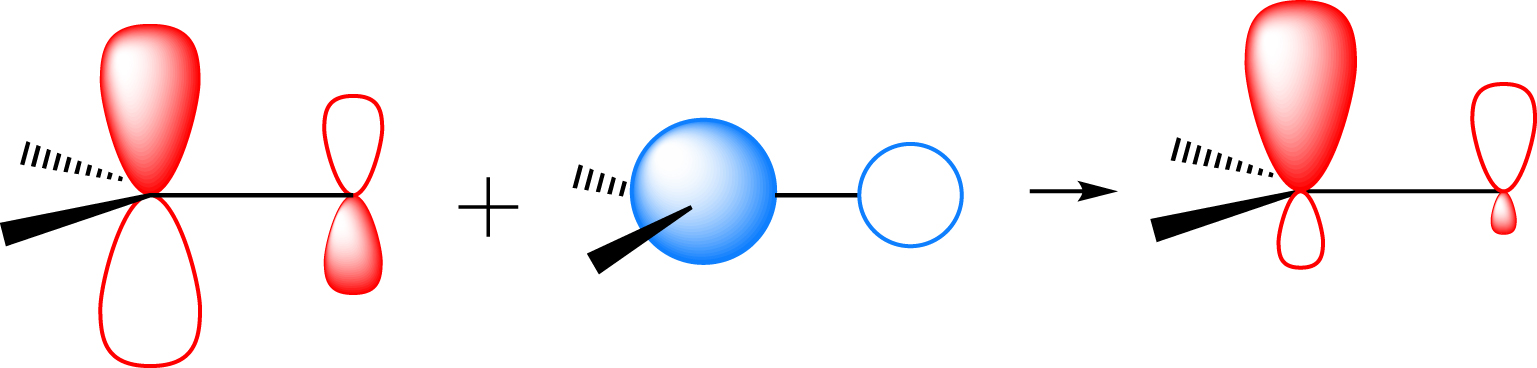
The relative importance and validity of these various criteria were the subject of an entire issue of Chem. Rev. in 1999, indicating how important these criteria were to the community of chemists. For example, in this issue, Dannenberg nicely discussed the pros and cons of electronic criteria that were used in those years [52]. He pointed out that it was unlikely that a single rule could rationalize all cases. Ohwada described how to use orbitals to rationalize the face selection in sterically unbiased cyclic systems [53]. Cieplak presented his interpretation of the effect of substituents on π-face selection [14]. Wipf and Jung discussed the role of dipole effects [54], Mehta and Chandrasekhar discussed various electronic effects for sterically unbiased ketones and olefins [55]. Adcock and Trout discussed the case of rigid saturated model substrates and in particular the influence of the substituents [56].

A study by Rosenberg et al. is notable by the number of systems studied experimentally and computationally and by the careful consideration of a large number of factors [57]. These authors considered a series of 2-X-4-tert-butylcyclohexanones (X = H, CH₃, OCH₃, F, Cl, Br; with X equatorial or axial), studied their reactivity with LiAlH₄ and, performed computational studies of the face selectivity. They used the simplified model of the hydride that was currently selected in the early 2000s (LiH, NaH, BH₃, AlH₃). They determined the transition states for all the systems and obtained a calculated selectivity which correctly identified the main isomer. The experimental trends were better reproduced by the calculations when the X substituent was equatorial than axial. The controlling factors appeared to be the electrostatic interactions between the nucleophile and the substituent X. When X was axial, the electrostatic effect or the Felkin–Anh rule rationalized the results but the Cieplak model failed.

Thus, in the early 2000s, it was clear that a large number of factors were controlling the face selectivity and that none was dominant. It was also encouraging that calculations were successful to determine the major isomer, although the observed trends were sometimes difficult to reproduce. Given the very small energy difference between the transition states of the addition of the nucleophile on the two faces of the carbonyl, this was very encouraging. Thus, in the following years, improved calculations were performed. This includes a more realistic modeling of the nucleophile, the presence of the counter cation, the almost systematic inclusion of the solvent which was represented either implicitly (by a continuum) or explicitly by the presence of one or two solvent molecules. This also includes the use of more elaborate computational methods, in particular DFT methods that were successful at representing together the strong covalent bonding and the weak non covalent interactions. The determination of the reaction pathway (transition states and intermediates) was systematic. This “static approach” was the state of the art for many years. It was powerful, relatively inexpensive and usually successful in calculating selectivity in good agreement with the experimental data. However, with this static approach, the ability to accurately represent the thermodynamics of a very complex system of solute and solvent could be limited.

3.4. Studies with improved representation of the nucleophilic reagent

Calculations were performed with LiBH₄, NaBH₄ or LiAlH₄ as reagents. This allowed to understand how the cation and the element (B or Al) carrying the hydride cooperate to transfer the hydride to the carbonyl carbon. The solvent was often but not always included although its presence seemed necessary in presence of charged species. Besides the determination of the reaction pathway, the stereoselectivity for acyclic and cyclic carbonyl remained the main goal of these studies.

The computational study of the reaction of LiAlH₄ with formaldehyde and cyclohexanone was carried out in the gas phase [58]. The authors stated that neglecting the solvent was justified because similar stereoselectivity had been observed in the gas phase and in solution [47]. Under these conditions, the calculations were performed with the DFT method with the widely popular B3LYP functional and a 6–31G^∗∗ basis set (a good level of calculation in the early 2000s). Two types of transition states with either bidentate (preferred) or tridentate Li/AlH₃ bonding were identified (Figure 7). All transition states yielded the same intermediate where Li is still bound to the oxygen. It rearranges to the more stable Al–O bound final product.

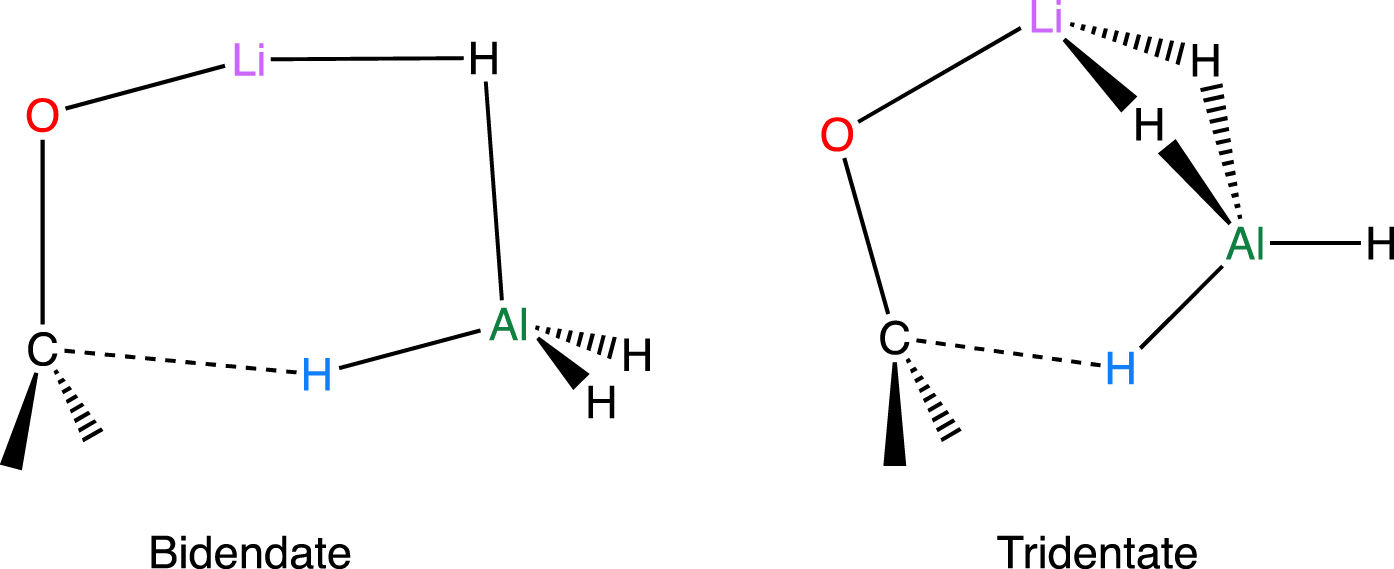
The calculations carried out for the cyclohexanone show a preference for an axial approach, which has already been found with nucleophiles such as LiH, SiH 5 −, BH₃ etc. The strain energy is again mentioned as disfavoring the equatorial attack. The hyperconjugation effect is suggested to be small since the C–H and C–C σ bonds, next to the reactive carbonyl group, do not lengthen or contract significantly. Thus, the greater extension of the π CO ∗ LUMO towards the axial face was suggested to be a favorable factor for the attack on this face. A similar study was carried out on the reduction of 2-X-substituted cyclohexanones (X = OMe, SMe, SeMe) with LiAlH₄ in the gas phase [59]. To interpret the results, the extension of the π CO ∗ LUMO towards one of the faces of the carbonyl and the electrostatic potential were considered. However, this was not sufficient because the conformations of the 6-membered ring and the complexation of X by lithium (Li) had a determining role in the stereoselectivity. To study cases where the X⋯Li interactions did not exist, calculations were also performed for X = CH₃ and CH(CH₃)₂  [60]. The conformational preferences of the 2-X-substituted cyclohexanones in the transition state gave a preference for the trans-isomer (Figure 8).

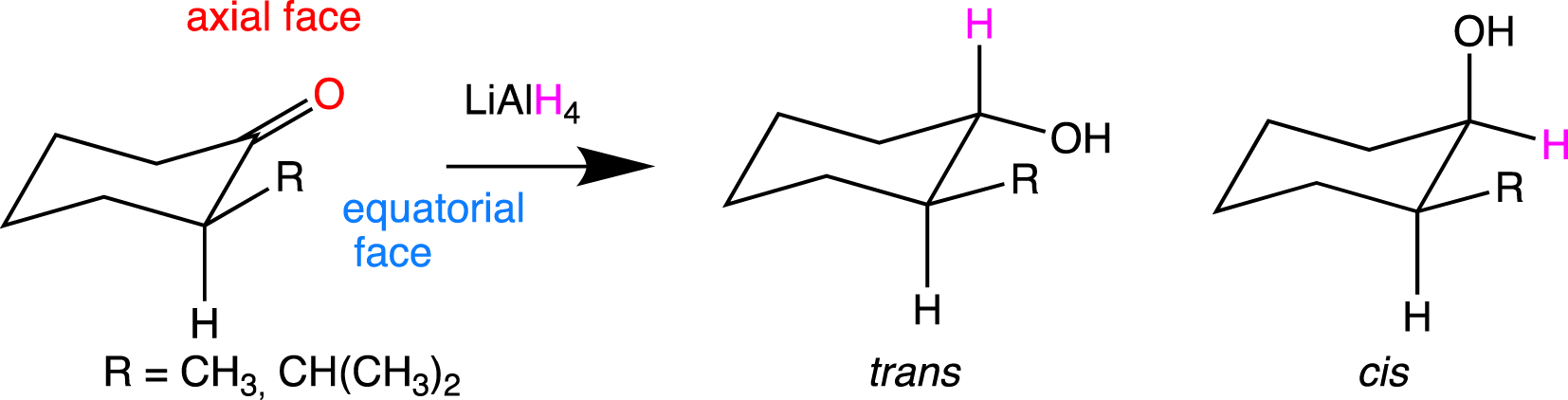
The reaction mechanisms for the addition of LiBH₄ and LiAlH₄ to formaldehyde were compared with the CAM-B3LYP/Aug-cc-pVTZ level for geometry optimization and with single point calculations at the CCSD(T)/Aug-cc-pVTZ level [61]. The solvent (THF) was represented by an SCRF/PCM continuum and selected calculations included an explicit molecule of THF. The energy barrier was significantly higher for LiBH₄ than for LiAlH₄. Thus, in agreement with the Hammond postulate, the transition state is product like for LiBH₄ and reactant like for LiAlH₄. In the product, O–B or O–Al bonds are formed and Li interacts either with the oxygen only (case of LiAlH₄) or with the oxygen and the hydride (case of LiBH₄). From, the evolution of the charge density along the reaction pathway, the authors suggested that the reaction started with an electron transfer from the hydride to the carbon of the carbonyl and is followed by the hydrogen transfer. This mechanism has not been suggested in other studies.

The experimental conditions were well represented in the relatively recent computational study of the face selectivity for reactions of small and large hydride species to 4-tert-butylcyclohexanone, cis-2,6-dimethyl N-acylpiperidone and N-acyltropinone (Figure 9) [62]. The substrates were considered in full and, small and large hydrides were represented by LiAlH₄ and by LiBH(CH₃)₃, respectively. LiBH(CH₃)₃ was used as a model for the experimental lithium tri-sec-butylborohydride, L-Selectride, whose conformational complexity was beyond the reach of calculations. The geometry optimization was carried out at the B3LYP/6-31(d,p) and the energies were refined by single point calculations with a larger basis set and implicit solvent effect represented with a recently developed powerful continuum method (SMD). These were high level calculations for such systems 10 years ago. The calculated free energies of activation (ΔG^≠) for the addition of the nucleophile to the two faces of the carbonyls differ by less than 1 kcal/mol and systematically, the transition state that yields the observed major isomer is calculated to have the lower energy. Thus, small diastereoisomeric excesses were correctly calculated. Small hydride species preferentially added to the axial face of the substituted cyclohexanones and tropinone. However, an equatorial attack to a twist boat conformation was preferred for the piperidone. In the case of the bulky hydride, the equatorial face was preferred in all systems. Torsional strain and steric effects control the selectivity and steric effects dominate in the case of large hydride.

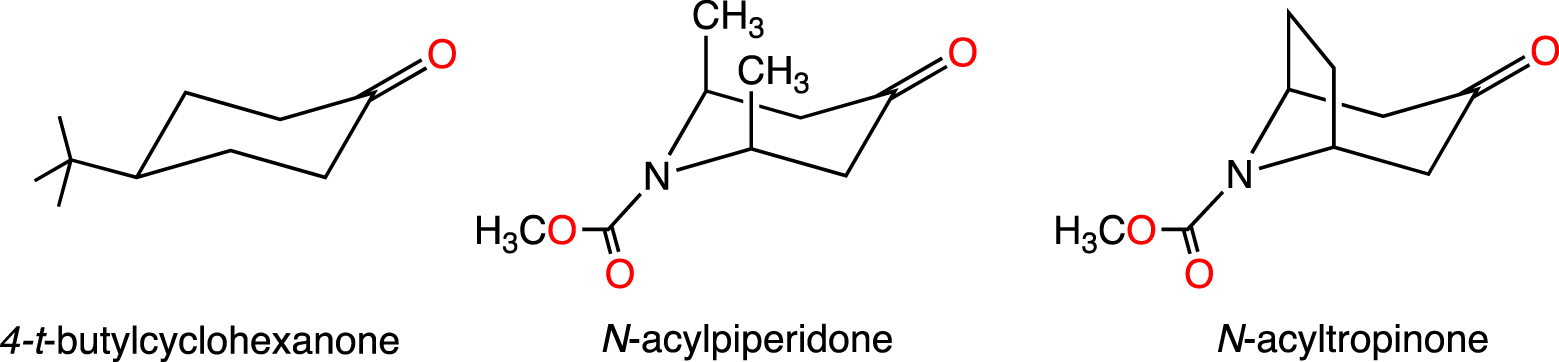
Recent years have seen an improved representation of solvation. Solvation has been implemented in calculations for many years using a continuum model which in particular allowed a correct representation of the electrostatic effects in solution. However, microsolvation was not present in implicit solvation and its omission was becoming increasingly questionable because microsolvation is recognized to be important when polar reagents are used. Thus, the selectivity of the reduction of 4-tert-butylcyclohexanone by LiAl(OR)₃H (R = tert-butyl for the experiments and methyl for the calculations) with THF mono- and bi-solvation was studied computationally with three functionals, B3LYP, B3LYP-D3 and M06-2X [63]. Implicit solvation was also included with the SMD method. Bi-solvation was found to be preferred. A two-step reaction was identified, with the first step describing the hydride transfer to the carbonyl carbon and the second step describing the formation of the Al–O bond. However, the intermediate between the two transition states is energetically high and close to the two transition states, questioning the existence of a two-step reaction and a strongly non-synchronous reaction cannot be ruled out. In fact, a recent high-level calculation of the reduction of 2-X-substituted cyclohexanones (X = H, Cl, Br) by NaBH₄ in which the solvent is explicitly represented by microsolvation and implicitly represented by a continuum showed a single transition state pathway [64]. This recent study highlights the need for this dual representation of the solvent. The calculations gave a late transition state with an almost formed C–H bond as actually found in most previous studies. This late transition state was said to be consistent with the mild reducing power of NaBH₄. The observation that 2-halo cyclohexanones are more reactive than cyclohexanone was only well represented when both solvation and microsolvation were considered. Thus, even if the solvent (ethanol) does not change the face selectivity, its explicit inclusion is necessary to better model a reaction pathway involving polar transition states. Today, the need for an explicit representation of the solvent molecules especially when highly polar or ionic species are present is fully recognized. The question remains on how to represent this explicit solvation. For years, calculations were performed with a reasonably small number of solvent molecules following some computational tests and chemical intuition. Today, this is an important issue in the study of reaction pathways and other methods are starting to be used [65] (see also below).

Computational chemists have also been concerned with the quality of the calculations and in particular with the method and level of calculation that must be used to represent the strong bonds and the weak interactions in a balanced way in order to correctly determine the face selectivity. Such a study has been carried out for substituted 2-X-substituted cyclohexanones (X = Me, OMe, SMe, Cl) and LiAlH₄ with eight different functionals, MP2 and CCSD(T) methods [66]. The energy barrier is found to be more sensitive to the calculation method than the conformational properties of the substrate. MP2 appears one of the poorest methods in this particular study. The coordination mode of AlH₄ to Li at the transition state was found to depend on the calculation method but not the face selectivity which is the same for all methods. An interesting analysis of the strain energy and steric effects, reinforces the accepted understanding that face selectivity results from a balance between them. The fact that the selectivity of the reaction does not vary with these already high-level computational methods is encouraging for further studies with more complex substrates and nucleophiles.

4.1. The metal hydride cases

The nature of the solvated species present in ethereal solutions of LiAlH₄ has been studied by combining experiments and computations based on IR spectroscopy. The result of this study is that LiAlH₄ in ethereal solutions forms contact ion pairs. The dissociated species are higher in energy than the associated species by about 2.3 kcal/mol and 4 kcal/mol for THF and dimethyl ether, respectively [67].

Car–Parrinello molecular dynamics simulation of NaBH₄ in methanol also suggested a preference for a solvated contact ion pair and found that the dissociation pair to be more than 4 kcal/mol higher in energy [68]. This led the authors to propose a transition state for the reduction of ketone that incorporates this finding in a set of static calculations. Using this solvated contact ion pair as reagent for the reaction with cyclohexanone derivatives dramatically lowers the activation energy. It also leads to calculated selectivities in very good agreement with observed values (4-methylcyclohexanone axial/equatorial: exp = 86:14, calc = 80.9:19.1; 2-tert-butcyclohexanone axial/equatorial: exp = 50:50, calc = 41:59). These results were used to calculate the complete mechanism for the reduction of resorufin by NaBH₄ in water [69]. As mentioned above, the effect of the solvent (ethanol) on the stereoselectivity and reactivity was also investigated in the case of the reduction of 2-X-substituted cyclohexanones (X = H, Cl, Br) by NaBH₄ [64].

4.2. The Grignard reaction

The Grignard reaction is a prominent process in organic synthesis for the formation of carbon–carbon bonds. Despite extensive experimental studies, the mechanism of the reaction at the molecular level remains unknown. This is because the nature of the Grignard reagent in solution is still unknown. As summarized by Dietmar Seyferth, “Generally written as RMgX, the Grignard reagents in ethereal solution are more complicated than this simple formula indicates” [70]. It is currently recognized that the nominal reagent, RMgX is a condensed representation of numerous mono- and poly-metallic species in rapid equilibrium and that the exact nature of the species is determined by the solvent. Thus, unfortunately, most of the studies attempting to characterize these species by the most advanced and diverse spectroscopic methods [71], and crystallization have identified them under conditions different from those of the reaction itself. Traditional static computational methods would also fail because they cannot properly calculate the free energy changes of the solvent organization and dynamics at close and intermediate distances from the organomagnesium species. A method of calculations capable of representing the thermodynamics of the solute and the solvent, as accurately as possible, is the ab initio molecular dynamics (AIMD). This method has been used to describe solvated NaBH₄ as mentioned above [68] and has thus been used to uncover the diversity of species representing the global Grignard reagent in ethereal solution and to propose a mechanism for the Schlenk equilibrium (Equation (1)), for CH₃MgCl in THF [72].

It appears that the solvation of the magnesium species is highly variable and also very dynamic. It takes very little energy to add or remove a solvent molecule from the coordination sphere of magnesium. As expected, solvation is higher when Mg is bound to the electron withdrawing-chloride atom than to the electron-donating methyl group. Thus, dimethyl magnesium is best solvated by two THF molecules, while magnesium dichloride prefers three THF molecules in its coordination sphere. Thus, a higher positive charge on Mg increases the solvation. Several chloride and methyl-bridged dinuclear magnesium species, which differ in their solvation, are present in equilibrium, (Figure 10). The calculations suggest that the Cl/Me exchange between the two magnesium centers is initiated by a solvation imbalance between the two metal centers. The least solvated attracts a bridging chloride more strongly. The chloride unequally bound to the two magnesium centers becomes terminal to the closer magnesium promoting the transfer of a methyl group from the terminal to the bridging position. This chloride-methyl-bridged dimer achieves the Cl/Me exchange. The dynamics of the solvent is thus essential in the Schlenk equilibrium.

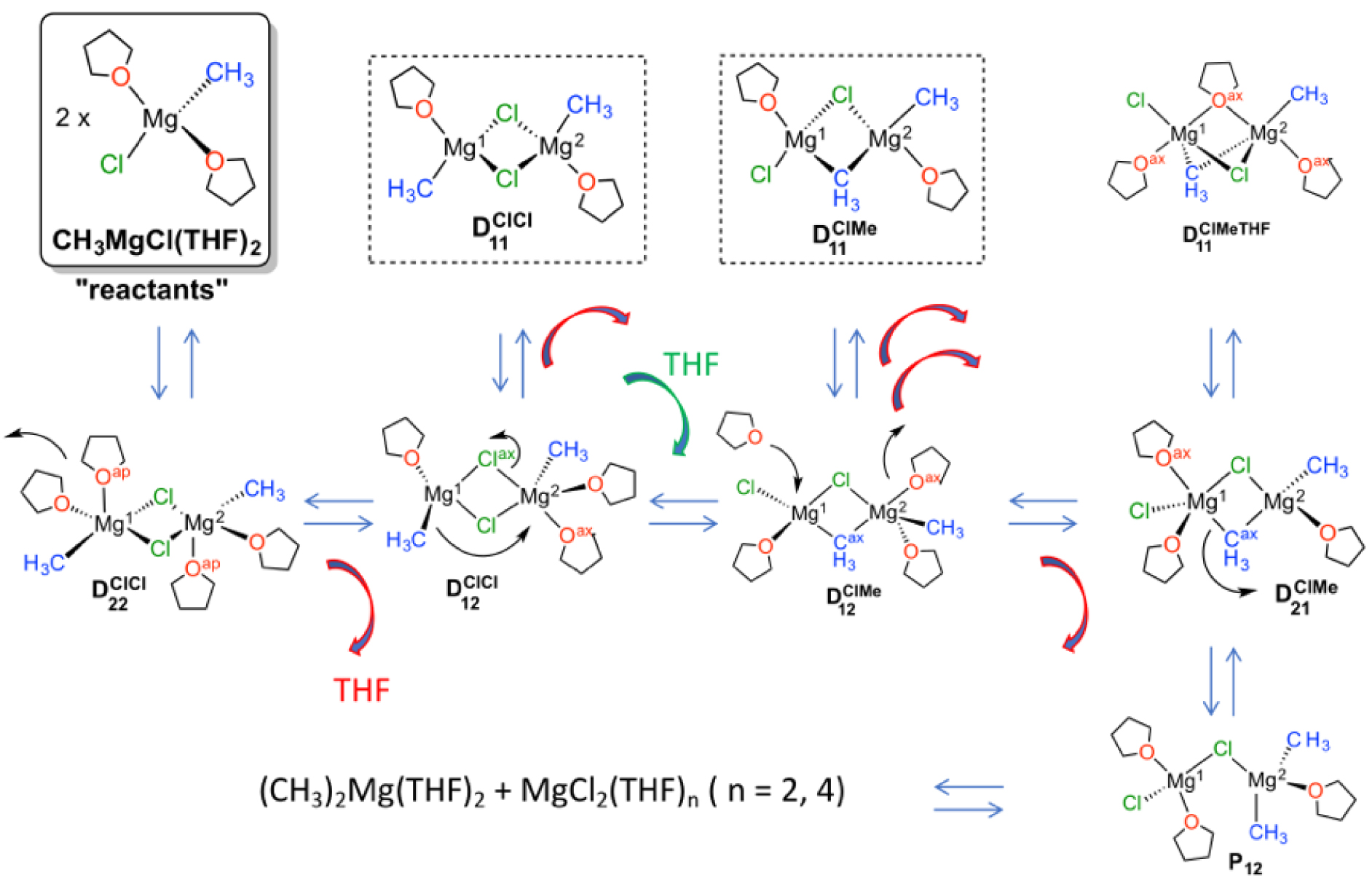
The Grignard reaction itself was studied with the AIMD method by considering the reaction of acetaldehyde with all identified forms of CH₃MgCl in THF [73]. It was found that all forms are competent in the Grignard reaction as the free energies of activation are within a narrow energy range. Since the different Grignard species are in rapid equilibria, they can all contribute to the reaction in parallel. Therefore, the reaction can occur via competing parallel pathways resulting in unclear kinetic order. Additional solvation may also be required to achieve the reaction. This is the case for the monomeric species, of which Mg(CH₃)₂ is found to be the most reactive. A highly solvated 𝜇²-Cl dimagnesium species is the most reactive dinuclear species. Importantly, the substrate and the nucleophile are initially bound to different magnesium centers and, in the transition state the acetaldehyde is strongly electrophilically activated by being O-coordinated to both magnesium centers (Figure 11). Previous studies of the reaction using traditional (static) DFT calculations also identified dinuclear magnesium complexes as the most reactive [74, 75, 76]. The direct role of the solvent in modulating the reaction pathway is the main reason for the structural and energetic differences between the earlier and later studies. Indeed, the AIMD calculations indicate that the solvent is an essential active partner in the reaction.

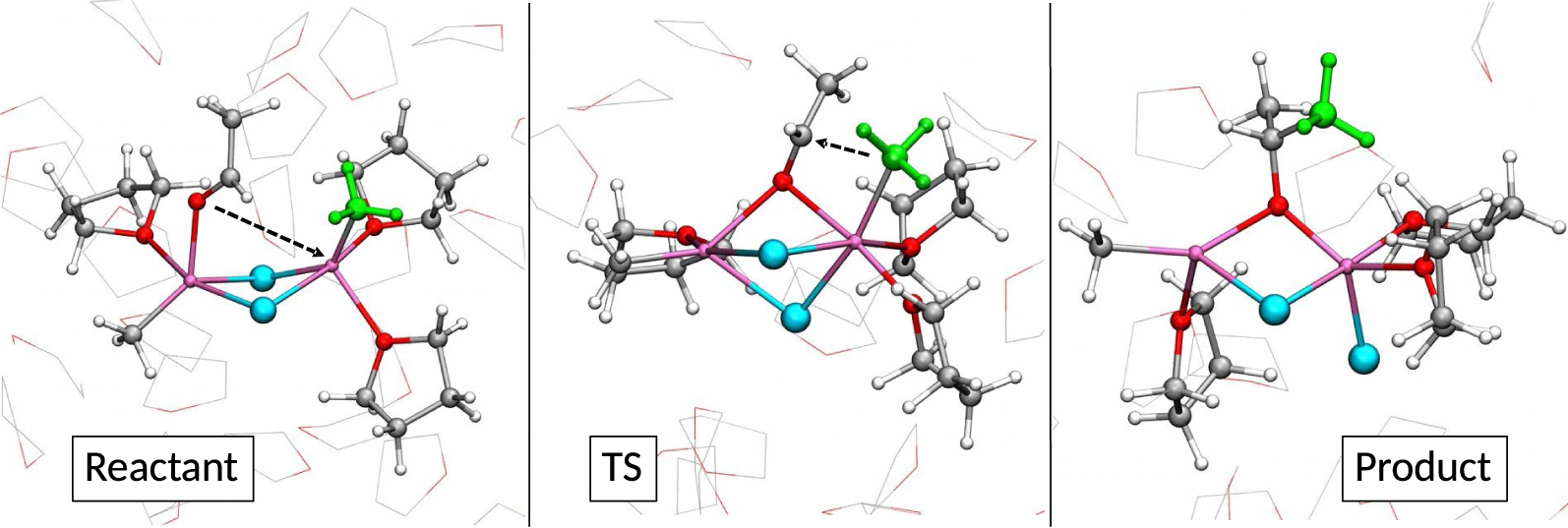
This study also clarified the issue of nucleophile vs single electron transfer (SET) mechanism. The SET mechanism has been proposed for substrates with low reduction potential. Recent studies have shown that the SET is rare and occurs only with aromatic carbonyl compounds [77, 78]. The computational study was limited to the formation of the organic radical and thus to the calculation of the bond dissociation energy (BDE) of the homolytic cleavage of the CH₃–Mg bond (DFT static calculations). The carbon–magnesium BDE in CH₃MgCl was calculated to be high (about 60 kcal/mol) with very little influence of the solvent. This high BDE would indicate that the radical cannot be formed. However, when the substrate is bonded to the magnesium, the carbon–magnesium BDE drops dramatically and the drop is increased as the energy of the π CO ∗ orbital of the substrate is decreasing. The reason is that the single electron of the magnesium species remains located on Mg in solvated MgCl species. However, the MgCl(substrate) species has a low-lying LUMO that is localized on the π CO ∗ empty orbital of the coordinated substrate. Thus, the single electron goes to the coordinated substrate π CO ∗ orbital, where it is stabilized compared to be located on Mg. In other words, the substrate itself assists the formation of the organic radical and the lowering of its reduction potential reinforces the assistance. The calculations show that the SET mechanism becomes competitive with the nucleophilic addition in the case of fluorenone in excellent agreement with Woerpel’s experimental results [77, 78].