1. Introduction
The incessant increase for energy demand and the important widespread of environmental pollution in relation with the depletion of fossil fuels has stressed the need for a green transition to renewable energy resources [1]. Green energy sources are considered as the best alternative to fossil fuels use. Green energy can meet the world’s energy demands and reduce greenhouse gas emissions and air pollution. As regards the utilization of alternative energy sources, the use of agricultural residues and organic wastes as biomass is a major challenge for the future and has attracted much attention. Biomass is an inexhaustible source and can exist over wide geographical regions in contrast to fossil fuels. Biomass has also a low impact on the environment due to its low sulphur and nitrogen contents [2, 3]. By the year 2050, the the use of biofuel and green electricity from biomass is expected to be approximately 38% and 17%, respectively [4].
Various agricultural residues are essentially composed of holocellulose (cellulose and hemicellulose) and lignin. These residues have high heating values (HHV) [5, 6, 7]. The thermochemical conversion process is one of the best and favoured methods for the turning of biomass into biofuels due to their high energy values under acceptable thermal conditions [8, 9]. Among these thermochemical conversion processes, pyrolysis has received special attention since it produces solid, liquid and gaseous products that could be recovered by different techniques [10]. The selection of a suitable recovery strategy depends strongly on the physical and chemical characteristics of the feedstock [10].
The climate conditions in the Mediterranean basin contribute to its diverse forests and natural and agricultural resources and consequently affect the variety of agricultural residues. Olive trees, palm trees and wheat fields are the major agricultural products in this region. Cistus monspeliensis and Aleppo pine trees are two of the most abundant natural species in the Mediterranean basin. The olive trees are essentially cultivated in the Mediterranean region. They are present in all the regions bordering the Mediterranean area from Madeira and the Canaries to Arabia and Mesopotamia. Spain is the world’s leading producer and exporter of olive oil and table olives. It also has the largest area of olive groves and the largest number of olive trees. Moreover, it is estimated that the number of date palm trees worldwide is about 105 million [11]. This number explains the global production of dates, which has undergone considerable expansion over the past decade, increasing from 6 million in 2004 to approximately 7.5 million tons in 2009 [12]. Egypt is the leading producer and Tunisia is the leading exporter of dates [13]. Regarding Aleppo pine trees, palaeogeography studies show that it is indeed North Mediterranean. It remains mainly native to semi-arid Mediterranean climate, and it is considered as a typical fruit in the French Mediterranean basin [14]. C. monspeliensis is mainly native to Spain and the Mediterranean Rim; it has the characteristics of easy regeneration and multiplying even after fires.
Several investigations have examined the characterization and the pyrolysis of various lignocellulosic materials such as palm kernel shells, corn cob, peanut shell, coffee husk [15], spent coffee grounds [16], Posidonia oceanica [17], kenaf stems [18] and grape marc [19]. Although the energy valorization values of olive [20, 21], date waste [4, 22, 23], wheat straw [24, 25] and Aleppo pine husks [26, 27, 28] are found in the literature, no information is available about the determination of reaction kinetics of C. monspeliensis using thermogravimetric analysis (TGA).
The biomass reactivity is often dependent on the content of holocellulose and lignin, the average size of the pellet and the presence of minerals [13].
It is well known that the distribution of the product of biomass pyrolysis varies according to operating conditions [29, 30, 31, 32, 33] and the nature of the biomass. Imam and Capered [34] examined the effect of temperature from 400 to 600 °C on the yield of pyrolytic products of switchgrass and found that an increase in the pyrolysis temperature led to an increase in the bio-oil and gas yields and a decrease in the the biochar yield. The optimization of this process therefore requires a better knowledge of the thermal and kinetic behaviour of biomass pyrolysis on the one hand and the characteristics of pyrolysis products on the other [22, 35, 36, 37]. The chemical valorization of bio-oil as a source of acids and sugars has been applied in the chemical industry. Acetic acid can be used in various industrial applications for the production of drugs, dyes and textures, while levoglucosan finds application in the pharmaceutical field such as in the synthesis of antibiotics. Phenol has various useful applications as an important chemical compound. Phenolic resins and caprolactam, for example, are used in nylon and synthetic fibres, and in the production of adhesives [38].
Several methods of biomass valorization can be found in the literature. The present work aims to study the production of a second-generation biofuel that can replace a conventional fuel such as gasoline or diesel by the pyrolysis of different biomasses.
The main objective of this study is to present a detailed characterization of some important parameters of pyrolysis reaction such as temperature, kinetics and product composition, which are required for the design of processes for thermochemical valorization. The pyrolysis of five biomasses of different origin (C. monspeliensis, olive and date kernels, Aleppo pine husks and wheat straw) was carried out in a thermogravimetric analyser.
2. Materials and methods
2.1. Biomasses
Five different biomasses were used in this work:
- C. monspeliensis (CM): This wild shrub is often found in Mediterranean forests and especially in southern Europe and North Africa. This plant can be a potential source of energy in mountainous and remote areas.
- Olive and date kernels (OK and DK, respectively): Olives are a typical Mediterranean product. They grow especially in the south of Europe and the north of Africa.
- Aleppo pine husks (APH) or Pinus halepensis: This is a type of woody biomass available in mountainous areas of Mediterranean countries.
- Wheat straw (WS): This is one of the most abundant agricultural residues in the Mediterranean region.
2.2. Sample preparation and characterization
After drying and crushing, the samples were sieved to an average size of 200 μm to avoid any constraints in heat and mass transfer according to the recommendations of Van de Velden et al. [39]. The characterization of the different biomass samples based on proximate and ultimate composition. For all of the samples, humidity was evaluated to 4%. The TGA was also used to conduct the proximate analysis following the process given by Garcia et al. [40]. This process involved carrying out pyrolysis and then a combustion of the sample (see Supporting Information for protocol details). The ultimate analysis was conducted using a CHNS analyser. A Parr bomb calorimeter (model 1356) was used for the determination of the calorific values of biomasses (HHV).
Ultimate and proximate analysis and HHV of the studied biomasses
| Sample | C (%) | H (%) | O (%)(1) | VM (%)(2) | FC (%)(3) | Ash (%) | HHV (MJ⋅kg−1)(4) |
|---|---|---|---|---|---|---|---|
| CM | 46.46 | 5.87 | 47.67 | 72.38 | 26.17 | 1.45 | 19.20 |
| OK | 45.56 | 5.8 | 48.64 | 75.42 | 23.79 | 0.79 | 20.86 |
| APH | 47.6 | 5.75 | 46.65 | 72.10 | 26.90 | 1.00 | 20.34 |
| WS | 47.35 | 5.74 | 46.91 | 70.44 | 28.83 | 0.74 | 19.10 |
| DK | 45.22 | 6.47 | 48.31 | 70.22 | 28.64 | 1.13 | 20.64 |
(1) Oxygen content was calculated by difference; (2) volatile matter fraction; (3) fixed carbon; (4) high heating value.
2.3. Experimental methods and modelling
The TGA is a useful tool for a wide variety of studies, including kinetic and thermal degradation of complex chemicals [41, 42]. An SDT/Q6000-TA analyser was used for thermogravimetric experiments, which were carried out at different heating rates ranging from 2 to 40 °C⋅min−1 under a nitrogen flowrate of 50 mL⋅min−1 and at atmospheric pressure. This gas flowrate allows a similar residence time of vapour pyrolysis in the laboratory-scale reactor (approximately 10 min). The weight of the initial samples was in the range of 5 ± 0.5 mg. The samples were introduced into the analyser at ambient temperature and then heated to 600 °C.
2.4. Thermal and kinetic study
The thermal pyrolysis of the biomass is usually expressed by the general equation
| (1) |
The conversion rate is calculated based on the mass loss of the sample:
| (2) |
The Arrhenius equation shows the dependence of the temperature and the rate constant as follows:
| (3) |
The kinetic model function mostly used [43] for biomass pyrolysis is
| (4) |
Combining Equations (1), (3) and (4), leads to
| (5) |
It should be noted that the first order is usually considered for the pyrolysis of biomass [44, 45]. The first order was considered in the present work, and several methods were used to determine the pre-exponential constants and the activation energies of the pyrolysis of five biomasses.
2.4.1. Kissinger method
The Kissinger relation [46] is widely used for solid and liquid decomposition under nonisothermal conditions. For biomass decomposition, the pyrolysis reaction is considered as a single reaction that produces bio-oil, gas and char. The Kissinger relation can be simplified as follows:
| (6) |
2.4.2. Kissinger–Akahira–Sunose method (KAS)
Isoconversional methods are widely used for studying kinetic parameters [47] and are recognized as the most appropriate approach for calculating the activation energy of reactions. These methods assume that the mechanism of biomass pyrolysis involves infinitely independent and parallel reactions with different kinetic rate constants and activation energies [48]. The KAS method is the most widely used approach for studying biomass pyrolysis kinetics in the literature [49]. After rearrangement and integration of (5), the KAS process can be written as:
| (7) |
The plot of versus 1∕T for a given value of the conversion rate (𝛼) yields a straight line. The slope of this line is used for determining the activation energy. Due to the complexity of the function g (relation (7)), the Kissinger relation is combined with the KAS method to determine the pre-exponential factor A𝛼.
2.4.3. Coats–Redfern method
This is a fitting method that is based on optimization of the order of the reaction, pre-exponential factor and activation energy. This method is well described in the literature [50, 51]. However, in the present case, the first order was already assumed for biomass pyrolysis as discussed above. The Coats–Redfern relation [52] is:
| (8) |
The plot of (8) versus the inverse of temperature gives a straight line whose slope is − Ea∕R. Equation (8) is applied in the temperature range [Ti, Tf] for different heating rates. In the literature, the term 2RT∕Ea is usually neglected in relation (8) [53]. The parameters Ea and A are calculated as average values based on different heating rates.
2.4.4. Distributed activation energy model (DAEM)
DAEM is the most recent method. It is based on the same principle as the KAS method: the distribution of activation energies. In general, a Gaussian-type distribution function is considered. Miura [54] developed a derivative equation that is simple to use and gives the same results as the real DAEM. The relation used by Miura is the following:
| (9) |
As described for the KAS method, this method requires plotting a straight line and then calculating the kinetic parameters.
2.4.5. Fitting method based on nonlinear least-squares minimization (NLSM)
This method is based on the minimization of error between the differential thermogravimetry (DTG) curves from the experiment and the curves estimated and optimized from the kinetic parameters ( and A). This method has also been compared to a method based on genetic algorithms [55], which in turn is based on the optimization of the following numerical system:
| (10) |
The convergence criterion is defined as
| (11) |
3. Results and discussion
3.1. Characterization of biomass products
Despite the different origins of biomasses, their ultimate and proximate analyses and HHVs show close values (Table 1). The analysis of mineral content in each sample is carried out using inductively coupled plasma atomic emission spectroscopy. According to these analyses, the major minerals in biomasses are K, Ca, Al, Na and Mg in different amounts (see Table S.1, Supporting Information).
3.2. Evaluation of thermal degradation and kinetic parameters
3.2.1. Evaluation of thermal degradation parameters
The kinetic derivative () for the five samples, at a heating rate of 10 °C⋅min−1 is shown in Figure 1. During pyrolysis, the weight loss associated with moisture evaporation occurs between room temperature and approximately 150 °C [56]. Above this temperature, the thermal degradation of the biomass samples shows three successive stages representing the decomposition of three biopolymers: hemicellulose, cellulose and lignin [57]. The temperature and the intensity of each of these steps (the shoulder or peak of the d𝛼∕dt curve) depend on the biomass and its biopolymer composition.
At a medium heating rate of 10 °C⋅min−1, the devolatilization of CM, DK, APH, WS and OK starts at approximately 210 °C, 174 °C, 200 °C, 171 °C and 215 °C (Ti or Tonset) and ends at 395 °C, 463 °C, 405 °C, 375 °C and 400 °C (Tf), respectively. These temperatures correspond to the initial temperature (Ti or Tonset) and the final temperature (Tf) of the pyrolysis reaction, respectively. The observed differences between these temperatures can be attributed to the biomasses composition in terms of holocellulose and lignin fractions as well as their mineral contents [8, 45].
Temperatures and maximum pyrolysis conversion rates of the studied biomasses at a heating rate of 10 °C⋅min−1
| Biomass materials | Ti (°C) | Tmax (°C) | Tf (°C) | Rmax (%⋅min−1) |
|---|---|---|---|---|
| CM | 210 | 359 | 395 | 0.98 |
| DK | 174 | 296 | 463 | 1.58 |
| APH | 200 | 344 | 395 | 1.42 |
| WS | 171 | 322 | 375 | 0.73 |
| OK | 215 | 330 | 400 | 1.26 |
Rmax is the maximum rate of pyrolysis.
The lowest initial temperature for biomass pyrolysis is 160 °C, which is exhibited for the WS pyrolysis at a heating rate of 2 °C⋅min−1. The highest final temperature (Tf) is approximately 495 °C and observed for the DK pyrolysis at a heating rate of 40 °C⋅min−1 (see Table S.2). It should be noted that Ti and Tf increase with the increase of the used heating rate. The major phenomenon that occurs at this temperature range is the pyrolysis of hemicellulose, cellulose and lignin [58]. It can be observed from the d𝛼∕dt curves in Figure 1 that in this range, the thermal degradation of biomasses consists of several overlapping steps. The first overlapping shoulder in the d𝛼∕dt curve represents the devolatilization of hemicellulose, whereas the second shoulder corresponds to cellulose devolatilization at Tmax [55]. The last shoulder, which also overlaps, corresponds to the decomposition of lignin at high temperatures. The temperature at which the decomposition rate of biomass is maximum is denoted by Tmax. At a heating rate of 10 °C⋅min−1, it was determined to 359, 296, 344, 322 and 330 °C for the CM, DK, APH, WS and OK samples, respectively, (see Table 2). The maximum rates Rmax (expressed in %⋅min−1) of weight loss are as follows—DK: 1.58 > APH: 1.42 > OK: 1.26 > CM: 0.98 > WS: 0.73. The differences in the maximum rate and Tmax are usually due to the reactivity of the biomass; the more volatile the matter, the more reactive the biomass. The evolution of the above-cited temperatures (Ti, Tf and Tmax) and the maximum pyrolysis rates with heating rate for the different samples based on principal component analysis (PCA) is shown in Figure 2 [59].
Kinetic rate curves of the studied biomasses (𝛽 = 10 °C⋅min−1).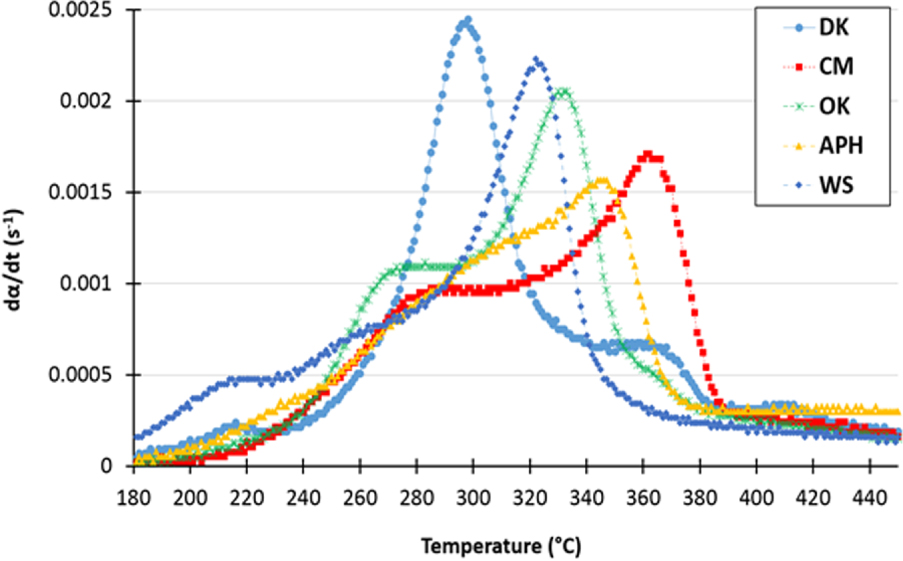
Behaviours of different characteristic temperatures and the maximum conversion rates of the studied biomasses according to PCA.
As shown in Figure 2(a), a strong linear correlation can be observed between the maximum rate Rmax and the heating rate 𝛽 on the one hand and between Tmax and Ti on the other. Figure 2(b) shows a global comparison of the different thermal parameters (Ti, Tf and Tmax and Rmax) for the different biomasses. This figure provides information about the similarity of biomass behaviour with respect to the different parameters depicted in Figure 2(a). The index behind each biomass name in Figure 2(a) represents the value of the heating rate (°C⋅min−1).
The parallel profiles show that globally the heating rate has the same influence on the behaviour of all biomasses. By combining Figures 2(a) and (b), a different behaviour can be observed between CM and DK. This can be confirmed by a comparative analysis of the different characteristics listed in Table S.2 and more particularly in relation to Tmax and Ti. On the other hand, the profiles of the APH and OK biomasses almost overlie each other and their behaviours are almost similar. Finally, the WS biomass exhibits an average behaviour between the different biomasses. This difference in behaviour can significantly influence the design of the pyrolysis process.
3.2.2. Evaluation of kinetic parameters
The Kissinger, KAS and Coats–Redfern methods are used in this work in order to determine the kinetic parameters. The linear correlation coefficients are high for all the methods used. In fact, in the Kissinger method, the coefficient of correlation varies between 0.995 and 0.999, confirming the existence of a strong linearization of the experimental points as shown in Figure 3.
Kinetic plots of the studied biomasses by the Kissinger method.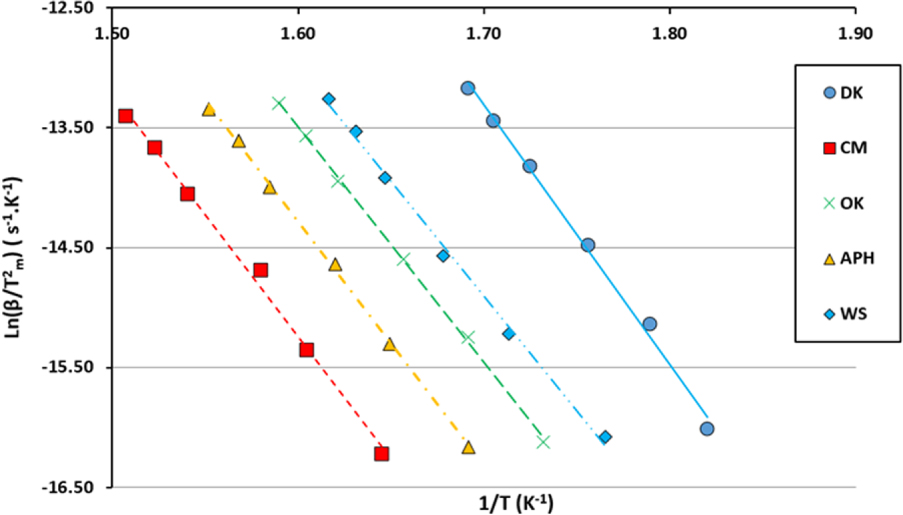
Figure 4 shows a plot of the CM sample according to the Coats–Redfern method at different heating rates. The correlation coefficient for the Coats–Redfern method also remains high; it varies between 0.926 and 0.990.
For the KAS method, the coefficient of correlation varies between 0.955 and 0.986 for conversion rates between 0.05 and 0.8. Above this conversion rate, linearization cannot be ensured in the KAS method, and the correlation coefficient drops to values between 0.4 and 0.8. Figure 5(a) shows a plot of the CM sample according to the KAS relation.
Kinetic plots of the studied biomasses by the Coats–Redfern method.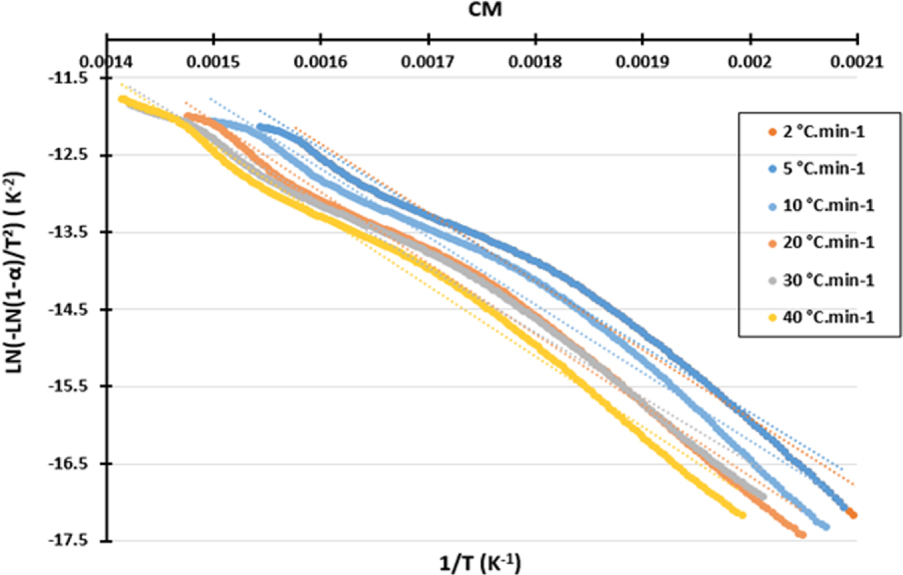
Cellulose, hemicellulose and lignin kinetic parameters for the studied biomasses according to the NLSM method
| Cellulose | Hemicellulose | Lignin | ||
|---|---|---|---|---|
| OK | ln(A) (s−1) | 15.15 | 10.46 | 1.84 |
| Ea (kJ/mol) | 195.98 | 132.96 | 60.34 | |
| CM | ln(A) (s−1) | 11.25 | 10.14 | 2.16 |
| Ea (kJ/mol) | 165.20 | 135.69 | 65.65 | |
| APH | ln(A) (s−1) | 10.99 | 8.79 | 2.31 |
| Ea (kJ/mol) | 154.50 | 118.60 | 68.15 | |
| WS | ln(A) (s−1) | 10.99 | 7.73 | 1.90 |
| Ea (kJ/mol) | 148.10 | 101.48 | 60.86 | |
| DK | ln(A) (s−1) | 11.02 | 15.89 | 1.06 |
| Ea (kJ/mol) | 154.85 | 193.85 | 53.87 | |
(a) Kinetic plots and (b) activation energy evolution versus the conversion rates of the studied biomasses according to the KAS method.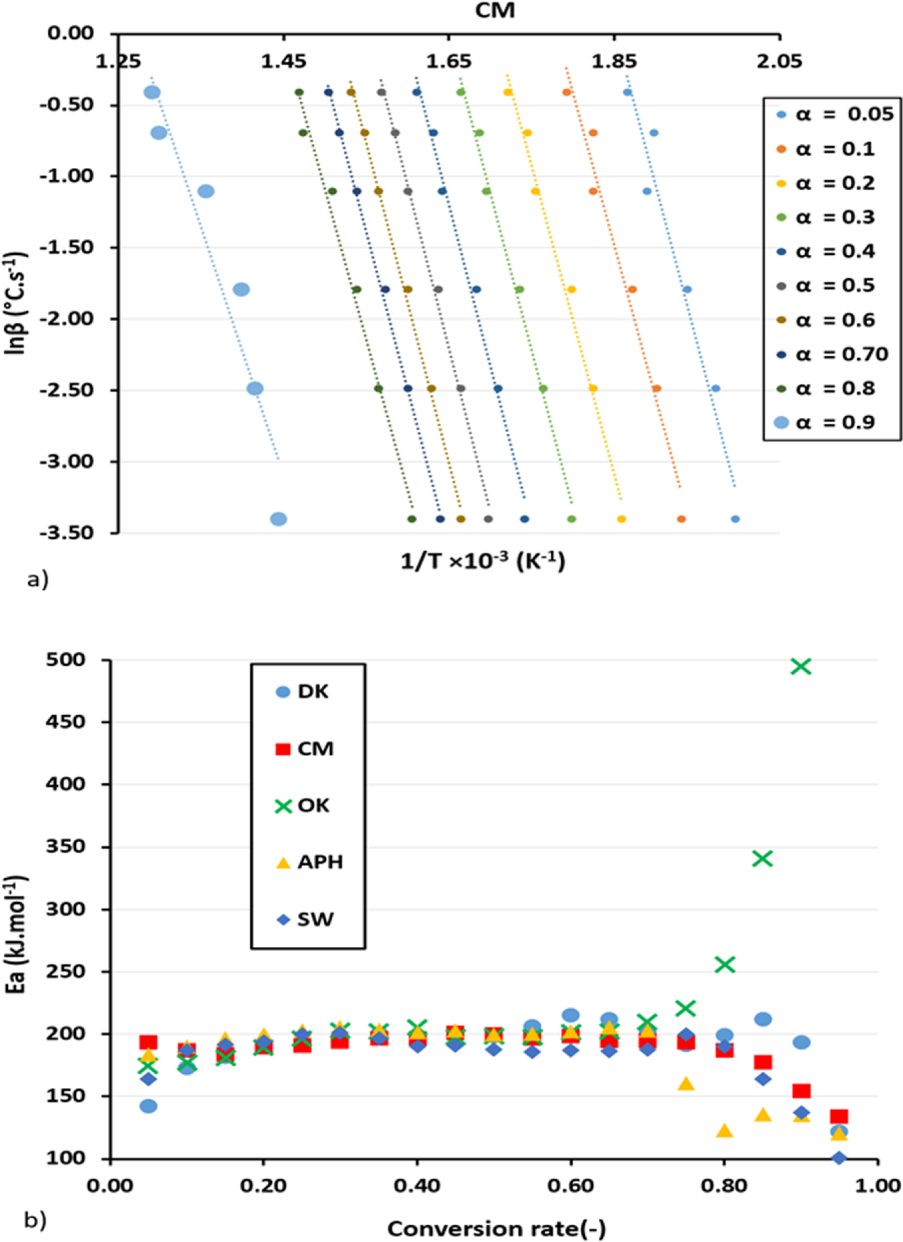
The plot of the different biomass samples according to the Coats–Redfern and KAS methods for different heating rates are given in Supporting Information (Figures S.1 and S.2 and Table S.4).
As reported in previous works, the Flynn–Wall–Ozawa (FWO) approach, which is another isoconversional method, can yield almost the same results as the KAS method. Table 4 summarizes all kinetic parameters for the different biomasses using the four methods mentioned above.
For the DAEM method, the biomasses have a close distribution. Furthermore, the curve trend of this distribution is very similar to that of the one estimated by the KAS method (Figure 6). However, the values of the corresponding activation energies were different. Moreover, at a high conversion rate, this method generates aberrant activation energy values similarly to those calculated by the KAS method.
For the NLSM method, the determination of the kinetics of the pyrolysis reaction is based on the evaluation and optimization of the kinetic parameters of the three biopolymers that constitute the biomass: cellulose, hemicellulose and lignin. From the kinetics of these three polymers, the overall biomass DTG curve can be reconstructed, which represents the pyrolysis reaction rate. The kinetic parameters are calculated from the DTG curves of the different heating rates and are presented in Table 3. Figure 7 shows experimental and modelled DTG curves superposed for a heating rate of 2 °C/min. As shown in this figure, the algorithm is able to reconstruct the DGT curve but only with a certain gap especially at the level of transition from one biopolymer to another (particularly for the biomasses CM and DK).
Activation energy evolution versus the conversion rates of the studied biomasses according to the DAEM method.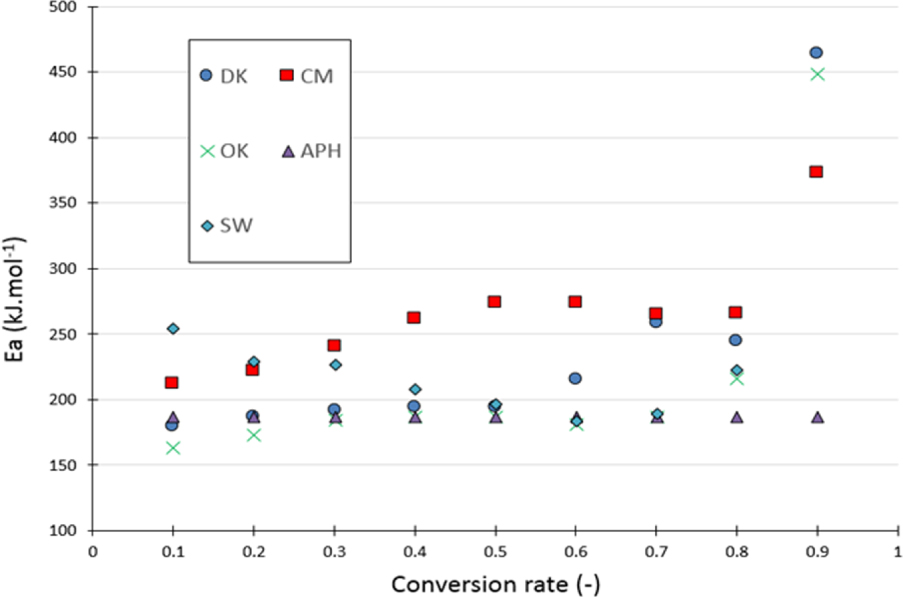
Experimental and modelling DTG curves of the studied biomasses according to the NLSM method at heating rate of 2 °C⋅min−1.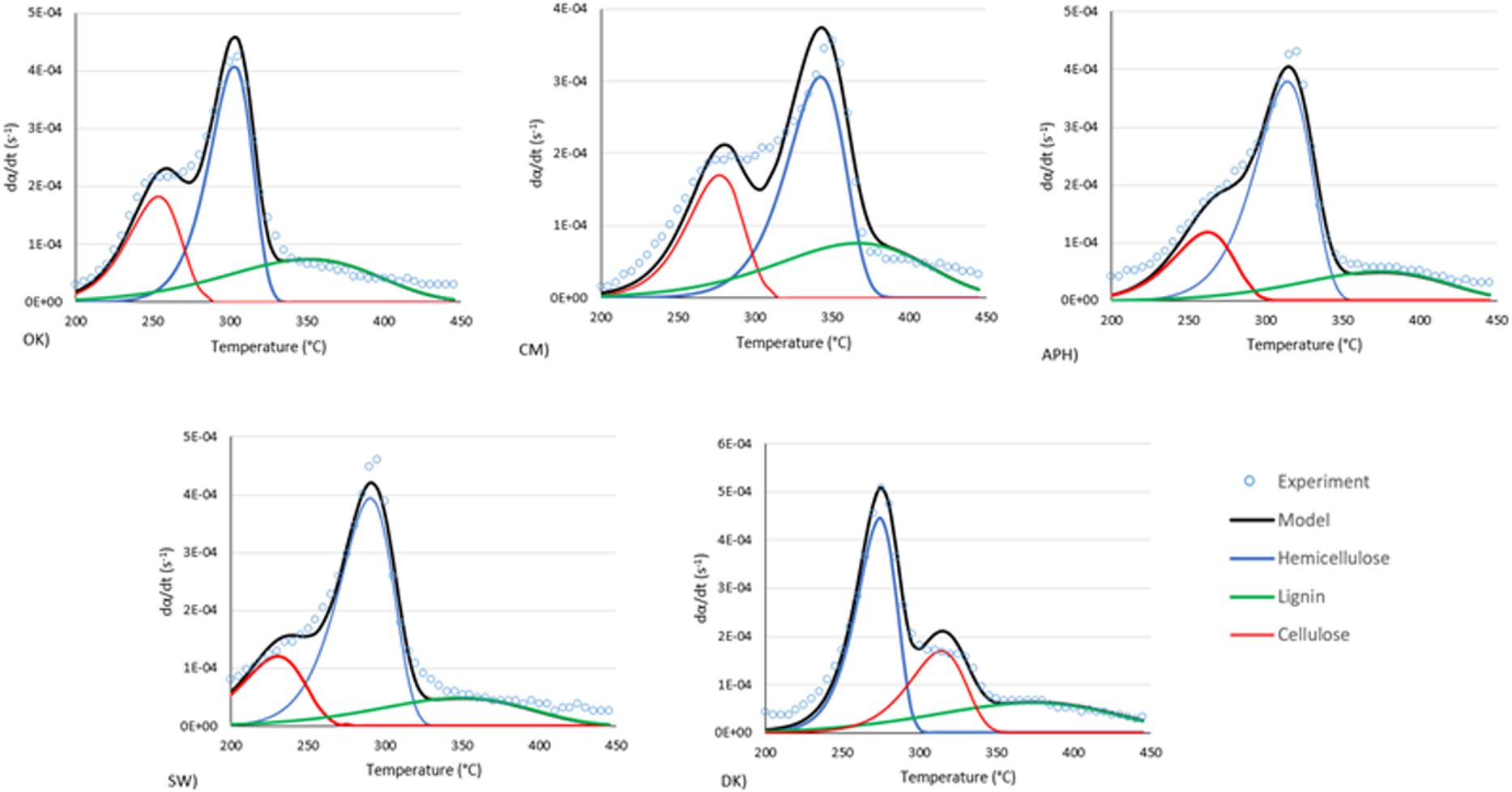
Comparison of the assessed kinetic parameters of the studied biomasses with the literature (Ea in kJ⋅mol−1and A in s−1)
| This work | Literature | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Biomass | Kissinger | KAS (𝛼 = 0.05 −−0.75) | Coats–Redfern | DAEM | Kinetic parameters | Method | Ref. | |||||
| Ea | A | Ea | A | Ea | A | Ea | A | Ea | A | |||
| CM | 169.62 | 7.37 × 108 | 194.16 | 1.02 × 1021 | 73.39 | 1.27 × 104 | 252.04 | 9.00 × 20 | No data available (N.A.) for this biomass | |||
| OK | 163.19 | 1.18 × 109 | 193.56 | 7.09 × 1020 | 74.08 | 1.43 × 104 | 184.85 | 2.68 × 1015 | 135.48 | 2.59 × 1014 | FWO | [20 ] |
| 130.03 (𝛼 = 0.1−−0.6) | 1.18 × 1010 | KAS | ||||||||||
| APH | 168.74 | 1.61 × 109 | 197.08 | 6.67 × 20 | 65.80 | 3.23 × 102 | 186.63 | 2.59 × 1016 | 253 (𝛼 = 0.3−−0.9) | N.A. | DAEM | [60] |
| WS | 159.10 | 8.64 × 108 | 197.27 | 1.03 × 1021 | 54.81 | 4.57 × 103 | 213.89 | 7.71 × 1023 | 130–175 (𝛼 = 0.15−−0.85) | N.A. | FWO | [24] |
| DK | 180.41 | 3.79 × 1011 | 190.17 | 3.48 × 1021 | 76.77 | 1.27 × 104 | 208.32 | 4.66 × 1019 | 20.24 | 1.64 × 103 | Coats–Redfern | [22 ] |
| 192.12 | 1.12 × 1014 | Kissinger | [4 ] | |||||||||
3.2.3. Discussion
Generally, the optimum temperature used for biomass pyrolysis is in the range 450–550 °C for increasing the bio-oil yield. As it can be seen from Table 2, this temperature range is higher than the characteristic temperatures estimated through TGA measurements (Ti, Tf and Tmax). Theoretically, the Tmax obtained by TGA is useful and essential for the design of pyrolysers. In fact, at this temperature (between 296 and 359 °C according to this work), the kinetic rate of pyrolysis is the highest. This allows better optimization of both the residence time of the biomasses’ particles in the reactor and its energy consumption. Nevertheless, this parameter is often neglected in the biomass pyrolysis for the reasons mentioned above (bio-oil yield). In the literature, thermal characteristics are often used to compare the reactivity of different biomasses or their chars. Some authors have even defined new parameters based on these temperatures to compare the reactivity of biomasses [8]. Besides this advantage, Ti and Tf are usually used to limit the temperature interval for kinetic studies.
As shown in Table 4, the kinetic methods, especially the Coats–Redfern method, generate some differences in the values of the activation energy and the pre-exponential factor. According to the literature, the Kissinger method is the oldest and the most widely used approach for kinetic determination by TGA. It was initially developed for monomolecular substances. However, as the biomass is composed of three complex biopolymers (cellulose, hemicellulose and lignin), the use of the Kissinger relation might lead to errors.
The KAS and DAEM methods are very useful methods for kinetic determination using TGA curves, but they have some limitations particularly at high temperatures, where the accuracy of the weight notably decreases due to the low mass present in the thermobalance. Above a conversion rate of 0.75, the activation energy is either very high or very low, and it has no physical significance (Table S.3). The average activation energy is therefore calculated based on conversion rates between 0.05 and 0.75. Despite the differences in the origins of the biomass samples and their varying values of Ti, Tmax and Tf, the KAS, Kissinger and DAEM methods provide close activation energies for the different samples.
The Coats–Redfern method provides activation energies in the range of 54.81–76.77 kJ⋅mol−1. They are much lower than those ones given in the literature (Table 4).
Contrary to the NLSM method, it is difficult to compare the kinetic parameters of the different biopolymers directly with the estimated values obtained when using the other four methods mentioned above. The advantage of this method is reproduction accuracy of the DTG curves and hence of the conversion rates as a function of temperature.
Activation energy distribution versus the conversion rate of the studied biomasses according to the methods used in this work.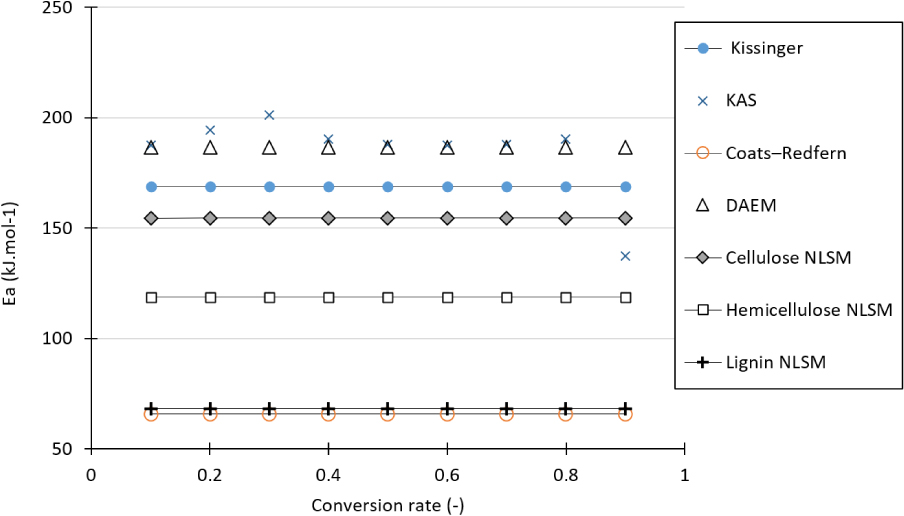
Figure 8 shows the evolution of activation energies calculated by different methods for the APH biomass. The KAS and DAEM methods exhibit an activation energy distribution almost overlying each other. The average activation energy estimated by these two methods is the highest (approximately 190 kJ⋅mol−1). The Kissinger method produces an activation energy close to that of cellulose by the NLSM method. This may be reasonable because the Kissinger method is dependent on the Tmax of the DTG curve. In general, this temperature corresponds to cellulose because it is the major component and the most reactive biopolymer of the biomass. Moreover, this figure shows that at a global scale, the activation energy remains essentially between 150 and 200 kJ⋅mol−1 except for the Coats–Redfern method, where a value of 70 kJ⋅mol−1 is obtained. This value is close to that of lignin determined by the NLSM method. Furthermore, hemicellulose generates an average activation energy of 118 kJ⋅mol−1.
4. Conclusion
Thermal and kinetic studies are carried out for five different biomasses of Mediterranean origin. Results highlight the crucial problem of choosing the most appropriate method for the determination of the corresponding kinetic parameters. In addition, different temperatures from the TGA curves are usually neglected in the case of biomass pyrolysis at laboratory scale. Despite the different origins of biomasses, the initial and final ranges of pyrolysis temperatures are globally 171–215 °C and 375–463 °C, respectively.
Except for the Coats–Redfern method, the estimated values of the activation energy and the pre-exponential factor are relatively close. It would be better to validate all these methods by means of a pilot-scale reactor. The idea is to design a device that applies the same conditions in the TGA devices (controlled heating rate, controlled residence time of solid and vapours, etc.). In addition to the kinetic analysis, extensive heat and mass transfer studies are also required to better understand the biomass pyrolysis reaction particularly when using biomass pellets. In further work, a comparison study between the results from a TGA and a laboratory-scale reactor will be attempted in order to better understand the kinetics of solid pyrolysis and the possible complementarity between the two devices.
Nomenclature
| A | pre-exponential factor (s−1) |
| APH | Aleppo pine husk biomass |
| A𝛼 | pre-exponential factor at a given conversion rate (s−1) |
| CM | Ciste of Montpellier biomass |
| DAEM | distributed activation energy model |
| DK | date kernel biomass |
| DTG | differential thermogravimetry |
| Ea | activation energy (kJ⋅mol−1) |
| E𝛼 | activation energy at a given conversion (kJ⋅mol−1) |
| f | kinetic model function |
| FID | flame ionization detector |
| FWO | Flynn–Wall–Ozawa |
| g | complex integral function |
| HHV | high heating value (MJ⋅kg−1) |
| k | rate constant (s−1) |
| KAS | Kissinger–Akahira–Sunose model |
| m0 | initial mass (kg) |
| mf | final mass (kg) |
| mT | mass at temperature T (kg) |
| n | reaction order (–) |
| NLSM | nonlinear least-squares minimization |
| OK | olive kernel biomass |
| R | gas constant (8.314 J⋅K−1⋅mol−1) |
| Rmax | maximum reactivity (%⋅min−1) |
| T | temperature (°C) |
| Tf | final temperature (°C) |
| TGA | thermogravimetry analysis |
| Ti | initial temperature (°C) |
| Tmax | maximum temperature (°C) |
| T𝛼 | temperature at a given conversion |
| WS | wheat straw biomass |
Greek symbols
| 𝛼 | conversion rate (–) |
| 𝛽 | heating rate (°C⋅min−1) |
Supplementary data
Supporting information for this article is available on the journal’s website under https://doi.org/10.5802/crchim.56 or from the author.



 CC-BY 4.0
CC-BY 4.0