1. Introduction
Nowadays, powerful computers and massive parallelization of numerical methods in combination with quantum chemical software offers the opportunity to address chemical and physical problems which cannot be solved analytically. Indeed, the precise calculation of energies, charge distributions and other properties in the field of computational chemistry can lead to a full understanding of molecular processes observed in experiments with the final aim of predicting them. Of course, a close interplay between theoretical and experimental methods is needed to guarantee optimal results.
Density Functional Theory (DFT) [1, 2, 3] is the most used approach to reach this goal and is being used in physics, chemistry, materials science and other related fields [4, 5, 6]. Furthermore, in medicine, DFT is a tool which aids in developing new drugs [7] or antibacterial materials [8], understanding enzyme active sites [9], improving the long-term stability of implants [10] and dental composites [11] and much more. The big advantage of DFT (and other molecular modelling tools) is that it allows building a theoretical model of real-world problems at a molecular level that is extremely hard to achieve experimentally. Furthermore, the predictive abilities allow to fast-track the experimental design of new materials and methodologies.
The big advantage of DFT (in contrast to other modelling tools) is that it offers a very good compromise between chemical correctness and computational cost. Indeed, it allows the calculation of very accurate specific properties (such as spectroscopic data) as well as a time evolution of the system through ab initio molecular dynamics. It manages this good balance between computational efficiency and accuracy by explicitly treating electronic effects (in contrast to faster, but less accurate methods such as classical molecular dynamics) at an affordable computational cost (in contrast to more accurate, but more expensive approaches such as wave function methods). Obviously this means also that there is still a limit on the size of chemical systems and the time scales that can be studied using DFT, whereby specifically the inclusion of a solvent or biological medium may be problematic as this renders the size of the system very large. Aside from these direct investigations at the DFT-level, it should be noted that DFT is often used to benchmark or fit lower-level theories for subsequent investigations on similar systems [12].
The aim of this publication is then to present recent results obtained in the field of physiological [13, 14] and mostly pathological calcifications [15, 16, 17] by means of DFT. To attain this goal, we will start by a brief (more details can be found in different excellent books [18, 19]) presentation of some of its underlying principles. Afterwards, a selection of recent publications will be presented, dedicated to chemical compounds—namely calcium oxalate (COM and COD) and calcium phosphate (apatite and whitlockite)—that have been identified in pathological calcifications. We will show that the use of DFT is instrumental to obtain a precise assignment of the signals present in infrared, Raman and NMR spectra, to offer important insights in the morphology of crystallites present in urine or pathological calcifications and to develop new inhibitors to stop the growing process of crystallites.
2. Main underlying principles of DFT
The existence of a wave function for every measurable system is one of the fundamental postulates of quantum mechanics. This function defines the state of the system in function of 3N variables, with N the number of electrons in the system, each having 3 spatial degrees of freedom. The knowledge of the wave functions of a system allows—in principle—to solve the fundamental equation of quantum mechanics formulated by Schrödinger [20] leading to a full understanding of the system
| (1) |
A major breakthrough in this problem was achieved by introducing the so-called Born–Oppenheimer approximation, which significantly reduces the amount of variables that needs to be calculated [21]. This approximation uses the fact that the mass of an electron is very small compared to the mass of a nucleus and thus assumes that the electrons react instantaneously to the movement of the nuclei. As such, the terms describing the coupling between the nuclei and the electrons are discarded from the Schrödinger equation, leading to a considerable reduction in the computational cost.
A second approximation that has led to a large increase of system size within computational reach, is the Hartree–Fock method. In this method, the many-electron Hamiltonian is replaced by a one-electron Hamiltonian acting on one-electron wavefunctions (orbitals). Furthermore, the Coulomb interaction between different electrons is only represented as an average over the entire system. Although this approach leads to unexpectedly good results in general, the error margin is too large to describe many of the chemically interesting systems as the energy differences at play are often subtle. More precisely, it was found that Hartree–Fock does not consider the correlated motions of different electrons, leading to problematic descriptions of many systems. Different (partly) solutions exist to overcome these issues and to further enhance the description, but many of them are computationally quite expensive. A radically different approach was introduced by the development of the density functional theory.
The main idea of DFT is to use an electron density instead of a complicated wavefunction, reducing the number of variables to only 3 variables instead of 3N and thus making the Schrödinger equation much easier to handle. Hohenberg and Kohn [1] proved that this approximation is valid, i.e. all ground state properties of a quantum system—in particular the ground state total energy—are unique functionals of the ground state density.
Finally, it is important to underline that the success of DFT lies in a further approximation related to the calculation of the electron density from a set of mathematical functions or orbitals introduced by Kohn and Sham [22].
| (2) |
The total energy is then decomposed into three contributions being the kinetic energy, a Coulombic energy describing the electrostatic interactions between all charged particles and the so-called exchange-correlation term describing the many-body interactions. The mathematical form of the latter term is, unfortunately, unknown and is therefore approximated by increasingly accurate functional forms. Many different approximations exist, in multiple types and flavours, but the most common family—especially for solids—are the generalized gradient approximations whereby the exchange-correlation functional depends on the gradient of the local electron density of the system.
A further issue of DFT is that it is inherently not capable of well-describing dispersion forces that are responsible for many chemical phenomena of interest. This means that specific corrections need to be introduced to circumvent this problem as, although the magnitude of a dispersion interaction is small, they dominate the behaviour of neutral physical systems at intermediate distance ranges .
Again, a plethora of methods and approximations exist, whereby the pairwise dispersion correction series proposed by Grimme et al. [23, 24, 25, 26] are arguably the most popular. It is an intuitive correction term, based on the interaction between two multipoles, that is orders of magnitudes cheaper to calculate than DFT itself, making it very suitable for the calculation of large systems. The main disadvantage of this correction term is that it is empirical and needs to be fitted for every density functional it is combined with. Of course, the fitting parameters for the most common density functional are readily available although the end-user should evaluate carefully whether the fitted parameters apply for the specific system of interest.
3. Calcium oxalates
3.1. Characterization of calcium oxalates
Pathological calcifications containing calcium oxalates have been identified in different organs namely kidney [27], prostate [28, 29] as well as thyroide [30, 31]. For example in Figure 1, a calcium oxalate monohydrate crystallite in kidney can be seen as well as a calcium oxalate dihydrate crystallite in prostate. Note the significant differences in the size and in the arrangement of the crystallites in these two organs.
(A) Calcium oxalate monohydrate crystallites in kidney, (B) calcium oxalate dihydrate crystallites in prostate.
Regarding kidney, among the different chemical compounds which have been identified in concretions, calcium oxalate (CaOx) is the main component of more than 70% of all stones that were analysed in Western countries [32]. In general, three different crystalline forms of CaOx exist which defer in the amount of water molecules that are present in the crystal structure. The first one, calcium oxalate monohydrate (COM), or whewellite, has a 1:1 ratio between calcium oxalate units and water molecules: CaC2O4 ⋅ H2O. It is the most frequent form and is linked to hyperoxaluria [33, 34]. Calcium oxalate dihydrate (COD) or weddellite has a 1:2 ratio between calcium oxalate units and water molecules (CaC2O4 ⋅ 2H2O). It is about two to three times less frequent than COM and is related to hypercalciuria [35, 36]. It should be noted that, due to the presence of free-ranging water molecules inside the oxalate, the brute formula is actually CaC2O4 ⋅ (2 + x) ⋅ H2O, see below. Finally, the prevalence of the third species, namely calcium oxalate trihydrate (COT) or caoxite (CaC2O4:H2O = 1:3, CaC2O4 ⋅ 3H2O), is rarely observed in kidney stones.
According to a morpho-constitutional analysis [37, 38, 39], the etiology of kidney stones is based on the morphology as well as the chemical composition of the formed crystals as shown by Fourier Transform InfraRed (FT-IR) spectroscopy. Indeed, there is a correlation between the morphology of the kidney stone and the morphology of the crystallite [40, 41] and therefore, the morphology of crystallites present in urine constitutes a key element to determine the underlying causes of the pathology [42]. Of course, the use of vibrational spectra (IR and Raman) implies the full understanding of the origins of the absorption and scattering bands in relation to the chemical properties of the material under investigation. The calculation of these spectra for well-defined chemical compositions can provide this understanding, enhancing the ability to interpret difficult experimental spectra obtained from natural mixed systems. Indeed, several dispersion-corrected DFT studies have been performed on calcium oxalate whereby the IR and Raman vibrational spectra were successfully predicted for the three different polyhydrates of calcium oxalate [12, 43, 44, 45, 46, 47].
Another successful example of a DFT study on calcium oxalate was the identification of the amount and distribution of zeolitic water molecules in COD by Petit et al. [47]. Indeed, as mentioned before, the crystal structure of COD includes empty pores that can readily be filled by diffusing water molecules. Because of this, the crystal structure of COD is rather CaC2O4 ⋅ (2 + x) ⋅ H2O than CaC2O4 ⋅ 2H2O, whereby x represents the number of zeolitic water molecules per calcium oxalate unit. The exact value of x has been under debate for a long time until Petit et al. determined it through DFT studies [48]. By systematically calculating vibrational spectra for COD crystals with different values for x, they were able to show that there are at most 4 zeolitic water molecules per unit cell (x = 0.5) and ideally 3.
Another important study [33] helped to resolve issues surrounding the crystal conversion from COD (being metastable) to COM. In these circumstances, the Fourier transform infrared spectra seemed to indicate the presence of the latter, while the morphology of the observed crystallites indicate presence of the former. As both forms are related to different etiologies and treatments, this posed important problems to clinicians. The DFT study was able to show, in combination with different experimental techniques, that a small amount of a less-ordered form of COM was formed that skewed the IR spectra. This resulted in the understanding that more attention should be paid to the stone morphology, rather than the spectra in these specific cases. Further on this less ordered form of COM, which had already been proposed in some experimental studies, DFT studies were needed to fully unravel the involvement of the structural water molecules in the structure and the related symmetry of the crystal [49].
Finally, we would like to note that, aside from the already mentioned experimental results such as IR and Raman spectra, also the calculation of NMR spectra is available. It was applied and validated specifically for calcium oxalates by Colas et al. [50]. The authors of the paper emphasized that it is yet another benchmark against which difficult experimental or clinical samples can be validated and assigned.
3.2. Interaction between calcium oxalates and small molecules
DFT has also been used to assess molecular interactions occurring on a COD surface which could promote an anisotropic crystal growth. More specifically, Parvaneh et al. [51] found that the crystallographic faces (100) and (101) of COD are hydrophilic and can therefore be solvated by a strongly bound layer of water. However, important differences in the respective adsorption mechanisms could explain the anisotropic growth of the crystals, which is favoured in the (100) direction, as observed in experiments. Similar results have been published by Debroise et al. [52, 53] which further underlined the key role of water in the prediction of calcium oxalate morphology. More specifically, it was shown that the adsorption mechanisms of water onto the different crystal surfaces, offer the needed stabilization to obtain the experimentally found crystal morphologies.
Moreover, for many types of pathological calcifications, but especially in the case of kidney stones, crystal growth inhibitors are at the centre of several investigations. Indeed, it is well known that the growing process of crystals can be stopped or altered by ions or molecules. More specifically, the adsorption of inhibitors on specific crystal surfaces impedes the addition of surface ions, thereby reducing the rate of growth. Chung et al. [54] have showed by means of DFT (in combination with in situ atomic force microscopy) that citrate and hydroxycitrate exhibit an adsorption mechanism different from classical theory as they induce a dissolution process of the pathological crystal instead of a reduced rate of crystal growth. Similarly, experimental evidence exists suggesting that catechin (as present in green tea) has a similar effect [55]. A conclusive, explanatory DFT model, supporting these experimental findings has not yet been developed although a manuscript on this subject has been submitted by the current authors, see also Figure 2.
A citrate molecule surrounded by water molecules adsorbed onto an oxalate surface of about 15 Å × 18 Å. Brown is carbon, cyan is calcium, red is oxygen and white is hydrogen.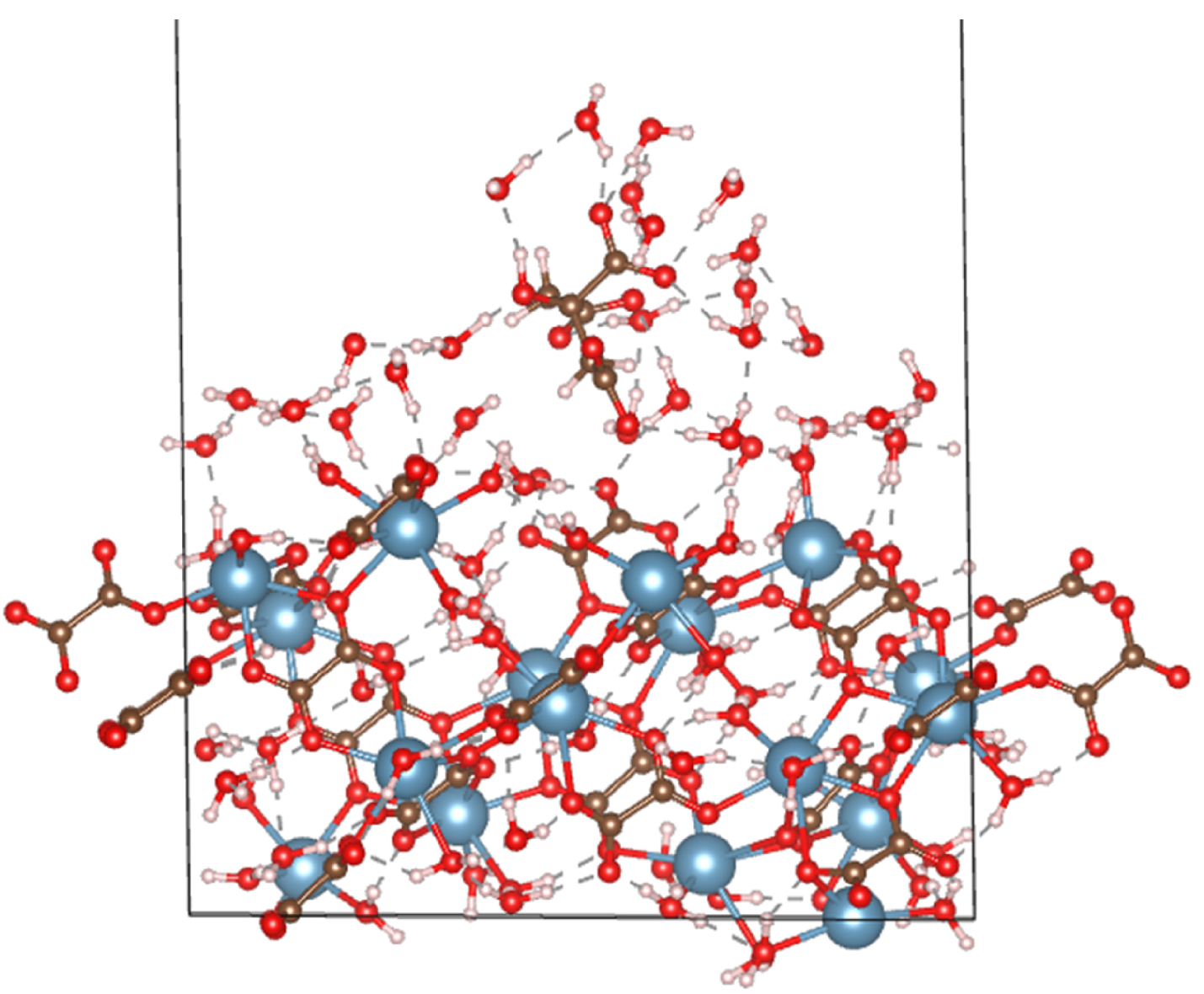
4. Calcium phosphates
4.1. Characterization of calcium phosphates
In general, it is well known that the chemistry of biological apatite is quite complex [56, 57] due to a lack of Ca2+ and OH− ions at the surface as well as their replacement by ions with different charges (for example substituted for and/or OH−). Regarding pathological calcification, calcium phosphate apatites are present in various parts of human body [58, 59] as well as on medical devices (Figure 3).
Spherical calcium phosphate apatite identified in thyroid calcifications (A) and on a medical device very common in urology, a JJ stent (B).
Although this makes it hard for a DFT study to capture all properties of an experimental system all at once (remember the size limit of the calculations), the method allows for a very detailed understanding of all the separate processes at work leading to an overall understanding of the system. Among such different investigations, we can quote the work of Deymier et al. [60] describing a mechanism by which crystal dimensions are controlled through carbonate substitution. Another study identified 2 types of carbonate substitutions and related this to the stability of the formed crystals [61]. A final example that we would like to mention here is the study of the mobility of the carbonate anion within the channels formed by apatite [62]. These results were well in line with experimental X-ray data and revealed that the carbonate is able to move almost freely through the channel. This may have important implications for the bioactivity of the apatite structure. It is worth to underline that all these results taken together, it is clearly demonstrated that carbonate substitution is sufficient to drive the formation of bone-like crystallites.
Also a derived material, hydroxyapatite (HAP) was studied by means of DFT to unravel its paracrystalline disorder and chemical composition [63]. By combining the theoretical calculations with synchrotron X-ray total scattering data, it was possible to unravel the atomistic structure of the material. Extending the range of possible DFT-compatible techniques, Chappell et al. [64] have characterized the material by comparing DFT-level and experimental NMR data opening up the possibility of studying surface reactivity.
In the case of kidney infection, it is worth to underline that two chemical compounds may be related to infection namely struvite and whitlockite [65, 66]. In that case, bacterial imprints (Figure 4A) can be revealed through observations at the micrometer scale by a scanning electron microscopy of the surface of calcium phosphate apatite [67, 68]. In whitlockite (Figure 4B), a complex structure whereby Ca2+ ions are substituted by Mg2+ ions leads to cation vacancies and protonation of phosphate groups as can be seen in the DFT model presented in Figure 5. Again, a careful theoretical characterization is detrimental for the understanding of the formation and removal of these crystals. In that sense, an important DFT-based contribution was delivered by Debroise et al. [69] who were able to quantify the ability of whitlockite to form the mentioned substitutions and vacancies. By relating these defects to the resulting IR, Raman and XRD spectra, important insights into diagnosis and treatment are available.
(A) bacterial imprints at the surface of calcium phosphate apatite deposits on a JJ stent. (B) Pseudo cubic whitlockite crystallites (blue arrows) and “bacterial imprints” (red arrows).
A DFT-based, molecular model for a Whitlockite bulk unit cell containing three Mg substitutions per unit cell of 10 Å × 9 Å × 18 Å. Blue is calcium, red is oxygen, pink is phosphorus, white is hydrogen and orange is magnesium.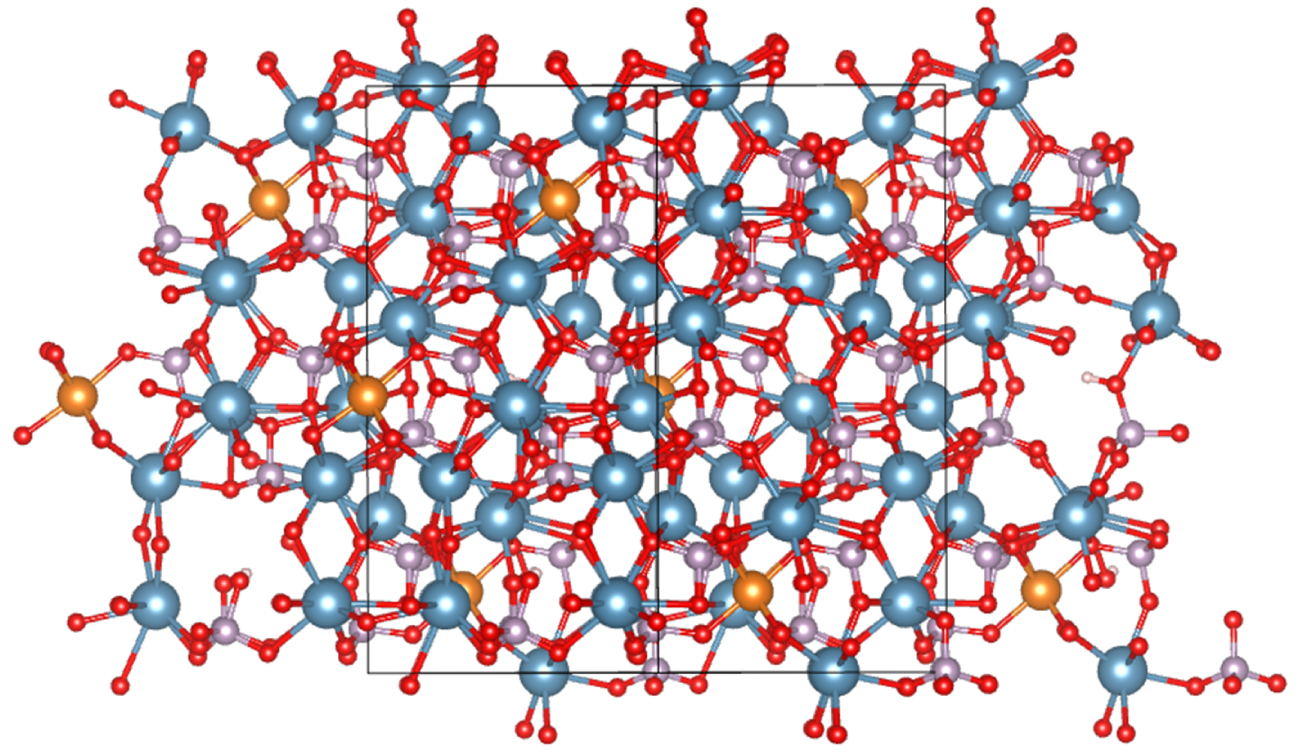
4.2. Interaction between calcium phosphates and small molecules
Most of the DFT studies dedicated to the interaction between organic and inorganic compounds have been performed within the context of physiological calcifications. As such, several studies were performed on the interface between the organic and inorganic parts in bone, namely the collagen protein and hydroxyapatite (HAP) (the most stable form of calcium phosphate in physiological conditions) [66]. A very important aspect of bone and teeth growth is the understanding of the nucleation and prenucleation phases of calcium phosphate. In that regard, an important study using DFT-driven simulations, was performed by Mancardi et al. [70] in identifying stable prenucleation clusters in aqueous solution.
The work of Cutini et al. [71] focuses on the interaction between a model of a single-collagen-strand with the most common dried P-rich (010) HAP surface. The authors discovered that the HAP adsorption process leads to a deformation of the polymer in order to create a relatively strong electrostatic interaction between the PRO carbonyl C =O group and the most exposed Ca ion of the P-rich (010) HAP surface. Other authors have investigated the interaction between water molecules and the HAP surface [69, 72]. Among them, Peccati et al. [73] have considered a set of HAP surfaces (namely (001), (010), and (101)) and their interaction with water using DFT simulations, predicting spontaneous water dissociation on these surfaces.
Quite recently, combining multinuclear solid-state NMR spectroscopy, powder X-ray diffraction, and first principles electronic structure, Davies et al. [74] have underlined the fact that citrate molecules form bridges between mineral platelets in bone. In fact, citrate molecules are well known as growth inhibitors and a recent investigation done by Fernandez et al. [75] has considered a set of the HAP crystal growth inhibitors namely pyrophosphate, etidronate, citrate and phytate. The complete set of numerical simulation showed that the adsorption energies of the inhibitors increased in the sequence: pyrophosphate < etidronate < citrate ≪ phytate. Such sequence is in line with the increase of functional groups of the molecules bounded with the HAP surface as well as the total molecular negative charge.
Finally, it is worth to note that DFT calculations can also be used to assess the interaction between metals such as Ag and HAP. Several antimicrobial studies have clearly shown that Ag-HAp nanoparticles have excellent in vitro antibacterial activity with E. coli.
5. Outlook on silica DFT studies
Although rather a mineralisation than a biological calcification, silicon dioxide—or silica—is found in skin in the case of sarcoidosis [76, 77] and also in kidney [78]. The chemistry of silica has been studied intensively due its importance in heterogeneous catalysis [79], yet not often at DFT level. Indeed, due to its amorphous nature and its complex solid/liquid interfaces, relatively little studies have been or are undertaken. Some of the authors of the current paper have been specializing in amorphous silica DFT modelling for over a decade. This resulted in the development of one of the first hydroxylated amorphous silica models in 2008 [80], published simultaneously with the model of the group of Ugliengo [79]. Recently, we reviewed the last decade on silica modelling with DFT [81, 82].
At DFT level, aside from some studies on the interaction of small amino acids with the silica interfaces, no other work has been done related to the silica mineralisation to the best of our knowledge. This is mainly due to the complexity of the molecular structure and the large size of the models when large biological molecules are investigated. However, with the still increasing computing power we expect that in a few years more realistic biological/silica interface studies will be studied at the DFT level.
6. Conclusion
We have demonstrated, through examples from the literature, the importance of density functional theory calculations in the field of pathological calcifications. Indeed, it is clear that the capability of theoretical methods—whereby density functional theory offers a very good balance between accuracy and computational cost—allows to zoom into the molecular level of the system of interest. Especially, the possibility to predict spectroscopic properties for different hypothesized molecular structures, allows to asses different possible models. Through careful comparison with experimental results, the validity of the proposed models can then be assessed. A careful analysis of the chemical structure of different surfaces, adsorption sites and geometries (conformations of functional groups), allows understanding and predictions that can have important repercussions at the macro level regarding prevention, diagnosis and treatment.




 CC-BY 4.0
CC-BY 4.0