1 Introduction
The spectroscopy of transition metal and rare-earth ions in glass has been of wide ranging importance in the optical glass industry for many years for a variety of reasons. In highly transparent materials they represent a source of energy loss because of the numerous absorptions they introduce throughout the UV, visible and near IR range. In other cases they are used to produce colour or active devices such as optical amplifiers, optical coolers, or solar energy converters based on fluorescence or scintillation. In all such cases their behaviour is related to the local environment and detailed optical studies have proved fruitful in structural analysis. Changes in the ligand (e.g., oxide or fluoride) cause significant peak shifts, while changes in matrix composition can alter the coordination number of the metal ion or shift the redox balance. More subtle changes can involve, for example, the lifetimes of excited states. A recent and increasingly active area of development is modifying the behaviour by partially crystallising the glass to phases that selectively partition the dopant ions, while controlling the crystal size to retain optical transparency. In the work reported here we have been interested in the combined effects of alkali and alkaline-earth metal ions on optical and other structurally sensitive properties. While these ions only occupy sites in the more distant coordination shells around the dopant ion, any tendency to medium-range order might be apparent and might also allow more accurate tailoring of optical absorption.
In particular, our studies have concentrated on iron species in glass. Such materials are vital for applications such as solar control, the deliberate attenuation of particular wavelengths of light to tailor optical behaviour. For example, automotive glass must have adequate visible light transmission whilst cutting out harmful ultraviolet (UV) rays and reducing heat transmission particularly by infrared (IR) radiation. UV radiation can severely damage polymeric materials, which now constitute a large proportion of vehicle interiors. With the depletion of the ozone layer, the need for UV protection is ever more important.
Iron species have unique optical absorption in the UV and near-IR spectral regions, which makes them well suited to solar control. Well-documented Fe2+ absorption bands occur in the near IR at 4 500 cm–1 and 10 000 cm–1 〚1–5〛, and Fe3+ absorption bands in the visible and near-UV range 〚1–12〛 in many different glass compositions. Fe species shift the UV edge to lower wavenumbers 〚1, 2, 8, 9, 10, 13〛, hence improving UV absorption of the glass.
Previously we have discussed the consequences of increasing Fe2O3 content in soda–lime–silica glasses 〚1〛. Here we report the effect of base-glass composition on redox, coordination, distribution and environment of Fe ions using a multi-technique approach involving wet chemical analysis and Mössbauer, ESR, optical absorption and photoluminescence spectroscopies. A large proportion of the previous studies on Fe species in glass have concentrated on binary alkali–silica or alkaline-earth–silica systems, and the results of such studies are of limited value when applied to commercial glass compositions. The ternary alkali–alkaline-earth–silica systems reported here model commercial glasses more closely whilst allowing a systematic study of the effects of compositional change.
2 Experimental
Compositions studied were, in molar percent: 70 SiO2–15 R2O (R = Li, Li/Na, Na, Na/K, K, Rb, Cs)–15 ŔO (Ŕ = Mg, Ca, Sr, Ba)–0.1 to 5 Fe2O3, with proportional replacement of the other oxides by Fe2O3. Most glasses containing 15% Li2O were phase-separated, making optical spectroscopy impossible. Mixed-alkali samples containing 7.5% of each of two alkalis were necessary to study the effects of lithium while avoiding phase separation. Mixed-alkali Na/K glasses were also made but were only included in the study by ESR spectroscopy.
Glass batches were made from high-purity chemicals to avoid contamination by unwanted oxides and other contaminants that might upset the redox equilibrium of the melt and its optical characteristics. Iron was introduced as Fe2O3. Most batches were designed to give 300 g of glass, but in just a few cases with more expensive components only 100 g of glass were melted. Only carbonates were used in melting to avoid additional redox species in the final melt. Glasses were melted in air in Pt–2% Rh crucibles at 1450 °C in electric furnaces. One-hour batch-free time was allowed, then the melt was stirred using a motorised Pt–2% Rh stirrer for 5 h. While not long enough to reach equilibrium with the atmosphere, the use of carefully controlled conditions allowed trends in behaviour to be identified. The melt was then poured into preheated moulds to make samples approximately 10-mm thick and annealed at 550 °C for 1 h, and cooled by 1 °C per minute to room temperature.
Density measurements of the glasses were made using Archimedes Principle and distilled water at a known temperature as the immersion medium. These results were used in the calculation of the volume concentrations of iron in the various glasses.
Chemical analysis was measured by the Inductively Coupled Plasma technique using an Applied Research Laboratories 3410 ICP. Fe redox measurements were also measured by wet chemical methods using a method that closely followed that of Close 〚14〛.
Samples were prepared for optical spectroscopy by cutting using a diamond wheel and using a cerirouge-impregnated wheel for chemical polishing of the sample. Typical specimen dimensions were 20 × 20 mm with thicknesses between 0.2 and 4 mm, depending on iron content. Optical spectra were recorded using a Hitachi U-3501 Spectrometer connected to a PC. The spectrometer was a dual beam instrument and measurements were made from 295–2200 nm using an integrated sphere attachment to reduce the effects of surface and bulk inhomogeneities in the glass samples. Additional data was collected using a Unicam UV/Vis spectrophotometer and a Perkin Elmer Spectrum 2000 FTIR spectrophotometer.
Photoluminescence Spectra were recorded at 293 K using an argon-laser excitation source at 476.5 nm, a combination of a Thorn EMI photomultiplier tube and a liquid N2-cooled germanium detector, and appropriate chosen gratings for the two detectors. A lock-in amplifier was used in combination with an Archimedes microcomputer for data capture. Data points were recorded every 2 or 5 nm.
ESR spectra were recorded using finely ground powder specimens placed inside clean sample tubes of 3-mm diameter. The spectra were recorded using a Varian Spectrometer connected to a Microcomputer for data capture.
Mössbauer spectra were recorded using a 25-mCi 57Co source. A 512-channel recorder was used for data capture, using velocity ranges of ±4, ±5, and ±12 mm s–1. Data collection times varied from 2 days to 2 weeks, according to iron concentrations used; most measurements were made at room temperature (293 K), but two samples were also studied at 7 K. Data were fitted by a least squares program that assumed Lorentzian profiles for the spectral lines. Results for centre shift values were corrected and quoted relative to those for α-Fe.
3 Results and discussion
3.1 Redox
Many studies have utilised the concept of optical basicity 〚15–17〛 to discuss the effect of different cations on redox equilibria. This is defined in terms of the effect of the cations present on the electron donating power of the oxygen ions in the melt and can be evaluated from published data 〚15–17〛. Increasing glass basicity in simple alkali–silica glasses shifts the redox equilibrium of Fe towards the oxidised state. This is a linear relationship 〚18–20〛 independent of Fe content 〚21〛. A similar linear relationship exists for binary alkaline-earth–silica glasses 〚22〛. It has, however, been noted that in some cases redox correlates less well with the optical basicity, attributed to “additional mechanisms” 〚20〛.
Wet chemical redox measurements for this study were made using a method similar to that of Close et al. 〚14〛. These measurements were only available for some samples. To obtain redox measurements for the remaining glasses, linear regressions of the wet chemical data were used in conjunction with peak intensities measured from optical absorption spectra. There was little deviation from the trends over the wide range of samples that were measured wet chemically and the redox calculations could be validated through the extinction coefficients and vice-versa.
Glasses containing 0.2 mol% Fe2O3 with varying alkali- and alkaline-earth-ion contents were studied. The results are shown in Figs. 1 and 2, and clearly show opposing effects of alkali and alkaline-earth ions on the Fe2+/ΣFe redox ratio when plotted against optical basicity. Increasing optical basicity brought about by increasing Z for the alkali ion resulted in a decrease in the Fe2+/ΣFe ratio. This is in agreement with a large body of previous work on binary alkali silica glasses 〚17–21〛. However, increasing optical basicity brought about by increasing Z for the alkaline-earth ion resulted in an increase in the Fe2+/ΣFe ratio. This is the opposite of the behaviour in binary alkaline-earth–silica systems 〚22〛. Our results have therefore shown that when the effects of the two different cation species are taken into account, the redox ratio no longer varies systematically with the optical basicity of the glass. Similar deviations in behaviour were found by Rüssel et al. 〚23, 24〛.
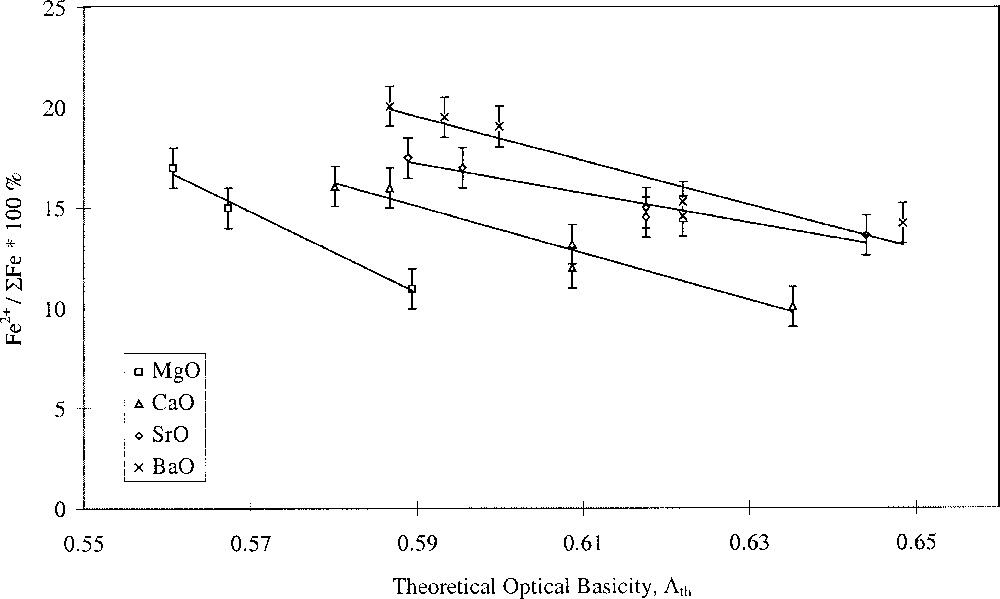
Fe2+/ΣFe redox ratio versus optical basicity in terms of alkaline-earth type.
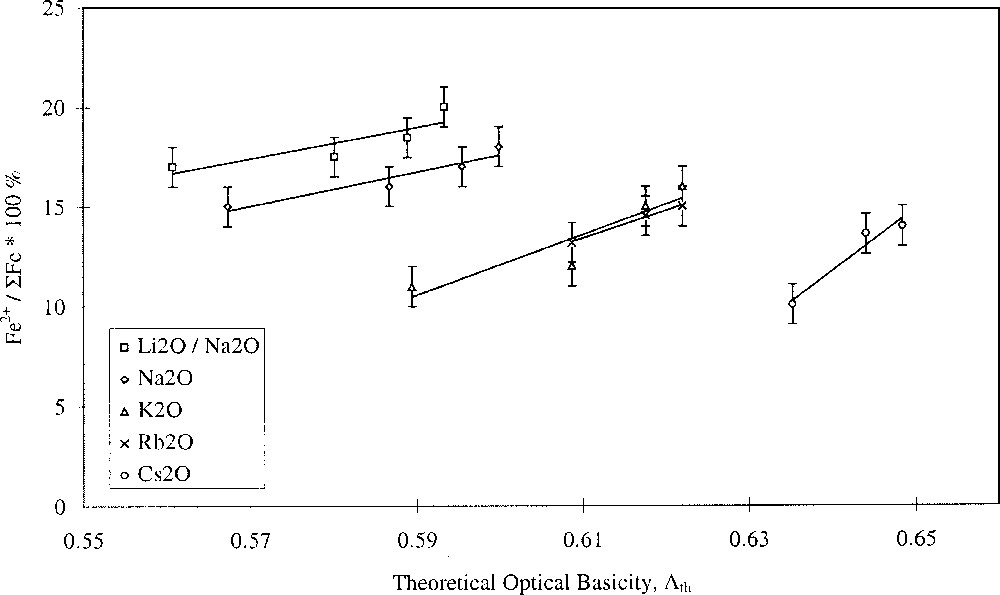
Fe2+/ΣFe redox ratio versus optical basicity in terms of alkali type.
Plotting the redox ratio, Fe2+/ΣFe, against the alkali/alkaline-earth ratio of either the Pauling ionic radii, the cation field strength Z/a2, or the optical basicities of the individual oxides, yielded linear relationships, as shown in Fig. 3. We have defined this as selective behaviour and it occurs when alkali and alkaline-earth ions have opposing effects on a property, suggesting competition or selectivity between ion types. Such behaviour is characterised by a linear relationship between the parameter being studied and the alkali/alkaline-earth ionic radius ratio. Here we have also found linear relationships between redox ratio and both the alkali/alkaline-earth cation field-strength ratio and oxide basicity ratio. Glasses where MgO was the alkaline-earth oxide gave a slightly offset line but with identical gradient. The anomalous structural role of magnesium in silicate glasses may explain this. It has been demonstrated in silicate glasses that Mg2+ ions behave somewhat differently to the other alkaline-earth ions, and this has been attributed to the presence of some Mg2+ ions in four-fold coordination 〚25–29〛. The unique behaviour of Mg2+ explains differences in molar volume 〚27〛 and glass hardness 〚29〛, and may also explain differences in redox and optical properties observed in iron-containing alkaline-earth phosphate glasses 〚30〛.
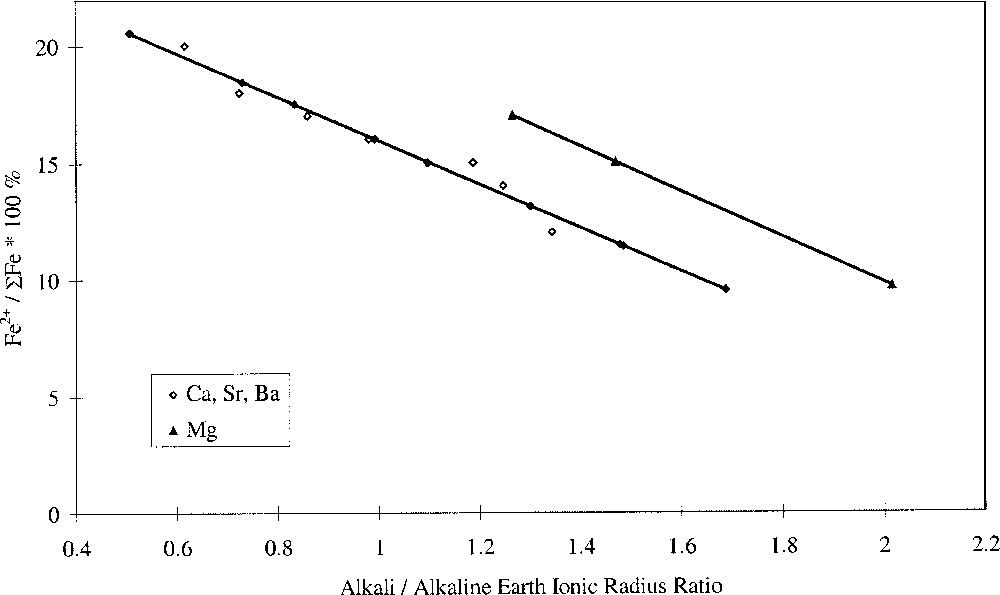
Fe2+/ΣFe redox ratio versus alkali/alkaline-earth ionic radius ratio.
3.2 Optical Absorption Spectroscopy: Fe2+ bands
Only one spin-allowed transition is expected for Fe2+, corresponding to the 5T2(D)→5E(D) transition for octahedral sites and 5E(D)→5T2(D) for tetrahedral sites, as illustrated in the energy-level diagram for Fe2+ ions. These are expected to occur at ∼10 000 cm–1 and ∼4 500 cm–1, respectively 〚1–6, 9–11, 13, 30〛. It is thought that, in agreement with mathematical fitting and observation of spectra, the width and asymmetry of the octahedral band is due to a range of site distortions and the dynamic Jahn–Teller effect 〚2, 4, 5, 11, 13, 30〛. There has been much debate over the coordination of Fe2+ ions in glass, and hence the origin of the absorption band at ∼4 500 cm–1. Some have attributed it to the 5E(D)→5T2(D) transition of Fe2+ ions in tetrahedral sites 〚1, 2, 4, 5, 11, 13, 31–33〛. The Laporte selection rule states that tetrahedrally coordinated ions absorb 10–100 times more strongly than octahedrally coordinated ions, so the relative weakness of this band suggests that the number of Fe2+ ions causing the absorption at ∼4 500 cm–1 is likely to be small. Optical spectroscopy of various silicate glasses indicated that less than 5% of Fe2+ ions were tetrahedrally coordinated 〚31–33〛.
When Fe ions are subjected to a ligand field, the 3d orbitals are split, and the energy difference between these split levels is known as the ligand field strength, 10 D q. This parameter is particularly useful for studying the local environment of Fe2+ ions, since it can be evaluated directly from optical absorption spectra. Glass composition strongly affects the octahedral Fe2+ band near 10 000 cm–1 〚3, 10, 30, 34, 35〛. Changes in band wavenumber indicate changes in 10 D q and the Racah B and C parameters. In alkaline-earth phosphate glasses, linear relationships were established between cation field strength of the alkaline-earth ion and Fe2+ band position, hence 10 D q(Fe2+), such that increasing size of the alkaline-earth ion shifted the peak to smaller wavenumbers 〚30, 35〛. It was asserted that the modifier cation was expected to reduce the ligand field strength of the oxygen ligands and that this effect would be greatest for the cation with the greatest polarising power, namely Mg2+. Hence the band would move to lower wavenumbers as the cation field strength of the alkaline-earth decreased. A similar study on ternary alkali–alkaline-earth silicate glasses found that the opposite occurs: with increasing field strength of alkali and/or alkaline-earth ion, the position of the peak near 10 000 cm–1 moved to larger wavenumbers 〚34〛. Possible explanations explored by these workers for the movement of the band were changes in the number of non-bridging oxygens and medium-range order effects due to modifier cations. Non-bridging oxygens (nbo’s) are bonded to one network-former and one network-modifier; hence they do not form bridges between glass-forming ions such as Si4+. A plot using cation field strength, Z/a2, of the various cations showed an approximately linear relation between peak wavenumber and {Z/a2 (alkali + alkaline-earth)}/{Z/a2 (Si + Al)} 〚34〛.
Optical absorption spectra in this study were corrected for intrinsic absorptions and reflection losses by subtracting the absorbance of glasses of the same composition but containing zero added Fe2O3. Gaussian peak fitting was then carried out using a computer program. A typical fitted spectrum is shown in Fig. 4.
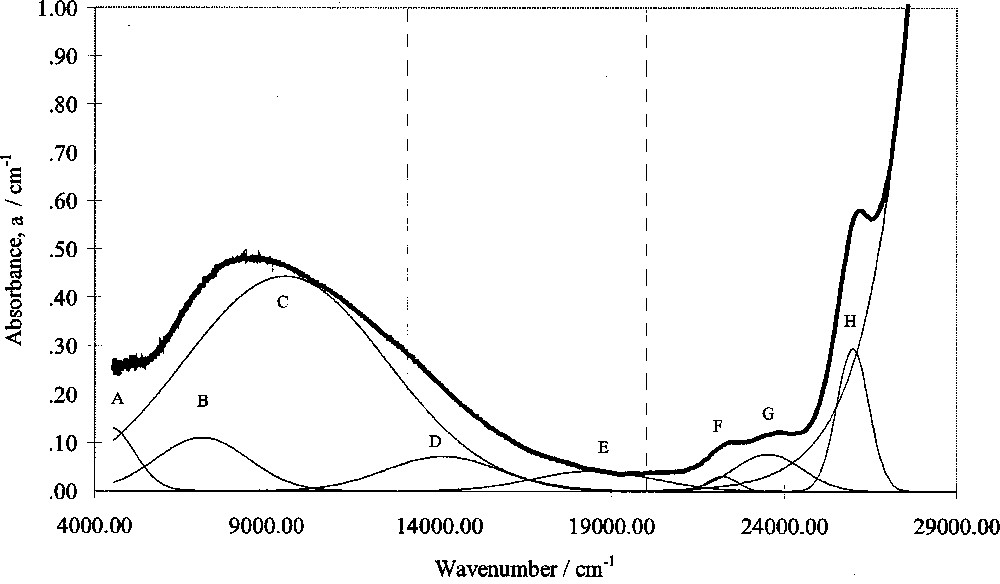
Computer-fitted optical absorption spectrum of SiO2–Cs2O–CaO–0.2% Fe2O3 glass.
Fig. 5 shows that the wavenumbers of the peaks attributed to Fe2+ ions, peaks A (tetrahedral), B (dynamic Jahn–Teller) and C (distorted octahedral), decrease linearly with optical basicity. This means that 10 D q(Fe2+) obeys a linear relationship with optical basicity. It was known that cation distributions in glass are not random as proposed by the original random network theory 〚36, 37〛. Application of our findings to the question of Fe coordination and environment shows that Fe2+ ions display collective behaviour, as evidenced by 10 D q(Fe2+). Hence their next-nearest-neighbour cation coordination spheres should contain alkali and alkaline-earth cations, though not necessarily both types in any one-coordination sphere. It is therefore possible that Fe2+ ions occupy regions in the glass that are rich with modifier ions. On the other hand there is no evidence that the Fe2+ ions do not define their own environment and use appropriate cations from their surroundings to satisfy bonding requirements. The intensity ratio of peaks A, B and C varied little with glass composition, indicating that the Fe2+ tetrahedral/octahedral ratio is largely unaffected by composition in these glasses, based on the widely-held view that the band at ∼4 500 cm–1 is caused by tetrahedral Fe2+ ions.
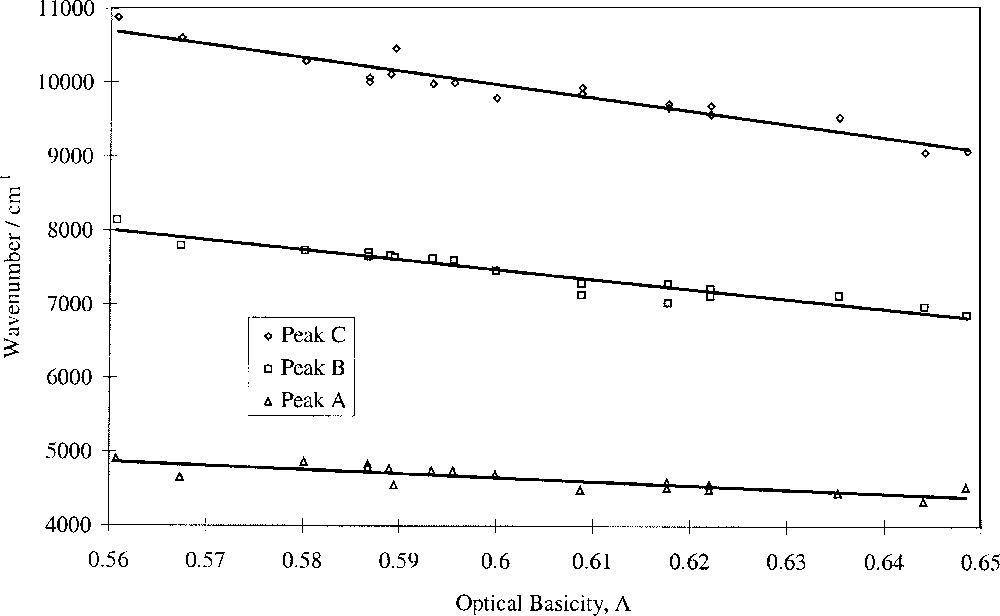
Fitted peak wavenumber vs optical basicity for Fe2+ bands.
3.3 Optical Absorption and Luminescence Spectroscopies: Fe3+ bands
It is not possible to evaluate 10 D q for Fe3+ ions directly from optical absorption spectra because Fe3+ has the 3d5 configuration so all d–d transitions are spin-forbidden. A large amount of work has been conducted on Fe3+ spectra in terms of optical parameters 〚2–10, 12, 30〛. Our band assignments agreed with those of Hannoyer et al 〚6〛, although values of 10 D q and Racah B and C differed slightly, due to compositional differences. The lowest energy Fe3+ transition, 6A1(S)→4T1(G) in absorption, is known from energy level diagrams to be strongly affected by the ligand field. This Fe3+ band can be observed using luminescence spectroscopy, whereas in absorption it occurs in a spectral region where it is obscured by strong Fe2+ bands. Previous studies indicated that this luminescence band occurs for tetrahedral Fe3+ at 14 000–16 000 cm–1 and for octahedral Fe3+ at 11 000–12 000 cm–1 〚3, 38–41〛.
In this study, the peak wavenumber of the transition assigned to 4T1(G)→6A1(S) of tetrahedral Fe3+ ions was measured in luminescence as a function of glass composition. Peak wavenumber varied linearly with the alkali/alkaline-earth ionic radius ratio, as shown in Fig. 6. Other workers have shown that changes in the Racah B and C parameters are too small alone to explain such peak shifts, instead attributing them to changes in 10 D q 〚3〛. The changes in wavenumber in this study therefore indicate changes in 10 D q as well as possibly B and C. We conclude therefore that 10 D q(Fe3+tetrahedral) decreases approximately linearly with alkali/alkaline-earth ionic radius ratio, i.e. exhibits selective behaviour. This is in marked contrast from the behaviour of 10 D q(Fe2+), shown in Fig. 5 and discussed in section 2.
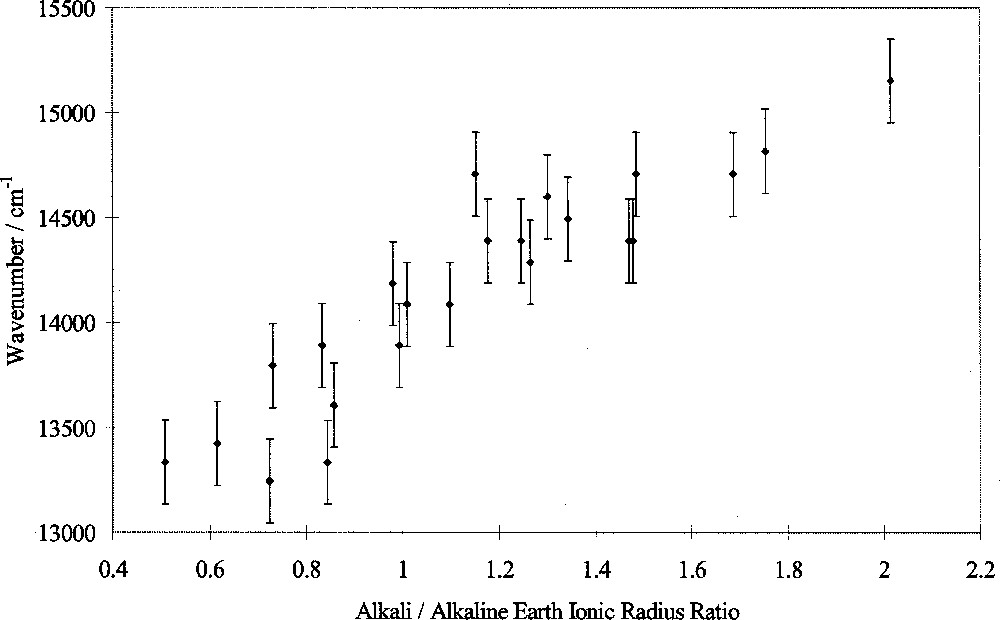
Fe3+ luminescence peak position versus alkali/alkaline-earth ionic radius ratio.
3.4 Electron Spin Resonance (ESR) Spectroscopy
The origins of the two main Fe3+ resonances at g ∼ 4.3 and g ∼ 2 have been intensively debated. Some have attributed them to Fe3+ ions occupying tetrahedral and octahedral coordination sites, respectively 〚35, 42–43〛. It is the current majority view, however, that the g = 4.3 resonance can be produced by isolated Fe3+ ions occupying either tetrahedral or octahedral sites with low-symmetry rhombic distortions 〚8, 11, 44–49〛. It has been suggested that these sites have a particular symmetry, C2v 〚44, 47, 48〛. The concentration dependence of the g = 2 resonance has been attributed to exchange interactions between clustered Fe3+ ions 〚8, 11, 45, 47–51〛. At low iron contents, the origin of the g = 2 resonance is less clear. Statistically, exchange interactions can occur at all iron concentrations, and indeed clustering of Fe3+ ions has been found at very low iron concentrations using both ESR 〚49, 50, 52〛 and Mössbauer spectroscopy 〚53〛. In a previous paper, we estimated relative amounts of isolated and clustered Fe3+ ions in a limited number of samples from Mössbauer spectroscopy 〚1〛. For any given Fe2O3 content, the ratio of peak-to-peak intensities of the g = 2/g = 4.3 resonances, Ip–p(g = 2)/Ip–p(g = 4.3), increased with increasing alkali ion size in single alkali-oxide–CaO–SiO2 glasses 〚42, 43, 47, 48〛, and also in mixed alkali-oxide–CaO–SiO2 glasses 〚48〛. Changing the CaO content had a smaller effect on Ip–p(g = 2)/Ip–p(g = 4.3) than changing the alkali content 〚48〛.
Analysis of ESR spectra measured at room temperature in this study was carried out in terms of Ip–p(g = 2)/Ip–p(g = 4.3). Figs. 7 and 8 show the results of this analysis plotted against alkali/alkaline-earth ionic radius ratio. Both graphs shows the same data points, but one highlights the effects of changing alkali oxide and the other highlights the effects of changing alkaline-earth oxide. Both Figs. 7 and 8 show that when the alkali ion was small, such as in the Li/Na or Na glasses, the type of alkaline-earth ion had little effect on the intensity ratio. Alkaline-earth ions had an increasing effect with increasing alkali ionic size, such that the effect of alkaline-earth ions was greatest in conjunction with Cs2O as the alkali oxide.
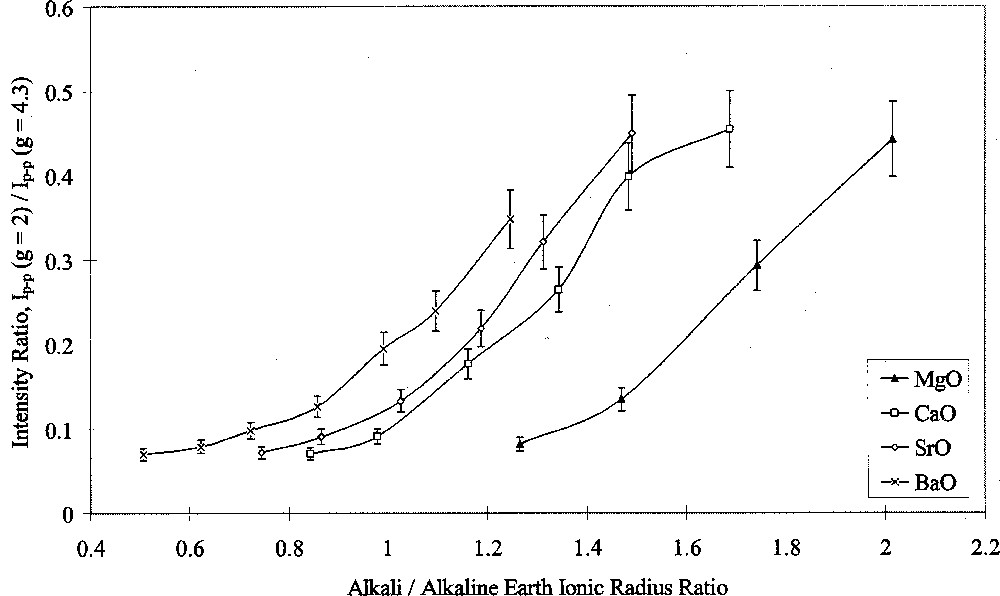
ESR Ip–p(g = 2/g = 4.3) ratio versus alkali/alkaline-earth ionic radius ratio, showing the effects of alkaline-earth type.
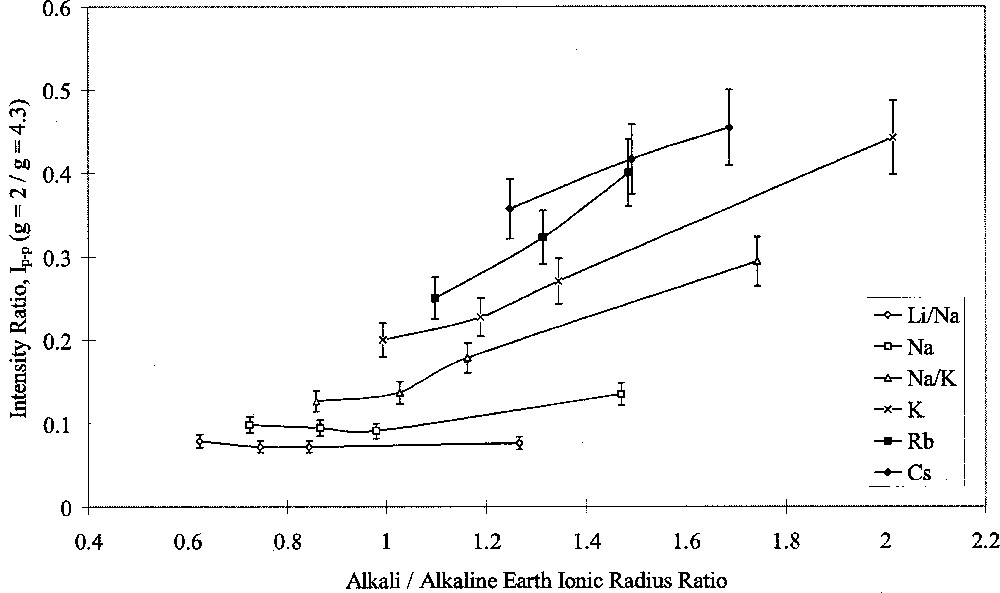
ESR Ip–p(g = 2/g = 4.3) ratio versus alkali/alkaline-earth ionic radius ratio, showing the effects of alkali type.
Based on the brief literature survey discussed here, the results of our study led us to the following conclusions:
- • (i) larger alkali ions promote Fe3+ cluster formation;
- • (ii) smaller alkaline-earth ions promote Fe3+ cluster formation;
- • (iii) this is more effective in conjunction with larger alkali ions.
These findings are also strong evidence for competition between alkali and alkaline-earth ions for stabilisation of Fe3+ ions, i.e. selective behaviour. For all the glasses studied, there is in theory an abundance of single-charged alkali ions present and able to provide sufficient charge balance for all the Fe3+ ions. Waff noted that alkali–Fe3+ complexes are more tightly bound than alkaline-earth–Fe3+ complexes and are therefore more stable 〚54〛. The fact that Fe3+ clustered/isolated distribution, as indicated by Ip–p(g = 2)/Ip–p (g = 4.3), is primarily determined by alkali ions confirms this statement. It also explains selective behaviour wherein tetrahedral Fe3+ ions preferentially use alkali ions for charge balance. A combination of larger alkali and smaller alkaline-earth ions gives the best stabilisation of tetrahedral Fe3+ ions.
3.5 Mössbauer Spectroscopy
Mössbauer spectra were measured in glasses containing 5 mol% Fe2O3. Previously we have shown that redox is unaffected by Fe2O3 content in these glasses, provided that redox equilibrium has been reached 〚1〛. Mössbauer spectra can be evaluated in terms of redox, centre shift (δ), quadrupole splitting (Δ), hyperfine splitting (hfs) and linewidth (Γ). For a detailed description of these parameters, the reader is referred to other works on Mössbauer spectra of iron-containing glasses 〚1, 6, 8, 22, 45, 53, 55–58〛. Based on the work of Williams et al. 〚53〛, it was safe to assume that at 5 mol% Fe2O3 any hfs due to isolated Fe3+ ions is very weak, and so measurements at room temperature were valid, resolving one doublet component for each redox state. Comparison of measured Mössbauer parameters obtained from peak fitting, shown in Tables 1 and 2, with those from literature 〚1, 6, 8, 22, 45, 53, 55–58〛 has led us to the following conclusions:
Mössbauer parameters for SiO2–Na2O–RO–5 mol% Fe2O3 glasses.
| alkaline-earth Oxide | MgO | CaO | SrO | BaO |
| Fe2+/ΣFe * 100%, ± 2 | 16.67 | 16.33 | 18.30 | 16.84 |
| CS (Fe2+) (mm s–1), ± 0.02 | 0.98 | 0.98 | 1.05 | 1.07 |
| QS (Fe2+) (mm s–1), ± 0.03 | 1.95 | 2.00 | 1.94 | 1.95 |
| LW (Fe2+) (mm s–1), ± 0.03 | 0.69 | 0.55 | 0.60 | 0.53 |
| CS (Fe3+) (mm s–1), ± 0.02 | 0.24 | 0.27 | 0.30 | 0.30 |
| QS (Fe3+) (mm s–1), ± 0.03 | 0.92 | 0.91 | 0.91 | 0.89 |
| LW (Fe3+) (mm s–1), ± 0.03 | 0.65 | 0.66 | 0.60 | 0.59 |
Mössbauer parameters for SiO2–R2O–BaO–5 mol% Fe2O3 glasses.
| Alkali Oxide | Li2O + Na2O | Na2O | K2O | Rb2O | Cs2O |
| Fe2+/ΣFe * 100%, ± 2 | 14.55 | 16.84 | 9.52 | 11.33 | 9.35 |
| CS (Fe2+) (mm s–1), ± 0.02 | 1.09 | 1.07 | 0.96 | 0.99 | 0.91 |
| QS (Fe2+) (mm s–1), ± 0.03 | 1.96 | 1.95 | 2.18 | 2.08 | 2.04 |
| LW (Fe2+) (mm s–1), ± 0.03 | 0.59 | 0.53 | 0.57 | 0.52 | 0.46 |
| CS (Fe3+) (mm s–1), ± 0.02 | 0.31 | 0.30 | 0.27 | 0.26 | 0.26 |
| QS (Fe3+) (mm s–1), ± 0.03 | 0.90 | 0.89 | 0.80 | 0.78 | 0.75 |
| LW (Fe3+) (mm s–1), ± 0.03 | 0.59 | 0.59 | 0.57 | 0.52 | 0.53 |
- • (i) the majority of Fe2+ ions are octahedrally coordinated; increasing alkali/alkaline-earth ionic radius ratio gave a small increase in the number of Fe2+ ions in tetrahedral coordination;
- • (ii) the majority of Fe3+ ions occur in tetrahedral coordination; increasing alkali/alkaline-earth ionic radius ratio leads to a greater preponderance of tetrahedral sites;
- • (iii) there is a greater dependency on alkali type than on alkaline-earth type;
- • (iv) smaller alkali and alkaline-earth ions give a wider range of site parameters for both redox states.
It must be noted that the Mössbauer results were obtained from glasses containing 5 mol% Fe2O3, rather than 0.2 mol% for the optical, redox and ESR results. The Mössbauer results show identical trends to the results from the other techniques and merit qualitative comparison.
6 Discussion
This study has shown that an increase in the alkali/alkaline-earth ionic radius ratio, cation field-strength ratio or oxide basicity ratio, is accompanied by increases in the Fe3+ tetrahedral/octahedral ratio and the Fe3+ clustered/isolated ratio. These changes in coordination and distribution are large compared with the changes in redox, hence the relationship between coordination and distribution are independent of redox in these glasses. Based on our findings, we suggest two different structural possibilities involved with the selective behaviour of redox, coordination of Fe3+ ions and distribution of Fe3+ ions.
(a) Only alkali cations stabilise Fe3+ ions, and alkaline-earth ions merely hinder their effectiveness by varying degrees based upon space/charge effects. The ability of the alkali ions to perform these various stabilisations increases linearly with size, and the ability of alkaline-earth ions to hinder the stabilisation increases linearly with size.
(b) Both alkali and alkaline-earth cations stabilise Fe3+ ions. A combination of large alkali ions and small alkaline-earth ions best achieves this. The ability of the alkali ions to perform the stabilisation is proportional to their size, and the ability of alkaline-earth ions to perform the stabilisation is inversely proportional to their size.
A slight exception to this rule is MgO, possible reasons for which were discussed in section 2.
7 Conclusions
Selective behaviour has generally been associated with the redox ratio and Fe3+ ions, whereas collective behaviour has generally been associated with Fe2+ ions. A relationship has been suggested between coordination and distribution of Fe3+ ions. These have implications for the local structure surrounding Fe species.
Acknowledgements
The principal author acknowledges with thanks the support of the EPSRC and Pilkington plc during this project, and Glass Technology Services Ltd. during the writing of this paper.


