1 Introduction
The process of sintering loosely packed particles is a very rich field of research, covering a wide range of materials with different atomic structures and dissimilar sintering behaviors. In some cases, sintering may be considered only a physical process when matter transport, such as atomic diffusion in crystalline systems or viscous flow in vitreous bodies, decreases the body’s surface area. Alternatively, sintering may follow a physicochemical course as, for instance, in some sol–gel systems in which a condensation reaction develops during sintering, with the concomitant problem of expelling the gases thus generated. In systems that sinter at high temperatures, a low melting second phase can be introduced or generated deliberately by chemical reaction to wet all the particles, aiding densification through capillarity. In addition, metallic crystalline nanoparticles, for instance, display newly discovered sintering mechanisms, such as particle rotation and plastic deformation, which do not occur in micron-sized particles.
The physical processes that control the densification kinetics of porous glass bodies by reducing their surface area are well known. In a variety of vitreous systems, the particle’s surface energy is the driving force, while viscous flow is the kinetic path through which the surface area is minimized. In some cases, however, a competing process, concomitant crystallization, typically surface crystallization, of the glass particles occurs. The crystallized surface of the particles does not flow, slowing down the sintering kinetics. The interplay between the kinetics of crystallization and sintering can result in a variety of microstructures with different porosities and crystallized fractions. Crystallization is a desirable effect only if one’s purpose is to produce sintered glass ceramics, in which case controlled crystallization is necessary; otherwise, it is a source of problems.
Different models have been developed to account for the kinetics of sintering. Frenkel’s model of viscous sintering 〚1〛, which describes the early stages of sintering of spherical, monodispersed particles, allows one to calculate the shrinkage rate of two equal particles whose centers approximate each other. The energy released by the decrease of surface area is used for viscous flow, which is responsible for the mass transport that produces densification. Frenkel’s model is valid roughly within the first 10% of linear shrinkage. For compacts beginning with a relative density of 0.6, 10% of linear shrinkage varies up to a density of 0.8.
Mackenzie and Shuttleworth 〚2〛 developed a model to explain the final sintering steps of a matrix with spherical monodispersed pores. This model applies to relative densities of more than 0.9.
There was also a gap between the densities of 0.8 and 0.9 to which no model applied. This gap was much larger when the initial density of the compact was about 0.15, as in gel-derived materials. This problem was solved by Scherer 〚3〛, who considered a geometric array of sintering particles that mimicked the structure of dry gels. Scherer’s calculations were similar to those of Frenkel: the energy dissipated in viscous flow was established as being equal to the energy change resulting from the reduction in surface area. He succeeded in describing the sintering of bodies from a very low relative density, 0.15, up to 0.94. Scherer’s model also applies for the densification of bodies having higher initial densities (even with particle arrangements that are unlike those of dry-gels), demonstrating that modeling results are virtually insensitive to geometric features. For instance, the results of Schererˈs and Frenkelˈs models almost coincide for the first 10% of linear shrinkage.
The Scherer model was successfully applied to the sintering of pure SiO2 preforms produced by flame hydrolysis of SiCl4 with a pore size distribution. In this case, the pore-size distribution data was required for the calculations 〚4, 5〛.
The Clusters model 〚6〛, which allows both Frenkel and M–S regions to occur simultaneously, was later developed to work with compacts having any particle-size distribution. This model is based on three sintering stages: a pure ‘Frenkel’ (F) first step, a mixed ‘Frenkel/Mackenzie-Shuttleworth’ stage, and a third, pure ‘Mackenzie-Shuttleworth’ (M–S) step. The model considers the sample’s shrinkage as the sum of the partial shrinkage of several clusters, each consisting of equally sized particles and each showing an independent F or M–S behavior. The overall set of clusters mimics the specimen’s real particle-size distribution. The model also introduced the ‘neck forming ability-ξr’, which allows for the formation of necks among different sized particles, thus relaxing the clustering condition.
The data necessary to calculate the sintering kinetics of non-devitrifying glasses are: viscosity vs temperature curve, glass–vapor surface energy, particle-size distribution and thermal history. If the particles are not spherical, an (empirical) shape factor is also needed. The Clusters model also allows one to introduce the number of necks that each particle forms with its neighbors. If there is concurrent crystallization or pre-existing refractory particles (or crystals) on the glass particle surfaces, not all particle–particle contacts are available for viscous flow 〚7–9〛. With such input data, the model offers the advantage of providing pore size distribution as an output.
It is common practice in modeling glass sintering to fit measured to theoretical density using viscosity as a free parameter, and to compare the viscosity thus obtained with measured data. When this procedure is used, it must be kept in mind that the fitted viscosity may include opposite effects on the sintering kinetics, such as a slowing down of the sintering kinetics by crystallization or an increase in the kinetics by shape factors greater than 1 for some jagged powders. To avoid such problems, in this article we use the experimental viscosity curve as an input parameter.
If crystallization occurs during sintering, viscous flow is hindered. When all particle surfaces crystallize, sintering (by viscous flow) ceases and a fully or partially crystallized porous body is obtained 〚7, 10〛. However, concurrent sintering and crystallization may have a significant technological importance, since various glass-ceramic products are made by viscous sintering followed by controlled crystallization 〚11〛.
The kinetics of homogeneous or heterogeneous crystallization is well described by the Johnson–Mel–Avrami–Kolmogorov (JMAK) equation of phase transformations 〚12〛. To calculate the surface fraction transformed on a given thermal path, all the data one needs are the density of nucleation sites Ns (for surface crystallization), the crystal growth rate U for each crystalline phase and the crystal geometry.
Most glasses crystallize from the surface, so a constant number of nucleation sites Ns at the particle’s surface is normally considered. The value of Ns is strongly dependent on the quality of the surface, which, in turn, depends on the method used to obtain the powder 〚13, 14〛. When the particle size is smaller than the product Ut (U = crystal growth rate and t = time), then the JMAK equation for surface crystallization describes only the first stages of crystallization kinetics.
Several authors have discussed the competition between sintering and crystallization. Ulhmann et al. 〚15〛, for instance, combined calculated TTT transformation curves with densification curves, calculated from the theory of viscous sintering, to discover whether densification of a porous body without simultaneous crystallization was possible. Zarzycki 〚16〛 noted that densification and crystallization are equally dependent on viscosity; thus, a decrease in viscosity causes the same acceleration in both processes. Due to this fact, Scherer showed that the real competition occurs between the driving forces for sintering and crystallization 〚10〛.
While the driving force for sintering – generally the solid–vapor surface energy – is almost temperature independent, the driving force for crystallization depends to a great extent on temperature. Therefore, a sintering temperature above the range in which the driving force for crystallization is too high will privilege sintering. However, because it may crystallize along the heating path, the sample must reach this temperature quickly.
Muller 〚14〛 studied the concurrence of sintering and crystallization in cordierite glass. The competition in this concurrency is so fierce that only very small particle compacts sintered to almost full density before crystallizing. Particle size and heating rate were used as variables to analyze this concurrence and the author found that, at a heating rate of 12 K min–1, only particles smaller than 1 μm sintered to full density.
Gutzow et al. 〚17〛 studied the problems that control surface-induced nucleation of glasses. They emphasized the influence of elastic strains, surface contamination by active substrates, and the dependence of crystal growth and overall crystallization kinetics on the average size of an ensemble of sintering glass grains. They also derived a formalism connecting overall crystallization with the average size of the glass particles. Finally, they investigated the interdependence of sintering and crystallization. Finite-particle effects on the crystallization kinetics were also studied by Weinberg 〚18〛.
Boccaccini et al. 〚19〛 experimentally demonstrated that cylindrical compacts (5 × 5 mm) of crushed Ba–Mg–Al–Si–O glass powder with a narrow particle-size distribution of around 10 μm can be fully densified when heated at q = 15 °C min–1 to 1050 °C. However, this same powder crystallized and the compact therefore densified to only 89% of the glass density, at a heating rate of 1 K min–1. Thus, the high heating rate favored sintering in detriment to crystallization.
Using the proposal of reference 〚20〛, the present authors extended the Clusters model to describe the concurrence of sintering and surface crystallization in isothermal and non-isothermal experiments 〚7, 8〛. This model considers the effect of the surface crystallization on the sintering rate, an approach unlike that of Uhlmann 〚15〛, who considered volume crystallization and treated sintering and crystallization as independent processes. The Clusters model was also used to predict the sintering kinetics and pore size distribution of an array of spherical soda–lime–silica glass particles having a partially crystallized surface at the beginning of sintering 〚9〛. In real systems, a pre-existing crystallized surface fraction or crystalline impurities on the particle surfaces strongly affect the sintering kinetics.
Non-stoichiometric crystallization, when the crystal phase composition differs from that of the parent glass, may cause variations in the glass matrix composition, viscosity and surface energy, complicating the analysis of the sintering kinetics. Finally, gas expelled from the growing crystals, gases entrapped during sintering or exiting the glass particles can generate porosity, which deteriorates the properties of sintered glasses or glass ceramics.
Next, we will summarize the governing models, describe relevant experiments and discuss several tests involving the Clusters model.
2 The models
2.1 Frenkel’s model
The Frenkel model (equations (1a) and (1b)) offers a description of the onset of isotropic sintering of monodispersed spherical particles
Equation (1b) is commonly used to describe the change in density during sintering:
A deviation from equation (1a) is found 〚21〛 when the particles are nonspherical. To account for the effect of particle shape on the sintering kinetics, an empirical constant, called shape factor, ks, is normally used to fit the measurements. The ks values used in the literature vary from 1.8 to 3. Nevertheless, when one compares the sintering kinetics of spherical particles having a size distribution with that of irregular particles (such as crushed particles) having the same size distribution, one is comparing not only shapes, because the particle packing is also different. Thus, the real effect of the particles’ shape on the sintering kinetics deserves further attention.
Frenkel’s equation, equation (1a), is actually derived for a linear arrangement of particles. In passing to volume shrinkage, one can use equation (1b). This passage assumes isotropic sintering behavior in three spatial coordinates, which is equivalent to considering a cubic array of particles. Thus, each particle should have six neighbors and should therefore develop six sintering necks in the beginning of the process. However, experimental data for an array of a narrow size distribution of spherical glass particles shows that there is a distribution of necks per particle (between 3 and 8) and that the average is 5 〚9〛. This distribution varies in different systems and should therefore be tested on a case-by-case basis.
2.2 The Mackenzie–Shuttleworth model
For higher relative densities (ρ>0.9), when the pores are spherical and isolated in the glass, the Mackenzie–Shuttleworth, M–S model, gives the following densification rate 〚2〛:
The original M–S kinetics, without approximations, is expressed as 〚23〛:
Although the initial particle boundaries have vanished by the time the M–S stage is reached, the pore size distribution is inherited from the initial particle-size distribution.
On a laboratory time scale, sintering is only accomplished above the glass transition temperature, Tg. In this range of temperatures, the viscosity η(T) is normally described by the Vogel–Fulcher–Tamman (VFT) equation 〚24〛:
The surface energy can be estimated from the glass composition. The other relevant parameters are measured.
2.3 The Scherer model
Scherer’s model 〚3〛 uses a basic cell, pictured as a cubic array of intersecting cylinders, which describes low-density microstructures such as those of dry gels and flame hydrolysis preforms. The cylinders stand for strings of particles. Because the particles, in this case, are aligned along the borders of a cubic structural unit, each particle has a small number of neighbors and, hence, a small number of contacts (six for particles in the string crossovers and two otherwise).
Scherer’s model is an excellent (and perhaps the only) way to deal with the sintering kinetics of these types of structures. Although it can also be applied to high-density systems, the geometry of the unit cell is very dissimilar to the geometry of packed particles. However, since the calculations are apparently insensitive to the geometry assumed in different models, this cylinder geometry has been applied to different situations with good results 〚25〛. It also solves the problem of describing the medium range densities, especially when one starts from low-density compacts.
Scherer’s model was developed to include, as input data, the measured pore-size distribution obtained through mercury porosimetry. However, one must consider that if a pore-size distribution is present, porosimetry can be misleading, because the access of Hg or of any other liquid to the large pores may be through the small ones. In addition, mercury porosimetry depends on the rate at which the pressure increases during measurement. Thus, the information provided by mercury intrusion porosimetry does not always reflect actual pore sizes and may be a source of problems (Fig. 1).
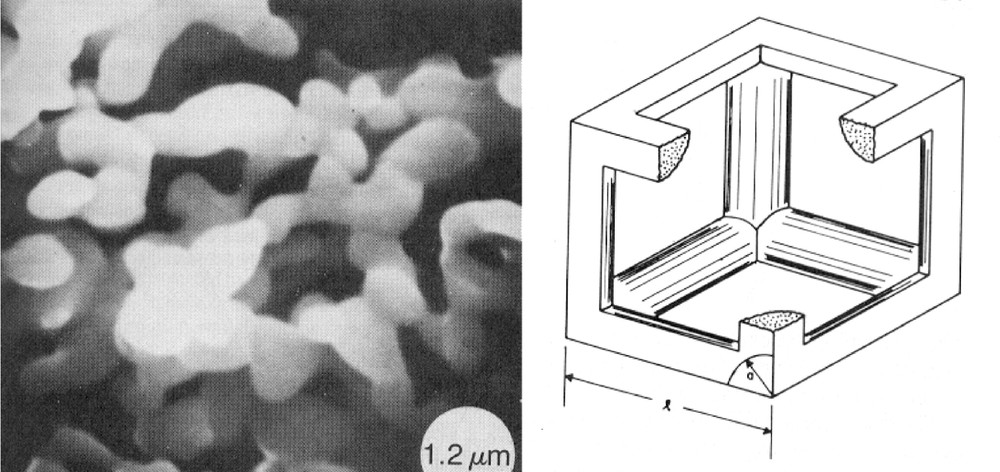
Low-density structure (left). Diagram of Scherer’s model (right) resembling the microstructure on the left-hand side. l is the cell length and a is equivalent to the particle size. After G.W. Scherer, Sintering of low-density glasses, part I 〚3〛.
2.4 The ‘Clusters model’. Glass densification with a particle-size distribution
Giess et al. 〚23〛 reported that a pure M–S analysis does not accurately describe the final stages of sintering of pressed compacts of polydispersed, irregular shape cordierite-glass particles. He suggested that this drawback may be the result of smaller-size particle fractions sintering more rapidly at the outset and of larger ones sintering towards the end of the process. Fig. 2 illustrates this fact in a cross-section of a compact of an alumino-borosilicate glass having a wide particle-size distribution, after a linear shrinkage of 8%.
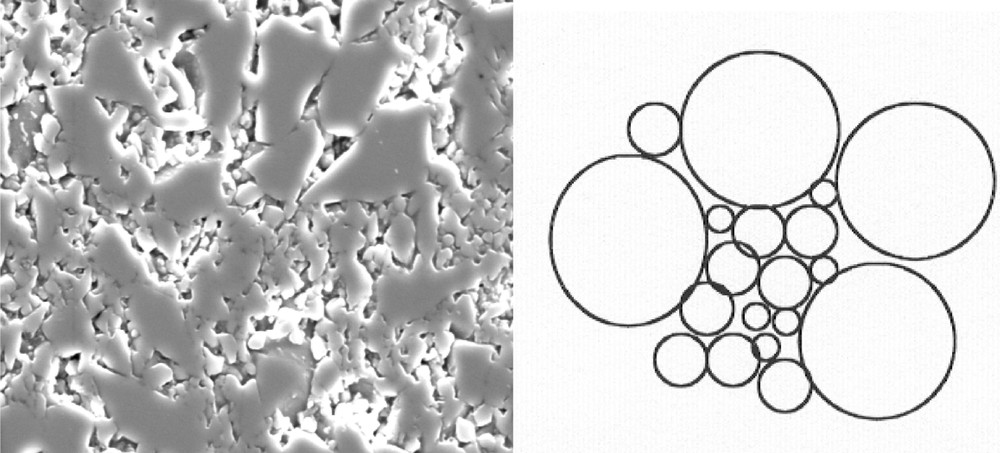
SEM micrographs of a polydispersed compact of an alumino-borosilicate glass after a linear shrinkage of 8%. Magnification of 1200 × 〚6, 7〛 (a). Width of the micrograph = 20 μm. (b) Diagram of the Custers model.
Fig. 2 gives experimental evidence of the fact that the Frenkel and M–S processes may occur simultaneously in a sample having a particle-size distribution. The Clusters model 〚6〛 is based on this experimental fact: small particles preferentially cluster in the open spaces left by larger particles and sinter faster. Thus, for a polydispersed compact with volume fraction vr of particles of radius r, the following expression holds true for the densification kinetics at a given temperature:
Equation (4) sums up the relative density for each particle size, r, as a function of time, t. During the Frenkel stage of sintering, the condition is met and ,t) is calculated using the Frenkel equation (equation (1b)). Later, , is calculated by the Mackenzie–Shuttleworth model (equation (2)). For each cluster, the passage from the Frenkel regime to the M–S regime is performed using the step functions θF(t0.8 – t) and θM–S(t – t0.8), whose values alternate between 1 and 0 at t = t0.8 when is reached. Thus, θF(t0.8 – t) = 1 and θM–S(t – t0.8) = 0 for t < t0.8, and θF(t0.8 – t) = 0 and θM–S(t – t0.8) = 1 for t > t0.8. ξr is the neck-forming ability of each particle, which can be calculated from the particle-size distribution, and ξr = 1/rc, where c is a constant that depends on the particle-size distribution, as proposed in reference 〚6〛.
The pore radius a0 in equation (2) is adjusted to ensure a continuous function at t = t0.8. The adjustment is achieved by first computing t0.8 with equation (1b), then calculating a0 with the integrated version of equation (2) at t = t0.8.
Equation (4) can be explicitly written as equation (5) for ξr = 1 (which corresponds to narrow size distributions):
Other microstructural facts that the model should consider in order to describe actual glasses are described below.
2.4.1 The number of necks that each particle develops with its neighbors
We have experimentally found that the actual number of necks per particle in green compacts of monodispersed spheres consists of a large distribution, from 3 to 8 necks pert particle, with an average value of about 5. Note that, in the Scherer scheme of particle arrangement, each particle may have either two or six contacts with its neighboring particles (i.e., particles at an edge or at a corner of the cell, respectively).
Fig. 3 shows that some necks are lacking for two possible reasons: there is a free gap between two neighboring particles (frustrated contact) or a neighbor is lacking (a hole in the random packed structure). Both types of lacking necks produce an arresting effect on densification.

Detail of an array of glass spheres sintered for a short time to form necks. White arrows show frustrated necks (although these particles are close they are not in actual contact) or lacking neighbors. Black arrows show developed necks. The width of each micrograph corresponds to 1.425 mm.
For both size distributions in Fig. 4, we found that the average number of necks is 5, i.e., one neck less than the six necks needed for a local cubic array of particles, as is implicitly assumed in equation (1b).

Number of neighbors of each particle, measured for two compacts corresponding to two different size distributions of spherical particles 〚9〛.
2.4.2 Pre-existing surface crystals or dust
When the glass particles to be sintered show pre-existing surface crystals or dust, only the glass–glass contacts contribute to sintering. For example, particles having only 90% of glassy surface have an effective fraction 0.9 × 0.9 = 0.81 of contacts that will develop necks during sintering.
The ‘Clusters model’ was developed to describe the system shown in Fig. 2: simultaneous Frenkel (F) and M–S kinetics. The model allows one to include the afore-mentioned microstructural packing and pre-crystallization details. The calculations are presented via summations of particle-size fractions, because it is not always possible to describe the particle-size distribution as simple analytical functions. Working with summations rather than integrals allows one to use the actual particle-size distribution.
To the best of our knowledge, there is no single model capable of describing all the sintering processes for every type of particle arrangement, from green density to full density. Even Scherer’s model assumes cylindrical arrays (that do apply to compacts having high initial densities) and only describes sintering up ρ∼0.94. In our case (compacts having a green density of about 0.6 or more), we use the Frenkel model for the first 10% of linear shrinkage – relative density range 0.6–0.8 – and the M–S model for the high-density range 0.8–1. Our model, however, does not apply to low-density green compacts. The choice of an appropriate pore size a0 allows one to obtain a smooth crossover of the Frenkel and M–S curves for the sintering kinetics at the desired value of relative density = 0.8.
The M–S mechanism should be strictly valid in the density range of 0.9 to 1, but, in our model, we extend its validity to 0.8–1.0. We justify this simplification by the fact that the sintering kinetics of various systems (including materials having a wide particle-size distribution and showing concurrent crystallization) can be described by the model. There is a good reason for choosing 0.8 as the beginning density of the M–S model. It has been experimentally observed that, at this density, a qualitative shift in porosity occurs from interconnected to isolated pores. Hence, the porosity is no longer interconnected.
The Clusters model uses the approximation suggested in 〚22〛 for the M–S process. This approximation gives a slightly slower kinetics for sintering than the exact solution. But the difference is negligible compared to all the other simplifications. Moreover, it drastically simplifies the calculations, allowing one to include other effects such as concurrent crystallization in isothermal and non-isothermal sintering, keeping in mind an additional advantage, i.e., the fact that the pore size distribution can be calculated as an output.
The particle-size distribution (which is easy to measure) is used as an input and allows one to calculate the pore-size distribution. This feature allows one to predict the evolution of pore size over time and to compare this calculated distribution with pore-size measurements from plane sections of the sample (careful stereological corrections must be made here). In a recent report 〚9〛, we demonstrated that calculations with the Clusters model provide a good prediction of the measured pore size distribution of sintered spherical particles.
2.5 The Clusters model with concurrent crystallization
Fig. 5 shows a spherical particle of soda–lime–silica glass that formed necks during sintering and whose surface is fully crystallized with cristobalite and devitrite. The crystals grow from the surface towards the particle’s interior. In this case, crystallization arrested viscous flow sintering.
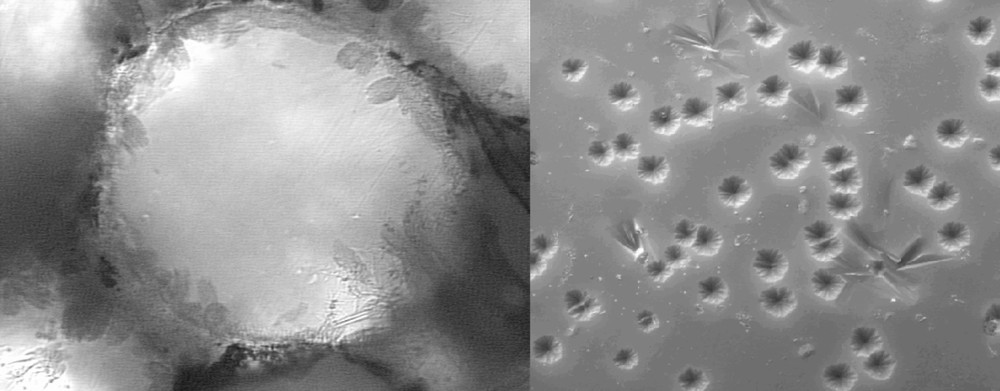
Crystals growing from the surface towards the volume of a spherical soda–lime–silica glass particle (radius ≈ 200 μm) in a sintering-crystallization experiment. Necks between particles are clearly shown 〚7〛 (a). SEM micrograph of a surface of the glass sphere heat-treated at 700 °C for 5 h (b).
2.6 Isothermal sintering with concurrent crystallization
Most glass powders have a tendency to crystallize starting from the external surfaces when heated 〚26〛, and any fraction of the surface that crystallizes hinders sintering by preventing viscous flow. It is, therefore, important to understand the effect of surface crystallization on the sintering kinetics.
For powdered glasses, we assume the most typical case: heterogeneous nucleation of spherical crystals growing with a linear growth rate, U(T), from a fixed number of sites per unit area, Ns. In this case, the JMAK 〚12〛 theory predicts the crystallized surface fraction, αs:
Müller 〚20〛 reasonably assumed that, regardless of the sintering model, the densification rate should decrease in proportion to the surface fraction of glass remaining after crystallization. Hence, in this case, the isothermal densification rate is:
By inserting appropriate expressions for dρ/dt (from equations (1b) and (2)) and αs (equation (6)) into equation (7), upon integration one arrives at equations (8) and (9)) for the Frenkel and Mackenzie–Shuttleworth cases, respectively:
In equation (8), xf stands for the initial vitreous surface fraction of the particles before sintering starts. When the particle surface is pristine, xf = 1. The probability that a neck between particles is of the type glass–glass is xf2. When both effects are considered, a term xf3 appears. Only xf appears in equation (9), since necks do not have to be considered in the M–S regime. The ease with which this microstructural data is introduced into the calculations is one of this model’s advantages. Another application is the possibility of predicting the pore-size distribution at any stage of densification.
With these equations and the appropriate physical parameters of the glass (surface tension, viscosity vs temperature, crystal growth rate vs temperature, number of active surface sites, particle-size distribution and green density), the densification kinetics (ρ or ρc vs time) can be predicted at any chosen temperature. With the exception of U(T) – which is fixed by the chemical composition of the glass – the other parameters can be estimated from the glass composition (η, γ) or can be used as simulation parameters (Ns, r, ρ0). Equations (8) and (9) can be extended to the case where more than one crystalline phase for M–S. Polydispersed distributions undergoing isothermal sintering and concurrent crystallization can be treated by introducing equations (8) and (9) into equation (4).
2.7 Non-isothermal densification with concurrent crystallization
In some situations, however, depending on how fast the sintering and crystallization rates are, a substantial part of these processes may occur on the heating path before the specimens reach the desired treatment temperature. Thus, it is fundamental to simulate which sintering and crystallization degrees are achieved at a given heating rate just before the designed annealing temperature is reached. Here, we follow the procedure presented in 〚8〛.
The time, t, may be treated as a temperature dependent variable, dt = dT/q, where q is a constant heating rate. Making the appropriate change of variables, the temperature-dependent crystallization, i.e., the surface fraction crystallized as a function of heating rate, can be written as follows:
The densification rates for both F and M–S stages may be similarly written.
From equations (1a), (7), and (10), one arrives to equations (11) and (12), respectively:
The corresponding M–S expression obtained from equations (2), (7), and (10) is:
With these equations and the appropriate physical parameters of the glass (particle-size distribution, green density, surface tension, viscosity vs temperature, number of active nucleation sites per unit surface and crystal growth rate vs temperature), it is possible to predict the densification kinetics, ρ or ρc vs time or temperature. Except for U(T), which must be measured, the other parameters can be estimated from the glass composition (η, γ) or they can be used as simulation parameters (Ns, vr, ρ0).
Polydispersed distributions undergoing non-isothermal sintering and concurrent crystallization can be treated by introducing equations (11) and (12) into equation (4).
2.8 Crystallization towards the volume
Most analyses of the concurrence between sintering and crystallization only take into account internal crystallization 〚10, 15, 16〛 or surface crystallization 〚7, 8, 20〛. Moreover, density changes are frequently neglected due to the volume transformed from the surface towards the particle’s center. This type of kinetics was studied by Gutzow et al. 〚17〛.
Interior crystallization is typically neglected, because, in practice, the effect of volume crystallization (crystals nucleating in the volume and rising to the particle’s surface) is generally smaller than surface crystallization. However, if growing crystals have a density that differs from that of the glass, the density variation must be considered in calculating the evolution of the body’s density.
Crystals nucleated at the particle’s surface not only cover the surface but also grow towards the particle’s core. Gutzow et al. 〚17〛 described the kinetics of this type of volume transformation for spherical crystals. Before the growing crystals begin to interact, the volume crystallization kinetics is a function of t3, but when they impinge, they only can grow towards the particle’s center and, thus, the kinetics of volume crystallization is a function of t1. Equations (13a) and (13b) hold true, in each case, for each crystalline phase p.
In equations (13a) and (13b), the subscript ‘p’ indicates a given crystalline phase and the subscripts ‘v’ and ‘r’ indicate volume crystallization and particle radius, respectively.
3 Results
In this section we summarize our calculations and experimental data for different systems: an alumino-borosilicate glass (ABS) powder having a widely dispersed distribution of jagged particles, which does not crystallize during sintering, and soda–lime–silica (SLS) glass sphere that crystallizes (in up to four different phases). We also show calculations based on experimental results of Muller 〚13〛 for a narrow sized cordierite glass powder.
3.1 Isothermal sintering of alumino-borosilicate glass
An alumino-borosilicate glass of composition 71.70 SiO2, 8.33 B2O3, 8.56 Al2O3, 1.00 MgO, 2.67 CaO, 7.44 Na2O (wt.%), which is a candidate for nuclear waste encapsulation, was used owing to its stability against devitrification 〚27, 28〛. This system was convenient for our studies, because the original surface and number of nucleation sites remained unchanged throughout the experiments.
The glass-transition temperature, TgDSC ≈ 845 K, was determined by differential scanning calorimetry at 10 K min–1. Fig. 6 shows the particle-size distribution measured with a Mastersizer μ Ver.2. High temperature viscosity measurements were taken using a rotating cylinder viscometer, and low temperature viscosity was measured by the penetration method. The viscosity showed a Vogel-Fulcher-Tamman behavior with η∞ = e–4.803 Pa s, Ev = 4983.2 K and T0 = 510.5 K.
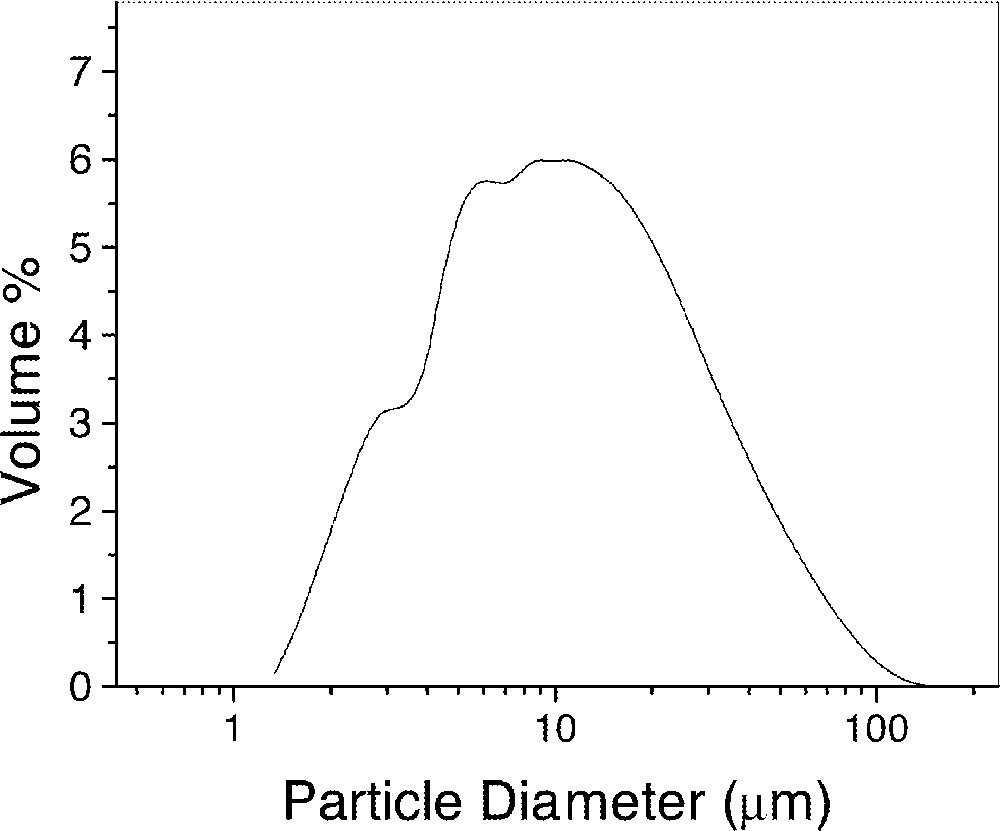
Particle-size distribution of the alumino-borosilicate glass powder 〚6〛.
The glass-vapor surface energy γ varies only slightly with temperature, but we lacked available data for our glass at temperatures near Tg, at which the sintering experiments were performed. Hence, extrapolated data was used employing Lyon’s method 〚29〛. The values of γ extended from 0.327 J m–2 at 959 K to 0.325 J m–2 at 1017 K.
Cylindrical powder compacts were prepared by uniaxial die pressing of around 0.75 g of sample glass powder at 0.5 MPa for 30 s. The cylinders were approximately 6.0 mm in height and 10.2 mm in diameter. The sample’s length, l, and diameter, φ, were measured after each sequential isothermal sintering step to determine the sample’s relative density. When the density stopped increasing with heat treatment, the final compact density was determined by the Archimedes method, using liquid mercury.
The fact that the samples did not reach thermal equilibrium instantaneously when brought to the sintering temperature was considered. The corrections performed are detailed in 〚6〛.
To gain a better understanding of the real sintering process, we calculated the sintering curves of idealized monodispersed powders together with the calculation corresponding to the real particle-size distribution. Fig. 7 shows the calculated sintering curves for a monodispersed distribution of the smallest particles, for the average particle size and for the largest particles of the measured particle-size distribution. The curves corresponding to the polydispersed distribution were calculated using the Clusters model with c = 1.23 and c = 0. c = 0 means that, in our calculations, every particle with the same size sintered as a cluster, while c = 1.23 relaxed this condition (for more details see 〚6〛). A comparison of the kinetics of these idealized processes with the real one highlights the effect of having a polydispersed distribution. The sintering kinetics of the real distribution is quite close to that of the smallest particles, at least for the particle-size distribution tested here.
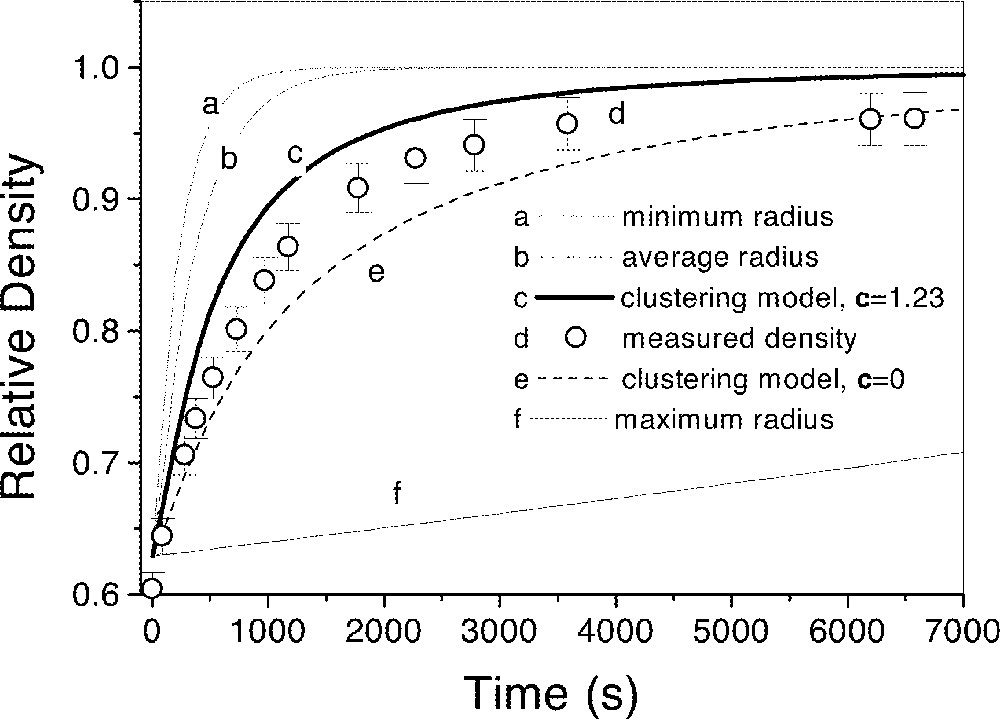
Relative bulk density ρ versus time at 989 K, showing (a) smallest particles, (b) average size particles, (c) clustering model with c = 1.23, (d) clustering model with c = 0, (e) largest particles of the distribution shown in Fig. 6.
When the compacts reach the M–S stage due to the pressure of entrapped gases in the closed pores, our samples never reached full density, ρ=1, but only ρf=0.96 in the final stage of sintering.
3.2 Isothermal sintering of soda–lime–silica glass spheres
Distributions D2 and D3 of the soda–lime–silica glass spheres (composition in wt%, 72.5 SiO2, 13.7 Na2O, 9.8 CaO, 3.3 MgO, 0.4 Al2O3, 0.2 FeO/Fe2O3) shown in Fig. 8 were used to determine the number of neighbors of each glass sphere. The average number of neighbors was found to be 5 for both distributions 〚9〛. In the same study, distribution D1 was used for the sintering experiment shown in Fig. 9 (the solid dots are experimental data and the solid line is the calculated sintering kinetics based on the Clusters model).
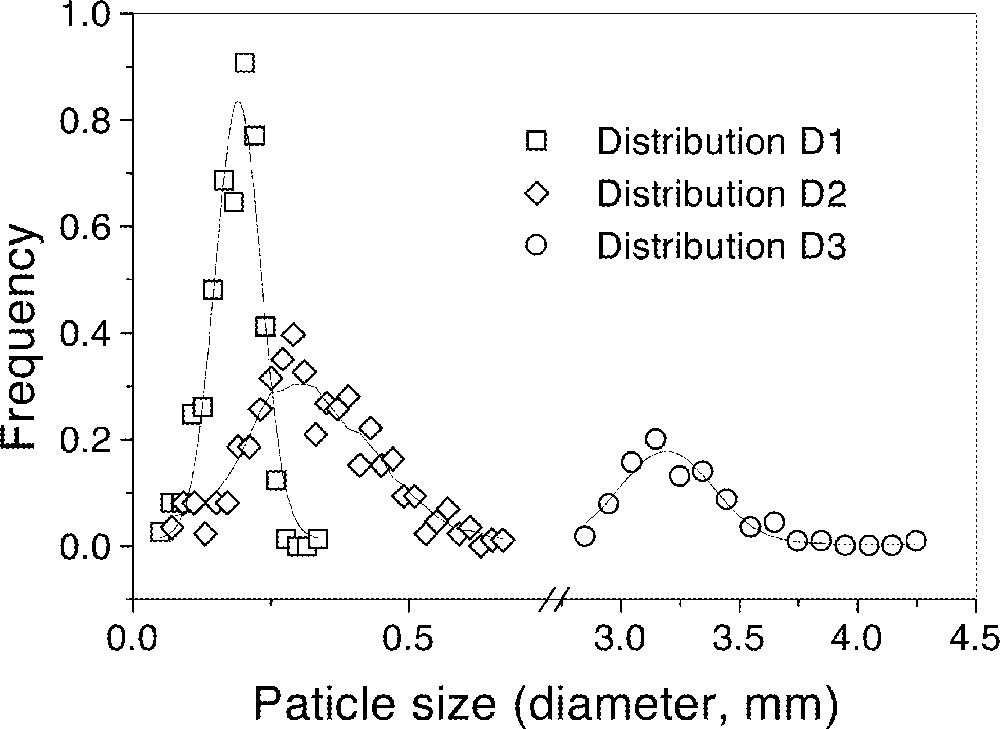
Three size distributions of soda–lime–silica glass particles used in 〚9〛.
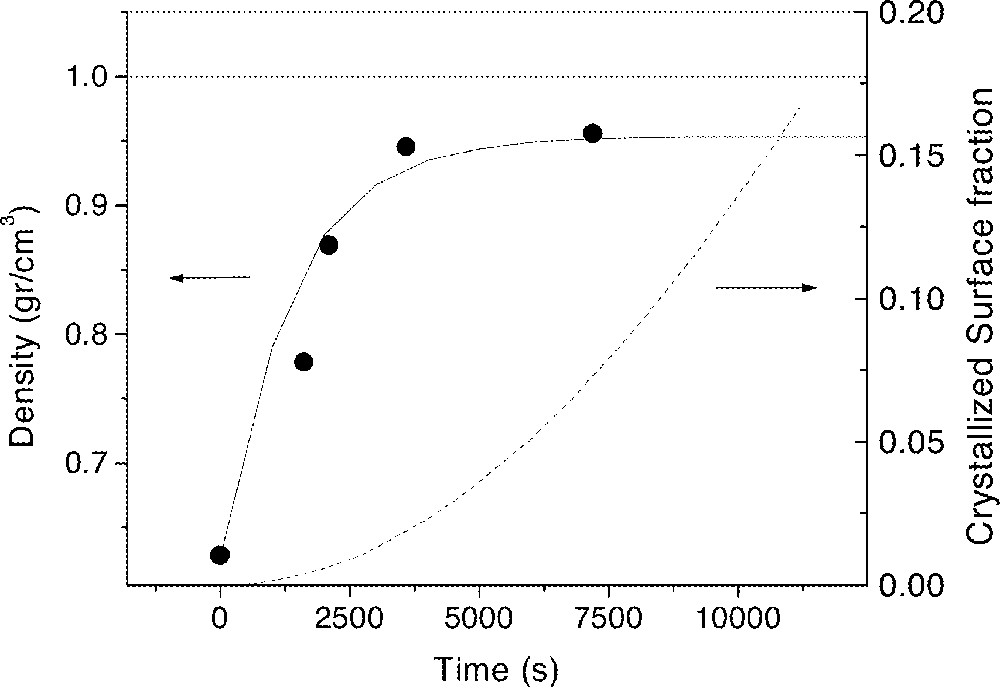
Sintering kinetics of soda–lime–silica glass spheres, size distribution D1, at 710 °C. Black dots: measured, solid line: calculated with the Clusters model, dashed line: calculated crystallized surface fraction.
The compacts never reach full density (ρ = 1), because pre-existent crystalline particles on the sphere’s surface reduce the area available for sintering and (probably) due to gases (entrapped or from degassing) that cannot diffuse out from the sample. Surface crystallization during sintering was negligible, i.e., only about 2% when the sample density saturated, causing no harm in this case.
An analysis was made of the measured and calculated porosity for a sample with density = 0.88. This density was chosen because, at this point, all particle sizes are in the Mackenzie–Shuttleworth regime.
The calculated pore size distribution is plotted in Fig. 10. The a0(r,0) (pore radius at t = 0) were calculated first. Equation (5) was then used to estimate the time at which the compact density reached 0.88. After that, using equation (2b), each pore radius was computed at that time. It is worth stressing that, although the overall density of the compact was 0.88, the local density depended upon the particle sizes existing in that region of the sample. The pore-size distribution measured is shown in the same figure. The sizes of about 800 pores were measured by microscopy on plane sections of the sample, and the size distribution thus found was converted to volume size distribution by standard stereological calculations. The calculated values were systematically smaller (about 10 μm) than the measured ones. We discuss this mismatch below.

Pore-size distribution. Calculated with the Clusters model (hollow squares). Measured: solid squares. The area under each curve is equal to 1.
The effects of the particle’s surface quality and particle size are shown in Fig. 11. Smaller particle size and better surface quality (no pre-existing crystals) favor sintering over crystallization.
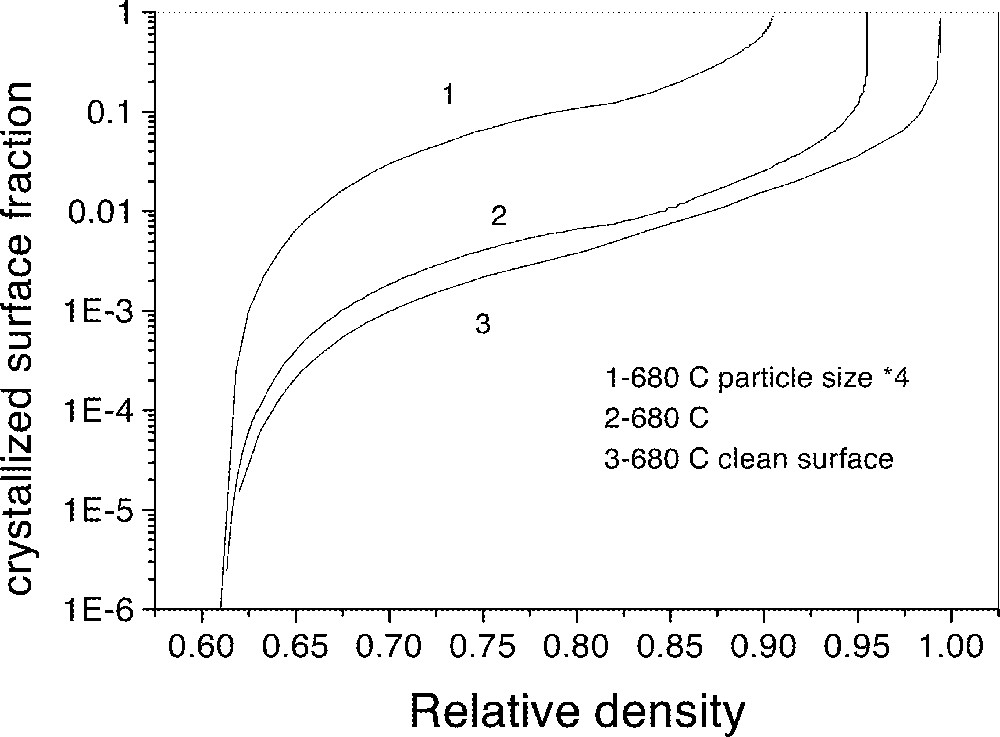
Effect of the particle’s surface quality and size on the sintering kinetics. Calculations for size distribution D1 of Fig. 8 (curves 2 and 3), and for a hypothetical distribution with particle size four times larger (curve 1). Curves 1 and 2 correspond to particles with glassy surface fraction = 0.9 (the remaining 0.1 fraction is occupied by pre-existing crystals or other inclusions).
3.3 Non-isothermal sintering of jagged polydispersed particles
The same ABS glass whose size distribution in shown in Fig. 6 was used for the non-isothermal tests. We chose this system to limit the number of variables to a controllable level, because it is stable against crystallization. Thus, in principle, viscous sintering proceeds undisturbed by crystallization until maximum densification is reached.
Fig. 12 shows the calculated and experimental densification curves for two heating rates. Due to the uncertainty caused by the unknown shape factor of the jagged particles, we present two types of calculated curves. One resulted from the cluster model ((equation (4)), with ks = 1 and ξr ≠ 1 (calculated from the particle-size distribution with no adjustable parameter 〚6〛), while the other curve resulted from ks = 1.8 (fit to isothermal data of 〚6〛 for the same glass powder) and ξr = 1. At both heating rates, there was a small temperature shift of about 5–10 K between experimental and calculated curves. The experimental density saturated at about ρ∼98%. A negligible degree of crystallization was observed at the temperature of maximum density for each heating rate.
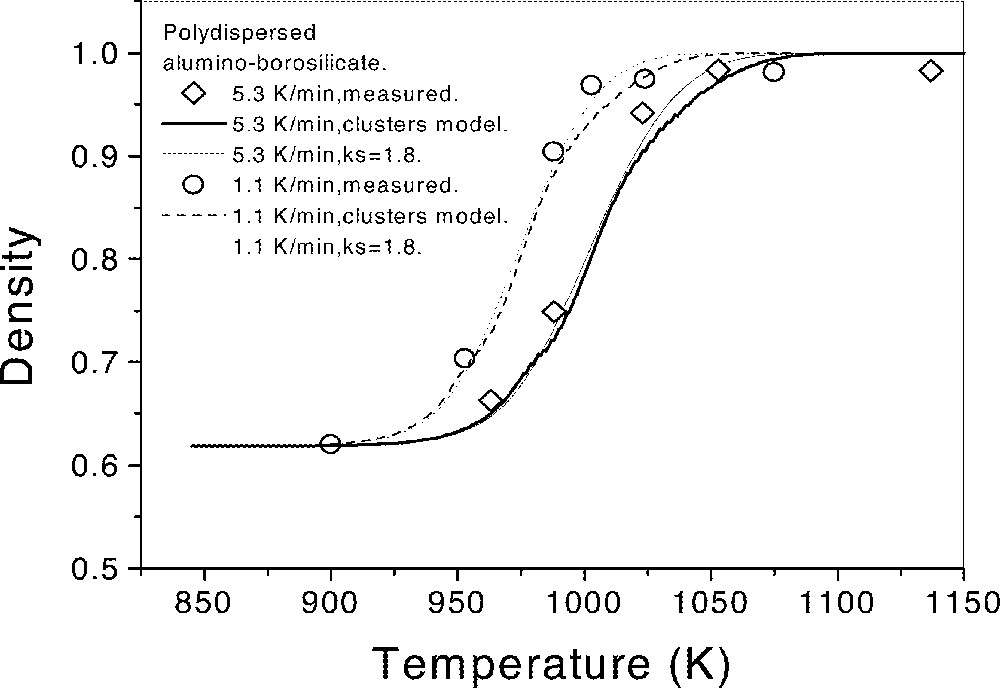
Calculated (lines) and experimental (circles) densification curves of ABS glass for two heating rates. q1=1.1 K min–1 (dotted lines and hollow circles) and q2 = 5.3 K min–1 (full lines and solid circles).
To further test the algorithm under stricter conditions, we also worked with a cordierite glass having a relatively narrow distribution of jagged particles. This glass has a tendency to devitrify concurrently with sintering; thus, we hoped to examine our model under this arresting condition.
Fig. 13 shows the calculated (this study) and experimental (from 〚13〛) densification curves of cordierite glass having average particle sizes of r = 1, 6.8, 8 and 11 μm, subjected to a heating rate of 12 K min–1. The crystallized surface fraction is also shown. Under these conditions, crystallization begins at ∼1150 K and is completed at ∼1250 K. At this point, densification is completely arrested.
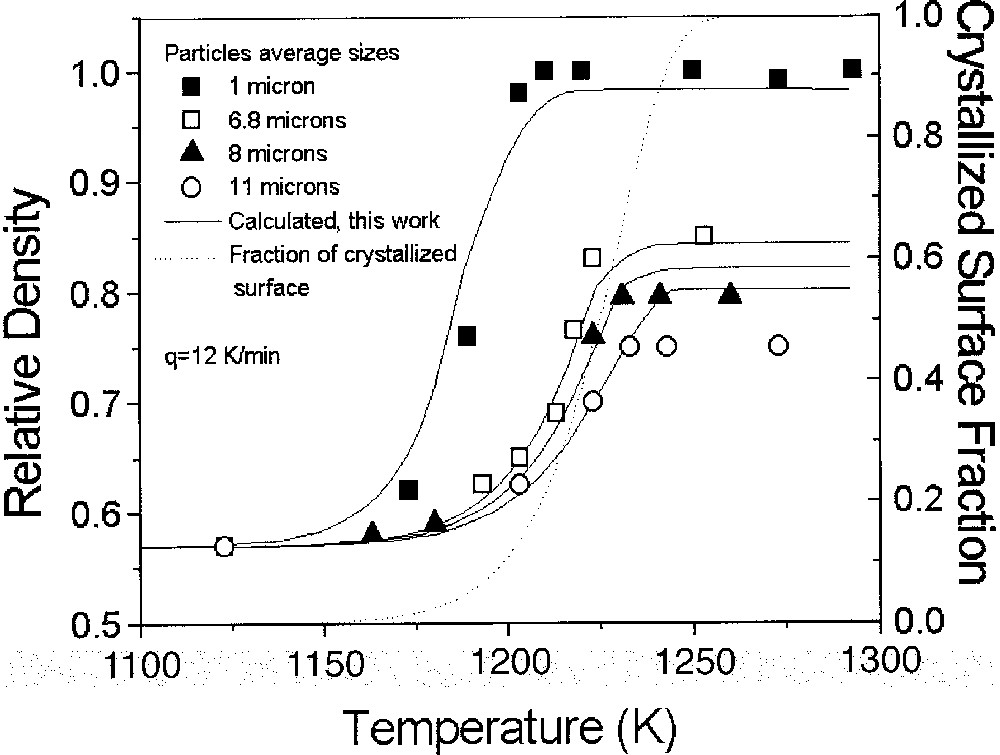
Simulated (this work) and experimental (from 〚13〛) densification curves for non-isothermal sintering of cordierite glass powders of different sizes. The crystallized surface fraction is also shown.
Due to the unknown shape factor of the jagged particles, it was used as a fitting parameter, resulting in ks ∼ 3. Only the finest particles densified fully; all the other curves saturated at ρ∼0.84, 0.82 and 0.80 (calculated curves) or at ∼ 0.85, 0.80 and 0.75 (experimental data) for increasing particle size, demonstrating the arresting effect of crystallization.
In every case, the experimental density saturated at slightly different values than predicted. If, for instance, the passage from the Frenkel to the M–S regime is forced to occur at 0.75 instead of 0.8, a better agreement is found for the two larger particle sizes, but not for the smallest one.
4 Discussion
In the previous section, the Clusters model was tested from the standpoint of the prediction of the sintering kinetics of a variety of glass-forming systems. These powdered systems include large and narrow particle-size distributions, spherical and irregular particles, crystallizing and stable glasses, particles with ‘clean’ surfaces and particles with embedded solid particles or pre-existing crystallization. These are only part of the different situations that may arise in the sintering of diverse materials. The ability of a given model to include the special characteristics of the system of interest in its formulation determines its applicability. For example, if the compact of interest has a low density, such as a dry gel, then the Scherer model is the most appropriate one to describe the sintering kinetics. However, no quantitative predictions of either sintering or crystallization rates of gels can be done, because of the retained OR groups (where R may be an H atom or an organic chain). During condensation reactions, the removal of the OR groups are responsible for a time dependence of the viscosity 〚10〛. For compacts with relative green densities of about 0.6 or higher, such as those of the systems discussed herein, and for quantitative predictions of sintering and crystallization rates, the Clusters model has the ability to include different aspects of diverse systems (number of neighbors per particle, particle-size distribution, crystallizing phases, etc.) in its formulation. Another interesting feature of the Clusters model is that it serves as a tool to predict the resulting porosity distribution in the sintered compact. For a soda–lime–silica sphere sintering test, the calculated porosity size distribution at ρ=0.88 is consistently smaller (about 10 μm) than the measured one. However, it agrees quantitatively with the measured distribution 〚9〛.
The surface viscosity of glass particles with pristine surfaces (free of embedded solid particles or pre-existing surface crystallization) is expected to be somewhat lower than the volume viscosity 〚30〛. In our case, because our soda–lime–silica glass spheres were produced by an industrial process, their surfaces were full of defects and embedded particles, which were difficult to characterize properly due to their small sizes. That is why, in this case, had we used the viscosity as a fitting parameter (considering clean particle surfaces), the viscosity obtained would have been about 70% higher than the measured one. It is remarkable that this high viscosity is found for both the isothermal and non-isothermal sintering kinetics of these glass spheres. In reality, this high viscosity value accounts for the embedded solid particles or pre-existing surface crystallization on the particles’ surfaces.
However, the extended Clusters model, which takes concurrent crystallization into account, allows one to include not only the information that contacts between particles of the crystal–crystal or glass–crystal type will not develop necks by viscous flow (only glass–glass contacts develop necks) but also that the rate of sintering is proportional to the glassy area. With these microscopic data included in the model, the experimental (not fitted) viscosity explains all isothermal and non-isothermal measurements.
Due to the crystallization of non-stoichiometric phases, the chemical composition of the glass matrix continuously changes with time. An estimate of the change in surface viscosity of the soda–lime–silica glass used in this work caused by these compositional shifts, considering the two main phases (devitrite and cristobalite) and using the SciGlass database 〚29〛, indicates a slight decrease in surface viscosity.
An exact computation of the surface fraction crystallized is impossible when the geometry of the crystals is as complex as that of devitrite. This phase can appear as needles or as bundles of needles, with no obvious symmetry. Moreover, devitrite is by far the most common crystalline phase in the sintering range. We approximated its surface morphology as a circle. The same geometry was used to compute the areas of other crystalline phases. This approximation slightly overestimated the crystallization kinetics.
The effect of particle-size distribution and of the number of contacts between different size particles is introduced in the Clusters model through the parameter ξ, which has an effect on the sintering kinetics when the size distribution is large. This parameter weighs the volume fraction of each particle size with the number of necks that each particle develops in all the surrounding particle sizes. As smaller particles develop more necks to surround other particles, their fractions are augmented in detriment to larger particles. But large size distributions are common to crushed irregular particles. In this case, the effect of size distribution is mixed with a ‘particle-shape effect’ and also a ‘packing effect’, since particles with different geometries may pack differently. When these three effects are simultaneously present, it may be impossible to decouple them.
The number of neighbors each particle has or, equivalently, the number of necks each particle develops, also depends on the particle-size distribution, particle shape, and packing. This information, if available, can be readily introduced into the Clusters model.
Another subject of interest is non-isothermal sintering. In this case, thermal gradients that develop within the compact on the heating path are not (although they can be) included in the model. Temperature gradients may arise when the sample’s dimensions or the heating rate are relatively large, for example in glassy blocks of about 50 cm for nuclear waste immobilization or for floor tiles.
In non-isothermal sintering, temperature gradients produced between the surrounding hot air and the specimen may arise on the sample’s surface (due to the small heat transfer coefficient, h) and inside the compact (due to the small thermal diffusivity, κ, of porous glass). We estimate these gradients, for a cylindrical geometry, in the following paragraphs.
The temperature profile T(r,t) in an infinitely long cylinder of finite radius a, 0 < r < a, with zero initial temperature and with an imposed surface temperature q t, where q is a constant heating rate and t is time, can be expressed as 〚31〛:
Actually, because the compact’s porosity varies with time (and temperature), so does its thermal conductivity and diffusivity. The other parameters, c and ρ, have typical values c = 0.3 cal g–1 K–1, and .
When the samples are sintered in air with natural convection, a heat transfer coefficient h must be considered 〚32〛 (this must be equally valid for both small and large samples). This actually causes the sample’s surface temperature, Ts, to be lower than the furnace’s temperature, which follows the imposed heating rate curve almost exactly.
The following equation of heat conservation on the sample’s surface can be written considering, for the sample’s surface:
A temperature difference at a stationary regime of about 4 K was found by plotting equation (14) with k = 0.01 cal K–1 cm–1, estimated from 〚33〛, for a cylindrical porous body, diameter = 1 cm and height = 1 cm (typical geometry used in the sintering experiments of this work, isothermal and non-isothermal), with a relative density = 0.6 and a continuous glassy matrix with isolated pores.
The estimated values of ΔT ≈ 31 K were found based on equation (15), where the temperature gradient at the sample’s surface (dT/dr)r = 0 ≈ 15 K cm–1 (from equation (14)), A is the area of the surface considered, ΔT = T∞ – TS and T∞ = qt, h ≈ 200 W K–1 m–2 (a maximum heat transfer coefficient h, from reference 〚32〛, was considered for heating in air with natural convection).
The complete uncertainty about the h value leads to doubts about the actual magnitude of the surface ΔT value. In our experiments with 5-mm pieces, we did not expect high values for ΔT. Residual porosity is frequently found in many viscous sintering experiments. The relative density of the alumino-borosilicate glass discussed herein also displayed a saturation density unlike 1 for both heating rates. It has also been observed 〚7–9〛 that, when sintered under thermal conditions in which crystallization is negligible, crystallizing systems (e.g., soda–lime–silica glasses) do not achieve a relative density = 1.
This saturation may be due to at least these factors: pre-existing surface crystals, partial or total surface crystallization during sintering, insoluble gases entrapped in the initial pores, and bubbles formed by the release of dissolved gas (which can be catalyzed by crystallization). While surface crystallization is taken into account in the model’s equations, the processes involving gases are not. Therefore, entrapped gases or degassing cause remnant porosity in SLS glass. This may also be the cause of the consistent mismatch between calculated and measured porosity.
5 Conclusions
Except for low-density compacts such as gel-derived preforms, to which the Cluster model is not expected to be applicable, we tested the model in a variety of situations. These comprise: (a) isothermal and non-isothermal sintering of widely polydispersed alumino-borosilicate glass having jagged particles, which is stable against devitrification; (b) isothermal sintering of soda–lime–silica glass having a narrow distribution of spherical particles with embedded solid particles or pre-existing surface crystallization – this glass readily crystallizes during sintering –; (c) devitrifying cordierite glass with a narrow size distribution. In each case, the model provided a good description of the experimental results. An analysis of the data published on cordierite shows that, for a given heating rate, there is a maximum particle size that can be sintered to full density. The model fits these data reasonably well and can be used to determine the maximum acceptable particle size for any other thermal treatment.
Based on our experiments with narrowly distributed glass spheres, we have shown that each glass particle can have a different number of neighbors, which vary from 3 to 8. The number of neighbors may vary according to size distribution and particle shape. This variable can be readily introduced into the Clusters model equations.
The effect of pre-existing surface crystals or embedded solid particles, which was also taken into account, proved to exert a strong effect on the Frenkel stage of sintering.
The effect on the sintering kinetics of wide-size distributions was also considered, but further work is needed to disassociate size distribution, particle shape and particle packing. The Clusters model assumes a homogeneous sample temperature. However, in the case of large samples or high heating rates, temperature gradients must be considered.
When all the particle sizes are in the Mackenzie–Shuttleworth regime, the model can readily predict the pore size distribution. A low percent of residual porosity at the saturation density, which is frequently found, may have different origins: gas expelled from the growing crystals, gases entrapped during sintering or degassing from the glass particles by diffusion. This important topic also deserves further research.
Finally, we have shown that different aspects of the sample’s microstructure, crystallization parameters and thermal treatment conditions can be included in the formulation of the Clusters model, providing a formidable tool to simulate the densification kinetics of powdered glasses in a variety of situations.
Acknowledgements
The authors gratefully acknowledge Dr Eduardo B. Ferreira for his critical comments, and CNPq, Cyted, PRONEX and FAPESP for funding this research.


