Dendritic encapsulation as probed in redox active core dendrimers

Christopher B. Gorman

doi:10.1016/j.crci.2003.05.004

Dendritic nanodevices

Dendritic encapsulation as probed in redox active core dendrimers

Christopher B. Gorman ¹

¹ Department of Chemistry, North Carolina State University, Box 8204, Raleigh, NC 27695–8204, USA

Comptes Rendus. Chimie, Volume 6 (2003) no. 8-10, pp. 911-918.

Résumé

The relationship between dendrimer primary structure, conformation, and core encapsulation behaviors is highlighted. This work has involved the synthesis of several novel types of redox-active core dendrimers. Assessment of diffusion measurements provides a first indication of molecular size. Conformation can be probed by exploiting electrochemical and magnetic properties of the core and correlation of these behaviors to computational models.

Métadonnées

Reçu le : 2003-04-09
Accepté le : 2003-05-20
Publié le : 2003-08-01

DOI : 10.1016/j.crci.2003.05.004

Affiliations des auteurs :

Christopher B. Gorman ¹

¹ Department of Chemistry, North Carolina State University, Box 8204, Raleigh, NC 27695–8204, USA

@article{CRCHIM_2003__6_8-10_911_0,
     author = {Christopher B. Gorman},
     title = {Dendritic encapsulation as probed in redox active core dendrimers},
     journal = {Comptes Rendus. Chimie},
     pages = {911--918},
     publisher = {Elsevier},
     volume = {6},
     number = {8-10},
     year = {2003},
     doi = {10.1016/j.crci.2003.05.004},
     language = {en},
}

TY  - JOUR
AU  - Christopher B. Gorman
TI  - Dendritic encapsulation as probed in redox active core dendrimers
JO  - Comptes Rendus. Chimie
PY  - 2003
SP  - 911
EP  - 918
VL  - 6
IS  - 8-10
PB  - Elsevier
DO  - 10.1016/j.crci.2003.05.004
LA  - en
ID  - CRCHIM_2003__6_8-10_911_0
ER  -

%0 Journal Article
%A Christopher B. Gorman
%T Dendritic encapsulation as probed in redox active core dendrimers
%J Comptes Rendus. Chimie
%D 2003
%P 911-918
%V 6
%N 8-10
%I Elsevier
%R 10.1016/j.crci.2003.05.004
%G en
%F CRCHIM_2003__6_8-10_911_0

Christopher B. Gorman. Dendritic encapsulation as probed in redox active core dendrimers. Comptes Rendus. Chimie, Volume 6 (2003) no. 8-10, pp. 911-918. doi : 10.1016/j.crci.2003.05.004. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2003.05.004/

Version originale du texte intégral

1 Introduction

The hyperbranched architecture of dendrimers has led to the proposal and subsequent study of these types of molecules for encapsulation. This type of encapsulation can involve small molecule guests within the dendrimer or covalent encapsulation of units within the molecule. In this latter class, the unit to be encapsulated is typically placed at the ‘core’ of the molecule – that is, at its topological center. Encapsulation in this sense implies that the dendritic arms around the core display themselves in space so as to efficiently sterically shield the core from the surrounding environment. Thus, the efficacy of encapsulation relies on a link between the hyperbranched, primary structure of the dendrimer and its conformation (e.g., its tertiary structure by analogy to a protein). Early theories of dendrimer conformation suggested that they adopted ‘dense shell’ or sterically congested conformations [1]. Later, it was argued that dendrimers tend to form conformations with a uniform radial density and substantial distribution of the tips of the molecule throughout it [2, 3]. This latter conformation may or may not offer ideal conditions for encapsulation. Here, we highlight work that illustrates that dendrimers can be useful in encapsulation strategies, but mere hyperbranching is insufficient to provide ideal encapsulation.

Covalent encapsulation of a core moiety is typically studied in two ways. The photophysical behaviors of a core moiety can be probed as a function of the type and generation of the dendrimer [4–6]. Specifically, the degree of exciton quenching (e.g. intermolecular self-quenching of luminescence) can be attenuated or eliminated by placing the lumophore at the center of a dendrimer [7, 8]. Also, the degree of quenching of luminescence by dioxygen and other small quencher molecules can be attenuated in a similar manner [9–11]. These functions have been discussed in detail previously [4–6].

The other manifestation of core encapsulation is via changes in the electronic (electrochemical) properties of the dendrimer core. Specifically, as a redox-active core moiety is shielded, the relative rate of electron transfer to/from that core decreases. The dendrimer can also create a different type of microenvironment around this moiety as compared to the surrounding solvent. To the extent that this occurs, the thermodynamic redox potential of the redox active unit can change. Here, the former effect is emphasized, although the latter has been studied [12] and reviewed [4–6] as well.

Molecules that encapsulate a redox center have two potentially important functions in the study of both materials sciences and life sciences processes. First, the shielding of a redox center is the dominant structural effect of metalloproteins. To date, the general effects that structure has on redox potential are still unclear. Redox active core dendrimers offer the opportunity to elucidate general structural effects [4, 5, 12–25]. Second, controlling rate, driving force and direction of electron transfer are key elements in the design of molecular electronic devices. As will be shown, dendrimers offer a model system to show how an “insulating” macromolecular architecture affects these parameters. Dendrimers may be potentially useful in the design of rational, molecular electronics.

2 Synthesis of metal cluster core dendrimers

The ideal, redox active core dendrimer involves a core with well-understood electrochemical properties and a geometry that disposes the dendron arms about it in a uniform (symmetrical) fashion [20]. With respect to mimicking protein function, Diederich et al. first showed that dendrimers could be used to model protein environment. This group synthesized several classes of porphyrin-core dendrimers and showed that the dendrimer structure could affect redox potential as well as the kinetics of oxygen binding [13,14,16,26–30]. The facility of encapsulating biologically relevant clusters into dendrimers has further been illustrated by Aida et al. [31], who prepared dendrimer encapsulated copper(μ-oxo)dimers (found in methane monooxygenase and ribonucleotide reductase) and Basu et al. who prepared dendrimer encapsulated oxo-Mo(V)tetrasulfide units (found in DMSO reductase) [32]. Significant contributions have also come from Kaifer et al. [33–38] who have reported dendrimers based on ferrocenyl and viologen core moieties and Zheng et al., who have reported dendrimers based on a Re⁶Se⁸ cluster core moiety [39–41].

The synthesis of dendrimers with these types of symmetric cores requires some type of ligand exchange reaction that is efficient. In general, it is very difficult or impossible to separate side products that result from the incomplete attachment of the requisite number of arms around the cluster. To this end, we have explored the conditions for efficient ligand exchange around two clusters, Fe₄S₄ and Mo₆Cl₈. Fig. 1 illustrates a general protocol for each type of ligand exchange. In the case of Fe₄S₄, Holm et al. had previously shown that bulky aliphatic thiolates can efficiently be displaced by aromatic thiols with the loss of the initial component to vapor [42–45]. This scheme works well for the synthesis of iron–sulfur cluster core dendrimers – molecules with molecular weights of ca. 25 000 have been illustrated [18,19,24]. In the case of Mo₆Cl₈, phenol derivatives can substitute for methoxy groups or potassium phenolate can substitute for triflate groups [23]. These types of reactions have had an important impact on the systematic study of dendritic encapsulation of redox active cores.

Fig. 1
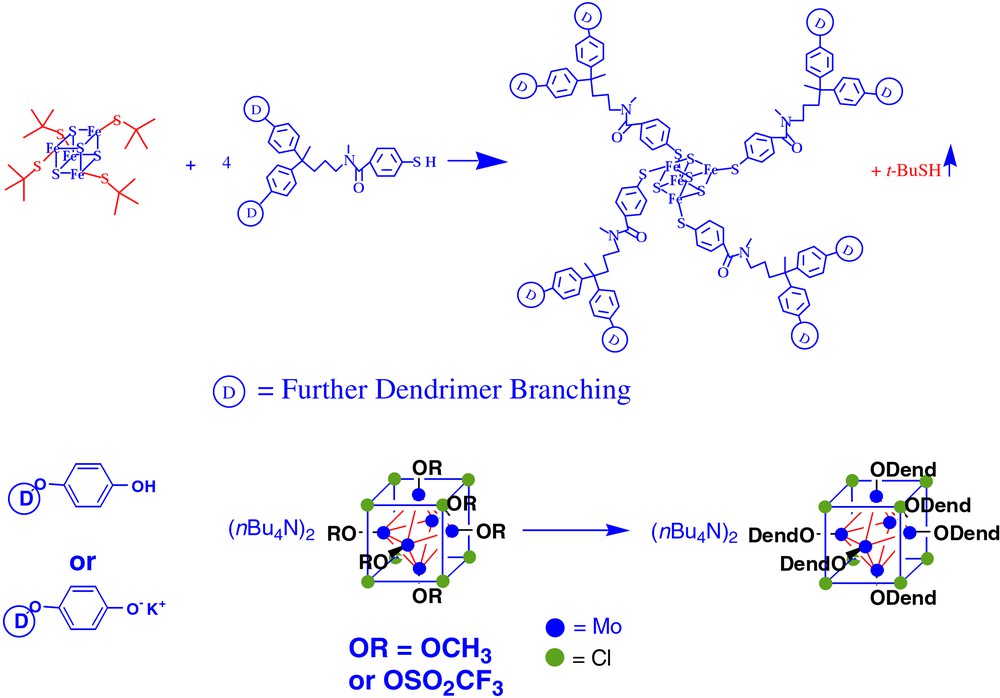
A general protocol for each type of ligand exchange used to form metal cluster core dendrimers.

3 Dendrimer size in solution

The size of a dendrimer as estimated from a diffusion coefficient gives a first indication of conformation. Moreover, diffusion coefficients provide the element of mass transfer that is required to calculate electron transfer rates from voltammetry as illustrated below. To this end, we sought to measure diffusion coefficients of dendrimers. In Fig. 2, the general structures of flexible and rigid iron–sulfur cluster core dendrimers are shown. Each type of dendrimer has been synthesized for generations one through four. Two complementary techniques have been employed to measure diffusion coefficients for these molecules. The results for the flexible series are shown in Fig. 3. Taking advantage of the electroactive nature of the iron–sulfur cluster, diffusion measurements could be obtained by chronoamperometry. These values compared well to those obtained by pulsed field gradient spin echo NMR. Both techniques gave values expected for a systematic increase in molecular size with generation. Comparison of radii of gyration for these molecules calculated using the Stokes-Einstein equation to those derived from computations (below) indicated that these molecules assumed globular, packed conformations [24].

Fig. 2
Generation-3 examples of flexible and stiff Fe₄S₄–cluster core dendrimers previously prepared in the Gorman group.

Fig. 3
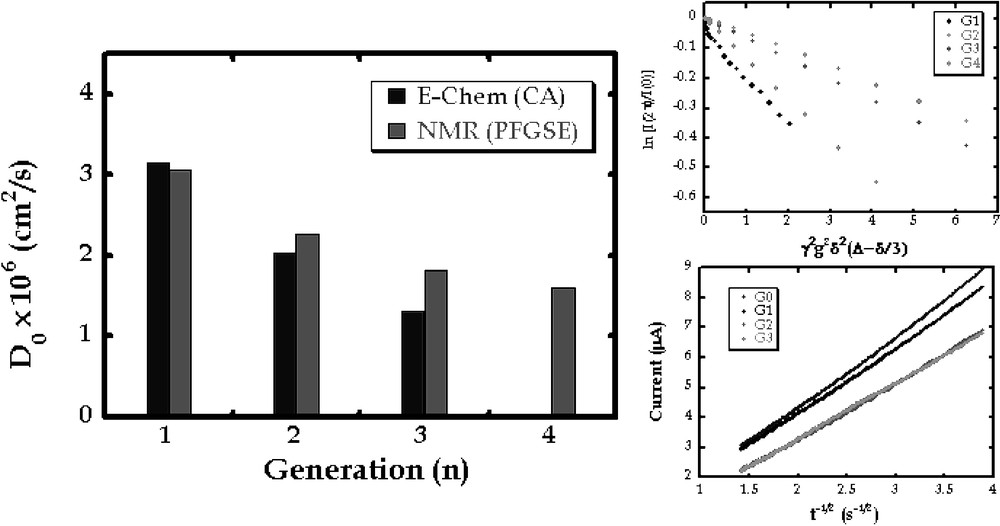
Illustration of diffusion coefficients for flexible dendrimers of generations 1 through 4. These data were obtained using pulsed field gradient spin echo NMR (Stejskal–Tanner plots are shown at the top right) and chronoamperometry (Cottrel plots are shown at the bottom right).

4 Dendritic encapsulation – Effect on electron transfer rates

Heterogeneous electron transfer rates for iron–sulfur cluster core dendrimers were determined by fitting Osteryoung square wave voltammetry data to a quasi-reversible heterogeneous electron transfer model as described previously [24]. The results are presented in Table 1. One can observe that increasing generation decreases the rate of electron transfer in the flexible dendrimers. Thus, the effective encapsulation increases with increasing generation. This effect has been examined nicely in the very slow rate regime by using thin layer voltammetry on large dendrimers [46].

Structure	k₀ (× 10³ cm s^–1) OSWV^a	E_1/2 (mV) OSWV or CV^a,c	α OSWV^a
G0Flex	7.43 (1.31)	–1344 (4)	0.57 (0.07)
G1Flex	6.15 (0.64)	–1359 (9)	0.54 (0.06)
G2Flex	3.29 (0.44)	–1374 (13)	0.33 (0.01)
G3Flex	0.76 (0.03)	–1374 (28)	0.29 (0.05)
G4Flex	0.13 (0.06)	NA^b	0.47 (0.01)

G0Rig	6.24 (0.59)	–1351 (5)	0.56 (0.08)
G1Rig	4.12 (0.78)	–1322 (14)	0.54 (0.04)
G2Rig	2.35 (0.09)	–1324 (9)	0.37 (0.03)

3,2 (extended)	4.79 (0.92)	–1494 (4)	0.48 (0.03)
3,2B (backfolded)	0.64 (0.15)	–1618 (2)	0.50 (0.005)

However, the decrease in rate does not reflect an increase in effective electron transfer distance that would be expected if the dendrimer were in an extended conformation. Examining an analogous series of rigid dendrimers, the electron transfer rate was found to decrease much faster with generation (or molecular weight). This result indicates that the primary structure of the dendrimer is important in biasing the conformation so as to maximize the effective distance (and thus rate) of electron transfer.

To further illustrate the effect of dendrimer structure on conformation, as evidenced by electron transfer rate, two dendrimer isomers were prepared and studied (Fig. 4). We and others [47–50] have hypothesized that primary structural elements that enforce backfolding should increase the degree of steric congestion around the core moiety of the dendrimer. This behavior should lead to more effective encapsulation. Indeed, as illustrated in Table 1, the backfolded isomer showed a lower rate of electron transfer than the extended isomer. This result is consistent with a more congested architecture and a higher effective distance for electron transfer in the former isomer as compared to the latter. Concomitant with this observation is a shift in the redox potential of the backfolded isomer compared to the extended isomer. This result is consistent with the iron–sulfur cluster being found in a more hydrophobic microenvironment in the backfolded molecule as compared to the extended molecule. Thus, primary structure can be used to bias dendrimer conformation in an experimentally observable manner.

Fig. 4
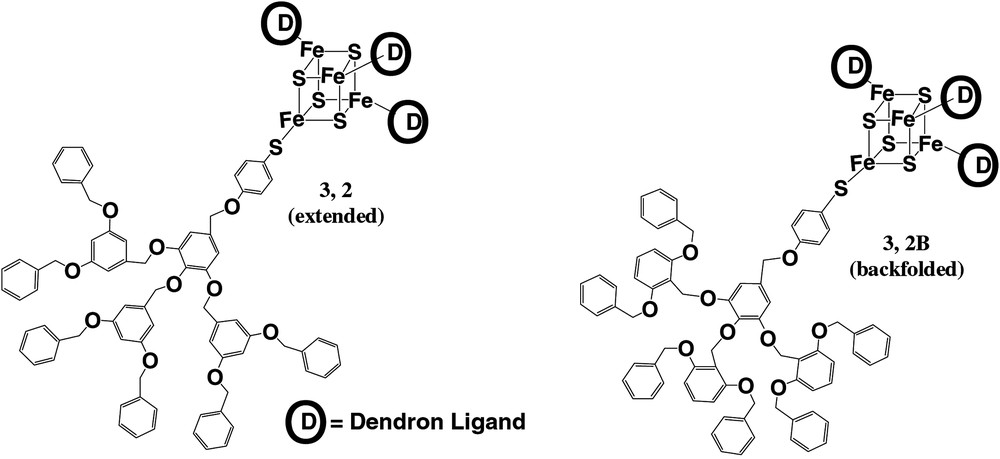
Structures of two iron–sulfur cluster core dendrimer isomers prepared.

5 Dendrimer conformation: the link between primary structure and encapsulation behavior

Regrettably, no methods to directly observe dendrimer conformation have been successful. However, we have explored two methods that indicate some important conformational features of these molecules and help to explain the encapsulation phenomena described above.

The longitudinal relaxation time constants (T₁) of the protons in a series of dendrimers that alternatively had paramagnetic ([Fe₄S₄(SR)₄]^2– R = dendron) and diamagnetic (tetraphenylmethane) cores were compared [21]. The T₁ values of the phenyl and benzyl protons in the paramagnetic core dendrimers were attenuated compared to analogous protons in the diamagnetic core dendrimers (Fig. 5). This observation indicated that protons in each set of topologically different repeat units (generation) of the dendrimer approach the core of the molecule closely in space. This conclusion is consistent with the computed radial density distributions of the different generations calculated from molecular dynamics simulations [25].

Fig. 5
T₁ values (in ms) of aromatic protons in an iron–sulfur cluster core dendrimer as compared to a diamagnetic analogue.

Using a conformational searching protocol, the number of low-energy conformers (within a Boltzman cutoff of 10 kcal mol^–1 at 500 K of the lowest energy conformer) were correlated with the relative offset of the core (Fig. 6) [24]. An offset of zero would find the core at the center of mass of the molecule. An offset of one would find the core at the edge of the molecule. One can see a substantially more offset core in all of the flexible models compared with all of the rigid models. In pictorial representations of the lowest energy conformations (Fig. 6, top), the core is observed to be very centrally located in the rigid molecule but virtually at the molecular edge in the flexible molecule. This model helps to explain why the effective electron transfer distance differs in these two types of molecules. This type of conformational search has been applied to the dendrimer isomer pair as well and will be reported separately.

Fig. 6
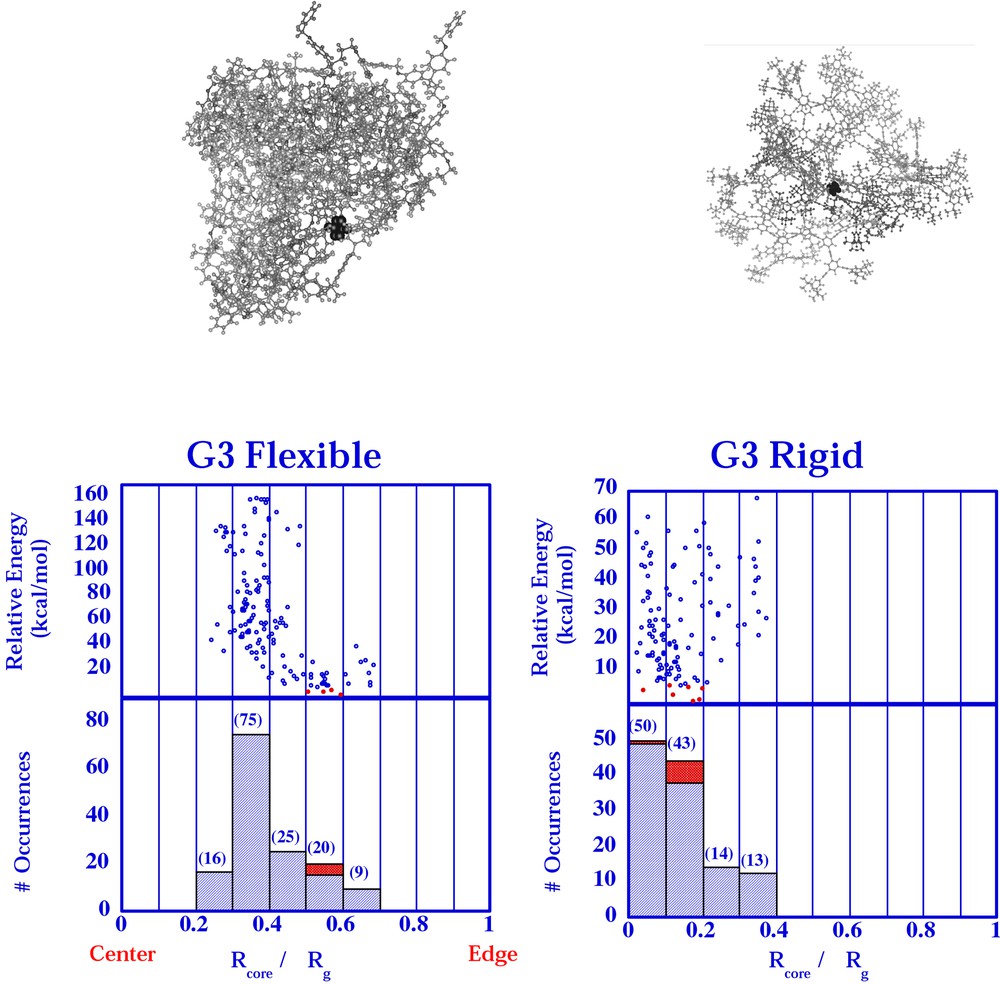
Relative core offsets (0 = core at center and 1 = core at edge) of flexible and stiff dendrimers from conformational search results presented previously [24]. Molecular models of conformation snapshots are shown above the histogram of each search result.

6 Conclusions

These data support several conclusions relevant to dendritic encapsulation. A simple dendrimer does encapsulate its core, but not necessarily in an efficient manner (at least for generations that are relatively accessible, synthetically). However, other structural elements can enforce a conformation in which the core is more closely held in the center of the molecule. Here, the relative rigidity and the use of backfolding have been illustrated as structural motifs to achieve this goal. Undoubtedly, other useful structural elements exist, and this gives an exciting purpose to the continued exploration of structure-property relationships that govern dendritic encapsulation.

Acknowledgements

This work was supported in part by the Air Force Office of Scientific Research MURI Program in Nanoscale Chemistry, and by the National Science Foundation (CAREER Award, DMR-9600138 and CHE-9900072).

Bibliographie

[1] P.G. Degennes; H. Hervet Statistics of Starburst Polymers, J. Phys. Lett., Volume 44 (1983), p. L351

[2] R.L. Lescanec; M. Muthukumar Configurational characteristics and scaling behavior of starburst molecules: a computational study, Macromolecules, Volume 23 (1990), p. 2280

[3] T.C. Zook; G.T. Pickett Hollow-core dendrimers revisited, Phys. Rev. Lett., Volume 90 (2003) (art. No. 015502)

[4] C.B. Gorman; J.C. Smith Structure-property relationships in dendritic encapsulation, Acc. Chem. Res., Volume 34 (2001), p. 60

[5] C.S. Cameron; C.B. Gorman Effects of site encapsulation on electrochemical behavior of redox-active core dendrimers, Adv. Funct. Mater., Volume 12 (2002), p. 17

[6] S. Hecht; J.M.J. Fréchet Dendritic encapsulation of function: applying nature's site isolation principle from biomimetics to materials science, Angew. Chem. Int. Ed. Engl., Volume 40 (2001), p. 74

[7] S. Lamansky; P. Djurovich; D. Murphy; F. Abdel-Razzaq; H.E. Lee; C. Adachi; P.E. Burrows; S.R. Forrest; M.E. Thompson Highly phosphorescent bis-cyclometalated iridium complexes: synthesis, photophysical characterization, and use in organic light emitting diodes, J. Am. Chem. Soc., Volume 123 (2001), p. 4304

[8] J.M. Lupton; I.D.W. Samuel; M.J. Frampton; R. Beavington; P.L. Burn Control of electrophosphorescence in conjugated dendrimer light-emitting diodes, Adv. Funct. Mater., Volume 11 (2001), p. 287

[9] A. Archut; G. Azzellini; V. Balzani; L. De Cola; F. Vögtle Toward photoswitchable dendritic hosts. interaction between azobenzene-functionalized dendrimers and eosin, J. Am. Chem. Soc., Volume 120 (1998), p. 12187

[10] J. Issberner; F. Vögtle; L. De Cola; V. Balzani Dendritic bipyridine ligands and their tris(bipyridine)ruthenium(II) chelates: syntheses, absorption spectra, and photophysical properties, Chem. Eur. J., Volume 3 (1997), p. 706

[11] F. Vögtle; M. Plevoets; M. Nieger; G.C. Azzellini; A. Credi; L. De Cola; V. De Marchis; M. Venturi; V. Balzani Dendrimers with a photoactive and redox-active [Ru(bpy)₃]²⁺-type core: Photophysical properties, electrochemical behaviour, and excited-state electron-transfer reactions, J. Am. Chem. Soc., Volume 121 (1999), p. 6290

[12] C.B. Gorman; J.C. Smith Iron–sulfur core dendrimers display dramatically different electrochemical behavior in films compared to solution, J. Am. Chem. Soc., Volume 122 (2000), p. 9342

[13] P.J. Dandliker; F. Diederich; M. Gross; C.B. Knobler; A. Louati; E.M. Sanford Dendritic porphyrins: modulating redox potentials of electroactive chromophores with pendant multifunctionality, Angew. Chem. Int. Ed. Engl., Volume 33 (1994), p. 1739

[14] P.J. Dandliker; F. Diederich; J.-P. Gisselbrecht; A. Louati; M. Gross Water-Soluble Dendritic Iron Porphyrins: Synthetic Models of Globular Heme Proteins, Angew. Chem. Int. Ed. Engl., Volume 34 (1995), p. 2725

[15] P.J. Dandliker; F. Diederich; A. Zingg; J.-P. Gisselbrecht; M. Gross; A. Louati; E. Sanford Dendrimers with porphyrin cores: Synthetic models for globular heme proteins, Helv. Chim. Acta, Volume 80 (1997), p. 1773

[16] P. Weyermann; J.-P. Gisselbrecht; C. Boudon; F. Diederich; M. Gross Dendritic iron porphyrins with tethered axial ligands: New model compounds for cytochromes, Angew. Chem. Int. Edit. Engl., Volume 38 (1999), p. 3215

[17] K.-Y. Chen; C.B. Gorman Synthesis of a series of focally-substituted organothiol dendrons, J. Org. Chem., Volume 61 (1996), p. 9229

[18] C.B. Gorman; B.L. Parkhurst; K.-Y. Chen; W.Y. Su Encapsulated electroactive objects based upon an inorganic cluster surrounded by dendron ligands, J. Am. Chem. Soc., Volume 119 (1997), p. 1141

[19] C.B. Gorman Encapsulated Electroactive Molecules, Adv. Mater., Volume 9 (1997), p. 1117

[20] C.B. Gorman Metallodendrimers: structural diversity and functional behavior, Adv. Mater., Volume 10 (1998), p. 295

[21] C.B. Gorman; M.W. Hager; B.L. Parkhurst; J.C. Smith Use of a paramagnetic core to affect longitudinal nuclear relaxation in dendrimers: a tool for probing dendrimer conformation, Macromolecules, Volume 31 (1998), p. 815

[22] C.B. Gorman; R.L. Miller; K.-Y. Chen; A.R. Bishop; R.T. Haasch; R.G. Nuzzo Semi-permeable, chemisorbed adlayers of focally substituted organothiol dendrons on gold, Langmuir, Volume 14 (1998), p. 3312

[23] C.B. Gorman; W.Y. Su; H. Jiang; C.M. Watson; P. Boyle Hybrid organic-inorganic, hexa-arm dendrimers based on an Mo₆Cl₈ core, Chem. Commun. (1999), p. 877

[24] C.B. Gorman; J.C. Smith; M.W. Hager; B.L. Parkhurst; H. Sierzputowska-Gracz; C.A. Haney Molecular structure-property relationships for electron transfer rate attenuation in redox-active core dendrimers, J. Am. Chem. Soc., Volume 121 (1999), p. 9958

[25] C.B. Gorman; J.C. Smith Effect of repeat unit flexibility on dendrimer conformation as studied by atomistic molecular dynamics simulations, Polymer, Volume 41 (2000), p. 675

[26] J.P. Collman; L. Fu; A. Zingg; F. Diederich Dioxygen and carbon monoxide binding in dendritic iron(II) porphyrins, Chem. Commun. (1997), p. 193

[27] P. Weyermann; F. Diederich Synthesis of dendritic iron(II) porphyrins with a tethered axial imidazole ligand designed as new model compounds for globins, J. Chem. Soc., Perkin Trans., Volume 1 (2000), p. 4231

[28] P. Weyermann; F. Diederich; J.-P. Gisselbrecht; C. Boudon; M. Gross Dendritic iron porphyrins with tethered axial ligands: New model compounds for cytochromes, Helv. Chim. Acta, Volume 85 (2002), p. 571

[29] P. Weyermann; F. Diederich Dendritic iron porphyrins with a tethered axial ligand as new model compounds for heme monooxygenases, Helv. Chim. Acta, Volume 85 (2002), p. 599

[30] A. Zingg; B. Felber; V. Gramlich; L. Fu; J.P. Collman; F. Diederich Dendritic iron(II) porphyrins as models for hemoglobin and myoglobin: specific stabilization of O–2 complexes in dendrimers with H-bond-donor centers, Helv. Chim. Acta, Volume 85 (2002), p. 333

[31] M. Enomoto; T. Aida Self-assembly of a copper-ligating dendrimer that provides a new non-heme metalloprotein mimic: dendrimer effects on stability of the bis(μ-oxo)dicopper(III) core, J. Am. Chem. Soc., Volume 121 (1999), p. 874

[32] S. Mondal; P. Basu Dendrimer encapsulation of [Mo^VOS₄] cores: implications for the DMSO reductase family of enzymes, Inorg. Chem., Volume 40 (2001), p. 192

[33] R. Toba; J.M. Quintela; C. Peinador; E. Román; A.E. Kaifer Dendritic cavitands: preparation and electrochemical properties, Chem. Commun. (2002), p. 1768

[34] Y. Wang; C.M. Cardona; A.E. Kaifer Molecular orientation effects on the rates of heterogeneous electron transfer of unsymmetric dendrimers, J. Am. Chem. Soc., Volume 121 (1999), p. 9756

[35] R. Toba; J.M. Quintela; C. Peinador; E. Roman; A.E. Kaifer A new series of dendrimers with 4,4′–bipyridinium cores capable of fast electron transfer reactions, Chem. Commun. (2001), pp. 857-858

[36] D.K. Smith Branched ferrocene derivatives: using redox potential to probe the dendritic interior, J. Chem. Soc. Perkin Trans., Volume 2 (1999), p. 1563

[37] W. Ong; A.E. Kaifer Unusual electrochemical properties of unsymmetric viologen dendrimers, J. Am. Chem. Soc., Volume 124 (2002), p. 9358

[38] C.M. Cardona; S. Mendoza; A.E. Kaifer Electrochemistry of encapsulated redox centers, Chem. Soc. Rev., Volume 29 (2000), p. 37

[39] R. Wang; Z. Zheng Dendrimers supported by the [Re₆Se₈]²⁺ metal cluster core, J. Am. Chem. Soc., Volume 121 (1999), p. 3549

[40] B.K. Roland; H.D. Selby; M.D. Carducci; Z.P. Zheng Built to order: molecular tinkertoys from the Re₆(μ₃–Se)₈²⁺ clusters, J. Am. Chem. Soc., Volume 124 (2002), p. 3222

[41] B.K. Roland; C. Carter; Z.P. Zheng Routes to metallodendrimers of the Re₆(μ₃–Se)₈²⁺ core-containing clusters, J. Am. Chem. Soc., Volume 124 (2002), p. 6234

[42] M.A. Bobrik; L. Que; R.H. Holm Synthetic analogs of the active sites of iron-sulfur proteins. IV. Ligand substitution reactions of the tetranuclear clusters [Fe₄S₄(SR)₄]^2–, J. Am. Chem. Soc., Volume 96 (1974), p. 285

[43] L. Que; M.A. Bobrik; J.A. Ibers; R.H. Holm Synthetic analogs of the active sites of iron-sulfur proteins. VII. Ligand substitution reactions of the tetranuclear clusters [Fe₄S₄(SR)₄]^2– and the structure of [(CH₃)₄N]₂[Fe₄S₄(SC₆H₅)₄], J. Am. Chem. Soc., Volume 96 (1974), p. 4168

[44] G.R. Dukes; R.H. Holm Synthetic analogs of the active sites of iron-sulfur proteins. X. Kinetics and mechanism of the ligand substitution reactions of arylthiols with the tetranuclear clusters [Fe₄S₄(SR)₄]^2–, J. Am. Chem. Soc., Volume 97 (1975), p. 528

[45] R.W. Johnson; R.H. Holm Reaction chemistry of the iron-sulfur protein site analogues [Fe₄S₄(SR)₄]^2–. Sequential thiolate ligand substitution reactions with electrophiles, J. Am. Chem. Soc., Volume 100 (1978), p. 5338

[46] Y. Rio; G. Accorsi; N. Armaroli; D. Felder; É Levillain; J.-F. Nierengarten Thin-layer cyclic voltammetry: an efficient tool to determine the redox characteristics of large dendrimers, Chem. Commun. (2002), p. 2830

[47] V. Percec; W.D. Cho; M. Möller; S.A. Prokhorova; G. Ungar; D.J.P. Yeardley Design and structural analysis of the first spherical monodendron self-organizable in a cubic lattice, J. Am. Chem. Soc., Volume 122 (2000), p. 4249

[48] V. Percec; W.D. Cho; G. Ungar; D.J.P. Yeardley Synthesis and NaOTf mediated self-assembly of monodendritic crown ethers, Chem. Eur. J., Volume 8 (2002), p. 2011

[49] H.W.I. Peerlings; D.C. Trimbach; E.W. Meijer Chiral dendrimers with backfolding wedges, Chem. Commun. (1998), p. 497

[50] B.H. Huang; J.R. Parquette Effect of an internal anthranilamide turn unit on the structure and conformational stability of helically biased intramolecularly hydrogen-bonded dendrons, J. Am. Chem. Soc., Volume 123 (2001), p. 2689

Commentaires - Politique