1 Introduction
The concept of frustration has proved to be very rich in condensed matter physics during the last 30 years. In this paper, we shall focus on geometrical frustration, as it was initially discussed for icosahedral order in amorphous systems and later generalized to other types of order. Frustration applies to cases where a given condensed matter system is subjected to uncompatible requirements, with a pronounced tendency to form well-defined local configurations, and the impossibility for the latter to perfectly fill the 3-dimensional Euclidean space.
In the icosahedral order case, this concept unifies, in the same approach, clusters, amorphous systems, quasicrystals, and even large cell crystals known as Frank–Kasper phases. A general approach to treat this problem has been introduced by Sadoc [1–3]. The method consists in a first step to relax the space-filling constraint to allow a free propagation of the local configuration throughout the space. The price to be paid is that the underlying space becomes curved (positively curved in this case), and one eventually gets a regular icosahedral structure, a polytope on a 3-dimensional hypersphere S3 embedded in 4 dimensions. One can then study, in this curved space model, those properties which are mainly due to the local order itself.
This curved space approach has later been successfully applied to other frustrated situations, like tetra-coordinated covalent structures [4], double-twisted cholesteric blue phases [5], frustrated polymers [6] and frustrated amphiphilic films [7,8].
Once the ideal curved space structure has been defined, one must, in a second step, find ways to “transform” the curved space ideal structure back to the Euclidean 3-dimensional space. For that purpose, the free propagation of local configurations must be interrupted by regions (that we shall call “defects”), which carry an opposite curvature content, in such a way that the underlying space be flat on the average. The final structure will therefore be described as a complex juxtaposition of (positively curved) regions where the order is very close to that of the ideal polytope, and of defective regions. An order of magnitude has been gained in the analysis and geometrical description of these structures. Their complexity is not coded in terms of the individual atomic coordinates, but in the mutual arrangement of the defects.
We shall see below that, among all possible defect types, disclination lines play a centre role. From a descriptive, but also conceptual point of view, an important result of this approach is to allow the following classification, in terms of the disclination lines' arrangements:
- - no disclinations: ideal structure defined in curve space;
- - periodic disclination networks: large cell crystals, like the Frank–Kasper metallic phases [9], and even some clathrates. In the liquid-crystal field, this corresponds to the cholesteric blue phases and to some complex crystalline amphiphilic films. The cholesteric case is particularly interesting, since disclination lines were studied at length in these systems, in particular by Bouligand [10] and Kleman [11];
- - hierarchical disclination network: quasicrystals;
- - disordered arrangement of disclinations: amorphous structures.
In this paper, after recalling the curved space model in the icosahedral order case, we shall focus on the unexpected analogy between two complex large cell crystals, the Frank–Kasper metallic alloys and the cholesteric blue phases. In both cases, the structure can be described as a periodic arrangement of disclination lines, whose origin is simply related to the presence of geometrical frustration, which is relaxed on the positively curved S3 hypersphere. An array of line defects carrying negative curvature is then necessary to embed the structure in a 3-dimensional Euclidean space.
2 Frustration in close sphere packings and icosahedral order
2.1 Sphere packing and “Lennard–Jonesium” solid
Atomic close-packings are widely met in condensed matter systems. A (classical) model consists in having spherical particles interacting through a pair potential displaying isotropic long-range (van der Waals-like) attraction (to eventually get a structure) and short-range repulsion (to prevent the system from collapsing). A widely studied such atomic pair potential is the Lennard–Jones potential:
Is is well known that, varying the clusters size, a large fraction of structures with (pseudo)icosahedral symmetry are found which minimize the Lennard–Jones total energy [12]. In the early seventies, this knowledge, and the experimental strong indication of a polytetrahedral (and therefore (pseudo)icosahedral) atomic order in amorphous metals [13], opened the way for a rich scientific exchange between the amorphous and the cluster scientific communities.
For the present purpose of introducing geometrical frustration, we can further simplify this potential, and consider situations where a pair of atoms sit at a distance were they minimize the Lennard–Jones energy, and then add the contribution −ɛ to the total energy. In such hard sphere limit, the total energy is just equal to −ɛ times the number of sphere contacts. We extend this to 2 dimensions as a hard-disk close-packing problem and compare the 2- and 3-dimensional cases (Fig. 1). In this simple model, one clearly sees that with four particles, the system minimizes its energy by adding the fourth particle in such a way to close a regular tetrahedron, instead of staying on a 2-dimensional space. The best configuration for the fifth particle consists in closing a second tetrahedron sharing a face with the first one. The sphere close-packing problem is thus mapped onto a tetrahedral packing in R3. In an equivalent way, had the configuration been restricted to be planar, the hard-disk close-packing problem would translate to a triangular packing in 2d.
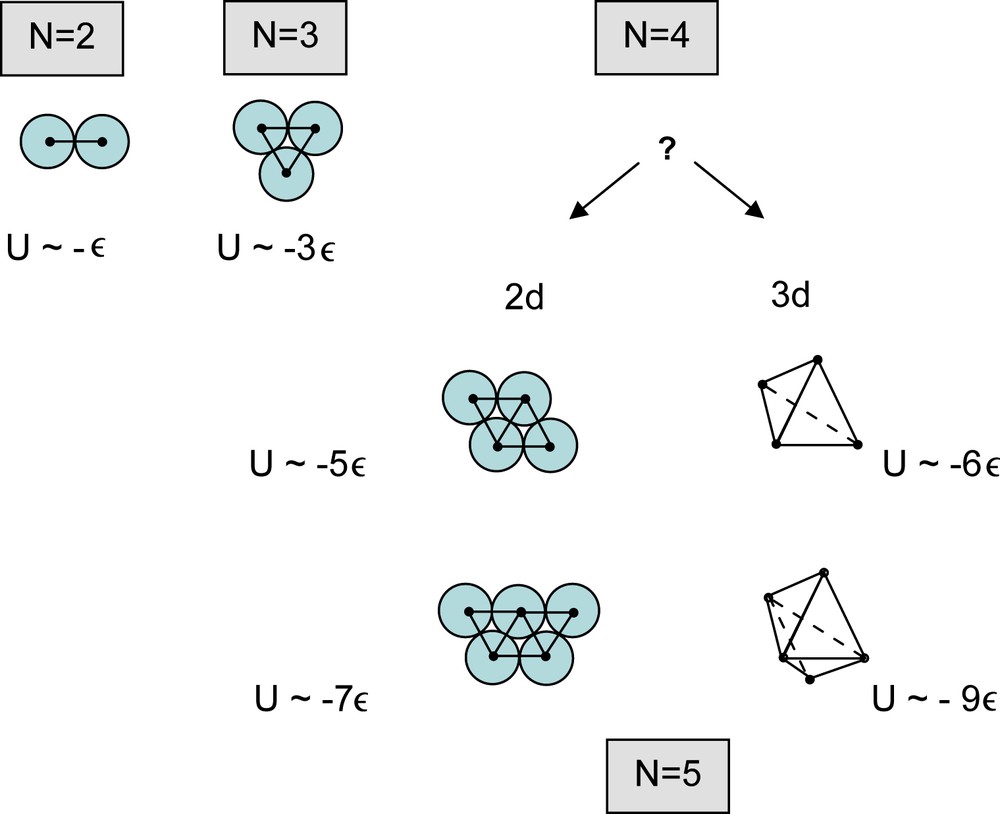
Packing sequence for few particles in 2 and 3 dimensions. With N = 4, the escape to a third dimension, with a perfect tetrahedral configuration, significantly lowers the energy. The close-packing problem is then related to the tetrahedral close-packing problem, which turns out to be frustrated.
And there comes the main difference between close-packing in two and three dimensions. A triangular packing can be freely propagated throughout a plane, the reason being that the corner angle (60°) is a submultiple of 2π. A triangular lattice, with six equilateral triangles sharing each vertex, results from that construction, and is well known to be the closest 2d lattice packing. This situation (local “best” configuration which can be freely propagated in space) is referred to as unfrustrated. On the contrary, propagation of the tetrahedral order quickly meets a problem, due to the fact that the regular tetrahedron dihedral angle (∼70°30′) is not an integer submultiple of 2π. Note that it falls short of being the fifth of 2π. This means that adding more and more tetrahedra, there is a trend toward arranging five tetrahedra sharing a common edge, but each time with a remaining small hole. These holes accumulate, and eventually destroy the perfect tetrahedral order. This is a typical frustrated system. Notice that a set of 20 tetrahedra sharing a common vertex would define a perfect centrered icosahedron, at the price of having slightly deformed tetrahedral symmetry. This is why close-packed tetrahedral order and icosahedral order are closely linked problems.
2.2 The ideal icosahedral order on a 3-dimensional curved space
In 1979, Jean-François Sadoc proposed a very original approach to analyse this frustration effect in sphere packing problems. He observed that perfect (unfrustrated) icosahedral order can propagate freely throughout the space if the latter gets positively curved. There is an analogous problem in two dimensions associated with pentagonal packing (Fig. 2). The regular pentagon vertex angle (108°) does not divide 2π, and therefore cannot perfectly tile an Euclidean plane. But if one tries instead to tile the surface of a sphere of appropriate radius, a regular tiling can be obtained: the dodecahedron (with 20 vertices and 12 faces). Sadoc observed that a correctly scaled, 3-dimensional sphere (noted S3) can also admit a perfect tetrahedral packing. One gets a polytope with 120 vertices and 600 tetrahedra cells; each edge is shared by five tetrahedra and each vertex is surrounded by a perfect icosahedron. High-dimensional polytopes, which are well known and classified by mathematicians [14], then found a new application as ideal templates for real atomic packing problems.
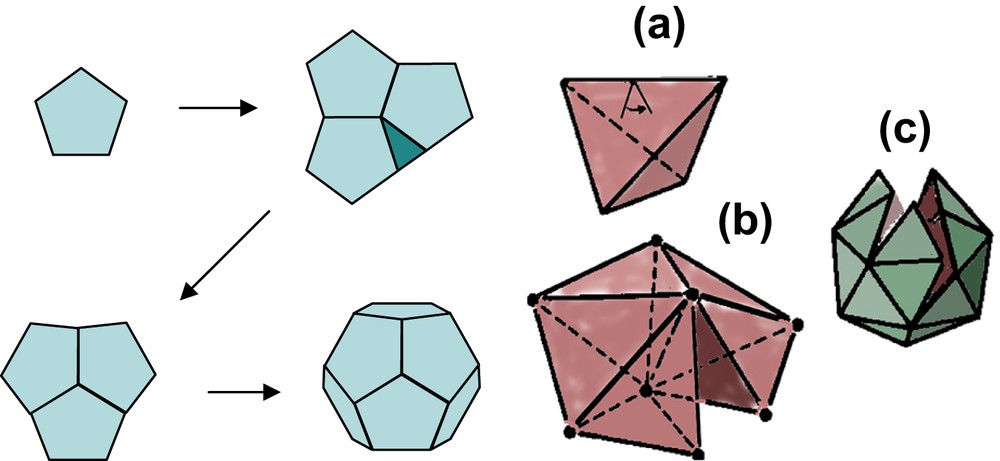
Frustration problem in 2 and 3 dimensions. Left: tiling the plane with regular pentagons is impossible, but possible on a sphere. Right: geometrical frustration in the close tetrahedral packing in R3. With 20 tetrahedra around a central vertex, an irregular icosahedral configuration is obtained.
An interesting computer simulation, done by Straley [15], illustrates quite well the frustration effect. Straley compares annealing of interacting particles in Euclidean and in spherical space. In the first case the structure is very slowly approaching equilibrium, while on S3, with adjusted radius, the ground state configuration, corresponding to the 120-vertex polytope, is reached very quickly.
Having this ideal template, the physical properties associated with the perfect icosahedral order can be computed (see for example [3], and references herein), keeping for a next step the analysis of how far these properties will survive in the more realistic structures.
Among the theoretical studies that took advantage of these ideal templates, one should cite the detailed analyses by David Nelson and co-workers [16–18], who elaborated on the concept of icosahedral order parameter, and proposed a Landau theory of frustrated system.
2.3 Decurving procedure and topological defects
Once the ideal structure has been defined, its relation with the real structure must be described. One can imagine several ways for that purpose. If one is interested in finite clusters of icosahedral symmetry, a simple prescription consists in directly mapping a piece of the ideal polytope onto an 3-dimensional Euclidean tangent space [19]. For infinite structures, the most valuable method consists in introducing disclination defects. Indeed, a disclination defect naturally carries curvature, as shown in a simple 2-dimensional example in Fig. 3.
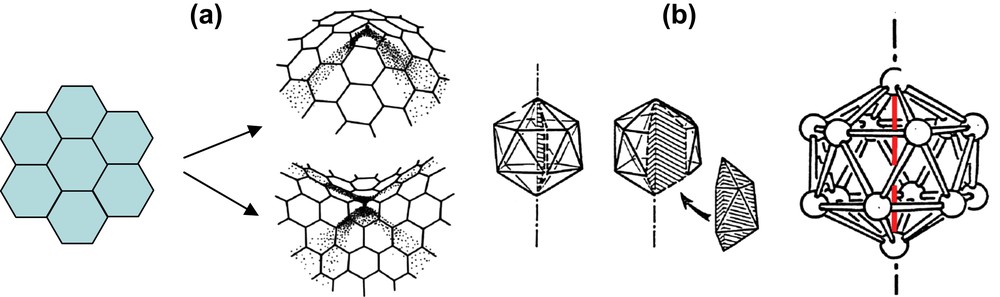
Disclination defects in 2 and 3 dimensions. A disclination defect is created, with the Volterra process, by cutting in the structure, and adding or removing a wedge of material between the lips of the cut. (a) A disclination point defect in an hexagonal tiling, of either positive or negative nature. (b) A disclination line in an icosahedral configuration changes the 5-fold axis to a 6-fold axis, and concentrates negative curvature.
Let us recall the standard Volterra process to create a disclination defect. One creates a cut in the structure, and add or remove a wedge of material along the edge of the cut (this is to be contrasted with adding or removing a half plane in the dislocation case), as illustrated in Fig. 3 for a 2(3)-dimensional point (line) defect, respectively. It is then clear that a disclination “carries” curvature, either positive or negative. It is then natural to propose, as decurving procedure from the ideal template on a 3-dimensional positively curved sphere to the “flat” Euclidean space, the creation of an adequate density of disclination lines (see for example [20]). Along this line, an interesting possibility is the so-called “Iterative Flattening Method”, which gives rise to infinite closely packed structures, with a hierarchical disclination order, and atomic arrangement close to that of quasicrystals [21].
2.4 The Frank–Kasper phases
Although the present curved space approach was initially meant to address the structural description of amorphous systems, it became rapidly clear that the method applies to large cell crystalline structures with complex local order inside the unit cell. The best example is provided by the Frank–Kasper metallic phases [9]. These phases present tetrahedrally close-packed atoms with many (pseudo)icosahedral local configurations, which are repeated periodically. An inspection of the unit cell arrangements indicates a rather large fraction of atoms with an almost perfect icosahedral coordination shell (with 12 neighbours, and denoted Z12 sites). Frank and Kasper showed that the remaining atoms have a higher coordination (mainly Z14, Z15 and Z16), and form uninterrupted networks (called the “major skeleton”) along the directions where the five-fold local symmetry is replaced by a six-fold one (Fig. 4). The Frank–Kasper skeleton has been since identified to a disclination line network threading a medium with the icosahedral polytope order [16,22,23]. The discovery of icosahedral quasicrystalline phases [24] renewed the interest toward the Frank–Kasper phases. Many large cell with such structures were found stable in the vicinity of the quasicrystal phase in most phase diagrams; to some respect, the true quasicrystalline phase can be understood as the asymptotic element of an infinite set of periodic structure with increasing large cell structures, the so-called approximant phases.
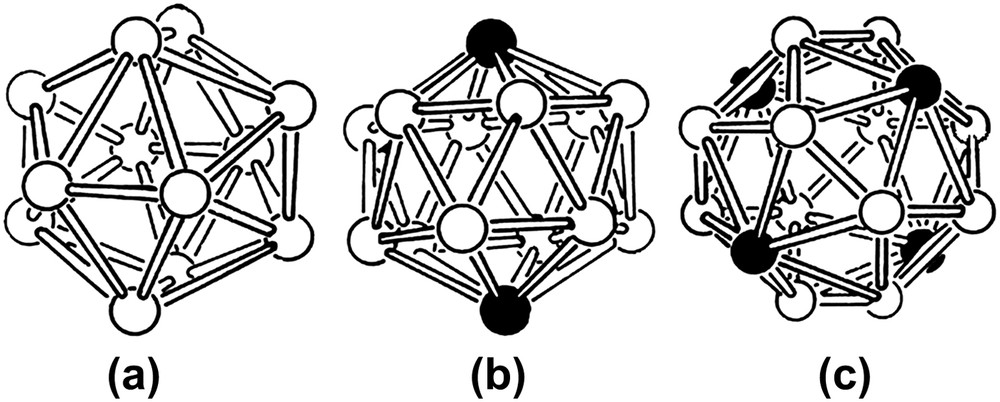
Frank–Kasper polyhedra: (a) the Z12 icosahedral shell; (b) the Z14 shell, with one 6-fold axis. A F-K line (negative disclination) joins the two dark vertices; (c) the Z16 shell, with four 6-fold local configurations. The F–K line network corresponds to 4 half-lines, threading the dark vertices and joining at the centre.
3 Frustration in cholesteric blue phases
Let us now turn to the, a priori different, frustration effect in cholesteric systems, made of chiral molecules. A pair of neighbouring molecules will have an equilibrium position corresponding to a minimal energy if they sit at a slight angle with respect to each other (imagine close “screws”). It is more convenient to leave the molecular scale and to consider molecular orientation averaged inside small space regions. The structure is then described, in this continuous approximation, by a field of directors (headless vectors), but, except for description and classification of topological defects, it is possible to consider a standard vector field.
3.1 The double-twist frustration
The classical cholesteric phases correspond to the case where the twist propagates along one direction only, leading to planar parallel configurations twisting in the perpendicular direction. But more complex structures, called the blue phases, are sometimes found in a narrow range of the phase diagrams. Their local order corresponds to more complex arrangements where the twist seems to propagate along all directions perpendicular to the molecular axis, the so-called “double-twist” configuration. Such a situation is frustrated, as it can be understood in Fig. 5, by following and keeping track of the director orientation along two different paths ending at the same point. It is then impossible to fill the space with a vector field which obeys everywhere the “double-twist” rule. This is therefore a new example of geometrical frustration, whose strength is characterized by the pitch of the associated rotation.
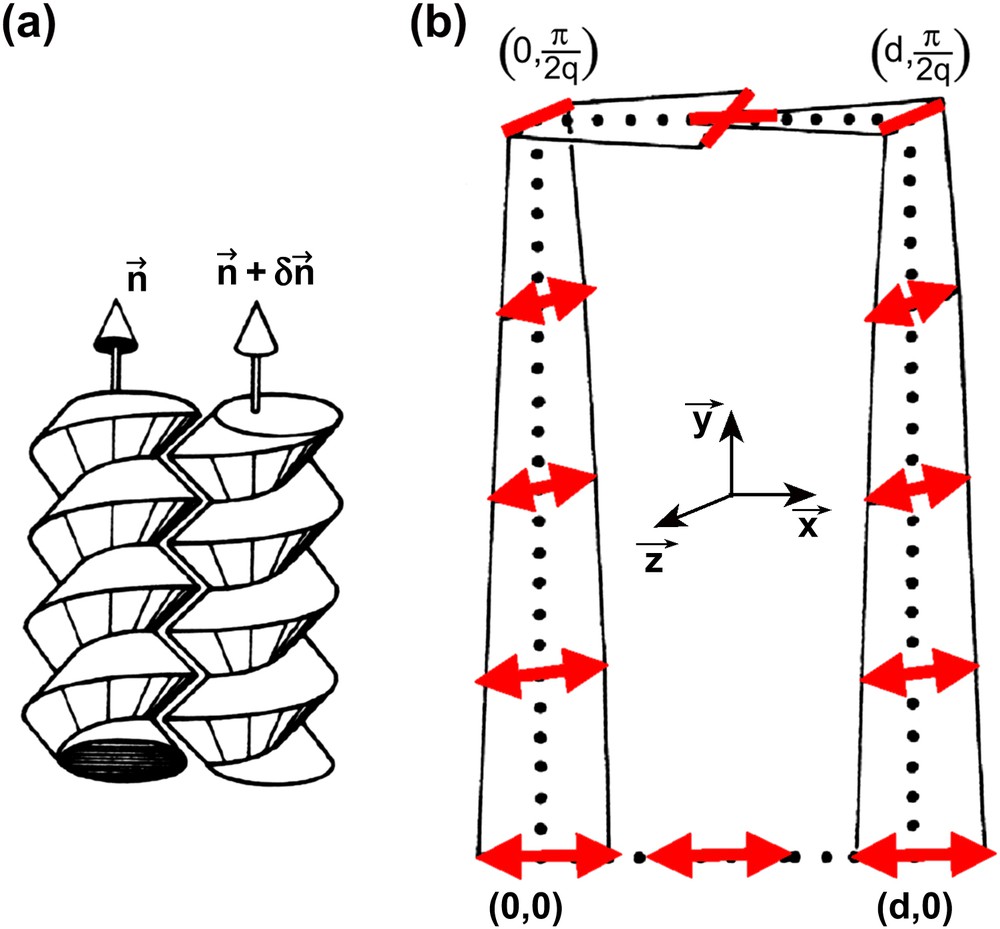
Frustration in double-twisted cholesteric phases. (a) Schematic representation of two chiral cholesteric molecules by screws. (b) Frustration in a double-twist system in R3. At a given point, the director orientations are different for two different paths which continuously satisfy the double-twist condition from the origin.
3.2 The unfrustrated double-twist blue phase on S3
This fascinating example of geometrical frustration was the first to be treated in a continuous system [5,25], using an ideal template in S3 whose radius is adjusted to the helicoidal pitch. Indeed, a vector field tangent to S3 can be defined such that the double-twist configuration is everywhere perfect. This field can be visualized, using the stereographic projection on R3, as shown in Fig. 6b.

(a) The double-twist condition is realized on the axis of a double-twist tube in R3. (b) A piece of the ideal blue phase in S3, stereographically mapped onto R3. The field is tangent to the Hopf fibration circles.
One way to describe this vector field is in relation with the S3 great circle Hopf fibration. It is possible to fill the whole S3 with non-intersecting great circles in such a way that any S3 point belong exactly to one circle. The ideal blue phase field is nothing but the vector field tangent to the Hopf great circles. The great circle gathers on a continuous set of coaxial tori, three of which being represented in Fig. 6b.
3.3 The cholesteric blue phase as a periodic arrangement of disclination lines
Topological defects must be introduced to lower the space curvature, in order to relate the ideal double-twist structure in S3 and real structures in R3 [26]. Blue phases are, along this line, similar to Frank and Kasper phases.
Note that it is already possible to minimize the “double-twist” energy in R3, along the central axis of a cylinder, called a “double-twist tube” (Fig. 6a). A standard model for the blue phases is then a 3-dimensional periodic arrangement of these tubes [27], as displayed in Fig. 7. But the director field cannot be defined everywhere and a periodic array of disclination lines, of type “π”, is present. The two well-known examples, blue phases I and II, correspond to different tube arrangements with cubic symmetry.
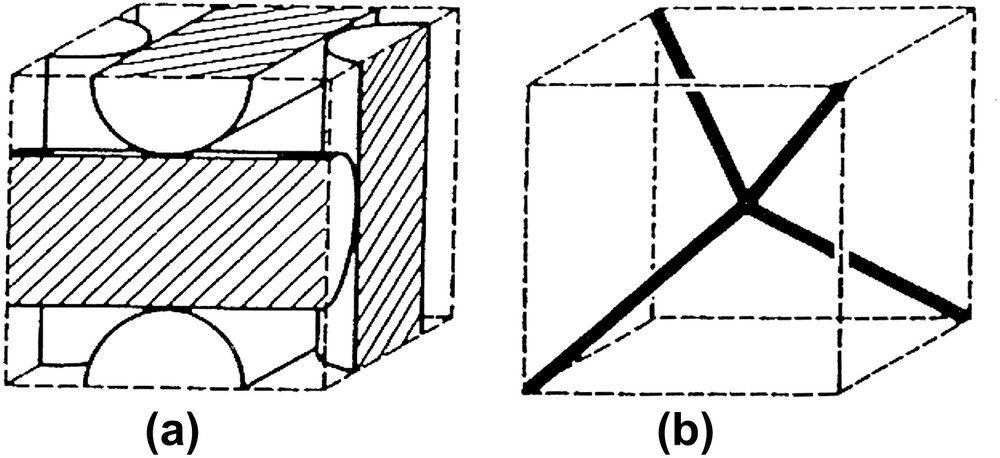
A model of the blue phase structure: (a) double-twist tubes arrangement in blue phase II; (b) the associated disclination network.
The analysis of the field configuration near the tube interfaces is made easier if one remarks the close relation with two Infinite Periodic Minimal Surfaces, called P and D. In particular, a local minimum of the energy is reached if the director field is tangent to the asymptotic lines of the surface [26]. Flat points on the surface, which are singularities for this field, are threaded by axes of type [111], which corresponds to the disclinations.
4 Conclusion
Geometrical frustration is rather common in condensed matter systems. A general approach, which unifies very different types of material (either metallic, covalent or liquid crystalline) have been introduced in the 1980s by different groups, following the pioneer work of Sadoc on icosahedral systems. The method follows two steps: first, the definition of an ideal unfrustrated structure in curved space; then an analysis of real space defects which follows a decurving process toward a R3 structure.
After having recalled this curved space approach in the icosahedral order case, we have focussed here on the description of two types of large cell crystalline structures, the metallic Frank–Kasper alloys, and the cholesteric blue phases. Both structures can be described as a periodic array of disclination line defects threading a medium with (slightly deformed) local and medium range order.
Acknowledgements
The content of this paper was presented at a scientific meeting in March 2006, at the College de France (Paris), centred on the scientific interests of Yves Bouligand. I would like to acknowledge many illuminating discussions with him, that I benefited in the mid-eighties, on the questions of linear defects in liquid crystals. I should also acknowledge the many years of a rich collaboration with Jean-François Sadoc, about geometrical frustration in diverse condensed matter systems.


