1 Introduction
Photochemical reactions play an important role in the removal of biologically refractory pollutants from surface freshwater. They consist of the direct photolysis of sunlight-absorbing molecules and of a number of indirect photoreactions [1,2]. The latter can involve pollutants that do not absorb sunlight, and include the transformation processes photosensitised by dissolved organic matter (DOM), most likely through the excited triplet states (3DOM*) [3,4], and the reaction with transient species such as OH, CO3−, 1O2, NO2, and Cl2− [5–9]. The cited transients can be produced upon irradiation by sunlight of photosensitisers such as DOM itself, nitrate, nitrite, and Fe(III). In some cases the interaction with inorganic anions such as bicarbonate, carbonate, chloride and nitrite is required. In many cases the transient species are consumed by natural scavengers, among which DOM is usually expected to play an important role [10]. Possible exceptions to the scavenging by DOM are the cases of 1O2 and NO2, for which deactivation by collision with water molecules [11] and hydrolysis [12], respectively, might be major removal pathways.
Recent research has enabled the modelling of the steady-state concentration of OH in the surface layer of natural waters, as a function of the chemical composition of photoactive species. It is, therefore, possible to assess the lifetime of pollutants with known reaction rate constant with OH, from the values of NPOC (non-purgeable organic carbon, which quantifies DOM), [NO3−], [NO2−], [HCO3−], and [CO32−] [13]. Such a result was mainly allowed by the quantification of the role of DOM as photochemical OH source. Interestingly the OH radical is involved not only into the degradation of organic pollutants but also in the production of other reactive transients such as CO3− from carbonate and bicarbonate, and NO2 from nitrite [14,15].
This work is focused on the modelling of the occurrence and reactivity of the carbonate radical in surface freshwater. The radical CO3− can be produced from OH and CO32− or HCO3− [16], from CO32− and 3DOM* [17], and possibly also from irradiated Fe(III) oxides and CO32− [18]:
| OH + CO32− → OH− + CO3− [k1 = 3.9 × 108 M−1 s−1] | (1) |
| OH + HCO3− → H2O + CO3− [k2 = 8.5 × 106 M−1 s−1] | (2) |
| 3DOM* + CO32− → DOM− + CO3− [k3 ≈ 1 × 105 M−1 s−1] | (3) |
The radical CO3− is less reactive than OH toward the degradation of organic compounds [16,19], but in surface freshwaters it is also scavenged by DOM to a lesser extent [17]. The consequence is that CO3− can reach a higher steady-state concentration than the hydroxyl radical, which would compensate to a variable extent for the lower reactivity. It is generally believed that CO3− can be an important sink for water-dissolved phenolates and sulphur-containing compounds [17].
2 The model for carbonate radicals in surface waters
The present model is based on the formation of CO3− by OH and 3DOM* (reactions (1)–(3)), and on its consumption by DOM itself (reaction (4)) and the pollutant(s) of interest.
| DOM + CO3− → DOM+ + CO32− [k4 = 102 (mg C)−1 s−1] | (4) |
The main issue with reaction (4) is that there is some disagreement among the values of k4 reported in the literature, either 40 [20] or 280 ± 90 [17] (mg C/L)−1 s−1. The value adopted in the present paper can be regarded as a reasonable estimate based on those figures. To apply the model, it is also necessary to know the second-order rate constant for the reaction of the pollutant with CO3−.
2.1 Production of CO3− from OH
As far as reactions (1) and (2) are concerned, it is essential to have an estimate of the formation rate of OH in the system (ROHtot) in order to derive the formation rate of the carbonate radical, RCO3−, from the concentration values of carbonate and bicarbonate. From the values of NPOC, [NO3−] and [NO2−] in the surface water layer, where most of the photochemical activity would occur [21], it is possible to derive the value of ROHtot (in mol s−1) under 22 W m−2 sunlight UV irradiance in a water volume V = Sd [22]. S = 1.26 × 10−3 m2 is the surface of the photoreactor adopted in the irradiation experiments that have been the experimental basis of the OH model [22], and d is the water column depth best expressed as the average depth of the water body. All the calculations will be referred to the standard volume V (in litres), but it would be the same as referring them to the whole aquatic system. Another input datum for ROHtot would be the absorption spectrum A1(λ) of the water over the optical path length b = 1 cm. However, in case where the spectrum is not available it would be possible to approximately model it from the NPOC value, as [22]:
| (5) |
Eq. (5) depends on NPOC because DOM is by far the main radiation absorber in surface waters in the very vast majority of the cases of environmental significance [23].
The formation rate of the carbonate radical, accounted for by OH, is equal to ROHtot times the fraction of the hydroxyl radicals that react with carbonate and bicarbonate (Eq. 6). It is expressed in mol s−1 in the volume V = Sd (S = 1.26 × 10−3 m2; d = average depth of the water body):
| (6) |
The numerical values in Eq. (6) are the rate constants for the reaction between OH and carbonate, bicarbonate, DOM and nitrite [22]. Usually DOM is by far the main sink for OH in surface freshwaters [10]. Table 1 reports the values of the chemical composition and those of ROHtot and RCO3− (OH) for the case of four lakes and one river. The chemical composition is referred to the surface water layer because the photochemical reactions mostly occur within the first meter of the water column [21,22]. The water absorption spectrum was not available for the river, and it was simulated according to Eq. (5). The absorption spectra of the relevant surface water samples are reported in Fig. 1. The error bounds of the values in Table 1 are referred to those of ROHtot as derived from the model reported in Ref. [22] (μ±α), modified according to the rules of error propagation.
Parameters of photochemical significance in the surface water systems under consideration. Note that d is the average depth, and V = Sd is the volume of the water column with surface S = 1.26 × 10−3 m2. The data in the lower section of the table were calculated based on those of the upper one. The four lakes (Avigliana Piccolo, Candia, Avigliana Grande and Rouen) are all located in NW Italy [22], the Blue Earth River is in Minnesota [10]. In the latter case the concentration of nitrite, not reported, was not considered. Standard sunlight UV irradiance was 22 W m−2. SSD means summer sunny days equivalent to 15 July at 45°N latitude. The conditions in which CO3− prevails over OH as reactive species are highlighted in bold italic, the reverse case is reported in normal font.
| Av. Piccolo | Candia | Av. Grande | Rouen | Blue Earth River | ||
| NPOC (mg C L−1) | 5.1 | 5.4 | 5.0 | 0.63 | 4.2 | |
| NO3− (M) | 1.9 × 10−5 | 1.6 × 10−6 | 9.6 × 10−6 | 1.9 × 10−5 | 6.3 × 10−4 | |
| NO2− (M) | 1.2 × 10−6 | 1.5 × 10−7 | 1.4 × 10−6 | 3.7 × 10−7 | ||
| HCO3− (M) | 4.0 × 10−4 | 1.1 × 10−3 | 3.6 × 10−3 | 2.4 × 10−5 | 2.2 × 10−3 | |
| CO32− (M) | 1.1 × 10−6 | 6.1 × 10−6 | 4.8 × 10−5 | 2.4 × 10−9 | 3.7 × 10−5 | |
| d (m) | 7.7 | 5.9 | 19.5 | 2.0 | 3 | |
| V (L) | 9.7 | 7.4 | 24.6 | 2.5 | 4 | |
| PaDOM (einstein s−1) | 3.2 × 10−7 | 2.5 × 10−7 | 3.2 × 10−7 | 2.2 × 10−7 | 2.6 × 10−7 | |
| ROHtot (mol s−1) | (4.1 ± 0.5) × 10−11 | (2.4 ± 0.2) × 10−11 | (8.4 ± 0.4) × 10−11 | (3.5 ± 0.3) × 10−11 | (1.5 ± 0.1) × 10−10 | |
| RCO3− (OH) (mol s−1) | (5.8 ± 0.7) × 10−13 | (1.0 ± 0.1) × 10−12 | (1.3 ± 0.1) × 10−11 | (2.0 ± 0.2) × 10−13 | (2.1 ± 0.2) × 10−11 | |
| RCO3− (DOM) (mol s−1) | 2.3 × 10−15 | 1.0 × 10−14 | 1.0 × 10−13 | 3.4 × 10−18 | 6.2 × 10−14 | |
| RCO3−tot (mol s−1) | (5.8 ± 0.7) × 10−13 | (1.0 ± 0.1) × 10−12 | (1.3 ± 0.1) × 10−11 | (2.0 ± 0.2) × 10−13 | (2.1 ± 0.2) × 10−11 | |
| (ΣikSi [Si]) OH (s−1) | 2.7 × 105 | 2.8 × 105 | 3.2 × 105 | 3.5 × 104 | 2.4 × 105 | |
| Diuron | (t1/2P,CO3−)SSD | (2.1 ± 0.3) × 104 | (9.7 ± 1.0) × 103 | (2.3 ± 0.1) × 103 | (1.9 ± 0.2)·103 | (1.9 ± 0.2)·102 |
| (t1/2P,OH)SSD | (2.5 ± 0.3) × 102 | (3.4 ± 0.3) × 102 | (3.6 ± 0.2) × 102 | 9.7 ± 1.0 | 25 ± 2 | |
| Atrazine | (t1/2P,CO3−)SSD | (4.1 ± 0.5) × 104 | (1.9 ± 0.2) × 104 | (4.6 ± 0.2) × 103 | (3.8 ± 0.4) × 103 | (3.9 ± 0.4) × 102 |
| (t1/2P,OH)SSD | (4.1 ± 0.5) × 102 | (5.6 ± 0.5) × 102 | (6.1 ± 0.3) × 102 | 16 ± 2 | 41 ± 4 | |
| Aniline | (t1/2P,CO3−)SSD | (3.3 ± 0.4) × 102 | (1.6 ± 0.2) × 102 | 37 ± 2 | 31 ± 3 | 3.1 ± 0.3 |
| (t1/2P,OH)SSD | 89 ± 11 | (1.2 ± 0.1) × 102 | (1.3 ± 0.1) × 102 | 3.5 ± 0.3 | 8.9 ± 0.9 | |
| Phenolate | (t1/2P,CO3−)SSD | (6.6 ± 0.8) × 102 | (3.1 ± 0.3) × 102 | 73 ± 3 | 61 ± 6 | 6.2 ± 0.6 |
| (t1/2P,OH)SSD | (1.3 ± 0.2) × 102 | (1.7 ± 0.2) × 102 | (1.9 ± 0.1) × 102 | 5.1 ± 0.5 | 13 ± 1 | |
| 4-Hydroxybenzoate | (t1/2P,CO3−)SSD | (1.7 ± 0.2) × 103 | (7.8 ± 0.8) × 102 | (1.8 ± 0.1) × 102 | (1.5 ± 0.2) × 102 | 16 ± 2 |
| (t1/2P,OH)SSD | (1.5 ± 0.2) × 102 | (2.0 ± 0.2) × 102 | (2.1 ± 0.1) × 102 | 5.7 ± 0.6 | 15 ± 1 |
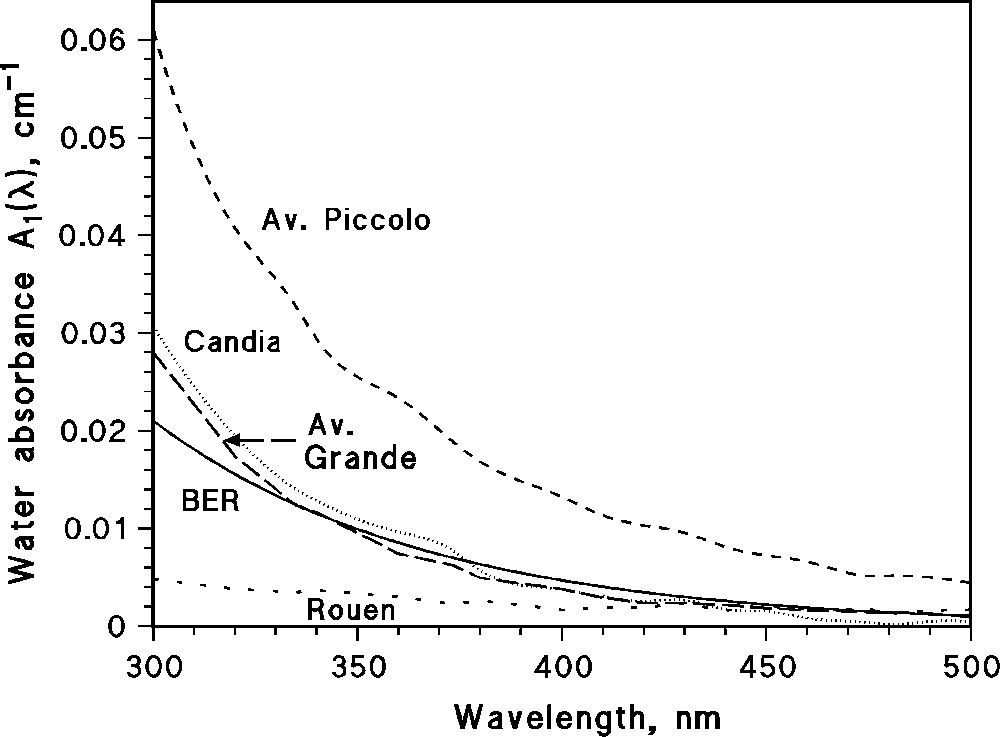
Absorption spectra of the surface water samples, the data of which are reported in Table 1. In the case of the Blue Earth River (BER) the spectrum (not available) was simulated according to Eq. (5).
2.2 Production of CO3− from 3DOM*
Canonica et al. [17] have quantified the generation rate of the carbonate radical from irradiated DOM and CO32− in the surface layer (1 m) of Lake Greifensee (Switzerland, 47°N). In the presence of NPOC = 3.5 mg C L−1 and [CO32−] = 1 × 10−5 M [24] one gets that the volumetric rate of formation of CO3− by irradiated DOM is RCO3− (DOM) V−1 = 1 × 10−14 M s−1 under noon summertime irradiation conditions [17]. With S = 1.26 × 10−3 m2 and d = 100 cm one gets V = Sd = 1.26 L, and RCO3− (DOM) ≈ 1.3 × 10−14 mol s−1 as a consequence. Under noon summertime irradiation the UV irradiance of sunlight would be around 30 W m−2 [25], namely 1.4 times more intense than our model conditions. It is possible to model the absorption spectrum of the Greifensee water by means of Eq. (5) and the reported NPOC value. From these data one gets that the photon flux absorbed by DOM is in the first meter of Lake Greifensee, where d = 100 cm and qn,p(λ)0 is the incident photon flux of sunlight, in einstein s−1 over the surface S = 1.26 × 10−3 m2 [22]. It is reasonable to hypothesise that RCO3− (DOM) = 1.3 × 10−14 mol s−1 is proportional to the product of PaDOM times [CO32−], from which one gets:
| (7) |
The dependence of Eq. (7) on the irradiation intensity is taken into account in PaDOM, which is also reported in Table 1 for the samples under consideration. The total formation rate of CO3− in a water system would be RCO3−tot = RCO3− (OH) + RCO3− (DOM). It can be observed that RCO3− (OH) ≫ RCO3− (DOM) in all the cases (Table 1). It is also RCO3−tot < ROHtot, and the ratio ROHtot (RCO3−tot )−1 varies in the range from 6 to 175. However, once CO3− is formed it is scavenged by DOM to a lesser extent compared with OH, and the reactivity of CO3−could therefore be significant.
Also note that the formation rate of CO3− in the systems under consideration might be higher in the case that the Fe(III) species were a significant source of the carbonate radical upon photo-oxidation of CO32− [18]. However, the exact quantification of the Fe(III) contribution to CO3− will require further studies, and for the moment that possible source will not be considered.
3 Modelling the reactivity of CO3− in surface waters
The carbonate radical reaches a steady-state concentration in surface waters [17], which implies that the rate of formation RCO3−tot is equal to that of consumption of CO3−, by DOM as the expected main scavenger (reaction (4)) and by the pollutant(s) that can be present in the system. Be P a pollutant molecule at molar concentration [P]0, with rate constant kP,CO3− with CO3− (in M−1 s−1). The scavenging rate constant for CO3− in the system would be ΣikSi [Si] = k4NPOC + kP,CO3− [P]0. In many cases kP,CO3− [P]0 ≪ k4 NPOC, and the value of ΣikSi [Si] would be independent of [P]0. In the most general case the degradation rate of P due to the carbonate radical (R′P,CO3−, in M s−1) will be (note that V = Sd, and that RCO3−tot should be divided by V to have it in M s−1):
| (8) |
Among the natural scavengers, low-molecular weight carboxylic acids (LMWAs) are expected to play an important role [26]. The most common LMWA is formate, which can reach μM levels in surface waters [27] and is for instance the main OH scavenger among LMWA in cloud water [28]. Given the reaction rate constants of formate with OH (3.2 × 109 M−1 s−1 [16]) and CO3− (1.5 × 105 M−1 s−1 [19]), in the presence of 1 mg C L−1 NPOC one can expect that 1 μM formate would account for about 5–10% of the OH scavenging by DOM, and for less than 0.5% of the scavenging of CO3−. The integration of Eq. (8) between [P]0 and 1/2 [P]0, and between 0 and t1/2 yields the following result for the half-life time of P (in seconds if V is in litres):
| (9) |
Indeed if kP,CO3− [P]0 ≪ k4 NPOC, the value of t1/2P,CO3− would be independent of [P]0. The result of Eq. (9) is valid for continuous irradiation under 22 W m−2 sunlight UV irradiance. However, the intensity of sunlight is not constant. It has been observed that the energy emitted by constant irradiation for 10 h at 22 W m−2 UV irradiance is equivalent to that reaching the ground on a summer sunny day (15 July) at 45°N latitude [29]. It is, therefore, possible to obtain t1/2P,CO3− in summer sunny day (SSD) equivalents by dividing its value in seconds by 10 h = 3.6 × 104 s.
| (10) |
The reported model was applied to five substrates (diuron, atrazine, aniline, phenolate, 4-hydroxybenzoate), for which the reaction rate constants with the carbonate radical are known and reported in Table 2. Table 2 also reports the rate constants for the reaction with OH, and it is interesting to observe that the ratio kP,OH (kP,CO3−)−1 varies from 800 for the least reactive compound (atrazine) to 28 for the most reactive one (aniline).
Comparison between our model, applied to the first meter of the Lake Greifensee (Switzerland), and the data derived from Ref. [17]. In the column of our model it was adopted 22 W m−2 sunlight UV irradiance, and 30 W m−2 in that of Ref. [17]. In the latter case the half-life time (in SSD) was calculated as: t1/2 = 0.693 (2.6 × 104 kP,CO3− [CO3−])−1. The conversion factor compensates for the different irradiation intensities. For our model it was adopted eq.(10). The value of [CO3−] was derived from the literature estimate of RCO3−tot V−1 [17], and from the rate of scavenging of the carbonate radical by DOM (reaction (4)). Only the entries required by each model have been inserted as data in the table. The main difference between our model and the approach of Ref. [17] is that in the latter case the contribution of nitrate only to OH photoproduction has been taken into account [17,24]. By doing the same with our model one obtains the t1/2 data reported in brackets. The table also reports the reaction rate constants of five organic compounds with the radicals CO3− and OH, together with the corresponding literature references.
| Lake Greifensee ([17], [25]) | Present model | Ref. [17] | |
| NPOC (mg C L−1) | 3.5 | 3.5 | |
| NO3− (M) | 1 × 10−4 | 1 × 10−4 | |
| HCO3− (M) | 2 × 10−3 | 2 × 10−3 | |
| CO32− (M) | 1 × 10−5 | 1 × 10−5 | |
| d (m) | 1 | 1 | |
| V (L) | 1.26 | ||
| PaDOM (einstein s−1) | 1.5 × 10−7 | ||
| ROHtot (mol s−1) | 2.7 × 10−11 (1.6 × 10−11) | ||
| RCO3−(OH) (mol s−1) | 3.3 × 10−12 | ||
| RCO3−(DOM) (mol s−1) | 1.0 × 10−14 | ||
| RCO3−tot (mol s−1) | 2.8 × 10−12 (1.7 × 10−12) | ||
| RCO3−tot V−1 (M s−1) | 2 × 10−12 | ||
| (ΣikSi [Si]) OH (s−1) | 2 × 105 | ||
| [CO3−], M | 6 × 10−15 | ||
| Diuron, (t1/2P,CO3−)SSD | kP,CO3− = 8 × 106 M−1 s−1 [17] kP,OH = 5 × 109 M−1 s−1 [30] | 300 (500) | 560 |
| Atrazine, (t1/2P,CO3−)SSD | kP,CO3− = 4 × 106 M−1 s−1 [17] kP,OH = 3 × 109 M−1 s−1 [31] | 600 (980) | 1100 |
| Aniline, (t1/2P,CO3−)SSD | kP,CO3− = 5 × 108 M−1 s−1 [19] kP,OH = 1.4 × 1010 M−1 s−1 [16] | 4.8 (8.0) | 8 |
| Phenolate, (t1/2P,CO3−)SSD | kP,CO3− = 2.5 × 108 M−1 s−1 [19] kP,OH = 9.6·109 M−1 s−1 [16] | 9.7 (16) | 18 |
| 4-Hydroxybenzoate, (t1/2P,CO3−)SSD | kP,CO3− = 1 × 108 M−1 s−1 [19] kP,OH = 8.5 × 109 M−1 s−1 [16] | 25 (41) | 42 |
The data of (t1/2P,CO3−)SSD for the five substrates, relevant to the different water bodies, are reported in Table 1, with [P]0 = 1 × 10−9 M for each substrate. The half-life times (in summer sunny day equivalents) due to reaction with the carbonate radical would vary from 3 days for aniline in the Blue Earth River, to 4 × 104 days for atrazine in Lake Avigliana Piccolo.
The results for the carbonate radical are compared with those of a corresponding model for OH, for which the half-life time of P in SSD equivalents is given by:
| (11) |
Table 1 reports the OH scavenging rate constant (ΣikSi [Si])OH for the surface water bodies under consideration [22], and the values of (t1/2P,OH)SSD calculated with Eq. (11) and [P]0 = 1 × 10−9 M. Also, in this case, a wide variability is estimated (from 3 to 600 days), albeit lower than for the case of CO3−. The comparison between (t1/2P,CO3−)SSD and (t1/2P,OH)SSD for the same substrate and the same aquatic system indicates that the hydroxyl radical would be more important as reactive species for degradation in 20 cases out of 25. In the other cases the carbonate radical would account for a higher reactivity and, what is most important, they are all cases in which photochemistry is expected to be a significant removal pathway. Actually, a half-life time in the 103–104 day range means that the relevant pathway(s) would play a negligible role in the degradation of the substrate, other routes being more important. Indeed, out of the 11 cases in which at least one of the two t1/2 values (relative to CO3− and/or OH) is lower than 100 days, therefore, pointing to a significant radical reactivity, in 5 of these the carbonate radical is a more important reactive species than OH.
Very interestingly, for CO3− to prevail over OH as reactive species, the combination of a water body rich of carbonate/bicarbonate (as Lake Avigliana Grande and the Blue Earth River in the present case) and an easily oxidisable substrate is required, which would be significantly reactive toward both CO3− and OH (e.g. atrazine, phenolate, 4-hydroxybenzoate).
4 Conclusions
The model that was developed for the reactivity of the carbonate radical toward target compounds in surface waters shows that the chemistry of CO3−, compared to that of OH, can be in some cases in which the radical reactions would be expected to play a significant role. For CO3− to play an important role one needs a carbonate-rich water and a reactive substrate. The application of the model to the reactivity of both OH and CO3− would be of great help in the assessment of the exposure of aquatic ecosystems and human communities to water-dissolved pollutants. Note that the actual lifetimes in water bodies could be significantly lower because of the presence of additional transformation pathways, including reaction with 3DOM*.
Table 2 reports a comparison between our model and the approach adopted in Ref. [17] to account for the production of CO3− in the first meter of Lake Greifensee (Switzerland). The main difference between our model and the calculations of Ref. [17] is that, in the latter case, nitrate was considered to be the only source of OH. According to our model nitrate would account for 60% of the OH generation in that system, the remainder being attributable to DOM. If one considers nitrate as the sole source of OH in our model also, the results (in brackets, Table 2) for the calculated half-life times of diuron, atrazine, aniline, phenolate and 4-hydroxybenzoate are in very reasonable agreement with those derived from the literature data of RCO3− V−1 [17].
Acknowledgements
Financial support from PNRA – Progetto Antartide, Università di Torino – Ricerca Locale and INCA (WG GLOB-CHEM) is kindly appreciated.


