1 Introduction
Polyoxometalates (POM) have the general formula [XxMmOy]q–, where X is typically a main-group element and M is usually molybdenum or tungsten; partial substitution of M with other transition metals, organic or organometallic groups leads to a huge variety of structures [1–3]. Owing to their polyanionic nature, the solubility of POM's can be tuned by selecting a suitable counter-cation, so that aqueous, organic and alternative media are viable as solvents [4]. For these reasons, the solution chemistry of POMs has wide implications for homogeneous catalysis, materials science and medicinal chemistry [2,3].
NMR of the 183W nucleus (I = 1/2, 14% natural abundance) is an essential tool for the characterization of polyoxotungstates, since 183W of chemical shifts are sensitive to structure, solvent and counterion [5,6]. However, its application is hampered by its very low sensitivity (γ = 1.128 × 107 rad s−1 T−1; ν0 = 16.6 MHz in a 9.4–T instrument). Moreover, these spectra often consist only of singlets, possibly with satellites owing to vicinal 2JWOW couplings, and their assignment is often problematic [7,8]. There is, therefore, a genuine need for tools to assign such spectra, even under unfavorable conditions and without recourse to empirical arguments. Such an avenue of investigation is offered by calculations by first-principles methods; the current state-of-the-art in computational modelling of POMs has been summarized by Poblet and his group [9]. More specifically, the prediction of NMR properties by density functional theory methods (DFT) has made rapid progress in recent years [10]. Most significantly, computational NMR of heavy-atom nuclei [11,12] has benefitted from the implementation of efficient DFT codes incorporating relativistic corrections by means of the Zero-Order Regular Approximation (ZORA) [13–19]. The main properties (chemical shift and coupling constants) of many such nuclei, including 183W, can now be predicted to an accuracy usable for spectral assignment [20–23].
Previous work [22] concerned an extensive validation and methodological study of polyoxotungstates having a well defined structure, which are briefly summarized here.
Application to 183W NMR of polyoxotungstates presents difficulties because tungsten atoms in POMs lie in very similar environments (WO6 octahedra), and their chemical shifts accordingly span only 500 ppm at most, and often much less; signals separated by 1–2 ppm are common. However, we have previously shown that a fair degree of accuracy can be attained (a mean absolute error of ca. 35 ppm), provided that one of the most prominent effects that influence the 183W shifts of POMs, i.e. solvation, is adequately accounted for through continuum-solvent calculations [22]. Further developments and improvements in the modeling of POM NMR have been recently presented [24,25].
In this framework, we previously examined a small series of POM chemical shifts by ZORA scalar methods with frozen-core basis sets, obtaining a fairly good correlation with experiment, and pointed out counterion effects for lacunary POMs [20]. Analogous findings were experimentally [26] and theoretically [24,27] reported. All these observations consistently point out that solvation effects and level of relativistic treatment play an important role.
The problem we try to address here is the counterion effect on the spectra of the lacunary Keggin POM [PW11O39]7–, whose general structure and numbering are displayed in Fig. 1.
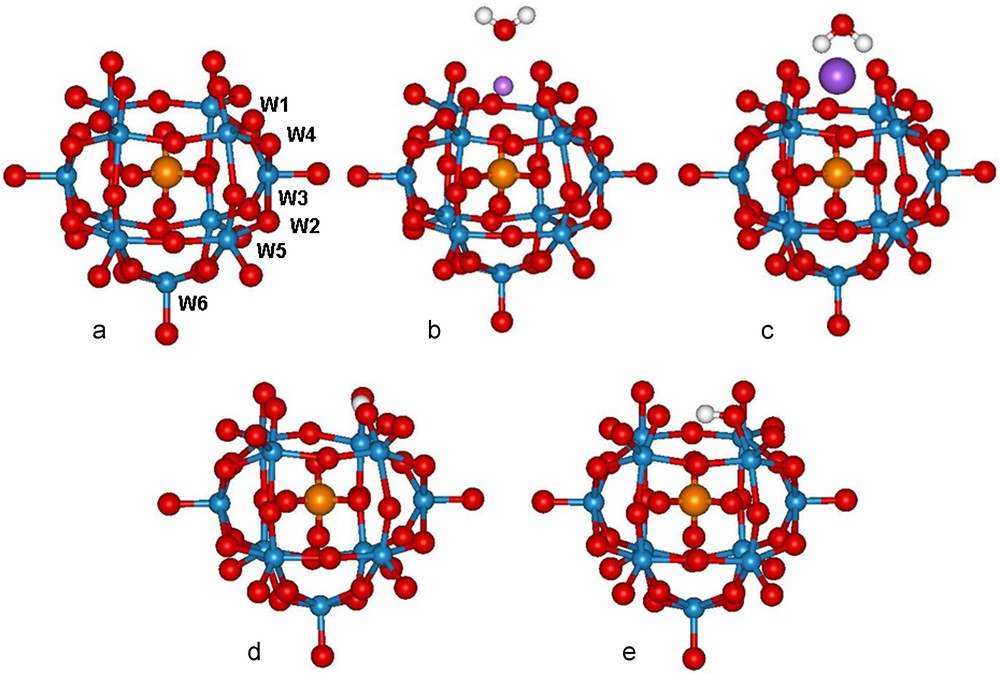
Structure and numbering of a: [PW11O39]7–; b: Li(H2O)[PW11O39]6–; c: Na(H2O)[PW11O39]6–; d: [PW11O39H]6–, protonated on O(W1) (e): [PW11O39H]6–, protonated on O(W4). COSMO-BP86-ZSC/TZP geometry. W blue, O red, P orange, H grey, Li purple, Na dark purple.
It has been known for a long time that its water-soluble salts with Li+ or Na+ as counterions exhibit significantly different spectra, with most signals rearranged in their ordering, the only pivot line being that of the W6 signal, characterized by half intensity (Table 1). Such spectra have been assigned by means of time-consuming 2D homonuclear correlation NMR [7,26] and it is of course of interest to understand such spectra in an independent way. The aim of such an understanding lies not only in the capability to predict the spectra but, even more importantly, in understanding their solution structure with regard to cation-anion association etc.
Experimental 183W NMR chemical shifts (ppm) for Li and Na salts of [PW11O39]7– in watera.
| Signal | Li+ | Na+ | ||
| δ | δ rel. W6b | δ | δ rel. W6b | |
| W1 | –99 | 23.1 | –110.7 | 7.9 |
| W2 | –152.3 | –30.2 | –154.8 | –36.2 |
| W3 | –133.2 | –11.1 | –134.0 | –15.4 |
| W4 | –99.7 | 22.4 | –103.9 | 14.7 |
| W5 | –104.3 | 17.8 | –99.0 | 19.6 |
| W6 | –122.1 | 0.0 | –118.6 | 0.0 |
a Experimental data from ref. [19].
b Internally referenced to the W6 signal.
Thus, we have carried out relativistic DFT calculations on [PW11O39]7– and models of its solution structure (ion pairs with Li and Na ions and protonated forms).
2 Computational details
All calculations have been carried out using DFT as implemented in the Amsterdam Density Functional (ADF) code [13]. Drawing on our previous results, [22] calculations in this work utilized a triple-zeta quality, singly polarized Slater basis set (TZP) for all atoms. Relativistic effects were taken into account by means of the two-component ZORA method [10b,14,17,28] including either only scalar effects (ZSC) or spin-orbit coupling as well (ZSO). The BP86 functional [29] was adopted.
Geometry optimization was performed at the ZSC level under the appropriate symmetry constraints. Single-point calculations were carried out at the ZSO level at the corresponding ZSC geometries.
The solvent effect was modeled by means of the ADF implementation [30] of the COSMO method [31]. Atomic radii (in Å) were set at the values (H: 1.8135; Li: 2.1294: O: 1.7784; Na: 2.6559; P: 2.106; W: 2.0) ([13], recommended radii from [32], for consistency with our previous studies [22]).
Nuclear shieldings were computed with the ADF nmr property module [13,14] from the ZSO density. The perturbed Kohn-Sham orbitals were determined at the ZORA level including spin-orbit coupling operators (“U1 K best” option in ADF) [13,17]. The isotropic shielding constant σ is given by the sum of dia-, para-magnetic and spin-orbit contributions (σ = σd + σp + σSO). Computed chemical shifts are then determined by difference with the shielding of a reference standard (for which δ = 0) as δ = σref –σ. Notice that, even though the accepted standard of experimental 183W NMR is aqueous WO42–, [5] we will mostly report chemical shifts internally referenced to the signal of W6, since it can be independently assigned and provides a natural reference for the problem, also avoiding calibration issues.
3 Results and discussion
3.1 Naked anion
The six symmetry-unique 183W chemical shifts of Li and Na salts are spread over a limited range of ca. 50 ppm [7,20]. In both cases, W2, W3 and W6 are the most shielded and appear in the order W2 < W3 < W6. The remaining three signals are scrambled according to the counterion.
Optimized geometries of [PW11O39]7– and associated ion pairs are reported in Fig. 1; results are collected in Table 2. A first approximation to the solution structure (and NMR) of [PW11O39]7– is of course represented by the “naked” anion itself. Three situations were considered: gas-phase geometry and NMR; gas-phase geometry and solution NMR; solution geometry and NMR. Fig. 2 displays the results where calculated shifts are plotted against experimental shifts of the Li and Na salt.
Calculated energies (au) and 183W NMR chemical shifts (ppm) for Li and Na salts of [PW11O39]7–, ion pairs and protonated formsa.
| δ (g) | δ (aq) | δ (aq geo) | |
| [PW11O39]7– | –243.261654 | –245.28869795 | –245.299592 |
| W1 | –30.9 | –44.8 | –43.7 |
| W2 | –88.3 | –89.0 | –59.4 |
| W3 | –13.0 | –12.9 | –9.1 |
| W4 | –17.1 | –26.9 | –7.9 |
| W5 | –10.9 | –12.3 | 3.5 |
| W6 | 0.0 | 0.0 | 0.0 |
| (H2O)Li[PW11O39]6– | –244.42849667 | –245.908855 | –245.912388 |
| W1 | 22.3 | 20.7 | 28.6 |
| W2 | –38.2 | –37.2 | –31.3 |
| W3 | –0.05 | 1.6 | 1.3 |
| W4 | 45.1 | 44.5 | 42.6 |
| W5 | –2.0 | –0.2 | 6.7 |
| W6 | 0.0 | 0.0 | 0.0 |
| (H2O)Na[PW11O39]6– | –244.394399 | –245.869000 | –245.872720 |
| W1 | 16.4 | 19.4 | 25.1 |
| W2 | –43.0 | –41.3 | –34.9 |
| W3 | –1.3 | 1.6 | 3.6 |
| W4 | 53.4 | 54.2 | 49.1 |
| W5 | –7.1 | –4.7 | 7.1 |
| W6 | 0.0 | 0.0 | 0.0 |
| [PW11O39H]6– (OW1) | –243.841712 | –245.339876 | –245.344377 |
| W1 | 47.8 | 40.2 | 33.3 |
| W2 | –8.4 | –8.9 | –8.3 |
| W3 | 19.1 | 18.7 | 14.9 |
| W4 | –0.9 | –5.8 | –2.2 |
| W5 | 45.7 | 31.4 | 33.5 |
| W6 | 0.0 | 0.0 | 0.0 |
| [PW11O39H]6– (OW4) | –243.841425 | –245.337776 | –245.342002 |
| W1 | –42.5 | –54.9 | –46.7 |
| W2 | –81.8 | –82.3 | –71.0 |
| W3 | –17.0 | –15.8 | –23.0 |
| W4 | 63.6 | 60.5 | 46.8 |
| W5 | –22.3 | –22.1 | –20.0 |
| W6 | 0.0 | 0.0 | 0.0 |
a Chemical shifts calculated at the BP86-ZSO/TZP level, with COSMO solvation where indicated, and are internally referenced to the W6 signal. Left to right: chemical shifts calculated with gas-phase geometry and NMR; gas-phase geometry and solution NMR; solution geometry and NMR.
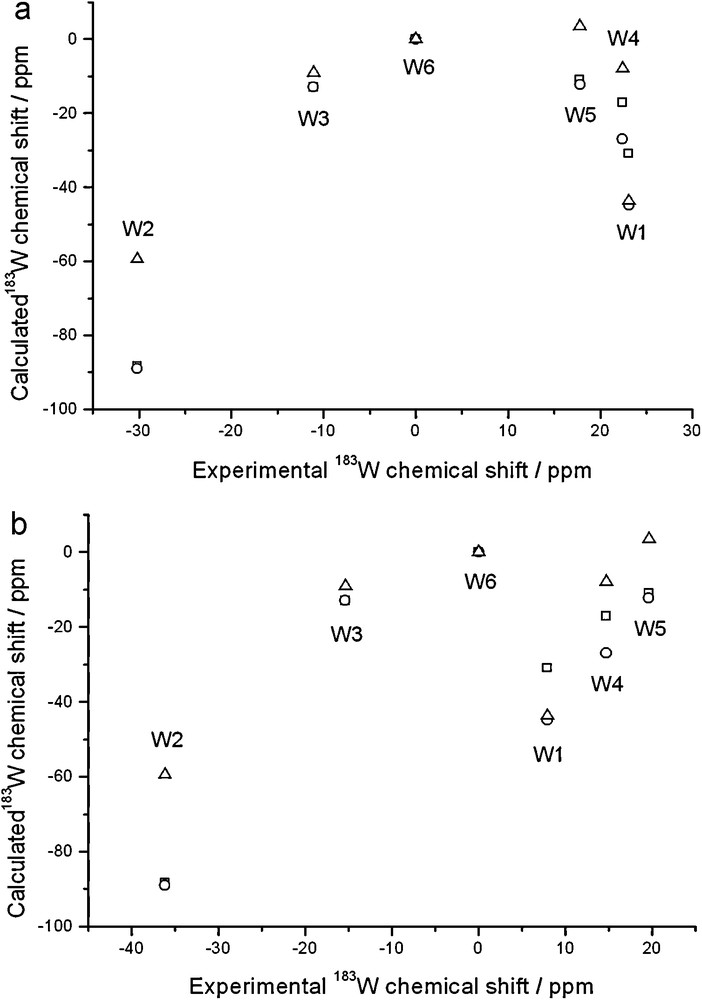
Calculated 183W chemical shifts of [PW11O39]7– plotted against experimental shifts of the Li (a, top panel) and Na (b, bottom panel) salts; ZSO-BP86/TZP calculations with COSMO solvation model where specified. Shifts are relative to W6. Gas-phase geometry and NMR (squares); gas-phase geometry and solution NMR (circles); solution geometry and NMR (triangles).
It is immediately apparent that in no case the signals are predicted in the correct order, and the most shielded signal (W2), which lies at ca. –30 ppm from W6, is predicted at ca. –90 ppm. Therefore, the naked anion is not a good model of the solution structure, even if non-specific solvent effects are taken into account.
3.2 Ion pairs
As a further step, we considered one counterion inserted into the POM lacuna. In a previous work, we had considered a simple model consisting just of a Li+ cation, and such a model fared somewhat better; [20] herein, we build on those results, extending the system to one in which the alkali metal ion is also solvated by one explicit water molecule (Fig. 1). One should keep in mind, however, that according to 7Li and 23Na NMR data the free aqueous and ion-paired cations must be under the fast exchange regime; [7,26], hence no stable ion pair can be invoked to understand the spectra. Similar models have been utilized by Vankova et al. for ion pairs of γ-[SiW10O36]8– [24]. Indeed, the need for inclusion of explicit solvent molecules was found to be necessary in the prediction of 195Pt chemical shifts [33].
The calculated structures of the Li and Na ion pairs are different (Fig. 1). The Li salt maintains a straightforward arrangement, the Li+ cation being solvated by the four oxygens of the lacuna and the water oxygen, whereas the Na salt features (upon optimization) the water molecule displaced toward the front end of the lacuna, its hydrogens pointing towards the W4 oxygens. Apparently, this arrangement reflects the smaller hydration energy of Na+ compared to Li+. The results for the Li salt are shown in Fig. 3.
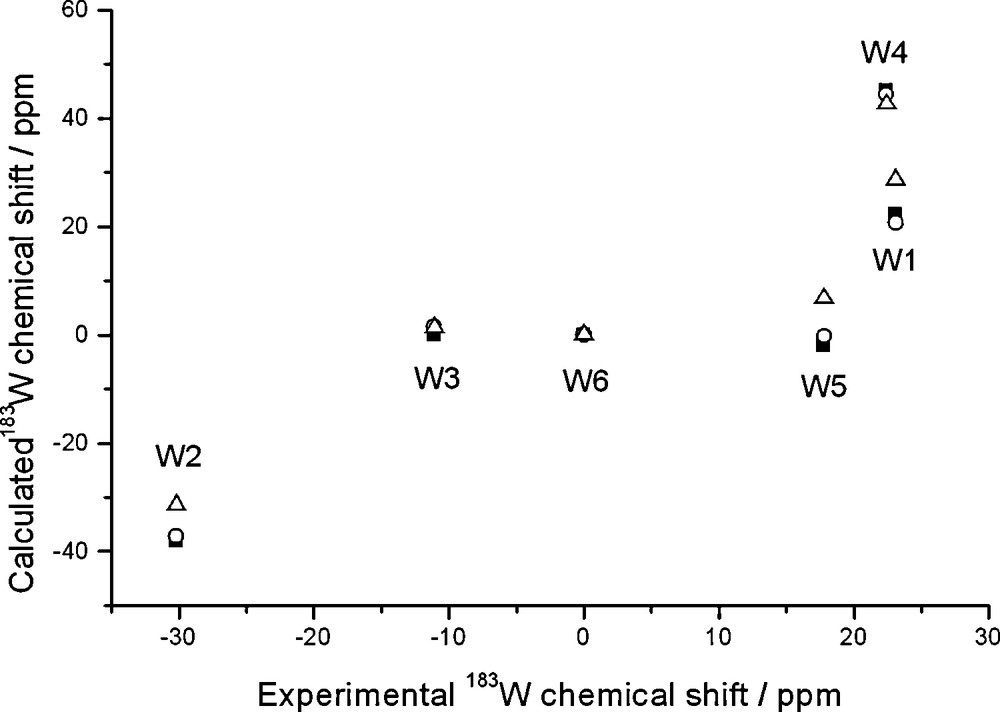
Calculated and experimental 183W chemical shifts of Li(H2O)[PW11O39]6– plotted against experimental shifts of the Li salt; ZSO-BP86/TZP calculations with COSMO solvation model where specified. Shifts are relative to W6. Gas-phase geometry and NMR (squares); gas-phase geometry and solution NMR (circles); solution geometry and NMR (triangles).
The inclusion of Li+ can be seen to be beneficial, in that at least the range of calculated tungsten shifts better matches the experimental one. In particular, the W1 and W4 signals (belonging to the lacuna) become much deshielded and their chemical shifts reach the positive region. However, their shifts (differing by just 1 ppm) are predicted in reverse order; most signals are predicted in essentially correct order even though relative spacings are not quite so. Hence, the accuracy of the current computational protocol is not sufficient to sort out such closely spaced signals.
The corresponding results for the Na ion pair are in Fig. 4.
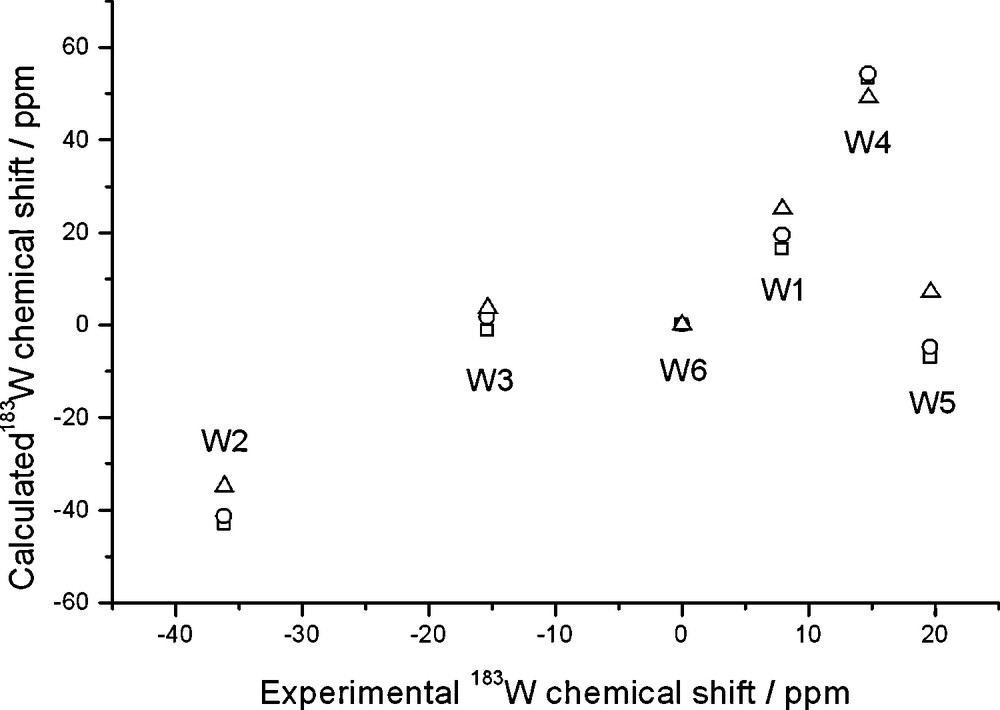
Calculated and experimental 183W chemical shifts of Na(H2O)[PW11O39]6– plotted against experimental shifts of the Na salt; ZSO-BP86/TZP calculations with COSMO solvation model where specified. Shifts are relative to W6. Gas-phase geometry and NMR (squares); gas-phase geometry and solution NMR (circles); solution geometry and NMR (triangles).
Also in this case, explicit inclusion of the solvated counterion is beneficial, in that it brings calculated shifts into the correct range. However, a much larger scatter is apparent, W3 and W5 strongly deviating from any correlation.
A preliminary conclusion would then be that the solution structure of the Li salt loosely resembles that of the ion pair depicted in Fig. 1b, whereas that of the Na salt seems more complex. This is not too surprising, in view of the smaller size of Li+ than of Na+, whereby the former may fit better into the lacuna, whereas in the Na case the interaction with the lacuna is weaker and donation of a hydrogen bond by the water molecule to the lacuna competes. Nevertheless, it is clear that such models are still far from a realistic view (the POM is assumed to be present only as ion pair) and, most importantly, from a reliable prediction of NMR spectra.
3.3 Protonated forms
A further step towards a realistic modeling of this lacunary POM can be taken considering the effect of protonation of the POM cage upon NMR spectra. POMs have multiple protonation sites, terminal oxygens being generally regarded as the most basic [34]. However, the lacuna region is the most reactive nucleophilic site [35], so it makes sense to investigate the effect of proton transfer to lacunary oxygen atoms, i.e. O(W1) and O(W4), keeping in mind that protonation is not complete and may occur also at other oxygen atoms.
Thus, we optimized the structures of [PW11O39H]6– with O(W1) and O(W4) alternatively protonated and computed the relevant 183W chemical shifts. For consistency with the previous calculations, data were collected for the gas-phase isolated structure, gas-phase geometry and solution NMR; solution geometry and NMR. All protonated structures have no symmetry, and therefore the results for each symmetry-unique tungsten atom were averaged under the assumption of fast proton exchange between equivalent sites. Also, no simultaneous ion pairing and protonation was considered. As a consequence, these further calculations should be considered as a framework for interpretation rather than an improved model of this system.
Geometry optimization, starting from structures featuring the O–H bond of the added proton pointing outwards, invariably leads to intramolecularly hydrogen-bonded structures (Fig. 1), which is not surprising in view of the limited stabilization that a continuum solvation model can offer.
The two isomeric protonated forms considered (OW1 and OW4) are slightly different in energy, OW1 being more stable by 0.2 kcal/mol in the gas phase and up to 1.5 kcal/mol in aqueous solution, which is somewhat smaller than analogous differences between terminal and bridging oxygens in non-lacunary POMs [34]. This small energy difference, obtained without zero-point corrections and for geometries which may not fully reflect the arrangement in solution, cannot be used to make reliable predictions on the relative stability of the two protonated forms. Nevertheless, it does qualitatively suggest that OW1 protonation is somewhat more favored; a Boltzmann analysis gives an estimated equilibrium constant K = [OW4]/[OW1] = 0.1. The proton affinity of [PW11O39]7– in water can be calculated (within the rough approximations employed here) as 28 kcal/mol, i.e. a very low value for a polyanion (cfr. ca. 300 kcal/mol for neutral amines [36]). As a consequence, one can hardly invoke a substantial presence of protonated forms.
However, even in the unlikely situation where the OW1-protonated species is the only species present, its shifts would not consistently improve the overall result.
Thus, making the realistic assumption that the observed shift is a weighted average of the free, protonated and ion-paired species, one can make an informed guess on reasonable trends. Thus, a substantially improved agreement with experimental shifts is attained by assuming that [PW11O39]7–, [PW11O39H]6– and M(H2O)[PW11O39]6– account for, respectively, 15%, 35%, 50% (M = Li) or 40%, 35%, 25% (M = Na); (note that in both cases the same amount of protonated form is assumed). These estimates are plotted against experimental values in Fig. 5 (in view of the generally better performance of COSMO geometries, only those were considered). The results are reasonable insofar as they feature a larger contribution of the Li, rather than the Na, ion pair, which seems consistent with the expected weaker interaction of Na+. We emphasize that the above weighting factors are simply reasonable guesses that do not derive from a consideration of themodynamic stabilities (which, as mentioned before, are not available). Therefore, the overall accuracy depends on the choice of several parameters, and these results should only be considered indicative of a trend rather than suggesting the actual composition of the solution. In other words, the data of Fig. 5 should only be taken as pointers to the factors that seem involved in determining the observed shift, and hopefully stimulate further experiments. Thus, one should keep in mind that the species that we considered are themselves simplified models of a system that is probably composed of many solvated, protonated and ion-paired species. Conceivable avenues for improvement would involve explicit consideration of different protonated, ion-paired and hydrated forms, including the possibility that more than one water molecule is included in the lacuna. Probably, a more consistent way to address the solution structure of lacunary POMs will require a full molecular dynamics simulation, as recently done by Poblet and Bo for related systems; [9,37] however, describing proton transfer shall require a quantum dynamics approach [38].
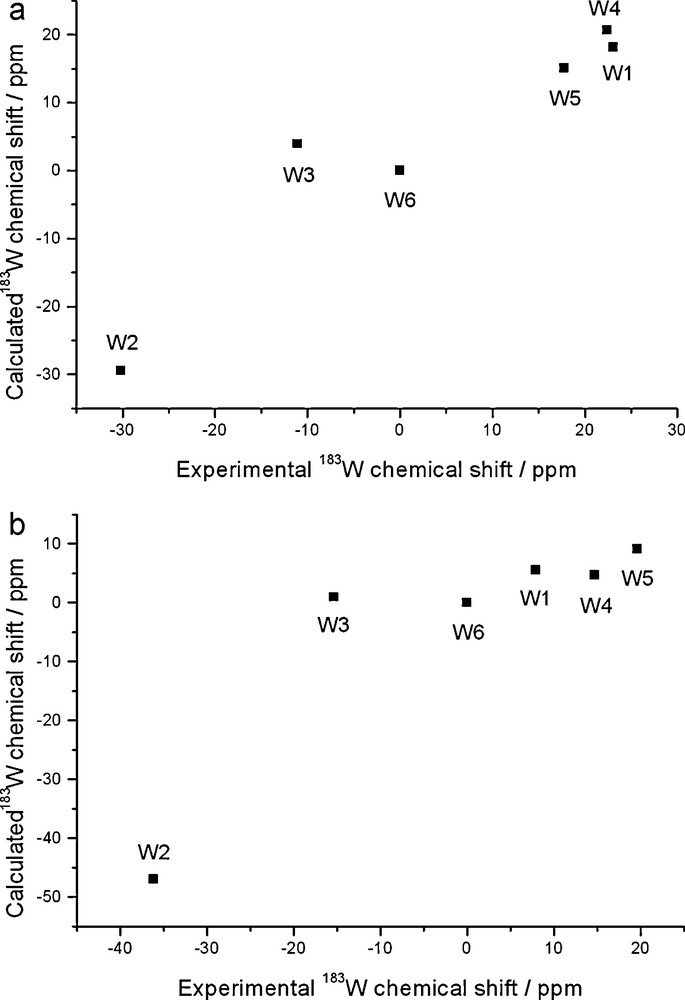
Population-averaged 183W chemical shifts of [PW11O39]7– plotted against experimental shifts of the Li (a, top panel) and Na (b, bottom panel) salts; ZSO-BP86/TZP calculations with COSMO solvation model. Shifts are relative to W6. See text for weighting scheme.
4 Conclusions
Modeling the solution NMR spectra of the lacunary Keggin polyoxometalate is a difficult problem that requires consideration of (besides state-of-the-art relativistic DFT calculations) several weakly bonded species whose structure is not well defined. Nevertheless, understanding such spectra (and especially the differences between two common counterions such as Li and Na) is helpful in allowing to assess the overall quality of our understanding of the solution structure. In this work, we have shown that the isolated anion is not a good model for either salt, regardless of the solvation model adopted. Consideration of a hydrated cation in the lacuna brings some improvement, as does the protonated species; using sensible (but tentative) estimates of the amounts of each species leads to a marked improvement, even though the agreement with experiment is only semi-quantitative.


