1 Introduction
Heteroallenes1,2 [1–10] and especially heterophosphaallenes ECP (E = Si [8], Ge [9,10]) have been the subject of intensive researches during the past 20 years. Due to their two double bonds allowing many types of additions and cycloadditions, heteroallenes present a great interest as powerful building blocks in organometallic and heterocyclic chemistry. By contrast, tin analogues are very difficult to synthesize and no phosphastannaallenes >SnCP– were obtained so far; only the stannaallene Tip2SnCCR2 (Tip = 2,4,6-triisopropylphenyl, CR2 = fluorenylidene) was postulated as intermediate in a reaction leading to a distannirane [11] and the stanna ketenimine R2SnCNR′ is more considered as stannylene–isocyanide complexes >Sn←CN– [7].
The first systematic computational study in the field of heavier group 14 analogues of allene was reported by Apeloig [12]. Ab initio and DFT methods have been used to determine the geometry of heteroallenes of the types ECC and CEC (E = group 14 element). In both cases, the deviations of the skeleton from linearity increase from Si to Pb. The singlet-triplet energy separation was estimated for XCPSi [13] and CPSiX [14] systems by ab initio and DFT calculations as a function of electronegativity of the X atom (X = F, Cl, Br, I). The stability of 1,3-diphospha-2-silaallenes –PSiP– relatively to possible isomers was also investigated through theoretical calculations [15].
The first computational study in the field of phosphagermaallenes refers to the calculations of the relative energies of the dimers of the parent H2GeCPH by restricted HF methods [9]: a small energy difference separates the head-to-head and head-to-tail forms for each pair of dimers. The geometries of all possible isomers of the model compound H2GeCPH were optimized at the B3LYP/6-31G(d,p) level of theory in order to determine the most stable isomers and the main geometrical parameters (GeC, PC bond lengths and GeCP bond angle) [16]. The most stable isomer is, as expected, the phosphaalkyne H3Ge–CP, which is lower in energy by 130.21 kJ/mol than the corresponding allene H2GeCPH. A recent computational study at DFT level explains the [3 + 2] cycloaddition of H2ECPH with HCCH (E = Si, Ge, Sn) by the presence of a heavier group 14 element [17].
Computational data are available for >SiCP– and >GeCP– derivatives, but so far, no extended theoretical studies have been reported in the case of 1-phospha-3-stannaallenes >SnCP–. As there are no examples in the literature of such compounds and in order to determine the right substituents to be successful in their synthesis and stabilization, we undertook a theoretical study to provide an insight on their structure and properties, especially in the case of the tin-carbon double bond within the phosphaallenic unit. We have thus investigated and herein report the results on a series of phosphastannaallenes with the general formula RR′SnCPR (R = H, Me, Ph, R′; R′ = F, Cl, OMe, SiMe3).
2 Results and discussion
2.1 Methods and basis sets
Several computational methods have been employed in this study. Both the BP86 and the B3LYP functionals were tested. Moreover, two different basis sets were considered for the tin atom, the Gaussian 09 [18] built-in LANLDZ [19] and the CRENBL [20] effective potential, both accounting for relativistic effects. High-correlated methods should also be included, although they prove to be time-consuming in the case of vibrational analysis in systems larger than Me2SnCPMe. However, all the model compounds presented in this study have also been optimized at the MP2/CRENBL/6-311+G(d,p) level. All calculations were carried out using the Gaussian 09 program.
Table 1 presents selected geometrical parameters obtained with each method in the case of the 1-phospha-3-stannaallene fully substituted with methyl groups (Scheme 1, color codes for atoms are also given).
Selected geometrical parameters for the Me2SnCPMe derivative.
| Method | SnC1 (pm) | SnC2 (pm) | C1P (pm) | PC3 (pm) | SnC2P (°) | C2SnC1 (°) | C1PC3 (°) |
| BP86/LANL2DZ | 2.00 | 2.17 | 1.69 | 1.96 | 165.4 | 115.5 | 106.4 |
| B3LYP/LANL2DZ | 1.97 | 2.15 | 1.68 | 1.94 | 167.2 | 117.7 | 106.2 |
| B3LYP/CRENBL/ | |||||||
| 6-311+G(d,p) | 2.05 | 2.21 | 1.64 | 1.89 | 159.5 | 115.4 | 108.7 |
| MP2/CRENBL/6-311+G(d,p) | 2.01 | 2.16 | 1.65 | 1.87 | 160.5 | 116.7 | 105.1 |
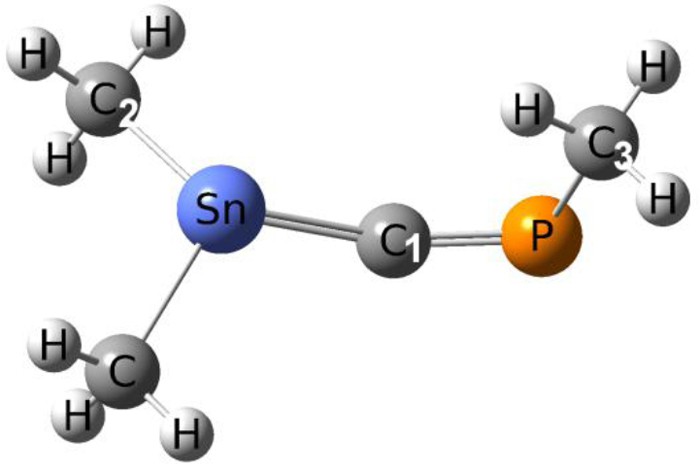
The data for Me2SnCPMe summarizes well the trends obtained for all the other derivatives. The calculated values for the Sn-C distances are close to those obtained experimentally in stannenes >SnC<: around 2 Å for the SnC double bond [21] and between 2.10 and 2.20 Å for the SnC single bond [22]. The B3LYP/LANL2DZ method seems to slightly underestimate the length of the SnC double bond for the models with RMe, but in the case of other substituents (R = H, Ph) the same trend is not observed. The larger basis sets give smaller values for the SnCP bond angle. The geometrical parameters obtained are also in agreement with experimental data for CP bonds [23] and there is a good correlation with the values obtained with all the methods studied. We will discuss further only the optimized structures using B3LYP/6-311+G(d,p)/CRENBL (which are almost identical to those obtained at the BP86 level). All the presented structures were identified as local minimas through frequency calculations.
2.2 Geometry and bond orders of RR′SnCPR and R2SnCPR′ derivatives
It is well known that the –PC< double bond is generally fairly stable with various groups on P and C atoms; thus, it is reasonable to presume that the instability of phosphastannaallenes should be mostly due to the weakness of the SnC double bond; so we particularly studied the influence on the tin–carbon bond order of the substituents at both the tin and phosphorus atoms; however, we also calculated the PC bond order; they have been calculated through an NBO analysis [24] which can also give us an intuitive look at the nature of the bonds and the electronic factors weakening them. The isomers of R2R′PCSn (R = H, Me or Ph; R′ = F, Cl, OMe, SiMe3) derivatives containing the SnCP unit were investigated, by varying the nature and the position of the R′ substituent on Sn or P.
Table 2 presents selected geometrical parameters and calculated Wiberg bond orders [25] for the considered phosphastannaallenes. The computed data for R3PCSn model compounds are also given for comparison.
Selective data for RR′SnCPR and R2SnCPR′, calculated at the B3LYP level.
| Molecule | ΔE (kJ/mol) | SnC (pm) | CP (pm) | SnCP (°) | W BO SnC | W BO CP |
| H2SnCPH | – | 2.06 | 1.64 | 162.7 | 1.37 | 2.09 |
| Me2SnCPMe | – | 2.06 | 1.64 | 159.5 | 1.28 | 2.04 |
| Ph2SnCPPh | – | 2.04 | 1.63 | 161.0 | 1.26 | 1.99 |
| HFSnCPH | 0.00 | 2.12 | 1.64 | 153.9 | 1.17 | 2.13 |
| H2SnCF | 7.26 | 2.01 | 1.62 | 161.0 | 1.34 | 1.99 |
| MeFSnCPMe | 0.00 | 2.10 | 1.63 | 150.6 | 1.14 | 2.09 |
| Me2SnCPF | 6.46 | 2.01 | 1.62 | 155.6 | 1.20 | 2.02 |
| PhFSnCPPh | 0.00 | 2.09 | 1.64 | 151.5 | 1.13 | 2.04 |
| Ph2SnCPF | 8.83 | 2.02 | 1.62 | 149.4 | 1.16 | 2.03 |
| HClSnCPH | 0.00 | 2.10 | 1.64 | 155.2 | 1.20 | 2.12 |
| H2SnCPCl | 14.05 | 2.01 | 1.61 | 164.4 | 1.29 | 2.06 |
| MeClSnCPMe | 0.00 | 2.09 | 1.63 | 152.0 | 1.17 | 2.08 |
| Me2SnCPCl | 12.67 | 2.02 | 1.61 | 160.9 | 1.15 | 2.09 |
| PhClSnCPPh | 0.00 | 2.08 | 1.64 | 153.0 | 1.16 | 2.03 |
| Ph2SnCPCl | 14.82 | 2.02 | 1.61 | 157.8 | 1.10 | 2.11 |
| H(OMe)SnCPH | 0.00 | 2.11 | 1.64 | 151.8 | 1.20 | 2.11 |
| H2SnCPOMe | 1.04 | 2.01 | 1.63 | 157.7 | 1.38 | 1.93 |
| Me(OMe)SnCPMe | 0.16 | 2.09 | 1.64 | 148.7 | 1.16 | 2.08 |
| Me2SnCPOMe | 0.00 | 2.02 | 1.63 | 151.4 | 1.24 | 1.95 |
| Ph(OMe)SnCPPh | 0.00 | 2.08 | 1.64 | 151.4 | 1.14 | 2.02 |
| Ph2SnCPOMe* | 4.52 | 2.02 | 1.63 | 146.3 | 1.21 | 1.96 |
| H(SiMe3)SnCPH | 1.34 | 2.06 | 1.65 | 151.1 | 1.37 | 2.06 |
| H2SnCPSiMe3 | 0.00 | 2.13 | 1.62 | 163.2 | 1.18 | 2.21 |
| Me(SiMe3)SnCPMe | 2.09 | 2.05 | 1.64 | 166.9 | 1.33 | 2.03 |
| Me2SnCPSiMe3 | 0.00 | 2.12 | 1.63 | 161.2 | 1.14 | 2.17 |
| Ph(SiMe3)SnCPPh | 0.00 | 2.04 | 1.64 | 170.1 | 1.31 | 1.97 |
| Ph2SnCPSiMe3 | 2.08 | 2.13 | 1.63 | 159.9 | 1.11 | 2.19 |
As predicted by other computational studies on similar derivatives (like >GeCP– [16] and –AsCP– [26]), the SnCP bond angle is strongly deviated from the ideal linearity of allenic units, even for the model compound H2SnCPH; thus, the steric effect is not a factor to explain this. The NBO analysis shows that this deviation is correlated with the SnC bond order. The most significant second order interaction involves the λ3σ2P lone pair as a donor and the antibonding σ* orbital on the SnC bond, which is present for all the derivatives discussed (Fig. 1).
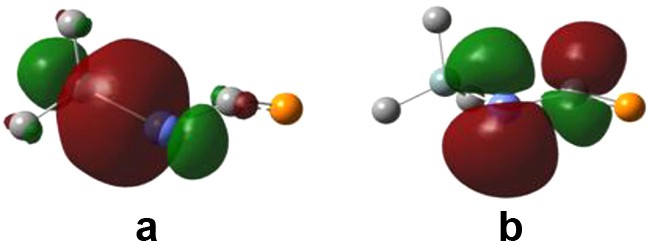
NB orbitals involved in second order perturbation interactions for H2SnCPH: (a) lone pair electrons on P; (b) antibonding non-Lewis orbital on the SnC bond.
A scan of the SnCP bond angle was performed, with a step of 10°, in the range 130°–180° and the value of the stabilization energy afforded by the LPP–σ*SnC interaction was examined. It is obvious (Table 3) that the higher the value of the SnCP bond angle, the stronger the interaction and thus the higher tin–carbon bond order becomes. Assuming that the instability of the phosphastannaallene is mainly due to the lability of this bond, it would be useful to identify a substituent that would allow a linear structure for the phosphaallenic moiety.
Correlation between the SnCP bond angle and SnC parameters.
| SnCP (°) | W BO SnC | W BO CP | SnC (pm) | CP (pm) | E(2)a kJ/mol |
| 130 | 1.34 | 2.04 | 216 | 167 | 60.71 |
| 140 | 1.35 | 2.06 | 209 | 166 | 74.61 |
| 150 | 1.36 | 2.07 | 208 | 165 | 89.01 |
| 160 | 1.37 | 2.09 | 206 | 164 | 102.24 |
| 162b | 1.37 | 2.09 | 206 | 164 | 105.47 |
| 170 | 1.38 | 2.09 | 205 | 164 | 112.88 |
| 178 | 1.39 | 2.09 | 204 | 163 | 117.19 |
a E(2) is the stabilization afforded by the interaction LP on P → BDnnon SnC (kJ/mol).
b Calculated global minimum.
From Table 2, we can conclude that the isomer substituted by an electron-withdrawing group at the phosphorus atom is less stable than that with the same group on the tin atom (for R′ = OMe the difference in energy is insignificant) while the SnC bond order tends to go higher. In the case of the substitution with SiMe3, the position of the group does not influence much the relative stability of the two isomers. However, the calculated Wiberg bond order for the SnC bond is always higher for the R(SiMe3)SnCPR than for the R2SnCPSiMe3 one. We can also note that the PC bond order is always around 2 and generally higher. The main interaction evidenced by NBO analysis contributing to the higher SnC bond order is a charge transfer from the bonding orbital situated along the SiSn bond to the antibonding orbital π* on the SnC bond (Fig. 2). The structure depicted by the natural bond orbital analysis is very close to an allenic Lewis structure H(Me3Si)SnCPH, with the tin valence orbitals participating in double bonding through a sp2 hybridized and an almost pure p orbital. It should be therefore interesting to envisage a silyl-substituted phosphastannaallene as an experimental target.
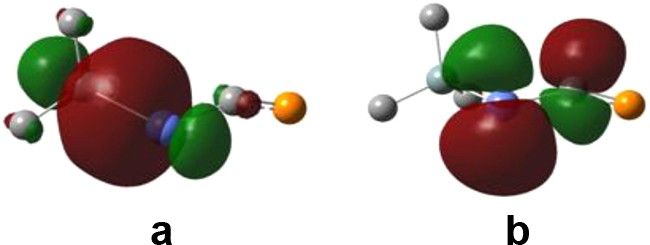
(a) NBO situated along the SiSn bond and (b) antibonding π*orbital on the SnC bond (hydrogen atoms were omitted for clarity).
The main problem encountered in the synthesis of heavy phosphaallenes of the type >ECP (E = Si, Ge, Sn) is the increased reactivity exhibited at the level of the EC bond once the unsaturated compound is formed. The “head-to-head” or “head-to-tail” dimers have been evidenced for both E = Si and Ge [10,11]. In most of the model compounds discussed above, both the HOMO and the LUMO are situated along the SnC bond (Fig. 3), which would favor the formation of the cyclic compounds, even in the absence of other reactive species. Only in Ph2SnCPPh and three other considered phosphastannaallenes bearing phenyl groups, the frontier orbitals are not situated on this bond, but along the PC or PX bond.

Calculated HOMO (a) and LUMO (b) for Me(Me3Si)SnCPMe (hydrogen atoms were omitted for clarity).
Mulliken charges for the atoms in the allenic unit are given in Table 4 for derivatives with R = H. Similar values are calculated for the other model compounds. As expected, the polarity of the SnC bond varies, depending on the nature of the substituent on the tin atom.
Mulliken charges for H2R′SnCP derivatives.
| Molecule | Mulliken atomic charges | ||
| Sn | C | P | |
| H2SnCPH | 0.62 | −0.34 | 0.05 |
| HFSnCPH | 0.84 | −0.32 | 0.09 |
| H2SnCPF | 0.76 | −0.50 | 0.24 |
| HClSnCPH | 0.71 | −0.31 | 0.08 |
| H2SnCPCl | 0.76 | −0.29 | 0.00 |
| H(MeO)SnCPH | 0.81 | −0.36 | 0.06 |
| H2SnCPOMe | 0.71 | −0.53 | 0.23 |
| H(Me3Si)SnCPH | 0.48 | −0.36 | 0.00 |
| H2SnCPSiMe3 | 0.47 | −0.12 | −0.20 |
2.3 Geometry and bond orders of R′2SnCPR and RR′SnCPR′ derivatives
Phosphastannaallenes bearing two R′ groups have also been investigated. Two types of isomers, R′2SnCPR and RR′SnCPR′ have been considered and compared. The results are summarized in Table 5.
Selective data for R′2SnCPR and RR′SnCPR′, calculated at the B3LYP level.
| Molecule | ΔE (kJ/mol) | SnC (Å) | CP (Å) | SnCP (°) | W BO SnC | W BO CP |
| F2SnCPH | 0.00 | 2.23 | 1.64 | 145.4 | 0.93 | 2.22 |
| HFSnCPF | 10.06 | 2.02 | 1.63 | 138.5 | 1.19 | 1.99 |
| F2SnCPMe | 0.00 | 2.19 | 1.63 | 143.6 | 0.94 | 2.21 |
| MeFSnCPF | 6.36 | 2.03 | 1.63 | 136.0 | 1.13 | 2.01 |
| F2SnCPPh | 0.00 | 2.18 | 1.63 | 146.5 | 0.94 | 2.17 |
| PhFSnCPF | 7.81 | 2.03 | 1.63 | 133.2 | 1.10 | 2.02 |
| Cl2SnCPH | 0.00 | 2.19 | 1.64 | 148.7 | 0.99 | 2.19 |
| HClSnCPCl | 16.64 | 2.03 | 1.62 | 150.2 | 1.19 | 2.05 |
| Cl2SnCPMe | 0.00 | 2.16 | 1.63 | 146.8 | 1.00 | 2.17 |
| MeClSnCPCl | 13.26 | 2.04 | 1.62 | 148.7 | 1.12 | 2.07 |
| Cl2SnCPPh | 0.00 | 2.15 | 1.63 | 149.4 | 1.01 | 2.13 |
| PhClSnCPCl | 14.93 | 2.04 | 1.62 | 146.0 | 1.10 | 2.08 |
| (MeO)2SnCPH | 0.00 | 2.17 | 1.65 | 142.3 | 1.03 | 2.15 |
| H(MeO)SnCPOMe | 2.23 | 2.04 | 1.64 | 131.2 | 1.18 | 1.96 |
| (MeO)2SnCPMe | 0.00 | 2.15 | 1.64 | 139.5 | 1.02 | 2.13 |
| Me(MeO)SnCPOMe | 0.77 | 2.05 | 1.64 | 126.1 | 1.11 | 1.99 |
| (MeO)2SnCPPh | 0.00 | 2.14 | 1.64 | 144.1 | 1.03 | 2.09 |
| Ph(MeO)SnCPOMe | 6.08 | 2.03 | 1.65 | 127.0 | 1.24 | 1.90 |
| (SiMe3)2SnCPH | 2.79 | 2.04 | 1.64 | 176.0 | 1.39 | 2.04 |
| H(SiMe3)SnCPSiMe3 | 0.00 | 2.12 | 1.63 | 155.0 | 1.22 | 2.12 |
| (SiMe3)2SnCPMe | 2.09 | 2.04 | 164 | 174.1 | 1.39 | 2.01 |
| Me(SiMe3)SnCPSiMe3 | 0.00 | 2.11 | 1.64 | 153.7 | 1.21 | 2.10 |
| (SiMe3)2SnCPPh | 0.00 | 2.03 | 1.64 | 178.3 | 1.40 | 1.95 |
| Ph(SiMe3)SnCPSiMe3 | 0.90 | 2.11 | 1.64 | 153.7 | 1.19 | 2.11 |
It can be noticed that by placing two electron-withdrawing groups on the tin atom, the bond order drastically drops. For R′ = Cl and OMe, the reason is a charge transfer from bonding orbitals along the SnC bond (both of σ and π symmetry) towards non-Lewis vacant orbitals situated on the SnCl or SnO bond of σ symmetry (see Fig. 4 for an example in the case of Cl2SnCPH). For the RR′SnCPR′ isomers, only one such interaction can exist, as the other electron-withdrawing group is placed on the phosphorus atom, and thus the bond order for SnC is higher than in the case of R′2SnCPR derivatives. Such interactions do not occur in the case of substitution with trimethylsilyl.
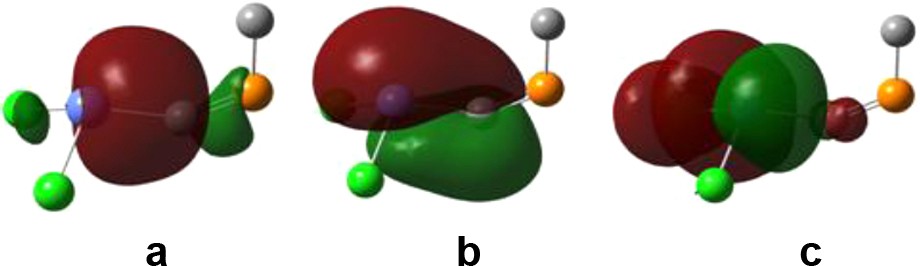
NB orbitals involved in electron-transfer interactions leading to a decrease in the SnC bond order for Cl2SnCPMe: (a, b) occupied bonding orbitals situated on the SnC bond; (c) vacant orbital with antibonding character on the SnCl bond.
In the case of F2SnCPR derivatives, the NBO analysis suggests a structure with a high charge on the tin atom (NPA gives a value of 1.91) and a lone pair on the carbon atom, while the SnF bond is depicted as a donation from F− lone pairs to tin. This is not the case for the RFSnCPF derivatives, where the allenic structure has a more important contribution to the correct description of bonding within the SnCP unit.
From this study, it appears that the trimethylsilyl substituent proves to be the best choice for the stabilization of a phosphastannaallene, as the Wiberg bond order of the SnC bond is the highest calculated for all considered compounds. Moreover, substitution of the phosphorus atom by a phenyl group appears also to be efficient. It can be noticed that the value of the SnCP bond angle also tends to an ideal value of 180°. A similar interaction to that mentioned for the silyl-monosubstituted derivatives R(Me3Si)SnCPR also occurs. As for the R2R′SnCP derivatives, the frontier orbitals of the considered model compounds are situated on the SnC bond, with HOMO displaying a bonding character and the LUMO an antibonding one, with a larger contribution from tin orbitals than the ones from the carbon atom. This is the case even for every phosphastannaallene with R′ = SiMe3; so in order to check the potential of the TMS groups for stabilizing the allenic unit, a preliminary evaluation of the dimerization tendency of such species was performed.
The energies of “head-to-head” and “head-to-tail” dimers of (Me3Si)2SnCPH by the SnC double bond were calculated at the B3LYP level. The dimerization energy was estimated by the formula E = Edimer − 2*Emonomer. For comparison, the same procedure was applied to the H2SnCPH derivative. The results are given on Fig. 5.
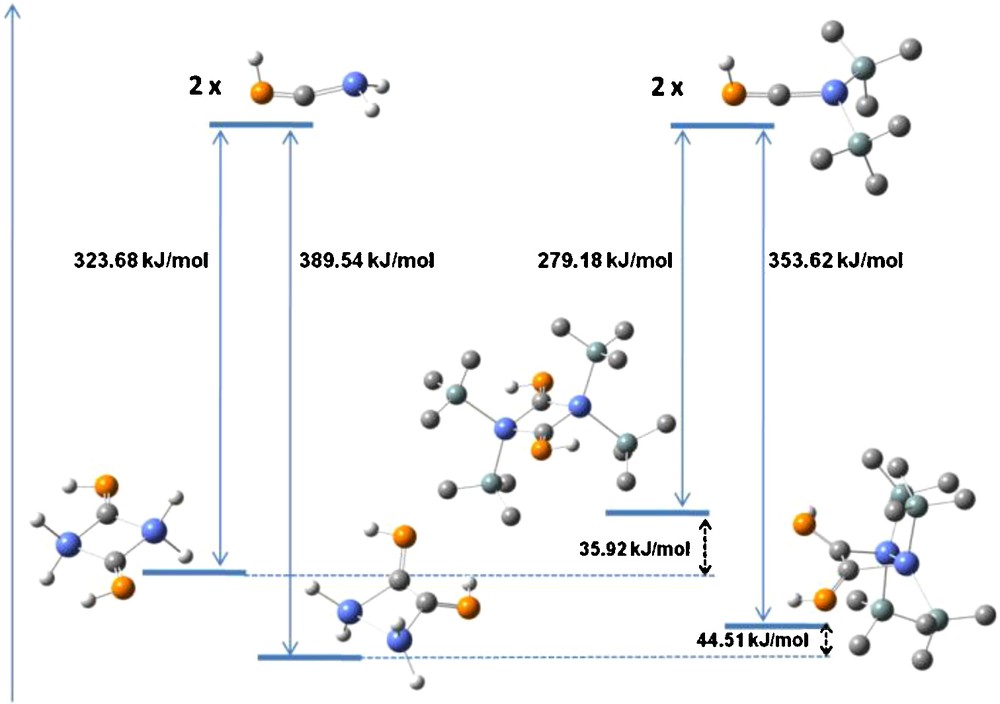
“Head-to-head” and “head-to-tail” dimerization energies for H2SnCPH and (Me3Si)2SnCPH.
As expected, both forms of dimerization are thermodynamically likely to occur for the two derivatives considered, with the formation of the “head-to-head” dimer being more energetically favored. However, the computational data show that the presence of the bulkier silyl groups on the tin atom disfavors the additions at the SnC double bond, the stabilization afforded by the dimeric structures compared with the monomeric units being smaller by 33–42 kJ/mol in the case of (Me3Si)2SnCPH than for H2SnCPH.
3 Conclusions
The bond order of the SnC bond in phosphastannaallenes depends on the nature of the substituents on both the tin and the phosphorus atoms. Electron-withdrawing groups on the tin atom induce orbital interactions that generally decrease the bond order whereas Me3Si groups increase it. The frontier molecular orbitals of such derivatives are usually situated on the SnC bond. PC bond orders are in all cases high, close to or greater than 2, regardless of the substituents.
We propose that a stable phosphastannaallene can be in theory obtained by substituting the tin atom with silyl groups, and further on, that it should have a linear SnCP unit, very close to that of the allenic carbon analogues. This kind of substituent would also afford steric hindrance around the SnC bond preventing the dimerization. A further amount of stabilization could be due to the presence of a phenyl (or of a bulkier substituted aromatic group) on the phosphorus atom.
Acknowledgments
This work is supported by UEFISCDI (Contract no. PCCE-129/2008). A.B. thanks POSDRU for financial support (Contract no. 88/1.5/S/60185).
1 The first heteroallenes to be synthesized were the phosphaallenes –PCX (XC, N, P, As, O, S) [1acde] followed by some metallaallenes >SiCC< [1,2] and >GeC=C< [1,4]. Such derivatives have been successfully obtained as stable compounds using bulky substituents, which prevent their dimerization and thus kinetically stabilize them.
2 When E15 is a nitrogen atom, SiCN derivatives generally behave as silylenes >Si and isocyanides C=N– due to their intermediary structure between azasilaallenes >SiCN– and silylene–isocyanide complexes >Si←CN– [5] at the exception of the compound prepared by Kira [6]. The same phenomenon has been reported for the tin derivative analogue SnCN [7]. By contrast, when E15 is a phosphorus atom, the SiC and GeC bonds in >E14CP– (E14 = Si, Ge) are not cleaved and these compounds behave as heteroallenic derivatives; transient phosphasilaallene >SiCP– [8] and phosphagermaallene >GeCP– [9] have been characterized by low temperature NMR and trapping reactions.


