1 Introduction
In medicinal and structural chemistry, one of the long-standing problems is the relationship between the bioavailability of a drug and its crystalline form, such as polymorphisms, salts, solvates or hydrates and cocrystals [1–7]. As a result, many efforts have aimed at elucidating this relationship and several computational methods and approaches have been developed for predicting crystalline forms, especially of polymorphs of organic molecules with (potential) bioactivity [6,8–12]. However, there are still several obstacles to overcome in order to obtain qualitative and quantitative understanding and predictions. In this context, compound 1-benzyl-5-amino-1H-tetrazole (BAT) was studied by DFT methods, whose results were compared to the X-ray crystallographic structure and to measured spectroscopic (NMR, FT–IR and UV–visible spectra) properties in solution. For comparisons between the calculated and crystallographic structures, several models that take into account the crystalline environment via a cluster approach were employed. Thus, these studies can be regarded as initial efforts towards understanding and predicting the molecular structure under approximated crystalline effects and the spectroscopic properties of this class of molecules that are relevant to medicinal chemistry. In fact, the tetrazole moiety has received considerable attention in recent years due to its unique structural and electronic properties. This moiety is present in many bioactive structures, which have been reported to show, for instance, anti-allergic, anti-asthmatic [13,14], antiviral [15], anti-inflammatory [16] and cognition disorder activities [17]. They are also used as activator in the synthesis of oligoribonucleotides [18–20], as anti-convulsants [21,22] and in the treatment of cancer and AIDS [23,24], resulting in a large number of tetrazole-containing drugs approved by the Food and Drug Administration (FDA) [25,26]. In addition, they have been used as anti-fog agents in photographic emulsions and photoimaging [27,28], as plant-growth regulators, herbicides, and fungicides in agriculture [27]. The nitrogen-rich rings are used as explosives and rocket propellants [29–31] and are important intermediates in synthetic organic chemistry [32–34]. Thus, structural and electronic information is relevant to understand the mechanism of biological activities of these compounds as well as their chemical properties.
Due to their relatively low computational cost, density functional theory (DFT) implementations based on the Kohn–Sham partitioning scheme have become one of the most important approaches for investigating the electronic structure and properties of medium- to large-size molecules. Indeed, DFT functionals have been used to study the electronic structures and molecular properties of several tetrazoles derivatives [35–46], including their molecular and electronic structures (HOMO–LUMO, natural bond orbital (NBO) analysis, dipole moment and electrostatic potential, etc.), spectroscopic properties (NMR, mass fragmentation, electronic, vibrational, etc.) and photochemical behavior mainly related to tautomeric processes. Most of these studies involved comparisons with ab initio methods (Hartree–Fock, HF, and second-order perturbation theory, MP2) and experimental results. Electronic structure methods were also used to study the energy contents of these highly nitrogenated species aiming at exploring structure–property relationships [47–49].
Thus, in this contribution, we used DFT functionals with different basis sets and coupled with cluster models and solvent effects to calculate the molecular structure, electronic and spectroscopic properties of 1-benzyl-5-amino-1H-tetrazole (BAT) and to perform comparisons with single-crystal X-ray crystallographic structure and spectroscopic techniques. One of the goals is to determine the reliability of these functionals and of the cluster model to reproduce the crystal structure as well as the spectroscopic properties of molecules in gas phase and in solution.
2 Experimental
2.1 Material and measurements
Benzyl chloride (CAS No.: 100-44-7) and 5-aminotetrazole monohydrate (CAS No.: 15454-54-3) were purchased from Fluka Chemika and Fluka AG, respectively, and all other reagents and solvents were obtained from common commercial sources and used without further purification. IR spectra over the range 4000–400 cm−1 were obtained with a Thermo Nicolet FT–IR-200 (USA) spectrometer using KBr pellets. Melting points were determined in open capillary tubes on Gallenkamp melting point apparatus. Elemental analysis for N, C and H were performed on Vario Micro Cube, Elementar, Germany. UV–Vis spectra were recorded on a PerkinElmer Lambda 20 UV–Visible spectrophotometer. Crystal determination was performed on Bruker KAPA APEX 11 CCD diffractometer equipped with graphite-monochromatized Mo Kα radiation (λ = 0.71073 Å) at room temperature. 1H NMR spectra was recorded on Bruker (300 MHz) AMX spectrometer at room temperature.
2.2 Synthesis of 1-benzyl-5-amino-1H-tetrazole
A mixture of dried 5-aminotetrazole (17.6 mmol, 1.5 g), sodium hydride (1.24 g, 52.9 mmol) and N,N-dimethylformamide (10.0 mL) was stirred at room temperature for 30 min, followed by addition of benzyl chloride (17.6 mmol, 2.03 mL). Stirring was continued for three extra hours. The progress of the reaction was monitored by TLC. On completion of the reaction, the precipitated product was isolated, washed using chloroform solvent and dried at room temperature. Suitable crystals for X-ray analysis were grown from methanol solution by slow evaporation. The yield of the reaction was 80% (2.47 g). mp 185–190 °C. UV–Vis (DMF) λmax: 190.15 nm. 1H NMR (DMSO, 300 MHz) δ: 5.35 (s, 2H, CH2), 6.83 (br. s, 2H, NH2), 7.21–7.36 (m, 5H, Ar–H). IR (KBr) ν (cm−1): 1290 (C–N str.), 1390 (NN str.), 1140 (N–N str.), 1629 (CN str.), 2875 (CH2 antisymm. str.), 2797 (CH2 symm. str.), 3157 (C–H aromatic symm. str.), 3065 (C–H aromatic antisymm. str.), 3277 (NH2 antisymm. str.), 3160 (NH2 symm. str.). Elemental analysis: calculated (%) for C8H9N5: N, 39.98; C, 54.85; H, 5.18; found (%): N, 38.97; C, 54.45; H, 4.97.
2.3 Single-crystal structure determination
A suitable colorless single-crystal with dimensions 0.28 × 0.14 × 0.07 mm3 was chosen for structure determination and refinement. The crystal data have been collected using APEX2 [50]. The structure was solved by direct methods using SHELXS-97 [51] and refined by full-matrix least-squares method on F2 using SHELXL-97 [51] within the WINGX [52] suite of programs. All hydrogen atoms were refined anisotropically. The structure has received code CCDC 824980 (Table 1).
Crystallographic data and refinement details for compound.
| Molecular formula | C8H9N5 |
| Formula weight | 175.20 |
| Crystal system | Triclinic |
| Density (calculated) | 1.365 g·cm−3 |
| Space group | P2(1)/c′ |
| Unit cell dimensions | |
| λ (nm) | 0.71073 |
| a (nm) | 1.4911(6) |
| b (nm) | 0.5121(2) |
| c (nm) | 1.1195(4) |
| α (°) | 90.00 |
| β (°) | 94.435(2) |
| γ (°) | 90.00 |
| V | 85.236(6) nm3 |
| Z | 4 |
| F(000) | 368 |
| μ (Mo Kα) | 0.92 mm−1 |
| θ range/(°) | 3.65 to 28.34 |
| Goodness-of-fit on F2 | 1.038 |
| R | 0.0428 |
| wR2 | 0.1011 |
| Data/restraints/parameters | 2109/3/125 |
2.4 Computational procedures
All molecular structures were obtained by geometry optimization with B3LYP [53] and PBE1PBE [54] functionals with 6-31G** and 6-311G** basis sets [55]. Vibrational frequency calculations were performed on the optimized structures with the same method to ensure that all force constants were positive. The solvent effects of DMF (N,N-dimethylformamide) and DMSO (dimethyl sulfoxide) were simulated by the standard Polarizable Continuum Model (PCM) [56] and radii derived from the UAKS approach [57]. Because these are aprotic, polar, hydrogen bonding solvent, two explicit solvent molecules were included in the structure of the monomer and denoted as DMF2/PCM or DMSO2/PCM. The absorption spectrum was calculated by time-dependent density functional theory (TD-DFT) using the PBE1PBE/6-311G** method in DMF. NMR calculations were performed with the WP04/aug-cc-pVDZ method [58] in DMSO. The TD-DFT and NMR calculations were performed at the PBE1PBE/6-311G** equilibrium geometry. All calculations were performed with the Gaussian 09 program [59] using its default criteria and installed in a computer with an 8-core Intel processor, 8 GB RAM memory and a 1 TB hard-drive. Typical CPU time ranged from a few hours for geometry optimizations to a few days for vibrational frequency calculations of tetramer structures.
3 Results and discussion
3.1 X-ray crystal structure and calculated structures of 1-benzyl-5-amino-1H-tetrazole
In the 1-benzyl-5-amino-1H-tetrazole (BAT) structure, the tetrazole and benzyl rings are not coplanar and a corresponding dihedral angle of 103.0° was measured. DFT calculations of the isolated molecule also support this conformation, where at the PBE1PBE/6-311G** level, this dihedral angle is 164.5°. The N1–C2 bond length is 1.454 Å, which is almost the same as the N–Cphenyl single bond length. The intermolecular N–H···N hydrogen bonds between the amino group and tetrazole N atoms are primarily responsible for the formation of a two-dimensional network that extends parallel to the ac plane of the crystal. Each molecule is hydrogen bonded to three neighbors, where both hydrogen atoms of the 5-amino group are involved in hydrogen bonds and two additional hydrogen bonds are formed with N3 and N4 nitrogen atoms of the tetrazole rings (see Fig. 1). Indeed, the global pattern can be depicted as dimeric structures formed by simultaneous hydrogen bonds between amino···tetrazole and tetrazole···amino, with the additional hydrogen bonds between the H atom of the amino group and the other N atoms of the tetrazole ring extend the structure into another dimension, as illustrated in Fig. 2. The structure presented the expected spatial relationships observed for compounds containing tetrazole and benzyl rings and 5-amino group. A comparison of tetrazole ring geometry with that of 5-aminotetrazole [60] did not reveal any influence of the substitution of the benzyl group on the tetrazole ring. However, comparing to the X-ray structure of 1-phenyltetrazole [61], it was found that the substitution of the H atom at the ring carbon C1 by an amino group in the BAT molecule results in the shortening of N2N3 bond by 0.014 Å and elongation of N4C1 and N1–N2 bonds by 0.026 Å and 0.016 Å, respectively. This indicates that the amino substitution causes a delocalization of the conjugated electronic density such that the N1–C1 and N3–N4 bonds lengths remain unaffected.
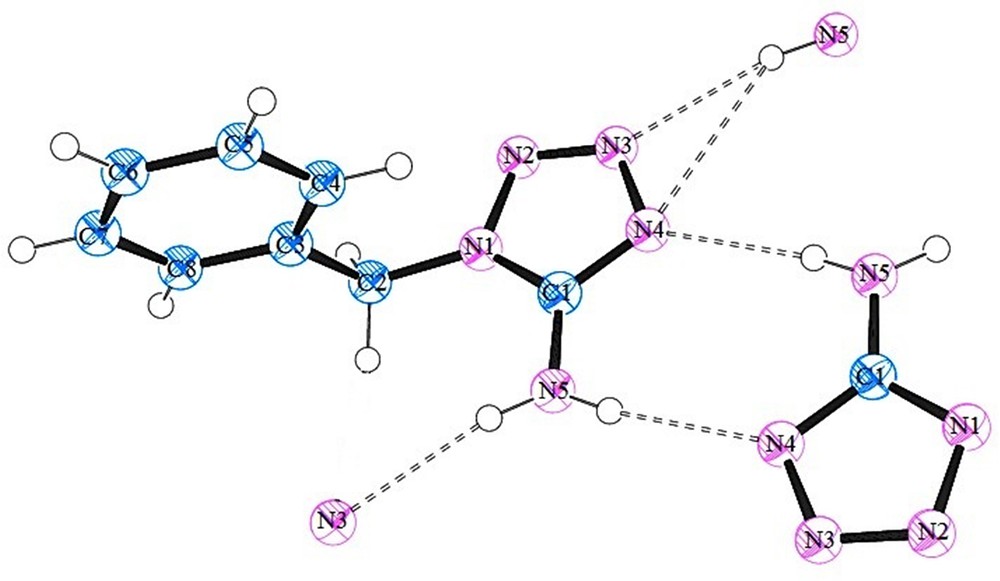
(Color online.) A view of the asymmetric unit of 1-benzyl-5-amino-1H-tetrazole (BAT), where the atoms involved in hydrogen bonding were included, whereas the other atoms were omitted for clarity. Thermal displacement ellipsoids are drawn at the 30% probability level. The atomic labels are also included.

(Color online.) Molecular strands within the crystal structures of 1-benzyl-5-amino-1H-tetrazole (BAT). Hydrogen bonds are represented as dashed lines.
As mentioned, the crystal structure exhibits intermolecular N–H···N hydrogen bonds between the amino group and atoms N3 and N4 of the tetrazole rings. The details of these hydrogen bonds are presented in Table 2.
Hydrogen bond geometries for 1-benzyl-5-amino-1H-tetrazole (BAT). Standard deviations are shown in parenthesis.
| D–H···A | D–H (Å) | H···A (Å) | D···A (Å) | D–H···A (°) |
| N5–H5···N4a | 0.862(9) | 2.169(10) | 3.010(16) | 168.3(17) |
| N5–H5···N3b | 0.853(9) | 2.231(10) | 3.073(16) | 169.0(17) |
a Symmetry code: −x + 2, −y, −z + 2.
b Symmetry code: x, −y + 1/2, z − 1/2.
Table 3 shows a comparison between the X-ray crystallographic bond lengths and the bond angles of 1-benzyl-5-amino-1H-tetrazole (BAT) and the respective calculated values with the PBE1PBE/6-311G** method for the isolated molecule. The overall agreement is quite good (ca. ± 0.01 Å for bond lengths and ca. ± 0.5°), except when atoms N5, C6, C7 and C8 are involved. The dependence of the calculated structure upon the DFT functional (B3LYP and PBE1PBE) and basis sets (6-31G** and 6-311G**) is displayed in Fig. 3 as overlaying with the X-ray structure. The RMSD (root-mean square deviation) between the calculated and the crystallographic structures is 0.00853, 0.00103, 0.00456, and 0.00599 for the B3LYP/6-31G**, B3LYP/6-311G**, PBE1PBE/6-31G**, and PBE1PBE/6-311G** method, respectively. Notice that the errors are similar and are mostly due to the differences in the dihedral angle of the benzyl ring. Taking into account only the bond distances, the relative unsigned deviations are 0.173, 0.151, 0.150, and 0.147 for the optimized structure at the B3LYP/6-31G**, B3LYP/6-311G**, PBE1PBE/6-31G**, and PBE1PBE/6-311G** levels, respectively, when compared to the experimental values (Table S1 and Table S2 in the Supplementary data), with the latter method presenting the lowest error.
Selected bond lengths (Å) and bond angles (degree) for 1-benzyl-5-amino-1H-tetrazole (BAT).
| Bond length (Å) | Expa | PBE1PBEb | Bond angle (°) | Expa | PBE1PBEb |
| N1–C1 | 1.337 | 1.344 | C1–N1–N2 | 108.4 | 107.6 |
| N1–N2 | 1.364 | 1.355 | N1–N2–N3 | 105.9 | 106.3 |
| N1–C2 | 1.454 | 1.445 | N2–N3–N4 | 111.8 | 111.9 |
| N2–N3 | 1.284 | 1.276 | C1–N4–N3 | 105.4 | 105.5 |
| N3–N4 | 1.361 | 1.350 | N4–C1–N1 | 108.5 | 108.6 |
| N4–C1 | 1.328 | 1.315 | N1–C2–C3 | 113.6 | 112.6 |
| C1–N5 | 1.337 | 1.368 | N5–C1–N4 | 126.0 | 127.2 |
| C2–C3 | 1.504 | 1.509 | C1–N1–C2 | 129.8 | 129.8 |
| C3–C4 | 1.378 | 1.393 | N2–N1–C2 | 121.6 | 122.6 |
| C4–C5 | 1.381 | 1.392 | H1–N5–H2 | 118.9 | 112.8 |
| C5–C6 | 1.361 | 1.388 | C4–C3–C2 | 122.8 | 120.5 |
| C6–C7 | 1.363 | 1.392 | C8–C3–C2 | 118.6 | 120.2 |
| C7–C8 | 1.380 | 1.387 | C3–C4–C5 | 120.6 | 120.5 |
| C8–C3 | 1.378 | 1.396 | C4–C5–C6 | 120.3 | 120.0 |
| N5–H1 | 0.862 | 1.009 | C5–C6–C7 | 119.6 | 119.8 |
| N5–H2 | 0.853 | 1.011 | C6–C7–C8 | 120.7 | 120.2 |
a Single-crystal X-ray structure.
b PBE1PBE/6-311G** level of theory of the isolated monomer.
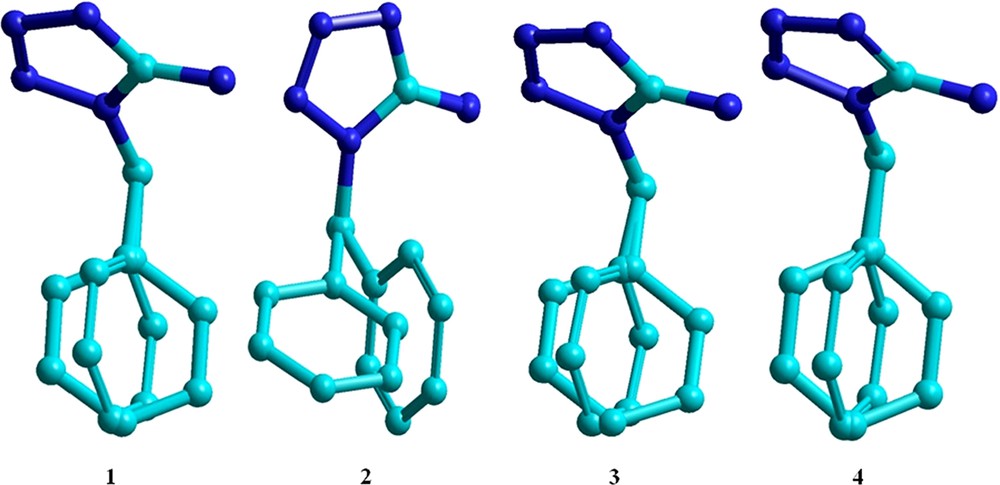
(Color online.) Overlay between the crystallographic and calculated structures with the (1) B3LYP/6-31G**, (2) B3LYP/6-311G**, (3) PBE1PBE/6-31G**, and (4) PBE1PBE/6-311G** methods for the 1-benzyl-5-amino-1H-tetrazole molecule.
As mentioned when analyzing Table 3, the largest deviations between the calculated and crystallographic structures are related to the atoms forming hydrogen bonds. These deviations can fairly be attributed to the fact that theoretical calculations were performed on isolated molecules. The deviations were minimized when interaction effects were considered through dimeric and tetrameric models. The tetrameric structure provided the smallest relative deviation (0.128) and was found to be in good agreement with the experimental data obtained by X-ray diffraction studies (Table S1 and Table S2 in the Supplementary data). A comparison of optimized and experimental data showed that the PBE1PBE/6-311G** level of theory is the most reliable and accurate for calculating the structure of BAT. Detailed comparisons between observed and computed bond lengths and bond angles for monomer, dimer and tetramer at different levels of the theory are presented in Figs. S2 and S3 of the Supplementary data.
3.2 Experimental and calculated 1H NMR, IR, and UV–Vis spectral analyses
In the 1H NMR spectrum of 1-benzyl-5-amino-1H-tetrazole (BAT), the singlet peak at 5.35 is assigned to the CH2 protons and the broad singlet peak observed at 6.83 is assigned to the NH2 protons (see Fig. S4 in the Supplementary data). A doublet peak observed at 7.22 is assigned to the CH(C4HC8H) protons of the substituted phenyl moiety. The two triplet peaks observed at 7.32 and 7.36 are due the CH(C6H) and CH(C5HC7H) protons of the phenyl moiety, respectively. The 1H chemical shifts were calculated with the WP04/aug-cc-pVDZ [58] method, whose assessment showed satisfactory accuracy for assignments and comparisons between isomers [62]. Indeed, the calculated 1H chemical shifts were used in the assignment of BAT in DMSO as presented in Table 4.
Observed and calculated 1H NMR chemical shifts values for 1-benzyl-5-amino-1H-tetrazole (BAT) in DMSO. Calculations at the WP04/aug-cc-pVDZ//PBE1PBE/6-311G** level with PCM-UAKS used to simulate the solvent effects and DMSO2/PCM included two explicit DMSO molecules forming hydrogen bonds with the NH2 group. The numbers in parenthesis are the calculated chemical shift values for the rigid structures.
Nucleus | Observed DMSO | Monomer PCM | Monomer DMSO2/PCM | Monomer DMF2/PCM | Dimer PCM |
| C4HC8H | 7.22 | 7.32 (7.55/7.10) | 7.71 (7.39/8.03) | 7.40 (7.02/7.78) | 7.21 (7.50/6.91) |
| C5HC7H | 7.36 | 7.33 (7.35/7.31) | 7.22 (7.13/7.31) | 7.40 (7.38/7.42) | 7.36 (7.27/7.45) |
| C6H | 7.32 | 7.27 | 7.13 | 7.51 | 7.35 |
| C2H2 | 5.35 | 5.17 (4.66/5.68) | 5.03 (5.01/5.04) | 5.23 (5.09/5.37) | 4.98 (4.53/5.43) |
| N5H2 | 6.83 | 3.57 (4.09/3.05) | 7.99 (7.76/8.23) | 7.01 (6.86/7.16) | 6.70 (9.99/3.40) |
Because the internal rotations of the N1–C2 and C2–C3 bonds are fast in the time scale of the NMR, the protons attached to carbons C4 and C8, C5 and C7, C2, and N5 are magnetically equivalent. Thus, the comparisons were performed with the mean of the chemical shifts values calculated at the rigid PBE1PBE/6-311G** equilibrium structure for the monomer and the dimer. Notice that the results obtained with the dimer are in much closer agreement with the experimental data than the calculations for the monomer, so it might be inferred that in DMSO solution the BAT is in dimeric form. However, because DMSO is a hydrogen bond acceptor molecule, the NMR calculations were also performed for the monomer species interacting with two DMSO molecules via the hydrogen atoms of the amino group. These calculations are referred to as DMSO2/PCM and they show, in Table 4, an improved agreement for the 1H in the amino group. However, the overall agreement between the calculated chemical shifts with the dimeric structure is still the best.
The IR spectrum of the BAT compound shows characteristic vibrational bands of NH stretching at 3277 cm−1, CN stretching at 1629 cm−1, NN stretching at 1390 cm−1, and C–N stretching at 1290 cm−1, as well as symmetric and antisymmetric stretchings of Cmethyl at 2797 cm−1 and 2875 cm−1, Caromatic stretchings in the range 3000–3200 cm−1 (Fig. S5 in the Supplementary data). As shown in Table 5 and Fig. 4, these assignments are in agreement with the harmonic vibrational frequencies obtained for the monomeric and dimeric calculated structures at the PBE1PBE/6-311G** level. However, because the C–N stretch were calculated with a very small intensity for both monomeric and dimeric structures, reassignment of this band was proposed, namely, the transition at 1290 cm−1 should be due to C–H aromatic in-plane bending modes calculated at 1310 cm−1 (4.5 km·mol−1) and 1346 cm−1 (20.3 km·mol−1) for the monomer, and 1315 cm−1 (7.8 km·mol−1) and 1348 cm−1 (38.5 km·mol−1) for the dimer. In fact, the vibrational wavenumbers are very similar for these two structures; however, the normal modes dominated by the hydrogen-bonded atoms differ quite significantly. More specifically, the NH2 symmetric stretch is redshifted by 320 cm−1 for the dimeric structure (3257 cm−1) compared to the monomeric one (3577 cm−1), and becomes much closer to the experimental data (3160 cm−1). Notice that the NH2 antisymmetric stretch is very similar for both structures because the stretching N–H bond is not participating in hydrogen bonding. In addition, the NH2 wagging is affected by the hydrogen-bonding formation where the intense band at 652 cm−1 in the monomer is separated into two medium intensity bands at 432 and 856 cm−1 in the dimeric structure. Overall, the calculated intensities of the infrared transitions are significantly enhanced in the dimer and the comparisons with the experimental data suggest that the dimeric structure provides a better description for the solid-phase infrared spectrum, as expected from the crystalline structure.
Experimental and calculated infrared spectrum of 1-benzyl-5-amino-1H-tetrazole (BAT). Wavenumbers in cm−1 and calculated intensities (km·mol−1) in parenthesis. Calculations at the PBE1PBE/6-311G**.
| Normal mode | Experimental | Monomer | Dimer |
| NH2 str. (antisymm) | 3277 | 3685 (66) | 3654 (233) |
| NH2 str. (symm) | 3160 | 3577 (32) | 3257 (2877) |
| C–H aromatic str. (symm) | 3157 | 3220 (10) | 3220 (28) |
| C–H aromatic str. (antisymm) | 3065 | 3210 (13)–3181 (5) | 3210 (26)–3182 (10) |
| C–H (CH2) str. (antisymm) | 2875 | 3132 (1) | 3129 (2) |
| C–H (CH2) str. (symm) | 2797 | 3073 (16) | 3070 (39) |
| CN str. | 1629 | 1687 (207) | 1725 (342) |
| N–H scissoring | 1534 | 1615 (9) | 1643 (117) |
| N–CN str. | 1496 | 1557 (92) | 1547 (208) |
| C–H (CH2) bending | 1465 | 1470 (8) | 1472 (16) |
| NN str. | 1390 | 1413 (17) | 1433 (45) |
| C–N str. | 1290 | 1329 (2) | 1340 (2) |
| N–N str. | 1140 | 1175 (15) | 1185 (42) |
| N–H rocking | 1086 | 1123 (23) | 1137 (110) |
| NH2 wagging | 696 | 652 (144) | 856 (159)/432 (128) |
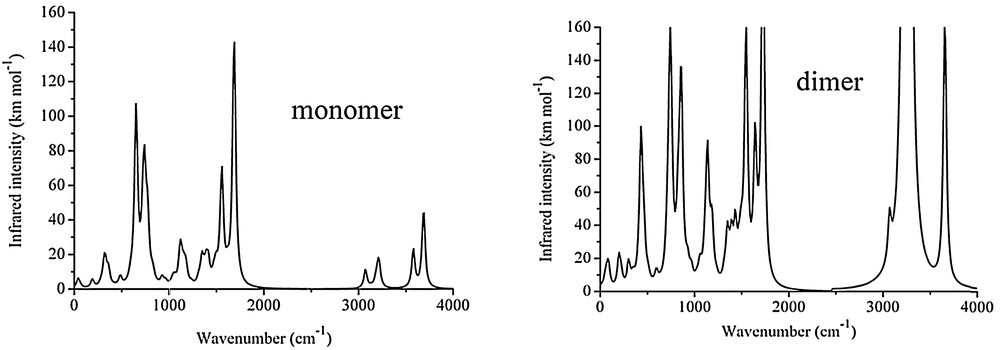
Calculated infrared spectrum of the monomeric (top panel) and dimeric (lower panel) structures of 1-benzyl-5-amino-1H-tetrazole (BAT). Simulated spectra with Gaussian lineshape and 20 cm−1 of half-width at half-height.
The UV–visible spectra in solvent DMF were calculated using polarized continuum model (PCM) by TD-DFT calculations at the PBE1PBE/6-311G** level of theory and are compared to the experimental spectrum in Fig. 5. The monomeric structure presents two strong absorption bands at 191 nm (oscillator strength = 0.055) and 204 nm (oscillator strength = 0.028), which are in excellent agreement with experimental data, namely, 190 nm (oscillator strength = 0.057) and 203 nm (oscillator strength = 0.03). Moreover, a broad absorption band in the region 224–234 nm was observed in the computed spectrum for the monomer, but the corresponding oscillator strengths are well below 0.005, so it is unlikely to be observed in the experimental spectrum. The absorption maximum for the dimer species has been calculated at 204 nm with an oscillator strength of 0.142. We observed a second and a third absorption peaks at 214 and 221 nm with oscillator strengths of 0.062 and 0.039, respectively. The absorption maximum for the monomer interacting with two DMF molecules through hydrogen bonds with NH2 protons is found at 204 nm with oscillator strength of 0.085. A second and a third absorption peaks have been calculated at 217 and 225 nm with oscillator strengths of 0.018 and 0.012, respectively.

(Color online.) A comparison of the experimental and calculated UV–visible spectra of 1-benzyl-5-amino-1H-tetrazole in DMF using TD-DFT at the PBE1PBE/6-311G** level of theory. Simulated spectra with Gaussian lineshape and 785 cm−1 width at half-height. The intensities were normalized with respect to the largest observed/calculated value.
The comparisons made in Fig. 5 suggest that the dominant form of BAT in DMF solution in the monomeric structure. This same species is also possible from the comparisons of the 1H NMR chemical shifts results (Table 4), despite the good agreement obtained with the dimeric structure. In fact, the effects of the hydrogen-bonding between BAT and the solvent molecules (DMSO and DMF) are overestimated by the DFT functionals. This is probably due to their inherent deficiencies to describe intermolecular interactions [63] as well as the model employed that is limited to only two solvent molecules, which could indeed lead to overestimation of the explicit hydrogen bonds considered in the geometry optimization.
The main contribution to the maximum absorption band is the HOMO (highest occupied molecular orbital)–LUMO (lowest unoccupied molecular orbital) transition, whose isovalue surfaces are depicted in Fig. 6.

(Color online.) Isovalue surfaces of the HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) of BAT computed at the PBE1PBE/6-311G** level. An isovalue of 0.02 was used for drawing the orbital surfaces.
Notice from Fig. 6 that the HOMO is localized over the tetrazole ring, whereas the LUMO is localized on the benzyl fragment. Therefore, it is expected that this HOMO–LUMO transition would be significantly affected by the solvent polarity because of its charge transfer character and the BAT molecule might be a good candidate for solvatochromic studies. The HOMO and LUMO energies and HOMO–LUMO energy gaps for the monomer, dimer and tetramer are represented in Table 6, and their dependence upon the functional and basis sets is reported.
The dependence of the HOMO (highest occupied molecular orbital), EHOMO, LUMO (lowest unoccupied molecular orbital), ELUMO, and HOMO–LUMO energy gap, Egap, on the molecular model (monomer, dimer, and tetramer) and the computational method. All energy values are in eV.
| B3LYP/6-31G** | B3LYP/6-311G** | PBE1PBE/6-31G** | PBE1PBE/6-311G** | |
| Monomer | ||||
| EHOMO | –6.99 | –6.99 | –6.912 | –7.102 |
| ELUMO | –0.846 | –0.844 | –0.681 | –0.925 |
| Egap | 6.144 | 6.146 | 6.231 | 6.177 |
| Dimer | ||||
| EHOMO | –6.313 | –6.503 | –6.558 | –6.694 |
| ELUMO | –0.653 | –0.898 | –0.489 | –0.707 |
| Egap | 5.66 | 5.605 | 6.069 | 5.987 |
| Tetramer | ||||
| EHOMO | –6.117 | –6.258 | –6.067 | –6.503 |
| ELUMO | –0.784 | –0.952 | –1.034 | –0.762 |
| Egap | 5.333 | 5.306 | 5.033 | 5.741 |
Notice from Table 6 that the HOMO–LUMO gap decreases as the BAT molecule aggregates, namely, Egap(monomer) > Egap(dimer) > Egap(tetramer). This trend is independent of the computational method (functional and basis set) employed and is due mainly to the destabilization of the HOMO. Thus, this property could be an interesting probe of the degree of aggregation of BAT in different solvents.
3.3 Molecular electrostatic potential (MEP)
The molecular electrostatic potential is a useful property to determine the preferred sites for the nucleophilic and electrophilic attack and hydrogen-bond interactions [64,65]. The H-donor and H-acceptor properties are related to the positive and negative regions, respectively. Thus, the formation of hydrogen bonds can be related to the electrostatic potentials [66]. Being a real physical property, electrostatic potential can be calculated by both experimental i.e. X-ray diffraction and computational methods [67]. In most of the MEPs, the regions with the most negative charge values, shown in red color, are assigned as the preferred site for electrophilic reactions, while the region of highly positive charge, shown in blue, is the preferred site for nucleophilic attack [68].
The molecular electrostatic potential map of the BAT computed at PBE1PBE/6-311G** is shown in Fig. 7. The negative electrostatic region is localized on N2, N3, and N4 atoms. However, the most positive region (blue) is localized on the hydrogens, with NH2 hydrogens being the highest positive region, which indicates the possible site for nucleophilic attack.

(Color online.) Molecular electrostatic potential map calculated at PBE1PBE/6-311G(d,p) level.
4 Conclusions
1-Benzyl-5-amino-1H-tetrazole was synthesized and characterized using spectroscopic techniques, and its crystal structure was determined by X-ray diffraction. The structure shows a good comparison with previously published related structures. The monomeric, dimeric, and tetrameric structures of BAT were determined with different DFT computational methods (functional and basis sets). The tetrameric structure calculated with the PBE1PBE/6-311G** method was found to be the best molecular model and computational level to reproduce the experimental crystal results. The calculated spectroscopic properties (1H NMR, IR, UV–Vis) are in good agreement with the experimental results as long as the proper molecular model is employed, including DMF and DMSO explicit solvent molecules. From the comparisons between the experimental and computational results, the BAT is dominated by the monomeric structure in polar DMF and DMSO solutions. However, the DFT methods employed appear to overestimate the effects of the hydrogen-bonding due to their intrinsic limitation as well as the limitation imposed by modeling the explicit solvent molecules via only two molecules. It was predicted that the BAT molecule could present solvatochromic properties and that the HOMO–LUMO energy gap could be used as a probe for the degree of aggregation of BAT in different solvents.
Acknowledgements
The authors are grateful of Shehzad Sharif for XRD data collection and Dr. Muhammad Nadeem Arshad for helpful discussions.


