1 Introduction
Tropane (8-methyl-8-azabicyclo-[3.2.1]octane) and granatane (9-azabicyclo[3.3.1]nonane) are bicyclic structures [1] found in numerous bioactive naturally occurring and synthetic compounds [2,3]. Tropinone (1, R = Me) and granatanone (also known as pseudopelletierine, pseudopelletrierin or N-methylgranatanone 2, R = Me) [4] are simple and are among the best-known representatives of these groups of compounds (Fig. 1). Tropane, granatane and their N-alkyl analogues are interesting in medicinal chemistry. Tropane-derived molecules, including cocaine analogues [5], have been studied as promising ligands for biological receptors [6–8]. The granatanone skeleton is an important substructure of some compounds possessing anti-Parkinsonian [9], neuroleptic [10,11], and hypotensive [12] activity. Granatanone and its derivatives were useful for the synthesis of potential cocaine-binding site ligands [13]. The relative stability of the N-alkyl invertomers of tropane alkaloids and related bioactive compounds may influence interactions with receptor binding sites [14].
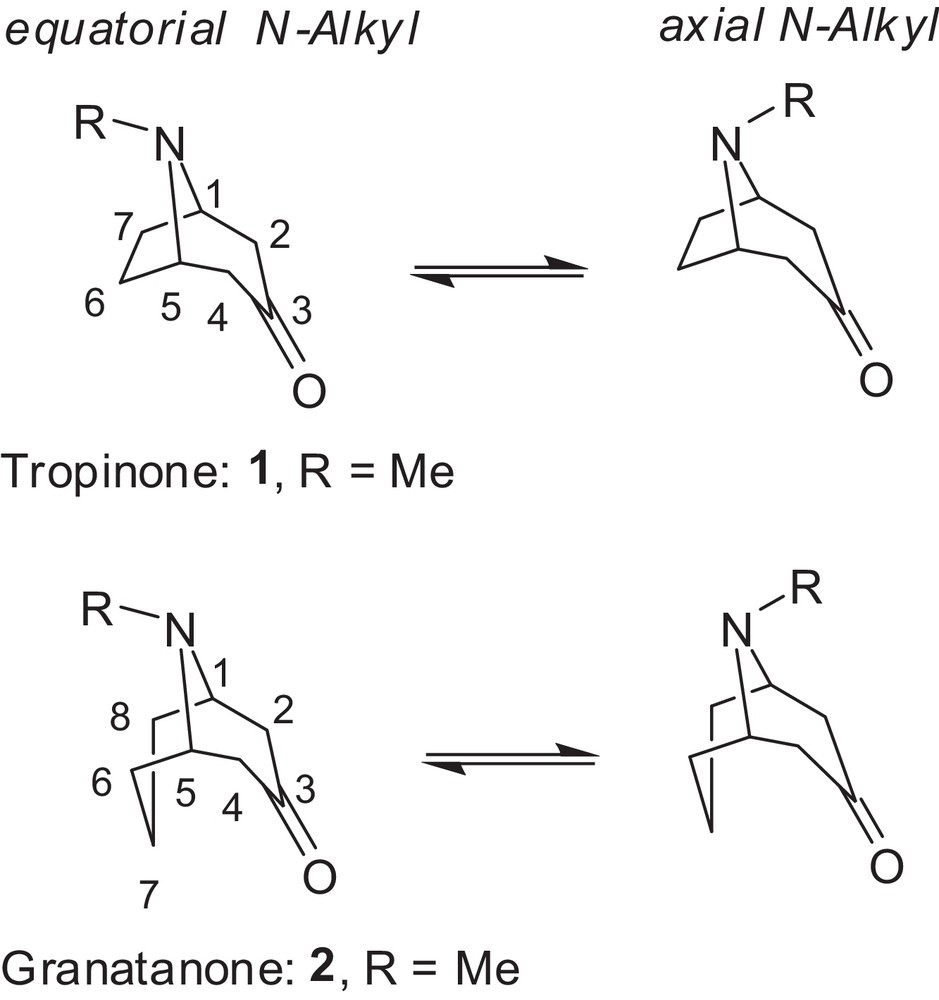
Invertomers of tropan-3-one and granatan-3-one analogues showing the equatorial and axial N-invertomer of the piperidone ring (tropane atom numbering shown).
Some of the most synthetically useful transformations of tropane- and granatane-derived ketones are the diastereoselective and enantioselective aldol reactions [15]. Tropinone has been successfully used in this capacity for the synthesis of several bioactive derivatives, such as cocaine [16] and its analogues [6,7], as well as of several other alkaloids [17–21]. Recently, we discovered and investigated stereoselective reactions of tropinone and granatanone promoted by water. The elucidation of the configurational preference of the N-methyl in water helped to rationalise reactivity and the origins of stereoselectivity in such aldol processes [22]. Similarly, the knowledge of N-invertomer preferences in N-substituted analogues in aqueous solutions may be useful for the rationalisation or the prediction of their reactivity in reactions that occur in water, including the aldol reaction.
Previous conformational studies by NMR spectroscopy in CDCl3 suggested axial or slight axial preferences for the N-substituents in tropinone [23], granatanone [24,25], and related N-substituted structures. However, preferences for the equatorial N-invertomer (by 0.62–1.2 kcal/mol) in some C-3 substituted tropanes in a CFCl3 solution at –100 °C was observed by a 13C NMR method [26]. Crystal structures indicated that the N-methyl in tropinone [27] and N-phenyl in the granatanone derivative [28] display the axial configuration in the solid state. The N-methyl configuration in the crystals depended on the derivative and was determined to be equatorial in cocaine [29] and its salts [30] as well as in phenyltropane [31], tropinone aldols [32,33], tropinone aldol tosylhydrazone [21], and granatanone aldols [34], but axial in scopolamine [35]. In some conformational studies of granatane derivatives by NMR methods [36], the N-methyl stereochemistry remained undetermined. The conformations of granatane and related systems have been reviewed by Zefirov and Palyulin [37]. An excellent computational and spectroscopic study of the conformational flexibility of tropinone in the gas phase reported equatorial preference 2:1 [38]. However, little is known about the N-invertomer preference of such compounds in polar solutions. The equatorial/axial invertomer ratio for deuterotropinone deuterochloride in D2O was determined to be 4.2 based on NMR spectra to be 4.2 [39]. Recently, we have determined the differences in the invertomer preferences for the N-methyl derivatives of tropane and granatane in polar solvents [40]. X-ray diffraction revealed the N-benzyl group in equatorial position in N-benzylnortropinone aldols [41] and aldol tosylhydrazone [21]. However, as far as we know, there has been no experimental or computational study concerning the distribution of the higher N-alkyl or N-aryl invertomers in tropanes or granatanes in water (or even other polar solvents), which are essential for biological systems and green synthetic reactions. The enantioselectivity of deprotonation and diastereoselectivity of aldol reactions of higher N-alkyl homologues of tropinone [21,42,43] and granatanone [34] is affected by the configurational preference of the N-substituents in reaction medium. In an effort to extend the aqueous aldol reactions [44] to higher N-alkyl substrates, we decided to examine their N-invertomer preferences. Herein, we report our results for the preferred N-invertomer stereochemistry and equilibriums in representative N-substituted tropinone and granatanone analogues.
2 Results and discussion
We investigated the N-invertomer distributions in aqueous and methanol solutions using computational and NMR spectroscopic methods. The use of protic deuterated solvents (D2O, methanol-d4) is hampered by spontaneous protium–deuterium exchange of the acidic hydrogens at the α-position to carbonyl groups. Direct NoD-NMR methods [45] for water or methanol solutions (e.g., ROESY technique) did not provide useful information due to interferences from the non-deuterated solvent, low sample solubility and fast rate of invertomer interchange. Therefore, we used proven methods based on 13C NMR combined with verified DFT calculations [40]. To probe the behaviour of these amino ketones in aqueous environments including the potential involvement of protonated amine forms in aldol and other reactions in aqueous media [44], we also included the N-invertomer equilibriums in the corresponding hydrochlorides.
2.1 Synthesis of N-substituted tropinone and granatanone derivatives
The higher N-alkyl analogues of tropinone 1 and granatanone 2 were prepared via an adapted two-step literature procedure [46], except for the N-benzyl derivatives (Scheme 1).
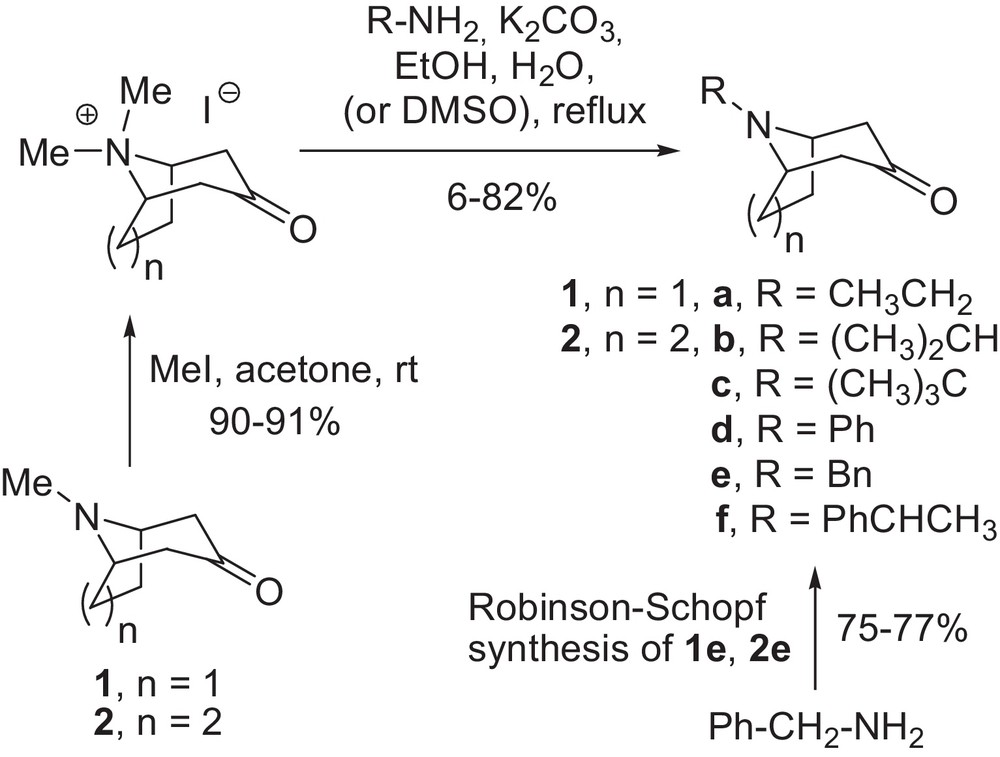
Synthesis of N-substituted nortropinone and norgranatanone analogues.
Tropinone and granatanone were N-methylated with methyl iodide to yield the corresponding quaternary salts. The quaternary salts were reacted with appropriate primary amines in an ethanol–water mixture. In most cases, fair or good overall yields of the desired products were obtained (30–82%). For the tert-butyl derivatives, incomplete reactions and low yields as well as problems with purification were encountered. Granatanone tert-butyl derivative 2c was obtained in 6% yield and satisfactory purity by PTLC. The reaction medium for N-tert-butylnortropinone (1c) had to be changed to DMSO, to obtain the product in acceptable yield (14%). N-benzyl derivatives 1e and 2e were conveniently obtained (75 and 77% yield, respectively) via Robinson–Schopf synthesis according to a previously published procedure [47]. The amine hydrochlorides for the spectroscopic studies were prepared from the amino ketones by vacuum evaporation with excess hydrochloric acid followed by drying. With the compounds in hand, we performed the experimental study of the N-invertomer equilibriums in solution.
2.2 Theoretical study of N-invertomer distributions
In this study, we chose a DFT functional with two basis sets and CPCM [48,49] to model solvent effects. The density functional calculations at the B3LYP/6-31G(d) level are not computationally demanding and are popular with organic chemists. The results from calculations at this level of theory have proven to be useful in the exploration of organic mechanisms and equilibrium states in both the gas and liquid phases [50–53]. This method also displayed excellent performance for aldol reactions of bicyclical amino ketones [22]. Therefore, this basic set was employed as the basis set of choice. In addition, reportedly a more accurate but much more computationally demanding B3LYP/6-311++G(3d,3p) level of theory was included for comparison for these particular structures. This basis set was chosen due to the satisfactory results obtained for the investigation of the N-methyl invertomer distributions for tropanes and granatanes [40]. All of the electronic structure calculations were performed using the GAUSSIAN 09 suite of programs. The equilibrium constant K (representing N-invertomer ratio) was calculated with the formula:
For comparison, distributions in the gas phase were also calculated at the same levels of theory and temperatures as for solution calculations. The calculated relative free energies, obtained from the DFT calculations, together with corresponding ratios of the equatorial to axial forms (Fig. 1) are listed in Table 1 (gas phase), Table 2 (water), and Table 3 (methanol). For comparison, Tables 2 and 3 contain also experimental data obtained directly from NMR spectra (vide infra).
Calculated free energies [kcal/mol] of equatorial to axial N-inversion with corresponding ratios of N-invertomer in the gas phase.
| Entry | Species (R) | Calculated at B3LYP/6-31G(d) | Calculated at B3LYP/6-311 + +G(3d,3p) | ||||||
| –90 °C | 25 °C | –90 °C | 25 °C | ||||||
| ΔG | eq/ax | ΔG | eq/ax | ΔG | eq/ax | ΔG | eq/ax | ||
| 1 | 1a (Et) | 0.14 | 1.5 | 0.15 | 1.3 | 0.24 | 1.9 | 0.24 | 1.5 |
| 2 | 1a•HCl (Et) | 1.3 | 34.5 | 1.3 | 8.6 | 1.3 | 35.1 | 1.3 | 9.1 |
| 3 | 1b (iPr) | –0.56 | 0.21 | –0.46 | 0.46 | –0.42 | 0.32 | –0.29 | 0.61 |
| 4 | 1b•HCl (iPr) | 0.30 | 2.3 | 0.31 | 1.7 | 0.49 | 3.8 | 0.50 | 2.3 |
| 5 | 1c (tBu) | 2.0 | 279.0 | 2.1 | 35.1 | 2.0 | 274.3 | 2.1 | 33.0 |
| 6 | 1c•HCl (tBu) | 4.0 | 62554 | 4.1 | 942.6 | 3.9 | 51153 | 4.0 | 792.6 |
| 7 | 1d (Ph) | –2.0 | 0.0045 | –1.8 | 0.046 | –1.8 | 0.0076 | –1.6 | 0.068 |
| 8 | 1d•HCl (Ph) | 1.7 | 98.9 | 1.7 | 17.0 | 1.8 | 133.3 | 1.8 | 20.6 |
| 9 | 1e (Bn) | 0.35 | 2.6 | 0.41 | 2.0 | 0.31 | 2. 3 | 0.30 | 1.7 |
| 10 | 1e•HCl (Bn) | 1.6 | 76.9 | 1.5 | 13.4 | 1.5 | 68.1 | 1.5 | 12.1 |
| 11 | 1f (PhMeCH) | –0.03 | 0.92 | 0.14 | 1.3 | 0.06 | 1.2 | 0.21 | 1.4 |
| 12 | 1f•HCl (PhMeCH) | 1.3 | 40.1 | 1.5 | 13.5 | 1.2 | 30.3 | 1.3 | 8.7 |
| 13 | 2a (Et) | –0.46 | 0.28 | –0.40 | 0.51 | –0.37 | 0.36 | –0.29 | 0.61 |
| 14 | 2a•HCl (Et) | –0.90 | 0.084 | –1.0 | 0.19 | –0.96 | 0.072 | –1.1 | 0.16 |
| 15 | 2b (iPr) | –0.42 | 0.32 | –0.35 | 0.55 | –0.64 | 0.17 | –0.63 | 0.35 |
| 16 | 2b•HCl (iPr) | –0.77 | 0.12 | –0.77 | 0.27 | –0.76 | 0.13 | –0.74 | 0.28 |
| 17 | 2c (tBu) | –0.19 | 0.60 | –0.16 | 0.76 | –0.32 | 0.42 | –0.36 | 0.54 |
| 18 | 2c•HCl (tBu) | –1.0 | 0.063 | –1.0 | 0.19 | –1.0 | 0.057 | –1.0 | 0.18 |
| 19 | 2d (Ph) | –0.45 | 0.29 | –0.36 | 0.54 | –0.49 | 0.26 | –0.42 | 0.49 |
| 20 | 2d•HCl (Ph) | –1.2 | 0.042 | –1.2 | 0.13 | –1.2 | 0.037 | –1.3 | 0.12 |
| 21 | 2e (Bn) | –0.53 | 0.23 | –0.56 | 0.39 | –0.74 | 0.13 | –0.92 | 0.21 |
| 22 | 2e•HCl (Bn) | –0.80 | 0.11 | –0.88 | 0.23 | –0.91 | 0.083 | –1.0 | 0.18 |
| 23 | 2f (PhMeCH) | –0.58 | 0.21 | –0.60 | 0.37 | –0.51 | 0.25 | –0.52 | 0.42 |
| 24 | 2f•HCl (PhMeCH) | –0.92 | 0.080 | –1.0 | 0.18 | –0.96 | 0.071 | –1.1 | 0.16 |
Calculated free energies [kcal/mol] of equatorial to axial N-inversion in water with corresponding equilibrium ratios compared to experimental equilibrium ratios.
| Entry | Species (R) | Calculated at B3LYP/6-31G(d) | Calculated at B3LYP/6-311++G(3d,3p) | Experimental (Inverse gated 13C NMR) eq/ax ratio at 25 °C | ||
| ΔG | eq/ax | ΔG | eq/ax | |||
| 1 | 1a (Et) | –0.07 | 0.89 | 0.02 | 1 | – |
| 2 | 1a•HCl (Et) | 1.0 | 5.4 | 1.2 | 7.1 | 3.5 |
| 3 | 1b (iPr) | –0.64 | 0.34 | –0.35 | 0.56 | – |
| 4 | 1b•HCl (iPr) | 0.49 | 2.3 | 0.88 | 4.4 | 1.0 |
| 5 | 1c (tBu) | 2.2 | 39.3 | 2.2 | 39.9 | – |
| 6 | 1c•HCl (tBu) | 3.9 | 753.3 | 4.1 | 1046.6 | > 43.6 b |
| 7 | 1d (Ph) | –1.7 | 0.053 | –1.7 | 0.061 | – |
| 8 | 1d•HCl (Ph) | 1.5 | 12.2 | 1.6 | 15.2 | 12.3 |
| 9 | 1e (Bn) | 0.06 | 1.1 | 0.19 | 1.4 | – |
| 10 | 1e•HCl (Bn) | 1.3 | 8.8 | 1.3 | 9 | 10 |
| 11 | 1f (PhMeCH) | 0.004 | 1.0 | –0.02 | 0.97 | – |
| 12 | 1f•HCl (PhMeCH) | 1.6 | 14 | 1.7 | 17.3 | 11.3 |
| 13 | 2a (Et) | –0.67 | 0.32 | –0.53 | 0.41 | – |
| 14 | 2aHCl (Et) | –0.82 | 0.25 | –0.85 | 0.24 | 0.25 |
| 15 | 2b (iPr) | –0.94 | 0.2 | –0.88 | 0.23 | – |
| 16 | 2b•HCl (iPr) | –0.73 | 0.29 | –0.71 | 0.3 | 0.083 |
| 17 | 2c (tBu) | –0.37 | 0.54 | –0.49 | 0.44 | – |
| 18 | 2c•HCl (tBu) | –0.77 | 0.27 | –1.1 | 0.15 | 0.33 |
| 19 | 2d (Ph) | –0.41 | 0.5 | –0.44 | 0.47 | – |
| 20 | 2d•HCl (Ph) | –0.94 | 0.21 | –1.0 | 0.18 | 0.17 |
| 21 | 2e (Bn) | –1.0 | 0.2 | –0.61 | 0.35 | – |
| 22 | 2e•HCl (Bn) | –1.0 | 0.17 | –1.2 | 0.13 | 0.51 |
| 23 | 2f (PhMeCH) | –0.73 | 0.29 | –0.54 | 0.4 | – |
| 24 | 2f•HCl (PhMeCH) | –0.76 | 0.28 | –1.7 | 0.056 | 0.18 |
| 25 | MADa | 188 | 275 |
a Mean absolute deviations (MAD) for the calculated and experimental ratios.
b No minor invertomers signals observed, the ratio is greater than the measured S/N value.
Calculated free energies [kcal/mol] of equatorial to axial N-inversion in methanol with corresponding equilibrium ratios compared to experimental equilibrium ratios.
| Entry | Species (R) | Calculated at B3LYP/6-31G(d) | Calculated at B3LYP/6-311 + +G(3d,3p) | Experimental (Inverse gated 13C NMR) eq/ax ratio at –90 °C | ||||||
| –90 °C | 25 °C | –90 °C | 25 °C | |||||||
| ΔG | eq/ax | ΔG | eq/ax | ΔG | eq/ax | ΔG | eq/ax | |||
| 1 | 1a (Et) | –0.05 | 0.86 | –0.06 | 0.90 | 0.04 | 1.1 | 0.03 | 1.0 | 1.1 |
| 2 | 1a•HCl (Et) | 1.1 | 21.6 | 1.0 | 5.7 | 1.3 | 32.0 | 1.2 | 7.3 | – |
| 3 | 1b (iPr) | –0.72 | 0.14 | –0.64 | 0.34 | –0.50 | 0.26 | –0.34 | 0.56 | 0.12 |
| 4 | 1b•HCl (iPr) | 0.44 | 3.3 | 0.49 | 2.3 | 0.75 | 7.9 | 0.89 | 4.5 | – |
| 5 | 1c (tBu) | 2.1 | 291.7 | 2.2 | 39.2 | 2.1 | 313.1 | 2.2 | 39.8 | > 22.5b |
| 6 | 1c•HCl (tBu) | 4.0 | 53343.7 | 3.9 | 759.1 | 4.1 | 72497.9 | 4.1 | 1027.7 | 25 °C |
| 7 | 1d (Ph) | –2.0 | 0.0046 | –1.8 | 0.053 | –1.9 | 0.0060 | –1.7 | 0.060 | 0.29 |
| 8 | 1d•HCl (Ph) | 1.4 | 51.9 | 1.5 | 11.8 | 1.6 | 75.8 | 1.6 | 14.7 | – |
| 9 | 1e (Bn) | 0.09 | 1.3 | 0.06 | 1.1 | 0.06 | 1.2 | 0.10 | 1.2 | 1.6 |
| 10 | 1e•HCl (Bn) | 1.5 | 62.5 | 1.3 | 8.7 | 1.5 | 56.5 | 1.3 | 9.1 | – |
| 11 | 1f (PhMeCH) | –0.16 | 0.64 | 0.01 | 1.0 | –0.13 | 0.70 | –0.02 | 0.97 | 0.24 |
| 12 | 1f•HCl (PhMeCH) | 1.5 | 59.2 | 1.5 | 13.5 | 1.6 | 80.4 | 1.7 | 17.2 | – |
| 13 | 2a (Et) | –0.73 | 0.13 | –0.67 | 0.32 | –0.62 | 0.18 | –0.52 | 0.41 | 0.076 |
| 14 | 2a•HCl (Et) | –0.74 | 0.13 | –0.82 | 0.25 | –0.77 | 0.12 | –0.85 | 0.24 | – |
| 15 | 2b (iPr) | –0.88 | 0.090 | –0.94 | 0.20 | –0.90 | 0.085 | –0.88 | 0.23 | 0.071 |
| 16 | 2b•HCl (iPr) | –0.64 | 0.17 | –0.74 | 0.29 | –0.63 | 0.17 | –0.72 | 0.30 | – |
| 17 | 2c (tBu) | –0.39 | 0.34 | –0.36 | 0.54 | –0.47 | 0.28 | –0.48 | 0.44 | 0.070 |
| 18 | 2c•HCl (tBu) | –0.76 | 0.12 | –0.76 | 0.28 | –0.97 | 0.069 | –1.0 | 0.17 | – |
| 19 | 2d (Ph) | –0.49 | 0.26 | –0.41 | 0.50 | –0.45 | 0.29 | –0.36 | 0.55 | 0.14 |
| 20 | 2d•HCl (Ph) | –0.90 | 0.085 | –0.94 | 0.20 | –0.72 | 0.14 | –0.78 | 0.27 | – |
| 21 | 2e (Bn) | –0.88 | 0.088 | –0.98 | 0.19 | –0.64 | 0.17 | –0.62 | 0.35 | 0.080 |
| 22 | 2e•HCl (Bn) | –0.87 | 0.092 | –1.1 | 0.17 | –0.91 | 0.081 | –1.2 | 0.14 | – |
| 23 | 2f (PhMeCH) | –0.73 | 0.13 | –0.73 | 0.29 | –0.59 | 0.20 | –0.54 | 0.40 | 0.14 |
| 24 | 2f•HCl (PhMeCH) | –0.70 | 0.15 | –0.76 | 0.28 | –1.4 | 0.024 | –1.8 | 0.051 | – |
| 25 | MADa | 175 | 203 |
a Mean absolute deviations (MAD) for the calculated and experimental ratios.
b No minor invertomer signals were observed, and the ratio is greater than the measured S/N value.
In the gas phase (Table 1), a general dominance of the equatorial forms for the tropane analogues (with the exception of N-isopropyl and N-phenyl) and the axial forms for the granatane analogues was observed. The gas phase calculations also indicated a shift to a higher content of equatorial forms upon protonation of the nitrogen atom in tropanes. In the granatanes, a shift to the axial form was observed. To verify the reliability of the chosen computational methods, a direct comparison with experiment is needed.
2.3 NMR study of N-invertomer distributions
We used a proven approach used by Sturm [26] and by us [40] for the N-methyl analogues based on integration of signals in inverse gated 13C NMR experiments. The 13C NMR spectra of some of the free amines 1 and 2 in methanol at –90 °C and many amines 1 and 2 hydrochlorides in water at room temperature exhibited separate signals for both N-invertomers (Tables 4 and 5). The basis for this phenomenon has been presented by Glaser et al. [55]. The separation of signals in 13C NMR spectra is a result of decreased rate of inversion on the nitrogen atom. Lowering temperature to ca.–100 °C [26] or protonation of the amine nitrogen atom slows down the inversion process enough to make the separate N-invertomers observable at the NMR time scale. The presence of excess acid increases the rate of exchange of hydrogens on amine nitrogen resulting often in sharper signals. Increasing the lifetimes of the two equilibrating invertomers enables the recording of spectra for two separate invertomers at the so-called NMR slow exchange limit (SEL) for isomer interconversion, e.g., at low temperature or for the protonated amine at room temperature. The separation of signals with decreasing temperature for the carbon atoms most sensitive to syn-γ effect is exemplified in Fig. 2. The syn-γ effect in tropanes is due to the relative shielding or de-shielding of carbon atoms C(2,4) and C(6,7) related to the axial or equatorial disposition of the N-alkyl group and associated position of the lone electron pair [26].
13C NMR chemical shifts of relevant carbon atoms (ppm) in methanol illustrating the syn-γ effect in the studied free amine tropinone and granatanone derivatives.
| Species carbon atom | Experimental (ppm) | Predicteda | ||||
| Averaged for both invertomers at 25 °C | Axial N-R invertomer at –90 °C | Equatorial N-R invertomer at –90 °C | Axial N-R invertomer at 25 °C | Equatorial N-R invertomer at 25 °C | ||
| 1a (Et) | C(2,4) | 46.9 | 42.7 | 49.3 | 52.6 | 60.3 |
| C(6,7) | 27.7 | 28.5 | 26.4 | 41.3 | 39.1 | |
| 1b (iPr) | C(2,4) | 44.8 | 42.7 | – | 52.6 | 60.5 |
| C(6,7) | 28.5 | 28.6 | – | 41.2 | 39.3 | |
| 1c (tBu) | C(2,4) | 53.0 | 52.3 | – | 58.4 | 62.2 |
| C(6,7) | 31.2 | 31.2 | – | 42.6 | 43.3 | |
| 1d (Ph) | C(2,4) | 45.5 | 45.1 | – | 54.7 | 59.6 |
| C(6,7) | 28.84 | 28.66 | – | 40.7 | 40.2 | |
| 1e (Bn) | C(2,4) | 47.8 | 44.0 | 50.3 | 52.8 | 60.3 |
| C(6,7) | 27.8 | 29.6 | 27.4 | 41.5 | 39.2 | |
| 1f (PhMeCH) | C(2,4) | 46.2, 45.9 | 43.2, 42.7 | – | 52.5 | 60.3 |
| C(6,7) | 28.4, 28.2 | 28.7, 28.6 | – | 41.2 | 39.0 | |
| 2a (Et) | C(2,4) | 41.8 | 40.0 | – | 50.6 | 57.6 |
| C(6,8) | 30.0 | 31.2 | – | 43.5 | 34.7 | |
| 2b (iPr) | C(2,4) | 42.0 | 40.2 | – | 50.3 | 57.7 |
| C(6,8) | 30.5 | 31.3 | – | 43.8 | 35.3 | |
| 2c (tBu) | C(2,4) | 46.9 | 45.9 | – | 55.8 | 59.0 |
| C(6,8) | 32.6 | 33.1 | – | 44.9 | 40.4 | |
| 2d (Ph) | C(2,4) | 43.6 | 42.7 | – | 53.2 | 56.4 |
| C(6,8) | 30.6 | 31.0 | – | 42.7 | 39.2 | |
| 2e (Bn) | C(2,4) | 43.2 | 41.6 | – | 50.7 | 57.6 |
| C(6,8) | 30.8 | 31.9 | – | 43.5 | 34.7 | |
| 2f (PhMeCH) | C(2,4) | 42.3, 42.0 | 40.4, 40.3 | – | 50.5 | 57.6 |
| C(6,8) | 30.34, 30.26 | 31.5, 31.4 | – | 43.6 | 34.9 |
a Predicted based on B3LYP/6-31G(d) optimised geometry in methanol using the CPCM model and SCF GIAO method (experimental and predicted shifts with the same relative position for equatorial versus axial invertomers are shown in bold).
13C NMR chemical shifts of relevant carbon atoms (ppm) in H2O at 25 °C illustrating the syn-γ effect in the studied N-protonated tropinone and granatanone derivatives.
| Species carbon atom | Experimental (ppm) | Predicted (ppm)a | |||
| Axial N-invertomer | Equatorial N-invertomer | Axial N-invertomer | Equatorial N-invertomer | ||
| 1a•HCl (Et) | C(2,4) | 43.6 | 48.3 | 51.5 | 56.6 |
| C(6,7) | 28.4 | 27.0 | 38.3 | 36.7 | |
| 1b•HCl (iPr) | C(2,4) | 44.5 | 49.2 | 49.2 | 51.6 |
| C(6,7) | 29.3 | 27.9 | 27.9 | 38.4 | |
| 1c•HCl (tBu) | C(2,4) | – | 51.2 | 53.7 | 59.0 |
| C(6,7) | – | 31.1 | 39.3 | 39.8 | |
| 1d•HCl (Ph) | C(2,4) | – | 48.1 | 51.8 | 57.4 |
| C(6,7) | – | 29.3 | 37.8 | 38.6 | |
| 1e•HCl (Bn) | C(2,4) | 45.1 | 49.3 | 51.9 | 56.7 |
| C(6,7) | 29.5 | 28.1 | 38.4 | 36.8 | |
| 1f•HCl (PhMeCH) | C(2,4) | – | 46.6 | 51.5 | 56.8 |
| C(6,7) | – | 25.9 | 38.4 | 36.6 | |
| 2a•HCl (Et) | C(2,4) | 41.7 | – | 49.1 | 54.5 |
| C(6,8) | 32.3 | – | 42.3 | 34.8 | |
| 2b•HCl (iPr) | C(2,4) | 42.6 | – | 49.1 | 54.4 |
| C(6,8) | 32.2 | – | 42.5 | 34.8 | |
| 2c•HCl (tBu) | C(2,4) | 43.8 | 48.6 | 51.3 | 56.7 |
| C(6,8) | 34.3 | 28.2 | 44.8 | 36.9 | |
| 2d•HCl (Ph) | C(2,4) | 44.2 | – | 50.4 | 56.3 |
| C(6,8) | 31.8 | – | 44.0 | 35.4 | |
| 2e•HCl (Bn) | C(2,4) | 41.6 | 46.2 | 49.2 | 54.6 |
| C(6,8) | 31.9 | 25.4 | 42.5 | 34.9 | |
| 2f•HCl (PhMeCH) | C(2,4) | 41.8 | – | 48.9 | 54.6 |
| C(6,8) | 31.7 | – | 42.4 | 35.1 |
a Predicted based on the B3LYP/6-31G(d) optimised geometry in methanol using the CPCM model and SCF GIAO method (experimental and predicted shifts with the same relative position for equatorial versus axial invertomers are shown in bold).
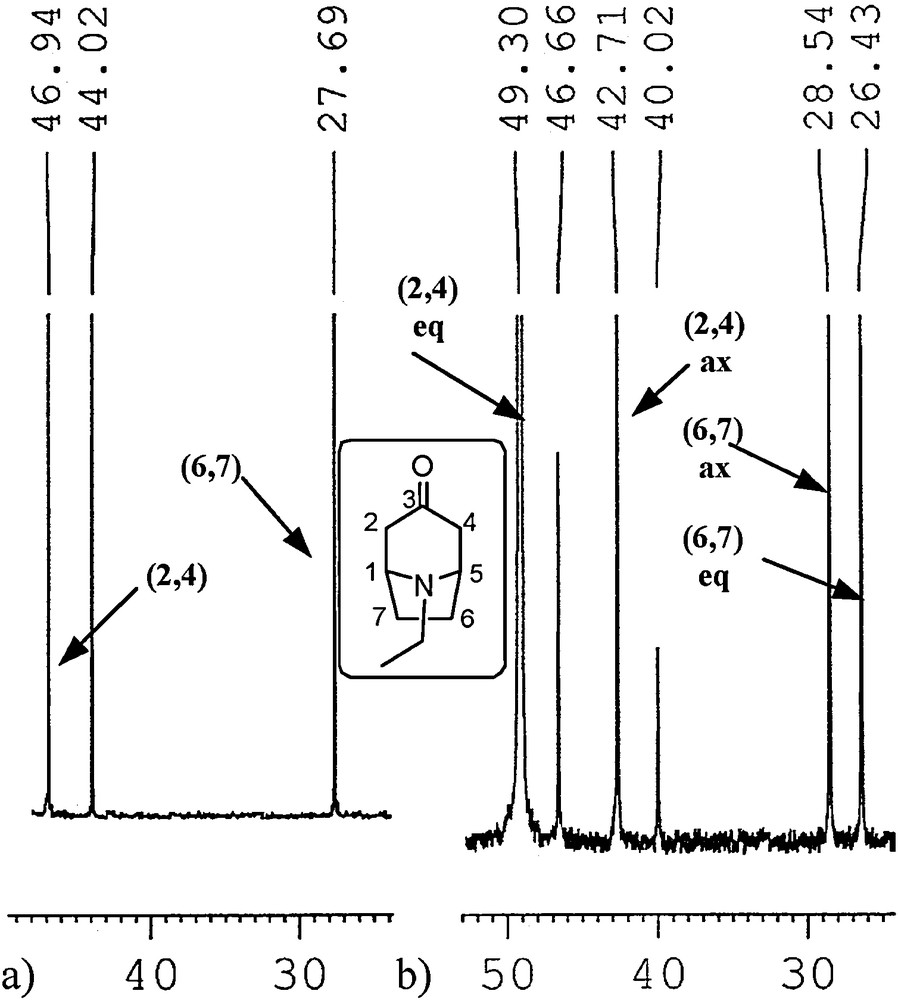
Fragments of 13C NMR spectra of N-ethylnortropinone in MeOH: (a) at room temperature, (b) at –90 °C.
It should be remembered that signals (chemical shifts) at the NMR fast exchange limit (FEL) for interconversion (recorded at room temperature for free amines) correspond to a time-averaged structure. Therefore, the position of the time-averaged signal for a specific carbon of both invertomers recorded at room temperature is found within a shift range set by separated signals (shifts) of the same carbon recorded at lowered temperature. Because of technical limitations, not all signals of the carbons may be separated (peaks may be broadened if the effect is subtle). When the invertomer ratio is higher than the signal-to-noise ratio for the major invertomer, the minor invertomer may be undetected, which results in an apparent lack of signal separation for any atom. Using our previous experience [40], by analogy with the described syn-γ effect applied to tropanes by Sturm [26], and correlation spectroscopy, the split signals were assigned to the specific carbons of two N-invertomers. As previously observed for granatanone (2 R = Me) [40], tropanes 1b–d, 1f and all granatanes 2 exhibited no detectable splitting of signals at –90 °C (Table 4) or even at lower temperatures (up to solvent freezing, ca. –105 °C). However, the signals in the spectra of these compounds shifted slightly as the temperature decreased from room temperature to –90 °C. For these cases, we concluded that only one N-invertomer was observed within the detection limits of the experiments at low temperatures. The content of the major invertomers was estimated from the signal-to-noise ratio in the spectra (Table 3, the actual ratio of major/minor invertomers was equal or higher than the signal-to-noise ratio). For cases where no minor invertomer was visible, comparing the position of signals in the 13C NMR spectra of the invertomer observed at –90 °C with the positions of the corresponding signals at room temperature, which are the time-averaged signals for both invertomers (the axial and the equatorial), we could infer the relative position of the undetected, minor invertomer signals to the major signals (as upfield or downfield to the detected invertomer). This inference combined with the syn-γ effect shown in the predicted relative position of invertomer signals of C(2,4) and C(6,7/8) by a computational model enabled the assignment of the split signals’ chemical shifts to the axial or the equatorial form (the assignments are shown in Tables 4 and 5). According to the computational model, the 13C shifts were calculated using the DFT optimised geometry and the SCF GIAO method as implemented in GAUSSIAN 09.
The calculated shifts for the relevant atoms and the experimental shifts for the free amines are compared in Table 4. The relative position of the calculated and experimental signals could not be used for invertomer identification in two cases (1c and 1d). In these cases, the experimental and predicted shifts for C(6,7) did not follow the trend. Thus, the dominating invertomer was assumed to be the one predicted on the basis of the calculated equilibrium distributions. To sum up, using the observed NMR shifts at low temperature and at room temperature (Table 4) and the invertomer distributions obtained from DFT calculations (Table 3), we accept that all granatanes and tropanes 1b, 1d, and 1f, at low temperatures in methanol solution, exhibit dominating invertomers with the N-axial group, which is in contrast to tropanes 1a, 1c, and 1e.
The room-temperature NMR spectra of the hydrochlorides of amines 1 and 2 in water exhibited the separation of many signals into resonances corresponding to species with axial and equatorial N-substituents analogous to their N-methyl analogues [39]. We assigned the signals (Table 5) based on literature data [39], correlation spectroscopy, and correspondence to the spectra of free amines (Table 4). The results from the calculations and the shift predictions from SCF GIAO also supported the assignments in the protonated amines, except 1b•HCl, where one pair of signals did not follow the trend (Table 5). However, for some of the protonated forms, no separation of signals of C(2,4) and C(6,7/8) corresponding to the separate invertomers was observed (Table 5). In these cases, the assignment could not be verified by the relative shielding prediction and was based only on calculated invertomer dominance (Table 2). We can conclude that, at room temperature in water, the preferred isomer of protonated granatanes has the axial N-substituent, while for tropanes the opposite N-equatorial isomer is preferred.
The experimental relative ratio of isomers (Tables 2 and 3) was obtained by dividing peak areas of signals corresponding to the same carbon atom (typically the carbonyl) in both isomeric species in the inverse gated 13C NMR spectra. In cases where no minor invertomer was detected, the signal-to-noise ratio was used as an estimate of the minimum value of the major-to-minor isomer ratio.
2.4 Comparisons and discussion of the calculated and experimental distributions
The invertomer distributions in methanol and water observed in the inverse gated 13C NMR experiments are quantitatively compared with the distributions calculated by the computational methods (Tables 2 and 3). The accuracy of methods, such as B3LYP, is only moderate, and this functional is able to predict stereoselectivities with errors of less than 0.5 kcal/mol [56]. Variation in the results of this order would yield a variation in the invertomer distribution ratio on the order 2.3 at T = 298 K and ca. 4 at T = 183 K.
To obtain a quantitative estimate of the accuracy of the theoretical methods, the mean (average) absolute deviation (MAD) values are defined as:
are reported in Tables 2 and 3. In the above formula, n is the number of experimental results available, ratioexp denotes the measured distribution, and ratiocalc represents the distribution calculated with a given computational method. Summation is extended over all the species for which the experimental distributions are available. Of course, a smaller MAD value indicates that the results from a given method agree more closely with the experimental data.
For the tert-butyl derivative 1c and its salt (Tables 2 and 3), the signals from the minor invertomers were too weak to observe by 13C NMR spectroscopy under the experimental conditions used. The relative amounts of N-invertomers were estimated from the signal-to-noise ratio for the major invertomers. The S/N was limited by the experimental time and solubility. Therefore, the experimental ratio of invertomers for the nortropinone tert-butyl derivatives was estimated as greater than 22.5 for 1c and greater than 43.6 for 1c•HCl. A comparison of these experimental data with those obtained from the calculations resulted in a very high relative error and overstated MAD values. The exclusion of these uncertain cases would improve the MAD values for B3LYP/6-31g(d) and B3LYP/6-311++g(3d,3p) in Table 3 to 83 and 105, respectively, and in Table 2 to 58 and 91, respectively. This indicates a good overall agreement of the computational methods with experimental results and points towards the simpler basis set as better choice for this type of problem.
The calculated ratio of equatorial/axial isomers for the tert-butyl nortropane derivative 1c in methanol at –90 °C reached the very high value of ca. 300 for the free amine and more than 50,000 for the protonated one; this stems from the calculated difference in the free energy of invertomers (ΔG of equatorial to axial inversion) ca. 2.1 and 4 kcal/mol for the free and the protonated forms, respectively (Table 3). This high invertomer ratios stand out from the other results; however, considering the commonly accepted A values [57,58] for the tert-butyl substituent (4.9 kcal/mol [59]) and the expected preference of the substituent in the tropane system, this is a reasonable result [60]. The lower free energy of inversion for derivatives with the bulky isopropyl and the benzyl group can be rationalized by their axial form attaining the lowest energy conformations in which the C–H bond is positioned between the pseudoaxial hydrogens of the C(4) and C(2) carbons of the tropane system (Fig. 3a and b). In case of the tert-butyl group, which has no such C–H bond but a C–CH3 group instead (Fig. 3c), much higher destabilising interactions in the axial N-invertomer are expected. The differences between the tert-butyl, and isopropyl and ethyl groups observed experimentally and calculated for the tropane system are less than the corresponding A values (ΔG° 4.9, 2.1, 1.8 kcal/mol, respectively [57,58]). This can be rationalized based on the flattening of the piperidone ring, compared to the cyclohexanone for which the A values are given, and the resulting diminished interactions with pseudoaxial hydrogens at C(2) and C(4). The flat phenyl substituent may adopt the lowest energy conformation with lessened steric interactions with the piperidone ring (Fig. 3d) favouring also the axial invertomer of the free amine (entry 7 in Tables 1, 2 and 3). In granatane derivatives, the interactions within the piperidine ring (equatorial N-substituent) are expected to be stronger than within the flattened piperidone ring (axial N-substituent). This accounts for reversed invertomer preferences in the granatane series; both free amines and protonated amine favoured the axial invertomers (Tables 1, 2 and 3).
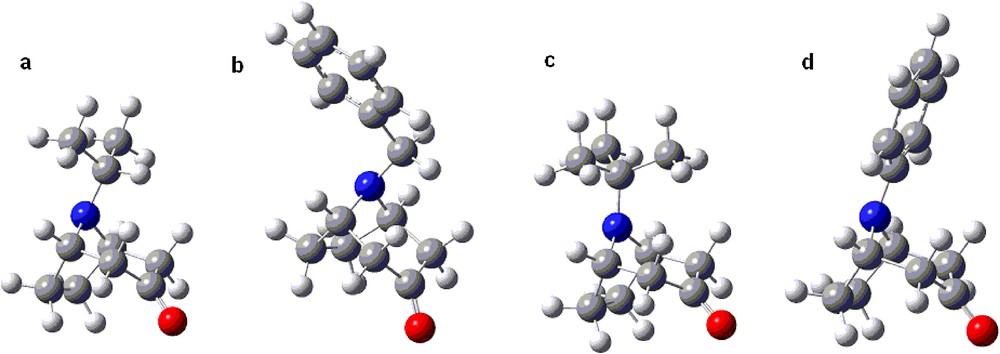
(Colour online.) a–d. The lowest energy conformations of representative N-axial invertomers.
The calculated invertomer ratios for free amines (Table 3) agreed qualitatively and reasonably well quantitatively with the experimental values. Experiments and calculations provided complementary data indicating that in methanol and water the free amine equatorial isomers dominated in the N-benzylnortropinone and especially in the N-tert-butylnortropinone. The axial forms dominated in the remaining tropanones, except 1a (N-ethyl) and all of the norgranatanone derivatives. The experimental results for protonated amines in water (HCl salts) were also qualitatively and fairly quantitatively reproduced by the calculations (Table 2). Both basis sets yielded a fairly good level of accuracy for reproducing the experimental results for free and protonated amines (Tables 2 and 3) with slightly lower MAD values for the 6-31G(d). Therefore, based on the much lower computational demands of the 6-31G(d) basis set, this level of theory is recommended for this type of problem. It can also be inferred, from both experiments and calculations, that the protonation of nitrogen in the nortropinone derivatives shifts the equilibrium toward the equatorial N-invertomers. Especially striking was the reversal of the dominant configuration of the N-isopropyl and N-phenyl groups of tropanones (e.g., for Ph from 0.29 to 12.3, experiment for 1d, entry 7, Table 3 versus entry 8, Table 2). According to experiment, the invertomer distributions in the norgranatanone derivatives appeared to be affected in the same way by protonation, but the axial forms remained dominant. According to both levels of theory, protonation in the granatane analogues shifted the invertomer equilibriums to some degree, and the direction of this shift was dependent on the N-substituent and temperature. In addition, in some cases, the predicted direction of the equilibriums shifts differed based on the basis set used. The protonation effect in the computed equilibriums in the granatanone series were within the errors of the method and as such could be regarded as inconclusive. However, the axial preference of the N-substituents in the protonated granatanones was clear. The found N-invertomers preference for the granatanes and for isopropyl and phenyl tropane derivatives agrees qualitatively with previous works [24,25,40]. For the rest of tropanes, e.g. benzyl derivative 1e, the differences with previous reports may be accounted for by the different solvents used (methanol and water in this study vs. CDCl3 [23]). The calculations, despite the known limited accuracy of the DFT methods, ca. 0.5 kcal/mol [56], and the relatively simple methodology commonly used by organic chemists (using comparisons of the lowest energy conformations and the B3LYP with moderate basis set) gave fairly good overall agreement with experiments.
3 Conclusions
The results from the calculations and experiments can be summarised as follows.
The DFT computational methods provide generally satisfactory reproduction of the distribution of axial and equatorial invertomers of N-substituted tropanones and granatanones in both the protonated and free amine forms.
Although both basis sets yielded results in reasonable agreement with experiment, the popular and less computationally demanding B3LYP/6-31G(d) level of theory provided slightly better reproduction of experimental data and is recommended for determining isomer distributions for these types of structures. A larger and much more CPU-demanding basis set with diffuse functions does not necessarily provide better quantitative results with respect to its ability to properly predict the invertomer distributions compared to the simple basis set.
Predominance of the equatorial invertomers in N-tert-butyl- and N-benzylnortropinone and the axial invertomers in N-isopropyl-, N-phenylnortropanes as well as all of the granatanone derivatives was experimentally observed and computationally determined in solution and in the gas phase. For N-ethyl- and N-phenethylnortropinone, the ratio between the equatorial and axial forms was close to 1 in solutions.
Our experiments indicated that nitrogen protonation shifted the invertomer equilibrium toward the equatorial forms. DFT calculations reproduced this effect for N-substituted nortropanes. Inversion of the equatorial/axial ratio was predicted by DFT calculations for N-isopropyl nortropinone.
For protonated amines, the results from the computational methods and experiments indicated a preference for the equatorial invertomers in tropanones and the axial forms in granatanones.
4 Experimental
4.1 General methods
Magnetic resonance spectra were recorded on a Bruker AVANCE II 400 spectrometer using 5-mm probes, operating at 400 MHz for 1H and 100 MHz for 13C. The chemical shifts are reported in ppm downfield of tetramethylsilane. The chemical shifts were determined relative to residual CD2HOD (1H δ 3.31) and internal CD3OD (13C δ 49.0) as secondary references for the methanol-d4 solutions and relative to DSS (1H and 13C δ 0.0) for the aqueous solutions. For low-temperature measurements, the temperatures of the probe were calibrated with methanol. No-D NMR spectroscopy [45] was used for experiments in non-deuterated solvents (i.e., H2O, CH3OH). In this case, the spectra were recorded using shimming of the FID signal. Quantification of the 13C signals was achieved using inverse gated mode spectra. When required, the analysis and assignment of the 1H and 13C NMR data were supported by homonuclear (COSY) and heteronuclear (HSQC and HMBC) correlation experiments.
4.2 General procedure for the synthesis of N-substituted tropanones 1 and granatanones 2
Step 1. Tropinone (1, R = Me) or granatanone (2, R = Me) (5.00 mmol, 1.00 equiv) was dissolved in acetone (5 mL). Methyl iodine (5.50 mmol, 1.10 equiv) was added dropwise over 45 min, and the reaction was stirred at room temperature for 1 h. The methiodide precipitate was filtered, washed with acetone and hexane and dried over P2O5 [46].
4.2.1 8,8-Dimethyl-3-oxo-8-azoniabicyclo[3.2.1]octane iodide [46]
White solid, (1.278 g, 91%) decomp. 200 °C, 1H NMR: (400 MHz, DMSO-d6) δ 4.15 (br s, 2H), 3.40 (s, 3H), 3.18 (s, 3H), 3.15–3.07 (m, 2H), 2.57–2.40 (m, 4H), 1.99–1.92 (m, 2H); 13C NMR: (100.6 MHz, DMSO-d6) δ 202.2, 68.1, 50.4, 44.4, 44.1, 26.0; IR: (KBr) 2942, 1727, 1205 cm−1.
4.2.2 9,9-Dimethyl-3-oxo-9-azoniabicyclo[3.3.1]nonane iodide
White solid, (1.327 g, 90%), decomp. 200 °C, 1H NMR: (400 MHz, DMSO-d6) δ 3.92 (br s, 2H), 3.36 (s, 3H), 3.31 (s, 3H), 3.26 (d, J = 7.0 Hz, 2H), 2.57 (d, J = 19.1 Hz, 2H), 2.43–2.30 (m, 2H), 1.82–1.72 (m, 2H), 1.65–1.57 (m, 1H), 1.49–1.25 (m, 1H); 13C NMR: (100.6 MHz, DMSO-d6) δ 202.4, 63.2, 50.8, 49.8, 41.1, 25.0, 12.3; IR: (KBr) 2935, 1720, 1193 cm−1; HRMS: (ESI, m/z) (M+–I) calculated for C10H18NO+: 168,1383, found: 168,1389.
Step 2. To a solution of the appropriate amine (2.00 mmol, 1.00 equiv) in 5 mL of ethanol, K2CO3 (4.20 mmol, 2.10 equiv) dissolved in water (2 mL) was added. The resulting solution was heated to reflux, and a solution of tropinone or granatanone methiodide (2.20 mmol, 1.10 equiv) in water (3.5 mL) was added dropwise over 45 min. The reaction mixture was refluxed for 4 h, cooled to room temperature and concentrated under vacuum. The residue was extracted with dichloromethane (3 × 25 mL), and the combined extracts washed with brine (2 × 15 mL), dried over Na2SO4 and concentrated under vacuum [46].
The amine hydrochlorides were obtained directly prior to analysis by evaporation under vacuum of mixtures of amino ketones 1 or 2 with excess hydrochloric acid followed by vacuum drying.
4.2.3 8-Ethyl-8-azabicyclo[3.2.1]octan-3-one (1a) [61,62]
Ethylamine hydrochloride (2.00 mmol, 1.00 equiv) and K2CO3 (6.20 mmol, 3.10 equiv) were used instead of free amine. The product was purified by Kugelrohr distillation (80 °C, 1 Torr). For 2.00 mmol scale: yellow oil (0.136 g, 44%); Rf 0.3 (50% AcOEt/hexane); 1H NMR: (400 MHz, CDCl3) δ 3.59 (br s, 2H), 2.75–2.61 (app m, 4H), 2.20 (d, J = 15.4 Hz, 2H), 2.10–2.01 (m, 2H), 1.67–1.57 (m, 2H), 1.20 (t, J = 7.2 Hz, 3H); 13C NMR: (100.6 MHz CDCl3) δ 210.1, 58.0, 47.1, 43.8, 27.9, 14.0.
4.2.3.1 8-Ethyl-8-azabicyclo[3.2.1]octan-3-one•HCl
Major invertomer 1H NMR: (400 MHz, CDCl3) δ 4.12 (br s, 2H), 3.64 (dd, J = 16.7, 3.3 Hz, 2H), 3.09 (quintet, J = 6.8, Hz, 2H), 2.39 (d, J = 16.5 Hz, 2H), 2.33–2.25 (m, 2H), 1.95–1.86 (m, 2H), 1.49 (t, J = 7.2 Hz, 3H); 13C NMR: (100.6 MHz, CDCl3) δ 202.1, 60.3, 47.1, 46.3, 25.5, 10.1.
Minor invertomer 1H NMR: (400 MHz, CDCl3) δ 4.12 (br s, 2H), 3.45 (quintet, J = 6.7 Hz, 2H), 2.95 (dd, J = 18.2, 4.1 Hz, 2H), 2.62–2.55 (m, 2H), 2.49–2.35 (m, 2H), 1.83–1.78 (m, 2H), 1.50 (app t, J = 4.2 Hz, 3H); 13C NMR: (100.6 MHz, CDCl3) δ 201.3, 57.2, 42.2, 41.4, 26.6, 10.4.
4.2.4 8-Isopropyl-8-azabicyclo[3.2.1]octan-3-one (1b) [23,61]
For 2.00 mmol scale: yellow oil (0.191 g, 57%); Rf 0.64 (7% MeOH/DCM); 1H NMR: (400 MHz, CDCl3) δ 3.79 (br s, 2H), 2.94 (septet, J = 6.2 Hz, 1H), 2.67 (dd, J = 16.0, 4.3 Hz, 2H), 2.15 (d, J = 15.8 Hz, 2H), 2.08–1.99 (m, 2H), 1.67–1.57 (m, 2H), 1.20 (d, J = 6.2, 6H); 13C NMR: (100.6 MHz, CDCl3) δ 210.1, 55.6, 45.3. 45.0, 28.6, 22.0.
4.2.4.1 8-Isopropyl-8-azabicyclo[3.2.1]octan-3-one•HCl
Major invertomer 1H NMR: (400 MHz, CDCl3) δ 4.33 (br s, 2H), 3.83 (d, J = 16.2 Hz, 2H), 3.21–3.11 (m, 1H), 2.45 (d, J = 16.4 Hz, 2H), 2.33–2.23 (m, 2H), 2.01–1.92 (m, 2H), 1.64 (d, J = 5.7, 6H); 13C NMR: (100.6 MHz, CDCl3) δ 202.4, 59.2, 53.5. 46.5, 25.7, 18.7.
Minor invertomer 1H NMR: (400 MHz, CDCl3) δ 4.26 (br s, 2H), 3.79–3.67 (m, 1H), 2.92 (d, J = 15.9 Hz, 2H), 2.81–2.70 (m, 2H), 2.52–2.48 (m, 2H), 1.92–1.83 (m, 2H), 1.62 (d, J = 5.6, 6H); 13C NMR: (100.6 MHz, CDCl3) δ 201.3, 56.4, 49.2, 42.2, 26.8, 18.7.
4.2.5 8-tert-Butyl-8-azabicyclo[3.2.1]octan-3-one (1c) [63]
tert-Butylamine (0.63 mL, 6.0 mmol) was added to a solution of 8,8-dimethyl-3-oxo-8-azonia-bicyclo[3.2.1]octane iodide (0.590 g, 2.00 mmol) in 3.5 mL of DMSO. The reaction was refluxed for 24 h, cooled to room temperature, extracted with hexane (3 × 25 mL), dried over Na2SO4 and reduced under vacuum. The compound was purified by column chromatography on neutral alumina with 1.5% AcOEt/hexane as the eluent to yield a yellow oil (0.050 g, 14%); Rf 0.55 (15% AcOEt/hexane, neutral alumina); 1H NMR: (400 MHz, CDCl3) δ 3.86 (br s, 2H), 2.55 (dd, J = 16.1, 4.6 Hz, 2H), 2.29 (d, J = 16.6 Hz, 2H), 1.94–1.85 (m, 2H), 1.69–1.59 (m, 2H), 1.14 (s, 9H); 13C NMR: (100.6 MHz, CDCl3) δ 212.2, 54.3, 53.2, 53.1, 31.1, 29.1.
4.2.5.1 8-tert-Butyl-8-azabicyclo[3.2.1]octan-3-one•HCl
1H NMR: (400 MHz, CDCl3) δ 4.39 (br s, 2H), 4.20 (dd, J = 16.3 Hz, 2H), 2.45 (d, J = 16.5 Hz, 2H), 2.40–2.27 (m, 2H), 1.99 (d, J = 8.7 Hz, 2H), 1.68 (s, 9H); 13C NMR: (100.6 MHz, CDCl3) δ 202.7, 64.3, 58.7, 48.5, 29.2, 26.4.
4.2.6 8-Phenyl-8-azabicyclo[3.2.1]octan-3-one (1d) [46,64,65]
The compound was purified by recrystallization from Et2O/hexane. For 2.00 mmol scale: yellow solid (0.326 g, 40%); mp 73–74 °C; Rf 0.7 (50% AcOEt/hexane); 1H NMR: (400 MHz CDCl3) δ 7.39–7.28 (m, 2H), 6.95–6.78 (m, 3H), 4.52 (br s, 2H), 2.72 (dd, J = 15.4, 4.2 Hz, 2H), 2.34 (d, J = 15.4, 2H), 2.28–2.15 (m, 2H), 1.87–1.77 (m, 2H); 13C NMR: (100.6 MHz, CDCl3) δ 208.1, 145.1, 129.8, 118.4, 114.9, 54.4, 45.6, 28.8.
4.2.6.1 8-Phenyl-8-azabicyclo[3.2.1]octan-3-one•HCl
1H NMR: (400 MHz CDCl3) δ 7.66–7.38 (m, 5H), 4.61 (br s, 2H), 3.90 (d, J = 16.3, Hz, 2H), 2.52 (d, J = 16.4, 2H), 2.45–2.29 (m, 2H), 2.05–1.95 (m, 2H); 13C NMR: (100.6 MHz, CDCl3) δ 202.0, 137.8, 130.1, 129.5, 121.6, 63.8, 46.1, 27.0.
4.2.7 8-Benzyl-8-azabicyclo[3.2.1]octan-3-one (1e)
The compound was synthesised by an adapted literature procedure [47].
For 2.00 mmol scale: yellow solid (0.323 g, 75%); mp 32–34 °C; Rf 0.4 (30% AcOEt/hexane); 1H NMR: (400 MHz, CDCl3) δ 7.48–7.22 (m, 5H), 3.76 (s, 2H), 3.57–3.43 (m, 2H), 2.70 (dd, J = 16.0, 4.6 Hz, 2H), 2.28–2.18 (m, 2H), 2.15–2.05 (m, 2H), 1.61–1.55 (m, 2H); 13C NMR: (100.6 MHz, CDCl3) δ 210.1, 139.3, 128.3, 128.2, 127.0, 58.4, 55.0, 48.1, 27.7.
4.2.7.1 8-Benzyl-8-azabicyclo[3.2.1]octan-3-one•HCl
Major invertomer 1H NMR: (400 MHz, CDCl3) δ 7.88–7.78 (m, 2H), 7.45–7.35 (m, 3H), 4.25 (d, J = 6.4 Hz, 2H), 3.86 (br s, 2H), 3.78 (d, J = 6.7 Hz, 2H), 2.51–2.33 (m, 4H), 2.05–1.92 (m, 2H); 13C NMR: (100.6 MHz, CDCl3) δ 202.2, 130.9, 130.2, 129.4, 128.7, 60.2, 55.2, 46.4, 25.8.
Minor invertomer 1H NMR: (400 MHz, CDCl3) δ 7.98–7.80 (m, 2H), 7.45–7.35 (m, 3H), 4.61 (d, J = 5.7 Hz, 2H), 4.05–3.98 (m, 2H), 3.20–3.11 (m, 2H), 2.82–2.70 (m, 2H), 2.51–2.41 (m, 2H), 1.90–1.79 (m, 2H); 13C NMR: (100.6 MHz, CDCl3) δ 201.6, 130.3, 130.2, 129.3, 128.7, 57.8, 49.8, 42.6, 26.9.
4.2.8 8-(1-Phenylethyl)-8-azabicyclo[3.2.1]octan-3-one (1f) [46,66]
The compound was purified by flash chromatography on silica gel with 15% AcOEt/hexane as the eluent. For 2.00 mmol scale: yellow solid (0.291 g, 63%); mp 60–62 °C; Rf 0.6 (50% AcOEt/hexane); 1H NMR: (400 MHz, CDCl3) δ 7.47–7.25 (m, 5H), 3.78 (q, J = 6.4 Hz, 1H), 3.70–3.65 (m, 1H), 3.56–3.50 (m, 1H), 2.77–2.65 (app m, 2H), 2.20–2.09 (app m, 2H), 2.08–1.95 (m, 2H), 1.65–1.56 (m, 2H), 1.42 (d, J = 6.4 Hz, 3H); 13C NMR: (100.6 MHz, CDCl3) δ 210.5, 145.5, 128.5, 127.1, 126.9, 56.7, 56.1, 56.0, 46.4, 46.2, 28.4, 28.1, 23.2.
4.2.8.1 8-(1-Phenylethyl)-8-azabicyclo[3.2.1]octan-3-one•HCl
Major invertomer 1H NMR: (400 MHz, CDCl3) δ 7.90–7.75 (m, 2H), 7.46–7.28 (m, 3H), 4.58–4.46 (m, 1H), 4.04 (d, J = 14.6 Hz, 2H), 3.67–3.51 (m, 2H), 2.70–2.52 (m, 1H), 2.46 (d, J = 16.6 Hz, 1H), 2.20 (d, J = 15.8 Hz, 2H), 1.97 (d, J = 6.0 Hz 4H), 1.88–1.67 (m, 1H); 13C NMR: (100.6 MHz, CDCl3) δ 202.6, 135.4, 129.7, 129.5, 128.2, 62.5, 60.2, 60.0, 46.4, 46.1, 25.8, 25.3, 19.1.
Minor invertomer 1H NMR: (400 MHz, CDCl3) δ 8.05–7.90 (m, 2H), 7.46–7.28 (m, 3H), 4.92–4.78 (m, 1H), 4.58–4.46 (m, 1H), 3.67–3.51 (m, 1H), 3.38–3.25 (m, 1H), 3.05–2.89 (m, 2H), 2.70–2.52 (m, 2H), 2.20 (d, J = 15.8 Hz, 1H), 1.98–1.89 (m, 4H), 1.88–1.67 (m, 1H); 13C NMR: (100.6 MHz, CDCl3) δ 201.5, 136.1, 129.5, 129.4, 127.8, 57.9, 57.1, 42.5, 42.3, 27.1, 26.5, 19.4.
4.2.9 9-Ethyl-9-azabicyclo[3.3.1]nonan-3-one (2a) [62,67,68]
Ethylamine hydrochloride (2.00 mmol, 1.00 equiv) and K2CO3 (6.20 mmol, 3.10 equiv) were used instead of free amine. The compound was purified by flash chromatography on silica gel with 3% MeOH/DCM as the eluent. For 2.00 mmol scale: yellow oil (0.123 g, 37%); Rf 0.4 (50% AcOEt/hexane); 1H NMR: (400 MHz, CDCl3) δ 3.45–3.38 (m, 2H), 2.77 (q, J = 7.2, 2H), 2.68 (dd, J = 16.7, 6.6 Hz, 2H), 2.26 (d, J = 16.7, 2H), 1.98–1.85 (m, 2H), 1.60–1.40 (m, 4H), 1.15 (t, J = 7.2 Hz, 3H); 13C NMR: (100.6 MHz CDCl3) δ 211.3, 53.3, 46.2, 42.3, 29.7, 16.5, 13.4.
4.2.9.1 9-Ethyl-9-azabicyclo[3.3.1]nonan-3-one•HCl
Major invertomer 1H NMR: (400 MHz, CDCl3) δ 3.94–3.87 (m, 2H), 3.80–3.68 (m, 2H), 3.48–3.33 (m, 2H), 2.55 (d, J = 16.5 Hz, 2H), 2.17–2.05 (m, 2H), 1.90–1.71 (m, 4H), 1.66–1.52 (m, 3H); 13C NMR: (100.6 MHz CDCl3) δ 203.0, 53.5, 46.3, 44.1, 23.5, 14.1, 9.8.
Minor invertomer 1H NMR: (400 MHz, CDCl3) δ 4.05–3.97 (m, 2H), 3.48–3.33 (m, 2H), 3.02–2.78 (m, 4H), 2.55 (d, J = 16.5 Hz, 2H), 1.90–1.71 (m, 4H), 1.66–1.52 (m, 3H); 13C NMR: (100.6 MHz, CDCl3) δ 201.3, 54.1, 47.3, 39.6, 29.3, 14.2, 9.7.
4.2.10 9-Isopropyl-9-azabicyclo[3.3.1]nonan-3-one (2b) [61,67]
For 2.00 mmol scale: yellow solid (0.328 g, 82%); mp 53–55 °C; Rf 0.6 (7% MeOH/DCM); 1H NMR: (400 MHz, CDCl3) δ 3.67 (br s, 2H), 3.05 (septet, J = 6.2 Hz, 1H), 2.64 (dd, J = 16.6, 6.6 Hz, 2H), 2.23 (d, J = 16.8 Hz, 2H), 1.93–1.83 (m, 2H), 1.68–1.46 (m, 4H), 1.16 (d, J = 6.2, 6H); 13C NMR: (100.6 MHz, CDCl3) δ 211.8, 50.5, 47.4, 42.5, 30.3, 21.8, 16.5.
4.2.10.1 9-Isopropyl-9-azabicyclo[3.3.1]nonan-3-one•HCl
Major invertomer 1H NMR: (400 MHz, CDCl3) δ 4.15 (br s, 2H), 3.95 (dd, J = 16.8, 5.6 Hz, 2H), 3.90–3.77 (m, 1H), 2.54 (d, J = 16.8 Hz, 2H), 2.20–2.03 (m, 2H), 1.90–1.82 (m, 4H), 1.80–1.75 (m, 6H); 13C NMR: (100.6 MHz, CDCl3) δ 203.4, 52.0, 44.0, 23.5, 18.2, 13.9.
Minor invertomer 1H NMR: (400 MHz, CDCl3) δ 4.24 (br s, 2H), 3.72–3.58 (m, 1H), 2.87 (dd, J = 18.2, 6.2 Hz, 2H), 2.55 (d, J = 18.2 Hz, 2H), 1.90–1.82 (m, 4H), 1.80–1.75 (m, 6H), 1.30–1.22 (m, 2H); 13C NMR: (100.6 MHz, CDCl3) δ 201.7, 52.7, 52.4, 39.6, 29.2, 17.8, 14.3.
4.2.11 9-tert-Butyl-9-azabicyclo[3.3.1]nonan-3-one (2c) [67]
The compound was purified by preparative thin-layer chromatography on silica gel with 25% AcOEt/hexane as the eluent. For 2.00 mmol scale: yellow oil (0.024 g, 6%); Rf 0.63 (30% AcOEt/hexane); 1H NMR: (400 MHz, CDCl3) δ 3.81 (br s, 2H), 2.50 (dd, J = 16.6, 6.7 Hz, 2H), 2.29 (d, J = 16.7 Hz, 2H), 1.80–1.68 (m, 2H), 1.59–1.49 (m, 4H), 1.20 (s, 9H); 13C NMR: (100.6 MHz, CDCl3) δ 213.4, 54.1, 48.3, 46.9, 32.1, 30.0, 17.1.
4.2.11.1 9-tert-Butyl-9-azabicyclo[3.3.1]nonan-3-one•HCl
Major invertomer 1H NMR: (400 MHz, CDCl3) δ 4.25 (br s, 2H), 4.23–4.18 (m, 2H), 2.42 (d, J = 14.8 Hz, 2H), 2.31–2.19 (m, 2H), 1.77–1.75 (m, 2H), 1.75 (s, 9H), 1.72–1.70 (m, 2H); 13C NMR: (100.6 MHz, CDCl3) δ 203.6, 67.2, 52.1, 46.2, 28.3, 26.1, 13.2.
Minor invertomer 1H NMR: (400 MHz, CDCl3) δ 4.32 (br s, 2H), 3.29 (t, J = 13.6 Hz, 2H), 3.05 (dd, J = 19.4, 6.7 Hz, 2H), 2.54 (d, J = 19.5 Hz, 2H), 1.85–1.79 (m, 1H), 1.72 (s, 9H), 1.69–1.65 (m, 2H), 1.58–1.64 (m, 1H); 13C NMR: (100.6 MHz, CDCl3) δ 201.9, 66.8, 53.0, 41.8, 31.0, 27.5, 14.4.
4.2.12 9-Phenyl-9-azabicyclo[3.3.1]nonan-3-one (2d) [28,69]
The compound was purified by flash chromatography on silica gel with 8% AcOEt/hexane as the eluent. For 2.00 mmol scale: yellow solid (0.132 g, 30%); mp 65–66 °C; Rf 0.73 (50% AcOEt/hexane); 1H NMR: (400 MHz, CDCl3) δ 7.36–7.28 (m, 2H), 7.03–6.95 (m, 2H), 6.89–6.78 (m, 1H), 4.48 (br s, 2H), 2.67 (dd, J = 16.4, 6.6 Hz, 2H), 2.41 (d, J = 16.4, 2H), 2.06–1.91 (m, 2H), 1.85–1.73 (m, 2H), 1.70–1.60 (m, 2H); 13C NMR: (100.6 MHz, CDCl3) δ 210.0, 147.9, 129.6, 118.4, 114.0, 50.9, 43.7, 30.4, 16.6.
4.2.12.1 9-Phenyl-9-azabicyclo[3.3.1]nonan-3-one•HCl
1H NMR: (400 MHz, CDCl3) δ 7.78–7.38 (m, 5H), 4.68 (br s, 2H), 3.60 (dd, J = 17.3, 5.6 Hz, 2H), 2.61 (d, J = 17.3, 2H), 2.45 (t, J = 12.4 Hz, 2H), 1.83 (d, J = 14.5 Hz, 2H), 1.79–1.60 (m, 2H); 13C NMR: (100.6 MHz, CDCl3) δ 209.4, 147.0, 129.7, 119.3, 114.7, 51.4, 43.6, 30.1, 16.4.
4.2.13 9-Benzyl-9-azabicyclo[3.3.1]nonan-3-one (2e)
The compound was synthesised by an adapted literature procedure [47].
For 2.00 mmol scale: white solid (0.353 g, 77%); mp 72–74 °C Rf 0.82 (10% MeOH/DCM); 1H NMR: (400 MHz, CDCl3) δ 7.45–7.22 (m, 5H), 3.92 (s, 2H), 3.39–3.28 (m, 2H), 2.73 (dd, J = 16.6, 6.4 Hz, 2H), 2.26 (d, J = 16.0, 2H), 2.10–1.74 (m, 2H), 1.61–1.41 (m, 4H); 13C NMR: (100.6 MHz, CDCl3) δ 211.3, 139.1, 128.2, 128.1, 127.0, 56.9, 53.4, 42.7, 29.2, 16.4.
4.2.13.1 9-Benzyl-9-azabicyclo[3.3.1]nonan-3-one•HCl
Major invertomer 1H NMR: (400 MHz, CDCl3) δ 8.16–7.80 (m, 2H), 7.55–7.31 (m, 3H), 4.69–4.35 (m, 2H), 3.90–3.69 (m, 4H), 2.55–2.40 (m, 2H), 2.35–2.19 (m, 2H), 1.89–1.60 (m, 4H); 13C NMR: (100.6 MHz, CDCl3) δ 203.0, 131.3, 130.2, 129.5, 128.3, 54.9, 53.6, 44.2, 23.8, 14.1.
Minor invertomer 1H NMR: (400 MHz, CDCl3) δ 8.16–7.80 (m, 2H), 7.55–7.31 (m, 3H), 4.69–4.35 (m, 2H), 3.90–3.69 (m, 2H), 3.39–3.05 (m, 2H), 3.01–2.79 (m, 2H), 2.55–2.40 (m, 2H), 1.89–1.60 (m, 3H), 1.59–1.32 (m, 1H); 13C NMR: (100.6 MHz, CDCl3) δ 201.9, 131.3, 130.2, 129.5, 128.3, 55.8, 54.6, 40.1, 29.2, 14.7.
4.2.14 9-(1-Phenylethyl)-9-azabicyclo[3.3.1]nonan-3-one (2f) [69,70]
The compound was purified by flash chromatography on silica gel with 1.5% MeOH/DCM as the eluent. For 2.00 mmol scale: yellow oil (0.195 g, 40%); Rf 0.7 (50% AcOEt/hexane); 1H NMR: (400 MHz, CDCl3) δ 7.46–7.22 (m, 5H), 4.01 (q, J = 6.5 Hz, 1H), 3.62–3.57 (m, 1H), 3.39–3.34 (m, 1H), 2.71 (dd, J = 16.4, 6.9 Hz, 1H), 2.51 (dd, J = 16.4, 6.9 Hz, 1H), 2.23 (d, J = 16.4, 1H), 2.19 (d, J = 16.4, 1H), 2.02–1.91 (m, 1H), 1.85–1.75 (m, 1H), 1.61–1.38 (m, 4H), 1.37 (d, J = 6.5 Hz, 3H); 13C NMR: (100.6 MHz, CDCl3) δ 211.7, 146.0, 128.4, 127.0, 126.7, 58.1, 50.9, 50.1, 42.5, 42.3, 29.5, 22.4, 16.5.
4.2.14.1 9-(1-Phenylethyl)-9-azabicyclo[3.3.1]nonan-3-one•HCl
Major invertomer 1H NMR: (400 MHz, CD3OD) δ 7.59–7.48 (m, 5H), 5.05 (q, J = 6.7 Hz, 1H), 4.59–4.52 (m, 1H), 3.51–3.44 (m, 1H), 3.38 (dd, J = 18.4, 6.5 Hz, 1H), 3.06 (dd, J = 18.4, 6.5 Hz, 1H), 2.64 (d, J = 18.4, 1H), 2.57–2.48 (m, 1H), 2.45 (d, J = 18.4, 1H), 2.38–2.26 (m, 1H), 2.09–2.01 (m, 1H), 1.92–1.87 (m, 1H), 1.82 (d, J = 6.7 Hz, 3H), 1.65–1.50 (m, 2H); 13C NMR: (100.6 MHz, CDCl3) δ 203.6, 135.2, 129.7, 128.7, 128.5, 61.2, 53.1, 52.6, 44.0, 43.9, 23.6, 23.2, 18.6, 13.8.
Minor invertomer 1H NMR: (400 MHz, CD3OD) δ 7.83–7.70 (m, 5H), 5.15 (q, J = 6.7 Hz, 1H), 4.50–4.46 (m, 1H), 3.55 (dd, J = 18.5, 6.7 Hz, 1H), 3.52–3.49 (m, 1H), 3.08 (dd, J = 18.5, 6.7 Hz, 1H), 2.72 (d, J = 17.9, 1H), 2.57–2.48 (m, 1H), 2.47 (d, J = 17.9, 1H), 2.15–2.08 (m, 1H), 2.06–1.97 (m, 1H), 1.88 (d, J = 6.7 Hz, 3H), 1.81–1.68 (m, 3H); 13C NMR: (100.6 MHz, CDCl3) δ 202.0, 135.3, 129.7, 128.7, 128.5, 62.1, 53.7, 53.4, 39.9, 39.5, 29.0, 28.8, 18.3, 14.4.
Acknowledgments
The work was supported by the University of Bialystok (BST-125) and the National Science Center, Poland (grant No. N N204 546939). The authors wish to thank the computational centre at the University of Warsaw (ICM) for providing access to supercomputer resources and the GAUSSIAN 09 program (Grant G33–03).


