1 Introduction
Les phosphoranes sont des composés organophosphorés où l’atome central P est pentavalent. Ils jouent un rôle important dans les systèmes chimiques ou biologiques tels que le transfert des motifs phosphorés ou l'hydrolyse de composés biologiquement actifs, comme par exemple l'ADN ou l'ARN. Ainsi les enzymes phosphatases, qui jouent un rôle biomédical très important, peuvent utiliser lors de leur action catalytique [1] des acides de Lewis pour changer l'état de transition des réactions de transfert de phosphoryle en un état plus associatif, ou encore à travers un mécanisme en deux étapes avec la participation d’un phosphorane intermédiaire. Bien que de telles structures ont été souvent proposées et caractérisées in situ, peu d’entre elles ont été réellement isolées. Toutefois, quelques structures phospohoraniques bien stabilisées ont été bien observées, comme dans le cas du transfert de phosphoryle à partir du C(1)O du glucose 1,6-(bis)phosphate vers le nucléophile ASP8 carboxylate [2] ou des réactions similaires [3–5].
Dans ce type de réaction, on détecte très souvent des réactions d’échange de ligands autour de l’atome de phosphore. Or, les réactions d’alcoolyse des liaisons P–N des composés phosphorés tri-coordinés constituent une voie de synthèse très utilisée de par les échanges de ligands qui en découlent autour de l’atome de phosphore [6–12].Ces réactions ont été intensivement étudiées depuis des décennies, mais les informations sur leur mécanisme sont plus rares [13–15]. En particulier, une étude cinétique [16] a concerné la réaction d’un alcool avec un aminophospholane monocyclique mettant en évidence la formation transitoire d’un phosphorane à liaison P–H qui disparait lentement en faveur de l’alcooxyphospholane final. Ce comportement est inhabituel et constitue une énigme depuis plusieurs décades, non encore résolue.
Notre travail va reprendre les aspects expérimentaux et y intègrera une étude théorique de cette réaction d’alcoolyse d’une liaison P–N extracyclique dans le but de mettre en évidence encore une fois le rôle important joué par les formes pentacoordinées dans les réactions d’échange de ligands autour d’un atome de phosphore tricoordiné. Nous avons choisi d’utiliser dans nos cinétiques le tétraméthyl-4, 4,5,5-dioxaphospholane à cause de la grande stabilité de son cycle [12].
2 Méthode de calcul
Les calculs ont été réalisés avec le programme GAUSSIAN 09 [17]. La théorie de la fonctionnelle de la densité (DFT) [18,19] a été appliquée aux différents structures avec la fonctionnelle corrigée de gradient de Becke, Lee, Yang et Parr (B3LYP) [20,21] avec la base 6-311G (d, p) de qualité triple zêta intégrant des fonctions de polarisations sur tous les atomes.
La méthode d’optimisation du gradient analytique de Berny a été utilisée pour localiser les points stationnaires sur la surface d’énergie potentielle, qui sont caractérisés, à travers le calcul des fréquences de vibration, par l’absence ou la présence d’une seule fréquence imaginaire associée respectivement aux minimas et aux structures de transition. Des calculs IRC (coordonnée intrinsèque de réaction) ont permis d’élucider le mécanisme réactionnel. Les calculs indices de réactivité de Fukui ont été effectués par la même méthode et sur la même base [22].
3 Résultats et discussions
3.1 Étude expérimentale
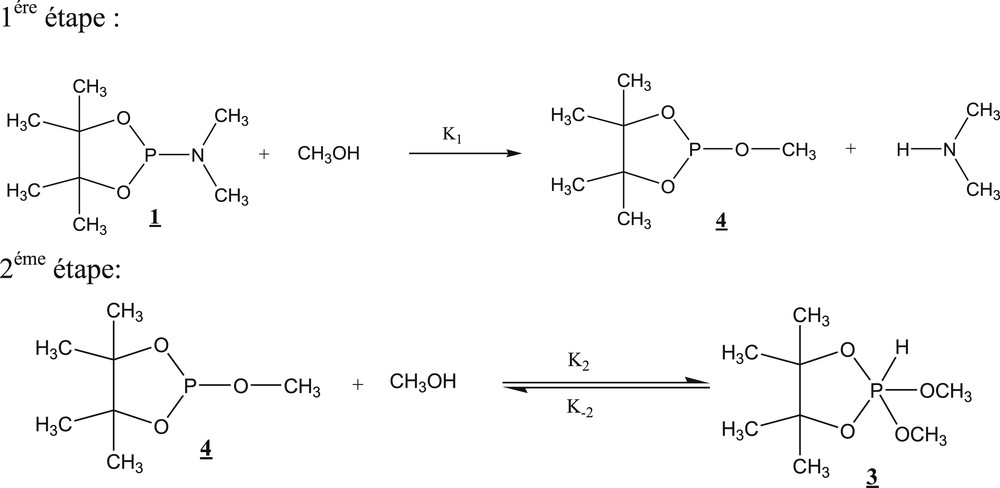
La réaction étudiée (Schéma 1) se caractérise par une stœchiométrie 1/1. Ce choix est classique en cinétique pour faciliter le traitement mathématique. Le phospholane 1 réagit avec le méthanol. Le phosphorane attendu 2 n’a pas été détecté. La réaction, suivie par le dosage de l’amine libérée, est très lente. L’analyse spectroscopique met en évidence la présence du phosphorane 3 dans le milieu réactionnel, qui commence à s’accumuler avant de disparaître en faveur du phospholane 4 après avoir atteint un maximum de l’ordre de 10%. Quand la réaction se fait dans le rapport 1/2 en faveur de l’alcool, le maximum du phosphorane 3 passe à près de 30%.
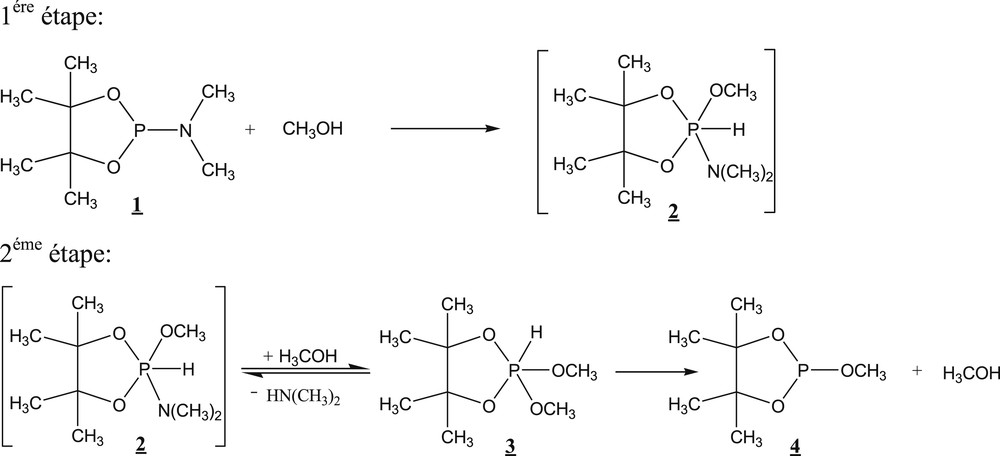
Déroulement supposé de la réaction d’alcoolyse du phospholane 1 en proportions stœchiométriques [16].
Ce mécanisme ne semble pas très probable pour les raisons suivantes :
- • le passage de 2 au 3 devrait faire intervenir un composé phosphoré hexacoordonné;
- • la loi d’action de masse indique que la présence de l’alcool en excès favorise la première étape mais défavorise la seconde et de ce fait cela ne peut expliquer la variation de la concentration maximale de 3;
- • des travaux plus récents [12] proposent que les réactions de réarrangement de ligands à hydrogènes mobiles dans les composés phosphorés tricoordonnés font intervenir des phosphoranes à liaison P–H.
Nous avons repris cette réaction avec un suivi cinétique par RMN du 31P. Ceci nous a permis de faire les observations suivantes :
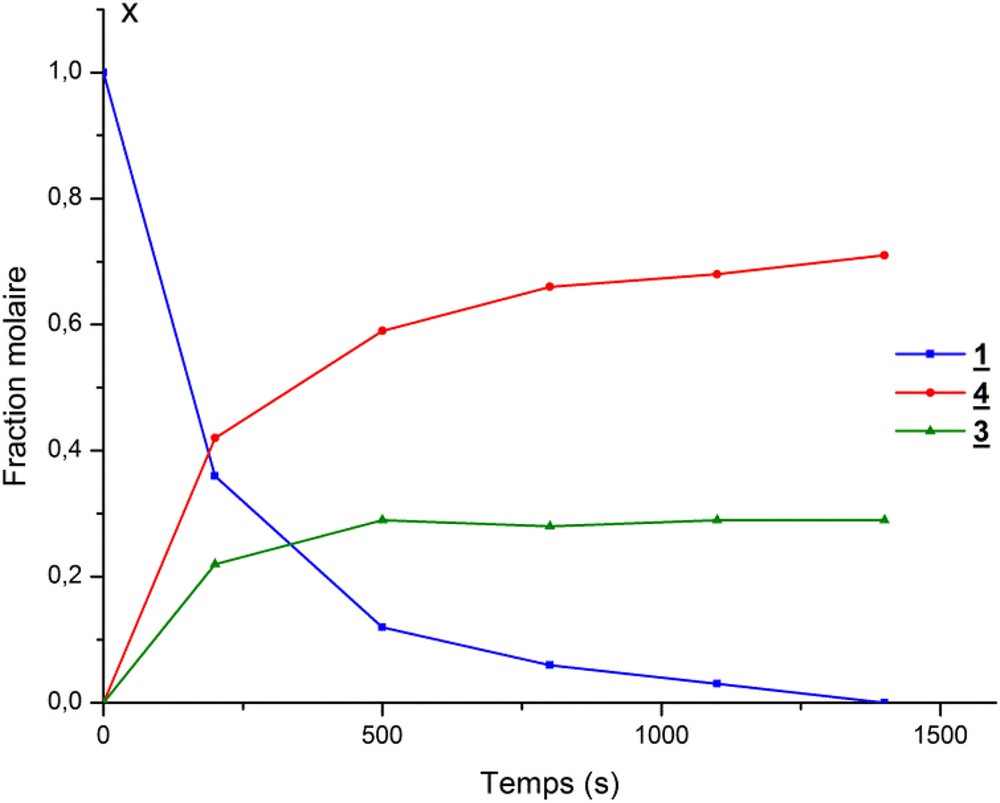
Les courbes obtenues (Fig. 1) mettent en évidence l’existence de deux réactions consécutives. La première est relativement rapide et finit par un palier correspondant au maximum de la concentration du phosphorane 3 ; elle est suivie d’une réaction très lente de décomposition de ce dernier en faveur du phospholane 4.

Mesures cinétiques de la réaction d’alcoolyse étudiée. X représente la fraction molaire des produits en présence de la réaction de méthanolyse du phospholane 1.
Nous proposons un déroulement différent de la deuxième étape de la réaction d’alcoolyse en proportions stœchiométriques selon le schéma 2. Pour bien cerner le mécanisme de cette réaction, nous avons entrepris des calculs théoriques.
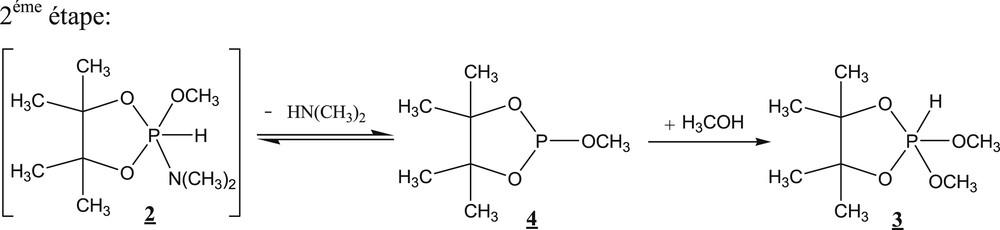
Nouvelle proposition de déroulement de la deuxième étape de la réaction d’alcoolyse en proportions stœchiométriques.
3.2 Étude théorique de la réaction d’alcoolyse
Nous nous plaçons dans l’hypothèse probable que le passage entre deux formes tricoordonnées du phosphore par échange d’un ligand se fait à travers la formation d’une forme pentacoodonnée [12]. Nous pouvons imaginer que le passage du composé 1 au composé 4 fait intervenir un ou plusieurs phosphoranes à liaison P–H, chacun ayant une géométrie en bipyramide trigonal (BPT). Pour optimiser le temps de calcul, nous avons remplacé les quatre groupements méthyle du cycle phospholanique par des hydrogènes.
Nous allons adopter la notation indiquée dans le schéma 3 où les ligands –N(CH3)2, –OCH3 et –H portent respectivement les numéros 2, 4 et 5.
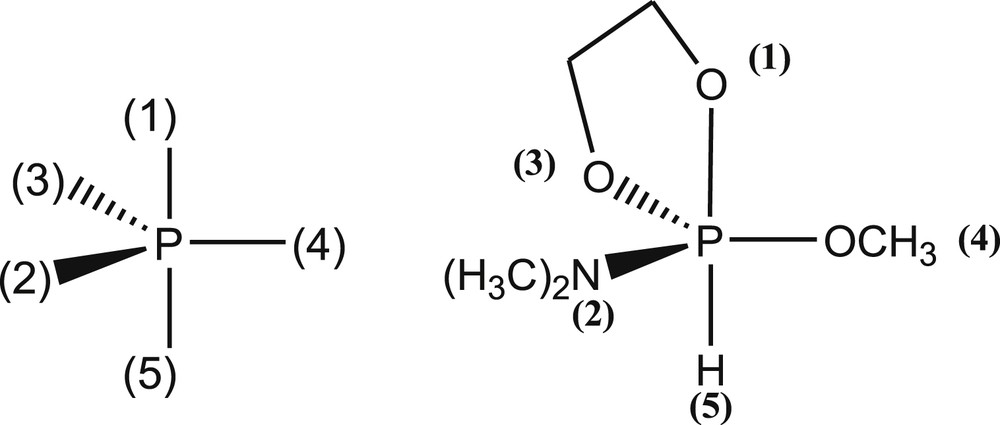
Numérotation des ligands dans les phosphoranes.
Nous présentons dans le Tableau 1 les valeurs des paramètres structuraux des composées étudiés et dans la Fig. 2 les géométries optimisées.
Valeurs des paramètres structuraux et thermodynamiques des composes étudiés. Les longueurs de liaison sont en Å, les angles en degrés, les énergies en unités atomiques et les moments dipolaires en Debyes.
| Composé | 1 | 2 | 3 | 4 | |||
| 12 | 14 | 15 | 12 | 15 | |||
| Longueur de liaison | |||||||
| P–O1 | 1693 | 1711 | 1741 | 1706 | 1680 | 1680 | 1662 |
| P–O3 | – | 1659 | 1668 | 1651 | 1668 | 1645 | 1660 |
| P–O4 | – | – | – | – | 1710 | 1641 | – |
| P–N | 1690 | 1793 | 1679 | 1695 | – | – | – |
| P–H | – | 1419 | 1410 | 1417 | 1350 | 1423 | – |
| Angle de liaison | |||||||
| O1–P–H | – | 84,020 | 84,85 | 174,44 | 85,66 | 174,78 | – |
| O1–P–N | 98,682 | 175,472 | 94,63 | 94,08 | – | – | – |
| O1–P–O3 | – | 89,541 | 172,87 | 87,20 | 91,26 | 91,06 | 92,37 |
| O1–P–O4 | – | – | – | – | 175,40 | 87,23 | – |
| Angle dièdre | |||||||
| O1–P–H-N | – | −176,59 | 92,35 | −146,22 | – | – | – |
| O1–P–N-O3 | – | 95,455 | −178,69 | −89,02 | – | – | – |
| O3–PH-O4 | – | – | – | – | 93,80 | 117,54 | – |
| Moment dipolaire | 2259 | 2831 | 1245 | – | 1,42 | 1,92 | 3,48 |
| Énergie E | −705,131 | −820,880 | −820,896 | −820,900 | −801,461 | −801,459 | −685,702 |
| Enthalpie H | −704,973 | −820,665 | −820,680 | −820,684 | −801,286 | −801,284 | −685,585 |
| Enthalpie libre G | −705,018 | −820,716 | −820,731 | −820,733 | −801,333 | −801,333 | −685,625 |
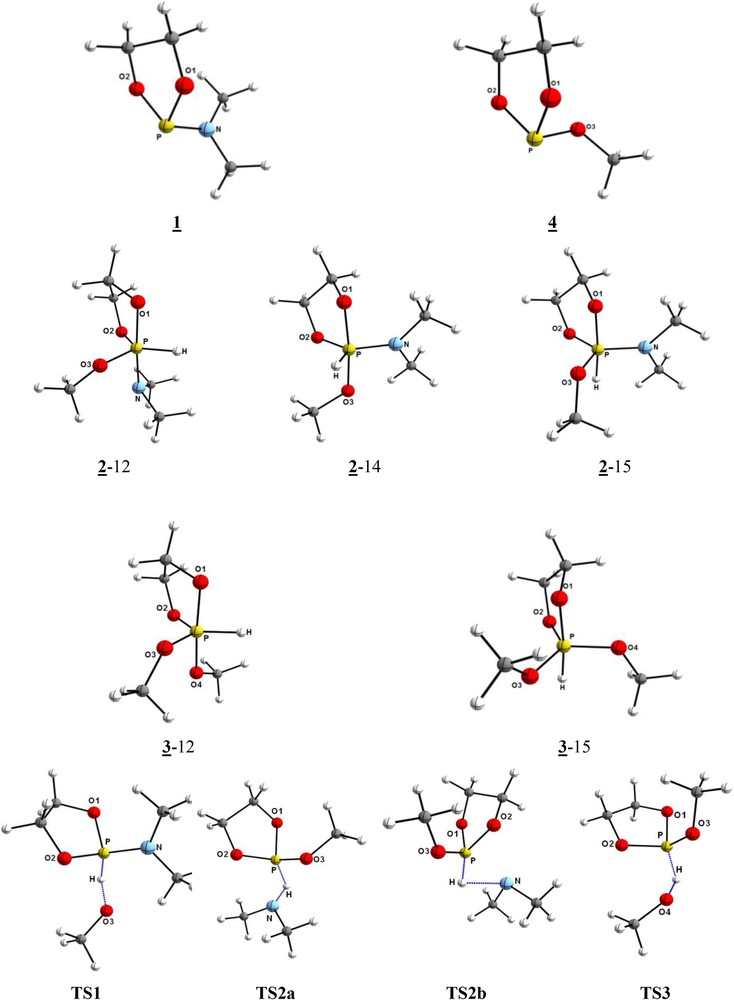
Géométrie optimisée des phospholanes 1, 4 et phosphoranes 2 et 3 et des états de transition intervenants TS1, TS2a, TS2b et TS3.
La présence du cycle phospholanique engendre une contrainte telle que les deux oxygènes, de numéros 1 et 3, se placent en général l’un en position axiale et l’autre en position équatoriale pour éviter un angle de 120° qu’ils formeraient s’ils occupaient deux positions équatoriales. Nous vérifierons cette hypothèse plus tard.
L’addition du méthanol sur le phospholane 1 peut engendrer trois phosphoranes avec –N(CH3)2 ou –OCH3 ou –H occupant la seconde position axiale, que nous allons noter respectivement 2–12, 2–14 et 2–15.
Le Tableau 1 et la Fig. 2 regroupent les résultats de nos calculs concernant les deux aspects, structural et thermodynamique de la réaction étudiée.
Nos calculs montrent que l’isomère 2–15 est le plus stable et le 2–12 est le moins stable, comme nous le voyons sur le diagramme énergétique de la Fig. 3.
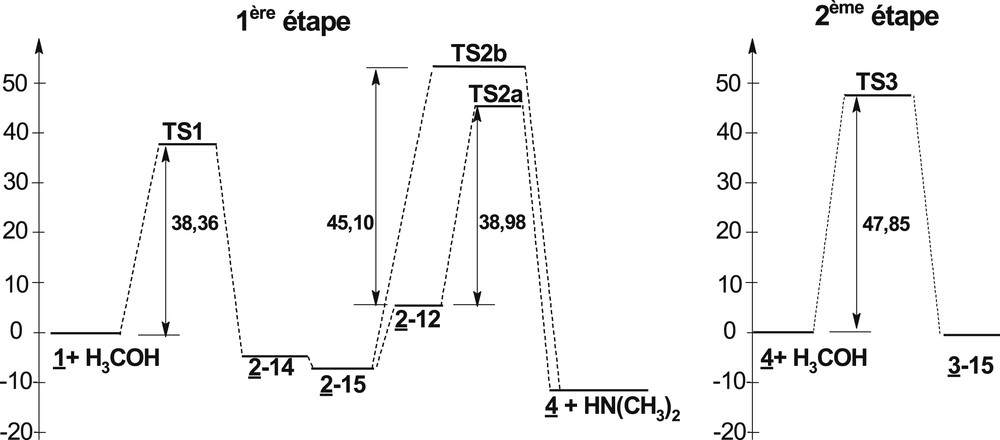
Diagramme énergétique de la réaction étudiée.
Nous pouvons envisager que ces trois isomères du composé 2 sont en compétition ou ils se partagent les rôles. Nous avons déterminé quatre états de transition (Tableau 2).
Valeurs des paramètres structuraux et thermodynamiques des états de transition étudiés. Les longueurs de liaison sont en Å, les angles en degrés, les énergies en unité atomique et les moments dipolaires en debye.
| Etat de transition | TS1 | TS2 | TS3 | |
| a | b | |||
| Longueur de liaison | ||||
| P–O1 | 1676 | 1725 | 1709 | 1696 |
| P–O2 | 1655 | 1666 | 1759 | 1648 |
| P–O3 | 2250 | 1643 | 1772 | 1608 |
| P–N | 1661 | 2000 | 1972 | – |
| P–H | 1467 | 1547 | 1513 | 1500 |
| P–O4 | – | – | – | 2081 |
| Angle de liaison | ||||
| O1–P–H | 124,76 | 127,42 | 171,02 | 128,04 |
| O1–P–N | 99,25 | 171,55 | 123,01 | – |
| O1–P–O3 | 163,36 | 98,92 | 122,44 | 99,16 |
| O1–P–O4 | – | – | – | 169,48 |
| Angle dièdre | ||||
| O1–P–H–N | – | −173,07 | 168,42 | – |
| O1–P–N-O3 | −172,34 | – | 159,05 | – |
| O3–P–H-O4 | – | – | – | −175,10 |
| Moment dipolaire | 4,52 | 1,36 | 1,67 | 4,72 |
| Enthalpie H* | −820,615 | −820,607 | −820,455 | −801,214 |
| Enthalpie libre G* | −820,667 | −820,658 | −820,500 | −801,265 |
| Entropie S* | 107,84 | 108,76 | 94,76 | 107,03 |
| Énergie E | −820,825 | −820,817 | −820,659 | −801.383 |
L’addition oxydante du composé à hydrogène mobile sur le phospholane est régiosélective. Le nucléophile (oxygène ou azote) et l’électrophile (l’hydrogène) s’approchent de la structure pyramidale du phospholane d’un même côté pour suivre le chemin de moindre énergie [23] (Fig. 4). Ainsi, les variations des angles du composés phosphorés restent les plus faibles, de 109,5° dans l’hybridation sp3 à 90° ou 120° dans l‘hybridation sp3d.
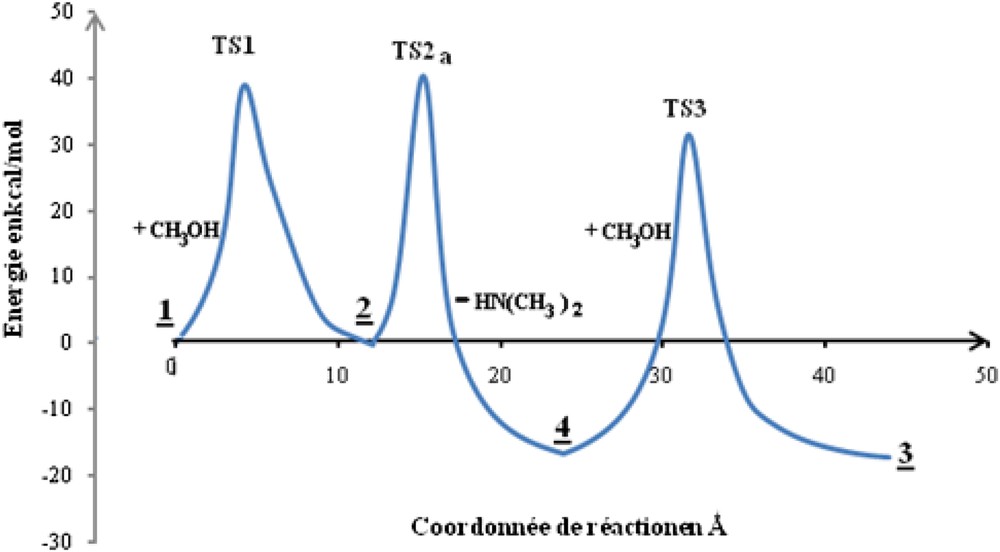
Profil énergétique relatif aux différentes séquences de la réaction.
La contrainte du cycle phopholanique que nous avons indiquée auparavant fait que nécessairement l’un des deux oxygènes occupera à la fin une position axiale et l’autre une position équatoriale. La plus grande apicophilie de l’oxygène par rapport à l’hydrogène est en faveur de la formation initiale du phosphorane 2–14.
Pour vérifier cette hypothèse, nous avons calculé les indices de Fucki [22] des atomes en présence, que nous avons regroupés dans le Tableau 3.
Indices de Fukui des réactifs et du produit final de la réaction étudiée.
| site | 1 | Méthanol | 4 | |||
| f− | f+ | f− | f+ | f− | f+ | |
| P | 0,051 | 0837 | – | – | 0,013 | 1808 |
| N | 0,347 | 0095 | – | – | – | – |
| O3 | – | – | 0,423 | 0403 | −0,010 | 0061 |
Nous voyons ainsi que le phosphore et l’hydrogène sont des électrophyles et l’oxygène du méthoxy et l’azote sont des nucléophiles. Puisque seul l’atome de phosphore est concerné par cette addition oxydante, la réaction serait initiée par l’attaque nucléophyle du méthoxy.
L’IRC associée à cette étape montre que le phosphoranes 2–14 est bien le produit de fin d’IRC (Fig. 4). L’état de transition correspondant TS1 engendre une énergie d’activation égale à 38,36 kcal mol−1. Comme l’isomère 2–15 est plus stable, nous pouvons envisager une pseudo-rotation de Berry [24,25] transformant le produit cinétique 2–14 en un produit thermodynamique 2–15.
Pour obtenir le composé 4, une molécule d’amine doit partir. C’est une élimination du type E1. Comme on peut envisager que le départ simultanée de deux ligands d’une géométrie bipyramide trigonal (BPT) est la réaction inverse de la formation du phosphorane, alors la réaction nécessite que ces deux ligands n’occupent ni deux position axiales ni deux positions équatoriales [26]. Ils doivent donc occuper l’un une position axiale et l’autre une position équatoriale.
Les deux isomères 2–15 et 2–12 sont des candidats potentiels. Nous avons déterminé leurs états de transition notés TS2a et TS2b, amenant respectivement à la décomposition de 2–12 et 2–15, d’énergies d’activation respectives 39,88 kcal mol−1et 45,10 kcal mol−1.
Il devient claire que la dissociation du composé 2 se fait à travers l’isomère 2–12. On doit envisager une seconde pseudo-rotation de Berry, qui transforme 2–15 en 2–12.
La dernière étape est une addition oxydante du méthanol sur le composé 4 amenant à la formation du phosphorane 3. Nous sommes en présence d’une compétition entre les atomes d’oxygène pour occuper les positions axiales.
Un état de transition, noté TS3, a été obtenu, qui engendre un mécanisme dont le composé de fin d’IRC est le composé 3–15 où un méthoxy occupe une position équatoriale. Son énergie d’activation est 47,85 kcal mol−1. Nous rassemblons dans le Tableau 4 les valeurs des grandeurs thermodynamiques associées à chaque séquence ou, étape, ou encore à la réaction totale.
Grandeurs thermodynamiques associées à chaque séquence ou étape, ou à la réaction totale.
| ΔE | ΔH | ΔG | ΔS | ||
| 1 + CH3OH→2–14 | Séquence | −4,50 | −3,16 | 9,82 | −43,56 |
| 2–12→4 + HN(CH3)2 | Séquence | −16,79 | −17,27 | −30,59 | 44,80 |
| 1 + CH3OH→4 + HN(CH3)2 | Étape | −11,37 | −11,11 | −11,16 | 0,32 |
| 4 + CH3OH→3 | Étape | −0,06 | 1,39 | 13,31 | −42,07 |
| 1+2CH3OH→3 + HN(CH3)2 | Réaction | −11,44 | −9,72 | 2,14 | −41,75 |
Nous remarquons que toutes les enthalpies ou enthalpies libres sont très faibles, indiquant que la réaction est modérément exothermique et qu’elle est limitée. Nous avons aussi calculé les paramètres spectroscopiques de RMN des composés étudiés. Nous voyons bien que les valeurs calculées et regroupées dans le Tableau 5 sont toutes proches uniquement du phosphorane 3, le seul détecté expérimentalement.
Les paramètres spectroscopiques (1JP–H et déplacement chimique) des composés 2 et 3.
| Valeurs théorique | Valeurs expérimentale | |||||
| 2-12 | 2-15 | 2-14 | 3-12 | 3–15 | 3 | |
| 1JP–H (Hz) | 698,4 | 687,4 | 749,3 | 775,1 | 627,5 | 694 |
| δ31P (ppm) | −15,85 | −36,58 | −42,04 | −31,41 | −26,72 | −26 |
| δH (P) (ppm) | 7,11 | 5,61 | 7,31 | 7,38 | 5,81 | 5,75 |
| δ OCH3 (ppm) | 3,54 | 3,48 | 3,46 | 3,56 | 3,49 | 3,22 |
Nous voulons indiquer pour clôturer cette partie théorique qu’à chaque fois que nous avons voulu optimiser des phosphoranes où les atomes O1 et O2 du cycle phospholanique occupent tous les deux des positions équatoriales, nous avons obtenu de manière systématique l’un des autres phosphoranes de la réaction.
Cette étude mécanistique a permis de quantifier les énergies d’activation associées aux séquences de la réaction étudiée. Les premières séquences ayant une barrière plus faible que la dernière, elles ne vont pas intervenir dans les mesures cinétiques. Ainsi, nous confirmons la non- détection expérimentale du phosphorane 2, car à la fois sa formation et sa décomposition en amine et en composé 4 sont rapides.
Toutefois, nous devons interpréter le phénomène inattendu de l’accumulation dans le milieu réactionnel du produit final de la réaction. L’interprétation concernera donc la partie qui voit décroître la concentration du compose 3 après le palier témoin de sa formation.
3.3 Retour à l'expérience
Les calculs théoriques ont permis d’élucider le mécanisme de la réaction d’alcoolyse du phospholane 1. Le phosphorane 3 est bien le composé final en équilibre avec le phospholane 4 et ne peut en aucun cas être considéré comme un intermédiaire réactionnel (Schéma 4).
Déroulement proposé pour le traitement cinétique de la réaction de formation du dimethoxyphosphorane 3.
Nous avons alors cherché à augmenter la quantité du composé 3 formé en travaillant en large excès d’alcool avec un rapport de 10/1. La réaction devient rapide, se limite à la partie avant le palier, finit en 25 min, mettant en évidence la présence classique de l’équilibre phospholane/phosphorane avec une constante d’équilibre égale au quotient des fractions molaires (l’alcool en large excès aurait une activité égale à 1) qui est de près de 0,33/0,66 (Fig. 5), c'est-à-dire de 0,5.
Mesures cinétiques de la réaction d’alcoolyse étudiée avec excès d'alcool. X représente la fraction molaire des produits 3 et 4 en présence de la réaction de méthanolyse du phospholane 1.
Nous présentons dans le Tableau 6 les valeurs des fractions molaires relatives à la réaction en 1/1. Nous calculons le quotient Q de la réaction liée à la deuxième étape. Nous remarquons qu’à partir de la deuxième minute, Q semble prendre une valeur constante sur les 15 mesures entre t = 120 s et t = 2280 s, dont la moyenne est 0,53. Cette valeur est quasiment égale à la constante d’équilibre obtenue dans la réaction avec excès d’alcool calculée précédemment. Après le palier, nous remarquons une diminution constante de ce rapport Q. La courbe représentative peut être décrite par une loi exponentielle avec un coefficient de régression R2 de 0,98, d’équation Q = 0,548 exp (−9,664.10−5 t) (Fig. 6).
Valeurs des fractions molaires relatives à la réaction en 1/1 et du quotient de la réaction Q de la deuxième étape.
| T (s) | 1 | 4 | 3 | Q |
| 60 | 0,88 | 0,07 | 0,05 | 0,861 |
| 120 | 0,82 | 0,12 | 0,06 | 0,658 |
| 130 | 0,73 | 0,2 | 0,08 | 0,615 |
| 240 | 0,7 | 0,23 | 0,07 | 0,491 |
| 300 | 0,67 | 0,24 | 0,09 | 0,647 |
| 360 | 0,64 | 0,26 | 0,1 | 0,712 |
| 420 | 0,63 | 0,27 | 0,1 | 0,699 |
| 480 | 0,61 | 0,3 | 0,09 | 0,566 |
| 660 | 0,59 | 0,32 | 0,09 | 0,563 |
| 1080 | 0,56 | 0,36 | 0,08 | 0,463 |
| 1320 | 0,54 | 0,37 | 0,09 | 0,541 |
| 1680 | 0,53 | 0,38 | 0,09 | 0,526 |
| 1800 | 0,51 | 0,38 | 0,09 | 0,538 |
| 2040 | 0,5 | 0,42 | 0,08 | 0,454 |
| 2280 | 0,47 | 0,44 | 0,08 | 0,466 |
| 3000 | 0,4 | 0,54 | 0,06 | 0,327 |
| 4440 | 0,34 | 0,62 | 0,04 | 0,215 |
| 5880 | 0,29 | 0,69 | 0,02 | 0,107 |
| 6600 | 0,27 | 0,72 | 0,01 | 0,053 |
| 8040 | 0,26 | 0,73 | 0,01 | 0,055 |
| 8760 | 0,25 | 0,75 | 0 | – |
| 10,920 | 0,21 | 0,79 | 0 | – |
| 11,640 | 0,17 | 0,83 | 0 | – |
| 13,080 | 0,16 | 0,84 | 0 | – |
| 13,800 | 0,15 | 0,85 | 0 | – |
| 14,520 | 0,13 | 0,87 | 0 | – |
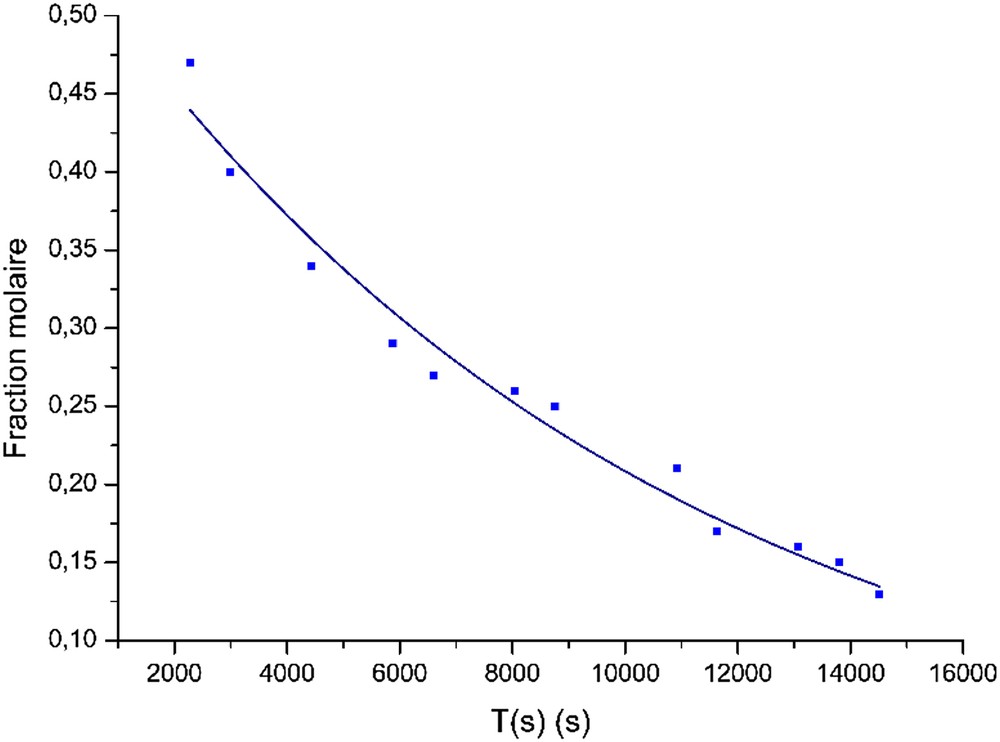
Variations du quotient de la réaction pour la partie suivant le palier.
Nous remarquons que la valeur avant le comportement exponentiel (t = 0 dans la dernière équation) est pratiquement la valeur de la moyenne des premières mesures obtenue précédemment.
Pour vérifier qu’après le palier, nous sommes en présence d’une relaxation des équilibres chimiques, nous avons porté les variations de Ln(1), composé qui n’intervient pas dans l’expression de Q, en fonction du temps. Nous avons obtenu une droite de coefficient directeur −9,433 10−5 avec le même coefficient R2 de 0.98 (Fig. 7). Nous remarquons que les deux étapes de la réaction sont régies dans cette partie de la cinétique après le palier par la même loi exponentielle de puissance de près de −9,5 10−5.

Variations du logarithme de la concentration de phospholane 1 après le palier.
Nous pouvons maintenant interpréter le résultat dans le cas de la réaction en 1/1. Au départ, quand la quantité d’alcool est importante, la réaction suit très bien le modèle issu des calculs théoriques et les composés 3 et 4 satisfont la situation d’équilibre.
Du moment que la quantité d’alcool présente dans le milieu ne satisfait pas la valeur de la constante d’équilibre, le phosphorane 3 formé doit se décomposer pour fournir la quantité de méthanol nécessaire. C’est une perturbation de l’état d’équilibre qui est régi par la constante de relaxation τ faisant intervenir à la fois les constantes de vitesse de la réaction directe et de la réaction inverse (Schéma 4) et qui suit en général une loi exponentielle [27].
4 Conclusion
Ce travail a concerné de manière complémentaire les aspects cinétiques expérimentaux et théoriques de la réaction d’alcoolyse d’une liaison P–N extracyclique d’un phospholane monocyclique. Un nouveau mécanisme a été proposé, réfutant le statut d’intermédiaire réactionnel au diméthoxyphosphorane attribué jusqu’à ce jour et le remplace par le statut de produit de fin de réaction, malgré le fait qu’il disparaît du milieu quand la réaction est étudiée dans les conditions stœchiométriques 1/1.
Pour confirmer cette hypothèse, les calculs théoriques ont permis de déterminer les structures des états de transition au niveau B3LYP/6-311G(d, p). Les chemins réactionnels correspondants ont été obtenus par le traçage des profils énergétiques en fonction de la coordonnée intrinsèque de la réaction (IRC).
Un retour à l’expérience a permis de valider les résultats théoriques et de montrer que la disparition du phosphorane formé en fin de réaction est une conséquence d’une modification continue de l’état d’équilibre diméthoxyphosphorane/méthoxyphospholane, mettant en évidence l’intervention de la relaxation chimique dans le déroulement de la réaction en 1/1 et son absence dans la réaction avec large excès d'alcool. Le traitement cinétique des équations indiquées plus haut est difficile et doit être résolu de manière numérique et itérative, étude qui est en cours dans notre laboratoire.
Remerciements
Nous voudrions remercier monsieur le professeur émérite Jean Barrans, de l’université Paul-Sabatier de Toulouse, qui a été à l’origine du problème posé, pour sa contribution fondamentale au traitement cinétique, et remercier le ministère de l’Enseignement supérieur et de la Recherche scientifique de la République tunisienne pour le financement du travail théorique.


