Sorption de biomolécules par membrane échangeuse d’ions : étude expérimentale et modélisation

Chalore Teepakorn; Catherine Charcosset; Koffi Fiaty

doi:10.1016/j.crci.2015.11.017

Sorption de biomolécules par membrane échangeuse d’ions : étude expérimentale et modélisation

Chalore Teepakorn ^1,^2,³ ; Catherine Charcosset ^1,^2,³ ; Koffi Fiaty ^1,^2,³

¹ Université de Lyon, 69622, Lyon, France
² Université Lyon-1, Villeurbanne, France
³ LAGEP, UMR 5007, CNRS, CPE, 43, bd du 11-Novembre-1918, 69100 Villeurbanne, France

Comptes Rendus. Chimie, Volume 19 (2016) no. 7, pp. 812-819.

Résumés

Anglais
Français

Microporous membranes are an alternative to conventional packed columns chromatography. They offer the main advantage compared to bulk material to reduce diffusion phenomena, reduce residence time and pressures drops, and thus, facilitate rapid purification of large quantities of molecules. A wide range of chromatographic membranes involving different molecules retention mechanism (ion exchange, affinity, etc…) is now commercialized. Despite their success, the influence of the geometry of the membrane chromatography devices remains relatively unexplored from a theoretical point of view.

This study on the sorption of bovine serum albumin (BSA) on a chromatographic ion exchange membrane (type Sartobind Q from Sartorius Stedim Biotech-Goettingen, Germany), aims to experimentally evaluate the influence of operating conditions (fluid flowrate, initial concentrations) on the breakthrough curves. Two types of geometries (plane module or spiral module) were used and helped to highlight the influence of the type of flow (axial or radial) on separation. The experimental study was conducted on an Akta Prime chromatography system (General Electrics, France). In order to understand the observed phenomena, to predict the performance of different modules and to develop a tool for improving the design of membrane chromatography capsule, a mathematical model was developed in CFD (Computational Fluid Dynamics) and successfully simulated.

Les membranes microporeuses sont une alternative aux supports de chromatographie classique sur colonne. Elles offrent l'avantage de diminuer les phénomènes de diffusion, de réduire les temps de séjour et les chutes de pressions, et donc de faciliter la purification rapide de quantités importantes de molécules. Une gamme importante de membranes chromatographiques mettant en jeu différents mécanismes de rétention des molécules (échange d’ions, affinité, etc.) est actuellement commercialisée. Malgré leur succès, l’influence de la géométrie des modules de chromatographie membranaire reste relativement peu étudiée du point de vue théorique.

Cette étude menée sur la sorption de l’albumine sérique bovine (ASB) sur une membrane chromatographique échangeuse d’ions (type Sartobind Q de la société Sartorius Stedim Biotech-Goettingen, Allemagne), vise à évaluer expérimentalement l’influence des conditions opératoires (débit de circulation, concentrations initiales) sur la courbe de perçage. Deux types de géométries différentes (module plan ou module en spiral) ont été utilisés et ont permis de mettre en évidence l’influence du type d’écoulement (axial ou radial) sur la séparation. L’étude expérimentale a été conduite sur un système de chromatographie Akta Prime (General Electrics, France)

Afin de comprendre les phénomènes observés, de prédire les performances des différents modules et de mettre au point un outil destiné à l’amélioration de la conception des capsules de chromatographie membranaire, un modèle mathématique en MFN (mécanique des fluides numérique) a été développé et simulé avec succès.

Métadonnées

Reçu le : 2015-06-01
Accepté le : 2015-11-09
Publié le : 2016-01-30

DOI : 10.1016/j.crci.2015.11.017

Keywords: Chromatographie membranaire, Albumine sérique bovine, Purification des protéines, Simulation numérique

Affiliations des auteurs :

Chalore Teepakorn ^{1, 2, 3} ; Catherine Charcosset ^{1, 2, 3} ; Koffi Fiaty ^{1, 2, 3}

¹ Université de Lyon, 69622, Lyon, France
² Université Lyon-1, Villeurbanne, France
³ LAGEP, UMR 5007, CNRS, CPE, 43, bd du 11-Novembre-1918, 69100 Villeurbanne, France

@article{CRCHIM_2016__19_7_812_0,
     author = {Chalore Teepakorn and Catherine Charcosset and Koffi Fiaty},
     title = {Sorption de biomol\'ecules par membrane \'echangeuse d{\textquoteright}ions : \'etude exp\'erimentale et mod\'elisation},
     journal = {Comptes Rendus. Chimie},
     pages = {812--819},
     publisher = {Elsevier},
     volume = {19},
     number = {7},
     year = {2016},
     doi = {10.1016/j.crci.2015.11.017},
     language = {en},
}

TY  - JOUR
AU  - Chalore Teepakorn
AU  - Catherine Charcosset
AU  - Koffi Fiaty
TI  - Sorption de biomolécules par membrane échangeuse d’ions : étude expérimentale et modélisation
JO  - Comptes Rendus. Chimie
PY  - 2016
SP  - 812
EP  - 819
VL  - 19
IS  - 7
PB  - Elsevier
DO  - 10.1016/j.crci.2015.11.017
LA  - en
ID  - CRCHIM_2016__19_7_812_0
ER  -

%0 Journal Article
%A Chalore Teepakorn
%A Catherine Charcosset
%A Koffi Fiaty
%T Sorption de biomolécules par membrane échangeuse d’ions : étude expérimentale et modélisation
%J Comptes Rendus. Chimie
%D 2016
%P 812-819
%V 19
%N 7
%I Elsevier
%R 10.1016/j.crci.2015.11.017
%G en
%F CRCHIM_2016__19_7_812_0

Chalore Teepakorn; Catherine Charcosset; Koffi Fiaty. Sorption de biomolécules par membrane échangeuse d’ions : étude expérimentale et modélisation. Comptes Rendus. Chimie, Volume 19 (2016) no. 7, pp. 812-819. doi : 10.1016/j.crci.2015.11.017. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2015.11.017/

Version originale du texte intégral

1 Introduction

Les chromatographies membranaires (CM) sont une alternative aux supports de chromatographie classique sur colonne. Elles sont basées sur le couplage en une seule opération d’une membrane de filtration fonctionnalisée par immobilisation d’un ligand connu pour interagir spécifiquement avec le soluté d’intérêt. Les CM offrent l'avantage principal, par rapport aux autres supports, de diminuer les résistances au transfert de matière, de réduire les temps de séjour et les chutes de pressions par rapport aux colonnes, et donc de faciliter la purification rapide de quantités importantes de molécules. Grâce à ces avantages, les CM connaissent un succès commercial croissant pour la purification de biomolécules comme les protéines, les acides nucléiques, les anticorps monoclonaux, l’ADN plasmatique pour la thérapie génique, les virus, etc. Une gamme importante de produits utilisant cette technologie est actuellement commercialisée, mettant en jeu différents mécanismes de rétention des molécules (échange d’ions, affinité, interaction hydrophobique, phase inversée, etc.) et différentes géométries du module membranaire (feuille, spirale, etc.). Malgré ses succès dans l’industrie, l’influence de la géométrie du module membranaire a été très peu étudiée. Ghosh et al. (2014) [1] ont étudié la sorption de protéines sur deux modules de CM de géométries différentes : un module axial de volume 0,08 mL et un module radial de volume égal à 1,2 L. La comparaison de ces deux modules a été difficile à réaliser à cause de la grande différence entre leurs volumes respectifs [1]. En revanche, en chromatographie traditionnelle sur billes [2,3], la comparaison entre les configurations axiale et radiale a bien été menée. Dans ce cas, aucune différence de performance en sorption n’a été observée.

Les procédés de CM sont principalement caractérisés par la forme de leurs courbes de perçage, qui sont influencées par les cinétiques de sorption et par l’hydrodynamique du fluide en circulation. Pour prédire en simulation le comportement des procédés de séparation par CM, un modèle mathématique est requis. Celui-ci est généralement basé sur l’établissement d'un bilan de matière incluant à la fois les phénomènes de diffusion, de convection et d’adsorption, et des quantités de mouvement. Les cinétiques d’adsorption sont souvent représentées, selon les mécanismes considérés, par des modèles d’isothermes de Langmuir, Freundlich, bi-Langmuir, modèle de propagation, modèle d’encombrement stérique, etc. en ce qui concerne les membranes d’affinité [4] et les membranes échangeuses d’ions [5,6]. Le modèle de bi-Langmuir peut être utilisé lorsque l’on observe au voisinage de la saturation l’élargissement des courbes de perçage indiquant l’existence d’un mécanisme de sorption autre que celui du simple mécanisme de Langmuir à un seul site de sorption. Ce phénomène a été mis en évidence par Boi et al. (2007) sur la sorption d’IgG (immunoglobulines de type G) sur une membrane Sartoepoxide A2P [7].

Récemment, la mécanique des fluides numériques (MFN) a été intégrée dans le développement du modèle de CM pour permettre de prendre en compte la non-idéalité des écoulements dans les modules des membranes. Ghosh et al. (2014) ont appliqué la MFN sur les deux types de modules axial et radial sans les comparer du point de vue théorique [1,8].

Cette étude, menée sur l’adsorption de l’albumine sérique bovine (ABS) sur une CM échangeuse d’ion (type Sartobind Q de la société Sartorius Stedim Biotech-Goettingen, Allemagne), vise à évaluer de manière expérimentale l’influence des conditions opératoires (débit de circulation et concentrations initiales) sur la courbe de perçage. Deux types de géométries différentes (module plan et module en spiral) sont utilisés pour permettre de mettre en évidence l’influence du type d’écoulement (axial ou radial) sur la séparation. L’étude expérimentale est conduite sur un système de chromatographie Akta Prime (General Electrics, France). Un modèle mathématique MFN a été utilisé pour simuler les courbes de perçage de l’ABS sur les modules Sartobind Q et Mini à partir des paramètres des modèles de Langmuir et bi-Langmuir obtenus dans une expérimentation menée en réacteur discontinu. Les simulations ont été réalisées avec le logiciel Comsol Multiphysics 4.3.

2 Théorie

Afin de donner une description appropriée du phénomène de sorption de la membrane chromatographique, l'ensemble du système chromatographique doit être considéré afin de tenir compte de la non-idéalité des flux à travers le volume de la capsule membranaire et les volumes externes à celle-ci, à savoir les rétentions liquides dans les tubes de connexion, la cellule de détection, la tête de pompe et les réservoirs d’alimentation, etc. Selon les travaux de Boi et al. (2007), ces volumes peuvent être modélisés par une combinaison en série de réacteurs idéaux : un réacteur parfaitement agité continu (RPAC) et un réacteur piston (RP) comme illustré sur la Fig. 1. Le réacteur RPAC est utilisé pour représenter la dispersion dans le système externe et le réacteur RP décrit le retard dû à l’écoulement du fluide dans ces différents volumes externes.

Fig. 1
Configuration du modèle de CM avec la connexion d’un RP, d’un RPAC et du module de CM en série.

Dans le module de CM, les champs de vitesse sont déterminés à partir de la représentation schématique des différents modules membranaires. Cette représentation a été facilitée à partir de la visualisation de l’imagerie par résonance magnétique (IRM) de chaque capsule membranaire (Fig. 2). Nous avons ainsi pu schématiser les deux types de modules étudiés par une coupe longitudinale en 2D sur l’interface de Comsol Multiphysics 4.3. Les modules étant symétriques par rapport à l’axe principal d’écoulement, la simulation sera effectuée sur la moitié comme schématisé sur la Fig. 3. Chaque module comporte deux zones : une zone d’écoulement libre et une zone dite de capsule membranaire où sont empilés des feuillets de membranes microporeuses (Fig. 2 et Fig. 3). Le fluide dans la zone libre est décrit par les équations de Navier–Stokes (Eq. (1) et (2)) en régime stationnaire et en écoulement laminaire sans force externe appliquée.

Fig. 2
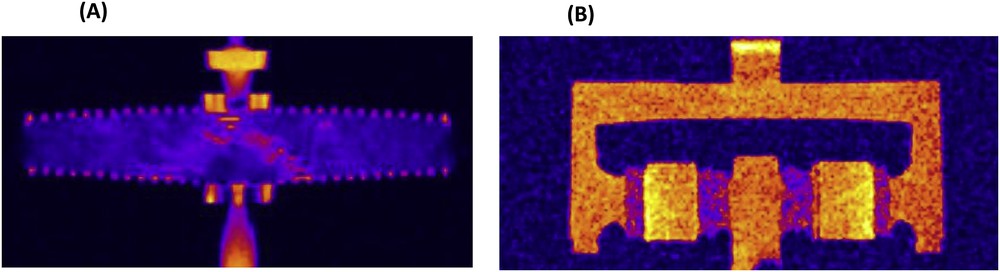
Imageries par résonance magnétique (IRM) des capsules membranaires : (A) Sartobind Q75 , (B) Sartobind Nano 1 ml.

Fig. 3
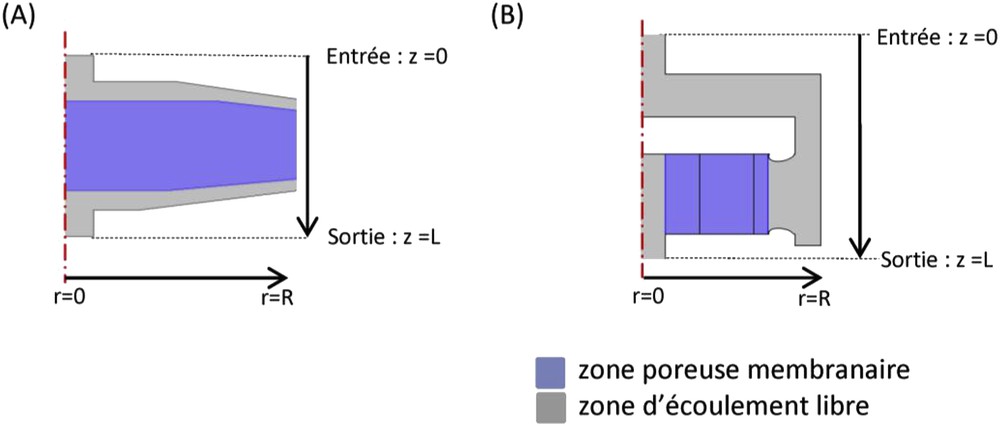
Image reconstruite des modules axial (A) et radial (B) à partir de l’IRM en section longitudinale. La morphologie est repérée dans les zones d’écoulement libre en gris et les zones membranaires en violet.

2.1 Les équations de Navier-Stokes

ρ (u \cdot \nabla u) = - \nabla p + μ \nabla^{2} u

(1)

\nabla \cdot u = 0

(2)

où ρ est la masse volumique du fluide, p la pression, μ la viscosité dynamique du fluide, u la vitesse du fluide en écoulement. Ces équations en coordonnées cartésiennes et en deux dimensions (x et y) deviennent :

ρ (u_{x} \frac{\partial u_{x}}{\partial x} + u_{y} \frac{\partial u_{x}}{\partial y}) = \frac{- \partial p}{\partial x} + μ (\frac{\partial^{2} u_{x}}{\partial x^{2}} + \frac{\partial^{2} u_{x}}{\partial y^{2}})

(1-1)

ρ (u_{x} \frac{\partial u_{y}}{\partial x} + u_{y} \frac{\partial u_{y}}{\partial y}) = \frac{- \partial p}{\partial y} + μ (\frac{\partial^{2} u_{y}}{\partial x^{2}} + \frac{\partial^{2} u_{y}}{\partial y^{2}})

(1-2)

\frac{\partial u_{x}}{\partial x} + \frac{\partial u_{y}}{\partial y} = 0

(2-1)

u_x et u_y sont les coordonnées du vecteur vitesse u.

La zone de la membrane microporeuse est décrite pour un fluide incompressible en écoulement laminaire et en régime stationnaire par les équations de Brinkman (Eqs. (3)-(4)).

2.2 Les équations de Brinkman

ρ (v \cdot \nabla v) = - \nabla p + μ \nabla^{2} v - \frac{μ}{κ} v

(3)

\nabla \cdot v = 0

(4)

avec v=u/ε la vitesse interstitielle, ε la porosité de la membrane et κ sa perméabilité.

Les équations (1) à (4) sont soumises aux conditions suivantes :

2.3 Les conditions aux limites

Entrée du module: à z = 0 u = 2 \bar{u} (1 - {(\frac{r}{R})}^{2})

(5)

Sortie du module: à z = L μ (\nabla u + {(\nabla u)}^{T}) = 0

(6)

où

\bar{u}

est la vitesse moyenne à l’entrée, c'est-à-dire le rapport du débit d’alimentation à la section de passage, R le rayon de la section droite à l’entrée du module.

Le transfert des solutés est décrit par :

– dans les retentions liquides :

\frac{\partial C}{\partial t} + u \cdot \nabla C = D_{a} \nabla^{2} C

(7)

– dans le lit poreux de membrane :

\frac{\partial C}{\partial t} + u \cdot \nabla C = D_{a} \nabla^{2} C - \frac{(1 - ε)}{ε} \frac{\partial q}{\partial t}

(8)

u représente les vitesses issues des équations de Navier–Stokes et de Brinkman, q est la quantité de soluté adsorbée par la membrane. Ce terme est nul lorsque le soluté n’a pas d’affinité avec les ligands greffés sur la membrane. La résolution des Eqs. (7) à (8) est soumise aux conditions aux limites suivantes :

Entrée du module: à z = 0 C (t) = C_{RP}^{sortie} = {\begin{matrix} 0 & t < τ_{RP} \\ C_{0} & t > τ_{RP} \end{matrix} |

(9)

Sortie du module: à z = L \nabla C = 0

(10)

\frac{{d C}_{sortie}^{RPAC}}{d t} = \frac{\bar{C} - C_{sortie}^{RPAC}}{τ_{RPAC}}

(11)

\bar{C}

est la concentration moyenne en soluté à la sortie du module de chromatographie membranaire, τ_RPAC et τ_RP sont les temps de séjour moyen respectivement des réacteurs RPAC et RP.

Les paramètres τ_RPAC et τ_RP sont identifiés par optimisation à partir d’une expérimentation à blanc, c'est-à-dire sans sorption avec de l’acétone. La routine SNOPT de Comsol Multiphysics 4.3 est utilisée dans ce cas.

La simulation de la courbe de perçage C/C₀ en fonction du temps, a été effectuée avec les Eqs. (1) à (11) auxquelles il faut joindre les cinétiques. Les modèles de Langmuir (Eq. (12)) et de bi-Langmuir (Eq. (13)) sont comparés dans cette étude.

2.4 Isotherme de Langmuir

\frac{\partial q}{\partial t} = k_{a} \cdot C \cdot (q_{m} - q) - k_{d} q

(12)

Dans l’équation de Langmuir, k_a et k_d sont respectivement les constantes de sorption et de désorption, q_m est la capacité maximale de sorption.

2.5 Isotherme de bi-Langmuir

\frac{\partial q}{\partial t} = \frac{\partial q_{1}}{\partial t} + \frac{\partial q_{2}}{\partial t}

(13a)

\frac{\partial q_{1}}{\partial t} = k_{a 1} C (q_{m 1} - q_{1}) - k_{d 1} q_{1}

(13b)

\frac{\partial q_{2}}{\partial t} = k_{a 2} C (q_{m 2} - q_{2}) - k_{d 2} q_{2}

(13c)

Dans l’équation de bi-Langmuir, la sorption s’effectue sur deux sites différents associés à deux énergies différentes de sorption et deux mécanismes différents. La quantité sorbée correspond à la somme des quantités sorbées sur chacun des sites représentés par les indices 1 et 2. Les constantes k_a, k_d et q_m avec les indices 1 et 2 correspondants ont, pour chaque site, la même signification que dans le cas du modèle de Langmuir à un seul site.

Les coefficients des modèles de Langmuir et bi-Langmuir ont été déterminés par ajustement paramétrique à partir d’expériences réalisées séparément en réacteur discontinu ou batch.

3 Matériels et méthodes

Les modules de CM utilisés dans ces études sont des modules Sartobind. Ils comportent des membranes échangeuses d’anion avec l’ammonium quartenaire comme ligand greffé sur leur surface. Trois différentes tailles du module axial ont été étudiées : Sartobind Q15, Q75 et Q100 et trois tailles également du module radial : Sartobind Nano-1mL, Nano-3mL et, Mini. L’ASB en poudre avec une pureté ≥ 98,0% provient de la société MP Biomedical (France) et a été dissoute dans 10 mM de la solution tampon de phosphate à pH 7,0 préparée à partir du mélange de K₂HPO₄ et KH₂PO₄ (Sigma Aldrich, France). Toutes les manipulations ont été réalisées avec le système chromatographique liquide: Aktaprime-Plus (General Electric, France). La courbe de perçage à blanc a été obtenue lors d’une expérience menée avec une solution d’alimentation en acétone à 5%vol. La solution d’ASB est alimentée sur le module de CM à une concentration initiale de 2,00 mg.mL⁻¹ et un débit d’écoulement de 10,0 mL.min⁻¹. Les courbes de perçage ont été mesurées en ligne par absorption UV à une longueur d’onde de 280 nm. L’ASB adsorbée a été récupérée en augmentant la force ionique du milieu avec la solution tampon saline NaCl 1M diluée dans la solution de phosphate. L’influence des concertations initiales d’ASB et des débits d’écoulement a été étudiée. Pour caractériser les performances de l’adsorption d’ASB sur les différents modules chromatographiques, la capacité de sorption dynamique à 10% de la concentration initiale (CAD_10%) a été calculée par l’Eq. (14). À la fin de l’expérience, la procédure de nettoyage et de régénération de la membrane a été effectuée suivant les procédures du manuel de Sartobind.

{CAD}_{10 %} = \int_{0}^{v_{10 %}} (C_{0} - C) d V - C_{0} V_{0}

(14)

4 Résultats et discussions

4.1 Capacité dynamique de sorption

Une série d’expériences est menée en faisant varier le débit d’alimentation de 5 à 30 mL.min⁻¹. Nous n’observons pas d’évolution de la capacité de sorption dynamique à 10% (CAD_10%) par unité de volume pour chaque type de module étudié, à savoir les modules Sartobind Q15, Q75 et Q100 pour la configuration axiale, Sartobind nano-1mL, 3 mL et mini pour la configuration radiale. Les valeurs obtenues sont d’environ 33, 22 et 19 mg.mL⁻¹, respectivement pour les trois modules axiaux et 30, 25 et 20 mg.mL⁻¹ pour les trois modules radiaux. Ces résultats confirment l’avantage qu’ont les CM de fonctionner à des débits d’écoulement très importants, avec une bonne performance de sorption des protéines. Le transfert massique dans ces modules de CM est dominé par le mouvement convectif, ce qui permet d’opérer à des débits plus élevés que dans une chromatographie classique. L’influence des concentrations initiales d’ASB est montrée sur les Fig. 4-A et Fig. 4-B pour les modules axiaux et radiaux. La CAD_10% augmente significativement avec la concentration initiale d’ASB. Elle est égale à 19,00 et 21,00 mg.mL⁻¹ de capacité à la concentration de 0,5 mg.mL⁻¹ pour Sartobind Q15 et Nano-1mL respectivement. À la concentration initiale de 8,0 mg.mL⁻¹, la CAD_10% s’élève à 59,4 et 58,4 mg.mL⁻¹, ce qui correspond à l’amélioration de la performance d’adsorption de CM de 213 et 178 %. La concentration des protéines est donc un facteur important pour l’augmentation de la capacité d’adsorption.

Fig. 4
Influence de la concentration initiale sur la capacité de sorption CAD_10% des modules axiaux (A) et radiaux (B).

D’un point de vue géométrique, la plus importante capacité par unité de volume de membrane a été obtenue avec le module dont la hauteur du lit de membrane est la moins importante : Sartobind Q15 (0,8 mm) pour le module axial et Sartobind Nano-1mL (4,0 mm) pour le module radial. Avec l’augmentation de la hauteur du lit de membrane sur Sartobind Q75 (4,0 mm) et Sartobind Nano-3mL (8,0 mm), la CAD10% par unité de volume est moins importante. Cette diminution de la CAD_10% sur Sartobind Q75 est estimée à 20% comparée au résultat du module Sartobind Q15. C’est la raison pour laquelle l’extrapolation des modules de CM est limitée, car la diminution de la capacité de sorption des protéines a été observée avec l’augmentation de la hauteur de lit dans les deux types de modules.

Ces résultats sont en accord avec ceux obtenus par le fournisseur de Sartobind, qui a étudié à un débit de 10 mL/min l’adsorption de l’ASB dilué dans la solution tampon de Tris/HCl à pH de 7,5. Leurs résultats sont d’environ 12-13 mg pour Sartobind Q75 et 29–30 mg pour Sartobind Nano-1mL.

4.2 Simulation numérique

Les profils de vitesse sont obtenus à partir de la résolution des équations de Navier–Stokes et de Brinkman sous Comsol Multiphysics 4.3 pour un débit de 5,0 mL.min⁻¹. Cette résolution, de même que celle de l’ensemble des équations différentielles considérées, est basée sur la méthode des volumes finis. Le maillage du domaine de résolution est réalisé sur Comsol Multiphysics. Les champs de vitesse résultant de cette simulation ont été ensuite intégrés dans les équations de bilan de matière couplées aux cinétiques de sorption pour la simulation du phénomène de sorption. Pour des raisons de symétrie axiale, cette simulation est réalisée sur la moitié du module. Les résultats issus du calcul sont illustrés sur la Fig. 5 pour les modules Sartobind Q75 et Sartobind Nano-1mL. Pour le module axial Sartobind Q75, les vitesses sont quasi homogènes sur toute la zone membranaire ; en revanche, sur la zone d’écoulement libre, à l’entrée et à la sortie du module, une distribution non idéale de l’écoulement est observée. La vitesse moyenne des fluides est de 5,87 × 10⁻³ cm.s⁻¹. Pour le module radial Sartobind Nano-1mL la vitesse moyenne est beaucoup plus élevée (5,39 × 10^-2 cm.s⁻¹), la distribution des vitesses est plus homogène dans la zone d’écoulement libre mais non idéale que dans la zone membranaire. Ces résultats nous montrent que la circulation des fluides est améliorée avec le module radial, qui permet d’atteindre des vitesses plus importantes et donc des temps de contact plus courts.

Fig. 5
Champs de vitesse issus de la simulation numérique du modèle de la MFN sur le module Sartobind Q75 (A) et le module Nano-1mL (B).

Les paramètres τ_RPAC et τ_RP du modèle de la MFN ont été optimisés à partir de l’essai à blanc, ces variables prennent en compte la dispersion et le volume mort du système externe. Avec le module Sartobind Q75 et au débit de 5 mL.min⁻¹, les valeurs suivantes sont obtenues : τ_RPAC = 29,1 s et τ_RP = 55,2 s. La diffusivité D_a = 4,06 × 10⁻⁹ m².s⁻¹ est calculée à partir de la corrélation de Polson appliquée à une solution de protéine très diluée [9]. Le modèle MFN a été simulé avec les différentes cinétiques de sorption (Langmuir et bi-Langmuir) pour prédire les courbes de perçage à la condition de sorption des protéines. Une étude préalable faite en faisant varier les valeurs de D_a montre que cette dernière a une influence négligeable sur le transfert. Sa valeur pour les protéines sera fixée à celle de l’acétone. Les paramètres des cinétiques de sorption des modèles de Langmuir et de bi-Langmuir sont résumés dans le Tableau 1. Les résultats issus de la simulation comparés aux valeurs expérimentales sont représentés sur la Fig. 6. Nous observons que le modèle de Langmuir prédit précisément la courbe de perçage jusqu'à 70% de la concentration initiale d’ASB avec le module Sartobind Q75. L’écart entre les résultats expérimentaux et théoriques apparaît sur la fin de la courbe de perçage lorsque la membrane arrive à saturation. Cet écart est corrigé avec le modèle de sorption de bi-Langmuir qui suppose l’existence de deux sites de sorption avec des vitesses de sorption différentes. Ce modèle sera retenu pour la suite de notre étude. Afin de valider notre modèle, nous avons simulé dans les mêmes conditions de débit d’alimentation, avec les mêmes paramètres de sorption, le module Sartobind Nano-1mL. La Fig. 7 montre les résultats expérimentaux et simulés. Les performances du modèle de MFN permettent de prédire précisément les courbes de perçage sur les deux géométries du module. Les différences de vitesse d’écoulement et la non-idéalité de la distribution du fluide proviennent des géométries des modules. Ces effets ont une influence sur les courbes de perçage.

Modèle cinétique d’adsorption	Paramètres optimisés du modèle
1 Langmuir	k_a = 0,043 ml.mg⁻¹.s⁻¹
k_d = 7,49 × 10⁻⁵ s⁻¹
q_m=223,81 mg.ml⁻¹
2 bi-Langmuir	k_a1 = 0,0498 ml.mg⁻¹.s⁻¹
k_d1 =6,74 × 10⁻⁵ s⁻¹
q_m1 = 172,718 mg.ml⁻¹
k_a2 = 0,0062 ml.mg⁻¹.s⁻¹
k_d2 =7,49 × 10⁻⁶ s⁻¹
q_m2 = 74,022 mg.ml⁻¹

Fig. 6
Simulation numérique des courbes de perçage d’ASB avec les différents modèles des cinétiques de sorption sur le module Sartobind Q75. Les conditions opératoires sont un débit d’écoulement de 5,0 mL/min et une concentration initiale d’ASB de 2,0 mg/mL.

Fig. 7
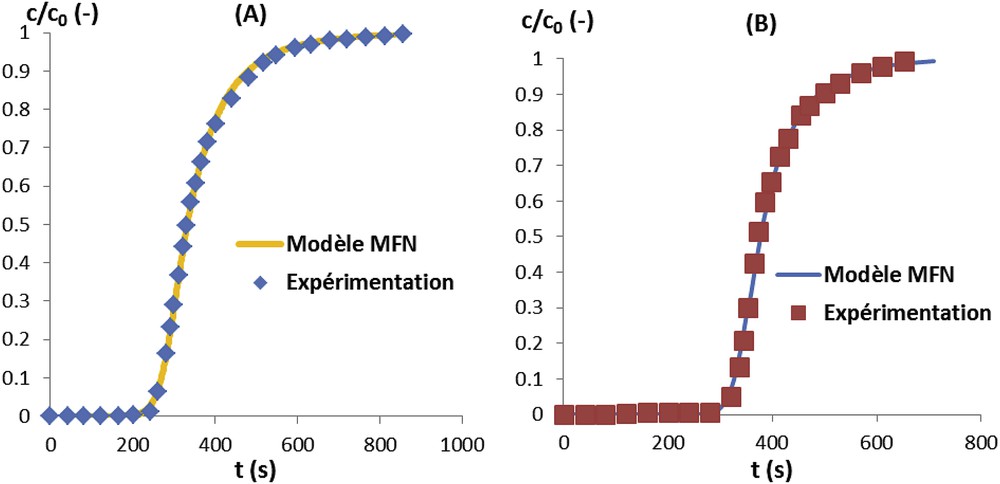
Comparaison entre les courbes de perçage expérimentales et celles issues du modèle de MFN sur le module de Sartobind Q75 (A) et de Sartobind Nano-1mL (B). Les paramètres des cinétiques de sorption sont identiques pour les deux modules. Les conditions opératoires sont un débit de 5,0 mL/min et une concentration d’ASB de 2,0 mg/mL.

4.3 Courbes de perçage aux différentes conditions opératoires

Pour cette partie, différentes conditions opératoires sont appliquées pour l’obtention des courbes de perçage. Sur le module Sartobind nano-1 mL, l’influence des débits d’écoulement sur la sorption de même que l’influence des concentrations initiales ont été étudiées. Les débits suivants : 5,0 10,0 20,0 et 30,0 mLmin⁻¹ ont été testés, pour une concentration initiale de 2,00 mg.mL⁻¹. Pour ce qui concerne les concentrations initiales, elles sont de 2,00, 4,00 et 8,00 mg.mL⁻¹ au débit d’alimentation de 5 mL.min⁻¹. D’une façon générale, on observe que l’allure des courbes de perçage n’est pas modifiée par les débits. La courbe de perçage apparaît plus tôt, avec un débit plus élev,é ce qui est normal car le temps de contact est réduit. Le phénomène de sorption est très rapide et efficace dans la CM, ce qui permet d’optimiser la productivité et le temps des procédés de purification des protéines. Lorsque les concentrations d’ASB augmentent, les temps de sorption diminuent. Les opérations préliminaires (sédimentation, filtration, etc.) qui permettent de concentrer les protéines sont de ce fait importantes afin d‘augmenter la capacité de sorption sur la CM.

Pour la simulation des courbes de perçage aux différents débits d’écoulement Q, les paramètres de sorption (k_a, k_d) sont corrélés au débit :

k_{a} = k_{a, 5} \frac{Q}{Q_{5}}

(15)

k_{d} = k_{d, 5} \frac{Q}{Q_{5}}

(16)

Q₁₀ est le débit de référence de 5 ml.min^-1, k_a,5 et k_d,5 sont respectivement les constantes d’adsorption et de désorption déterminées aux débits Q₅ et indiquées dans le Tableau 1.

À travers ces relations des équations cinétiques de Langmuir, les résistances aux transferts de matière ainsi que les limitations par la cinétique sont regroupés dans les constantes d’adsorption et de désorption. Cela ne modifie en rien l’équation de l’isotherme d’adsorption en régime statique puisque la constante d’équilibre thermodynamique n’est pas affectée par les débits. D’ailleurs nos résultats sont en accord avec les travaux publiés par van Beijeren et al. [10], qui relient leurs constantes à la vitesse d’écoulement du fluide par une relation linéaire.

Les constantes du modèle de bi-Langmuir sont adaptées en tenant compte de ces relations. Grâce à cette méthode, les courbes de perçage théoriques ont pu être simulées aux différents débits pour les deux configurations de modules. La comparaison avec les résultats expérimentaux est faite dans les Figs. 8. et 9. La performance du modèle de MFN permet d’observer précisément la prédiction des courbes de perçage aux différents débits. De plus, ce modèle permet d’obtenir de bons résultats sur les courbes de perçage aux différentes concentrations initiales (Fig. 9). Aucune modification des paramètres de la cinétique d’adsorption n’est nécessaire lorsqu‘on passe d’une géométrie à l’autre.

Fig. 8
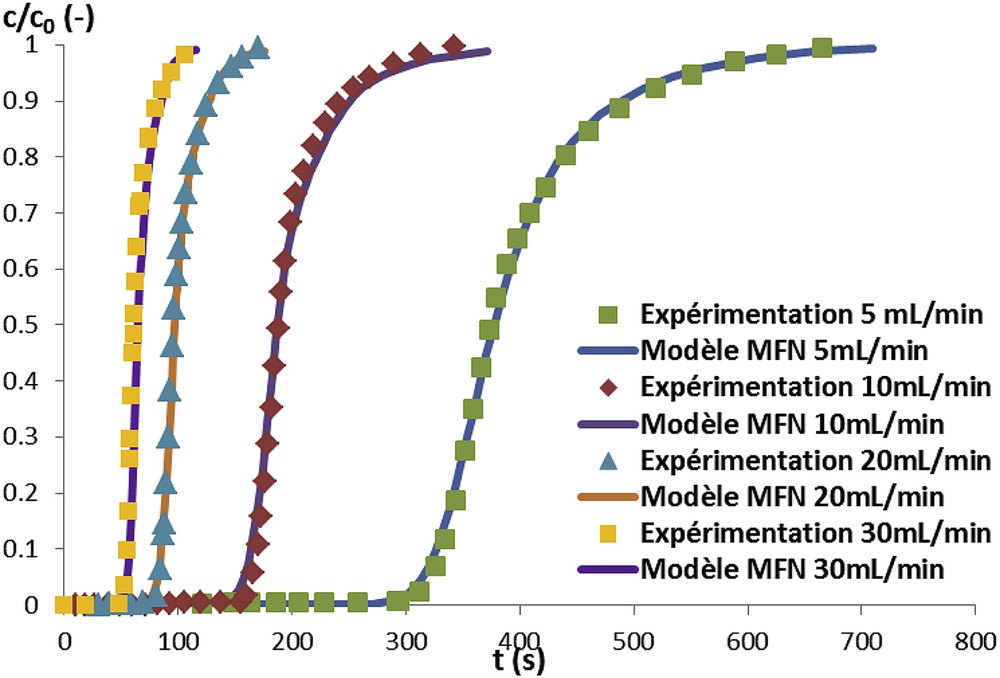
Comparaison des courbes de perçage obtenues aux différents débits d’écoulement par la simulation numérique de MFN et les résultats expérimentaux sur le module Sartobind Nano-1mL. La concentration initiale d’ASB est de 2,0 mg/mL.

Fig. 9
Comparaison des courbes de perçage obtenues à différentes concentrations initiales : 2,0 4,0 et 8,0 mg/mL par la simulation numérique de MFN et les résultats expérimentaux sur le module Sartobind Nano-1mL. Le débit d’alimentation est de 10 mL/min.

5 Conclusion

Ce travail a permis de clarifier l’influence du type d’écoulement (axial ou radial) sur la séparation dans la chromatographie membranaire à partir d’études expérimentales et théoriques. Un modèle de la MFN a été établi sur les modules de CM, ce qui permet de prédire précisément les résultats aux différentes conditions opératoires et d’optimiser ces procédés. La performance de la CM est confirmée avec une bonne capacité de sorption à débits importants. L’extrapolation des modules de CM à l’échelle industrielle sur les deux géométries d’écoulement : radial et axial est limitée, car la capacité de sorption diminue avec l’augmentation de la hauteur du lit membranaire. Le module radial semble plus approprié pour l’extrapolation à l’échelle industrielle car il offre une surface de transfert plus importante. Ainsi, l’épaisseur du lit du module radial peut rester relativement faible pour un volume d’opération plus important, ce qui permet une bonne capacité de sorption.

Bibliographie

[1] P. Ghosh; K. Vahedipour; M. Leuthold; E. von Lieres J. Chromatogr. A., 1332 (2014), pp. 8-13 | DOI

[2] T. Besselink; A. van der Padt; A.E.M. Janssen; R.M. Boom J. Chromatogr. A., 1271 (2013), pp. 105-114 | DOI

[3] M.B.J. Tharakan J Chromatogr. A., 702 (1995), pp. 191-196 | DOI

[4] S.-Y. Suen; M.R. Etzel Chem. Eng. Sci., 47 (1992), pp. 1355-1364 | DOI

[5] A. Shiosaki; M. Goto; T. Hirose J. Chromatogr. A., 679 (1994), pp. 1-9 | DOI

[6] K.H. Gebauer; J. Thömmes; M.R. Kula Chem. Eng. Sci., 52 (1997), pp. 405-419 | DOI

[7] C. Boi; S. Dimartino; G.C. Sarti J. Chromatogr. A., 1162 (2007), pp. 24-33 | DOI

[8] P. Ghosh; K. Vahedipour; M. Lin; J.H. Vogel; C. Haynes; E. von Lieres J. Chromatogr. A., 1305 (2013), pp. 114-122 | DOI

[9] C. Frerick; P. Kreis; A. Gorak; A. Tappe; D. Melner Chem Eng. Pro., 47 (2008), pp. 1128-1138

[10] Peter van Beijeren; Peter Kreis; Achim Hoffmann; Martina Mutter; Sven Sommerfeld; Werner Backer; Andrzej Gorak Chemical Papers, 62 (2008) no. 5, pp. 458-463 | DOI

Commentaires - Politique