1. Introduction
Aqueous biphasic systems (ABS) recently deserve a lot of attention thanks to their environmental friendly composition, with a large water content. They have been investigated for multiple extraction purposes in order to substitute the use of traditional highly polluting organic solvents [1, 2]. Among ABS, the family comprising the ionic liquid (IL) tributyltetradecylphosphonium chloride ([P4,4,4,14]Cl) mixed with water and a strong acid has been proposed for metallic ion extraction [3, 4, 5]. Metallic ions have preferential phases, as for example Co(II) prefers the upper, ionic liquid-rich phase while Ni(II) prefers the lower highly acid solution. Beside the interest in metal extraction, these ternary systems are surprising with a very rich phase diagram, either in presence of a strong acid or a salt (for example, HCl or NaCl). The solutions are thermomorphic, i.e. reversibly change from a monophasic to a biphasic liquid state with temperature, and with the particularity to separate upon an increase of temperature, meaning that the biphasic region of the phase diagram increases with temperature, therefore also having a Lower Solution Critical Temperature (LCST). The mono- or biphasic states are related to the composition and, at any fixed temperature, the increase of both IL or salt/acid content triggers the phase separation. The metallic ions extracted will therefore play themselves a determinant role in their own extraction [6, 7, 8]. Understanding the mechanisms of phase separation in such family of systems is therefore a challenging task that we partially address in this paper. Our previous investigation [9] was focused on the structural organization of the acidic (HCl, H2SO4) solutions with concentration and temperature. We highlighted that the IL [P4,4,4,14]Cl, which could be assimilated to a cationic surfactant, forms spherical micelles in solution. Upon temperature rise, the micelles aggregate until eventually causing the phase separation. The aggregation is due to an adsorption of chloride ions at the micelles surface with temperature, as proved by the titration of free chloride ions in solution: the adsorption of ions causes a variation in the Electric Double Layer (EDL) composition around the micelles and a screening of electrostatic repulsion bewteen micelles. Our previous structural investigation also shows an aggregation of the micelles when the acid content increases. Here, we question the similarity of the phase separation with temperature and salt concentration in the system. Using the former chloride titration technique at fixed temperature but variable salt content, we aim at rationalizing the electrostatic interactions responsible for the state of the solution. After describing the experimental methods, we present the experimental results: the investigated points are presented in the Figure 1 on the phase diagram of the particular solution investigated here: [P4,4,4,14]Cl, NaCl and water. We then detail the theoretical approach based on a classical charge regulation theory to model the results. We eventually discuss the validity and limits of the model.
Binodal curve of the system [P4,4,4,14]Cl, NaCl and water, and points investigated by chloride titration. Binodal data (black squares) from [10]. The three series of points correspond to the following IL wt%: 8.12 (blue squares), 14.55 (red circles) and 20.48% (green triangles).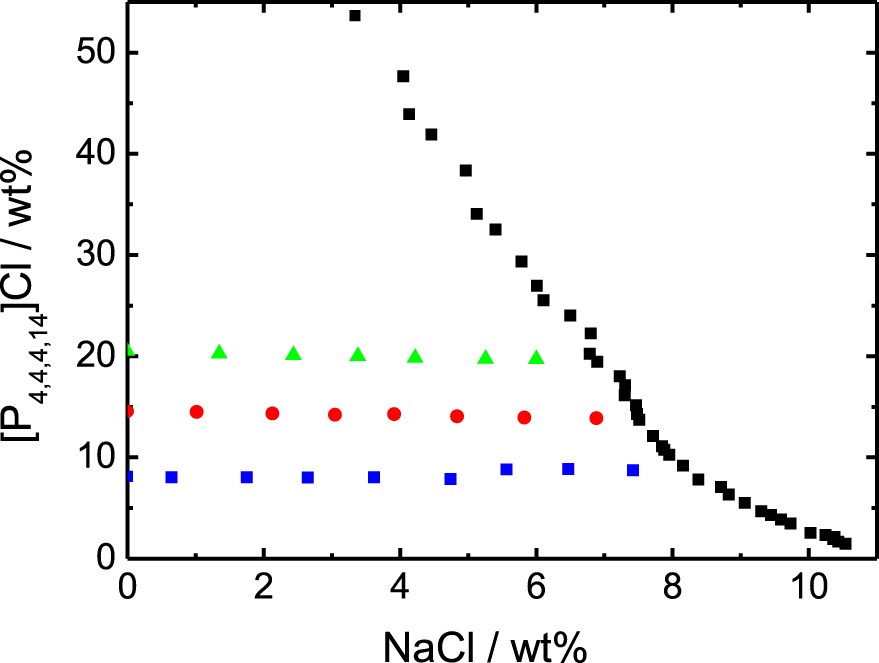
2. Materials and methods
2.1. Chemicals
Tributyltetradecylphosphonium chloride ([P4,4,4,14]Cl) has been provided by Interchim, while NaCl was purchased from Honeywell. All chemicals were used as received. All samples were made using ultra-pure water (Millipore system, 18 MΩ).
2.2. Samples
Desired amounts of NaCl and of a concentrated aqueous solution of [P4,4,4,14]Cl were weighted in a 10 mL gauged flask and then ultra-pure water was added to the line. The composition of all the samples can be found in the ESI.
2.3. Apparatuses and methods
A balance (Fisherbrand, Analytical Series, precision 0.0001 g) was used to prepare the samples. Free chloride ions concentration (M) was determined by use of a chloride specific electrode (ThermoScientific, chloride half cell Orion 9417SC and reference cell), which was calibrated by seven standard aqueous solutions of NaCl with concentrations ranging from 6 × 10−3 M to 1.1 mol⋅L−1. The calibration was found linear with very good regression parameter and under the experimental procedure followed, reproducibility is within ±2%. For both calibration and measurement of the samples, temperature was controlled at T = (25 ± 0.5) °C by a thermostated bath. Densities at T = 25 °C were measured by use of a density-meter (Anton-Paar, DMA 4001, precision 10−4 g⋅cm−3). Concentrations in moles per liter (M) were calculated from the weighted masses and flask volume while NaCl and [P4,4,4,14]Cl wt% were calculated from added masses, density and flask volume. Samples are sorted within three series, for which a fixed mass of IL is mixed with increasing amounts of NaCl. To label the series, we use the IL wt% in the absence of NaCl, i.e. 8.12/14.55/20.48 wt% of IL. This corresponds respectively to 0.185, 0.329 and 0.462 mol⋅L−1.
The binodal data obtained by Schaeffer et al. [10] have been obtained with Iolitech as the IL provider, while our samples are prepared with an Interchim batch of IL. Nevertheless, both data sets agree very well in terms of monophasic domain (see Figure 1). In addition, we prepared one sample supposedly being biphasic and very close to the binodal, according to the data by Schaeffer et al. and it actually appears to be biphasic (see ESI).
3. Experimental results
In the Figure 2 are plotted the experimental measurements of the chloride concentrations in the solutions. The first point of each experimental series corresponds to the case without any addition of NaCl and the horizontal lines are the experimental averages of each series. The line x = y would be the behavior without any adsorption at the micelle surface (see caption). The chloride specific electrode is sensitive to the chemical potential of the ion, which is converted directly into the equivalent concentration of chloride ion in an aqueous electrolyte solution in equilibrium with the system. By neglecting the activity coefficient corrections, which are relatively small in this chloride concentration range [11], one can consider that this quantity corresponds to the bulk free chloride ion concentration [Cl−]free, i.e. the Cl− concentration far away from the micelles. The quantity of chlorides adsorbed at the micelle surface is therefore equal to [Cl−]ads = [Cl−]tot − [Cl−]free. The data are presented up to the limit of linearity of the electrode, that does not allow a reliable measurement of the region too close to the binodal line. For this reason, more points are plotted in the Figure 1 than in the Figure 2.
Chloride titration for three different ionic liquid contents, as a function of total amount (in mol⋅L−1) of chloride. The [Cl−]free are directly measured and the [Cl−]ads are deduced from the measurement by the relation [Cl−]tot = [Cl−]ads + [Cl−]free. The line x = y would be the behavior without any adsorption at the micelle surface.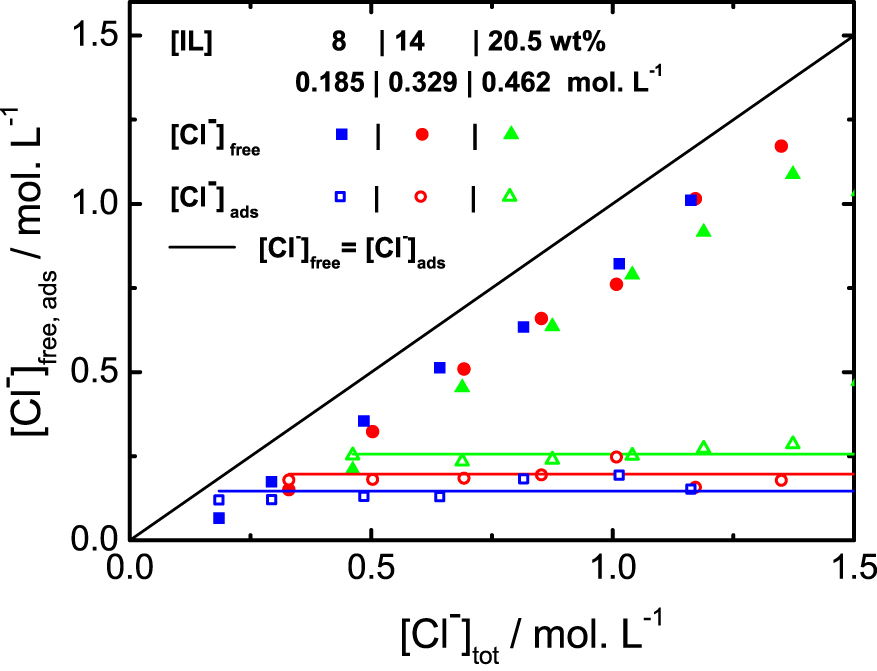
As observed in the Figure 2, without any addition of NaCl, about 40% of the Cl− are free in the solution, whatever the mass fraction of ionic liquid. More precisely, the fraction of adsorbed chloride at the surface follows the linear behaviour given by the equation: [Cl−]ads = 0.39 ⋅ [LI] + 0.071, both concentration in mol⋅L−1. The micelles therefore carry an effective charge for any fraction of IL. This result is consistent with the structural characterization of the binary mixture (IL + water) [9], where a strong correlation peak between micelles is observed, arising from the electrostatic repulsion between the objects in solution in absence of additional charges. Upon addition of NaCl, the adsorbed quantity of chloride is constant, all the ions are dispersed into the solution, in opposition to what is observed with temperature.
4. Theory
As previously expressed, we consider that the quantity measured by the electrode corresponds to the bulk free chloride ion concentration far away from the micelles, where the aqueous solution plays the role of a reservoir. The measurement can therefore be used to establish a link between the total concentration of introduced chlorides [Cl−]tot and [Cl−]free.
This result can then be compared with those obtained using an Electrical Double Layer (EDL) model with charge regulation. The total chloride concentration reads
| (1) |
The mass action law for the equilibrium between free ions and ions bound specifically to the surface reads as follows:
| (2) |
The SI practical unit of the mass action law constant K° is meter if the reservoir salt concentration C0 = [Cl−]free is the volume number density (i.e. the number of electrolyte per unit volume). The effective charge of the micelles is then:
| (3) |
| (4) |
| (5) |
Then we calculate the chloride excess in the EDL. Considering the Gouy–Chapmann equation [13] yielding the anion concentration C−(x) as a function of the position x with respect to the surface, we obtain the excess chloride area number density
| (6) |
These area number densities and must then be transformed into volume number densities to obtain the total experimental concentration [Cl−]tot. So multiplying by the specific surface area of the micelles , we finally obtain from (1):
| (7) |
In the Figure 3, we inverted the axes in order to stick to the experimental observables. Despite the simplicity of the model we have a quantitative agreement with the data for the range of chloride and ionic liquid concentrations investigated, although some deviations are observed and discussed below.
Free chloride in the solution (i.e. chloride concentration in the reservoir) as a function of total amount of chloride in the systems, as measured by titration and computed, for the three sets of samples (different colors/symbols).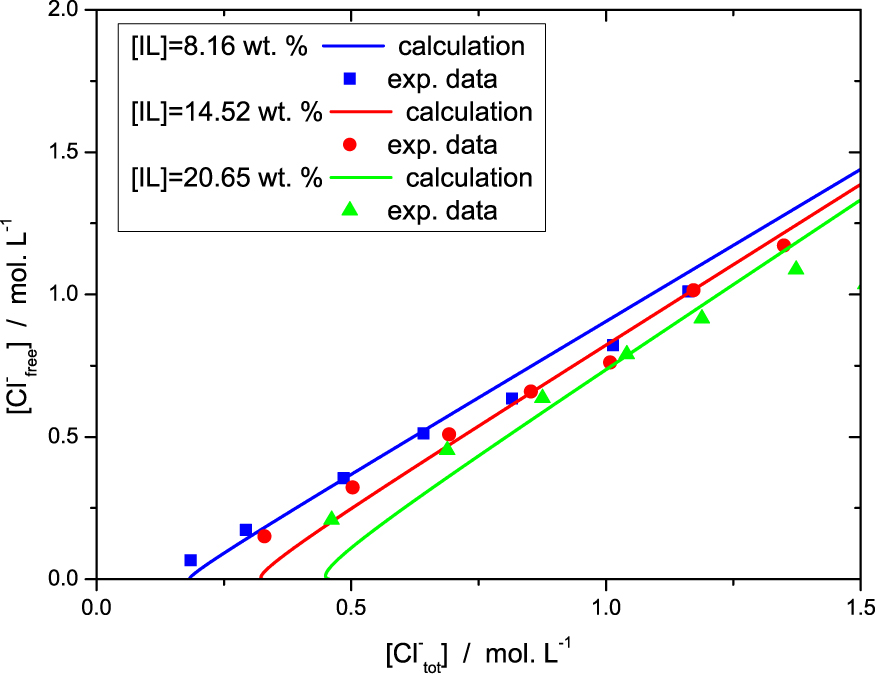
5. Discussion
The Figure 4 enables to analyse the different chloride populations. When no salt (NaCl) is added to the solution, the reservoir salt concentration C0 = [Cl−]free is 0. In this limit the model is not rigorously valid for two reasons. First, as long as the salt concentration is less than 2 × 10−2 mol⋅L−1, the strong electrostatic screening regime is not reached. Second we neglected the critical micellar concentration (cmc) and the concentration of free IL in solution. The cmc of [P4,4,4,14]Cl was evaluated from the variation of the surface tension as a function of IL wt% in aqueous mixture, measured by pending drop method (see SI). It was found to be equal to 0.05 ± 0.02 wt%, and drops consequently (<0.02 wt%) when acid or salt is added to the solution. There is therefore a proportion of free chloride not taken into account by the model for these two effects for low salt concentration C0 = [Cl−]free, as shown in Figure 3.
Different chloride populations (colors/groups) for three solutions of various IL mass fraction (full, dashed and dotted lines) as function of the free chloride in the solution (chloride concentration in the reservoir).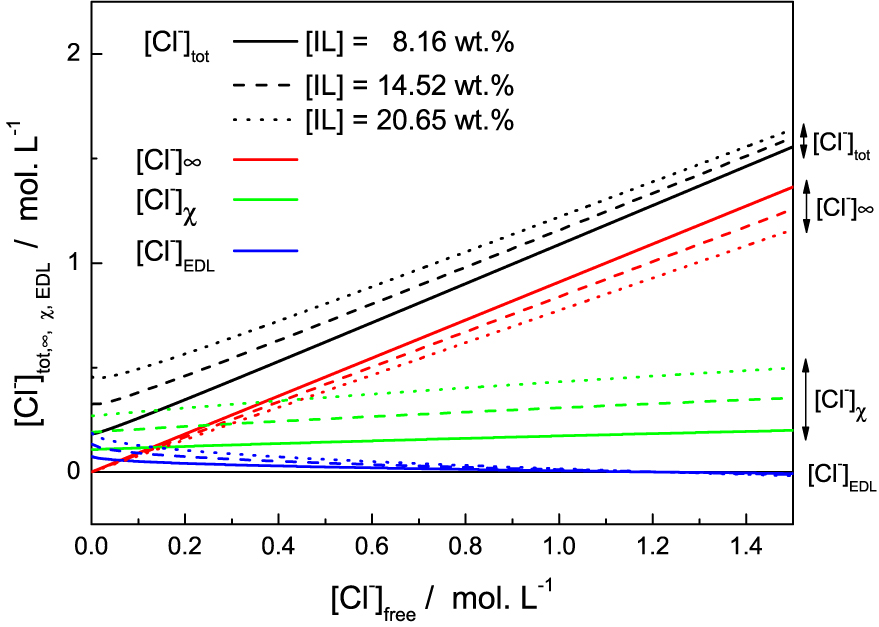
Adding more chloride into the solution, therefore having more chloride into the reservoir, leads to a slight increase of the bounded ions while the concentration into the EDL decreases. For a reservoir concentration of 1.25 mol⋅L−1, the EDL concentration [Cl−]EDL even becomes negative. [Cl−]EDL is actually an excess term with respect to bulk concentration. This means that above this limit, adsorption onto the surface is strong enough so that it reverses the surface charge, which becomes negative. We note that in absence of well-defined adsorption sites, there is no chemical saturation of the surface. Adsorption is therefore not limited and inversion is possible. In practice, this means that the electrostatic repulsion between micelles breaks down. The system can then become destabilised because the attractions due to Van der Waals forces are no longer counterbalanced by electrostatic forces. Phase separation is then possible. This is precisely what happens experimentally. Despite its simplicity, the model allows us to represent the destabilisation mechanism of the solutions and the appearance of this phase separation. At some chloride addition, the effective charge of the micelles becomes very small, leading to a complete screening of the electrostatic repulsion between the objects and therefore a flocculation of the micelles followed by the phase separation.
This effect is due to the increase in [Cl−]𝜒 population. Although the increase in [Cl−]𝜒 population in the Figure 4 is fairly small, it is enough to neutralise the charge on the micelles. Because of the high charge of the micelles due to their high aggregation number, adsorption is already high in the absence of salt, even if the K° constant is low. The addition of chloride further increases this phenomenon and the charge is eventually reversed.
We eventually examined the influence of the bounding constant K°. The Figure 5 shows the effect of varying the binding constant between 0.5 and 10 on the solution at 8.6 wt% of IL. The figure is understandable if we remember that [Cl−]free = C0 is the concentration of chloride in an electrolyte solution in equilibrium with the system. Thus the free ions far from the micelles [Cl−]∞ are directly proportional to it and do not depend on the adsorption constant which only controls the adsorbed Cl− and the ions in the Debye EDL. Overall, an increase in K° logically increases chloride ions adsorption. This then reduces the counter-ions concentration and the co-ion depletion in the EDL: the effective charge being lower, fewer counter-ions are needed to screen the micelles and the repulsive force on cations is weaker.
Different chloride populations (colors/groups) for the the 20.65 wt% IL solution as functions of the free chloride in the solution (chloride concentration in the reservoir). The values are given for different binding constants K° (full, dashed, dotted or dash-dotted lines).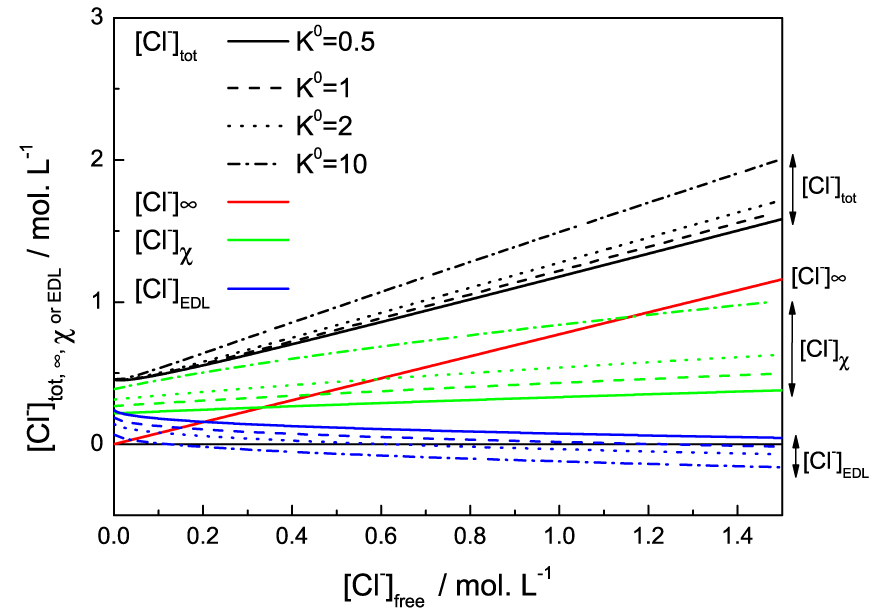
We first remark that increasing the value of K° indeed increases the slope of [Cl−]𝜒 with the chloride reservoir concentration, as previously mentioned. But the main effect is that increasing the binding constant will increase [Cl−]𝜒, reducing the effective potential at the micelle surface, therefore shifting to lower concentration the EDL and the term [Cl−]EDL. This leads to the effective charge of the micelle to be screened at lower NaCl addition, then the phase separation to be induced at lower NaCl or acid content. This behaviour is exactly what is observed upon increase of temperature, where the free chloride concentration decreases with temperature until phase separation. The higher is the temperature, the lower the salt (or acid) addition needed to observe the phase separation. The increase of temperature can therefore be modelled by an increase of K°. All this means that the adsorption reaction is favoured at high temperature and is therefore endothermic. It is this phenomenon that allows us to understand why this system shows a Lower Solution Critical Temperature (LCST). Eventually, we could assume that if K° increases enough, i.e. at high enough temperature, the charge inversion of the micelles could lead to repulsion again and the system would turn homogeneous again upon NaCl addition. This was however never tested experimentally, since the solubility of NaCl limits the phase diagram.
6. Conclusion
The aqueous biphasic systems formed by the mixture of the ionic liquid [P4,4,4,14]Cl with salt or acid present a strong interest from a fundamental as well as potential application point of view. The phase diagram is complex, with self aggregation and organisation varying with the addition of charges and temperature in different ways. Following a detailed structural investigation of acidic solutions with temperature and an insight into the phase transition mechanisms upon heating, we complete here our rationalisation of electrostatic effects. We propose a simple still relevant charge regulation model to describe the electrical double layer and screening of electrostatic interactions in the solution with addition of ions. The only fitted parameter is the binding constant taking into account the chemically or, in this case, physically bound ions to the micelle surface. The model is not rigorously valid at low salt concentration. Nevertheless, it provides a qualitative but strong insight into the mechanisms at play between the micelles upon addition of charges or increase of temperature, leading to the phase separation.
This approach could therefore be the first step in describing the phase diagram and thermodynamics of these complex systems, for which electrolyte theory can explain their behaviour and in particular their phase diagram. It would thus be possible to take into account more complex geometries of aggregates (e.g., beyond a spherical organisation) or to look at the limit of weaker electrostatic screening and the influence of the non-micellised part of the ionic liquid. A model combining the DLVO approach and Hamaker’s constant could thus enable the full prediction of the phase diagram versus ions concentration and temperature. Investigating the effect of salt versus acid, H+ versus Na+ or other ions, will eventually lead to another world of physical chemistry.
Declaration of interests
The authors do not work for, advise, own shares in, or receive funds from any organization that could benefit from this article, and have declared no affiliations other than their research organizations.
Dedication
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
Funding
This research was funded by the French National Agency for Research (Grant No. ANR-ITALLIX-22-CE29-0023-01). A CC-BY public copyright license has been applied by the authors to the present document and will be applied to all subsequent versions up to the Author Accepted Manuscript arising from this submission, in accordance with the grant’s open access conditions.




 CC-BY 4.0
CC-BY 4.0