1 Introduction
Les nitrures de fer ont suscité beaucoup d’intérêt depuis les premiers travaux de K.H. Jack 〚1〛, du fait de leurs applications dans les domaines de l’enregistrement magnétique de haute densité 〚2〛 et, sur le plan des procédés thermochimiques, de l’amélioration de la dureté des métaux ferreux 〚3〛. Sur le plan de l’approche théorique, les possibilités quant à une détermination précise des structures électroniques et magnétiques, au sein de la théorie de la fonctionnelle de la densité (DFT) 〚4〛, ont suscité un examen approfondi de ce système, visant à donner une description quantitative des amplitudes des moments magnétiques portés par les atomes de fer appartenant aux différents sites du réseau cristallin, en relation avec la proximité de l’azote 〚5–7〛.
Au sein du système fer–azote, les nitrures Fe8N, Fe4N et Fe3N s’ordonnent de manière ferromagnétique 〚8〛. Avec l’augmentation du taux d’azote dans la série, l’aimantation baisse et, à plus forte concentration d’azote, on observe l’absence d’ordre magnétique : Fe2N est paramagnétique 〚9〛. Leurs structures cristallines peuvent être considérées comme résultant de l’insertion d’azote dans le réseau métallique du fer, respectivement dans ses variétés cubique centré (Fe-α), cubique à faces centrées (Fe-γ), hexagonal compact (Fe-ϵ) et orthorhombique (Fe-δ). En effet, Fe8N (ou Fe16N2-α”) se forme comme une structure intermédiaire entre la martensite azotée α'-(structure dérivée du Fe-α) et le nitrure, plus riche en azote Fe4N (structure dérivée du Fe-γ). Sachant que seul Fe-α est ordonné ferromagnétiquement à l’ambiante, il faut conclure que l’ordre magnétique et les amplitudes des moments atomiques portés sont le résultat de l’insertion de l’azote, qui a pour conséquence la redistribution des atomes de fer en trois (Fe8N), deux (Fe4N) et un (Fe3N) sous-réseaux. Nous nous proposons dans cette note d’en étudier le double rôle chimique et magnétovolumique pour un des nitrures, Fe4N, et d’en dégager des tendances pour la série Fe8N, Fe4N et Fe3N.
2 Structure cristalline de Fe4N
Les études antérieures menées sur Fe4N en tant que pigment pour l’enregistrement magnétique 〚2〛 étaient suscitées par une aimantation à saturation élevée (σs300 K ≈ 180 uem g–1), voisine de celle de Fe-α (σs300 K ≈ 190 uem g–1), associée toutefois à une plus grande inertie chimique. Sa structure cristalline est dérivée de la perovskite cubique, de formulation générale ABX3 (A, B = métal, X = anion). En fait, la Fig. 1 représente le composé comme une antiperovskite, dans la mesure où les sites X sont occupés par un des deux sous-réseaux de fer, donnant : FeINFeII3. FeI, au sommet du cube porte un moment de ∼3 μB ; FeII, aux centres des faces, a un moment réduit de ∼2 μB ; l’ordre est ferromagnétique, avec TC ≈ 700 K 〚10〛.

Représentation de la structure de Fe4N. Par ordre de tailles de sphères décroissantes : Fe I, Fe II, N.
Representation of the crystal structure of Fe4N. By decreasing order of size of sphere: Fe I, Fe II, N.
La structure peut être également visualisée comme l’arrangement cubique à faces centrées du fer (variété γ), avec l’azote inséré au centre du cube. L’insertion d’azote provoque une forte augmentation du paramètre de maille a = 7,1777 bohr (1 bohr = 0,529 Å) comparativement au paramètre de Fe-γ (a = 6,5217 bohr). Compte tenu des distances fer–azote, les atomes de fer au sommet (FeI) sont à a√3/2, avec 12 FeII proches voisins à a√2, comme dans Fe-γ ; ceux des centres des faces, FeII, ont, en plus des 12 FeI proches voisins, deux atomes d’azote à a/2.
3 Méthode de calcul
Pour l’examen de la structure électronique et magnétique, il a été fait usage d’une méthode de calculs auto-cohérents, au sein de la théorie de la fonctionnelle densité (DFT), c’est-à-dire la méthode de l’onde sphérique augmentée (ASW) 〚11〛. Outre l’utilisation qu’elle fait de l’approximation de la densité électronique locale de spin (LSDA) 〚12〛, la méthode ASW est basée sur l’approximation de la sphère atomique (ASA). L’ASA stipule que chaque atome est entouré d’une sphère où une moyenne sphérique est effectuée pour la densité et le potentiel ; en outre, le volume occupé par les sphères doit être égal au volume de la maille. Il en résulte un problème de représentation de l’espace interstitiel pour les structures dites ouvertes comme la fluorine, le rutile ainsi que la perovskite. Afin d’éviter un recouvrement trop important des sphères atomiques, rendant le sens physique des résultats peu probant, des sphères vides (ES : empty sphere) sont introduites dans l’espace vide, afin d’y représenter la densité électronique. Les ES sont des pseudo-atomes sans états de cœur et dont les charges proviennent des atomes avoisinants ; de plus, les sphères vides permettent la prise en compte des effets de covalence au sein du réseau. Dans la structure du nitrure de fer Fe4N, des sphères vides ont été introduites aux milieux des arêtes : (,0,0), etc. Outre l’obtention et la discussion des densités d’états (DOS), les propriétés de liaison chimique seront détaillées sur la base des populations de recouvrement (COOP = Crystal Orbital Overlap Population), calculées au sein de la méthode ASW 〚13〛. Selon le signe des COOP, positives, négatives ou nulles, les liaisons seront liantes, anti-liantes ou non liantes.
4 Effet chimique de l’introduction de l’azote
Afin de démontrer cet effet, deux calculs ont été effectués au paramètre expérimental. Le premier correspond au nitrure Fe4N (FeINFeII3) ; le second, pour un réseau simulant l’absence d’azote, FeIESFeII3, formulation dans laquelle la sphère vide (ES) au site de l’azote en (,,) ne joue pas le même rôle que celles introduites en (,0,0), etc. Notons qu’un calcul de FeIESFeII3 au paramètre de Fe-γ (a = 6,5217 bohr) donne un moment magnétique très faible, donc sans éclatement d’échange pour les DOS, ce qui empêche d’établir les comparaisons permettant de souligner le rôle de l’azote. Laissant l’étude magnétique détaillée pour la section suivante, nous examinons ici les caractéristiques de transfert de charges, de densités d’états et de liaison chimique.
Dans le cadre de ces calculs, basés sur l’approximation de la sphère atomique, le transfert de charges entre les différents constituants est fonction du choix des rayons des sphères atomiques, qui n’est pas unique. Dans le cadre de nos calculs, qui minimisent le recouvrement entre les sphères atomiques et vides, le transfert s’effectue essentiellement depuis les sphères atomiques FeII vers l’azote et les sphères vides, alors que seul un faible transfert est observé depuis les atomes FeI vers l’azote. De tels résultats peuvent s’expliquer par les distances respectives et montrent que le site FeI est moins engagé dans la liaison chimique avec l’azote.
4.1 Densités d’états (DOS)
Pour les deux populations de spins, majoritaire (↑) et minoritaire (↓), les densités d’états pour chaque site, tenant compte de sa multiplicité par unité formulaire (u.f.), c’est-à-dire 1 FeI, 3 FeII et 1 N, sont présentées sur la Fig. 2 ; le zéro des énergies sur l’axe des x est pris au niveau de Fermi EF. Quoique pris en compte dans les états de valence pour lesquels les calculs sont entrepris explicitement, les états N(2s) se trouvant à des énergies beaucoup plus basses que la fenêtre énergétique (–8, 8 eV) ne sont pas reportés. Les sphères vides présentant peu de contribution aux DOS ne sont pas représentées sur la Fig. 2. Du point de vue de l’aspect général, le moment magnétique est dû à un déplacement énergétique entre les états des deux populations de spins – éclatement d’échange –, plus important pour FeI que pour FeII. Les états N(2p) ne sont pas affectés par le shift énergétique ; ils prédominent au bas de la bande de valence entre –8 et –6 eV, où ils se mélangent principalement avec les états de FeII, contrairement aux états de FeI, qui présentent une moindre hybridation avec l’azote. Ceci est en accord avec une liaison FeII–N, plus forte compte tenu des distances interatomiques détaillées plus haut. Les deux sites métalliques présentent des DOS très différentes, hormis les intensités : pour les populations (↑), celles de FeI tombent à un minimum avant EF, signalant un comportement de ferromagnétique fort au sens d’une sous bande pleine, alors qu’une densité d’états finie et relativement élevée est observée pour FeII à EF. Ces états, dont la nature est détaillée au paragraphe suivant décrivant la liaison chimique, sont responsables du comportement de ferromagnétique faible du nitrure et sont absents dans le système FeIESFeII3 (cf. § 4.3). Pour les deux populations de spins, les DOS de FeII sont étendues sur une fenêtre énergétique plus importante que celles de FeI ; ceci est en rapport avec une localisation plus importante, donc un moment plus élevé de ce dernier par rapport au moment de FeII. Ces observations, liées à la présence de l’azote, pourront être explicitées davantage par l’examen de la liaison chimique.

Densités d’états spin polarisées de Fe4N.
Spin polarized density of states for Fe4N.
4.2 Propriétés de liaison chimique (COOP)
Les interactions entre les sites métalliques et entre les atomes de fer et d’azote sont explicitées par les COOP partielles représentées sur la Fig. 3, permettant d’attribuer un caractère liant (+) ou antiliant (–) à une liaison. Ces COOP sont montrées pour les populations de spins majoritaires (↑) ; pour l’autre direction de spin, elles sont semblables, avec un déplacement vers les énergies plus élevées, comme pour les DOS. Pour permettre des comparaisons entre les différentes amplitudes, seule la contribution d’un unique atome de chaque espèce est prise en compte.

COOP partielles pour les populations (↑) pour les différentes interactions dans Fe4N.
Spin up (↑) partial COOP for Fe4N.
Malgré la symétrie ponctuelle D4h du site FeII, plus basse que Oh du site FeI, nous considérons l’éclatement des orbitales d en t2g (dxy, dxz et dyz) et eg (dz2 et dx2-y2) pour faciliter la discussion.
L’interaction fer–azote a un caractère covalent impliquant un électron 3d dans une orbitale eg (soit dz2) de FeII et un des trois électrons 2p de l’azote (soit pz), formant une liaison σ ayant un caractère liant prédominant entre –8 et –6 eV. Dans le reste de la bande de valence, son caractère, tout en restant liant, diminue en intensité, car les états d du fer sont impliqués dans la liaison métallique FeI–FeII. Compte tenu de la liaison plus longue entre le sommet du cube et le site de l’azote à a√3/2, cette liaison est nettement moins importante pour FeI–N, comme le montre le tracé en pointillés par rapport au tracé en traits pleins entre –8 et –6 eV. Les orbitales FeII–t2g participent principalement à la liaison métallique entre les deux sous-réseaux de fer, FeI–FeII, qui est pour moitié liante et pour moitié anti-liante en dessous de EF, indiquant que la stabilité du système ne peut être due à cette interaction. La liaison chimique Fe–Fe dans Fe-γ (FeIFeII3) ajoutée au tracé, montre un comportement similaire. Les orbitales t2g sont non liantes par rapport à la liaison Fe–N, sauf pour la faible liaison π, qui a lieu, par exemple, entre N–px et Fe–dxz. Les états correspondant à π* se trouvent au-dessus des DOS des états Fe–d au voisinage du niveau de Fermi. Grâce à l’azote (il faut tenir compte des trois liaisons fer–azote dans l’octaèdre « N–FeII6 »), la majeure partie de la bande de valence reste liante, malgré la présence de liaisons π* près du niveau de Fermi.
On retrouve la même nature de liaison fer–azote dans les autres nitrures Fe8N et Fe3N, qui comprennent respectivement trois et un sous-réseau(x) Fe : les états π* identifiés à EF dans Fe4N se retrouvent alors respectivement en dessous et au-dessus de EF. Avec des états σ* et π* dans la bande (vide) de conduction, Fe3N serait le nitrure ferromagnétique le plus stable, contrairement à Fe8N. Ces observations permettent de suggérer une tendance à l’augmentation de « l’ionicité » de la liaison globale dans la série. De fait, Fe3N est facilement obtenu comme produit secondaire lors des essais de préparation des pigments Fe4N lorsque les conditions de nitruration n’étaient pas suffisamment contrôlées (température, mélange NH3–H2, durées…).
4.3 Le composé FeIESFe3II
La Fig. 4a montre les DOS partielles aux sites du fer du composé FeIESFe3II. Cette formulation correspond en réalité à Fe-γ, dans lequel les atomes de fer en (0,0,0) et ceux en (,,0)… ont été rendus cristallographiquement différents. Les DOS confirment les observations formulées ci-dessus sur le rôle de l’azote par trois aspects principaux :


a. Densités d’états spin polarisées de « Fe4ES », la sphère vide ES remplaçant l’azote. b. Densités d’états et liaison chimique (FeI–FeII) spin-polarisées de Feγ, (FeIFe3II) au paramètre de Fe4N.
a. Spin polarized density of states for “Fe4ES”, the empty sphere replacing nitrogen. b. Spin polarized density of states and COOP (FeI–FeII) for Feγ (FeIFe3II) at the lattice parameter of Fe4N.
- • (i) l’absence d’états dans le domaine énergétique de l’azote, c’est-à-dire entre –8 et –6 eV ;
- • (ii) l’aspect peu modulé des DOS de la sphère vide du site de l’azote (dans laquelle un faible transfert de charges s’opère), contrairement au cas des DOS de l’azote de la Fig. 2, provenant davantage d’une certaine délocalisation que d’un transfert de charge depuis les atomes de fer, essentiellement FeII ;
- • (iii) l’allure des DOS des deux sites de fer, qui est la même, et le gap, signalant un comportement de ferromagnétique fort pour FeI ainsi que pour FeII, d’ailleurs devenus équivalents, comme dans le fer cubique à faces centrées.
Afin de montrer les aspects de liaison chimique au sein d’un réseau Fe-γ, nous montrons sur la Fig. 4b les DOS partielles et les COOP pour l’interaction entre deux atomes dans FeIFe3II. L’aspect essentiel de la Fig. 4a est retrouvé et la liaison chimique FeI–FeII présente la même allure que celle des COOP obtenues pour le nitrure (Fig. 3). L’énergie des COOP(↑) FeI–FeII dans le métal vis-à-vis du niveau de Fermi est plus basse que dans le nitrure, vis-à-vis du niveau de Fermi du nitrure, du fait de la covalence introduite par la liaison Fe–N. Notons enfin que, si la liaison FeI–FeII (↑) est liante et anti-liante dans la bande de valence, défavorisant la stabilité du réseau métallique, elle est surtout liante dans la BV pour les COOP(↓) FeI–FeII.
5 Effets magnétovolumiques
L’insertion d’azote a pour conséquence, outre la création de la liaison chimique fer–azote, l’augmentation du volume. Nous examinons cet effet par la variation volumique, d’une part, pour l’énergie électronique totale et, d’autre part, pour le moment magnétique porté par chaque sous-réseau.
5.1 Variation volumique de l’énergie totale
Autour de la valeur expérimentale de Fe4N, c’est-à-dire dans la gamme 250–550 bohr3, la variation de l’énergie avec le volume est obtenue en menant les calculs auto-cohérents avec les mêmes conditions de rapport de rayons des sphères dans l’ASA et d’intégration dans la zone de Brillouin, utilisant le même maillage du réseau réciproque en points k pour différents couples (Ei,Vi). À la convergence des calculs, on obtient une courbe Ei = f(Vi), dont l’allure quadratique présente un minimum, permettant de retrouver l’énergie et le volume à l’équilibre, soit le couple (E0,V0), d’une part, ainsi que le module de compressibilité B0, d’autre part, au travers de son ajustement par une équation d’état de type Birch–Murnaghan 〚14〛, dont une forme simplifiée est : E = E0 + βV + γV2. Dans cette expression, β et γ sont reliés respectivement au module de compressibilité et au volume à l’équilibre. Malgré un grand soin apporté au calcul de l’énergie E(k) sur un maillage fin de la zone de Brillouin, la Fig. 5 montre que cette variation présente une déviation par rapport au comportement quadratique (voir l’insert dans la figure). En fait, cet aspect est en relation avec le comportement discontinu du moment au site du FeII observé sur la Fig. 6, comme il en sera discuté à la section suivante 5.2. Cette déviation par rapport au comportement quadratique de la courbe E(V) a rendu plus difficile la détermination de B0, dont la valeur moyennée sur l’ensemble des points du graphe donne B0 = 150 GPa. Compte tenu de la difficulté de sa détermination, cette valeur présente un écart par rapport à l’expérience : B0(exp.) = 196 GPa 〚15〛. La valeur théorique du paramètre à l’équilibre est trouvée inférieure de 3% (indiquée par une ligne verticale sur la Fig. 6) à la valeur expérimentale. Un tel résultat est attendu dans le cadre de calculs dans la fonctionnelle LSDA, connue pour être « sur-liante », car basée sur une distribution d’un gaz homogène d’électrons (jellium).
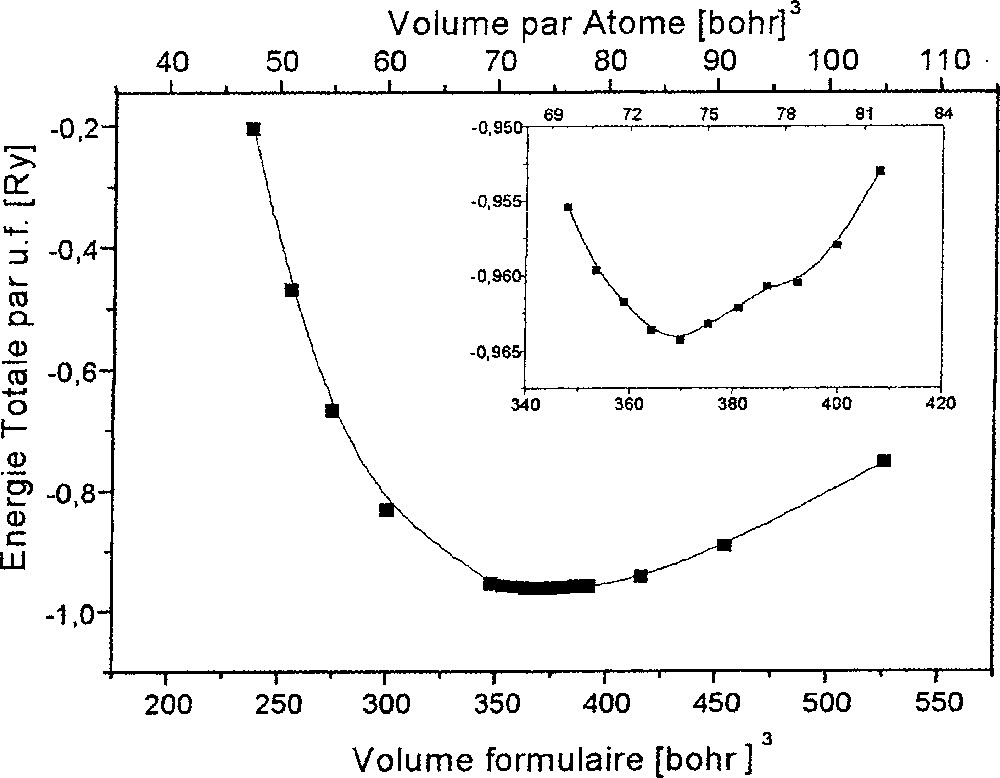
Variation volumique de l’énergie totale dans Fe4N (1 Ry = 13,6 eV). L'insert montre le comportement irrégulier autour du minimum d'énergie.
Variation of the total energy with volume for Fe4N (1 Ry = 13.6 eV). The insert shows the irregular behaviour around the minimum of energy.
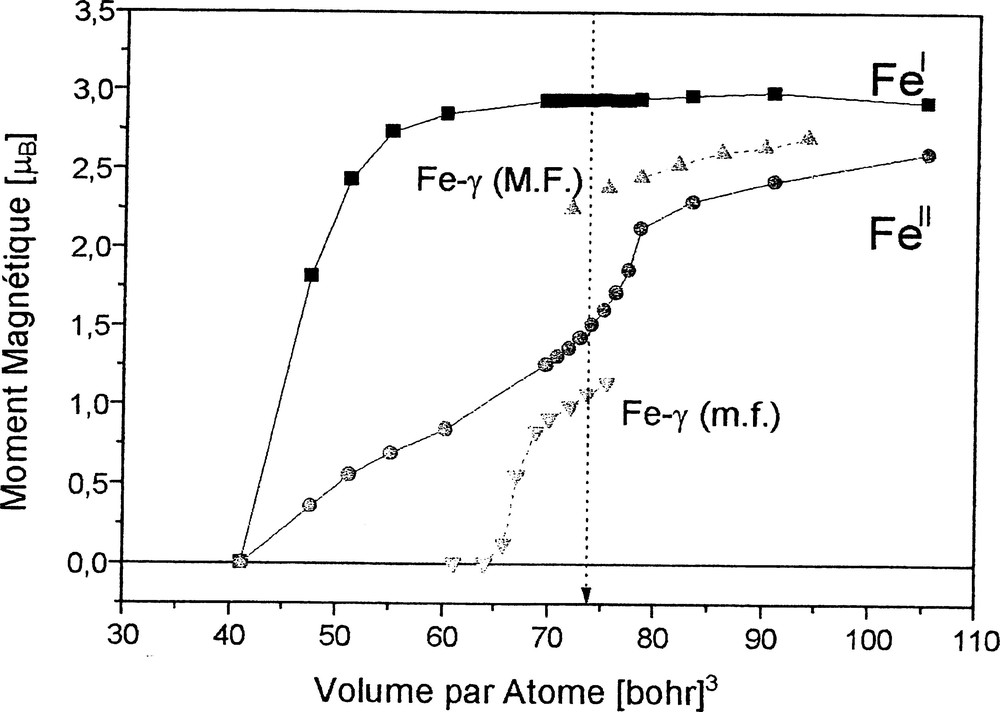
Variation volumique du moment magnétique dans Fe4N et Fe-γ.
Variation of the magnetic moment with atomic volume for Fe4N and γ Fe.
5.2 Variation volumique du moment magnétique
La variation volumique du moment magnétique sur chaque site dans Fe4N, pour des valeurs proches de l’équilibre, est représentée sur la Fig. 6. Partant de volumes très faibles (∼40 bohr3 atome–1), pour lesquels aucune polarisation de spins n’est observée, le moment au site FeI croît rapidement jusqu’à environ 2,85 μB (proche de la limite sur la courbe Slater–Pauling pour le fer ferromagnétique fort 〚16〛). En revanche, le moment du site FeII croît lentement, pour atteindre une valeur d’environ 1,6 μB au volume à l’équilibre. Un accroissement supplémentaire du volume montre qu’une transition du deuxième ordre vers un état à moment fort a lieu, accompagnée d’une variation irrégulière de l’énergie (cf. insert de la Fig. 5). La variation volumique, différente pour les moments des deux sites, est à rapprocher de celle dans Fe-γ (courbes en tirets), qui montre une transition d’un état à moment faible vers un état à moment élevé, ressemblant davantage à une transition de premier ordre. Une telle comparaison rapproche d’une manière originale les comportements magnétiques des deux systèmes. Ce qui fait de Fe4N un cas spécial dans ce contexte est le fait qu’il contienne deux sites de fer, à rapprocher des deux états de Fe-γ à différents volumes : alors que le fer au site FeI a un comportement à « moment élevé–volume élevé », celui au site FeII, assujetti à la pression chimique produite par deux atomes d’azote voisins (appartenant à deux mailles adjacentes), montre quant à lui un comportement « moment faible–volume faible ». Ce comportement reflète aussi les distances moyennes pour les plus proches voisins, exprimées plus haut.
6 Discussion
Nous venons de montrer que l’insertion d’azote peut avoir deux effets, chimique et volumique, sur les propriétés des nitrures d’insertion. Si l’on considère, dans la série des nitrures, le volume expérimental (en bohr3) ramené à un atome de fer, on a : Fe8N (87,54), Fe4N (92,41), Fe3N (92,75). L’expansion volumique est en effet observée. Ceci est d’autant plus visible si l’on inclut le fer sous ses deux variétés Fe-α (79,03) et Fe-γ (69,31). Si c’est cet effet qui prédomine, on devrait observer une augmentation du moment magnétique avec l’accroissement du taux d’azote dans la série, conduisant à une augmentation de la pression magnétique, donc à l’exaltation de l’aimantation. Ceci est effectivement observé, mais seulement sur le plan local : le moment du site FeI approche 3 μB dans Fe4N (cf. Fig. 6), de même que dans Fe8N pour l’atome de fer le plus éloigné de l’azote 〚5〛. En considérant l’effet moyen, le contraire est observé pour les moments atomiques de fer à ces volumes : Fe8N (∼ 2,40 μB) 〚5〛 Fe4N (∼ 2,20 μB) 〚6〛, Fe3N (∼ 1,95 μB) 〚7〛 ; Fe-α (2,22 μB). On devrait alors conclure que la liaison chimique Fe–N, impliquant l’appariement d’un spin de N(2p) et d’un spin de Fe(3d), comme cela a été illustré pour Fe4N, s’impose comme l’effet majeur dans les nitrures.
Le fait que les trois nitrures considérés montrent respectivement trois, deux et un sous-réseaux de fer permet de visualiser, hors considérations structurales, un effet de ségrégation de plus en plus important des atomes de fer autour de l’azote, en allant des nitrures dilués (Fe8N) vers les nitrures concentrés (Fe3N). On peut suggérer que l’utilisation de ces derniers (dans leur large domaine d’existence : FexN-ϵ) pour le durcissement en surface des pièces en alliages à base de fer 〚3〛 se justifie par la liaison covalente Fe–N, impliquant tous les atomes de fer (d ≈ 3,59 bohr, soit 1,899 Å), plus courte, d’une part, que la somme des rayons métalliques du fer, 1,274 Å, et covalent de l’azote, 0,702 Å 〚17〛, et, d’autre part, que la distance Fe–C dans la cémentite, soit 2,041 Å.
Enfin, les relations structurales entre Fe2N paramagnétique (groupe d’espace Pbcn) 〚9〛 et une variété orthorhombique du fer à haute température et haute pression (groupe d’espace Pbcm), récemment mise en évidence 〚18〛, sont des aspects qui suscitent une étude complémentaire dans ce même cadre.



