Impacts in the primordial history of terrestrial planets

Alessandro Morbidelli

doi:10.1016/j.crte.2007.09.001

Geochemistry (Cosmochemistry)

Impacts in the primordial history of terrestrial planets
[Le rôle des impacts dans l’histoire primitive des planètes]

Présenté par : Written on invitation of the Editorial Board

Alessandro Morbidelli ¹

¹ Observatoire de la Côte d’Azur, BP 4229, 06304 Nice cedex 4, France

Comptes Rendus. Géoscience, Volume 339 (2007) no. 14-15, pp. 907-916.

Résumés

Anglais
Français

Collisions played a very important role in the formation of terrestrial planets. These planets are believed to have formed from a system of planetary embryos, with masses comparable to that of the Moon or of Mars. Giant collisions between proto-planets and embryos were, therefore, the rule. The collision which gave origin to the Earth’s moon was just one of these collisions. We review the state of the art concerning numerical modeling of the terrestrial planets accretion process and we compare the results with the available observational or geochemical constraints. After the completion of the formation process, the history of the bombardment of the terrestrial planets was peculiar. After a period most likely characterized by a weak bombardment rate, about 3.9 Gyr ago, the planets experienced the ‘Late Heavy Bombardment’, a cataclysmic episode characterized by a bombardment rate of about 20,000 times the current one, during a time-span of 50–150 Myr. We review a recent model that has been proposed to explain the origin of this cataclysm.

Les collisions ont joué un rôle très important dans la formation des planètes telluriques. On pense que les planètes telluriques se sont d’abord formées à partir d’un système d’embryons planétaires de masses comparables à celle de la Lune ou de Mars. Les collisions géantes entre proto-planètes et embryons étaient donc la norme. La collision à l’origine du disque proto-lunaire était l’une de ces collisions. Nous faisons une revue de l’état de la modélisation de la croissance des planètes telluriques en comparant les résultats aux contraintes observationnelles. Une fois les planètes formées, l’histoire du bombardement a été très particulière. Après une periode vraisemblablement caractérisée par un taux de bombardement météoritique faible, le système des planètes telluriques a subi, il y a environ 3,9 Ga, le «grand bombardement tardif», un épisode cataclysmique caractérisé par un taux de bombardement égal à 20 000 fois le taux de bombardement actuel, et qui a perduré entre 50 et 150 Ma. Nous exposons un modèle récent qui explique l’origine de ce bombardement.

Métadonnées

Reçu le : 2007-05-02
Accepté le : 2007-09-05
Publié le : 2007-10-25

DOI : 10.1016/j.crte.2007.09.001

Keywords: Impacts, Planet formation, Teuestial planets, Lunar basins
Mot clés : Impacts, Formation planète, Planètes telluriques, Bassins lunaire

Affiliations des auteurs :

Alessandro Morbidelli ¹

¹ Observatoire de la Côte d’Azur, BP 4229, 06304 Nice cedex 4, France

@article{CRGEOS_2007__339_14-15_907_0,
     author = {Alessandro Morbidelli},
     title = {Impacts in the primordial history of terrestrial planets},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {907--916},
     publisher = {Elsevier},
     volume = {339},
     number = {14-15},
     year = {2007},
     doi = {10.1016/j.crte.2007.09.001},
     language = {en},
}

TY  - JOUR
AU  - Alessandro Morbidelli
TI  - Impacts in the primordial history of terrestrial planets
JO  - Comptes Rendus. Géoscience
PY  - 2007
SP  - 907
EP  - 916
VL  - 339
IS  - 14-15
PB  - Elsevier
DO  - 10.1016/j.crte.2007.09.001
LA  - en
ID  - CRGEOS_2007__339_14-15_907_0
ER  -

%0 Journal Article
%A Alessandro Morbidelli
%T Impacts in the primordial history of terrestrial planets
%J Comptes Rendus. Géoscience
%D 2007
%P 907-916
%V 339
%N 14-15
%I Elsevier
%R 10.1016/j.crte.2007.09.001
%G en
%F CRGEOS_2007__339_14-15_907_0

Alessandro Morbidelli. Impacts in the primordial history of terrestrial planets. Comptes Rendus. Géoscience, Volume 339 (2007) no. 14-15, pp. 907-916. doi : 10.1016/j.crte.2007.09.001. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2007.09.001/

Version originale du texte intégral

1 Introduction

Impacts have played a relevant, if not fundamental, role in the history of terrestrial planets, as it can be realized just by looking at the heavily cratered highlands on the Moon or Mars. Impacts, however, did not only sculpt the surface geology of the planets after their formation. The planets themselves built from a disk of planetesimals and planetary embryos through a sequence of impacts, some of which with an energy that a human mind can difficultly imagine. For instance, the best model of the Moon’s formation argues that an impact of a Mars-mass body on the proto-Earth ejected a disk of debris around our planet, out of which our satellite accreted.

In this paper, we review the role of impacts during the primordial history of terrestrial planets. We divide the review into two parts. In Section 2 we describe the formation process of the terrestrial planets and the kind of impacts that we expect to have occurred during that phase. In Section 3, we discuss how the impact flux should have decayed after the planets’ formation and address the issue of the Late Heavy Bombardment (LHB).

2 Impacts during the terrestrial planets formation process

According to modern astronomical models, the growth of terrestrial planets occurs in two stages. First, a system of numerous planetary embryos with masses comparable to the mass of the Moon or that of Mars forms from a disk of planetesimals, by processes denominated ‘runaway growth’ and ‘oligarchic growth’. Then, the planetary embryos start to interact with each other and develop eccentric orbits that lead to mutual giant collisions, thus forming a smaller number of bigger and bigger bodies: the planets as we know them. Each of these stages is characterized by different kinds of impacts, for what concerns impact energy and the origin of the projectiles. We review them separately below.

2.1 Formation of planetary embryos

Once the protoplanetary disk is inhabited by planetesimals of several kilometers in size, the dynamics of accretion starts to be dominated by the effect of mutual gravitational attraction, which increases the collisional cross-sections. A runaway growth phase starts, during which the big bodies grow faster than the small ones, hence increasing their relative difference in mass [15] with respect to the rest of the planetesimals population. This process can be summarized by the equation:

\frac{d}{d t} \frac{M_{1}}{M_{2}} = \frac{M_{1}}{M_{2}} (\frac{1}{M_{1}} \frac{d M_{1}}{d t} - \frac{1}{M_{2}} \frac{d M_{2}}{d t}) > 0

(1)

where

M_{1}

and

M_{2}

are respectively the characteristic masses of the ‘big’ and of the ‘small’ bodies, and can be explained as follows.

Generally speaking, accretion is favored by a high collision rate, which occurs when the relative velocities are large, but also by large collisional cross-sections and gentle impacts, which occur when the relative velocities are low. Therefore, the relative velocities between the different planetesimal populations govern the growth regime.

At the beginning of the runaway growth phase, the large planetesimals represent only a small fraction of the total mass. Hence the dynamics is governed by the small bodies, in the sense that the relative velocities among the bodies is on the order of the escape velocity of the small bodies $V_{esc}^{(2)}$ . This velocity is independent of the mass $M_{1}$ of the big bodies and is smaller than the escape velocity of the large bodies $V_{esc}^{(1)}$ . For a given body, the collisional cross-section is enhanced with respect to the geometrical cross-section by the so-called gravitational focusing factor:

F_{g} = 1 + (\frac{V_{esc}^{2}}{V_{rel}^{2}})

(2)

where

V_{esc}

is the body’s escape velocity and

V_{rel}

its relative velocity with respect to the particles in its environment. Because

V_{rel} \sim V_{esc}^{(2)}

, the gravitational focusing factor of the small bodies (

V_{esc} = V_{esc}^{(2)}

) is of order unity, while that of the large bodies (

V_{esc} = V_{esc}^{(1)} > > V_{esc}^{(2)}

) is much larger. In this situation one can show that the mass growth of a big body is described by the equation:

\frac{1}{M_{1}} \frac{d M_{1}}{d t} \sim M_{1}^{1 / 3} V_{rel}^{- 2}

(3)

[16]. Therefore, the relative growth rate is an increasing function of the body’s mass, which is the condition for the runaway growth (see Fig. 1).

Fig. 1
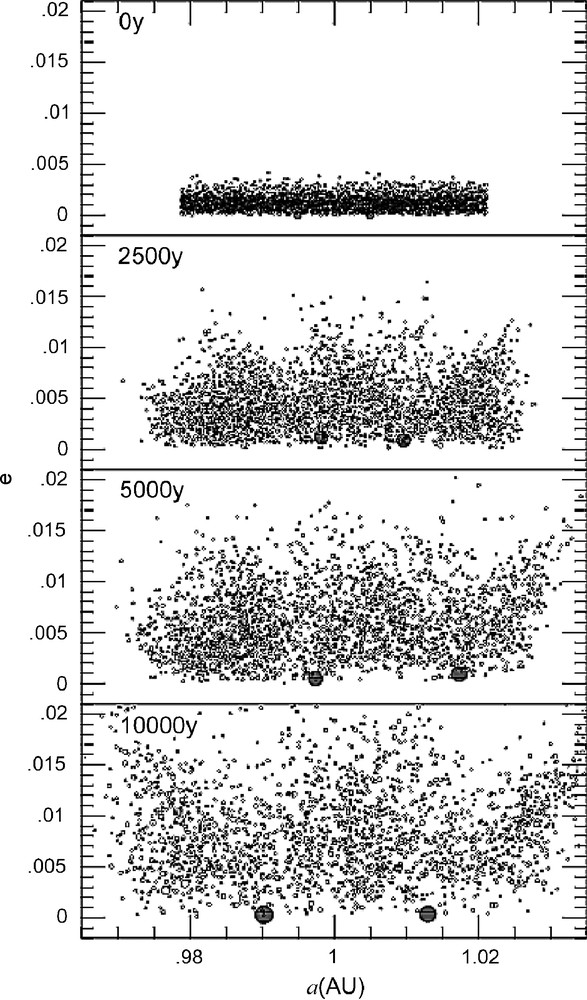
A simulation of the runaway growth process for planetary embryos. In a disk of equal mass planetesimals, two ‘seeds’ (planetesimals of slightly larger size) are embedded. As time passes, the two seeds grow in mass much faster than the other planetesimals, becoming planetary embryos (the size of each dot is proportional to its mass). While the growing planetary embryos keep quasi-circular orbits, the remaining planetesimals have their eccentricities (and inclinations) excited by the close encounters with the embryos. Notice also that the separation between the embryos slowly grows in time (i.e. passing from one panel to the subsequent one). From [18].
Fig. 1 Simulation du processus de croissance exponentielle runaway d’embryons planétaires. Initialement, deux objets légèrement plus gros ont été insérés dans un disque de planétésimaux de masses égales. Au fur et à mesure que le temps passe, ces deux objets grossissent beaucoup plus rapidement que les autres planétésimaux, et deviennent ainsi des embryons planétaires (dans la figure, la taille de chaque cercle est proportionnelle à la masse de l’objet correspondant). À la différence des embryons, qui restent sur des orbites presque circulaires, les planétésimaux évoluent sur des orbites de plus en plus excentriques, à cause des perturbations gravitationnelles exercées par les embryons, lors des rencontres proches. Notez aussi que la separation orbitale entre les embryons augmente avec le temps (c’est-à-dire d’un panneau à l’autre sur la figure). Figure reproduite d’après [18].

The runaway growth stops when the mass of the large bodies becomes important [16] and the latter start to govern the dynamics. The condition for this to occur is:

n_{1} M_{1}^{2} > n_{2} M_{2}^{2}

(4)

where

n_{1}

(resp.

n_{2}

) is the number of big bodies (resp. small bodies). In this case,

V_{rel} V_{esc}^{(1)} \sim M_{1}^{1 / 3}

, and hence

1 / M_{1} (d M_{1} / d t) \sim M_{1}^{1 / 3}

. The growing rate of the embryos gets slower and slower as the bodies grow, and the relative differences in mass among the embryos also slowly become smaller. In principle, one could expect that the small bodies keep growing, narrowing their mass difference with the embryos. But in reality, the now large relative velocities prevent the small bodies to accrete with each other. The small bodies can only participate to in the growth of the embryos: this phase is called ‘oligarchic growth’.

The runaway growth phase happens through the disk, with timescales that depend on the local dynamical time (Keplerian time) and on the local density of the available solid material. This density will also determine the maximum size of the embryos and/or planets when the runaway growth ends [22]. Assuming a reasonable surface density of solid materials, the runaway growth process forms planetary embryos of Lunar to Martian mass at 1 AU in $1 0^{5}$ – $1 0^{6}$ yr, separated by a few $1 0^{- 2}$ AU. Therefore, planetary embryos should not be confused with terrestrial planets. They are too small, too numerous, too narrowly separated, and they form too quickly with respect to geochemical constraints. Notice that the embryos grow essentially from collisions with small bodies and that their growth is a local process, in the sense that the planetesimals that participate in the formation of an embryo come essentially from the embryo’s neighborhood. Both these properties are very different for the second stage of the terrestrial planets formation process, reviewed below.

2.2 Formation of the terrestrial planets

The system of planetary embryos mentioned above probably extended over the entire inner solar system, namely in both the terrestrial planets region and in the asteroid belt. According to numerical simulations, the system of embryos is unstable on the long term. Thus the embryos’ orbits become dynamically excited (increase of eccentricity and inclination) and begin to intersect. Accretional collisions among neighboring embryos start to occur, giving origin to bigger objects (proto-planets). The process accelerates dramatically when Jupiter and Saturn acquire their current masses. These two planets strongly perturb the dynamical evolution of the embryos in the asteroid belt region between 2 and 5 AU. The latter acquire a strong dynamical excitation, begin to cross each other, and cross rather frequently the orbits of the embryos in the terrestrial planets region. The collision rate increases. Despite the high relative velocity, these collisions lead to accretion because of the large mass of the embryos. The typical result of this highly chaotic phase – simulated with several numerical N-body integrations – is the elimination of all the embryos originally situated in the asteroid belt and the formation of a small number of terrestrial planets on stable orbits in the 0.5–2 AU region, in a timescale of $\sim$ 100 Myr (see Fig. 2)

Fig. 2
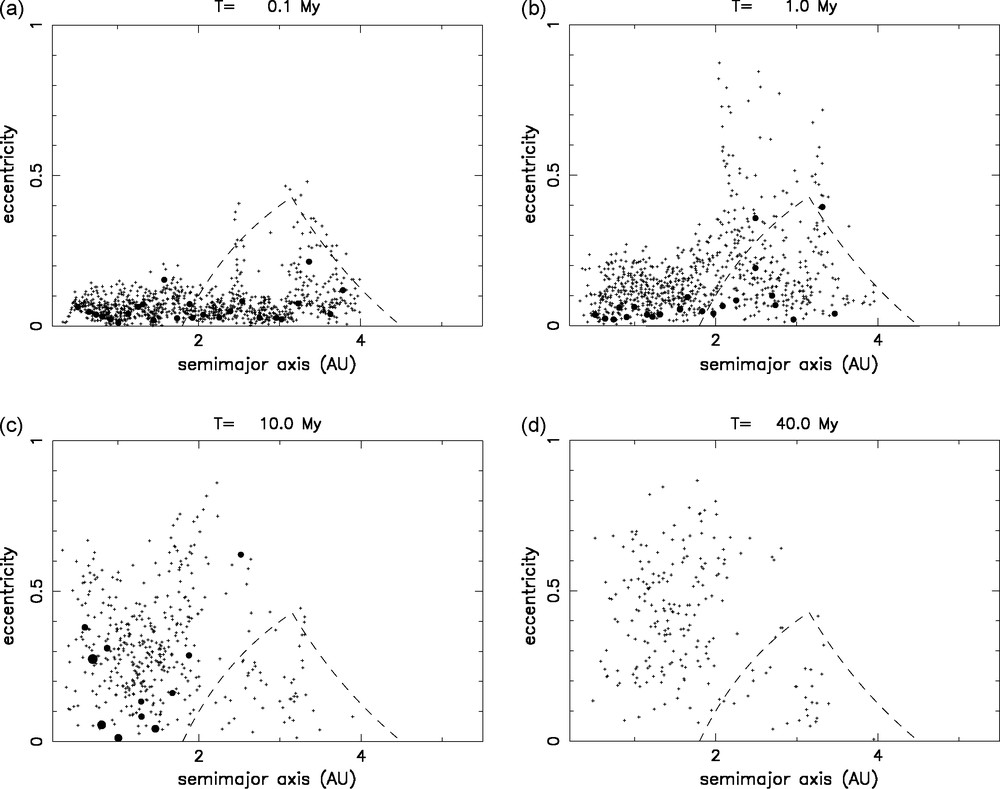
The growth of terrestrial planets from a disk of planetary embryos and planetesimals. Each panel shows the semi-major axis and eccentricity of the bodies in the system, the size of each dot being proportional to the mass of the embryo. The giant dot on the lower right corner of the plot represents Jupiter. The planetesimals are represented by small crosses. The dashed curves delimit approximately the current boundaries of the asteroid belt. The simulation time is reported on top of each panel. From [30,31].
Fig. 2 Croissance des planètes telluriques depuis un disque d’embryons planétaires et planétésimaux. Chaque panneau montre le demi-grand axe et l’excentricité des orbites des objets. Les tailles des cercles pleins sont proportionnelles aux masses des embryons plantaires correspondants. Le cercle géant en bas à droite de chaque panneau représente l’orbite de Jupiter. Les planétésimaux sont représentés par de petites croix. Les courbes en pointillés montrent les limites approximatives de la ceinture des astéroïdes. Le temps correspondant est indiqué au-dessus de chaque panneau. Figure produite à partir des simulations de [30,31].

This scenario has several strong points:

(i) planets are formed on well-separated and stable orbits only inside 2 AU. Their number typically ranges from 2 to 4, depending on the simulations, and their masses are in the range Mars mass–Earth mass [1,8,30];
(ii) quasi-tangent collisions of Mars-mass embryos onto the proto-planets are quite frequent [1]. These collisions are expected to generate a disk of ejecta around the proto-planets, from which a satellite is likely to accrete [5,6]. This is the standard, generally accepted, scenario for the formation of the Moon;
(iii) the accretion timescale of the terrestrial planets is $\sim$ 100 Myr. This is compatible with several constraints on the chronology of accretion coming from geochemistry [2];
(iv) all the embryos located beyond 2 AU are eliminated in most of the simulations [9,30]. They either are dynamically ejected from the solar system, or collide with the Sun, or are accreted by the forming terrestrial planets;
(v) in the same time, the small planetesimals are subject to the combined perturbations of the giant planets and of the embryos [31,32]. The dynamical excitation increasing very rapidly (timescale 1–2 Myr), most of the small planetesimals are eliminated in a few million years by either the ejection from the solar system, or the collision with the Sun or with a growing planet. In the asteroid belt (2–4 AU range), this leads to a remaining population of small bodies (the asteroids) on stable orbits with quite large eccentricities and inclinations, which contains only a very small fraction of the total mass initially in the region. This scenario explains well the mass deficit of the asteroid belt, the eccentricity and semi-major axis distribution of the largest asteroids and other more subtle properties of the asteroid belt population, such as the partial mixing of taxonomic types.

However, this general scenario of terrestrial planets formation suffers from some weaknesses:

(i) in many simulations, the final orbits of the planets formed in the simulations are too eccentric and/or inclined with respect to the real ones;
(ii) the Hf–W chronology (whose interpretation is still the object of a controversy) may indicate that the formation of the Earth’s core occurred within the first 30 Myr [17,40]. This may suggest that the Earth accretion was faster than it appears in most simulations;
(iii) obliquities of the terrestrial planets should have random values. However, in reality, only one planet has a retrograde spin (Venus). Moreover, all planetary obliquities are compatible with an initial 0-degree obliquity, modified by the subsequent evolution in the framework of the current architecture of the planetary system [20];
(iv) the planet formed in the simulations approximately at the location of Mars is typically too massive.

The first two problems listed above may find a solution if the simulations take into account not only the planetary embryos, but also a population of planetesimals with a total mass equivalent to that of the system of embryos. In fact, with the improvement of computer technology, simulations have taken into account a progressively larger number of individually smaller bodies, achieving terrestrial planets on orbits with progressively smaller eccentricities and inclinations and shorter accretion times.

The most recent simulations in the field are those in [30], which started from a system of 50 embryos of Martian mass between 0.5 and 4 AU, embedded in a disk of 2.5 Earth masses of planetesimals, modeled with 1000 particles. Thus, the mass ratio between individual embryos and planetesimals was 40, larger than ever used before. In the simulations of [30], for the first time, terrestrial planets have an angular momentum deficit (a measure of the orbital excitation of the planets, defined as the difference between the total angular momentum of the planets and the one that the planets would have if they were on circular and co-planar orbits with the same semi-major axes) that is smaller than that of the real terrestrial planets ( $1 0^{- 3}$ instead of $1.8 \times 1 0^{- 3}$ ). For the sake of comparison, in the previous ‘best’ simulations [7], the resulting angular momentum deficit was $7 \times 1 0^{- 3}$ . Moreover, the simulations by [30] give a median timescale for the acquisition of 90% of the final planetary mass equal to 40 Myr, and a median time of the last giant impact with an embryo of 30 Myr. These timescales are in perfect agreement with the Hf–W chronology of the formation of the Earth/Moon system.

Unfortunately, these great results have been obtained by assuming that Jupiter and Saturn were initially on their current, somewhat eccentric orbits. However, there is now growing evidence that the giant planets should have formed and evolved in the gas disk on quasi-circular orbits (see for instance [24]) and that they acquired their orbital eccentricity only much later [14,39]. O’Brien et al. [30] also did simulations of terrestrial planets accretion starting with the same set-up concerning embryos and planetesimals, but with Jupiter and Saturn initially on quasi-circular, co-planar orbits, with smaller mutual separation. The mean angular momentum deficit of the planets produced in these simulations ( $3 \times 1 0^{- 3}$ ) was still larger than that of the real planets; the median time of the last giant impact with an embryo was $\sim 100$ Myr. Clearly, with this initial configuration of the giant planets, more work is needed in order to obtain, in the simulations, terrestrial planets more in agreement with observational and geochemical constraints. Perhaps, a future generation of simulations, allowing for an even larger number of smaller planetesimals and for the regeneration of planetesimals during the giant impacts among the embryos, might achieve better results in the future, from the quantitative point of view.

Concerning the collisional history of the terrestrial planets, the simulations show that giant impacts of the kind of that giving origin to the Moon are not exceptional. On the contrary, they constitute the growth mode of the planets themselves. Moreover, given the large orbital excitation that the embryos may achieve during their evolution, the growth of the terrestrial planets is not a local process, in which the planets accrete only material from the local neighborhood. In the simulations, the terrestrial planets incorporate material coming from essentially everywhere in the inner solar system. This may include a quite large amount of mass coming from the asteroid belt. In particular, if the giant planets are initially on a circular orbit, about or more than 10% of the final mass of the planets can be accreted from beyond 3 AU. This region is considered to be the source of carbonaceous chondrite meteorites, which are notoriously rich in water (the latter accounting for 5 to 10% of total meteorite mass). The formation of water-rich planets is, therefore, quite the rule [25]. In this scenario, water is not delivered after the formation of the terrestrial planets, as in the late veneer scenario that was popular among the astronomical community in the recent past, but rather during the formation of the planets themselves.

3 Impacts after planet formation: early decay and late heavy bombardment

Once the terrestrial planets are formed, a large number of planetesimals are still in the inner solar system, on orbits with large eccentricities and inclinations, that still cross those of the terrestrial planets. These planetesimals continue to bombard the planets. However, their total number decays very rapidly in time. As for the current Near-Earth Asteroid population, the dynamical lifetime of the individual objects is of order of $\sim 10$ Myr, although some, those with the largest orbital inclinations for example, can have lifetimes 10 times longer. Most of the planetesimals are eliminated by being driven into the Sun, or by being ejected from the solar system by encounters with Jupiter.

Simulations of the dynamical decay of the left-over planetesimal population [3,26] show that the number of objects (and hence the impact rate on the planets) decays by one order of magnitude in the first 50 Myr and by 4 orders of magnitude in 600 Myr (see Fig. 3).

Fig. 3
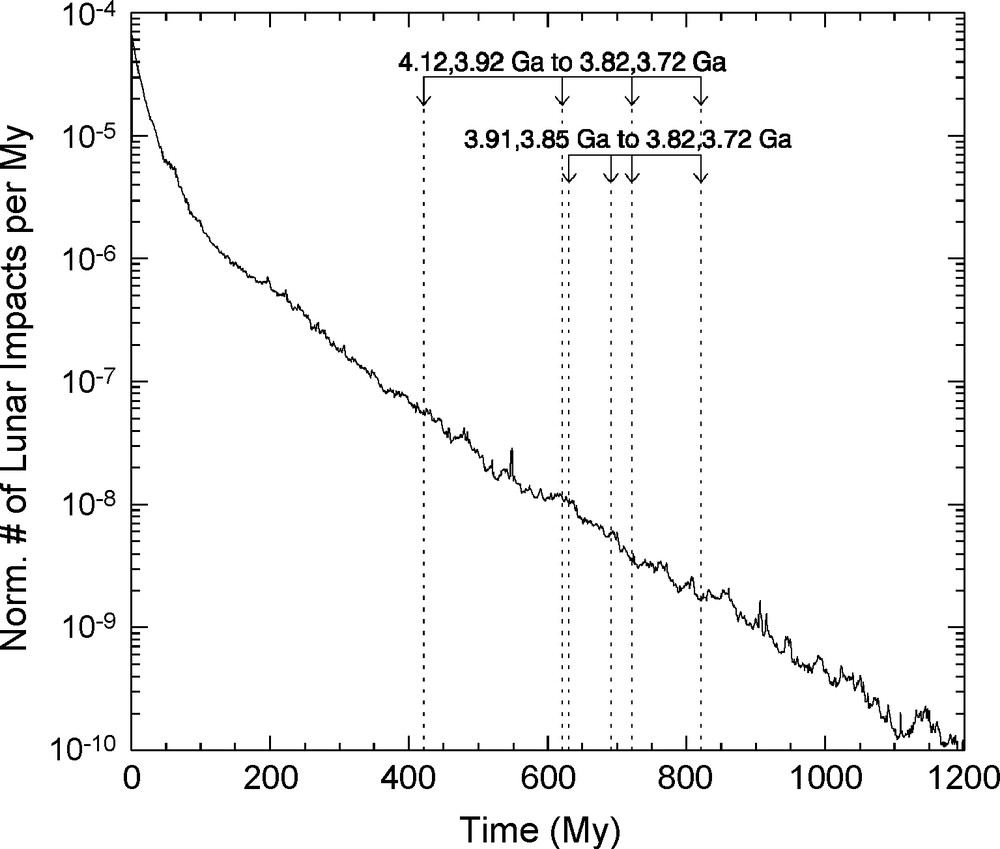
The decay rate of the impact rate on the Moon due to planetesimals left-over from terrestrial planets accretion, according to [3]. The arrows and the vertical dashed lines indicate the putative ages of the lunar basins Nectaris, Serenitatis, Imbrium and Orientale (from oldest to youngest). The ages of the first two basins are somewhat uncertain, so that two possible extreme values are given.
Fig. 3 Décroissance du taux d’impacts sur la Lune, dus aux planétésimaux restants à la fin du processus de formation des planètes telluriques, selon les simulations de [3]. Les flèches et les lignes verticales indiquent les âges estimées des bassins Nectaris, Serenitatis, Imbrium et Oriental (du plus ancien au plus récent). Les âges des deux premiers bassins sont incertains, et donc deux valeurs possibles sont indiquées sur la figure.

Nevertheless, the Moon shows many signs of a heavy bombardment at about 3.9 Gyr ago, namely 650 Myr after its own formation. The isotopic dating of the samples returned by the various Apollo and Luna missions revealed many impact melts about 3.9–3.8 Gyr old [33,34]. The lunar meteorites confirm this result. The meteorites provide a particularly strong constraint, because they likely originated from random locations on the Moon [11], unlike the lunar samples collected directly on its surface. The U–Pb isochron of lunar highland samples indicates a single metamorphic event at 3.9 Gyr ago, whereas the Rb–Sr isochron for the same rocks determines distinct metamorphic events in the interval between 3.85 and 4 Gyr ago [38]. Moreover, 15 out of the largest impact structures on the Moon, the so-called basins, with diameters between 300 and 1200 km, have been dated to have formed between 4.0 and 3.9 Gyr ago. Chapman et al., [10] have recently argued that the absence of evidence for an intense bombardment before 4.0 Gyr ago might be due to biases, but admitted that the intensity of the bombardment at about 3.9 Gyr ago and the rapid decline after the formation of the Imbrium basin appear secure from lunar data.

This late, heavy bombardment (LHB) cannot be the tail of the cratering process caused by the left-over planetesimals in the inner solar system, given the extremely rapid decay of this population, discussed above. Together with the absence of evidence of an intense bombardment prior to 4 Gyr ago (no impact melts, nor basins, have been found to be older than 3.9 Gyr), this suggests that the LHB was rather a sudden spike in the impact history of the planets.

Accepting a cataclysmic origin of the LHB (i.e. an impact spike) is however problematic. If an impact spike really happened late after the formation of the planets, it means that somewhere in the solar system a massive reservoir of small bodies had to remain stable for about 600 Myr, and then be suddenly destabilized. Where was such a reservoir? What did destabilize it? One possibility is that the solar system suffered a close stellar encounter that destabilized a distant planetesimal disk. However, stellar encounters are highly unlikely once the Sun has left its natal stellar environment, which typically happens in the first 10 Myr. Moreover, the orbital structure of the inner Oort cloud constrains the closest stellar encounters suffered over the age of the solar system to have happened at a distance of about 1000 AU [4,23]. If stellar encounters could not cause an LHB, then the remaining possibility is that the orbital structure of the giant planets suddenly changed, thus changing the stability properties of the small body reservoirs.

A model in this direction has been recently developed [14,28,39]. In this model, the giant planets are assumed to be initially on nearly circular and coplanar orbits, with orbital separations significantly smaller than the ones currently observed. More precisely, the giant planet system is assumed to lie in the region from $\sim 5.5$ AU to $\sim 14$ AU, and Saturn is assumed to be closer to Jupiter than their mutual 1:2 MMR. A planetesimal disk is assumed to exist beyond the orbits of the giant planets, on orbits whose dynamical lifetime is at least 3 Myr (the supposed lifetime of the gas disk). The outer edge of the planetesimal disk is assumed to lie at $\sim 34$ AU and the total mass is $\sim 35 M_{\oplus}$ (see Fig. 4 a).

Fig. 4
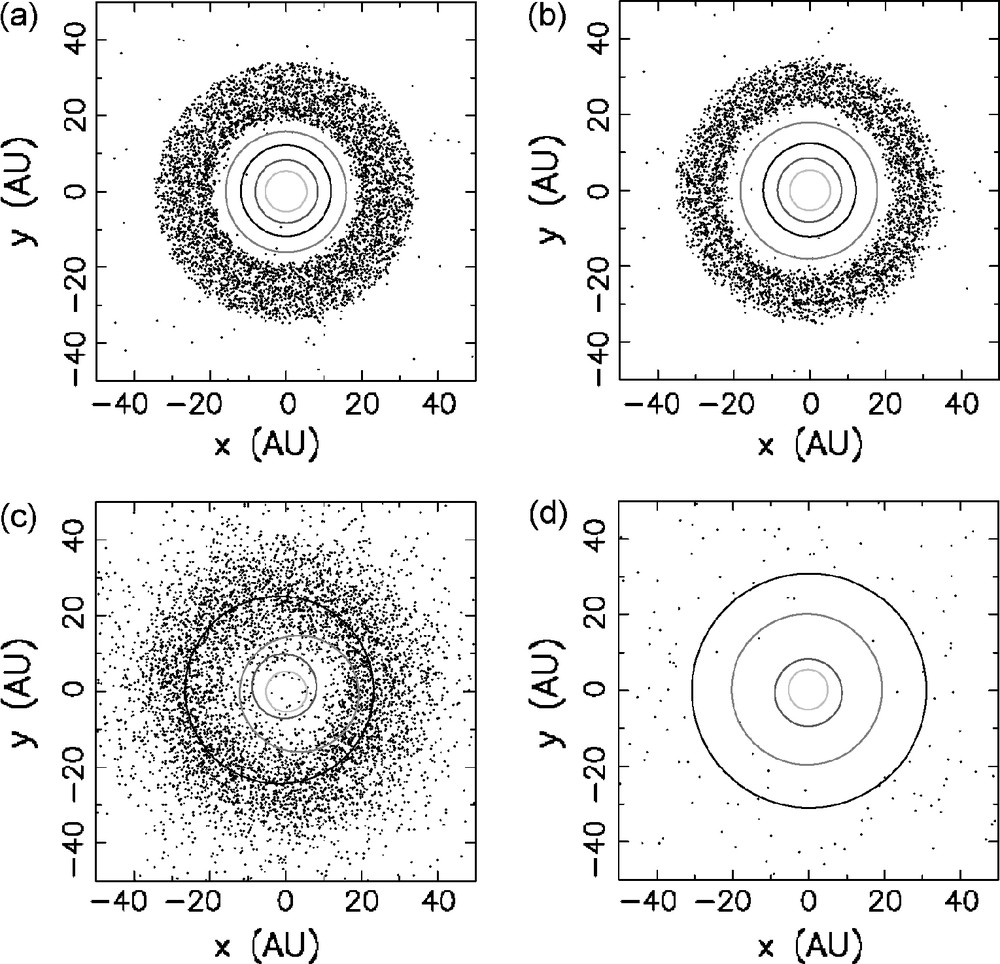
Solar system evolution in the LHB model. (a) At a time close to the beginning of the evolution. The orbits of the giant planets (concentric circles) are very close to each other and are quasi-circular. They are surrounded by a disk of planetesimals, whose inner edge is due to the perturbations from the planets and the outer edge is assumed to be at 34 AU. (b) Immediately before the great instability. Saturn is about crossing the 1:2 resonance with Jupiter. (c) At the time of the instability. Notice that the orbits of the planets have become eccentric and now penetrate the planetesimal disk. (d) After the LHB. The planets are parked on orbits very similar (in terms of separation, eccentricity, and inclination) to their current ones. The massive planetesimal disk has been destroyed. Only a small fraction of the planetesimals remains in the system on orbits typical of the scattered disk, Kuiper belt,and other small body reservoirs. From [14].
Fig. 4 Évolution du système solaire selon notre modèle sur l’origine du LHB. (a) Au début de l’évolution, les orbites des planètes géantes (cercles concentriques) sont très rapprochées et quasi circulaires. Elles sont entourées par un disque de planétésimaux, dont le bord interne est dû aux perturbations planétaires et le bord externe est supposé être à 34 UA. (b) Juste avant la grande instabilité, quand Saturne est prêt à traverser la résonance 1:2 avec Jupiter. (c) Au temps de l’instabilité. Notez que les orbites planétaires sont devenues excentriques et pénètrent désormais dans le disque des planétésimaux. (d) Après le LHB, quand les planètes se retrouvent sur des orbites très semblables aux orbites actuelles, en termes d’excentricités, inclinaisons et séparations mutuelles. Le disque des planétésimaux a été détruit; seulement une petite minorité des planétésimaux reste dans le système solaire, sur des orbites typiques du « disques dispersé », de la ceinture de Kuiper, et d’autres réservoirs de petits corps. Figure reproduite d’après [14].

With the above configuration, the planetesimals at the inner edge of the disk evolve onto Neptune-scattering orbits on a timescale of a few million years. These planetesimals are eventually eliminated, mostly by being ejected from the solar system by an ultimate close encounter with Jupiter. Because of the conservation of energy and angular momentum during the scattering process, the dispersion of the scattered planetesimals by the planets forces the planets to migrate [12]. More precisely, the semi-major axes of Saturn, Uranus and Neptune increase with time, while that of Jupiter decreases. Because the escape rate of planeteimals from the trans-planetary disk is slow, the migration of the giant planets also proceeds at a very slow rate. This slow migration continues for a long time, slightly damping out as the unstable disk particles are removed from the system (Fig. 4). Eventually, after a time ranging from 350 Myr to 1.1 Gyr in the simulations of [14] – which is consistent with the timing of the LHB – Jupiter and Saturn cross their mutual 1:2 mean-motion resonance (Fig. 4b). This resonance crossing excites their eccentricities to values slightly larger than those currently observed. Consequently, the ice giant’s orbits become chaotic and start to approach each other. Thus, a short phase of encounters follows the resonance-crossing event. Both ice giants are scattered outward, onto large eccentricity orbits ( $e \sim$ 0.3–0.4) that penetrate deeply into the disk (Fig. 4c). This destabilizes the full planetesimal disk. The planetesimals are scattered all over the solar system. The eccentricities of Uranus and Neptune, and – to a lesser extent – of Jupiter and Saturn, are damped on a timescale of a few megayears due to the dynamical friction exerted by the planetesimals. Thus, the planets decouple from each other, and the phase of mutual encounters rapidly ends. During and after the eccentricity damping phase, the giant planets continue their radial migration, and eventually reach final orbits when most of the disk has been eliminated (Fig. 4d).

With a planetesimal disk of about $35 M_{\oplus}$ , the simulations of this process reproduce the current architecture of the orbits of the giant planets remarkably well, in terms of semi-major axes, eccentricities and inclinations [39]. This model is also consistent with the existence and the orbital distribution of Jupiter’s Trojan asteroids [27], of the irregular satellites of Saturn, Uranus and Neptune [29], and of the Kuiper belt [28].

The main properties of the LHB are also reproduced. The late and abrupt triggering of the bombardment is due to the fact that most of the planetesimal disk remains stable until Jupiter and Saturn cross their mutual 1:2 resonance, and is rapidly dispersed after the resonance crossing. The mass of planetesimals originally from the trans-planetary disk that hit the Moon after the resonance crossing is consistent with the mass ( $6 \times 1 0^{21}$ g) estimated from the number and size distribution of lunar basins that formed around the time of the LHB epoch [14].

The planetesimals from the trans-planetary disk – which can be identified as ‘comets’ – were not the only ones to hit the terrestrial planets. The radial migration of Jupiter and Saturn forced secular resonances to sweep across the asteroid belt [13,21], exciting the eccentricities and the inclinations of asteroids. The fraction of the main belt population that acquired planet-crossing eccentricities depends quite crucially on the orbital distribution that the belt had before the LHB, which is not well known. As we have seen in Section 2, the asteroid belt got dynamically excited and substantially depleted during the terrestrial planets formation process, well before the LHB. If, at the end of the planet formation phase, the orbital distribution in the belt was comparable to the current one, as the simulations of [30,31] suggest, the secular resonance sweeping at the time of the LHB would have left $\sim$ 10% of the objects in the asteroid belt [14]. Assuming this figure, the pre-LHB main belt contained roughly $5 \times 1 0^{- 3} M_{\oplus}$ (10 times its current mass) and the total mass of the asteroids hitting the Moon was comparable to that of the comets. However, slight changes in the pre-LHB asteroid distribution, and the migration rate of Jupiter and Saturn (also highly variable from simulation to simulation, depending on the chaotic evolution of Neptune), can change this result for the asteroidal contribution to the Lunar cratering rate by a factor of several unities. In conclusion, the model of [14] cannot state whether asteroids or comets dominated the impact flux on the terrestrial planets. What it can say, however, is that the asteroidal contribution came later and more slowly than the cometary contribution, possibly erasing much of the signature of the cometary bombardment.

The issue of which population dominated the impact rate can be solved by looking for constraints on the Moon. In [19], analysis of Lunar impact melts indicated that at least one of the projectiles that hit the Moon, and probably more, had a chemistry inconsistent with carbonaceous chondrites or comets. In [37] it was found that the impact melt at the landing site of Apollo 17 was caused by a projectile of LL-chondritic composition. These results imply that the bombardment was dominated by asteroids typical of the inner belt.

In [35], the comparison of size distributions of the craters formed at the time of the LHB on Mercury, Mars and the Moon allowed the calculation of the ratios of the impact velocities on these planets, leading to the conclusion that most projectiles had a semi-major axis between 1 and 2 AU. Comets never acquire such a small semi-major axis during their evolution; so this argument again favors a dominant contribution from the inner main belt. More recently, [36] found that the crater size distribution on the lunar highlands is consistent with the size distribution of objects currently observed in the main belt.

Taken altogether, these results point with little doubt to asteroids being the dominating (or, possibly, latest-arriving) projectile population for the terrestrial planets at the time of the LHB. However, they do not imply that the asteroids triggered the LHB. On the contrary, the result in [36] implies that the LHB was triggered by a distant disk of comets (as in [14]), for the reasons explained below.

The remarkable match between the size distributions of craters and the main belt asteroids, pointed out in [36], implies that – at the LHB time – asteroids were ejected from the main belt onto planet-crossing orbits in proportions independent of their size¹. Only the sweeping of secular resonances can give a size-independent ejection throughout the main belt. At the time of the LHB, the gas disk was already totally dissipated. Thus, secular resonance sweeping could only be caused by the radial displacement of Jupiter and Saturn. Now, even assuming that the entire LHB on the terrestrial planets was caused by asteroids, from the mass hitting the Moon at that time and the collision probability typical of NEAs with the Moon, one can easily compute that the total asteroid mass on planet crossing orbits was about 0.01 $M_{\oplus}$ . This mass was too small to cause a significant migration of the giant planets. In conclusion, a more massive disk – which could only be trans-Neptunian – had to trigger and drive planet migration. Comets mandated the bombardment and asteroids executed it.

4 Conclusions

Collisions played a fundamental role for the accretion and the evolution of the terrestrial planets. First, collisions among planetesimals formed planetary embryos of masses in the range of the Lunar to Martian mass in about $1 0^{6}$ years. Then, giant collisions among the embryos led to the formation of the terrestrial planets as we know them, on a timescale of 30–100 Myr. After the last rogue embryos were eliminated, the bombardment of the terrestrial planets due to left-over planetesimals dropped dramatically, by 4 orders of magnitude in 600 Myr. However, 650 Myr after terrestrial planet formation, there was a sudden spike in the cratering rate, known as the Late Heavy Bombardment, during which impacts occurred at a frequency of about 10,000 times relative to the current epoch, for about 100 Myr. This cataclysmic bombardment was likely caused by a sudden instability of the orbits of the giant planets, that re-shaped the structure of the outer solar system. After the LHB was over, the solar system was finally like the current one, and the bombardment of the terrestrial planets, dominated by the so-called Near-Earth Asteroids, has remained more or less constant.

¹ Unlike the current Near- Earth Asteroids (NEAs) which, escaping from the belt due to size-dependent non-gravitational forces, have a size distribution significantly steeper than that of the main belt population.

Bibliographie

[1] C.B. Agnor; R.M. Canup; H.F. Levison On the character and consequences of large Impacts in the late stage of terrestrial planet formation, Icarus, Volume 142 (1999), pp. 219-237

[2] C.J. Allègre; G. Manhès; C. Göpel The age of the Earth, Geochim. Cosmochim. Acta, Volume 59 (1995), pp. 1445-1456

[3] W.F. Bottke; H.F. Levison; D. Nesvorný; L. Dones Can planetesimals left over from terrestrial planet formation produce the lunar Late Heavy Bombardment?, Icarus, Volume 190 (2007), pp. 203-223

[4] R. Brasser; M.J. Duncan; H.F. Levison Embedded star clusters and the formation of the Oort Cloud, Icarus, Volume 184 (2006), pp. 59-82

[5] R.M. Canup; L.W. Esposito Accretion of the Moon from an impact-generated disk, Icarus, Volume 119 (1996), pp. 427-446

[6] R.M. Canup; E. Asphaug Origin of the Moon in a giant impact near the end of the Earth’s formation, Nature, Volume 412 (2001), pp. 708-712

[7] J.E. Chambers Making more terrestrial planets, Icarus, Volume 152 (2001), pp. 205-224

[8] J.E. Chambers; G.W. Wetherill Making the terrestrial planets: N-Body integrations of planetary embryos in three dimensions, Icarus, Volume 136 (1998), pp. 304-327

[9] J.E. Chambers; G.W. Wetherill Planets in the asteroid belt, Meteorit. Planet. Sci., Volume 36 (2001), pp. 381-399

[10] C.R. Chapman; B.A. Cohen; D.H. Greenspoon What are the real constraints on the existence and magnitude of the Late Heavy Bombardment?, Icarus, Volume 189 (2007), pp. 233-245

[11] B.A. Cohen; T.D. Swindle; D.A. Kring Support for the Lunar cataclysm hypothesis from Lunar meteorite impact melt ages, Science, Volume 290 (2000), pp. 1754-1756

[12] J.A. Fernandez; W.H. Ip Some dynamical aspects of the accretion of Uranus and Neptune – The exchange of orbital angular momentum with planetesimals, Icarus, Volume 58 (1984), pp. 109-120

[13] R.S. Gomes Dynamical Effects of Planetary Migration on the Primordial Asteroid Belt, Astron. J., Volume 114 (1997), pp. 396-401

[14] R.S. Gomes; H.F. Levison; K. Tsiganis; A. Morbidelli Origin of the cataclysmic Late Heavy Bombardment period of the terrestrial planets, Nature, Volume 435 (2005), pp. 466-469

[15] R. Greenberg; W.K. Hartmann; C.R. Chapman; J.F. Wacker Planetesimals to planets – Numerical simulation of collisional evolution, Icarus, Volume 35 (1978), pp. 1-26

[16] S. Ida; J. Makino Scattering of planetesimals by a protoplanet – Slowing down of runaway growth, Icarus, Volume 106 (1993), pp. 210-227

[17] T. Kleine; C. Münker; K. Mezger; H. Palme Rapid accretion and early core formation on asteroids and the terrestrial planets from Hf–W chronometry, Nature, Volume 418 (2002), pp. 952-955

[18] E. Kokubo; S. Ida On Runaway Growth of Planetesimals, Icarus, Volume 123 (1996), pp. 180-191

[19] D.A. Kring; B.A. Cohen Cataclysmic bombardment throughout the inner solar system 3.9–4.0 Ga, J. Geophys. Res. (Planets), Volume 107 (2002), pp. 4-11

[20] J. Laskar; P. Robutel The chaotic obliquity of the planets, Nature, Volume 361 (1993), pp. 608-612

[21] H.F. Levison; L. Dones; C.R. Chapman; S.A. Stern; M.J. Duncan; K. Zahnle Could the Lunar ‘Late Heavy Bombardment’ have been triggered by the formation of Uranus and Neptune?, Icarus, Volume 151 (2001), pp. 286-306

[22] J.J. Lissauer Timescales for planetary accretion and the structure of the protoplanetary disk, Icarus, Volume 69 (1987), pp. 249-265

[23] A. Morbidelli; H.F. Levison Scenarios for the origin of the orbits of the trans-Neptunian objects 2000 CR₁₀₅ and 2003 VB₁₂ (Sedna), Astron. J., Volume 128 (2004), pp. 2564-2576

[24] A. Morbidelli, A. Crida, The dynamics of Jupiter and Saturn in the gaseous proto-planetary disk, Icarus, in press.

[25] A. Morbidelli; J. Chambers; J.I. Lunine; J.-M. Petit; F. Robert; G.B. Valsecchi; K.E. Cyr Source regions and time scales for the delivery of water to Earth, Meteorit. Planet. Sci., Volume 35 (2000), pp. 1309-1320

[26] A. Morbidelli; J.M. Petit; B. Gladman; J.E. Chambers A plausible cause of the Late Heavy Bombardment, Meteorit. Planet. Sci., Volume 36 (2001), pp. 371-380

[27] A. Morbidelli; H.F. Levison; K. Tsiganis; R.S. Gomes Chaotic capture of Jupiter’s Trojan asteroids in the early Solar System, Nature, Volume 435 (2005), pp. 462-465

[28] A. Morbidelli; H.F. Levison; R. Gomes; K. Tsiganis Origin Of The Structure Of The Kuiper Belt During A Giant Planets Orbital Instability, Bull. Am. Astron. Soc., Volume 38 (2006), p. 583

[29] D. Nesvorný; D. Vokrouhlický; A. Morbidelli Capture of irregular satellites during planetary encounters, Astron. J., Volume 133 (2007), pp. 1962-1976

[30] D.P. O’Brien; A. Morbidelli; H.F. Levison Terrestrial planet formation with strong dynamical friction, Icarus, Volume 184 (2006), pp. 39-58

[31] D.P. O’Brien, A. Morbidelli, W.F. Bottke, The primordial excitation and clearing of the asteroid belt revisited, Icarus, in press.

[32] J.M. Petit; A. Morbidelli; J.E. Chambers The primordial excitation and clearing of the asteroid belt, Icarus, Volume 153 (2001), pp. 338-347

[33] G. Ryder Lunar samples, lunar accretion and the early bombardment of the Moon, Eos Trans. AGU, Volume 71 (1990), pp. 313-323

[34] G. Ryder; C. Koeberl; S.J. Mojzsis Heavy bombardment on the Earth at 3. 85: The search for petrographical and geochemical evidence (R.M. Canup; K. Righter, eds.), Origin of the Earth and Moon, University of Arizona Press, Tucson, Arizona, 2000, pp. 475-492

[35] R.G. Strom; G. Neukum The cratering record on Mercury and the origin of impacting objects (F. Vilas; C. Chapman; M. Matthews, eds.), Mercury, University of Arizona Press, Tucson, Arizona, 1988, pp. 336-373

[36] R.G. Strom; R. Malhotra; T. Ito; F. Yoshida; D.A. Kring The Origin of planetary impactors in the Inner Solar System, Science, Volume 309 (2005), pp. 1847-1850

[37] R. Tagle LL-Ordinary chondrite impact on the Moon: Results from the 3.9 Ga impact melt at the landing site of Apollo 17, Lun. Planet. Sci. Conf., Volume 36 (2005), p. 2008

[38] F. Tera; D.A. Papanastassiou; G.J. Wasserburg Isotopic evidence for a terminal lunar cataclysm: Earth Planet, Sci. Lett., Volume 22 (1974), pp. 1-21

[39] K. Tsiganis; R.S. Gomes; A. Morbidelli; H.F. Levison Origin of the orbital architecture of the giant planets of the Solar System, Nature, Volume 435 (2005), pp. 459-461

[40] Q. Yin; S.B. Jacobsen; K. Yamashita; J. Blichert-Toft; P. Télouk; F. Albarède A short timescale for terrestrial planet formation from Hf-W chronometry of meteorites, Nature, Volume 418 (2002), pp. 949-952

Commentaires - Politique

Ces articles pourraient vous intéresser

A coherent and comprehensive model of the evolution of the outer Solar System

Alessandro Morbidelli

C. R. Phys (2010)

Planetary formation and early phases

Aurélien Crida

C. R. Phys (2023)

The primordial sculpting of the Kuiper belt

Alessandro Morbidelli; Hal F. Levison

C. R. Phys (2003)