1 Introduction
Cation exchange capacity (CEC) is a physicochemical characteristic of soils that gives insight about the ability of a soil to bind cations and release them in soil solution at the soil pH. This cation holding capacity is related to the amount of soil colloids with negative charges, like humus and clay.
CEC determination is of considerable importance for agronomical topics. As CEC reflects soil ability to retain cations available for plants, CEC is used, among other soil's parameters like colloid and nutrient content, to discuss soil fertility [13]. CEC evaluation is also relevant for environmental purposes. For instance, trace element exchangeable fraction in polluted soils or sediments is known to be part of the most labile fraction, can be more or less bioavailable, and may also indicate trace element origin [29].
Soil CEC has recently received attention in ecotoxicological studies. For Rieuwerts et al. [22], CEC is a predictive factor of metal extractability in soils but with little consistency when compared to soil pH. Predictability of U concentration in soil solutions has been demonstrated to be based on multiple parameters. On the opposite, a backward stepwise multiple regression analysis excluded CEC from being an explanatory variable [30]. Beside this, Zn, Fe and Cu accumulation in the leguminoseae plant Trigonella foenum-graecum was positively correlated to the CEC values of six experimental soils [27]. In a related study, but comprising only three soils, Gupta and Sinha [12] observed a similar trend for the accumulation of Ni, Cr and Pb in Chenopodium album. The bioavailability of 137Cs to various plant species was shown to be dependent on soil CEC for only one of a three-year study [14]. On the contrary, Sauras Yera et al. [25] showed that soil CEC was not a good predictor for 137Cs root uptake while it was the case for 90Sr. In invertebrates, heavy metals accumulated in enchytraeids and earthworms as a function of total metal soil concentrations and CEC values [31]. In Enchytraeus crypticus, Peijnenburg et al. [21] demonstrated that soil CEC together with pH were the most important parameters for heavy metal uptake rate constants and bioaccumulation factors. CEC was also one of the most important parameters determining Cd, Zn and Cu accumulation in the ground-dwelling spider Pirata piraticus [11].
Moreover, several works related the ecotoxicity of metal-contaminated soils to CEC values. When studying the influence of soil properties on Ni toxicity to barley root and tomato shoot growth using 16 European soils, Rooney et al. [23] identified soil CEC as the best single predictor for toxicity. Similarly, the toxicity of Zn and Cd toward the enchytraeid Enchytraeus albidus, exposed in artificial soil with different organic matter and clay types, were correctly predicted from soil CEC [16]. For non-oligochaete species, similar trends were suggested by Lock et al. [17] who reported on the ecotoxicity of Co on the springtail Folsomia candida. On a functional viewpoint, microbial cellulose decomposition in metal polluted soils was related to chemical parameters such as CEC, or readily oxidizable carbon rather than to total metal content [8].
Finally, beside metal studies, organic compound fate in soil has been related to CEC: phenanthrene and atrazine sequestration was indeed correlated to soil organic C content, nanoporosity and CEC values [9].
Even if these results do not absolutely concluded to identify CEC as a systematic key variable of metal fate and availability in soils, they strongly suggest to quantify its value when dealing with metal (and probably some organic compounds) fate, transfer and availability in soils.
Operationally, CEC is defined as the sum of the ion amounts released when mixing a fixed mass of soil with a fixed volume of reactant solution. Methods for CEC determination consist in the complete saturation of soil exchange complex by a mono-ionic solution. The CEC is quantified by measuring the difference between initial and remaining added ion concentration. Alternatively, the added ion adsorbed to soil can be removed and subsequently quantified. Another way is to sum up the soil cations removed from exchange sites.
Different methods have been already published for the determination of CEC. They differ by the reactant used, the variables measured, and the pH conditions during extraction (Table 1). In all cases, the CEC is generally expressed as milliequivalent per 100 g of soil dried at 105 °C (meq 100 g−1), that equals SI unit centimoles of positive charge per kilogramme of soil dry weight (cmol+ kg−1). Orsini and Rémy [20] proposed to use Co(NH3)63+ as the exchange ion and to quantify the CEC through the measurement of the concentration of Co remaining in solution. This method applies to a large range of soils due to the use of a dilute reagent simulating field soil solution conditions. Furthermore, exchange takes place at similar pH to soil pH as the cobaltihexamine chloride is a non-buffered reagent. This method is thus appropriate for soils with large amount of pH-dependent charges.
Common methods for CEC determination.
Tableau 1 Méthodes courantes pour la détermination de la CEC.
| Reagent | pH conditions | Reference |
| Ammonium acetate | Buffered | Metson [19] |
| Barium chloride | Buffered | Mehlich [18], Bascomb [6] |
| Silver-thiourea | Buffered | Chhabra et al. [7] |
| Ammonium acetate | Buffered | AFNOR [2] |
| Cobaltihexamine chloride | Soil pH | |
| Ammonium oxalate | Buffered |
As the cobaltihexamine chloride solution is coloured and absorbs at 472 nm, the objective of the present work was to assess the possibility to derive soil CEC values more simply from the absorbance of the extractive solution.
2 Material and methods
2.1 Soil samples
Soils were sampled from four sites located in the surroundings of the city of Nancy (France). They were selected with regard to their various colloid contents and different soil pH in order to cover a wide range of experimental conditions for CEC determination. Soils were collected as follows:
- • three samples in the A, AB and C horizon of a Rendzic Leptosol [15] developed on a limestone parent material;
- • two samples in the A, E and two others in the Bt horizon of a Luvisol [15] developed in a silty deposit parent material;
- • three samples in the A, B and C horizons of a Vertic Cambisol [15] developed on a marl;
- • four samples in the A, E, Bs and C horizons of a Podzol [15] developed on a sandstone parent material (Table 2).
General characteristics of the four soil profiles.
Tableau 2 Caractères généraux des quatre profils étudiés.
| Soil type | Horizon | Depth (cm) | Particle size fractions (%) | CaCO3 (%) | Organic C (g kg−1) | pH | ||
| Clay | Silt | Sand | H2O | |||||
| Rendzic Leptosol | A | 0–7 | 26.4 | 24.1 | 8.8 | 40.7 | 106.2 | 7.5 |
| AB | 7–25 | 8.0 | 28.9 | 6.8 | 56.3 | 38.8 | 7.9 | |
| C | > 25 | 14.0 | 17.4 | 8.0 | 60.6 | 9.6 | 8.4 | |
| Luvisol | A | 0–8 | 23.3 | 61.1 | 15.6 | 0 | 33.8 | 5.4 |
| E | 8–20 | 21.5 | 62.0 | 16.5 | 0 | 11.4 | 4.8 | |
| Bt1 | 20–60 | 57.2 | 32.4 | 10.4 | 0 | 4.5 | 4.9 | |
| Bt2 | > 60 | 69.0 | 23.3 | 7.7 | 0 | 4.2 | 4.8 | |
| Vertic Cambisol | A | 0–10 | 58.4 | 33.4 | 8.2 | 0 | 14.5 | 6.6 |
| B | 10–30 | 43.6 | 43.2 | 13.2 | 0 | 22.3 | 6.5 | |
| C | > 30 | 49.8 | 38.5 | 11.7 | 0 | 7.4 | 7.0 | |
| Podzol | A | 0–5 | 4.9 | 11.3 | 83.8 | 0 | 27.0 | 3.8 |
| E | 5–30 | 4.0 | 9.4 | 86.6 | 0 | 8.0 | 4.0 | |
| Bs | 30–50 | 12.7 | 13.3 | 74.0 | 0 | 30.2 | 4.4 | |
| C | > 50 | 10.7 | 11.3 | 78.0 | 0 | 2.8 | 4.6 |
The main characteristics of these four soils are compiled in Table 2 and were obtained by standard methods. Particle size analysis and carbonate content were performed by INRA's national soil analysis laboratory. After organic matter dissolution and, for Rendzic Leptosol only, carbonate removing, fractions below 50 μm were determined by the pipette method [1]. Carbonate content was estimated by volumetric method [3]. Total carbon was determined by dry combustion [4] and organic carbon was derived by difference with mineral carbon calculated from carbonate content. Soil pH in the supernatant of a soil–water suspension was measured [5].
After air drying (24 h at ambient temperature, this procedure was previously shown to result in dry weight values that differed by less than 4% to the ones derived from drying the soils at 105 °C), these 14 samples were sieved on 2 mm stainless steel mesh and then kept in the dark at ambient temperature before CEC analysis. For clayey horizons, samples were hand-crushed prior to sieving.
2.2 CEC measurements
For CEC determination, 2 g dry weight (d.w.) soil were placed in 50 ml polypropylene tubes and 40 ml of 0.05 N cobaltihexamine chloride solution were added. After continuous shaking for one hour (duration previously shown appropriate to reach equilibrium) on a rotating device (60 rpm), tubes were centrifuged at 7000 g for 10 min and supernatants filtered on 0.22 μm Millex GP filters. Absorbencies at 472 nm (A472) and pH were immediately measured. The A472 of the 0.05 N cobaltihexamine chloride solution was also determined. Then, Co concentration in supernatants was quantified by flame atomic absorption spectroscopy (Perkin-Elmer AAnalyst 100) together with Fe3+, Ca2+, Mg2+ and Mn2+. Na+ and K+ concentrations were measured by flame atomic emission spectroscopy. At last, Al3+ was determined by furnace AAS (Varian spectra-300) and H+ was estimated from pH measurement (pH 3000 pH meter WTW) of the supernatant. Certified solutions from Panreac Quimica SA were used to obtain calibration curves.
The whole experiment was repeated twice, the 0.05 N solution of cobaltihexamine chloride (CAS 10534-89-1, sigma H7891) being freshly prepared before each CEC determination.
2.3 Data analysis
According to Orsini and Rémy [20], CEC can be derived from the concentration of Co remaining in the supernatant, determined by flame emission or atomic absorption spectrometry, as
with the following notation: CECCo: cation exchange capacity (meq 100 g−1 or cmol+ kg−1) in terms of the concentration of Co in the supernatant; [Co]0.05N and [Co]assay: Co concentration in 0.05 N cobaltihexamine chloride solution and sample supernatant, respectively, in g l−1; V: volume in l of 0.05 N cobaltihexamine chloride solution added to soil sample (0.04 l); m: soil dry mass used (2 g).
As cobaltihexamine chloride solution absorbs at 472 nm, Co concentration in solution can be determined from A472 measurements. Considering the A472 of a solution of a given normality (i.e. 0.05 N), a CECA472 (meq 100 g−1 or cmol+ kg−1) can be calculated as:
where A4720.05N and A472assay correspond respectively to the absorbencies at 472 nm of 0.05 N (= 50 meq l−1) cobaltihexamine chloride solution and of sample supernatant; V: volume in l of 0.05 N cobaltihexamine chloride solution added to soil sample (0.04 l); m: soil dry mass used (2 g).
For each experiment, we plotted CECA472 versus CECCo values and run a regression analysis. All calculations were made according to published methods [26,32].
Moreover, we calculated CEC considering the sum of the soil cations determined in supernatants (Fe3+, Ca2+, Mg2+, Mn2+, Na+, K+, Al3+ and H+). In this case, the CECsum (meq 100 g−1 or cmol+ kg−1) can be derived as follows:
where [Mi] stands for individual cation concentration corrected for cobaltihexamine chloride solution values (mol l−1) and vi for the ion valence, respectively. V and m were already defined above.
Then, we studied the relationship between CECA472 and CECsum as described previously.
3 Results
CECA472 and CECCo values determined from the 14 horizons in two independent experiments are plotted in Fig. 1. The slopes and intercepts resulting from simple linear regression analyses were tested by using a two-sided Student's t test with 12 degrees of freedom (Table 3).

Scatter plot of CECA472 versus CECCo in the two independent experiments (exp1 and exp2). CECA472 and CECCo correspond respectively to CEC values derived from 472 nm absorbencies and Co concentrations of the cobaltihexamine solution after exchange.
Fig. 1. Graphe de la CECA472 versus CECCo pour deux expériences indépendantes (exp1 et exp2). CECA472 et CECCo correspondent respectivement aux valeurs de CEC calculées à partir des absorbances à 472 nm et des concentrations en Co de la solution de cobaltihexamine après échange.
Regression coefficients as obtained from the regression analysis of CECCo as a linear function of CECA472, for experiment 1 and 2 data.
Tableau 3 Paramètres de la régression linéaire établie entre la CECco et la CECA472, pour les données des expériences 1 et 2.
| Slope (P value) | Y-Intercept (P value) | |
| Experiment 1 (n = 14) | 0.987 (P < 10−11) | −0.41 (P = 0.417) |
| Experiment 2 (n = 14) | 0.957 (P < 10−11) | 0.248 (P = 0.257) |
Thus, the tests on both slopes were highly significant (P < 10−11), whereas the corresponding intercepts did not significantly differ from zero (P = 0.417 and 0.257, for experiment 1 and 2, respectively). Moreover, a test of comparison performed on the two slopes showed that they were not significantly different (Student's t test with 24 df; P = 0.257), suggesting that data from experiment 1 and 2 could be pooled together to derive a unique final model. To this end, and considering the above-mentioned results, a regression line crossing the origin was further fitted to the entire set of pooled data. The fitted model (r2 = 0.99) was as follows (Fig. 2):
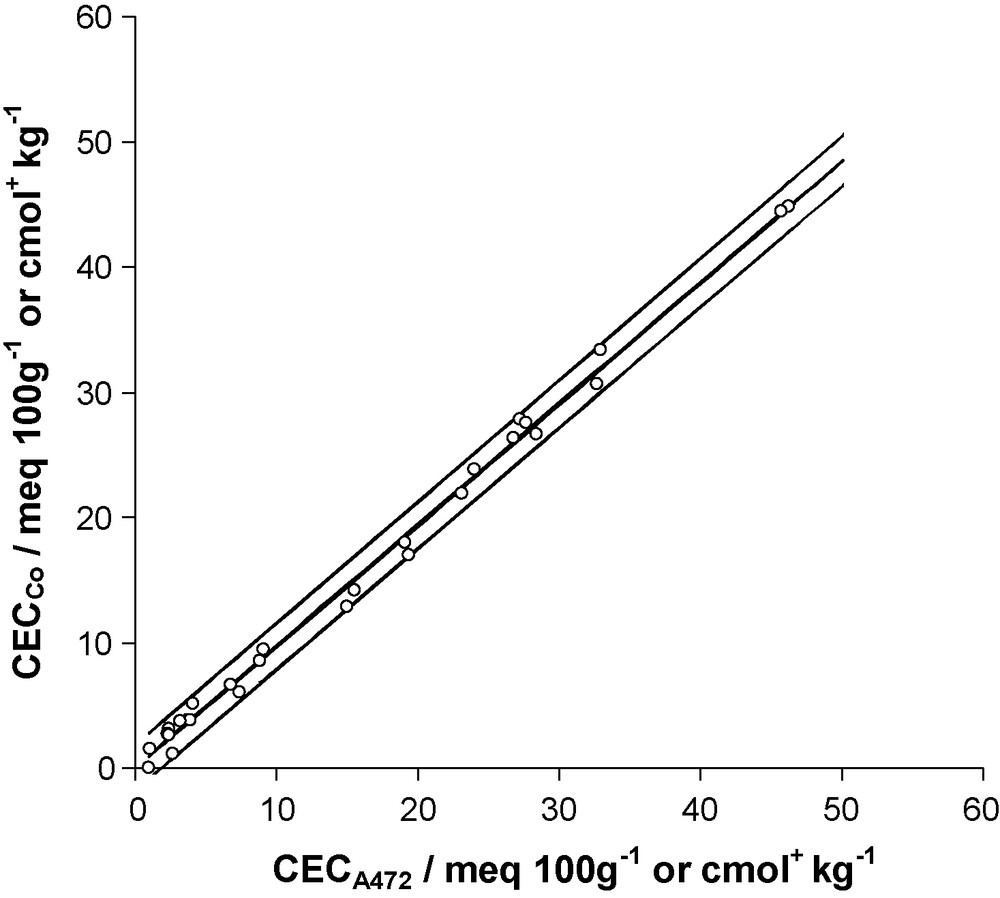
Regression of CECCo on CECA472 (data obtained from experiment 1 and 2 were pooled). Plot of fitted regression line (bold) and 95% prediction limits (light). CECA472 and CECCo correspond respectively to CEC values derived from 472 nm absorbencies and Co concentrations of the cobaltihexamine solution after exchange.
Fig. 2. Régression de la CECCo en fonction de la CECA472 (les données des expériences 1 et 2 ont été regroupées). La droite de régression est représentée en trait gras, les limites de prédiction à 95 % en traits fins. CECA472 et CECCo correspondent respectivement aux valeurs de CEC calculées à partir des absorbances à 472 nm et des concentrations en Co de la solution de cobaltihexamine après échange.
As the slope of this common model was significantly different from unity (two-sided Student's t test with 27 df; P = 6.7 × 10−4), CECA472 cannot be considered as a direct (i.e. with no correction) estimate of CECCo. The corrective factor 0.969 should therefore not be omitted, to prevent from a 3% overestimation of CECCo value. However, the meaning of this factor is limited. Indeed, if a classical regression was run, the slope would be slightly higher (0.972) and would differ significantly from 1 to a lesser extend (p = 0.039) and, at the same time, the Y-intercept would not differ significantly from 0. We preferred a regression through the origin analysis (RTO) since no Y-intercept at all was justified in our model.
Then, for any given experimental A472assay value, and considering A4720.05N (typically 0.941 in our experiments), it becomes possible to estimate the corresponding CECA472 and CECCo values. Moreover, a prediction interval at probability level (1 – α), for any CECCo corresponding to a given value of CECA472, can be obtained as:
where s stands for the residual standard deviation, equalling . As the square root term of the equation is, in our case, close to the unit, it can be neglected. Therefore, the expression simplifies to:
In particular, a 95% prediction interval can be calculated as:
The same procedure was followed to study the relationship between CECsum and CECA472. The fitted regression model (r2 = 0.99) resulted in the following equation:
The slope differed significantly from 1 (two-sided student t test with 27 df, P = 1.9 × 10−5) and this could result from an hypothesized release of cations (Fe3+, Ca2+, Mg2+, Mn2+, Na+, K+, Al3+ and H+) from the soil not due to an exchange with the cobaltihexamine ion.
Once again, a prediction interval at level (1 – α), for any CECsum, corresponding to a given value of CECA472, can be derived as:
The value of s in that case being . As previously explained, the expression simplifies to:
Notably, a 95% prediction interval is given by:
4 Discussion and conclusions
Two models were derived from our experiments, allowing to obtain estimations of soil CEC values, expressed either as CECCo or CECsum. Values will not differ to a large extent but reporting results as CECCo would be preferable since the model is based on a single determination (the concentration of Co in the medium), whereas the other model was derived from multiple measurements (i.e. Fe3+, Ca2+, Mg2+, Mn2+, Na+, K+, Al3+ and H+ concentrations), each one being a source of uncertainty. The relationship between CEC values determined by absorbance measurement of cobaltihexamine ion and values issued from the analytical determination of cobalt has already been reported [10]. The authors concluded that both measurements methods were interchangeable but the slope of the regression line was not statistically tested toward the unit and no confidence intervals were calculated. Here, we show that CECCo and CECA472 values are indeed extremely close one to the other but not interchangeable. Mechanistically, the discrepancy between both values may result from a tight loss of absorbance in the sample extracts which is not paralleled by a loss of Co. A lysis of the cobaltihexamine complex could lead to such phenomenon but it remains unexpected due to its high stability (dissociation constant Kd = 10−35). Also, the complex Co(NH3)63+ may react with solubilized soil components leading to a putative less absorbing compound. However, literature data does not allow to comfort such hypothesis.
As expected from soil selection, results of CECCo determination cover a large range of values, from 0.0 – 1.0 cmol+ kg−1 for the E horizon of the Podzol to 44.8 – 44.3 cmol+ kg−1 for the A horizon of the Rendzic Leptosol. Results are consistent with colloids content of the various samples: sandy or clay-poor samples (the whole profile of the Podzol and the illuvial E horizon of the Luvisol) show the lowest CEC, while organic or swelling clay-rich samples (A and AB horizons of the Rendzic Leptosol, and the whole profile of the Vertic Cambisol) exhibit the highest ones.
The null CECCo value for the E horizon of the Podzol found in experiment 1 (Fig. 1) is due to the extremely low colloids content of this sample. Due to a quartzic sandstone parent material and podzolization process, this profile is sandy-textured with very low clay content. Furthermore, E horizon is depleted in organic colloids as metal-humus complexes migration takes place through this horizon. Therefore, for low CEC samples (below 2.4 cmol+ kg−1 in this experiment) the method for CEC determination presented here shows insufficient accuracy.
On account of the significance of the CEC evaluation in the various topics presented in the introductive part, a rapid method for CEC determination, even with low accuracy, is required for screening purposes. The method presented here consists in a short exchange followed by measurement of absorbance after centrifugation and filtration, and therefore is rather not time-consuming and simple to perform. The variability observed between experiment 1 and 2 was tiny and mainly due to the subsampling of soils. It could be possible to reduce it again by increasing the mass of the subsamples. The use of cobaltihexamine chloride reagent proposed by Orsini and Rémy [20] is of great relevance for a large range of soils because this non-buffered reagent provides an exchange at soil's pH. Thereby this method is appropriate for both acid soils and soils with high pH-dependent charges.
Moreover, since a wide range of soil CEC were chosen for deriving the models, these ones may be used as predicting tools for a large variety of soils. For instance, a statistical distribution analysis of the CEC values of the French soil database [24] revealed that the 1st and 9th deciles reached 6.2 and 18.90 cmol+ kg−1, respectively, for a data set of approximately 170 000 values. In the same way, the US soil survey database [28] comprises more than 100 000 CEC values from various samples and pedons, and the 1st and 9th deciles were in this case 4.4 and 34.2, respectively. Then, it arises from these distributions of CEC data that the proposed method would be applicable for most of the soil samples.
Acknowledgements
The authors would like to thank Philippe Rousselle (université Paul-Verlaine-Metz, LIEBE, CNRS UMR 7146, France) for excellent technical work.


