1 Introduction
In recent years ambient noise imaging has been successfully and repeatedly used to generate tomographic images of the crust (Ritzwoller et al., 2006; Shapiro and Campillo, 2004; Shapiro et al., 2005; Stehly et al., 2006; Weaver, 2005). Studies of known regions have demonstrated that the Earth's background noise can be reliably used to retrieve crustal velocity structures that are in good agreement with both known regional geology and with tomographic results obtained using discrete earthquake sources. A particularly exciting development has been the use of ambient noise tomography to image time-dependent changes in the crust (Brenguier et al., 2007, 2008a). Although other sources (earthquakes, large explosions) have sufficient energy for crustal tomography, ambient noise imaging is the most suitable for time-lapse tomography. The technique's use of an ever-present seismic energy source could potentially enable the continuous monitoring of crustal changes down to seismogenic depths (∼20 km), and so may be the only tool capable of measuring stress-induced changes in the crust, a pre-requisite for reliable earthquake forecasts (Wood and Gutenberg, 1935).
As has been discussed in multiple publications, implicit to all noise correlation techniques is the assumption that the source distribution is isotropic. The Earth's ambient noise is dominated by ocean wave-generated seismic signals. While some signal is generated directly by the ocean swell crashing on the Earth's coasts (known as the primary microseisms), and thus is dominated by the swell period, a far more energetic source is the double-frequency (or secondary) microseismic noise in the frequency band ∼3–10 s, generated when opposing ocean surface gravity waves of overlapping frequency content interact and generate a nearly unattenuated acoustic wave that impinges on the ocean floor (Longuet-Higgins, 1950). Both primary and secondary microseisms have been successfully used in ambient noise tomography studies. Averaged over periods of months and years these ocean sources are generally believed to have a wide azimuthal distribution sufficiently random for ambient noise imaging. Tsai (2009) has used a ray theory approximation to calculate the effect of deviation from isotropic distribution on the accuracy of noise tomography travel-time measurements. He has shown that a collection of anistropic sources (similar to a perceived distribution of multiple ocean sources) may result in a small (few percent) velocity measurement error. He also demonstrated that a single source may result in a much larger error. This error is likely to increase as the correlation time decreases. The challenge for time-dependent correlation is to monitor and quantify the ambient source anistropic distribution, and correct for the errors it introduces, as was suggested by Tsai (2009).
In this article I describe what is currently known about the source distribution of ocean microseisms. I begin with a review of the theory of ocean microseisms, and discuss its excitation mechanisms in the deep ocean and along the coasts. I follow with a case study of microseisms generation in North America and discuss the differences between the source of microseisms in the western Atlantic Ocean, and the deeper Pacific Ocean. I conclude with an analysis of the source anisotropy as predicted by a Wave Action Model.
2 A review of the theory
Ocean microseisms have been observed since the first long-period seismometers were emplaced on the Earth's surface. The observation attracted tremendous scrutiny in the early days of seismology, and a variety of theories of their origin have been suggested. In 1950, Longuet-Higgins published his seminal paper “A Theory of the Origin of Microseisms”, based on Miche (1944), where he proposed that when two opposing surface gravity waves of the same period interact, a second-order acoustic wave is generated at half the period of the gravity waves, which travels unattenuated to the ocean floor where it generates a surface (Stoneley) wave. He then followed with a derivation of ocean depth dependent Stoneley wave excitation functions, and proceeded with a prediction of the amplitudes and excitation locations and intensities of microseisms in the world's oceans. In a wave tank test Cooper and Longuet-Higgins (1955) confirmed the theory.
While Longuet-Higgins’ basic idea is widely understood and has been heavily referenced, key aspects of his theory have unfortunately been either misunderstood or ignored for decades. I therefore provide here a brief summary of the complete theory, using a pendulum analogy (Fig. 1) following the example of Longuet-Higgins (1953). For consistency, I use the same notation as Longuet-Higgins (1950). For small motions of a pendulum, to a first-order approximation, there is no vertical pressure fluctuation in the pendulum system. Nevertheless, a second-order fluctuation does exist. As the pendulum swings, its center of mass is raised twice per cycle. The only force that can counteract it is a vertical force that, according to Newton's third law, would be felt at the pendulum's base. A downward vertical force would necessarily generate seismic waves in the elastic medium. Similarly, when a standing wave is generated by opposing surface gravity waves in a fluid the first order dynamic pressure fluctuation decays exponentially downward from the fluid surface, as is the case for a traveling wave or a linear combination of traveling waves. However, just as in the pendulum case, in a standing wave the center of mass of the water column is raised twice per cycle relative to the equilibrium condition. Again, the only force that can counteract it is a vertical pressure at the bottom of the fluid column, which in turn would generate seismic waves. Therefore, when two regular trains of waves travel in opposite directions with amplitudes a1 and a2 and radian frequency σ interact, it can be shown that they result in a pressure oscillation,
| (1) |
| (2) |
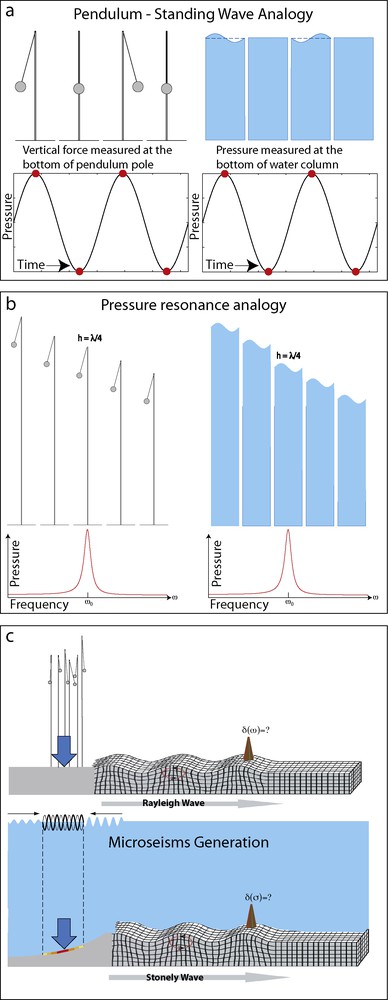
Double frequency (secondary) microseisms excitation process and a pendulum analogy. a: double frequency vertical pressure generated as a result of raising and lowering the systems’ centers of mass twice per cycle; b: when the speed of sound in the compressible media is taken into consideration and the propagation time of the pressure pulse is calculated, fundamental mode resonance is achieved when the pendulum pole and water column depths are ¼ of the acoustic wavelength in the respetive media; c: the Longuet-Higgins theory estimates the amplitude of seismic ground motion a large distance r away from the double frequency source. Masquer
Double frequency (secondary) microseisms excitation process and a pendulum analogy. a: double frequency vertical pressure generated as a result of raising and lowering the systems’ centers of mass twice per cycle; b: when the speed of sound in the compressible ... Lire la suite
Mécanisme d’excitation de microséismes à fréquence double (secondaire) et analogie avec un pendule. a : pression verticale à fréquence double, obtenue à la suite d’élévation et d’abaissement des centres des systèmes de masse deux fois par cycle ; b : quand la vitesse du son en milieu compressif est prise en considération et l’impulsion de la pression calculée, la résonance de mode fondamental est atteinte, quand la longueur du pendule et la profondeur de la colonne d’eau représentant ¼ de la longueur d’onde acoustique dans les milieux respectifs ; c : la théorie de Longuet-Higgins estime l’amplitude du mouvement sismique à une grande distance r loin de la source de fréquence double. Masquer
Mécanisme d’excitation de microséismes à fréquence double (secondaire) et analogie avec un pendule. a : pression verticale à fréquence double, obtenue à la suite d’élévation et d’abaissement des centres des systèmes de masse deux fois par cycle ; b : quand la vitesse ... Lire la suite
One way of intuitively understanding the dependency of
Next, the theory considers the effect of fluid compressibility. Again, using the pendulum analogy, if the pendulum pole is sufficiently long compared to the wavelength of an acoustic wave in the pole, the propagation time of the pressure pulse in the pole has to be considered. If the pole length is ¼ of the acoustic wavelength, the fundamental mode of pressure oscillation in the pole is excited, and resonance is achieved. Similarly, if the water column is ¼ of the acoustic wavelength in water, acoustic resonance will be achieved, and therefore a stronger excitation of seismic waves at the bottom of the water column. The theory proceeds to calculate local response kernels of a compressible liquid-solid system to a vertical oscillatory pressure source on the surface of the ocean. The kernels cm(h,σ,β) represent discrete modes of excitation of integer order m and are dependent upon the ratio σh/β, where σ is the surface gravity wave frequency, h is the depth of the liquid layer, and β is the elastic shear velocity of the solid half-space. These functions display resonant behavior when the ocean depth is close to ½(m − 1)+1/4 of an acoustic wavelength in water. Summing the contributions of all modes of excitation and accounting for geometrical spreading, a function W is introduced, which describes the contribution of a unit area of ocean experiencing oscillatory pressure force on its surface to a seismic wave recorded some distance r away:
| (3) |
Finally, the theory calculates the displacement amplitude at a large distance r from the source of double frequency oscillation. Again, using the pendulum analogy it answers the question: What would the displacement amplitude be at a distance r from a field of pendulums of random phases and random pole lengths. In the ocean, this is equivalent to estimating the amplitude of ground motion at distance r from the source of (double frequency) wave-wave interaction. That displacement, δ, is shown to be:
| (4) |
It should be noted, that since Longuet-Higgins theory uses a one-dimensional Earth model, within the confines of the theory a vertical source can only result Rayleigh or Stoneley waves. However, in reality, due to two-dimensional variations in the ocean bottom topography at the source region, and due to multipath effects, Love waves can be generated by the same mechanism, as has been recently discussed by various authors. A full development of the theory of Love wave generation by ocean wave-wave interaction has yet to be presented, and is beyond the scope of this article.
Certain consequences follow from Eq. (4) (Equation 198 in the original 1950 paper). Most notably, microseisms amplitudes may increase if the wave-wave interactions occur over ocean of resonant depth. This theoretical prediction has been almost completely ignored until recently when it was confirmed by Kedar et al., 2008. In addition, many misconceptions have been perpetrated in the literature. The two most common misconceptions are: (1) microseisms are generated within the storm area; (2) microseisms locations are correlated with regions of strong wave amplitudes. While both assertions may be correct some of the time, they are by no means always correct. Rather, the theory predicts that microseisms will be generated wherever opposing waves of overlapping frequency content interact, regardless of their origin. Also, as was pointed out by Tabulevich et al. (1976), the seismic recordings of ocean microseisms at a given site are typically composed of the sum total of microseisms emanating from several source regions. In many cases microseisms locations have been deduced by correlating seismic time series with significant wave height. Since microseisms are typically generated by interactions of high amplitude swells, a positive correlation is achieved and many authors’ mistakenly conclude that the source region has been thus identified. As will be shown below, this is not necessarily the case, and while the correlation indicates a causal relationship, it does not identify the precise location of the seismic source. To do that, one has to identify the regions in the ocean where wave-wave interaction occurs. This point is illustrated by a case study of microseisms generation in North America during fall and winter months.
3 Source distribution of microseisms observed throughout North America
The distribution of measured amplitudes of ground displacements throughout North America averaged over the entire month of November 2003 is displayed in Fig. 2. It clearly shows that during this period the North Atlantic Ocean generates substantially stronger microseisms than the Pacific. The microseism amplitudes measured along the Pacific coast decay rapidly away from the coasts, while along the North Atlantic they are of greater magnitude and propagate significantly deeper into the continent. This suggests a fundamental difference between the wave-wave interaction excitation in the western North Atlantic and the eastern North Pacific.
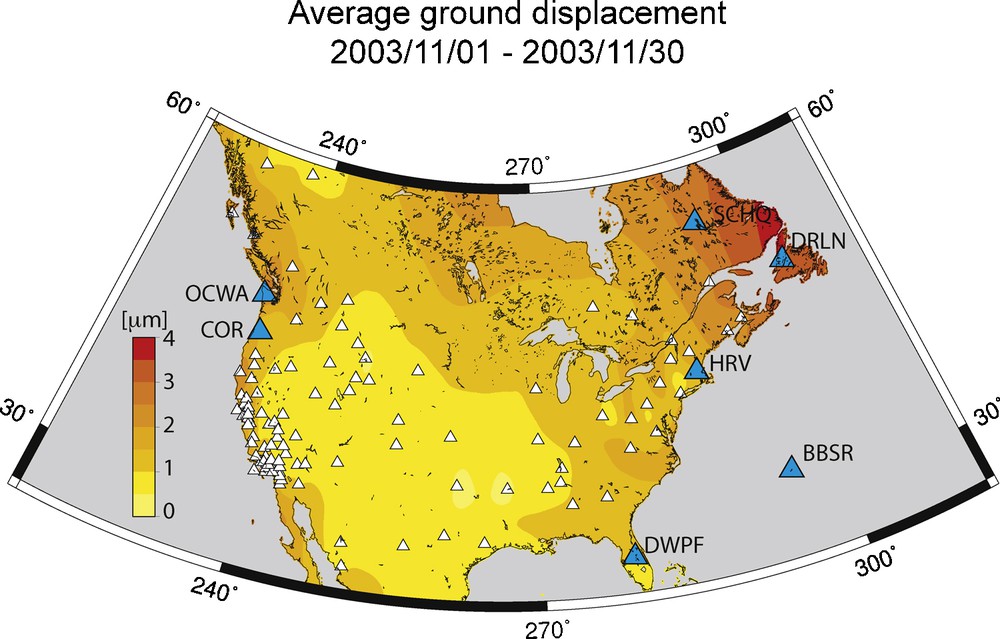
Average ground displacements throughout North America. Large earthquakes were removed from the data, and a 3–7 s band pass filtered was applied. A map showing the average vertical ground displacement throughout North America during the month of November, 2003 was derived from hourly time domain averages of the observed seismic amplitudes. The stations used for the displacement measurements are marked by triangles. The stations marked by triangles were used for the 6-month test depicted in Fig. 4.
Déplacements moyens du sol à travers l’Amérique du Nord. Les grands tremblements de terre ont été retirés des données et un filtre à bande passante 3–7 s a été utilisé. Une carte montrant le déplacement vertical moyen du sol à travers l’Amérique du Nord pendant le mois de novembre 2003 a été déduite de moyennes horaires des amplitudes sismiques observées dans le domaine temporel. Les stations utilisées pour les mesures de déplacement sont marquées par des triangles. Les stations figurées par des triangles ont été utilisées pour un test sur 6 mois, représenté à la Fig. 4. Masquer
Déplacements moyens du sol à travers l’Amérique du Nord. Les grands tremblements de terre ont été retirés des données et un filtre à bande passante 3–7 s a été utilisé. Une carte montrant le déplacement vertical moyen du sol à travers ... Lire la suite
From Kedar et al., 2008
Kedar et al. (2008) have shown that wave-wave interaction maps can be calculated from wind-driven Wave Action Models (WAMs), which may subsequently be used to calculate the seismic amplitudes anywhere on the surface of the Earth using Longuet-Higgins’ theory. Scaling the wave-wave interaction by the bathymetry-controlled microseisms potential, according to Eq. (4), and summing over all potential source regions, results in an intense microseismic source south of Greenland and only a weak, poorly defined source in the deep Pacific (Fig. 3).
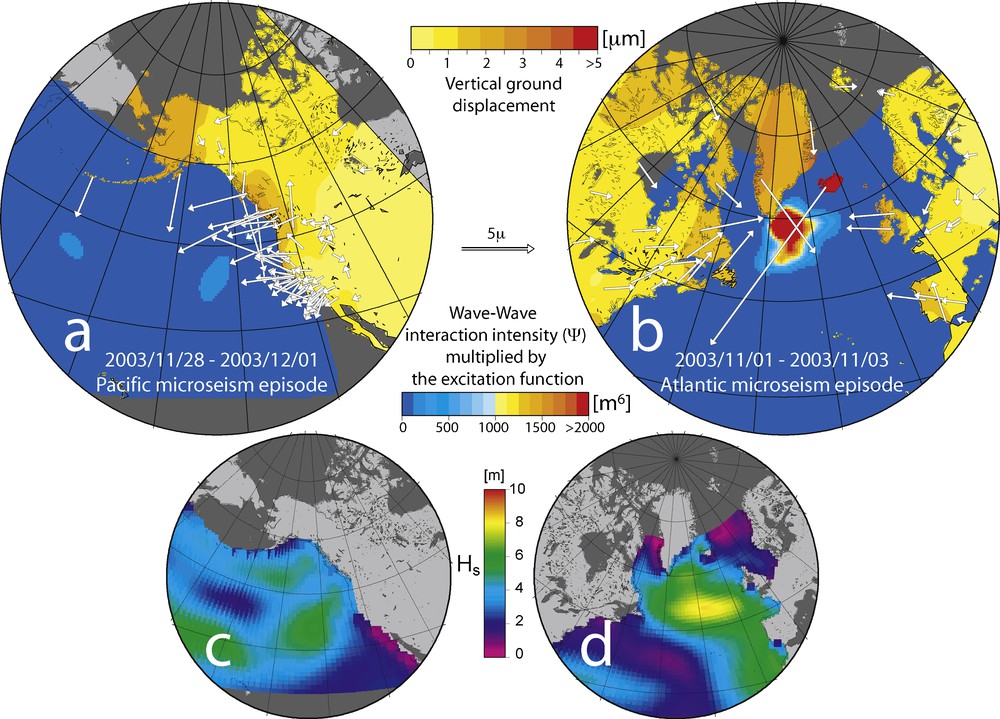
Qualitative comparison of data and modeled deep ocean sources. Measurements of vertical ground displacements on land (a and b) and Rayleigh wave polarities during two microseisms episodes in the North Atlantic and North Pacific. Vectors whose length is proportional to the ground displacement amplitude at each station, indicate the direction of Rayleigh wave arrivals, determined from cross-correlations of the horizontal components with the vertical component. A Gnomonic projection, in which great circles appear as straight lines, is chosen. Also shown are the corresponding average wave-wave intensities in the ocean, Ψ, multiplied by the bathymetry-controlled excitation function and the averaged significant wave heights, Hs (lower panels), during the same time periods. The amplitude pattern and the seismic wave directions around the North Atlantic suggest the seismic energy emanates from a deep-ocean source located south of Greenland. This is consistent with the model, which places an intense source in the same region. In the North Pacific, the deep ocean excitation is significantly lower, (Ψ peaks in the Pacific are a factor of 20 smaller than in the Atlantic) and the Rayleigh waves’ back azimuths are directed predominantly perpendicular to the nearest coastlines, suggesting a dominant local source of microseisms. The significant wave heights for the same period are displayed for reference (c and d). The wave heights are not significantly higher in the Atlantic than in the Pacific, and the peak wave heights do not coincide with peak wave-wave interaction intensities. Masquer
Qualitative comparison of data and modeled deep ocean sources. Measurements of vertical ground displacements on land (a and b) and Rayleigh wave polarities during two microseisms episodes in the North Atlantic and North Pacific. Vectors whose length is proportional to ... Lire la suite
Comparaison qualitative des données et des sources océaniques profondes modélisées. Mesures de déplacements verticaux du sol sur le continent (a et b) et polarisation des ondes de Rayleigh pendant deux épisodes de microséismes dans l’Atlantique Nord et le Pacifique Nord. Les vecteurs dont la longueur est proportionnelle à l’amplitude du déplacement du sol à chaque station, indiquent la direction d’arrivée des ondes de Rayleigh, déterminée à partir de corrélations croisées des composantes horizontales avec la composante verticale. Une projection gnonomique dans laquelle les grands cercles apparaissent comme des lignes droites a été choisie. Sont aussi présentées les moyennes correspondantes des intensités onde-onde dans l’océan, ψ, multipliées par la fonction d’excitation contrôlée par la bathymétrie et les hauteurs d’onde moyennes significatives, Hs (panneaux du bas), pendant les mêmes périodes de temps. Le diagramme d’amplitude et les directions d’ondes sismiques autour de l’Atlantique Nord suggèrent que l’énergie sismique émane d’une source d’océan profond, localisée au sud du Groenland. Ceci concorde avec le modèle qui place une source interne dans la même région. Dans le Pacifique Nord, l’excitation de l’océan profond est significativement plus faible (les pics ψ dans le Pacifique sont inférieurs à ceux de l’Atlantique d’un facteur de 20) et les azimuths d’arrivée des ondes de Rayleigh ont une direction principalement perpendiculaire aux rivages les plus proches, suggérant une source principalement locale pour les microséismes. Les hauteurs de vagues significatives pour la même période sont présentées comme référence (c et d). Les hauteurs de vagues ne sont pas significativement plus importantes dans l’océan Atlantique que dans l’océan Pacifique et les pics des hauteurs de vagues ne coïncident pas avec les pics d’intensité de l’interaction onde-onde. Masquer
Comparaison qualitative des données et des sources océaniques profondes modélisées. Mesures de déplacements verticaux du sol sur le continent (a et b) et polarisation des ondes de Rayleigh pendant deux épisodes de microséismes dans l’Atlantique Nord et le Pacifique Nord. ... Lire la suite
The location of the source at the southern tip of Greenland is consistent with the amplitude and direction of propagation of the Rayleigh waves at seismic stations around the North Atlantic. By contrast, in the Pacific, wave amplitudes sharply decrease away from the coast, and the incoming seismic wave azimuths typically point perpendicular to local coastlines and not towards any consistent deep ocean source. This is in agreement both with the model, which sees a very weak source in the Pacific, and with previous observations that traced the source to local Pacific shorelines (Bromirski and Duennebier, 2002; Gerstoft and Tanimoto, 2007; Schulte-Pelkum et al., 2003).
The vertical ground displacement amplitudes in space and time at several seismic stations were compared with model calculations in the double-frequency band of 0.14–0.3 Hz (Fig. 4) for both the Atlantic and the Pacific Oceans. The model values using a shear wave velocity β = 2800 m/s, and water density ρ = 1000 m/s, were calculated by adding the contributions from the entire ocean using Eq. (4), during the period from October 1, 2003 to March 31, 2004. The ocean was divided into rectangular elements 1 × 1.5 degrees in latitude and longitude, respectively. The wave-wave interaction intensity and the excitation were calculated at each ocean patch in 3-h increments. The vertical ground motion at a point of interest was calculated by taking the r.m.s. of all contributions and comparing it to the average vertical ground motion measured during the same 3-h period after large earthquakes were removed from the measured data (Fig. 4). Neglecting seismic wave propagation time differences was justified given the fact that they are an order of magnitude shorter than the three-hour time step of the model. Three-dimensional propagation effects such as multipathing and scattering, which are significant for short period (5–10 s) Rayleigh waves, are not explicitly taken into account. Rather, these effects are accounted for by selecting a low quality factor (Q = 125) in agreement with the known attenuation and scattering of short-period (5–10 s) Rayleigh waves (Canas and Mitchell, 1981; Langston, 1989; Mitchell, 1973; Mitchell et al., 1976). Assuming a one-dimensional model, the surface wave attenuation was approximated by calculating the number of wavelengths, n, in the distance r between the source area element and the station, then scaling the wave energy exponentially by n/Q. Sources of error include ignoring coastal interaction (which may play a significant role in regions such as the steep Labrador, Oregon and Washington coasts), neglecting propagation effects, and the use of a simplified Earth model.

Quantitative comparison of measured and modeled ground displacements. A comparison between modeled vertical ground displacements using the theory (red) and measured ground amplitudes (black) performed over the fall and winter of 2003–2004, at the sites marked on Fig. 4 (station BORG is located in Iceland). The seismic station names and the corresponding correlation coefficients are indicated. Note that in the Atlantic the agreement is significantly better than in the Pacific, where the model is consistently underestimating the ground displacements. The storms analyzed in Fig. 3 are indicated. The correlation coefficient is displayed on the left of each time series. Masquer
Quantitative comparison of measured and modeled ground displacements. A comparison between modeled vertical ground displacements using the theory (red) and measured ground amplitudes (black) performed over the fall and winter of 2003–2004, at the sites marked on Fig. 4 ... Lire la suite
Comparaison quantitative entre déplacements du sol mesurés et modélisés. Une comparaison entre les déplacements du sol verticaux modélisés en utilisant la théorie (en rouge) et les amplitudes mesurées (en noir) a été réalisée sur la période automne–hiver 2003–2004, aux sites marqués à la Fig. 4 (la station BORG est localisée en Islande). Les noms des stations sismiques et les coefficients de corrélation correspondants sont indiqués. À noter que dans l’océan Atlantique, la concordance est meilleure que dans l’océan Pacifique, où le modèle sous-estime considérablement les déplacements du sol. Les tempêtes étudiées à la Fig. 3 sont indiquées. Le coefficient de corrélation est fourni sur la gauche de chaque série temporelle. Masquer
Comparaison quantitative entre déplacements du sol mesurés et modélisés. Une comparaison entre les déplacements du sol verticaux modélisés en utilisant la théorie (en rouge) et les amplitudes mesurées (en noir) a été réalisée sur la période automne–hiver 2003–2004, aux sites ... Lire la suite
As seen in Fig. 4, the model does remarkably well in estimating both the phase and amplitude of the vertical ground motion during microseisms episodes in eastern North America, providing a first order quantitative confirmation of the theory. By contrast, in the North Pacific the model significantly under-predicts the observed ground amplitudes. I attribute this to the fact that, as was illustrated in Fig. 3, the Pacific Ocean is a very poor source of deep-ocean microseisms, and that in the North Pacific, depths are generally too great for efficient near-resonance excitation of deep-ocean microseisms. Rather it seems likely that in agreement with past studies, in the North Pacific it is the interaction of incident swell with its coastal reflection (an effect not modeled in the Wave Action Model) that is the dominant source of microseisms generation. In the Atlantic, though still a source of error, neglecting coastal interactions is secondary to a very powerful deep-sea source that has more than enough energy to account for the observed amplitudes.
A close examination of the characteristics of microseisms sequences generated in the Atlantic and the Pacific show inherently different behaviors, which suggest a different mechanism of wave-wave interactions responsible for their generation (Fig. 5). On the Pacific side, a typical microseisms sequence displays all the characteristics of a well developed swell generated thousands of miles away. In particular, it displays the typical linear dispersion of ocean swell (Haubrich et al., 1963) and, since it has propagated from farther away, it has lower frequency content originating from “older” longer-period swell. On the Atlantic side, the characteristics are of younger swell without pronounced linear dispersion and of typically higher frequency. The Atlantic wave-wave interaction occurs in regions where winds with opposing components are formed such as at the southern tip of Greenland, Iceland and the Labrador Sea. It is this coincidental combination of persistent wave conditions over an ocean area of the right depth that creates this particular powerful source in the North Atlantic. As was shown by Kedar et al. (2008) (Fig. 3), deep ocean wave-wave interactions do take place in the deep Northern Pacific ocean, but their contribution is significantly weakened as they take place over non-resonant ocean depths.
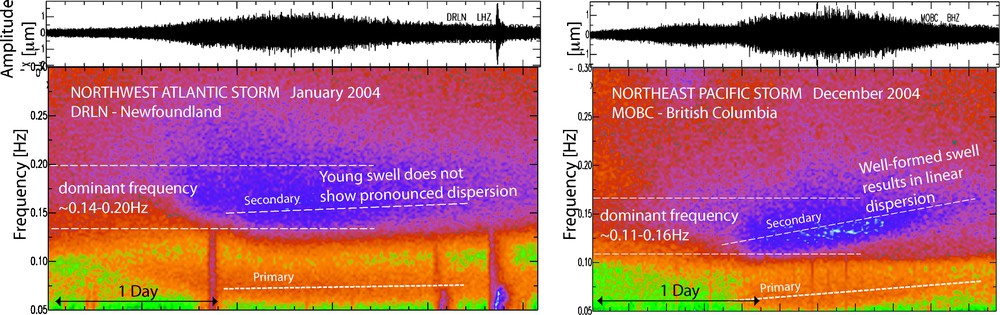
A comparison between two microseims sequences generated near the northwestern US-Canada coast (right) and in the northwestern Atlantic (left). The Pacific OMS appears to be generated by a well-formed, dispersed swell (i.e. swell that has traveled outside of its generation area), whereas the Atlantic OMS is generated by young swell. Since OMS requires opposing waves of similar frequency content, the “old” dispersed Pacific swell would require an opposing swell of same “age”. The likely source of such swell is its coastal reflection. Masquer
A comparison between two microseims sequences generated near the northwestern US-Canada coast (right) and in the northwestern Atlantic (left). The Pacific OMS appears to be generated by a well-formed, dispersed swell (i.e. swell that has traveled outside of its generation ... Lire la suite
Comparaison entre deux séquences de microséismes prenant naissance près de la côte nord-ouest US-Canada (en haut) et l’Atlantique nord-ouest (en bas). L’état de mer du pacifique apparaît comme étant le résultat d’une houle bien formée et dispersée (c’est-à-dire d’une houle dont le parcours s’est effectué en dehors de la zone où elle est née), tandis que dans l’Atlantique il est généré par une houle jeune. Comme l’OMS requiert des ondes opposées et de fréquences similaires, la « vieille » houle pacifique dispersée nécessitera une houle opposée, de même âge. La source probable d’une telle houle est sa réflexion sur la côte. Masquer
Comparaison entre deux séquences de microséismes prenant naissance près de la côte nord-ouest US-Canada (en haut) et l’Atlantique nord-ouest (en bas). L’état de mer du pacifique apparaît comme étant le résultat d’une houle bien formée et dispersée (c’est-à-dire d’une houle ... Lire la suite
4 Discussion
In spite of the differences between the way microseisms are generated in the North Atlantic and North Pacific Oceans during northern hemisphere winter, they share one characteristic – the microseisms generation patterns are repeated with great regularity due to persistent climactic conditions, topography, and bathymetry. The implication to noise tomography is that time averaging of the background noise may not necessarily result in a quasi-isotropic noise field. On the Pacific coast, the swell observed during winter months typically originates in the northwestern Pacific Ocean. It usually arrives from the northwest and propagates southwards along the western North America coast. By the time it travels across several thousands of miles of ocean and reaches the coasts it is well dispersed, giving rise to the linear dispersion pattern shown in Fig. 5. It continues dispersing as it travels down the west coast and a spatio-temporal pattern of swell evolution and interaction with the coast is generated (Fig. 6). This pattern is repeated regularly during the winter (Fig. 6a). During northern hemisphere summer, the swell arrives from the southern Pacific Ocean, yet summer patterns are repeated as well (Fig. 6b). Similarly, excitation of microseisms in the deep North Atlantic Ocean is repetitive. The source region near the southern tip of Greenland is dominant, where a combination of climatic conditions and bathymetry provides a persistent and efficient source of microseism generation. This has been confirmed not only by Wave Action Models, but also by independent location of P wave sources carried out by Landes et al. (2010) (Fig. 7).
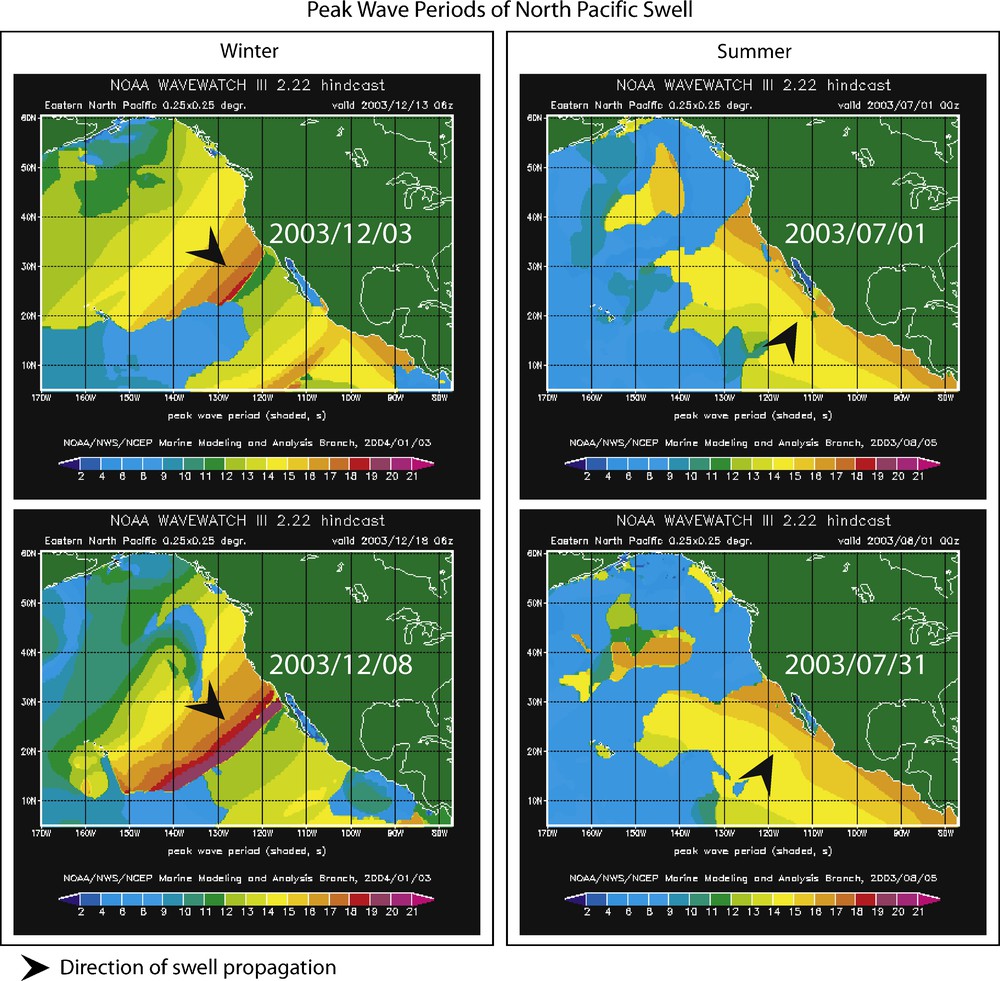
NOAA Wavewatch III (Tolman, 1999, 2005) Wave Action Model snapshots of swell period in the Northeast Pacific during northern hemisphere winter (left) and summer (right). Repeated swell patterns are observed in both seasons. Black arrows indicate direction of swell propagation.
NOAA Wavewatch III (Tolman, 1999, 2005). « Wave Action Model » : images instantanées de la période de houle dans le Nord-Est Pacifique pendant l’hiver (à gauche) et l’été (à droite) de l’hémisphère Nord. Des configurations répétées de houle sont observées pour les deux saisons. Les flèches noires indiquent la direction de propagation de la houle.
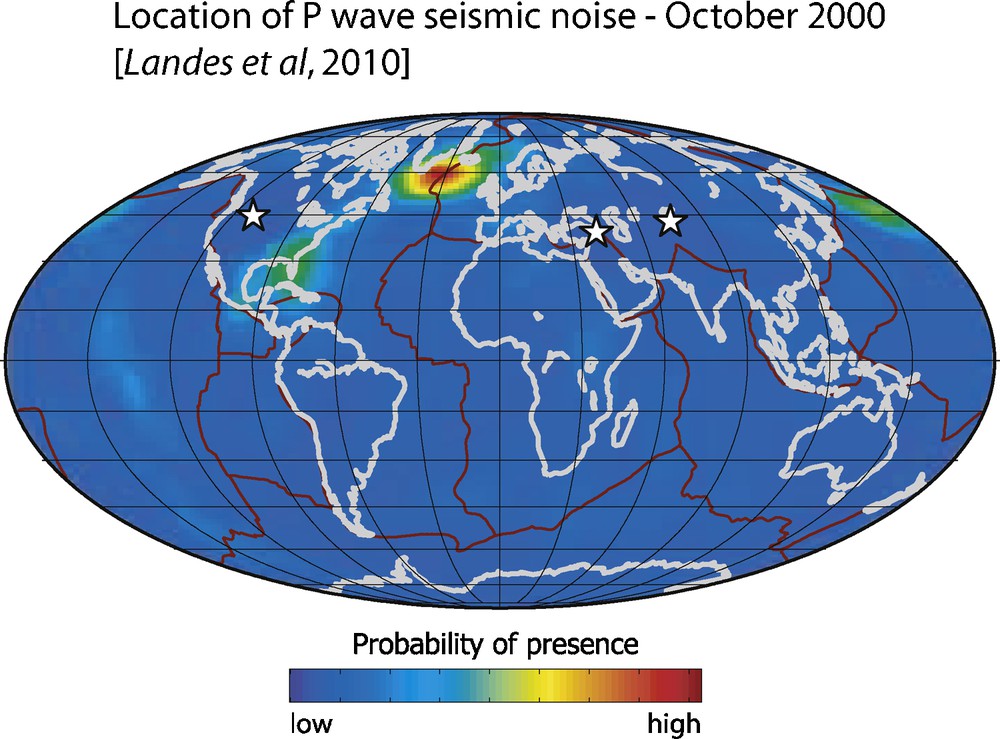
Probability of P-wave noise source during October 2000. The excitation pattern shows a persistent source south of Greenland, rather than a diffuse source distribution.
Probabilité de source du bruit d’onde-P pendant le mois d’octobre 2000. Le diagramme d’excitation montre une source persistante au sud du Groenland, plutôt qu’une distribution de sources diffuse.
From Landes et al., 2010
The repeated ocean patterns may in fact be of some benefit to time dependent noise tomography. Correcting for a repeated noise source distribution is easier than for a non-random yet non-repetitive source distribution. Moreover, it is possible that because of the persistence of microseisms excitation patterns, temporal changes in the Earth's crust, though not accurately determined, would still be detectable, in spite of the bias they introduce into the travel-time estimates. The bias can be studied by analyzing varying time averages of microseismic noise contributions as a function of source azimuths (Fig. 8). A 180-day average of modeled seismic amplitudes at a station in Newfoundland, Canada, reveals that during a ∼6-month period most of the noise energy is dominated by arrivals from a ∼30°-wide zone to the east-by-northeast. Therefore, in spite of the time averaging, the source is strongly anisotropic. Averaging the same information in 30-day bins shows that while the segments containing the main lobe are recurrent, they vary in absolute intensity and in the details of the source azimuthal distribution. While it is observed that during calmer periods the source distribution is less heterogeneous (Fig. 8, days 61–90), at no time is it approaching isotropic distribution. Therefore it would be difficult to argue that concentrating only on less noisy days would eliminate the need for a correction or elimination of the source directionality.

Source distribution at varying time scales calculated from wave-wave interaction maps. The contribution of each ocean segment is weighed by the expected amplitude at station DRLN (Fig. 2) calculated using Eq. (4). The top panel shows a 180-day azimuthal average. The six bottom panels display consecutive 30-day averages spanning the same period.
Distribution des sources à différentes échelles de temps, calculée à partir de cartes d’interaction onde-onde. La contribution de chaque segment océanique est estimée par l’amplitude attendue à la station DRLN (Fig. 2), calculée en utilisant l’Éq. (4). Le panneau du haut montre une moyenne azimuthale de 180 jours. Les six panneaux inférieurs présentent des moyennes de 30 jours consécutifs balayant la même période.
Tsai (2009) demonstrates that for periods shorter than the time it takes the signal to travel the distance Δx between correlated stations, even for highly anisotropic source distributions the estimated velocity error is minimal. Following his calculation, considering the periods in the above analysis (3–8 s) and a medium velocity of ∼3 km/s, correlation between stations that are Δx ∼20 km apart would see less than 1% error in their estimate. While this may be of little consequence for a regular tomographic study, it is significant compared to the amplitude of temporal changes in the crust. For example, Brenguier et al. (2008b) infer post-seismic velocity changes that are less than 0.1% over a period of 1–2 years. Moreover, the main focus of time varying ambient noise imaging would be analysis of changes near fault zones, which requires short correlation distances and therefore is more sensitive to anisotropic source distribution in the microseisms frequency band. The time variation in source distribution shown in Fig. 8 would map into the time varying velocity estimates for the same period. The travel time error may be reduced by using cross-correlation codas, where most of signal is from scattered waves that are significantly less sensitive to noise source distribution (Brenguier et al., 2008b).
Using the theoretical framework of Tsai (2009) a correction can be applied if the source distribution can be independently constrained. As shown above, wave-wave interaction maps can provide a good first estimate of the source distribution in the deep ocean. However, where the dominant source is coastal reflection, as is the case along the Pacific North American coast, such analysis may be significantly more difficult. Coastal reflections are complex processes dependent on beach slope, tides and bathymetry, and are inherently hard to model. Nevertheless, the above analysis highlights the need to include approximations of coastal reflections in the Wave Action Models, and to look for alternative approaches to estimating the microseisms source distribution throughout the entire ocean.
5 Conclusions
Microseisms dominate the spectrum of ambient noise used for crustal tomography. Examination of microseisms source distributions in the North Pacific and North Atlantic Oceans during fall and winter months reveals that they are distinctly different. The micoseismic noise observed along the eastern North American coast is dominated by a persistent deep ocean source south of Greeland, while the source of microseisms observed along the Pacific coast is predominantly generated by near-coastal wave-wave interactions of traveling swells with their coastal reflected image. Nevertheless, both sources are caused by repeated wave patterns that give rise to a non-random source distribution. Analysis of the azimuthal source distribution in the North Atlantic reveals that it is highly anisotropic, and that time averaging of the source does not substantially randomize it. This may introduce a relative small source of error (∼1%) into a single tomographic image. However, when considering time-varying ambient noise imaging, which aims to resolve a fraction of a percent of changes in the crust over short distances (as within the width of a of fault zone) and short periods (months-1 year), the source anisotropy error is significant and needs to be accounted for.
The source anisotropy in the Pacific Ocean is harder to model and quantify because of the inherent complexity of the coastal reflection process. However, the observed repeated swell patterns suggest that the source distribution would be anisotropic as well even after time averaging. Modeling of coastal reflection and independent measurements of source distribution is necessary for constraining the source anisotropy in the entire ocean.
Acknowledgements
The work presented here is based in part on work done in collaboration with Dr Michael Longuet-Higgins, Dr Frank Webb, Dr Nicholas Graham, Dr Robert Clayton, and Dr Cathleen Jones. The author wishes to thank Dr Anthony Sibthorpe of the Jet Propulsion Laboratory for his helpful suggestions. The author wishes to also thank the reviewers and editor for their thorough review. This research was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration and funded through the National Science Foundation Geophysics Program, Project # EAR-0838247, and through internal Research and Technology Development program.



Vous devez vous connecter pour continuer.
S'authentifier