1 Introduction
Mountain ranges are key environments in global and regional biogeochemical cycles. They are the main sources of dissolved matter (including nutrients such as N and Si) provided to the oceans by the continents (Meybeck, 1976, 2003), and they are particularly active in the continental weathering budget and associated CO2 consumption that control the climate over the geological timescale (e.g., Gaillardet et al., 1999; Godderis et al., 2017; Raymo and Ruddiman, 1992; Gaillardet et al., 1999; West et al., 2012). Moreover, these environments are occupied by 1480·106 inhabitants (∼20% of the world population) over 25% of the continents (Meybeck et al., 2001). They are, therefore, particularly sensitive to both water resource quality and quantity. However, global estimates of continents and mountains dissolved fluxes are generally based on the fluxes of major rivers (Meybeck, 2003; Milliman and Farnworth, 2011), and local, small equatorial rivers are generally misrepresented, because of the low availability of river chemistry data.
The Andes are the second main orogenic area in the world; however, estimates of hydrochemical budgets for this mountainous range are limited and generally focus on its eastern slope, in the Amazon basin (e.g., Armijos et al., 2013; Baronas et al., 2017; Bouchez et al., 2017; Dellinger et al., 2015; Guyot et al., 1993, 1996; Moquet et al., 2011, 2016; Torres et al., 2015, 2017 and references within) or in other Andean rivers, such as the Pilcomayo (Smolders et al., 2004). By contrast, geochemical information on Pacific Andean rivers in Ecuador and Peru is limited and scarce. This is mainly due to the difficulty in monitoring the abundant number of rivers in this area. According to a global discharge-TDS (total dissolved solids) relationship, the non-monitored Pacific basin TDS flux in Ecuador and Peru is estimated at ∼30 Mt·yr–1 (Milliman and Farnworth, 2011). In situ hydrochemical data available in these regions focused on the local scale in various environments, as in glaciers in Peru (Fortner et al., 2011) and Argentina (Leon and Pedrozo, 2015), or in basins impacted by mining activity in Ecuador and Peru (e.g., Betancourt et al., 2005; Skierszkan et al., 2016). Only one TDS budget has been reported at the outlet of a Pacific Andean river in this area by Armijos et al. (2013) in the Esmeraldas basin. Considering the great importance of Pacific sea margin productivity (e.g., Mollier-Vogel et al., 2012), it is crucial to estimate fluxes of solutes delivered by rivers to this area to better estimate the availability of nutrient inputs and to better constrain regional elemental cycles. Moreover, the hydrology of this region is particularly affected by the El Niño Southern Oscillation (ENSO) events (e.g., Morera et al., 2017; Rau et al., 2017a). Therefore, through the study of concentration vs. discharge relationships (“C–Q relationships”), the sensitivity of dissolved matter production to changes in hydroclimatological conditions can be determined.
In the present study, we present inorganic dissolved matter fluxes in the Andean Pacific basins based on discrete sampling for solute measurements at 23 stations along the Pacific coast, from Ecuador to southern Peru. Moreover, we describe the TDS variability during the hydrologic cycle based on monthly samples for solute concentrations acquired between 2007 and 2010 at five gauging stations (SNO-HYBAM database). Based on this unedited database, we identified the main factors controlling TDS production as a function of time and space discharge variability in Andean rivers along the Pacific coast. More specifically, we first discuss the C vs. Q relationship of solute concentrations during the hydrologic cycle at the monitored stations. Second, we discuss the discrete TDS and solute-specific flux distributions along the north-south climate gradient. We finally estimate a TDS Pacific basins budget, and we compare it with the Andean basins budget of the Amazon.
2 Studied area
The 28 sampled basins are located on the western slope of the Andes, between 0.5°N and 18°S and 80.5°W–70°W, and along 2400 km of the Pacific coast from Ecuador to southern Peru. All headwaters of the studied basins are in the Andes and reached a maximum elevation of ∼6500 m.a.s.l., and their outlets are located along the Pacific coast (Fig. 1, Table S1). The studied basins cover between 0.8 and 19.6 × 103 km2 and represent approximately 40% of the total Pacific coast drainage area for Ecuador and Peru and approximately 54% of the Andean domain of this area (> 500 m.a.s.l.) (Table S1).
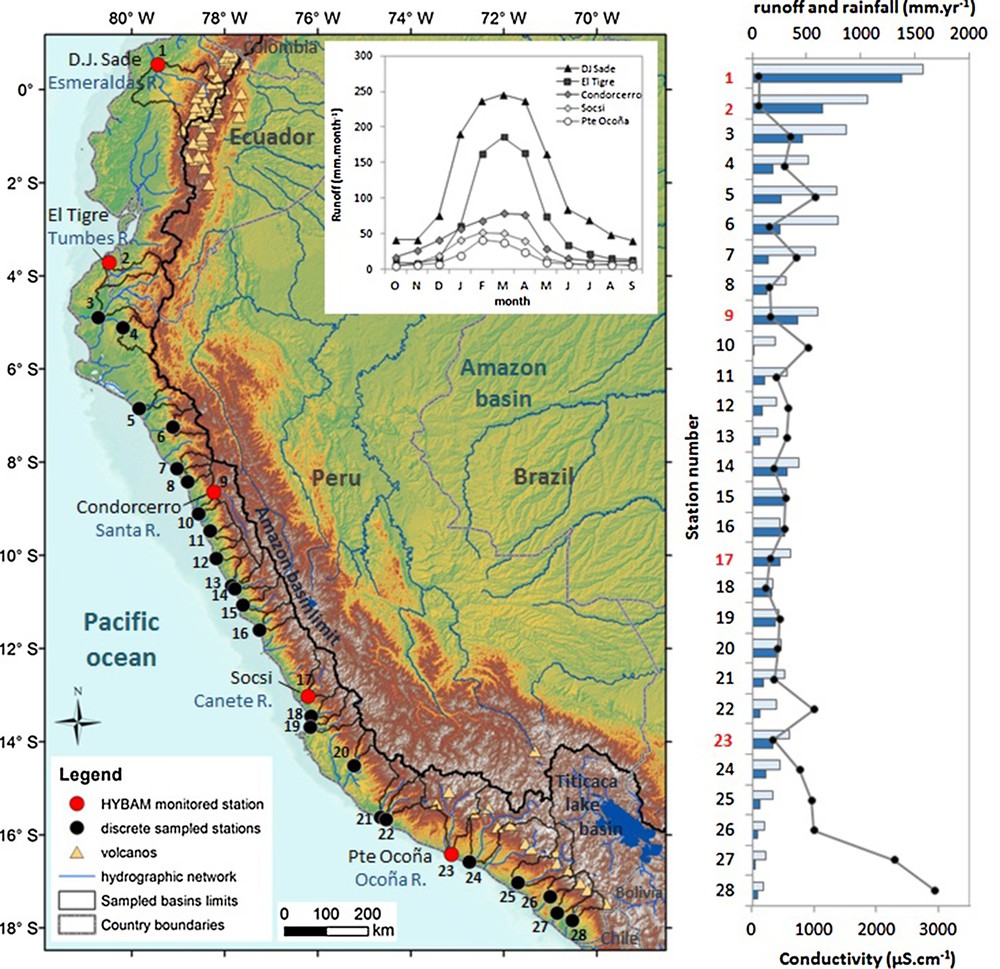
Location map of the discrete sampled and monitored Pacific Rivers in Ecuador and Peru. Mean monthly runoff of Esmeraldas, Tumbes, Santa, Cañete and Ocona rivers at monitored stations (covering the years 2007–2011). Variation of annual rainfall (light blue bars; TRMM), annual runoff (dark blue bars; this study, Lavado Casimiro et al., 2012, Senamhi database) and conductivity at each sampled stations. The red numbers correspond to HYBAM monitored stations. List of rivers (Table S1): 1–Esmeraldas, 2–Tumbes, 3–Chira, 4–Piura, 5–Reque, 6–Jequetepeque, 7–Moche, 8–Viru, 9–Santa, 10–Lacramarca, 11–Casma, 12–Huarmey, 13–Fortaleza, 14–Pativilca, 15–Huaura, 16–Chancay, 17–Cañete, 18–Chincha/San Juan, 19–Pisco, 20–Grande, 21–Acari, 22–Yauca, 23–Ocoña, 24–Camana–Majes, 25–Tambo, 26–Osmore, 27–Locumba and 28–Sama.
According to the 1:1,000,000 geological map of Ecuador (Baldock, 1982) and Peru (INGEMMET, 1999), the studied basins drain several types of lithologies that are variably dominated by volcanic rocks, sedimentary rocks, and plutonic and metamorphic rocks (Table S2, supplementary material). Volcanic rocks (e.g., andesites, basalts, and dacites) are present in all studied basins and cover between 8% and 70% of the basin, with a lower covered area in the central basins between the Santa and Chancay basins. However, active volcanos are only present in the Esmeraldas basin (Ecuador), as well as the southern basins in Peru from Ocoña to Sama basins. Plutonic and metamorphic rocks generally represent between 13% and 34% of the sampled basins. Silico clastic sedimentary rocks cover is highly variable, and represents between 11% and 74% of the sampled basins. When they are sensed, carbonates cover only a small part of the basins. With a relative surface ranging between 1% and 7% of the basins area, this lithology is significant only in the Tumbes, Cañete, and Chincha basins. The evaporite outcrop is not significant in the studied basins. However, even if carbonates and evaporites are not reported in lithological maps, they can occur in Andean formations (Rosas et al., 2007) or appear as neoformations in arid and semi-arid basins, similar to the Upper Madeira basins (Guyot et al., 1993; Magat, 1981). According to the Peruvian mining map (INGEMMET: geocatmin.ingemmet.gob.pe), pyrite is present in most of the studied basin; however, its relative abundance is not quantified.
The climate of Ecuadorian and Peruvian Pacific andean slopes depends on large-scale circulation patterns associated with the Andes cordillera, contrasting oceanic boundary conditions and landmass distribution (Garreaud et al., 2009). Rainfall is more abundant along the Ecuadorian and northern Peruvian coast and declines towards the south, where conditions of extreme aridity occur (Fig. 1; Garreaud et al., 2009; Rutlland et al., 2003). According to the TRMM rainfall data (1998–2009 period; freely downloaded from http://www.geog.ucsb.edu/∼bodo/TRMM/), the mean rainfall for these studied basins ranges from 1570 mm·yr–1 in the Esmeraldas basin to 107 mm·yr−1 in the Sama basin, located at the extreme North and extreme South of the studied area, respectively (Fig. 1; Table S1). The studied basins are influenced by a strong rainfall seasonality and exhibit a decreasing latitudinal gradient in mean annual rainfall from north to south (Fig. 1). In addition, a rainfall gradient is observed following the elevation on the west–east axis. According to the Köppen–Geiger climate classification, semi-arid conditions are found along the Peruvian Pacific coast at low elevations with an increase in mean annual rainfall with elevation up to 1500 m.a.s.l. (Lavado et al., 2012; Rau et al., 2017a). The El Niño Southern Oscillation (ENSO) also has an important influence on interannual precipitation and runoff variability along the Ecuadorian and northern Pacific coasts (Bourrel et al., 2015; Lavado and Espinoza, 2014; Rau et al., 2017a). During warm episodes (El Niño), rainfall and runoff are higher than normal at low elevations and drier at high elevations. During cold episodes (La Niña), the normal pattern is enhanced, and there are drier than normal episodes along the Ecuadorian and northern Peruvian coasts. Strong ENSO events were not observed during the studied period, according to the Oceanic Niño Index. The annual rainfall gradient is associated with a runoff gradient ranging from 25 to 1383 mm·yr−1 from southern to northern basins (Fig. 1, Table S1).
In Peru and Ecuador, the population is mostly concentrated along the Pacific slope, especially along the ocean coast. While mining activity is present in most of the studied Pacific basins (e.g., Cuba et al., 2014 and INGEMMET website: http://www.geocatminapp.ingemmet.gob.pe/), urban, agricultural, and industrial activities are mostly concentrated along the Pacific coast near the main cities. Thus, in most cases, studied basins do not include them because the gauging station is located upstream of the populated coastal areas (Rau et al., 2017b). Mining activity can affect the chemistry of the Pacific rivers (e.g., Betancourt et al., 2005); however, the dissolved load produced in mining areas must be considered as a potentially enhanced process for local weathering associated with acid mining drainage, for example, and not as an external solute input into the hydrosystem.
3 Material and methods
We present the TDS and major element concentrations measured in 28 rivers. 23 rivers were sampled between 1 and 11 times and 5 rivers (Esmeraldas, Tumbes, Santa, Cañete, and Ocoña Rivers) were monitored by the HYBAM monitoring program framework following a monthly sampling frequency between 4 and 10 years (Table S1). All data presented here are available for free download on the SNO-HYBAM website (http://www.ore-hybam.org). The description of the hydroclimate data source, of the hydrochemistry acquisition method, of the flux calculation and of the atmospheric correction methods are reported in supplementary material S1.
4 Results
4.1 Hydrology
Annual runoff increases from 188 to 1382 mm yr–1along the Pacific coast following a south-north gradient (Table S1; Fig. 1). According to the database, the 28 sampled rivers produced a total discharge of approximately 59 km3·yr−1, which corresponds to ∼49% of the Ecuadorian and Peruvian Pacific rivers’ total discharge (∼89% of the Peruvian R. discharge and ∼32% of the Ecuadorian R. discharge) (Autoridad Nacional del Agua, 2012; Milliman and Farnsworth, 2011; Table S1). All gauging rivers respond to homogenous unimodal seasonality, with a higher discharge between December and May (approximately 80% of the annual river discharge) and a low water stage during the June–November period. The seasonality index (SI = (Qm max−Qm min)/Qm mean, with Qm the monthly discharge) varies from 1.7 to 2.8 in the five studied basins.
4.2 Hydrochemistry spatial variability
The 28 sampled rivers range from neutral to slightly alkaline, and exhibit pH values from 6.6 to 7.8. The annual average electrical conductivity and TDS concentration are highly variable throughout the studied area and range between 122 and 2940 μS·cm−1 and between 107 and 1915 mg·L−1, respectively. These values are equivalent to or higher than the global riverine concentration average (∼100 mg·l–1; Milliman and Farnsworth, 2011). Conductivity is highly correlated to TDS concentration (R2 = 0.96; P < 0.001; TDS = 0.63 × cond. + 48 with TDS in mg·L−1) (Table S3; Fig. S2). The two highest values (cond. > 2290 μS cm−1; TDS > 1400 mg·L−1) are recorded in the two southern basins (Locumba and Sama Rivers), which are the driest basins, while all the other values exhibit a conductivity and a TDS concentration less than 1000 μS cm−1 and 600 mg·L−1, respectively. The conductivity (and TDS concentration) followed a north–south gradient, a general trend inversely proportional to the annual runoff (Fig. 1, S3). Interestingly, the Cl−, SO42−, Na+, Ca2+, Mg2+ and K+ concentrations are highly correlated with the TDS concentration (R > 0.89; P > 0.001), while Si and HCO3− are significantly correlated, but at a lower level (For HCO3–,R = 0.59; for Si, RSi = 0.72; P > 0.001). This observation implies that the concentrations of all solutes tend to increase together from north to south (Fig. S3 in supplementary material). Cl− and SO42−concentrations vary by a magnitude > 100 (magnitude = maximum concentration/minimum concentration). TDS, Na+, Ca2+, Mg2+, and K+ vary by magnitudes of 14 to 32, and the HCO3− and Si concentrations vary only by a magnitude of 6 and 7, respectively, while the runoff varies by a magnitude of 54 along the coast. However, the relative contribution of each element to the anionic or cationic charge is not homogenous along the climate gradient. The ternary diagram (Piper diagram) is often used as a diagnostic tool to characterize water (Fig. S4A in supplementary material). The sampled rivers exhibit contrasting water types. In the ternary cation diagram, Mg2+ fluctuates moderately, and represents 10%–28% of the cationic charge. K+ accounts for only 1%–6% of the cationic charge. Ca2+ dominates the cationic charge in northern basins, while Na+ dominates the cationic charge in southern basins. In the ternary anion diagram, bicarbonates dominate the anionic charge in northern basins, while the southern basins generally exhibit an SO4–Cl type. Some central rivers (Santa and neighboring rivers) are of SO4 type.
4.3 Concentration vs. discharge relationships
At the five monitored stations, the TDS concentration decreases with discharge during the hydrologic cycle (Fig. 2), showing a typical dilution/concentration pattern. This behavior is observed for all major elements concentrations in the five sampled rivers, except for the HCO3− and Si concentrations, which remain almost constant in the Santa and Cañete R., respectively. However, with variation coefficients ranging between 0.2 and 0.4, the magnitude of the TDS concentration is lower than that of the daily discharge (0.8–1.3). This implies that the TDS flux is mainly controlled by discharge variability during the hydrologic cycle. This dilution behavior is not homogenous for the major elements considered.

Variation of TDS concentration as a function of discharge at the monitored HYBAM stations. The complete dilution curves (concentration variability of a constant flux) are added for reference.
The slope b of the Ci = a Qb regression indicates the dilution behavior of the element i, with C and Q representing the concentration and daily discharge, respectively, and a and b the regression parameters. When b = −1, the element i is totally diluted and the flux is consequently constant through time. When b = 0, the concentration of the element i remains constant and the flux variability of the element is totally controlled by discharge variability. With values ranging between −0.72 and 0.05, the value of b is very variable according to both the element and the monitored station (Table S4). With values ranging between −0.20 and 0.05, the Tumbes R. exhibits values of b less variable than the four other monitored stations. For these four stations, a similar pattern is recorded, and the values of b increase according to the following hierarchy: Cl−(−0.72 to –0.50) < Na+ (−0.62 to −0.35) < SO42−(−0.48 to −0.40) ∼ Mg2+ (−0.50 to−0.35) < K+ (−0.31 to −0.20) ∼ Ca2+ (−0.36 to−0.21) < HCO3−(−0.41 to −0.09) ∼ Si (−0.17 to −0.01).
The relative proportion of the major elements with respect to the TDS concentration also varies along the hydrologic cycle (Fig. S4B). As observed for the Napo and Pastaza basins along the Amazonian slope (Moquet et al., 2011), Ca2+, Mg2+ and Na+ + K+ co-vary proportionally and represent approximately the same proportion as the cationic charge in Esmeraldas R. In the Santa and Cañete R., the cationic charge is dominated by Ca2+ during the rainy season, and the relative proportion of Na+, K+ and Mg2+ increase during the dry season. In the Ocoña and Tumbes R., the relative proportion of Mg2+ remains relatively constant during the hydrologic cycle (Mg2+ Ocoña ∼ 10%; Mg2+ Santa ∼ 20%). Ca2+ dominates the cationic charge during the rainy season, and the Na+ + K+ proportion increases during the dry period. Concerning the anionic charge, HCO3–dominates the anionic charge in the Esmeraldas and Tumbes R. However, the relative contribution of SO42− and Cl− increase during the dry period. SO42− dominates the anionic charge of the Santa R., but the relative contribution of HCO3− increases during the rainy period. In the Cañete and Ocoña R., HCO3− dominates the anionic charge during the rainy period and the contributions of the SO42− and Cl− increase during the dry period.
5 Discussion
5.1 Concentration vs. discharge relationships
The distribution of b generally responds to a typical dilution/concentration pattern, as recorded in numerous rivers in mountainous environments (e.g., Ollivier et al., 2010; Zakharova et al., 2005). This behavior shows that the reactions are either kinetically limited, when the minerals involved are present over the entire watershed (as silicate minerals, for example), or when they are limited by the availability of weathered minerals, which dominate the solutes production. The values of b measured in this study are similar compared to the observations performed on the eastern slope of the Andes (Torres et al., 2015–for the catchment MLC, which is the same surface area range as the studied basins; Bouchez et al., 2017; Moquet et al., 2016). Indeed, with a slope b generally lower than –0.4, the elements characteristic of evaporite inputs (Cl−, Na+, and SO42−) are highly diluted during the hydrologic cycle. As observed for the Marañón and Ucayali basins in the upper Amazon (Moquet et al., 2016), this implies that evaporite sources tend to produce a constant flux independently of discharge variability. This is consistent with the fact that evaporites (for these elements) or pyrites (for SO42−) are generally local formations and easily dissolved. Thus, their production depends on local weathering processes and on whether the flux is diluted by the runoff contribution from the remaining part of the basin.
TDS and the other solutes (HCO3−, Mg2+, K+, Ca2+, SiO2) also exhibit a dilutional pattern, but with values of b generally higher than –0.5, as generally recorded in most rivers at the global scale (Gislason et al., 2009; Walling and Webb, 1986). This shows that the dissolved flux produced by other weathering endmembers (carbonates, silicates) mainly responds to discharge variability in the basin. As observed by Baronas et al. (2017) under the Andean Amazon catchment of the Madre de Dios, this observation highlights that major elements exhibit significant C–Q relationships and depend on various degrees of dilution with increasing runoff under Andean catchment conditions. At the large river basin scale (Bouchez et al., 2017; Moquet et al., 2016), or at a smaller basin scale (Madre de Dios R.; Torres et al., 2015), the Andean basins generally exhibit a value of b smaller than those downstream, because less concentrated lowland water would dilute more chemostatic mountain inputs. Interestingly, the values of b recorded over the Pacific basins are commensurate to those recorded over the rivers monitored near the Amazonian Andes outlet. However, even though the values of b recorded in both Pacific basins and Amazonian Andean basins are all generally higher than –0.5 (Baronas et al., 2017; Bouchez et al., 2017; Moquet et al., 2016; Torres et al., 2015; 2017), they are variable. The C–Q relationship (and the related value of b) can either depend on conservative water mixing (e.g., a tributary confluence or groundwater vs. surface mixing; Baronas et al., 2017; Bouchez et al., 2017; Kirchner, 2016; Torres et al., 2015, 2017) and parameters that control the mean reaction rate, such as temperature (Li et al., 2016), lithological weatherability (Ibarra et al., 2016), water availability (West, 2012) and flow path length (Maher and Chamberlain, 2014). These studies were generally conducted over monolithological basins to identify the model governing the C–Q relationship. In this case, considering all Andean data available (Batonas et al., 2017; Bouchez et al., 2017; Moquet et al., 2016; Torres et al., 2015, 2017), no quantifiable relationship between b and either annual runoff, elevation or lithology is observed. The absence of relationship between b and the basin characteristics can be attributed to the fact that the shape of the C–Q relationship for each solute depends on a mixing of various sources. Considering the lithological heterogeneities over all these areas, their relative contribution to each solute concentration and their influence on the respective values of b can vary from one sub-basin to another. This result shows that even under a given geomorphological domain (an active mountain, in this case), contrasting spatial runoff variability does not control the variability of b for these solutes (HCO3−, Mg2+, K+, Ca2+). Therefore, under orogenic context, water availability alone does not control the shape of the C–Q relationship. The mineral weatherability and flow path of each individual source (lithologies) need to be considered.
5.2 Sources of major ions
According to the atmospheric correction model applied to the monitored station data, atmospheric inputs contribute to less than 6% at all sampled stations. Atmospheric inputs generally contribute less than 5% of the individual solutes Cl−, SO42−, Na+, Ca2+ and Mg2+, except for the three northern basins, where this proportion can be higher than 15% (Table S5). K+ is more sensitive to atmospheric inputs, but generally atmospheric inputs contribute to less than 15% of the K+ concentration. Indeed, these atmospheric inputs are generally negligible for solute production in these basins. Throughout the 28 sampled rivers, the identification of the main lithological sources controlling dissolved load concentrations is not straightforward. For example, the Ca2+ concentration is significantly correlated (P < 0.001) with both HCO3− and SO42− along the Pacific coast, and respectively follow the CaSO4 (gypsum) and CaCO3 dissolution lines (Fig. S5A and S5B). Consequently, it is not possible to quantify the relative part of Ca2+ released by the evaporites and the carbonate weathering based only on major element concentration variability. Moreover, the lithological map is not precise enough to report all the lithological formations that contribute to dissolving loads, especially for carbonates and evaporites. However, considering that Cl− is a qualitative index of halite (NaCl) dissolutions, it can be observed that evaporite inputs tend to increase from north to south (Fig. S5C; S6). Indeed, the relative mass abundance of Cl– increases from 4% to 29% following the north–south runoff gradient and is particularly high for basins located south of Cañete basins, where Cl− represents more than 15% of the TDS (Fig. S5). This result highlights that in the context of dry basins, evaporite inputs are related to climate conditions, i.e. a semi-arid context would favor evaporite formation and particularly affect the riverine hydrochemistry. Silicon is only released by silicate minerals, so this element can be considered as a good proxy of silicate weathering distributions (e.g., Maher and Chamberlain, 2014). Interestingly, in a fashion similar to TDS concentrations, Si concentrations follow a global north–south increase, according to the runoff gradient (Table S3; Fig. S3c, f). This result is interesting because it suggests that, in semi-arid conditions, the silicate weathering rate is less dependent on water availability and, consequently, silicates in this environment are highly reactive. However, drier basins in the southern area (from Ocoña to Sama) are also characterized by the presence of active volcanos (Fig. 1). Hydrothermal inputs associated with volcanism can therefore explain the high Si concentration recorded in these rivers (Hurwitz et al., 2010). The combination of low discharge with high hydrothermal inputs can consequently explain the high Si concentrations recorded in this area (Fig. S3c, f). The highest HCO3− and Ca2+ concentrations are recorded in three regions along the Pacific coast, which corresponds to 13 rivers: between the Chira and Reque basins, between the Lacramarca and Chancay Rivers and in the southern basins from the Camana to the Sama Rivers (Fig. S3a, b, d, e). HCO3− and Ca2+ are both released in natural water by silicate and carbonate weathering. In some cases, the lithological information can help to estimate carbonate inputs (e.g., Li and Bush, 2015; Sun et al., 2010). Indeed, higher Ca2+ and HCO3− concentrations would be expected in basins where carbonates are present because of their higher sensitivity to weathering processes (e.g., karst formations in the Cañete R.; Guyot et al., 2014). However, no clear relationship between HCO3− and Ca2+ concentrations and carbonate outcrop cover (extracted from lithological maps) is recorded for the studied basins (Tables S2 and S1).
5.3 Control of TDS budget
Spatially, we observed a north–south increase in TDS concentration with decreasing discharge value (Fig. 1 and S3). This gradient may be attributed to an increase in evaporites (either neogenous or unreported by the lithological map), because the SO42− + Cl− concentration increase together with the TDS concentration (Fig. S5). However, the magnitude of the TDS concentration is lower than that of the annual discharge (and annual runoff) of sampled rivers. Spatial discharge (and spatial runoff) distribution is consequently the first-order parameter that controls the TDS flux (and spatial specific flux) variability along the Pacific coast (Fig. 3, Fig. S5A). The range of the specific TDS flux is large and varies from 5 to 182 t·km–2·yr−1. This range is comparable to the values reported by Milliman and Farnworth (2011; based on the Meybeck, 1994 database) for wet young tropical mountainous rivers. The specific flux values are generally lower than those measured over the eastern Andes, but follows the same general trend as a function of the annual runoff (Fig. 3). The TDS specific flux follows a power-law relationship with the runoff and exhibits a slope of 0.46, which shows that the increase in runoff does not proportionally affect the TDS specific fluxes due to the diversity of the individual solute behaviors.
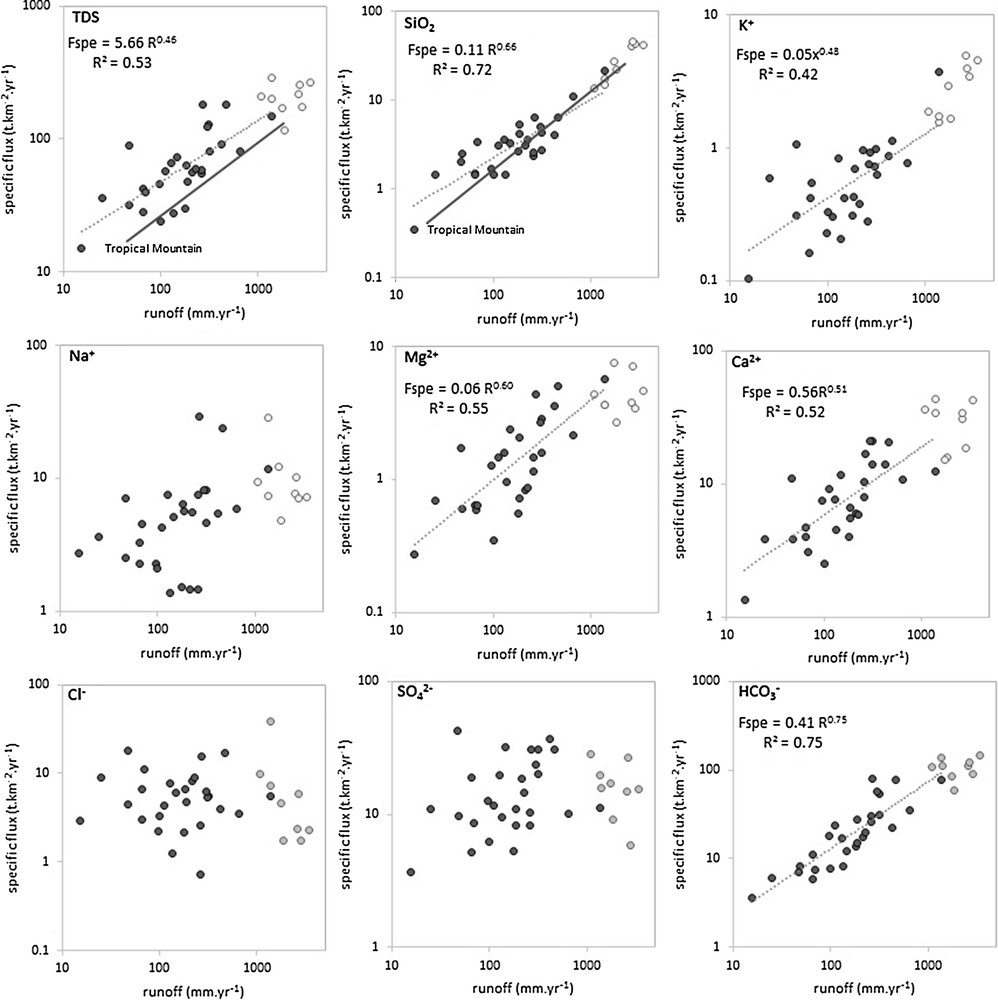
Annual TDS and individual solutes specific fluxes vs. annual runoff over the 28 sampled stations. Values from Andean basins (Aguarico, Coca, Jatunyacu, Napo, Pastaza, Santiago, Upper Maranon, Huallaga, Ucayali) are also reported for reference (Moquet et al., 2016). For TDS and SiO2, the relationship reported by Milliman and Farnworth (2011; based on Meybeck, 1994) for tropical wet young mountains is also shown for reference.
The specific fluxes of individual solutes exhibit a significant (P < 0.01) power-law relationship with runoff for most of the elements. These relationships exhibit a slope higher than 0.65 for SiO2 and HCO3− and a slope between 0.48 and 0.6 for K+, Mg2+ and Ca2+ (Fig. 3). Interestingly, as observed for TDS, these specific flux values are lower than those observed in the eastern Andes, but follow the same general trend as a function of runoff (Fig. 3). The SiO2 specific flux vs. runoff relationship is particularly close to the regression performed over the wet young tropical mountainous rivers and, therefore, confirms this empirical relationship (Milliman and Farnworth, 2011). Conversely, Cl−, SO42− and Na+ (Fig. 3) do not exhibit a significant relationship, which shows that the evaporite dissolution budget is not sensitive to runoff distributions throughout the studied area. This confirms previous observations made based on a C–Q relationship for individual catchments; i.e. these lithologies, which are particularly sensitive to dissolution, are not homogenously distributed throughout the studied area. When they are present, the solute production is independent of the runoff intensity received by the basin. The respective response for each basin, in terms of solute export, can be contrasted according to the occurrence and/or absence of these lithologies. The specific fluxes for elements purely released by silicates (SiO2) or by silicates and carbonates (HCO3−) increased northward almost proportionally to runoff. This observation highlights that these lithologies are particularly sensitive to hydroclimatological conditions. This region is affected by drastic climate variability from interannual (ENSO events; Morera et al., 2017; Sanabria et al., 2017) to multi-millennium timescales (Carré et al., 2012; Jorneli et al., 2009). Together with the C–Q relationship analyses, this result suggests that the Si and HCO3− fluxes respond almost proportionally to rainfall variability, following both the rainfall distribution changes along the Pacific coast and the annual to inter-millennial intensity variations on the scale for each individual catchment. This is explained by the fact that, under an active mountain context, the weathering processes are controlled by thermodynamic limit conditions (Maher and Chamberlain, 2014) and, more generally, that runoff is a dominant process that controls continental weathering (e.g., Hartmann et al., 2009; Meybeck, 2003). The fact that K+, Mg2+ and Ca2+ exhibit intermediate slope values is probably due to the diversity of their sources, including carbonates, silicates and evaporites which contrastingly respond to the runoff spatial variability.
5.4 Solute input into the Pacific Ocean
Concentration values, available over the sampled Peruvian and Ecuadorian rivers, allow the estimation of total TDS and individual solute fluxes exported annually by the Ecuadorian and Peruvian coasts to the Pacific Ocean. This estimate is performed for basins between northern Ecuador (Santiago R.) and southern Peru (Caplina R.), and is representative of the annual budget not influenced by an ENSO event. The sampled rivers produce ∼15 Mt·yr−1 TDS for a total discharge of ∼59 km3·yr−1 and a total area of 157 103 km2. Discharge from the sampled rivers correspond to approximately 49% of the total discharge from the Ecuadorian and Peruvian Pacific rivers (ANA, 2012; Milliman and Farnsworth, 2011; Table S1). Considering that the sampled rivers are representative of the Pacific rivers, this area could produce ∼30 Mt·yr−1 over ∼400 103 km2 (Table S1). Interestingly, this estimate is equal to Milliman and Farnsworth's (2011) estimate for the same area, which was based only on a first order estimate from a discharge vs. flux relationship interpolation. According to global budget estimates, the studied area contributes to less than 1% of the TDS flux annually exported to all oceans (3250 and 3800 Mt·yr−1; Meybeck, 1976 and Milliman and Farnsworth, 2011) and to less than 2% of the Indian and the Pacific oceans inputs (1775 Mt·yr−1; Milliman and Farnsworth, 2011). In terms of TDS specific flux, this area produces ∼70 t·km–2·yr−1, which is about two times higher than the global mean value (30 to 50 t·km−2·yr−1; Meybeck, 1976, 2003; Milliman and Farnworth, 2011). This shows that, even under low rainfall conditions, this region is active in terms of solute production. Individual solute fluxes (and specific fluxes) vary from 0.3 Mt·yr−1 (0.8 t·km−2·yr−1) to 11 Mt·yr−1 (27 t·km−2·yr−1) according to the following hierarchy: HCO3– > SO42− > Ca2+ > Na+ > Cl− > SiO2 > Mg2+ > K+ (Table 1; Fig. 3C). This budget is representative of the annual budget not influenced by an ENSO event. During El Niño events, the rainfall and discharge of the northern rivers can increase by one order of magnitude with respect to the average (e.g., Tumbes and Piura basins; Morera et al., 2017), whereas the southern basins (south of 7°S) exhibit a very low sensitivity to these events (Morera et al., 2017; Rau et al., 2017a). If the C vs. Q relationships for individual rivers and the annual specific flux vs. runoff relationships along the coast are stationary during these events, HCO3− and SiO2 fluxes (and specific fluxes) would increase almost proportionally to the increase in discharge. The associated K+, Mg2+, and Ca2+ fluxes would also increase with discharge, but to a lower relative extent in comparison, and Cl–and SO42− exports would be almost insensitive to these climate events.
TDS and solutes fluxes of Andean Pacific basins (this study) and Andean Amazon basins (Moquet et al., 2016).
| Units | Flux | Units | Specific flux | ||||
| Pacific basins | Amazon basins | % Pacific basins (/total) | Pacific basins | Amazon basins | |||
| Area | 103 km2 | 398 | 581 | 41 | |||
| Discharge | 106 m3·yr−1 | 120 | 715 | 14 | mm·yr−1 | 301 | 1231 |
| TDS | Mt·yr−1 | 28 | 121 | 19 | t·km−2·yr−1 | ||
| Cl− | 2.3 | 7.8 | 23 | 19 | 11 | ||
| SO42− | 5.6 | 10 | 36 | 47 | 14 | ||
| Na+ | 2.7 | 6.5 | 29 | 22 | 9.1 | ||
| Ca2+ | 3.2 | 21 | 14 | 27 | 29 | ||
| Mg2+ | 0.76 | 2.2 | 26 | 6.3 | 3.0 | ||
| K+ | 0.34 | 1.0 | 26 | 2.9 | 1.4 | ||
| HCO3− | 11 | 65 | 14 | 90 | 91 | ||
| SiO2 | 2.0 | 7.9 | 20 | 16 | 11 |
5.5 Comparison with eastern side of the Andes and total Andean budget between ∼1°N to ∼18°S
The Andean Amazon basins located at the same latitude (Solimões Andean tributaries: Napo, Maranon and Ucayali Rivers) produce a TDS flux of approximately 123 Mt year–1, with a total annual discharge of 695 km3·yr−1, over a surface of 581 km2 (budget extracted from Moquet et al., 2016). Therefore, the Andean Pacific rivers produce approximately 20% of the TDS flux and 14% of the discharge over an area that represents approximately 41% of the total western and eastern Andean area located between ∼1°N and ∼18°S (Fig. 4B). This budget is valuable in the absence of ENSO events. This result shows that even if the Pacific slope of the Andes receives a low amount of rainfall compared with Amazonian basins, this area will significantly contribute to the TDS annual production of the Andes, almost proportionally to the relative discharge (Fig. 4A). The flux and the specific flux of each individual element is also systematically lower in the Pacific basin budget than in the Atlantic basin budget (Fig. 4C; Table S3). The solute flux ratios between eastern and western slopes vary from 2 to 6 (ratio = Fx Amazon/Fx Pacific, where Fx is the flux of the element x). Higher ratios are observed for HCO3− and Ca2+ due to the high contribution of carbonate weathering to TDS export over the Amazonian slope (Moquet et al., 2011). This ratio is lower for SO42−, which shows that Pacific basins are particularly active in term of SO42− production linked to evaporite and/or sulfide weathering. TDS exports also differ between the two Andean sides, in terms of mean chemical composition. On both side of the Andes, the HCO3− dominated the TDS composition; however, this element contributes to more than 50% of the TDS over the Amazonian Andes, while it contributed to approximately 40% in the Pacific basin. This is probably due to higher contribution of carbonate weathering over the Amazonian Andean watersheds. In Pacific basins, the SO42− largely contributes to TDS production (20% of the TDS), while it contributes to only 8% of the TDS in the Andean Amazon basins. This observation shows that processes that release SO42− are highly active over Pacific basins. Over the Amazonian slopes, Ca2+ contributes to 17% of the TDS, while it contributes to only 12% over the Pacific basins, illustrating the dominance of carbonate weathering over the Amazonian basins. With 7% of the TDS, SiO2 contributes commensurately to TDS over both sides of the Andes. Finally, K+ and Mg2+ contribute less than 2% of the TDS over both sides of the Andes.
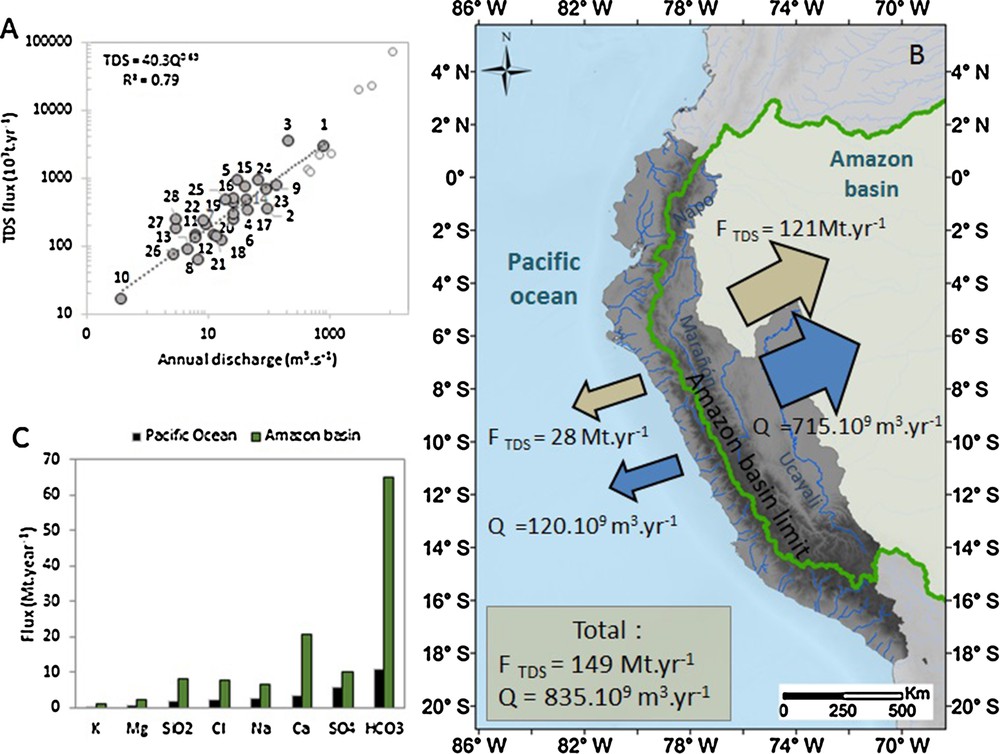
A. Relationship between net discharge and net TDS flux in the sampled Pacific basins (Values from Andean Amazon basins (Aguarico, Coca, Jatunyacu, Napo, Pastaza, Santiago, Upper Maranon, Huallaga and Ucayali) are also reported for reference (Moquet et al., 2016). B. Net budget of TDS and discharge fluxes of the Andes between 1°N and 18°S for western (398.103 km2) and eastern (581.103 km2) slopes. C. Net flux of individual solutes produced by the Andes towards the Pacific Ocean and the Amazon basin between 1°N and 18°S.
6 Conclusion
This study presents, for the first time, the geochemical water measurements from five monthly monitored rivers and 23 discrete sampled rivers distributed along a runoff/rainfall gradient of the Pacific coast, from Ecuador to South Peru.
At the five monitored stations, the C vs. Q relationships respond to a dilution pattern for all elements, but under different extents. As observed in the Amazonian context, the elements that are particularly submitted to dilution behaviors are those related to evaporite dissolution. For the other elements, the values of b are variable but closer to 0. For these elements, no clear relationship between b and the geographical characteristics are observed over the considered Andean basins (Pacific and Amazonian basins), likely due to basin source heterogeneities. This result shows that under orogenic domains, water availability is not the main controlling factor for the shape of the C–Q relationships.
Along the 28 sampled rivers, TDS, Ca2+, HCO3−, K+, Mg2+, and SiO2 specific fluxes decrease southward and are, on the first order, controlled by runoff distribution. However, for TDS, Ca2+, K+ and Mg2+ this first order is perturbed by the relative contribution of evaporite weathering, which increases southward. As shown by SiO2 and HCO3− budgets, silicate and carbonate weathering specific fluxes are almost proportionally controlled by runoff and are, therefore, more sensitive to climate variability (as ENSO events for example). Evaporite neoformation in the southern Peru semi-arid context could explain the north–south gradient of Cl− and SO42− concentrations.
The sampled rivers cover approximately 40% of the land area, as well as 49% of the discharge from Ecuadorian and Peruvian Pacific rivers, allowing estimates of the total TDS flux annually exported by the Andes to the Pacific Ocean between 1°N and 18°S in the absence of ENSO events. According to these results, this area contributes to approximately 30 Mt·yr−1 TDS, which corresponds to approximately 20% of the eastern and western Andean TDS production at these latitudes, but contributes a low proportion of the global TDS flux exported to oceans. The TDS specific flux is consequently estimated at ∼70 t·km–2·yr−1, showing that, even under low rainfall conditions, this orogenic context is more active in terms of TDS production than the global average and is commensurate to mountain environments. Individual solute fluxes (and specific fluxes) vary from 0.3 Mt·yr−1 (0.9 t·km−2·yr−1) to 11 Mt·yr−1 (27 t·km−2·yr−1) according to the following hierarchy: HCO3− > SO42− > Ca2+ > Na+ > Cl− > SiO2 > Mg2+ > K+. These budgets are systematically lower than those in the Amazonian Andes at the same latitudes, mainly because of a contrast in terms of rainfall intensity.
Acknowledgments
We thank the two anonymous reviewers for their constructive recommendations under the review process. This work was funded by the French “Institut de recherche pour le développement” (IRD), the French “Institut des sciences de l’univers” (INSU), and the “Observatoire Midi-Pyrénées” (OMP) through the HYBAM Observatory (Hydrogeodynamics of the Amazon basin). We especially thank Pascal Fraizy, Philippe Vauchel, Elisa Armijos, William Santini, Nore Arevalo, the SENAMHI (“Servicio Nacional de Meteorología e Hidrología”, Lima, Peru), the INAMHI (“Instituto Nacional de Meteorología e Hidrología”, Quito, Ecuador), the UNALM (“Universidad Nacional Agraria de La Molina”, Lima, Peru), as well as all members of the Observatory for Environmental Research HYBAM, for providing hydrological, suspended solids, and water chemistry data.


