Wavelet application to the time series analysis of DORIS station coordinates

Zahia Bessissi; Mekki Terbeche; Boualem Ghezali

doi:10.1016/j.crte.2009.03.010

Internal geophysics (Geodesy)

Wavelet application to the time series analysis of DORIS station coordinates
[Application des ondelettes à l’analyse des séries temporelles de coordonnées des stations DORIS]

Présenté par : Michel Petit

Zahia Bessissi ¹ ; Mekki Terbeche ¹ ; Boualem Ghezali ²

¹ Département de mathématiques, faculté des sciences, université d’Oran–Es-senia, BP 1524, El Menaouer, Oran, Algeria
² Centre des techniques spatiales, division géodésie, Arzew, Oran, Algeria

Comptes Rendus. Géoscience, Volume 341 (2009) no. 6, pp. 446-461.

Résumés

Anglais
Français

The topic developed in this article relates to the residual time series analysis of DORIS station coordinates using the wavelet transform. Several analysis techniques, already developed in other disciplines, were employed in the statistical study of the geodetic time series of stations. The wavelet transform allows one, on the one hand, to provide temporal and frequential parameter residual signals, and on the other hand, to determine and quantify systematic signals such as periodicity and tendency. Tendency is the change in short or long term signals; it is an average curve which represents the general pace of the signal evolution. On the other hand, periodicity is a process which is repeated, identical to itself, after a time interval called the period. In this context, the topic of this article consists, on the one hand, in determining the systematic signals by wavelet analysis of time series of DORIS station coordinates, and on the other hand, in applying the denoising signal to the wavelet packet, which makes it possible to obtain a well-filtered signal, smoother than the original signal. The DORIS data used in the treatment are a set of weekly residual time series from 1993 to 2004 from eight stations: DIOA, COLA, FAIB, KRAB, SAKA, SODB, THUB and SYPB. It is the ign03wd01 solution expressed in stcd format, which is derived by the IGN/JPL analysis center. Although these data are not very recent, the goal of this study is to detect the contribution of the wavelet analysis method on the DORIS data, compared to the other analysis methods already studied.

Le thème développé à travers cet article porte sur l’analyse des séries temporelles des coordonnées résiduelles des stations DORIS par la transformée en ondelettes. Plusieurs techniques d’analyse, déjà développées dans d’autres disciplines, ont été employées dans l’étude statistique des séries temporelles géodésiques des stations. La transformée en ondelettes permet, d’une part, de fournir des paramètres temporels et fréquentiels des signaux résiduels et, d’autre part, de déterminer et de quantifier les signaux systématiques tels que périodicité et tendance. La tendance est le changement à moyen ou long terme du signal ; c’est une courbe moyenne qui représente l’allure générale de l’évolution du signal. En revanche, la périodicité est un processus qui se répète identique à lui-même après un intervalle de temps appelé période. C’est dans ce contexte que s’inscrit le thème de cet article qui consiste, d’une part, à déterminer les signaux systématiques par l’analyse en ondelettes d’une série temporelle de coordonnées des stations DORIS et, d’autre part, à appliquer la transformée en paquet d’ondelettes pour le débruitage du signal qui permet d’obtenir un signal bien filtré et plus lisse que le signal original. Les données DORIS utilisées lors du traitement sont constituées d’une série hebdomadaire de jeux de coordonnées résiduelles de huit stations : DIOA, COLA, FAIB, KRAB, SAKA, SODB, THUB et SYPB, conduite entre 1993 et 2004. Il s’agit de la solution ign03wd01 exprimée en format stcd, issue du centre d’analyse IGN/GPL. Bien que ces données ne soient pas les plus récentes, le but de cette étude est de mettre en évidence l’apport de la méthode d’analyse par ondelette des données DORIS par rapport aux autres méthodes d’analyse déjà étudiées.

Métadonnées

Reçu le : 2008-08-25
Accepté le : 2009-03-30
Publié le : 2009-06-01

DOI : 10.1016/j.crte.2009.03.010

Keywords: DORIS, Time series, Wavelet analysis, Period, Tendency, Denoising
Mot clés : DORIS, Série temporelle, Analyse, Ondelettes, Période, Tendance, Débruitage

Affiliations des auteurs :

Zahia Bessissi ¹ ; Mekki Terbeche ¹ ; Boualem Ghezali ²

¹ Département de mathématiques, faculté des sciences, université d’Oran–Es-senia, BP 1524, El Menaouer, Oran, Algeria
² Centre des techniques spatiales, division géodésie, Arzew, Oran, Algeria

@article{CRGEOS_2009__341_6_446_0,
     author = {Zahia Bessissi and Mekki Terbeche and Boualem Ghezali},
     title = {Wavelet application to the time series analysis of {DORIS} station coordinates},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {446--461},
     publisher = {Elsevier},
     volume = {341},
     number = {6},
     year = {2009},
     doi = {10.1016/j.crte.2009.03.010},
     language = {en},
}

TY  - JOUR
AU  - Zahia Bessissi
AU  - Mekki Terbeche
AU  - Boualem Ghezali
TI  - Wavelet application to the time series analysis of DORIS station coordinates
JO  - Comptes Rendus. Géoscience
PY  - 2009
SP  - 446
EP  - 461
VL  - 341
IS  - 6
PB  - Elsevier
DO  - 10.1016/j.crte.2009.03.010
LA  - en
ID  - CRGEOS_2009__341_6_446_0
ER  -

%0 Journal Article
%A Zahia Bessissi
%A Mekki Terbeche
%A Boualem Ghezali
%T Wavelet application to the time series analysis of DORIS station coordinates
%J Comptes Rendus. Géoscience
%D 2009
%P 446-461
%V 341
%N 6
%I Elsevier
%R 10.1016/j.crte.2009.03.010
%G en
%F CRGEOS_2009__341_6_446_0

Zahia Bessissi; Mekki Terbeche; Boualem Ghezali. Wavelet application to the time series analysis of DORIS station coordinates. Comptes Rendus. Géoscience, Volume 341 (2009) no. 6, pp. 446-461. doi : 10.1016/j.crte.2009.03.010. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2009.03.010/

Version originale du texte intégral

1 Introduction

The Doppler Orbit Determination and Radiopositioning Integrated by Satellite (DORIS) system inaugurates a new means of scientific measurement based on the determination of orbit and radiopositioning [8,17]. It is a French civil system conceived and developed by CNES (French Space Agency), GRGS (French Research Group in Space Geodesy) and the IGN (French Mapping Agency) [3].

Since 1990, the beginning of the first DORIS mission, all of the measurements collected by the instruments embarked on SPOT2, SPOT 3, SPOT 4, TOPEX POSEIDON and JASON represent several tens of millions of precise observations placed at the disposal of the scientific community through the International DORIS Service [16].

The initial objectives of the Doris systems were Precise Orbit Determination of Low Earth Orbiting (LEO) satellites, gravity field determination and precise positioning [3] (expected to be at the 10 cm level before launch of SPOT2). In eight years, because of the restoration and installation of new stations and also by the improvement of models and strategies of computation, a significant improvement in the quality of network [7] was carried out, making it possible for the DORIS system to contribute significantly to the realization of the international reference terrestrial frame.

The richness of the measurements collected by the DORIS space system makes it possible today to represent the displacement of the stations on the ground in the form of station coordinate time series. Such series make it possible to detect, starting from analysis methods of observational, instrumental or geophysical parasitic phenomena origins, the local motion study of the stations; some methods are more sensitive to the different types of noises and their levels (autocorrelation function, spectral concentration of Allan variance, etc.) [12]; others are based on the search for periodicity, such as Fourier analysis, Singular Spectral Analysis (SA), Method of Maximum of entropy (MEM) [9], and also the wavelet method used in this article, which treats the non-stationary signals and makes it possible to extract information from the structures and the local irregularities.

The Fourier transform application provides only one piece of information on the total regularity of the signal and does not allow one to easily obtain information located in time. The following idea consists in representing our signal according to time and frequency. One of the first to have applied this principle to Fourier transforms is the physicist Dennis Gabor in 1940. One speaks then about Fourier transforms with windowing of the signal. The basic idea consists in cutting the signal in temporal sections and adapting, on each section, the Fourier transform. This analysis depends on the localisation of the section.

The main inconvenience of this technique is that the length of the bench (the scale) is fixed (Fig. 1) which prevents one from retaining the time-frequency representation and achieving a multiscale/multiresolution. In this case, we use the signal processing wavelet which takes into account the local regularity and makes a kind of zoom in/out on a portion of the signal by playing on the scale factor.

Fig. 1
Difference between the Fourier transform of windowing technique and the wavelet transform.
Fig. 1. Différence entre la transformée de Fourrier à fenêtre glissante et les ondelettes.

In the present article, we present an analysis methodology based on the wavelet technique using times series of DORIS station coordinates provided by the IGN/JPL center [18], and we apply the wavelet packet transform for denoising the signal. Our objective is to provide certain information useful to later geodynamic interpretations.

2 Discrete wavelet analysis

A wavelet is a function $ψ (x)$ of L₂(R) (L₂(R): space continuous functions square integrable having properties of localization and oscillation [6]. Just as the Fourier transform can be defined as being a projection on the basis of the complex exponential, we introduce the wavelet transform as projection on the base of wavelets functions:

TO (a, b) = \frac{1}{\sqrt{a}} \int_{- \infty}^{+ \infty} x (t) ψ (\frac{t - b}{a}) dt

(1)

with: (a, b) ∈R²

Starting from a mother wavelet [15], we can create a Hilbert base of L₂(R) by translation and dilation of mother wavelet $ψ$ :

\{ψ_{a, b} (t) = \frac{1}{\sqrt{a}} ψ (\frac{t - b}{a}), (a, b) \in R^{2}\}

Thus, we break up a signal x(t) in a basis of the Hilbert space L₂(R) defined by the family of functions $ψ_{a, b} (t)$ and the expression of the wavelet coefficients becomes:

TO (a, b) = \int_{- \infty}^{+ \infty} x (t) ψ_{a, b} (t) dt

with

ψ_{a, b} (t) = 1 / \sqrt{a} ψ (t - b / a)

.

Here, a and b represent the scale factor and the translation factor, respectively.

The functions $ψ_{a, b} (t)$ are obtained starting from dilation and translation of the mother function $ψ (t)$ .

A. Grossmann and J. Morlet showed that if $ψ (t)$ is real valued, all of these wavelets can be considered as an orthonormal base, which means that any signal of energy can be written as a linear combination of wavelets $ψ_{a, b} (t)$ [11].

The wavelet coefficients (1) depend on the real a and b. We can decide on an infinite number of values for these two parameters which vary continuously, i.e.: a∈R⁺\{0}, b∈R; we speak therefore about a continuous wavelet transform (CWT), which makes it possible to give us a better description of the pace of the signal. When we have a discretisation of the resolution parameter a and position b, we speak thus about the discrete wavelet transform (a = 2^j, b = k2^j, j, k∈Z²).

The wavelet transform can be also considered as a process of decomposition of the signal into approximations and details; we speak then about the multiresolution analysis.

The concept of the multiresolution is to use several times the wavelet transformation (discrete case) in order to break up the starting signal f into several signals (scale of signal) containing different information. We define thus the family of sub-spaces {Vj} of L₂ (R) which verifies:

V_{j} \subset V_{j + 1} \subset L_{2} \forall j \in Z; \cap V_{j} = {0} \cup V_{j} = L_{2}

The approximation with the resolution j is defined by following projection:

A_{n}^{j} = < f / Φ_{j, n} >

Φ_j,n constitutes a basis of V_j and verifies:

Φ_{j, n} (t) = {(\sqrt{2})}^{- j} Φ (2^{- j} t - n) with j, n \in Z

Φ (t) ∈ V₀ called the mother function or the scale function [10] defined by:

Φ (t) = \sum_{n} h (n) Φ_{- 1, n} = 2^{1 / 2} \sum_{n} h (n) Φ (2 t - n)

with h(n) = <Φ/Φ_-1,n> and Φ_-1,n = 2^1/2 Φ (2t − n).

The loss information during this projection corresponds to f projections on a detail space of Wj, which satisfies: V_j ⊕ W_j = V_j+1, the detail coefficient is defined:

d_{n j} = < f / Y_{j, n} > such as : ψ_{j, n} (t) = {(\sqrt{2})}^{- j} ψ (2^{- j} t - n)

with j,n∈Z. The function ψ is called wavelet function.

All this can be also translated like a filtering of our signal by two filters, a high-pass filter and a low-pass filter such as:

A_{n}^{j} = \sum_{k} \tilde{h} (2 n - l) A_{n}^{j - 1} and d_{n}^{j} = \sum_{k} \tilde{g} (2 n - l) A_{n}^{j - 1}

where

\tilde{h}

and

\tilde{g}

are discrete filters.

The original signal passes through two complementary filters (Fig. 2): a high-pass filter gives a signal of details and a low-pass filter, a signal from the approximations. In its formulation, the wavelet transform can be interpreted as an analysis band of constant overpressure filter. In such a bench, each filter (band pass) can result from a single gauge by a dilation or compression frequency.

Fig. 2
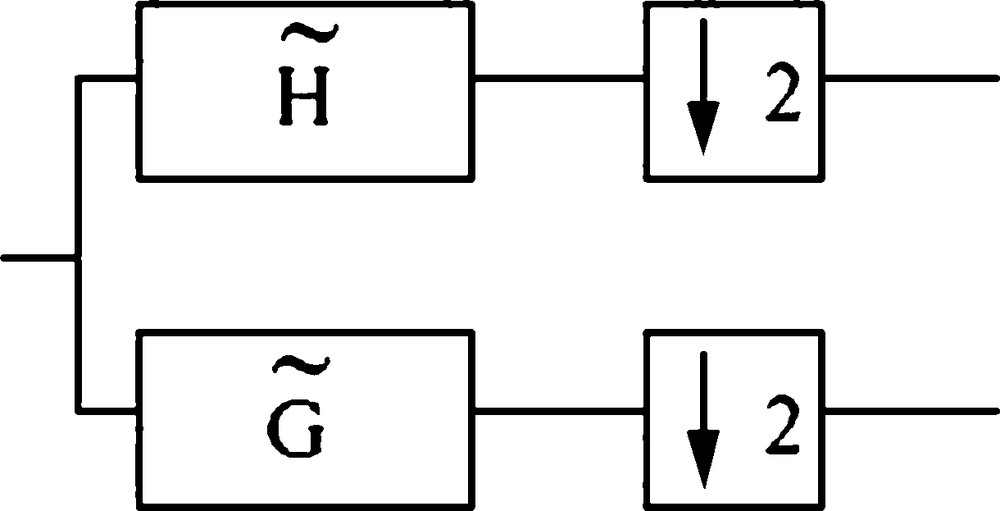
Passage of signal to high-pass filter and low-pass filter.
Fig. 2. Passage du signal au filtre passe-haut et filtre passe-bas.

3 Wavelet packet transform

The analysis of the signal by the wavelet transform makes it possible to extract the noise from the original signal and to obtain a filtered signal, which causes a loss of information on the high frequencies of the original signal. The wavelet packet analysis [4] offers a rich analysis of the signal, thanks to its best model of decomposition in the tree form. The wavelet packet allows one to break up the signal on many bases and to choose within the meaning of certain criteria which represent the signal as closely as possible. In fact, in other words, not only the low-pass filtered versions of the signal are broken up, but also the high-pass filtered versions. The high frequencies are also cut out in sub-bands and the decomposition tree becomes symmetrical (Fig. 3). The resulting coefficients from this decomposition are characterised by three parameters: the level of decomposition, frequency index and temporal index. Each wavelet packet is carrying triple information (f: frequency, s: scale and p: position). This brings different techniques to code the signal and offers a richer range of possibilities for analysing it. We use in our application the wavelet packet of Meyer [14].

Fig. 3
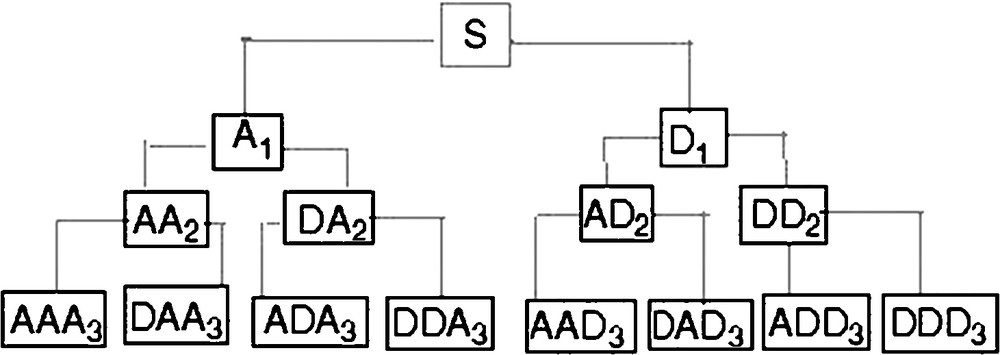
Wavelet packet decomposition tree.
Fig. 3. Décomposition en arbre de la transformée en paquet d’ondelettes.

4 Denoising signal methods by wavelets

Denoising is a problem of signal treatment that is well-known and largely studied.

Let y(t) = x(t) + n(t), be the signal noise observed. The problem is to obtain an estimate of the original signal x(t). According to the model employed for these random variables x and n, several principles of denoising have been proposed. Some methods are based on the calculation of the Hodler exhibitors [13], and others use the thresholding method of denoising proposed by Donoho and Johnstone [5,6]. This work treats the second criterion based on the thresholding method. In the general case two types of thresholdings are used:

• a hard thresholding:
$S_{hard} = \{\begin{array}{l} X & if | X | > T \\ 0 & if | X | < T \end{array}\}$
If the observation signal coefficient is lower than a certain threshold T, it is considered as being pure noise and it is replaced by zero; if not, it is kept such at its value.
• a soft thresholding:
$S_{soft} = \{\begin{array}{l} s i g n (X) (| X | - T) & if | X | > T \\ 0 & if | X | < T \end{array}\}$

If the observation signal coefficient is lower than a certain threshold T, it is regarded as being pure noise and is replaced by zero; if not it is set to a narrowed value of the threshold.

In the case of a Gaussian additive white vibration, Donoho and Johnstone also proposed the universal thresholding (1994) defined as follows [5,6]: $T = σ \sqrt{2 \log (n)}$ , n is the number of signal points and σ is the estimated noise level: σ = M/0.6745 and M represents the absolute median estimated on the first scale.

In the case of correlated noise, Johnstone and Silverman proposed the thresholding (level depend) defines as follows [10]:

T = σ_{t} \sqrt{2 \log (n_{t})}

where i is the scale comprising n_i points and σ = M_i/0.6745.

Within the framework of this article, we noted that the Gaussian white vibration is more appropriate for our signal. We thus studied only the white vibration case and we used the thresholding minimax suggested by Donoho and Johnstone which uses the risk minimum principle [5,6].

The noise reduction method employing the wavelet transform consists in applying the signal decomposition concept in a wavelet adaptive base. This method is summarised by the four following stages:

• the signal decomposition by choosing a wavelet and a resolution level N;
• the choice of the best tree for this decomposition;
• the selection of a threshold to the wavelet coefficients;
• the signal reconstruction by wavelet starting from the coefficients of the resolution level N and the details coefficients of the level 1 to N.

5 Time series analyzes by wavelets

When we observe a time series of station coordinates, we want to detect the station displacement, therefore we search a slope, a tendency (change in the short or the long term of the series), periodic terms or irregular movements. This article proposes an analysis by wavelet transform of time series of DORIS station coordinates.

DORIS data used during the treatment make up of a set of weekly residuals time series coordinates East (dE), North (dN) and Vertical (dH) from the eight DORIS stations as we can see in Table 1.

Stations	Geographical situation	Latitude	Longitude	Observation period (year)
DIOA	Greece	38°05′	23°56	1216
COLA	Sri Lanka	6°53′	79°52′	11.76
FAIB	Alaska	64°58′	−147°31′	5.42
KRAB	Krasnoyarsk	56°	92°48′	7.47
SAKA	Yuzhno-Sakha linsk	47°1′	142°43′	11.5
SODB	Scomo	18°43′	−110°57′	6.82
THUB	Greenland	76°32′	−68°49′	2.29
SYPB	Japan	−69°	39°35′	5.94

They were selected on the following criterion basis [20]:

• stations presenting discontinuities: KRAB and SAKA;
• stations affected by the earthquakes: COLA, FAIB, SAKA;
• stations affected by volcanic movements: SODB;
• stations presenting data gaps and an antenna instability: DIOA;
• station representing better quality of geodetic data with high latitudes: SYPB and THUB.

5.1 Temporal representation of the Doppler Orbit Determination and Radiopositioning Integrated by Satellite (DORIS) time series

This stage consists in representing on a graph the residual coordinates (dE, dN and dH) of the DORIS stations according to time in order to carry out an examination a priori on the series distributions for the observation period. Fig. 4 represents the series distributions of the eight DORIS stations:

Fig. 4
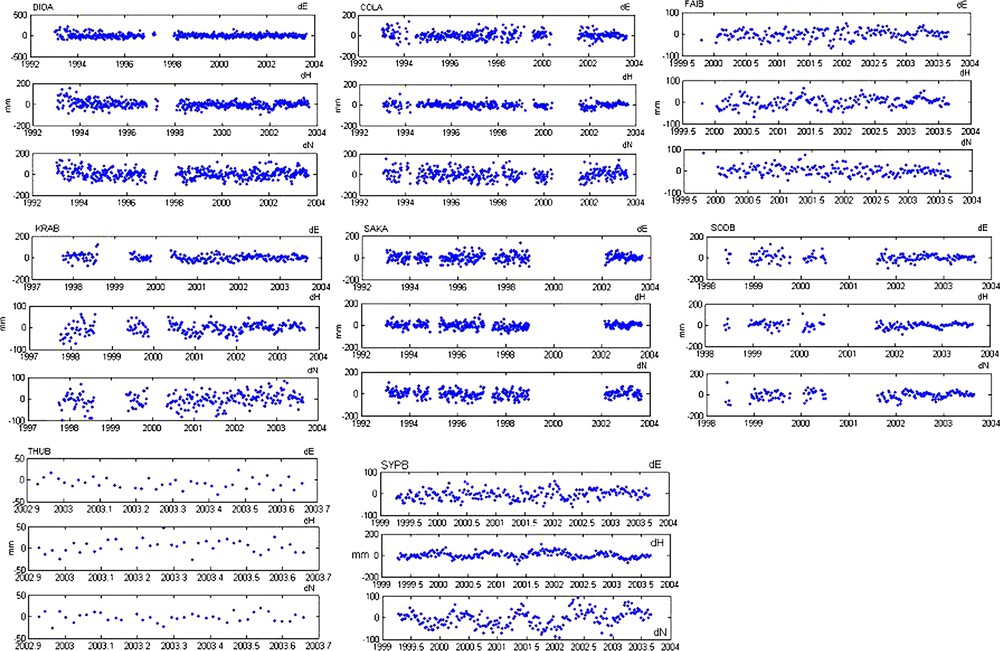
Representation of the original signal of the eight stations used.
Fig. 4. Représentation du signal original des huit stations utilisées.

5.2 Discrete wavelet transform – study of tendencies and periods

5.2.1 Tendencies

Knowing that the tendency represents the change in the short or the long term signal, wavelet analysis makes it possible to extract the tendency and the change in tendency of the series starting from the last resolution of the approximations (the 8th approximation) by using the discrete wavelet treatment of Meyer [14] which is very appropriate to our signal (Fig. 5).

Fig. 5
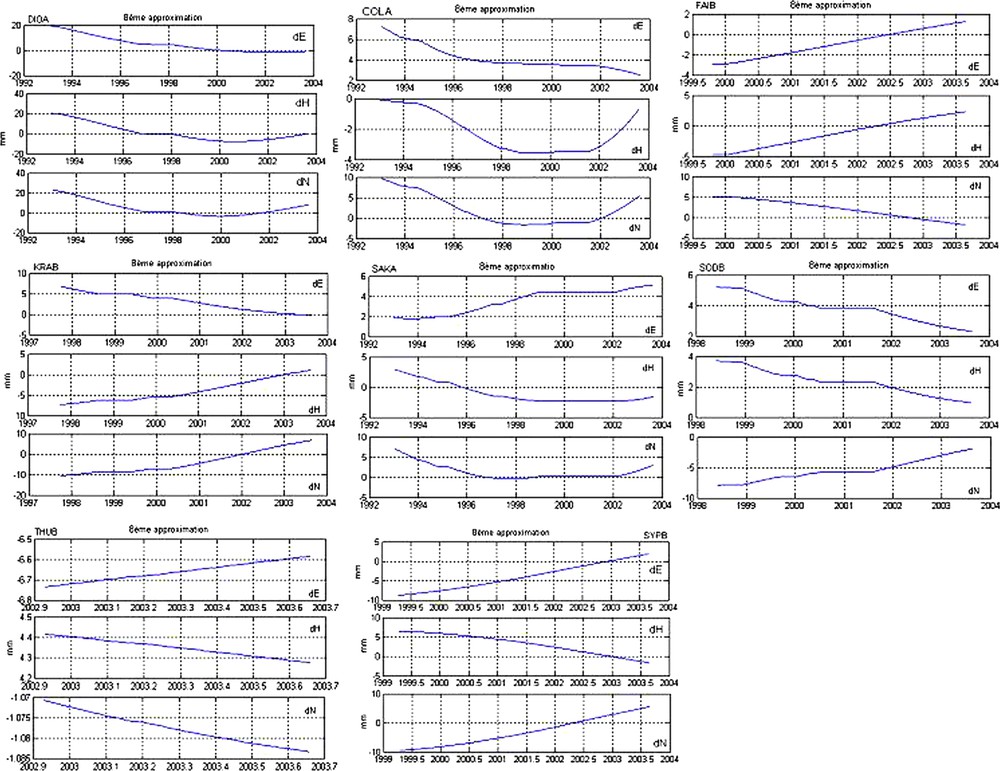
Representation of the 8th approximation of three components of eight DORIS stations.
Fig. 5. Représentation de la 8^e approximation des trois composantes des huit stations DORIS.

The examination of the signal series of the eight DORIS stations (Fig. 5) enabled us to detect:

• for DIOA station (Fig. 6): a descendent tendency from the beginning of the signal to 1997 and a data gap between 1997 and 1998 (null tendency). Another change of tendency (ascendent tendency) starting from 2001, and that for the three components dE, dH and dN;
• for COLA station (Fig. 7): an overall descendent tendency for dE component. The descendent tendency becomes ascendent from the end of 2001 for both components dH and dN;
• for FAIB station (Fig. 8): an ascendent tendency on all the signals for the two components dE and dH and a descendent tendency for the dN component;
• for KRAB station (Fig. 9): an overall descendent tendency on all the signal for the dE components and ascendent tendency for the two other components, dH and dN;
• for SAKA station (Fig. 10): an overall ascendent tendency on all the signal for the dE component, an overall descendent tendency for the two other components dH and dN. From the beginning of 2002 the tendency becomes ascendent for the three components;
• for SODB station (Fig. 11): an overall descendent tendency on all the signal for the dE and dH components, and overall ascendent tendency for the dN component;
• for THUB station (Fig. 12): an ascendent tendency on all the signal for the dE component and a descendent tendency for the two other components dH and dN;
• for SYPB station (Fig. 13): an ascendent tendency on all the signal for the two components dE and dN and an overall descendent tendency for the dH component.

Fig. 6
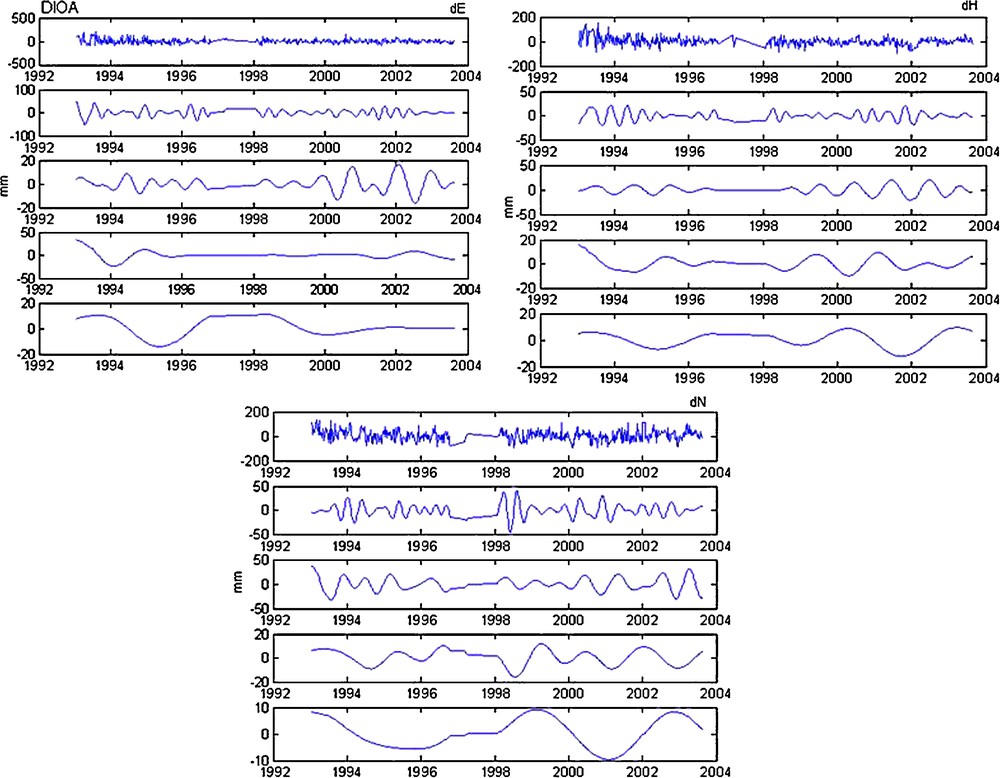
Decomposition in details (from 4th to the 7th detail) of dE, dH and dN (**DIOA** station).
Fig. 6. Décomposition en détails (du 4^e au 7^e détail) de dE, dH et dN (station **DIOA**).

Fig. 7
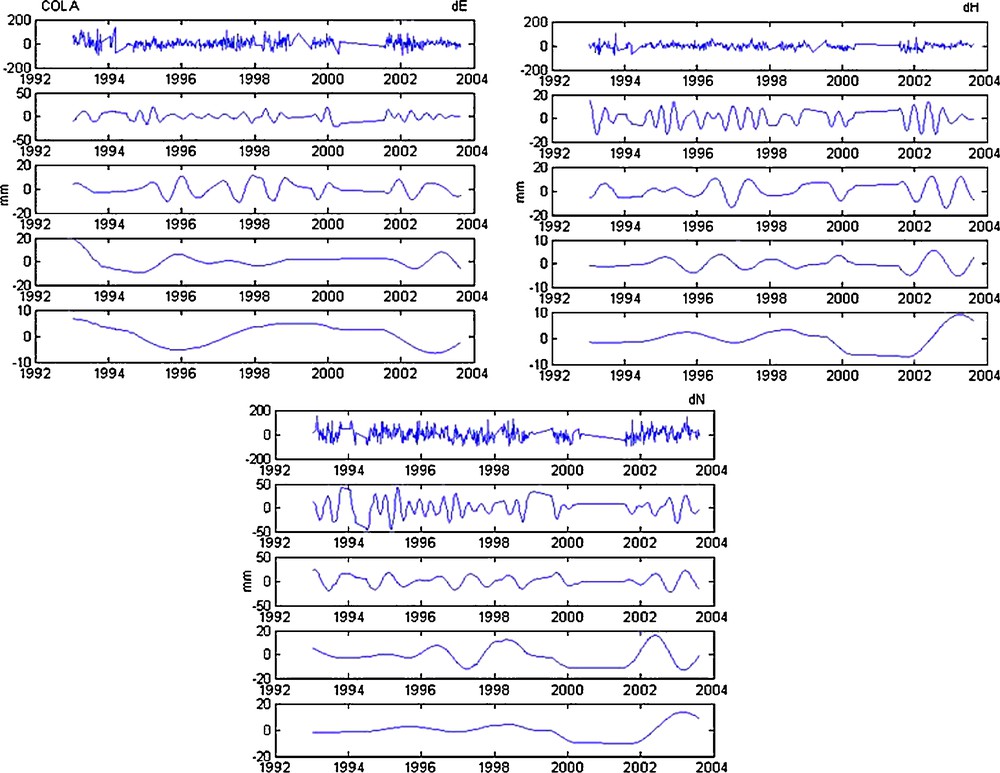
Decomposition in details (from 4th to the 7th detail) of dE, dH and dN (**COLA** station).
Fig. 7. Décomposition en détails (du 4^e au 7^e détail) de dE, dH et dN (station **COLA**).

Fig. 8
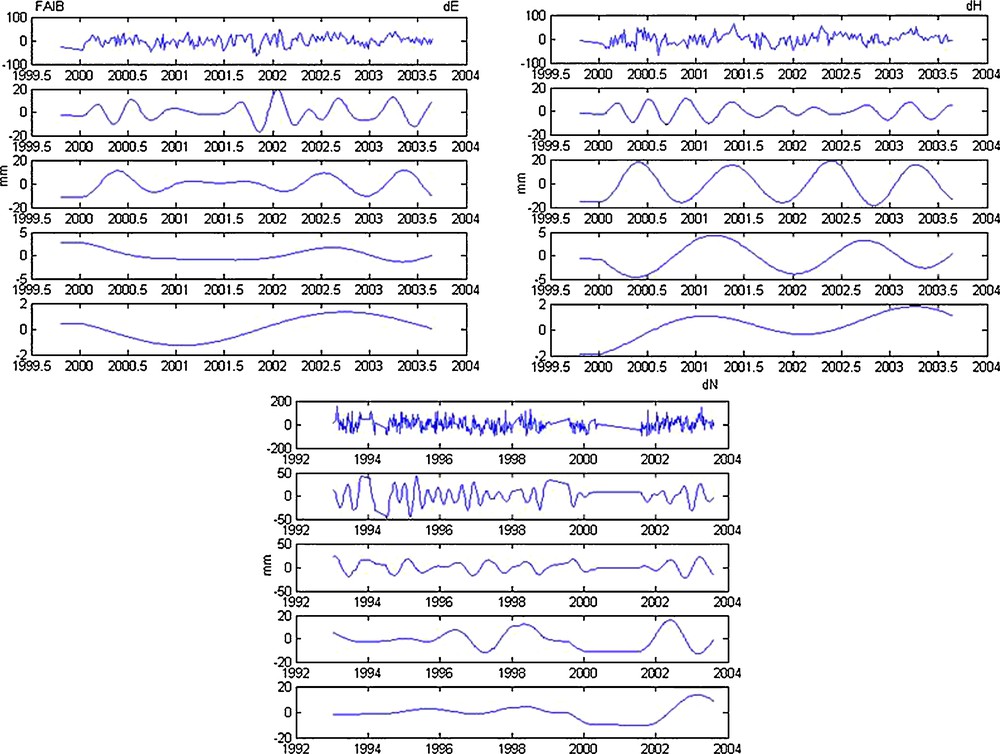
Decomposition in details (from 4th to the 7th detail) of,dE, dH and dN (**FAIB** station).
Fig. 8. Décomposition en détails (du 4^e au 7^e détail) de dE, dH et dN (station **FAIB**).

Fig. 9
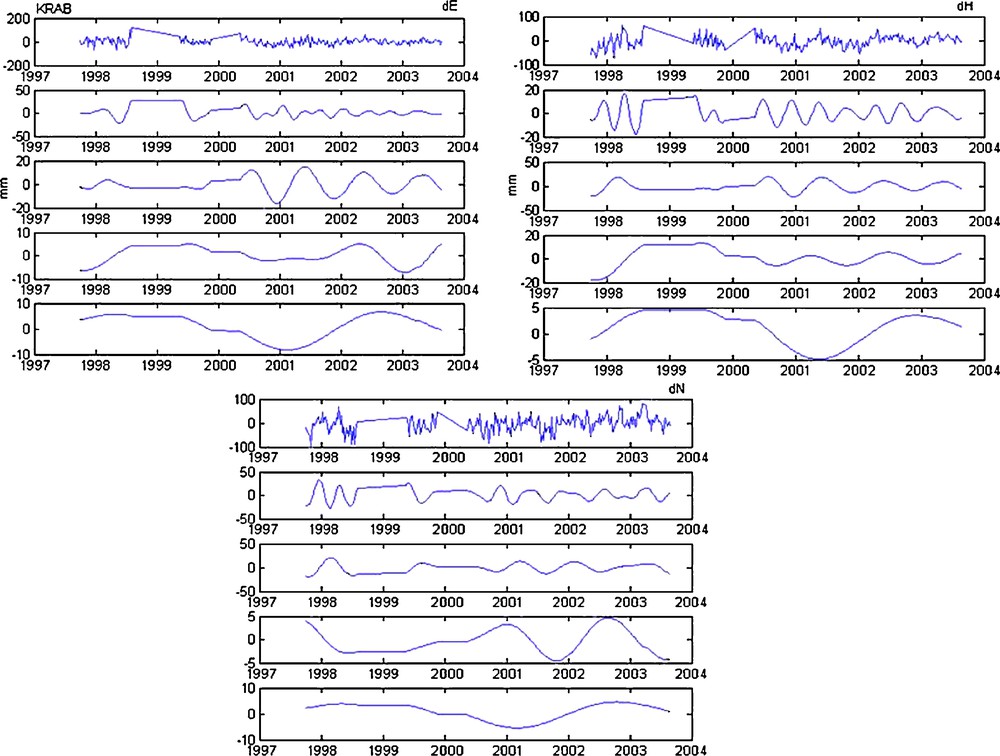
Decomposition in details (from 4th to the 7th detail) of dE, dH and dN (**KRAB** station).
Fig. 9. Décomposition en détails (du 4^e au 7^e détail) de dE, dH et dN (station **KRAB**).

Fig. 10
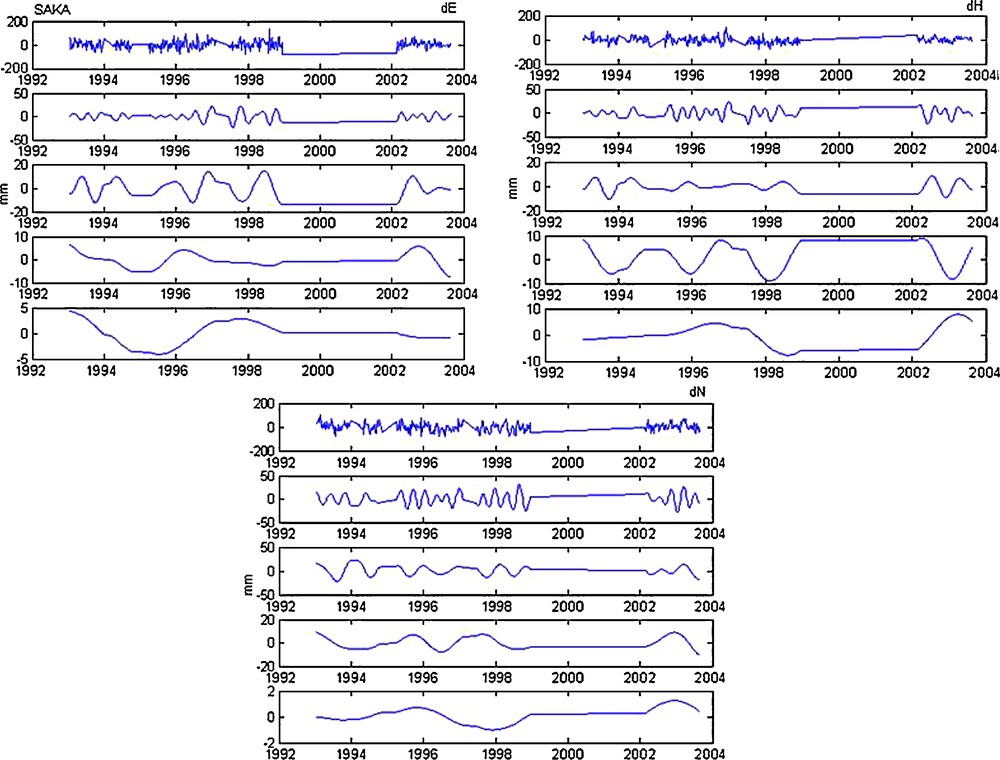
Decomposition in details (from 4th to the 7th detail) of dE, dH and dN (**SAKA** station).
Fig. 10. Décomposition en détails (du 4^e au 7^e détail) de dE, dH et dN (station **SAKA**).

Fig. 11
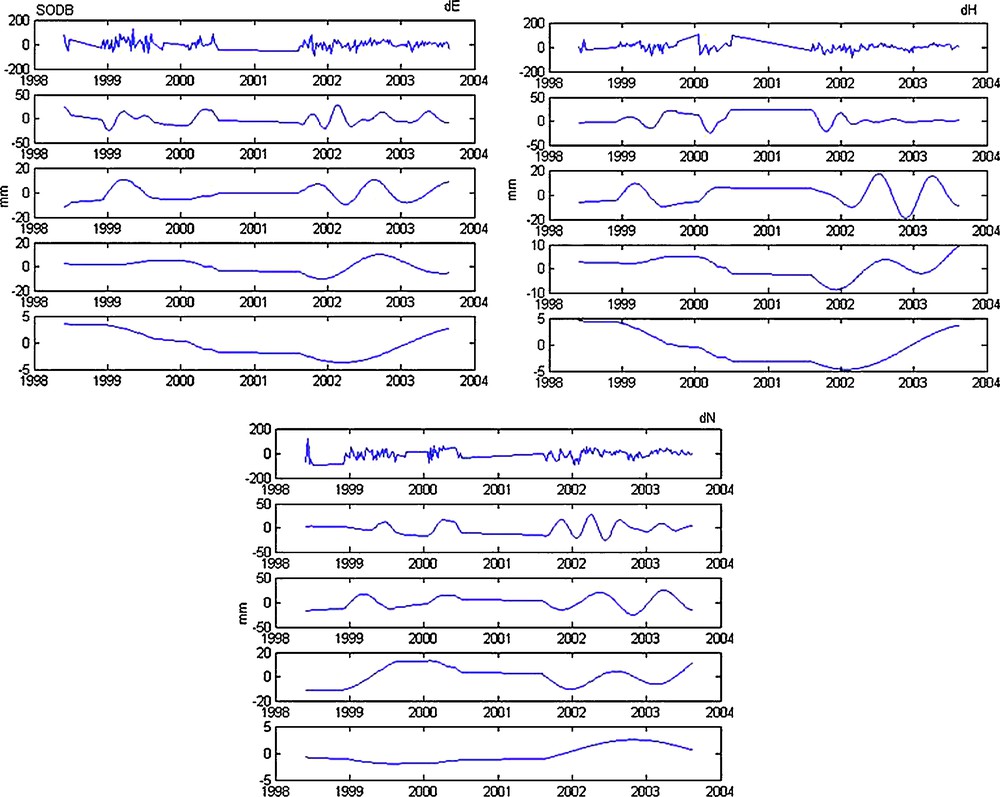
Decomposition in details (from 4th to the 7th detail) of dE, dH and dN (**SODB** station).
Fig. 11. Décomposition en détails (du 4^e au 7^e détail) de dE, dH et dN (station **SODB**).

Fig. 12
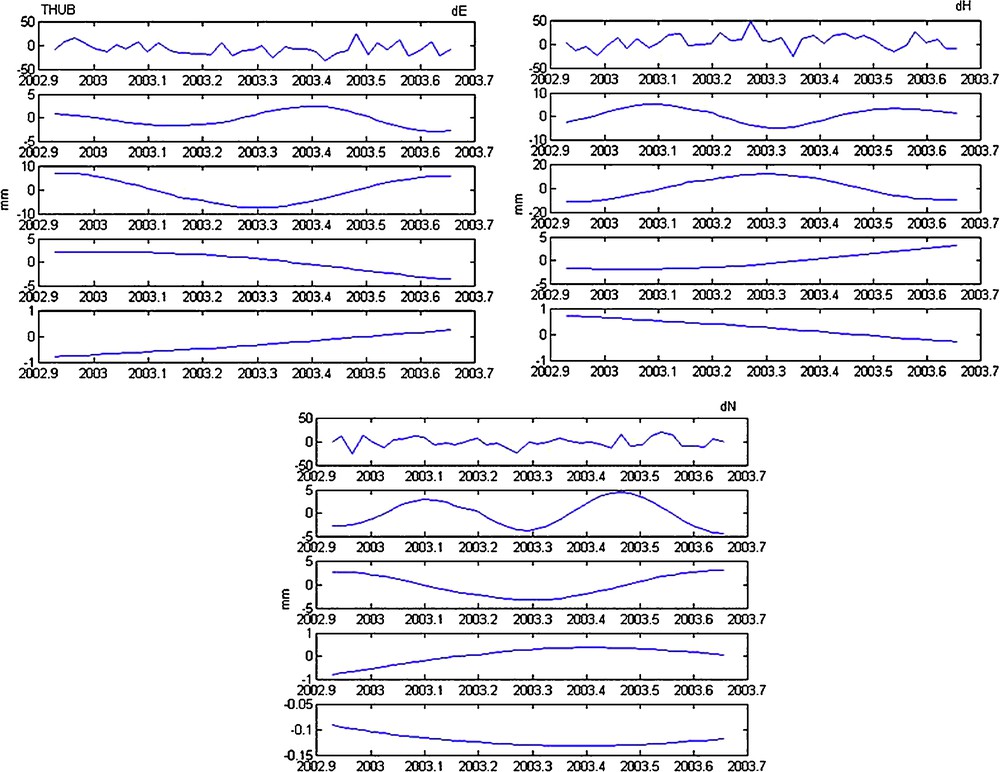
Decomposition in details (from 4th to the 7th detail) of dE, dH and dN (**THUB** station).
Fig. 12. Décomposition en détails (du 4^e au 7^e détail) de dE, dH et dN (station **THUB**).

Fig. 13
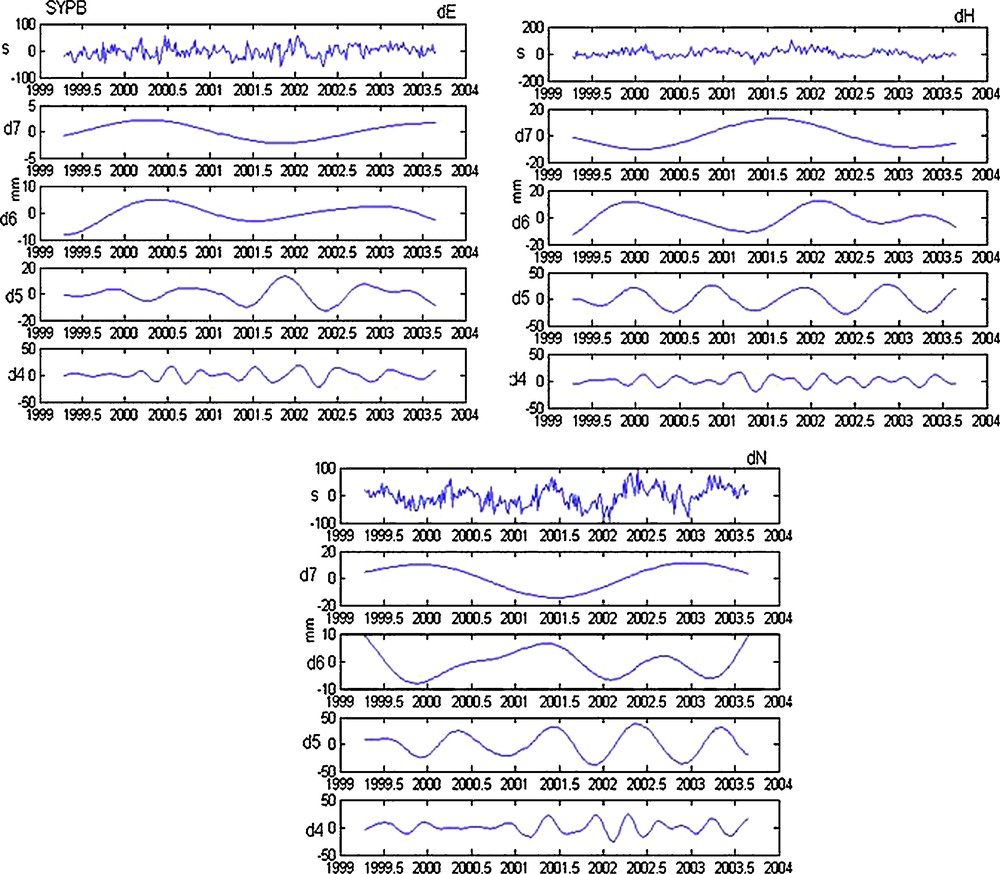
Decomposition in details (from 4th to the 7th detail) of dE, dH and dN (**SYPB** station).
Fig. 13. Décomposition en détails (du 4^e au 7^e détail) de dE,dH et dN (station **SYPB**).

Finally, we notice that tendencies are almost identical for:

• three components dE, dH and dN for DIOA station;
• two components dH and dN for COLA, KRAB, SAKA and THUB stations;
• two components dE and dH for FAIB and SODB stations;
• two components dE and dN for SYPB station.

The signal evolution of the vertical component (dH) is similar to the North component (dN) which is due probably to the fact that the SPOTS satellites are heliosynchronous, the traces are north-south to the equator and consequently the East component (dE) of stations is not as well determined as the other components.

5.2.2 Periods

The approximations are used to detect a tendency, a slope and irregularities of a signal, the details are employed to identify cycles (periodic signals). Fig. 6–13 represent the detailed signals starting from the 4th resolution of the three components for the eight stations.

According to these figures, we observe that the first details represent very important frequential extensions, i.e. small periods, but which are vague to distinguish. More the level of resolution increases, less the components become rich in frequencies (component periodicals are important). We can thus identify various periodic components on the resolutions and various levels of the details for the three components (dE, dH and dN) of the eight stations. Their periods increase with the resolution level. By making a zoom in the graph of the 4th detail of the vertical component of station SYPB, we notice a four-months period (= 118 days) (Fig. 14) which can result in a possible period error on the Z component of the geocentre [12,19].

Fig. 14
Representation of the period of four months starting from the detail D4 of the vertical component dH of station SYPB.
Fig. 14. Représentation de la période de quatre mois à partir du détail D4 de la composante verticale dH de la station SYPB.

We also note, on the vertical component level of DIOA, FAIB, KRAB and SYPB stations, a periodic signal of one year which is detached clearly on the level from the 5th detail D5. Concerning THUB station, we identified a six-months period on the level of the 4th detail of the East component, but we could not obtain the one-year periodic component owing to the fact that the observation period of this station is very short. For the other stations COLA, SAKA which are affected by earthquakes [19], the periodic components appear with difficulty from the graphs. Table 2 summarizes the various cycles detected on the level of the three components of the eight DORIS stations.

Components	Details
	D4	D5	D6	D7
dE, dH and dN	Period of 4 to 6 months	Period of 6 to 12 months	Period of 12 months with more than 24 months	Period of 24 months with more than 36 months

The examination of these characteristics of the time series, revealed by the wavelets, will be able to help identify the natural geophysical phenomena related to the systematical error in the spatial geodesic computations (earthquakes, imperfections of the ITRF2000 model [2] which is replaced by the ITRF2005) [1].

5.3 Continuous wavelet transform (CWT): characterization of the series in time frequency

The CWT is the sum during the time of the signal multiplied by the function-shifted wavelet along the signal. This process produces the wavelet coefficients which depend on the scale and time; it allows us to characterize the time series in time and frequency, to give us a qualitative idea of the time series contents and to emphasize unexpected components (cycles, transitory problems), and to carry out a denoising of the series.

The wavelet coefficients obtained during our analysis are represented in coloured mode, in 3D (Fig. 15). The marked color represents the importance of the amplitude coefficients: dark shows small coefficients and light expresses high values.

Fig. 15
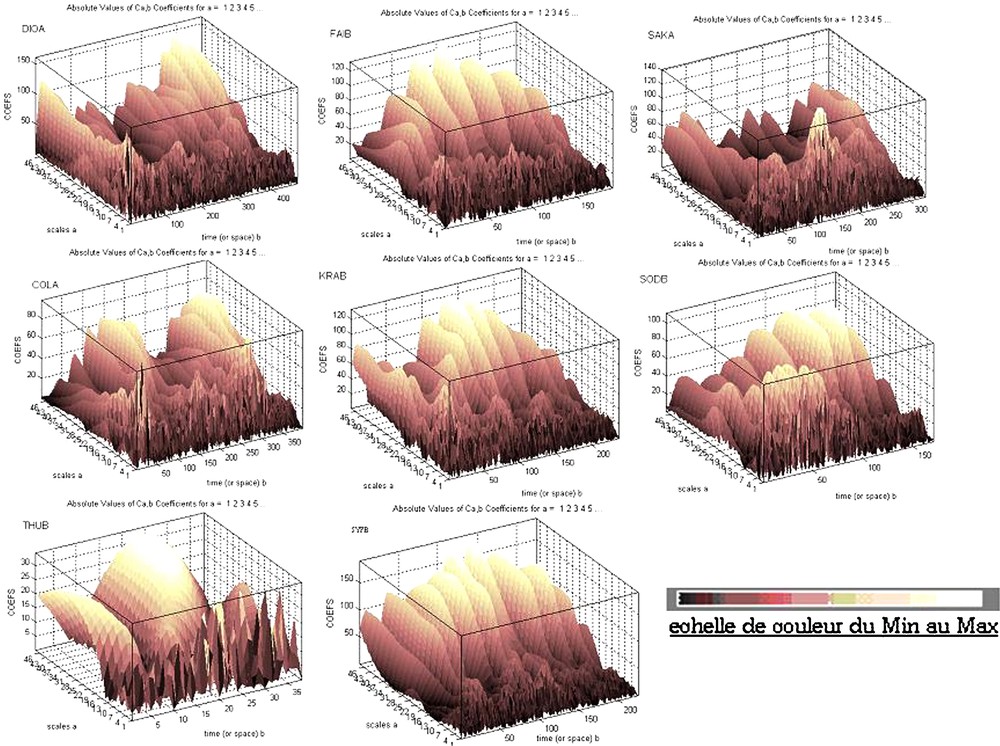
Representation of the wavelet coefficients (coloured mode) in 3D.
Fig. 15. Représentation des coefficients d’ondelette (mode coloré) en 3D.

Fig. 15 represents the periodic components along the signal; more the scale increases, more the signal has low frequencies and high values of coefficients. The periodic terms are variable in frequency or in amplitude.

A second analysis was applied (Fig. 16) to the denoised signal. We obtain new wavelet coefficients with better periodic components. We notice thus, for the eight vertical components of the eight stations, we detect the one-year periods for a low scale and six-months periods for large scale.

Fig. 16
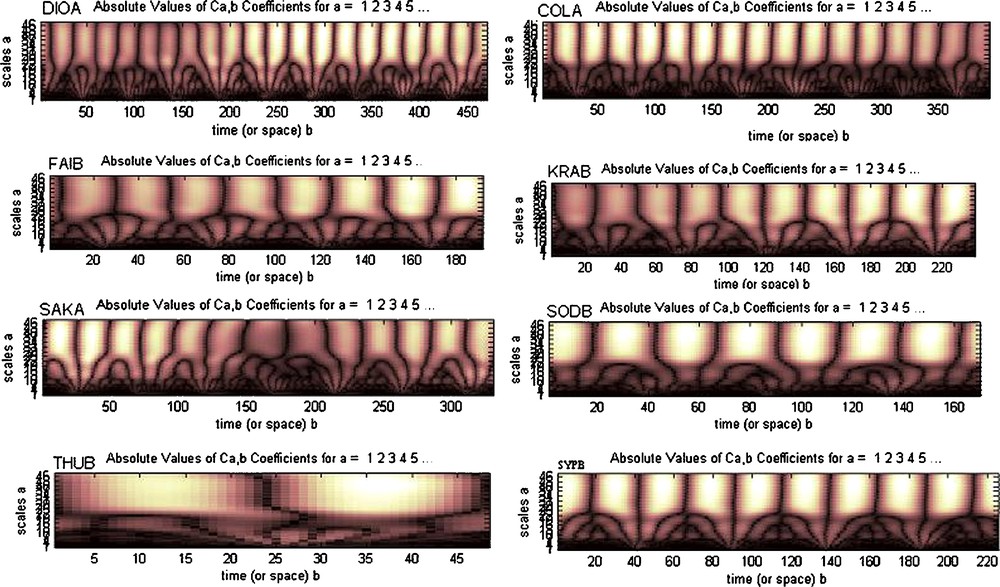
Graphs of the absolute values of the continuous wavelet coefficients applied for the 2nd time.
Fig. 16. Graphes des valeurs absolues des coefficients d’ondelettes continues appliquées pour la 2^e fois.

6 Wavelet packet transform

An interface of denoising signal using the wavelet packet transform with the soft thresholding applied to the vertical components (dH) of the eight DORIS stations was developed under MATLAB. The results obtained enabled us to notice that the analysed signal (filtered) of the eight stations (Fig. 17) became smoother, except that there remains some fluctuations on the level of the following stations:

• DIOA: at the beginning of the signal;
• COLA: towards the end of 1994 and also at the end of 2001 and at the beginning of 2002;
• FAIB: in the middle of the year 2000;
• KRAB: towards the beginning of 1998 and also the end of 1999;
• SAKA: towards the beginning of the year 1993et 1995 and also beginning and at the end of 1997;
• SODB: in the middle of the year 1998 and 1999 and also towards the end of 2001 and the beginning of 2002;
• SYPB: towards the beginning of the year 2000 and the end of 2002.

Fig. 17
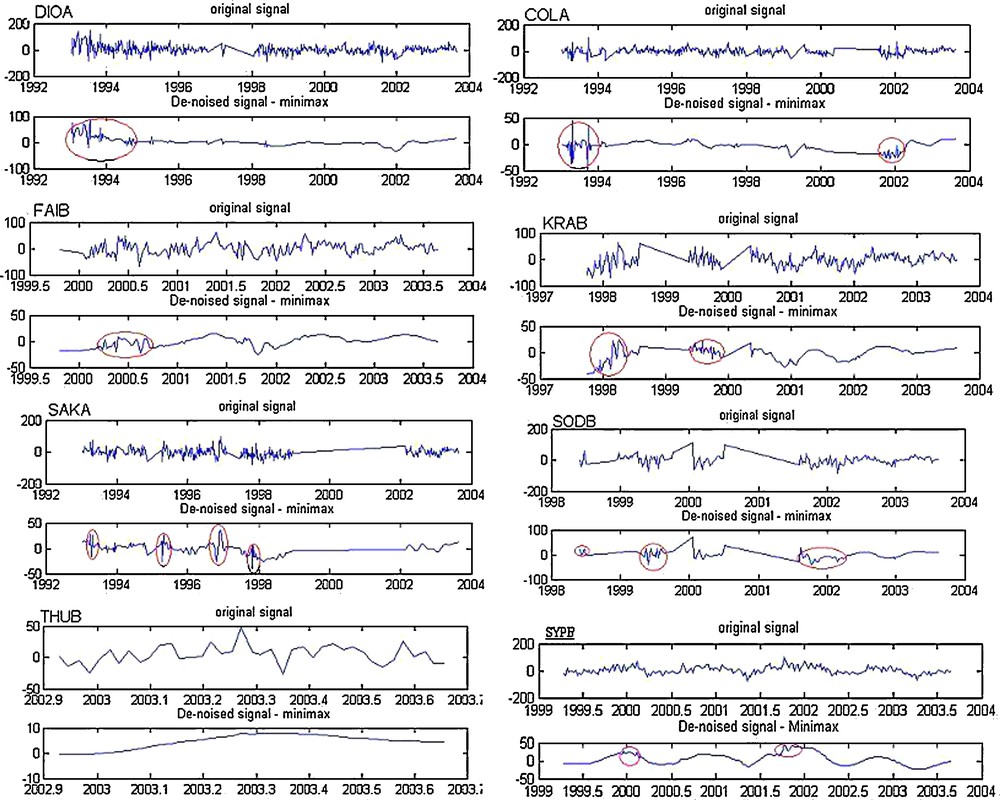
Representation of the filtered signal and original signal of the eight stations by the wavelet packet transform.
Fig. 17. Représentation du signal filtré et du signal original des huit stations par la transformée en paquet d’ondelettes.

On the other hand, at the THUB station, we note that the signal is smooth, which is certainly due to the fact that the observation period is relatively important.

All these fluctuations can be caused by a geophysical phenomenon (an earthquake), or by an antenna change or bad knowledge of one of the parameters being used with the estimate of the residues as coordinates. We also notice that all these fluctuations represent the high frequencies, which translates the analysis effectiveness of the wavelet packet transform.

7 Conclusion

The results obtained during the analysis of the residual time series of DORIS station coordinates showed that the wavelet method makes it possible to better determine and to quantify the systematic signals such as periodicity and tendency. Indeed, the tests carried out highlighted, on the one hand, the tendencies of the components (dE), (dN) and (dH) of each DORIS station. We notice almost identical tendencies of the vertical and the North component which is due probably to the fact that the East component less well determined as the other components because the SPOTS satellites are heliosynchrones. In addition, the annual and semi-annual periodic terms appear clearly on the detailed level of the wavelet coefficient for the eight station coordinates. Moreover, the 118 days period which arises from the graph of the 4th detail (D4) of the SYPB station provides a possible explanation error on the Z component of the geocentre. The extraction of the original signal noise by the wavelet transform can cause an information loss at high frequencies. The wavelet packet transform offers a richer analysis of the signal, thanks to its best model of decomposition in tree form and makes it possible to store more information on the high frequencies. Indeed, the wavelet packet transform application to the time series of DORIS station coordinates has allowed us, on the one hand, to obtain a smoother filtered signal, and on the other hand, to detect fluctuations representing the great frequencies which can be the cause of parasitic phenomena of observational, instrumental or geophysical origin.

The analysis of the geodetic time series is a field of research which is currently in a phase of development of the statistical studies adapted to the criteria of this new geodesy with four dimensions, while being often based on methods already developed in other disciplines. The work presented in this article is a contribution to these methodological developments based on the technique of the wavelets.

Acknowledgements

The authors are very grateful to the referees for their suggestions, comments, constructive criticisms and hints which lead to substantial improvement of the paper. They also would like to thank the University of Oran Es-senia for supporting this research topics under CNEPRUS B01820060148 and B3101/01/05.

Bibliographie

[1] Z Altamimi, X Collilieux, J Legrand, B Garayt, C. Boucher, ITRF2005: A new release of the International Terrestrial Frame based on time series of station positions and earth orientation parameters, J. Geophys. Res.-Solid Earth. (2007) 112, B09401, . | DOI

[2] Z. Altamimi; P. Sillard; C. Boucher New trends for the realization of the International Terrestrial Reference System, Adv. Space. Res., Volume 30 (2002), pp. 175-184 | DOI

[3] F. Barlier The DORIS system, a fully operational tracking system to get orbit determination at centimeter accuracy in support of earth observations, C.R. Geoscience, Volume 337 (2005), pp. 1223-1224 | DOI

[4] R.R. Coifman; Y. Meyer; M.V. Wickerhauser Wavelet analysis and signal processing, in : wavelets and their applications, Jones and Bartlett (Eds), Boston, MA, USA, 1992 (pp. 153–178)

[5] D. Donoho; I.M. Johnstone Ideal Spatial adaptation via wavelet shrinkage, Biometrika., Volume 41 (1994), pp. 425-455

[6] D. Donoho; I.M. Johnstone; G. Kerkyacharian; D. Picard Wavelet shrinkage: Asymptotia, Journal of the Royal Statistical Society, Ser. B., Volume 57 (1995), pp. 3019-3069

[7] H. Fagard Twenty years of evolution for the DORIS permanent network:from its initial deployment to its renovation, DORIS special Issue, J. Geod., Volume 80 (2006), pp. 429-456 | DOI

[8] M. Feissel-Vernier; O. de Viron; K. Le Bail Stability of VLBI, SLR, DORIS and GPS positioning, Earth Planets Space., Volume 59 (2007), pp. 475-497

[9] M. Ghil et al. Advanced spectral methods for climatic time series, Rev. Geophys., Volume 40 (2001), pp. 1-41 | DOI

[10] I. Johnstone, W. Silverman, Wavelet threshold estimators for data with correlated noise, Technical Report, Dept. of Statistics, Stanford University, 1996.

[11] P. Landrin, Temps-frequence, Edition Hes, collection traitement du signal, 1998.

[12] K. Le Bail Estimating the noise in space-geodetic positioning: the case of DORIS, DORIS. Special Issue, J. Geod., Volume 80 (2006), pp. 541-565 | DOI

[13] S. Mallat; W.L. Hwang Singularity detection and processing with wavelets, IEEE Trans. Theory., Volume 38 (1992), pp. 617-643

[14] Y. Meyer Ondelettes et opérateurs. I. Actualités mathématiques, Hermann, Paris, France, 1990

[15] P. Steffen; P.N. Heller; R.A. Gopinath; C.S. Burrus Theory of regular M-band wavelet bases, IEEE Trans. on Signal Proc., Volume 41 (1993), pp. 3497-3511

[16] G. Tavernier; H. Fagard; M. Feissel-Vernier; K. Le Bail; F. Lemoine; C. Noll; R. Noomen; J.C. Ries; L. Soudarin; J.J. Valette; P. Willis The International DORIS Service: genesis and early achievements, DORIS. Special Issue, J. Geod., Volume 80 (2006), pp. 403-417 | DOI

[17] S.D.P. Williams; P. Willis Error Analysis of Weekly Station Coordinates in the DORIS Network, DORIS. Special Issue, J. Geod., Volume 80 (2006), pp. 525-539 | DOI

[18] P. Willis; Y.E. Bar-Sever; G. Tavernier DORIS as a potential part of a global geodetic observing system. The Global geodetic observing system, J. Geodyn., Volume 40 (2005), pp. 494-501 | DOI

[19] P. Willis; J.-P. Berthias; Y.E. Bar-Sever Systematic errors in the Z-geocenter derived using satellite tracking data, A case study from SPOT-4 DORIS data in 1998, J. Geod., Volume 79 (2006), pp. 567-572 | DOI

[20] P. Willis; J.C. Ries Defining a DORIS core network for Jason-1 precise orbit determination based on ITRF2000: methods and realization, J. Geod., Volume 79 (2005), pp. 370-378 | DOI

Commentaires - Politique