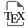Boundedness of classical solutions to a chemotaxis consumption system with signal dependent motility and logistic source

Khadijeh Baghaei

doi:10.5802/crmath.519

Équations aux dérivées partielles

Boundedness of classical solutions to a chemotaxis consumption system with signal dependent motility and logistic source

Khadijeh Baghaei ¹

¹ Pasargad Institute for Advanced Innovative Solutions, No.30, Hakim Azam St., North Shiraz St., Mollasadra Ave., Tehran, Iran

Comptes Rendus. Mathématique, Volume 361 (2023), pp. 1641-1652.

Résumé

We consider the chemotaxis system:

\{\begin{matrix} u_{t} = \nabla \cdot (γ (v) \nabla u - u ξ (v) \nabla v) + μ u (1 - u), & x \in Ω, t > 0, \\ v_{t} = Δ v - u v, & x \in Ω, t > 0, \end{matrix}

under homogeneous Neumann boundary conditions in a bounded domain $Ω \subset ℝ^{n}, n \geq 2,$ with smooth boundary. Here, the functions $γ (v)$ and $ξ (v)$ are as:

γ (v) = {(1 + v)}^{- k} and ξ (v) = - (1 - α) γ^{'} (v),

where $k > 0$ and $α \in (0, 1) .$

We prove that the classical solutions to the above system are uniformly-in-time bounded provided that $k (1 - α) < \frac{4}{n + 5}$ and the initial value $v_{0}$ and $μ$ satisfy the following conditions:

\begin{matrix} 0 < ∥ v_{0} ∥_{L^{\infty} (Ω)} \leq {[\frac{4 [1 - k (1 - α)]}{k (n + 1) (1 - α)}]}^{\frac{1}{k}} - 1, \end{matrix}

and

μ > \frac{k n (1 - α) ∥ v_{0} ∥_{L^{\infty} (Ω)}}{(n + 1) (1 + ∥ v_{0} ∥_{L^{\infty} (Ω)})} .

This result improves the recent result obtained for this problem by Li and Lu (J. Math. Anal. Appl.) (2023).

Reçu le : 2023-05-05
Révisé le : 2023-05-27
Accepté le : 2023-05-29
Publié le : 2023-11-17

DOI : 10.5802/crmath.519

Affiliations des auteurs :

Khadijeh Baghaei ¹

¹ Pasargad Institute for Advanced Innovative Solutions, No.30, Hakim Azam St., North Shiraz St., Mollasadra Ave., Tehran, Iran

Licence :

CC-BY 4.0

Droits d'auteur : Les auteurs conservent leurs droits

@article{CRMATH_2023__361_G10_1641_0,
     author = {Khadijeh Baghaei},
     title = {Boundedness of classical solutions to a chemotaxis consumption system with signal dependent motility and logistic source},
     journal = {Comptes Rendus. Math\'ematique},
     pages = {1641--1652},
     publisher = {Acad\'emie des sciences, Paris},
     volume = {361},
     year = {2023},
     doi = {10.5802/crmath.519},
     language = {en},
}

TY  - JOUR
AU  - Khadijeh Baghaei
TI  - Boundedness of classical solutions to a chemotaxis consumption system with signal dependent motility and logistic source
JO  - Comptes Rendus. Mathématique
PY  - 2023
SP  - 1641
EP  - 1652
VL  - 361
PB  - Académie des sciences, Paris
DO  - 10.5802/crmath.519
LA  - en
ID  - CRMATH_2023__361_G10_1641_0
ER  -

%0 Journal Article
%A Khadijeh Baghaei
%T Boundedness of classical solutions to a chemotaxis consumption system with signal dependent motility and logistic source
%J Comptes Rendus. Mathématique
%D 2023
%P 1641-1652
%V 361
%I Académie des sciences, Paris
%R 10.5802/crmath.519
%G en
%F CRMATH_2023__361_G10_1641_0

Khadijeh Baghaei. Boundedness of classical solutions to a chemotaxis consumption system with signal dependent motility and logistic source. Comptes Rendus. Mathématique, Volume 361 (2023), pp. 1641-1652. doi : 10.5802/crmath.519. https://comptes-rendus.academie-sciences.fr/mathematique/articles/10.5802/crmath.519/

Bibliographie
Cité par

[1] Jaewook Ahn; Changwook Yoon Global well-posedness and stability of constant equilibria in parabolic-elliptic chemotaxis systems without gradient sensing, Nonlinearity, Volume 32 (2019) no. 4, pp. 1327-1351 | MR | Zbl

[2] Nicholas D. Alikakos $L^{p}$ bounds of solutions of reaction-diffusion equations, Commun. Partial Differ. Equations, Volume 4 (1979), pp. 827-868 | DOI | MR | Zbl

[3] Khadijeh Baghaei; Ali Khelghati Global existence and boundedness of classical solutions for a chemotaxis model with consumption of chemoattractant and logistic source, Math. Methods Appl. Sci., Volume 40 (2017) no. 10, pp. 3799-3807 | DOI | MR | Zbl

[4] Khadijeh Baghaei; Ali Khelghati Les solutions classiques d’un modèle de chimiotaxie avec consommation de chimioattracteurs sont bornées, C. R. Acad. Sci. Paris, Volume 355 (2017) no. 6, pp. 633-639 | Zbl

[5] Tobias Black; Michael Winkler Global weak solutions and absorbing sets in a chemotaxis-Navier–Stokes system with prescribed signal concentration on the boundary, Math. Models Methods Appl. Sci., Volume 32 (2022) no. 1, pp. 137-173 | DOI | MR | Zbl

[6] Xinru Cao; Johannes Lankeit Global classical small-data solutions for a three-dimensional chemotaxis Navier-Stokes system involving matrix-valued sensitivities, Calc. Var. Partial Differ. Equ., Volume 55 (2016) no. 4, 107, 39 pages | MR | Zbl

[7] Kentaro Fujie; Jie Jiang Boundedness of classical solutions to a degenerate Keller-Segel type model with signal-dependent motilities, Acta Appl. Math., Volume 176 (2021), 3, 36 pages | MR | Zbl

[8] Kentaro Fujie; Takasi Senba Global boundedness of solutions to a parabolic-parabolic chemotaxis system with local sensing in higher dimensions, Nonlinearity, Volume 35 (2022) no. 7, pp. 3777-3811 | DOI | MR | Zbl

[9] Kentarou Fujie; Jie Jiang Global existence for a kinetic model of pattern formation with density-suppressed motilities, J. Differ. Equations, Volume 269 (2020) no. 6, pp. 5338-5378 | DOI | MR | Zbl

[10] Jiayi Han; Changchun Liu Global weak solution for a chemotaxis Navier-Stokes system with p-Laplacian diffusion and singular sensitivity, Nonlinear Anal., Real World Appl., Volume 73 (2023), 103898, 24 pages | MR | Zbl

[11] Dirk Horstmann; Michael Winkler Boundedness vs. blow-up in a chemotaxis system, J. Differ. Equations, Volume 215 (2005) no. 1, pp. 52-107 | DOI | MR | Zbl

[12] Hai-Yang Jin; Yong-Jung Kim; Zhi-An Wang Boundedness, stabilization, and pattern formation driven by density-suppressed motility, SIAM J. Appl. Math., Volume 78 (2018) no. 3, pp. 1632-1657 | MR | Zbl

[13] Hai-Yang Jin; Yong-Jung Kim; Zhi-An Wang Boundedness in the higher-dimensional Keller–Segel model with signal-dependent motility and logistic growth, J. Math. Phys., Volume 60 (2019) no. 1, 011507, 14 pages | MR

[14] Hai-Yang Jin; Zhi-An Wang Critical mass on the Keller-Segel system with signal-dependent motility, Proc. Am. Math. Soc., Volume 148 (2020) no. 11, pp. 4855-4873 | MR | Zbl

[15] Evelyn F. Keller; Lee A. Segel Initiation of slime mold aggregation viewed as an instability, J. Theor. Biol., Volume 26 (1970) no. 3, pp. 399-415 | DOI | MR | Zbl

[16] Ali Khelghati; Khadijeh Baghaei Boundedness of classical solutions for a chemotaxis model with rotational flux terms, Z. Angew. Math. Mech., Volume 98 (2018), pp. 1864-1877 | DOI | MR | Zbl

[17] Ali Khelghati; Khadijeh Baghaei Boundedness of classical solutions for a chemotaxis system with general sensitivity function, Appl. Anal., Volume 98 (2019) no. 3, pp. 611-621 | DOI | MR | Zbl

[18] Johannes Lankeit; Michael Winkler Depleting the signal: Analysis of chemotaxis-consumption models–A survey (2023) | arXiv

[19] Dan Li; Jie Zhao Global boundedness and large time behavior of solutions to a chemotaxis-consumption system with signal-dependent motility, Z. Angew. Math. Phys., Volume 72 (2021) no. 2, 57, 21 pages | MR | Zbl

[20] Xue Li; Liangchen Wang; Xu Pan Boundedness and stabilization in the chemotaxis consumption model with signal dependent motility, Z. Angew. Math. Phys., Volume 72 (2021) no. 4, 170, 18 pages | MR | Zbl

[21] Yan Li; Shuying Lu Global solutions to a chemotaxis-growth system with signal-dependent motilities and signal consumption, J. Math. Anal. Appl., Volume 521 (2023) no. 1, 126902, 17 pages | MR | Zbl

[22] Youshan Tao Boundedness in a chemotaxis model with oxygen consumption by bacteria, J. Math. Anal. Appl., Volume 381 (2011) no. 2, pp. 521-529 | MR | Zbl

[23] Youshan Tao; Michael Winkler Eventual smoothness and stabilization of large-data solutions in a three-dimensional chemotaxis system with consumption of chemoattractant, J. Differ. Equations, Volume 252 (2012) no. 3, pp. 2520-2543 | MR | Zbl

[24] Youshan Tao; Michael Winkler Global solutions to a Keller-Segel-consumption system involving singularly signal-dependent motilities in domains of arbitrary dimension, J. Differ. Equations, Volume 343 (2023), pp. 390-418 | MR | Zbl

[25] Idan Tuval; Luis Cisneros; Christopher Dombrowski; Charles W. Wolgemuth; John O. Kessler; Raymond E. Goldstein Bacterial swimming and oxygen transport near contact lines, Proc. Natl. Acad. Sci. USA, Volume 102 (2005) no. 7, pp. 2277-2282 | DOI | Zbl

[26] Liangchen Wang Global dynamics for a chemotaxis consumption system with signal-dependent motility and logistic source, J. Differ. Equations, Volume 348 (2023), pp. 191-222 | DOI | MR | Zbl

[27] Liangchen Wang Global dynamics for a chemotaxis consumption system with signal-dependent motility and logistic source, J. Differ. Equations, Volume 348 (2023), pp. 191-222 | DOI | MR | Zbl

[28] Liangchen Wang; Chunlai Mu; Pan Zheng On a quasilinear parabolic-elliptic chemotaxis system with logistic source, J. Differ. Equations, Volume 256 (2014) no. 4, pp. 1847-1872 | DOI | MR | Zbl

[29] Michael Winkler Stabilization in a two-dimensional chemotaxis-Navier–Stokes system, Arch. Ration. Mech. Anal., Volume 211 (2014) no. 2, pp. 455-487 | DOI | MR | Zbl

[30] Yamin Xiao; Jie Jiang Global existence and uniform boundedness in a fully parabolic Keller-Segel system with non-monotonic signal-dependent motility, J. Differ. Equations, Volume 354 (2023), pp. 403-429 | DOI | MR | Zbl

[31] Changwook Yoon; Yong-Jung Kim Global existence and aggregation in a Keller-Segel model with Fokker-Planck diffusion, Acta Appl. Math., Volume 149 (2017) no. 1, pp. 101-123 | DOI | MR | Zbl

Cité par Sources :

Commentaires - Politique

Ces articles pourraient vous intéresser

Blow-up of nonradial solutions to the hyperbolic-elliptic chemotaxis system with logistic source

khadijeh Baghaei

C. R. Math (2023)

Improvement of conditions for boundedness in a fully parabolic chemotaxis system with nonlinear signal production

Xu Pan; Liangchen Wang

C. R. Math (2021)

Uniform boundedness of solutions for a predator-prey system with diffusion and chemotaxis

René Dáger; Víctor Navarro; Mihaela Negreanu

C. R. Math (2020)