1 Introduction
Usually, wastewater originated from urban areas or industry undergoes a physical/chemical/biological treatment in a purifying plant. From there, wastewater is discharged through a submarine outfall into an aquatic media like a lake, a river or a coastal area, at a suitable distance from protected areas like beaches, fisheries or marine recreation zones. When several purifying plants are going to discharge wastewater into the same domain, the problem of design and management of the whole treatment system arises. To solve this problem, optimal control theory and optimization methods can be very useful: they can help decision makers in formulating rational policies in order to minimize costs while keeping the prescribed levels of water quality. Sections 4 and 5 are devoted to present two typical examples: the optimal management of a wastewater treatment system and the optimal location of the submarine outfalls.
Obviously, the knowledge of mathematical models for the evolution of pollutant concentration is a unavoidable first step if one wants to use optimal control techniques. So, the first part of this work is devoted to study in detail one of them, related with Biochemical Oxygen Demand (BOD) and Dissolved Oxygen (DO), which is frequently used in the case of domestic discharges. In Section 2 we deal with the complete two-dimensional model consisting of two uncoupled system of partial differential equations which give us the height of water, the depth-averaged horizontal velocity of water and the depth-averaged concentration of BOD and DO. In Section 3 we obtain a new zero-dimensional model, by integrating the previous one, which can be very useful to study the global performance of the system. We apply this model in the ría of Arousa (Spain) to obtain the global concentration of BOD and DO along the time.
2 A complete two-dimensional model for Biochemical Oxygen Demand and Dissolved Oxygen
We consider a domain Ω occupied by shallow water (as can be a ría or an estuary), where polluting wastewater are discharged through submarine outfalls located at points and connected to their respective purifying plants located at points (see Fig. 1). Moreover, we assume the existence of several areas , representing fisheries, beaches or marine recreation zones where it is necessary to guarantee the water quality with pollution levels lower than some allowed threshold levels.
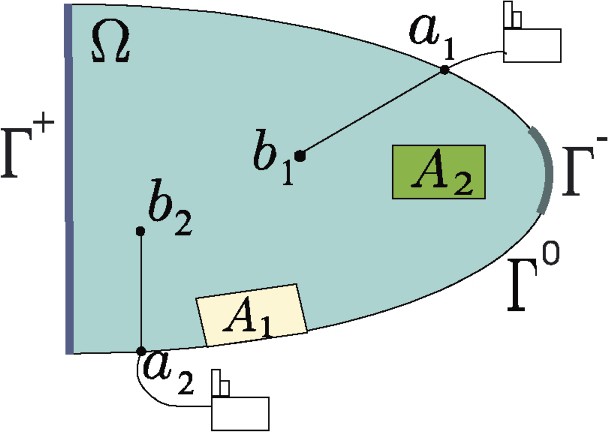
Domain Ω.
The flow of an effluent from a submarine outfall in a shallow water domain is mainly governed by horizontal transport due to currents (produced by tides, wind …) and turbulent diffusion. It allows uncouple hydrodynamical equations and transport equations. The former give the height and the velocity field which are used in latter to obtain the pollution levels.
2.1 Hydrodynamic model: the shallow water equations
In this section we recall the shallow water equations which constitute an useful mathematical model for hydrodynamic flows in shallow regions. If we consider Γ, the boundary of Ω, divided into three parts: (corresponding to the effluent), (corresponding to open sea) and (corresponding to the cost), then the shallow water equations can be written in the following way:
| (1) |
There are several works related to the existence, uniqueness and regularity of solution of (1) in particular cases (see, for instance, [1–5]) but in the general case it is still an open problem. A numerical approximation of h and in can be obtained by finite difference, finite element or finite volume methods (see, for instance, [6–9]) in order to be employed in the pollutant dispersion model.
2.2 Pollutant dispersion: the BOD-DO model
Firstly, in order to simulate the water quality in Ω, we have to choose some indicators of pollution levels. Two of the most important (especially in the case of domestic discharges) are the Dissolved Oxygen (DO) and the organic matter, which can be measured in terms of the need of oxygen to decompose it, the so-called Biochemical Oxygen Demand (BOD). If the pollution level is not too high the BOD can be satisfied by the DO. However, if the organic matter increases beyond a maximum value the DO is not enough for its decomposition, leading to important modifications (anaerobic processes) in the ecosystem. To avoid them a threshold value of BOD may not be exceeded and a minimum level of DO must be guaranteed.
The evolution of the BOD and the DO in the domain is governed by a system of partial differential equations (cf. [10]). Let us denote by and the concentrations of BOD and DO at point and at time , respectively. Then these concentrations are obtained as the solution of the following two initial-boundary value problems:
| (2) |
For this system we can prove the existence and uniqueness of solution (cf. [11]). A numerical solution for (2) can be obtained by a method which combines characteristics for time discretization with finite elements for space discretization (cf. [12]).
3 The global performance: a zero-dimensional model
The main aim in this paper is to study the global performance of the BOD-DO model in a ría, an estuary or a lake. In order to do it we integrate the system (2) in the region occupied by water. Thus, we obtain a new simple zero-dimensional model.
Let and be, respectively, the total mass of BOD and DO in the region at time t, that is to say,
| (3) |
If we study a stationary region (as can be a closed lake) A and V are constant along the time. In this case, if we also suppose that Q, and are constant, the exact solution of (3) is given by:
| (4) |
In order to develop an asymptotic study, for and , the terms with and can be negligible in (4) and the asymptotic values of BOD and DO are and . However, it is as well to point out that, in a shallow water domain, the typical values of and a are, respectively, of the order of 10−5 and , and then, the previous asymptotic values would be reached 300,000 years later!
For (only about some days later), we can neglect and approximate . Then we obtain an asymptotic value for the BOD and a linear approximation for the DO:
When we are working in an open region (as can be a ría or an estuary), we must take into account the water renewal. For example, in a ría, we can assume that inflow water is more pure than outflow water (in the sense that DO concentration is greater and BOD concentration is lesser) and, moreover, we know that DO concentration in inflow water is always lesser than oxygen saturation density (). In this case, if denotes the height over a fixed level (half tide) at the mouth of the ría and denotes the water volume corresponding to half tide, then, by geometrical reasons, we have
Moreover, taking into account the purification of the water in the ría because of the seawater renewal, we obtain the following expressions for the mass flow rates across the boundary:
| (5) |
This system can be easily solved by finite difference methods. We have used the backward Euler scheme to solve it for data corresponding to the ría of Arousa (Spain). Moreover, in order to study the weight of the water renewal in the ría, we have compared the result with the exact solution of (3) with and (in this case the exact solution is given by (4)). As one can see in Figs. 2 and 3, for data given in Table 1, the BOD concentration reaches an asymptotic value in both cases, but the DO concentration observes a linear decrease without water renewal and reaches an asymptotic value (very close to saturation) when the water renewal is considered.
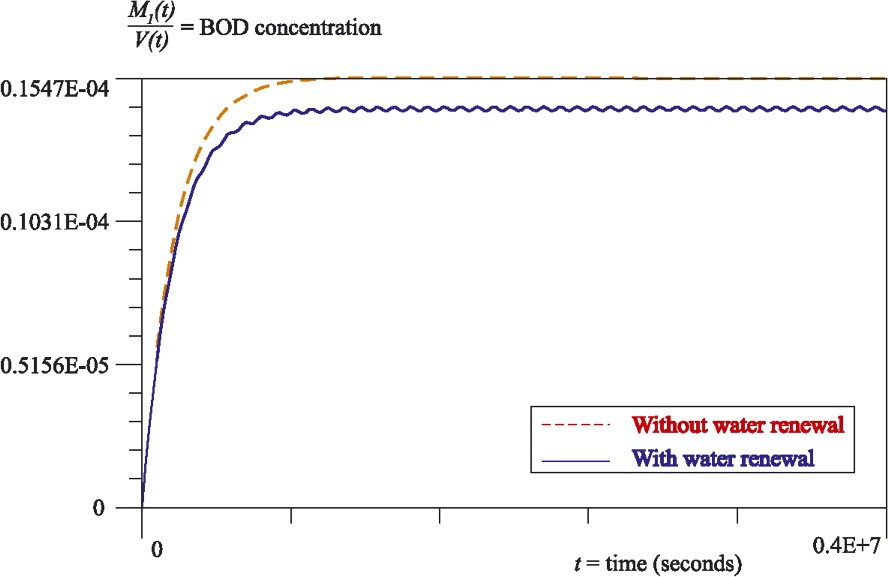
BOD concentration in the ría of Arousa (Spain) along the time.
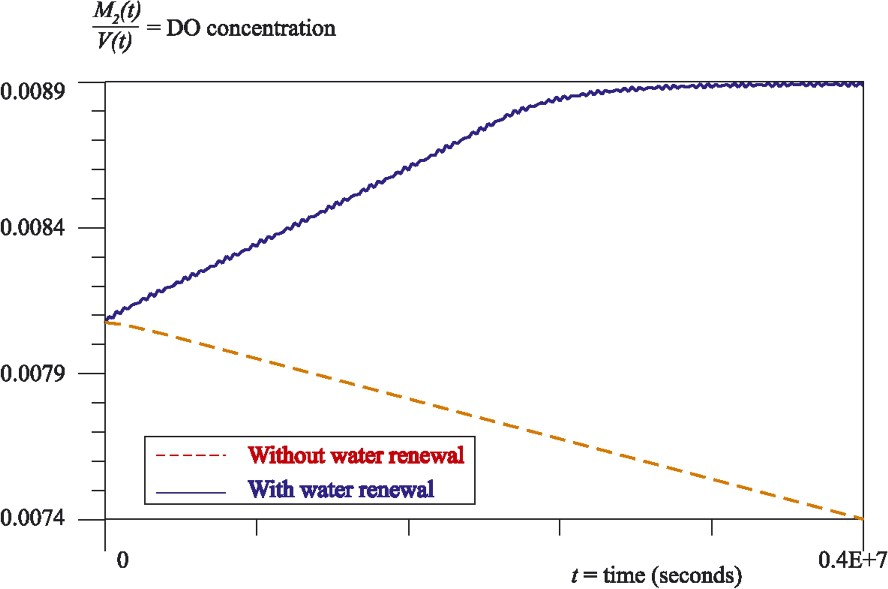
DO concentration in the ría of Arousa (Spain) along the time.
| – Total time | T=4⋅106 s |
| – Initial mass of BOD | |
| – Initial mass of DO | |
| – Mass flow rate of BOD discharged in the region | |
| – Oxygen saturation density | |
| – Kinetic coefficients and | |
| – Area of water surface in contact with air | |
| – Water volume corresponding to half tide | |
| Exclusive data for model (5) | |
| – Height over a fixed level at the mouth of the ría | |
| – Parameters α and β if | α=1, β=1 |
| – Parameters α and β if | α=0.95, β=1.02 |
4 Problem 1: Optimal management of a wastewater treatment system
In this section we pose an optimal control problem related to the management of a wastewater treatment system. We recall the situation is Section 2: we consider a domain occupied by shallow water where polluting wastewater is discharged through submarine outfalls (in this section we suppose that these outfalls are located at fixed points ). Moreover, there exist several sensitive areas, , in the domain, where it is necessary to guarantee the water quality with pollution levels lower than an allowed threshold. We suppose that wastewater arrives to the purifying plants with a certain BOD concentration. Before discharging it into the sea, its BOD concentration can be reduced in the plants by different biological or biochemical treatments. From the ecological point of view the depuration in each plant must be as high as possible but, from the economical point of view, there is a cost proportional to the developed depuration. Then, the optimal management problem is determining the depuration at each plant along the time, in such a way that the global depuration cost is minimized and the above constraints on the water quality are satisfied.
4.1 Mathematical formulation
In order to formulate this problem we need to take into account some issues. Firstly, if denotes the BOD of wastewater arriving to the jth plant and is the BOD corresponding to the maximum depuration at that plant, then determining the depuration at the jth plant is equivalent to finding the mass flow rate of BOD, , discharged through the corresponding outfall. We assume that they satisfy the constraints
| (6) |
| (7) |
Finally, we suppose that the cost of the depuration process at the jth plant is known and it is a strictly convex -function of the BOD discharged through the corresponding outfall. Hence, if denotes the cost function at jth plant, the cost of the whole depuration is given by,
| (8) |
This is an optimal control problem with pointwise state constraints and with pointwise control. We can obtain the existence and uniqueness of solution and an optimality system in order to characterize it (see [11] for further details).
4.2 Numerical resolution
The numerical solution of the optimal control problem requires a discretization of the state system (2). Moreover, in practice, because of the particular shape of the functions , the constraints can be suppressed. Thus, we are led to consider the discretized constraints:
Then, the optimal control problem can be written as follows,
4.3 Numerical results
In this work we resolve this problem in a realistic situation posed in the ría of A Coruña (Spain). We consider one purifying plant and one protected area (see Fig. 4). We assume pollutant concentration of the wastewater arriving to the purifying plant is (then the depuration cost above this value is constant and equal to 100) and we suppose that the complete depuration is not possible. Thus, we take the following cost function
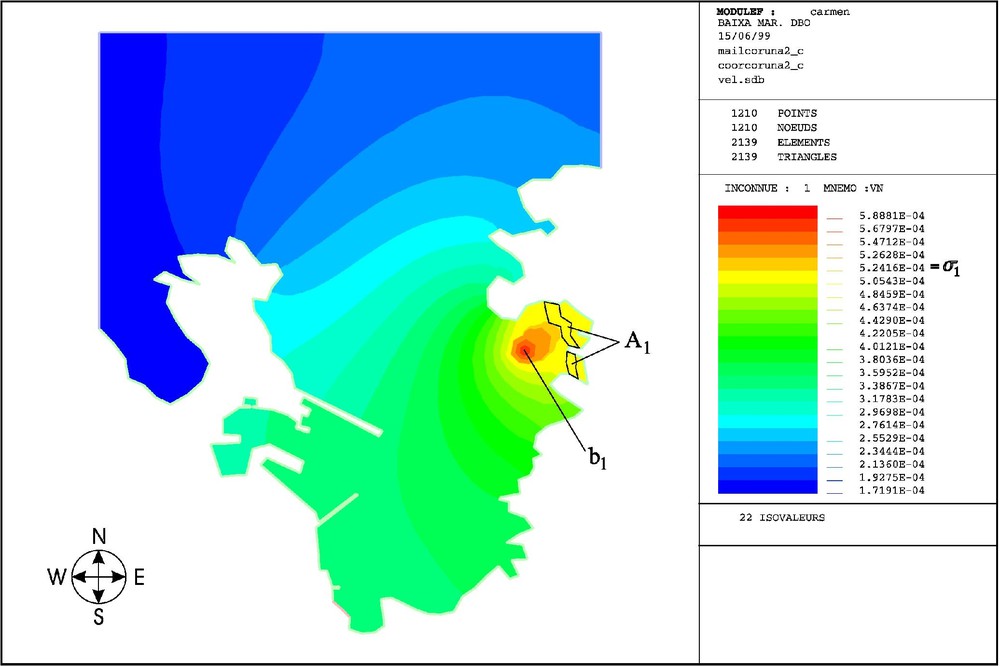
BOD concentration at the end of the tidal cycle, for the discharge in Fig. 5 (ría of A Coruña).
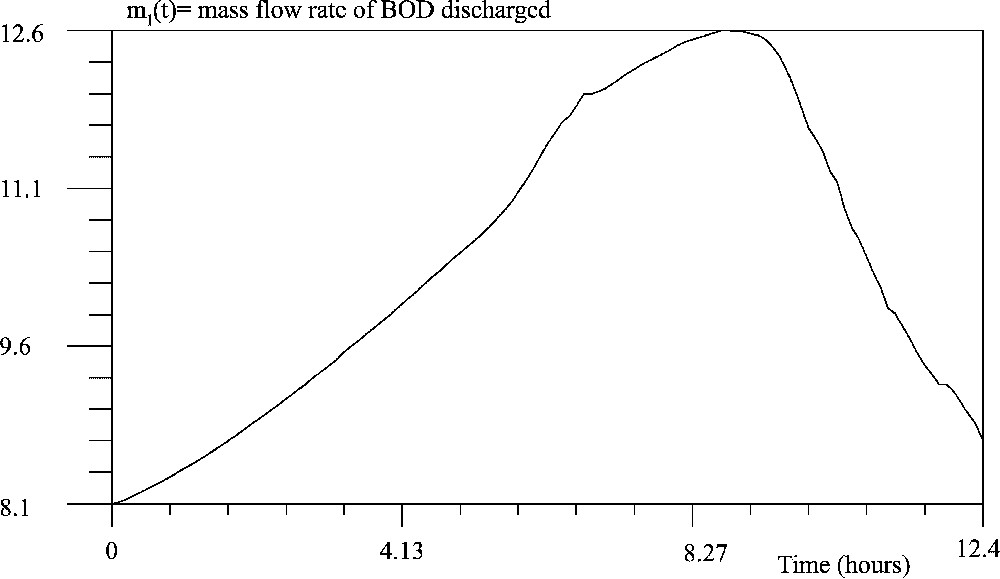
Optimal discharge during a complete tidal cycle (ría of A Coruña).
In order to make sure that the previous interpretation is correct we have found the optimal discharge during several tidal cycles. In Fig. 6, we show the optimal discharge during three cycles. In effect, we observe some periodicity, however, because of BOD accumulation, the discharge is greater in the next cycle than in the previous one. The DO concentration at the last point of time, when the saturation of the constraints takes place, can be seen in Fig. 7.
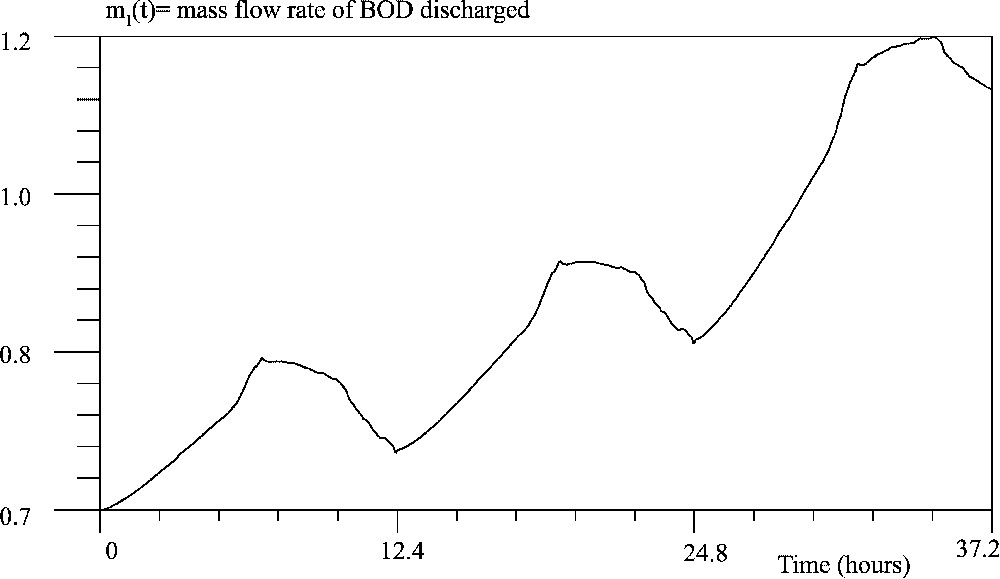
Optimal discharge during three tidal cycles (ría of A Coruña).

DO concentration at the end of the three cycles, for the discharge in Fig. 6 (ría of A Coruña).
5 Problem 2: Optimal location of wastewater outfalls
The second problem is connected with the optimal design of a wastewater treatment system. Particularly, it consists of finding the optimal location of the submarine outfalls.
We consider a similar situation to the previous one: a domain occupied by shallow water where we are going to discharge polluting wastewater through submarine outfalls and where there exist several sensitive areas in which we have to guarantee the water quality in terms of BOD and DO. Moreover, we also suppose that there are purifying plants (located at points ) but, unlike the previous problem, we now assume that the depuration in every plant is fixed (the functions are known beforehand) and our goal is to determine the points where wastewater will be discharged. These points must be determined in order to minimize the construction cost of the submarine outfalls while guaranteeing the water quality at the protected areas.
5.1 Mathematical formulation
The constraints on the water quality are given in (7). Moreover, taking into account technological limitations, the jth outfall must be placed in a suitable region , where is a compact convex polyhedral set representing all the admissible points where outfalls can be located. Thus, the optimal locations must verify . If we define , this constraint can be written in the simpler way
| (9) |
| (10) |
This is a control problem with quadratic cost but with nonconvex pointwise state constraints which makes difficult its analysis and resolution. A complete theoretical analysis of this problem can be seen in [14].
5.2 Numerical resolution
Now, in order to solve the problem , we introduce a discretization of the control problem in the same way that the previous problem. Firstly, the function collecting the discretized state constraints is denoted by ,
Then the optimal control problem is approximated by the following discrete optimization problem,
In [15], three different algorithms are used to obtain the numerical solution of namely an admissible points algorithm, the Nelder–Mead simplex method and a duality method. As we can see in that paper, due to the geometric nature of the problem, the three algorithms present a good performance, specially the Nelder–Mead method.
5.3 Numerical results
In this section we present the numerical results obtained when solving the problem for a realistic situation posed in the ría of Vigo (Spain) during a complete tidal cycle. We have taken two purifying plants, located near the coast at points and , and two protected areas (see Fig. 8).
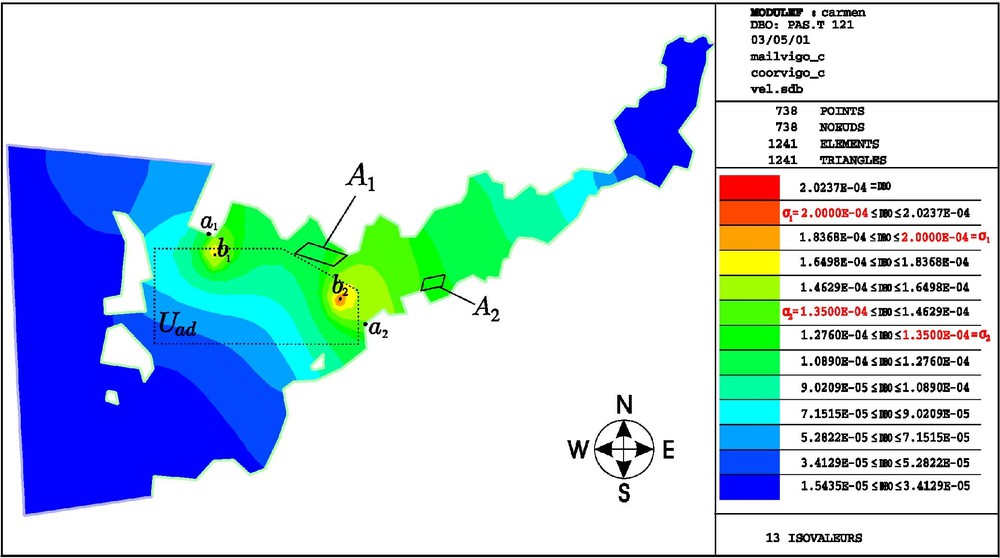
Optimal BOD concentration (hight tide, ría of Vigo).
The state constraints for both protected areas corresponds to , , , . The admissible set and the optimal locations and , given by the Nelder–Mead method can be seen in Fig. 8. Moreover, this figure shows the BOD concentration at high tide, at the end of the tidal cycle that we have simulated.
6 Conclusions
In this work, mathematical modelling and optimal control theory have been successfully applied to an interesting ecological problem: the management and design of a wastewater treatment system for coastal areas. In the last sections of the paper we present numerical results for two different cases related to this ecological problem.
However, the main contribution of this paper is the obtaining of a zero-dimensional model, which can be used in the study of the global performance of the system; we present an application of this simple model in a realistic situation posed in the ría of Arousa (Spain).
Obtained results indicate the good performance of our models and show how mathematical tools can be very useful in the study of a wide range of ecological problems.
Acknowledgments
This work was supported by Project BFM2003-00373 of Ministerio de Ciencia y Tecnología (Spain).


