1 Introduction
Usually, wastewater originated from urban areas or industry undergoes a physical/chemical/biological treatment in a purifying plant. From there, wastewater is discharged through a submarine outfall into an aquatic media like a lake, a river or a coastal area, at a suitable distance from protected areas like beaches, fisheries or marine recreation zones. When several purifying plants are going to discharge wastewater into the same domain, the problem of design and management of the whole treatment system arises. To solve this problem, optimal control theory and optimization methods can be very useful: they can help decision makers in formulating rational policies in order to minimize costs while keeping the prescribed levels of water quality. Sections 4 and 5 are devoted to present two typical examples: the optimal management of a wastewater treatment system and the optimal location of the submarine outfalls.
Obviously, the knowledge of mathematical models for the evolution of pollutant concentration is a unavoidable first step if one wants to use optimal control techniques. So, the first part of this work is devoted to study in detail one of them, related with Biochemical Oxygen Demand (BOD) and Dissolved Oxygen (DO), which is frequently used in the case of domestic discharges. In Section 2 we deal with the complete two-dimensional model consisting of two uncoupled system of partial differential equations which give us the height of water, the depth-averaged horizontal velocity of water and the depth-averaged concentration of BOD and DO. In Section 3 we obtain a new zero-dimensional model, by integrating the previous one, which can be very useful to study the global performance of the system. We apply this model in the ría of Arousa (Spain) to obtain the global concentration of BOD and DO along the time.
2 A complete two-dimensional model for Biochemical Oxygen Demand and Dissolved Oxygen
We consider a domain Ω occupied by shallow water (as can be a ría or an estuary), where polluting wastewater are discharged through
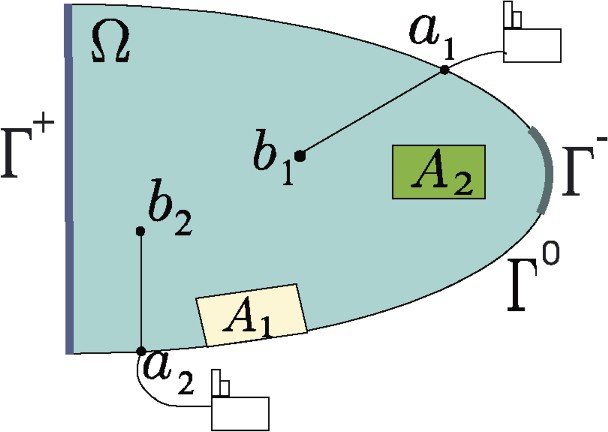
Domain Ω.
The flow of an effluent from a submarine outfall in a shallow water domain is mainly governed by horizontal transport due to currents (produced by tides, wind …) and turbulent diffusion. It allows uncouple hydrodynamical equations and transport equations. The former give the height and the velocity field which are used in latter to obtain the pollution levels.
2.1 Hydrodynamic model: the shallow water equations
In this section we recall the shallow water equations which constitute an useful mathematical model for hydrodynamic flows in shallow regions. If we consider Γ, the boundary of Ω, divided into three parts:
| (1) |
There are several works related to the existence, uniqueness and regularity of solution of (1) in particular cases (see, for instance, [1–5]) but in the general case it is still an open problem. A numerical approximation of h and
2.2 Pollutant dispersion: the BOD-DO model
Firstly, in order to simulate the water quality in Ω, we have to choose some indicators of pollution levels. Two of the most important (especially in the case of domestic discharges) are the Dissolved Oxygen (DO) and the organic matter, which can be measured in terms of the need of oxygen to decompose it, the so-called Biochemical Oxygen Demand (BOD). If the pollution level is not too high the BOD can be satisfied by the DO. However, if the organic matter increases beyond a maximum value the DO is not enough for its decomposition, leading to important modifications (anaerobic processes) in the ecosystem. To avoid them a threshold value of BOD may not be exceeded and a minimum level of DO must be guaranteed.
The evolution of the BOD and the DO in the domain
| (2) |
For this system we can prove the existence and uniqueness of solution (cf. [11]). A numerical solution for (2) can be obtained by a method which combines characteristics for time discretization with finite elements for space discretization (cf. [12]).
3 The global performance: a zero-dimensional model
The main aim in this paper is to study the global performance of the BOD-DO model in a ría, an estuary or a lake. In order to do it we integrate the system (2) in the region occupied by water. Thus, we obtain a new simple zero-dimensional model.
Let
| (3) |
If we study a stationary region (as can be a closed lake) A and V are constant along the time. In this case, if we also suppose that Q,
| (4) |
In order to develop an asymptotic study, for
For
When we are working in an open region (as can be a ría or an estuary), we must take into account the water renewal. For example, in a ría, we can assume that inflow water is more pure than outflow water (in the sense that DO concentration is greater and BOD concentration is lesser) and, moreover, we know that DO concentration in inflow water is always lesser than oxygen saturation density (
Moreover, taking into account the purification of the water in the ría because of the seawater renewal, we obtain the following expressions for the mass flow rates across the boundary:
| (5) |
This system can be easily solved by finite difference methods. We have used the backward Euler scheme to solve it for data corresponding to the ría of Arousa (Spain). Moreover, in order to study the weight of the water renewal in the ría, we have compared the result with the exact solution of (3) with
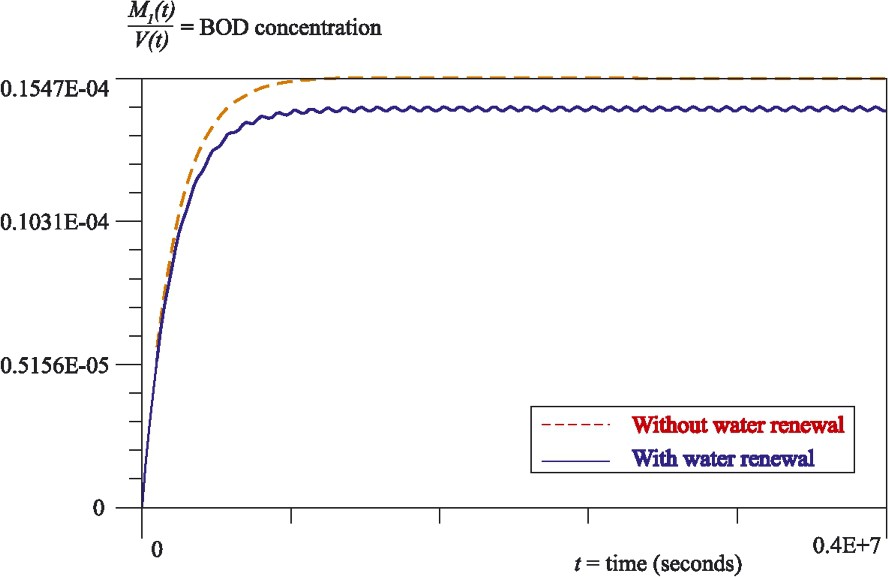
BOD concentration in the ría of Arousa (Spain) along the time.
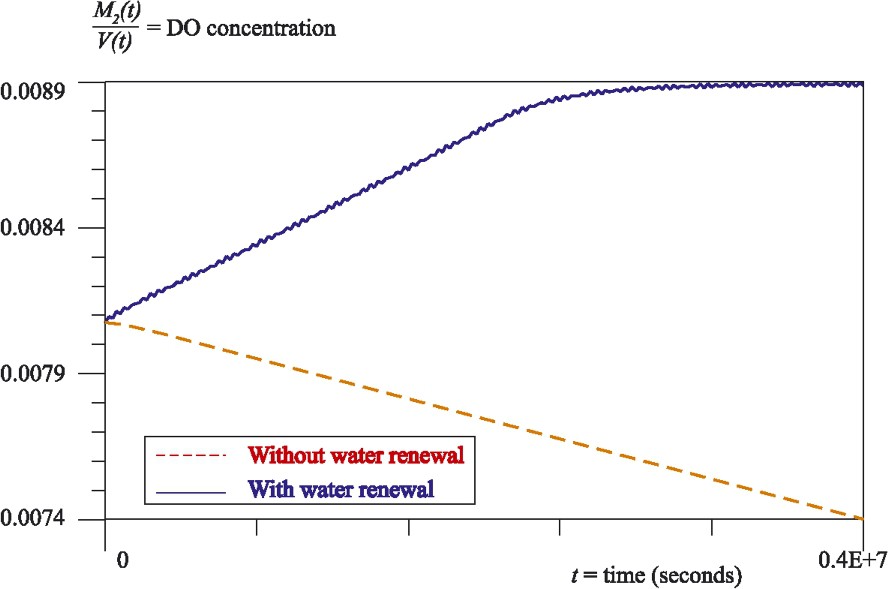
DO concentration in the ría of Arousa (Spain) along the time.
| – Total time | T=4⋅106 s |
| – Initial mass of BOD |
|
| – Initial mass of DO |
|
| – Mass flow rate of BOD discharged in the region |
|
| – Oxygen saturation density |
|
| – Kinetic coefficients |
|
|
|
|
| – Area of water surface in contact with air |
|
| – Water volume corresponding to half tide |
|
| Exclusive data for model (5) | |
| – Height over a fixed level at the mouth of the ría |
|
| – Parameters α and β if |
α=1, β=1 |
| – Parameters α and β if |
α=0.95, β=1.02 |
4 Problem 1: Optimal management of a wastewater treatment system
In this section we pose an optimal control problem related to the management of a wastewater treatment system. We recall the situation is Section 2: we consider a domain occupied by shallow water where polluting wastewater is discharged through
4.1 Mathematical formulation
In order to formulate this problem we need to take into account some issues. Firstly, if
| (6) |
| (7) |
Finally, we suppose that the cost of the depuration process at the jth plant is known and it is a strictly convex
| (8) |
This is an optimal control problem with pointwise state constraints and with pointwise control. We can obtain the existence and uniqueness of solution and an optimality system in order to characterize it (see [11] for further details).
4.2 Numerical resolution
The numerical solution of the optimal control problem
Then, the optimal control problem
4.3 Numerical results
In this work we resolve this problem in a realistic situation posed in the ría of A Coruña (Spain). We consider one purifying plant and one protected area (see Fig. 4). We assume pollutant concentration of the wastewater arriving to the purifying plant is
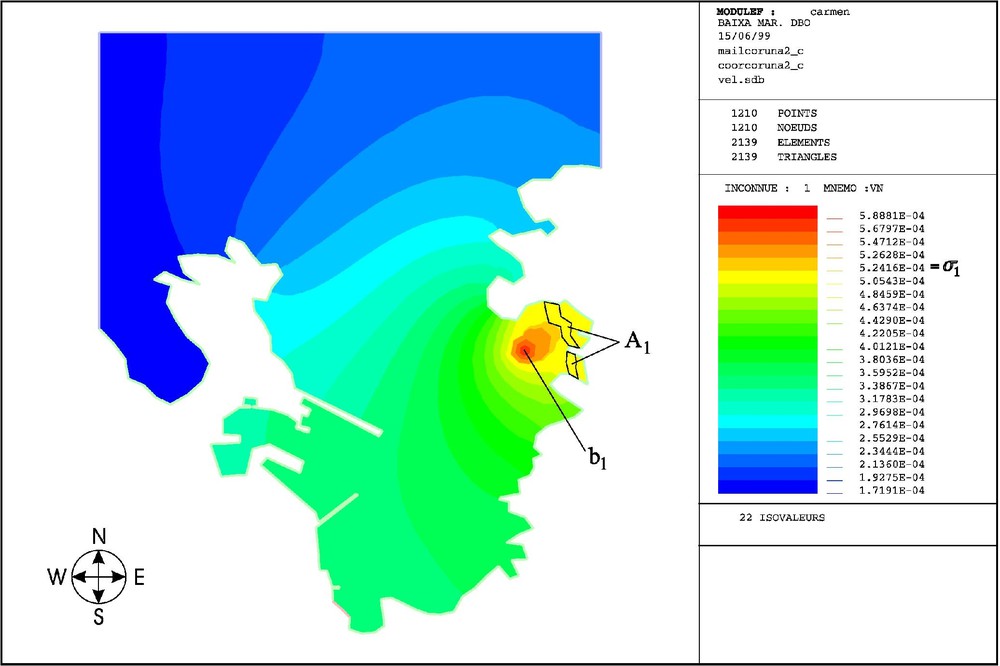
BOD concentration at the end of the tidal cycle, for the discharge in Fig. 5 (ría of A Coruña).
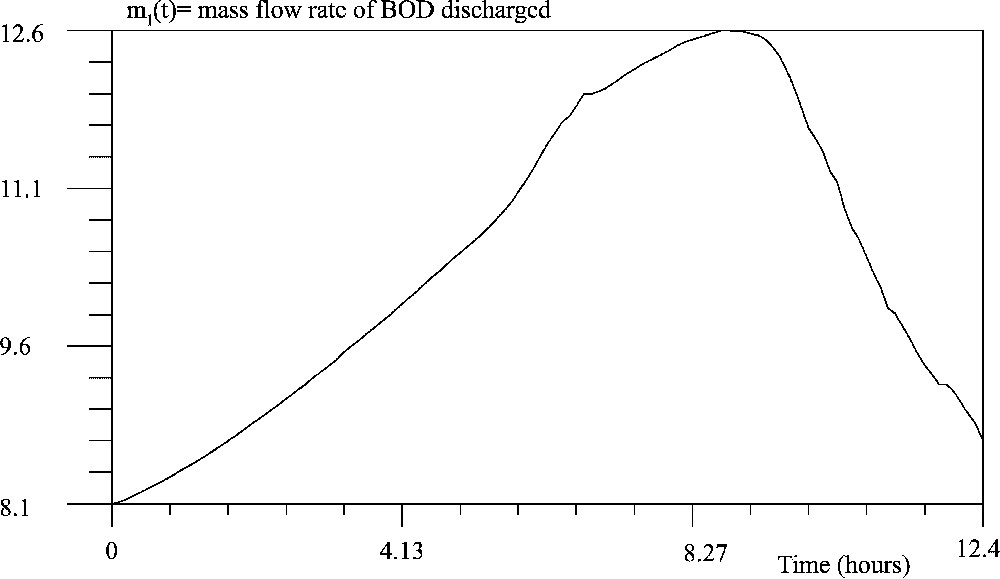
Optimal discharge during a complete tidal cycle (ría of A Coruña).
In order to make sure that the previous interpretation is correct we have found the optimal discharge during several tidal cycles. In Fig. 6, we show the optimal discharge during three cycles. In effect, we observe some periodicity, however, because of BOD accumulation, the discharge is greater in the next cycle than in the previous one. The DO concentration at the last point of time, when the saturation of the constraints takes place, can be seen in Fig. 7.
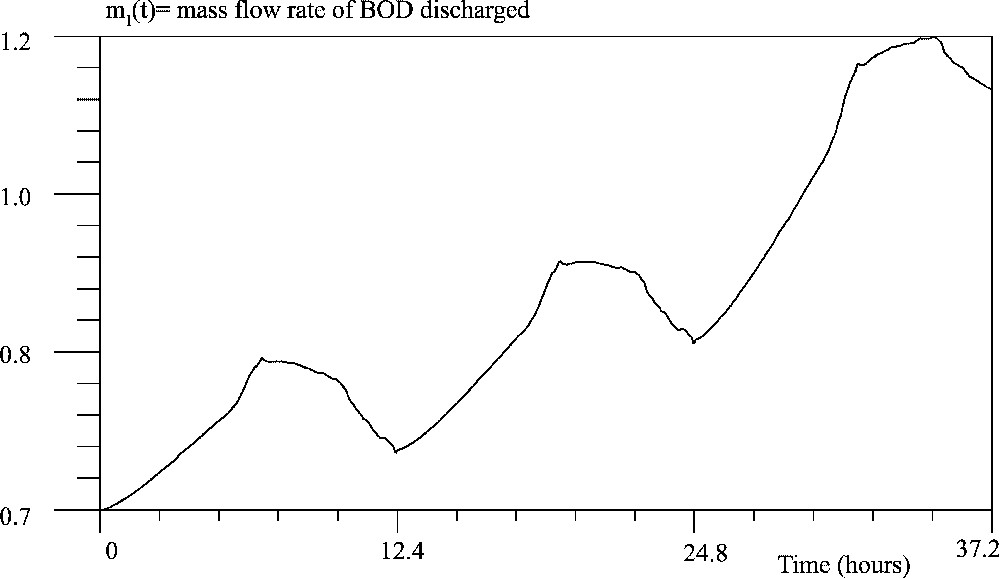
Optimal discharge during three tidal cycles (ría of A Coruña).

DO concentration at the end of the three cycles, for the discharge in Fig. 6 (ría of A Coruña).
5 Problem 2: Optimal location of wastewater outfalls
The second problem is connected with the optimal design of a wastewater treatment system. Particularly, it consists of finding the optimal location of the submarine outfalls.
We consider a similar situation to the previous one: a domain occupied by shallow water where we are going to discharge polluting wastewater through submarine outfalls and where there exist several sensitive areas in which we have to guarantee the water quality in terms of BOD and DO. Moreover, we also suppose that there are
5.1 Mathematical formulation
The constraints on the water quality are given in (7). Moreover, taking into account technological limitations, the jth outfall must be placed in a suitable region
| (9) |
| (10) |
This is a control problem with quadratic cost but with nonconvex pointwise state constraints which makes difficult its analysis and resolution. A complete theoretical analysis of this problem can be seen in [14].
5.2 Numerical resolution
Now, in order to solve the problem
Then the optimal control problem
In [15], three different algorithms are used to obtain the numerical solution of
5.3 Numerical results
In this section we present the numerical results obtained when solving the problem
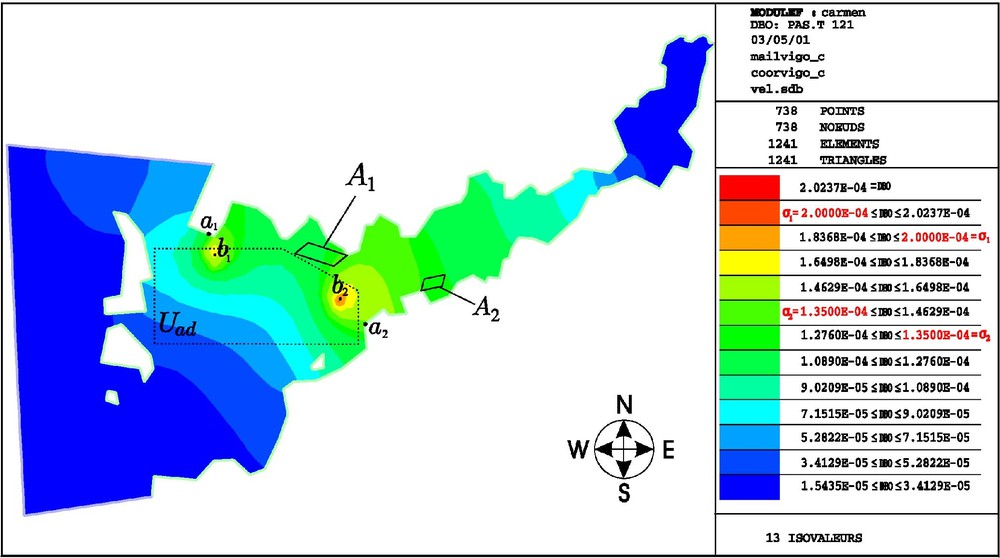
Optimal BOD concentration (hight tide, ría of Vigo).
The state constraints for both protected areas corresponds to
6 Conclusions
In this work, mathematical modelling and optimal control theory have been successfully applied to an interesting ecological problem: the management and design of a wastewater treatment system for coastal areas. In the last sections of the paper we present numerical results for two different cases related to this ecological problem.
However, the main contribution of this paper is the obtaining of a zero-dimensional model, which can be used in the study of the global performance of the system; we present an application of this simple model in a realistic situation posed in the ría of Arousa (Spain).
Obtained results indicate the good performance of our models and show how mathematical tools can be very useful in the study of a wide range of ecological problems.
Acknowledgments
This work was supported by Project BFM2003-00373 of Ministerio de Ciencia y Tecnología (Spain).


