1 Introduction
Since the initial discovery by Kubas and co-workers of the transition metal dihydrogen complex W(η2-H2)(PiPr3)2(CO)3 〚1,2〛, the chemistry of dihydrogen complexes has developed very rapidly, as manifested by a number of relevant reviews 〚2–8〛. A large majority of these isolable dihapto-H2 complexes has been found to be singly charged cationic species. This is mainly due to the common synthetic route of protonating a neutral metal hydride; an underlying aspect may be that the positive charge confers additional stability on the H2 complexes 〚9–11〛. While in this kind of compounds, monocationic ruthenium dihydride or dihydrogen complexes of the type 〚Cp’RuH2L2〛+ (Cp’ = C5H5, C5H4R or C5Me5; L2 = one diphosphine or two monodentate phosphine ligands) are common and their structures well established 〚12–15〛, their half-sandwich iron-based counterparts are scare. We have reported on the isolation and spectroscopic characterizations of the first half-sandwich organo-iron dihydrogen 〚Cp*Fe(dppe)(η2-H2)〛+ (2+; Cp* = C5Me5, dppe = 1,2-bis(diphenylphosphino)ethane) 〚16〛. It was obtained by protonation of Cp*Fe(dppe)H (1) with HBF4 in Et2O at –80 °C. The dihydrogen complex rearranges irreversibly into its tautomeric iron(IV) dihydride form trans-〚Cp*Fe(dppe)(H)2〛+ (4+), as the temperature is raised. Two years later, Puerta and co-workers 〚17〛 published the synthesis and the X-ray crystal structure of another stable iron(IV) dihydride derivative trans-〚Cp*Fe(dippe)(H)2〛BPh4– (dippe = 1,2-bis(diisopropylphosphino)ethane). The iron(IV) dihydride complex trans-〚CpFe(CO)(PEt3)(H)2〛+ was also spectroscopically characterised at –78 °C by Brookhart and co-workers 〚18〛. In this latter case, the dihydrogen compound is the thermodynamically more stable isomer.
On the other hand, steric interactions between the phosphine ligands and the C5 ring associated with their respective electron richness have been established to play an important role in determining the position of the dihydrogen/dihydride equilibrium for ruthenium complexes 〚6,19〛. However, such dihydride/dihydrogen equilibrium has not been observed in the case of related iron complexes. Nevertheless, a subtle balance of the steric and electronic environments around the metal is reached with the Cp*Fe(dppe) fragment that allows the isolation of both classical and non-classical dihydride isomers. Since the earlier theoretical studies on dihydrogen complexes 〚20,21〛, the electronic effects that govern the dihydride/dihydrogen equilibrium have been extensively investigated by various types of quantum chemical calculations 〚8,22〛. It is generally admitted that strong π-donor metal centres tend to favour full dissociation of the H–H bond, i.e. to favour the dihydride form over the dihydrogen one. Therefore, the observation of both isomers requires a fine-tuning of the metal π-donor ability.
We report in this paper (i) full experimental details on the synthesis of both non-classical 〚Cp*Fe(dppe)(h2–H2)〛+X– (2+X–) and classical 〚Cp*Fe(dppe)(H)2〛+X– (4+X–), cationic iron hydride complexes (X = BF4, PF6), (ii) NMR characterisation of the complexes, (iii) the X-ray crystal and molecular structure of the dihydride derivative trans-〚Cp*Fe(dppe)(H)2〛+BF4–, and (iv) a theoretical analysis of the electronic structure of 2+ and 4+ by means of DFT calculations. A significant part of the experimental work has been reported in a preliminary form 〚16〛.
2 Experimental section
2.1 Materials
All manipulations were carried out under an argon atmosphere using Schlenk techniques. Reagent grade tetrahydrofuran (THF), diethyl ether and pentane were dried and distilled from sodium benzophenone ketyl prior to use. Dichloromethane and acetone were distilled under argon from P2O5 and B2O3, respectively. Complexes Cp*Fe(dppe)H 〚23〛, Cp*Fe(dppe)D 〚23〛 and 〚Cp*Fe(dppe)〛+PF6– 〚24〛 were prepared following the published procedures, and other chemicals were purchased from commercial sources and used as received. NMR spectra were recorded on multinuclear Bruker AM300WB (300 MHz) or DPX 200 (200 MHz) spectrometers. Chemical shifts are reported (in ppm) relative to internal tetramethylsilane (TMS) or to the residual proton resonance resulting from incomplete deuteration of the NMR solvents for 1H NMR; the carbon of the deuterated NMR solvents for 13C NMR; external 85% H3PO4 for 31P NMR, and external CFCl3 for 19F NMR. Proton T1 studies were performed using the standard inversion recovery 180°–τ–90° pulse sequence method 〚25〛. Temperatures within the NMR probe were controlled by a Bruker VT unit, and temperature calibration was accomplished by following the Van Geet methanol calibration method 〚26〛, and found to be accurate within 1 °C. The samples for variable-temperature NMR were prepared in degassed CD2Cl2 in 5 mm NMR tubes. Elemental analyses were performed at the Centre for Microanalyses of the CNRS at Vernaison, France.
2.2 Synthesis and characterisation
2.2.1 〚Cp * Fe(dppe)( η2-H2)〛+BF4– (2+BF4–)
To a cooled (–80 °C) orange diethylether solution (20 ml) of 0.59 g (1.0 mmol) of Cp*Fe(dppe)H were added by syringe 187 μl (1.5 mmol) of HBF4·OEt2. A yellow suspension formed and the stirring is maintained for 3 h. The solid was filtered off, washed with cold pentane (4 × 50 ml), and dried under vacuum at temperature always below –50 °C. Complex 〚Cp*Fe(dppe)(η2-H2)〛+BF4–is isolated as a lemon–yellow powder in 95% yield (0.64 g). 1H NMR (300 MHz, CD2Cl2, 193 K) δ: 7.96–7.39 (m, 20 H, Ph), 2.07–1.92 (2m, 4 H, CH2), 1.45 (s, 15 H, C5Me5), –12.39 (bs, w1/2 = 50 Hz, 2 H, Fe(η2-H2); T1 min (223 K, 300 MHz) = 7 ms). 13C NMR (75 MHz, CD2Cl2, 193 K) δ: 136.5–129.1 (m, Ph), 91.1 (s, C5Me5), 31.1 (m, CH2, JCH = 136 Hz), 10.1 (q, C5Me5, JCH = 128 Hz). 31P NMR (121 MHz, CD2Cl2, 193 K) δ: 93.6 (s, dppe).
2.2.2 〚Cp * Fe(dppe)( η2-H2)〛+PF6– (2+PF6–)
A Schlenk tube under argon, containing a cooled (–80 °C) THF solution (30 ml) of 〚Cp*Fe(dppe)〛+PF6– (0.734 g, 1.0 mmol), is pressurised with 2 bar of H2. The initial orange–red color of the solution turned immediately yellow and the stirring is continued for 15 min. Low temperature work up, as described above, provided 0.662 g (90% yield) of 〚Cp*Fe(dppe)(η2-H2)〛+PF6–, authenticated by comparison of its 1H NMR data with those of its corresponding BF4– salt (see § 2.2.1.).
2.2.3 〚Cp * Fe(dppe)(H)2〛+BF4– (4+BF4–)
A yellow solid sample of 〚Cp*Fe(dppe)(η2-H2)〛+BF4– (0.405 g, 0.6 mmol), prepared as described above in § 2.2.1., was kept in a Schlenk tube under argon, at 20 °C for 48 h. The colour of the solid material turned light orange–yellow. The solid is dissolved in 10 ml of acetone. The solution is filtered off, concentrated to 2 ml and layered with 10 ml of pentane. A yellow–orange precipitate formed. After filtration and drying under vacuum, 0.381 g (94%) of 〚Cp*Fe(dppe)(H)2〛+BF4– are recovered as air and thermally stable microcrystals. Anal. calcd for C36H41BFeF4P2: C, 63.75%; H, 6.09%; P, 9.13%. Found: C, 63.39%; H, 5.85%; P, 9.22%. 1H NMR (200 MHz, CD3COCD3) δ: 8.01–7.35 (m, 20 H, Ph), 2.33 (m, 2 H, CH2), 2.27 (m, 2H, CH2), 1.58 (s, 15 H, C5Me5), –7.65 (t, 2 H, Fe-H, JHP = 69 Hz). 13C {1H} NMR (50 MHz, CD3COCD3), δ: 135.3 (t, Ph), 131.8 (s, Ph), 129.6 (t, Ph), 96.1 (s, C5Me5), 33.7 (t, CH2), 9.8 (s, C5Me5). 31P NMR (81 MHz, CD3COCD3), δ: 90.8 (t, dppe, JPH = 69 Hz). 19F NMR (188 MHz, CD3COCD3) δ: 127.0 (BF4–).
2.2.4 〚Cp*Fe(dppe)(H)2〛+PF6– (4+PF6–)
A Schlenk tube under argon, containing a THF solution (30 ml) of 〚Cp*Fe(dppe)+PF6– (0.734 g, 1.0 mmol), is pressurised with 2 bar of H2. The initial orange color of the solution turned immediately yellow and the stirring is continued for 5 min. The solvent is then evaporated under reduced pressure and the yellow residue is washed with pentane (3 × 20 ml). Following the extraction with dichloromethane, concentration of the extracts, filtration and precipitation with an excess of diethyl ether, 0.660 g (90% yield) of 〚Cp*Fe(dppe)(H)2〛+PF6– are isolated, and identified by comparison of its 1H NMR parameters with those of its corresponding BF4– salt (see § 2.2.3.).
2.3 Crystallographic data collection and refinement of the structure of 4+BF4–
X-ray quality crystals of 〚Cp*Fe(dppe)(H)2〛+BF4– were grown as described above in § 2.2.3. section. Diffraction data were collected at 293 K with an Enraf-Nonius CAD-4 diffractometer, using graphite monochromated MoKα radiation (λ = 0.710 69 Å). Crystal parameters and refinement results are summarised in Table 1. Complete details of the crystal data, X-ray data collection, and structure solution are provided as Supporting Information. Cell constants and orientation matrix for data collection were obtained from a least-squares refinement using 25 high-θ reflections. After Lorenz and polarisation corrections 〚27〛, the structure was solved with SIR-97 〚28〛, which revealed all non-hydrogen atoms of the molecule. A riding model was applied to hydrogen atoms bound to carbon (C–H = 0.96 Å), which were included in the model at idealised positions, while hydrogen atoms bound to iron were located in Fourier difference maps and were not refined. Isotropic thermal parameters were considered for all H-atoms equal to 1.2 times the equivalent isotropic thermal parameters of the corresponding parent atom. The whole structures were next refined with SHELXL97 〚29〛, by the full-matrix least-square techniques based on F2, including all reflections. Atomic scattering factors were taken from the literature 〚30〛. The refinements converged at conventional R-factors of 0.0677, for 3045 reflections with I > 2 σ(I) (R = 0.1916 for all reflections). ORTEP view of the molecule (Fig. 1) was generated with PLATON98 〚31〛. All the calculations were performed on a Pentium NT Server computer.
Crystal data, data collection, and refinement parameters for complex trans-〚Cp*Fe(dppe)(H)2〛+BF4– (4+BF4–).
| Formula | C36H41BF4FeP2 |
| FW | 678.29 |
| Temperature (K) | 293(2) |
| Crystal system | monoclinic |
| Space group | P21/c |
| a (Å) | 11.838(6) |
| b (Å) | 13.216(9) |
| c (Å) | 22.186(12) |
| α (°) | 90 |
| ß (°) | 103.21(2) |
| γ (°) | 90 |
| V (Å3) | 3379(3) |
| Z | 4 |
| D(calcd) (g cm–3) | 1.333 |
| Crystal size (mm) | 0.35 × 0.32 × 0.25 |
| F(000) | 1416 |
| Diffractometer | CAD4 |
| Radiation λ | 0.710 69 |
| Absorption coefficient (mm–1) | 0.587 |
| θ range (°) | 1.77–24.98 |
| Range h,k,l | 0/14, 0/15, –26/26 |
| Number of total reflections | 6234 |
| Number of unique reflections | 5927 |
| Number of observed reflections 〚I > 2 σ(I)〛 | 3045 |
| Restraints/parameters | 0/398 |
| ω = 1/〚σ2 (Fo)2 + (a P)2 + b P〛 | a = 0.1470 |
| (where P = 〚Fo2 + 2 Fc2〛/3) | b = 0.0000 |
| Final R | 0.0677 |
| Rω | 0.1747 |
| R indices (all data) | 0.1916 |
| Rω (all data) | 0.2252 |
| Goodness of fit / F2 | 0.962 |
| Largest diffraction peak & hole (e Å–3) | 0.537 –0.763 |
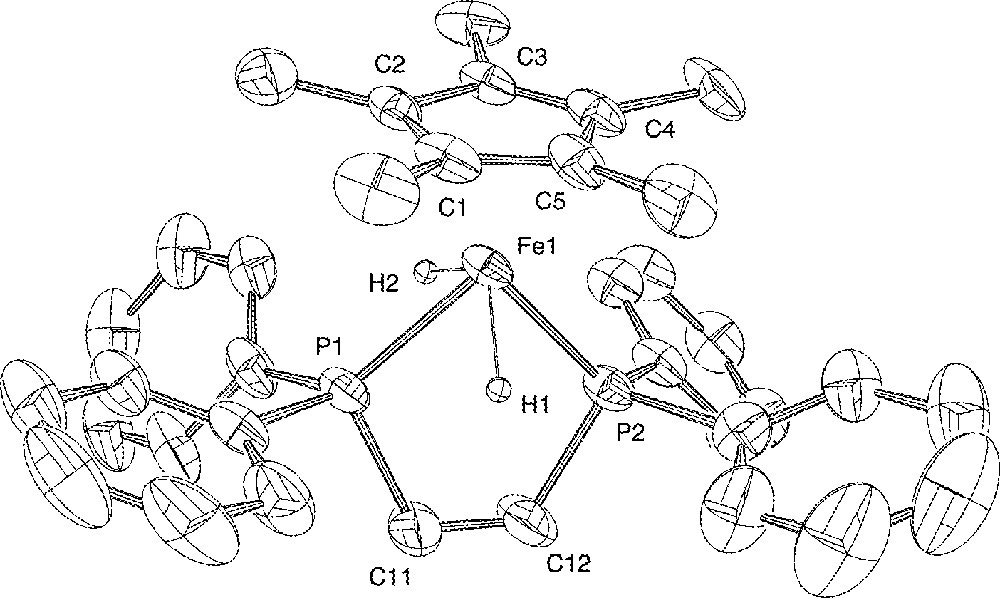
ORTEP view of the trans-〚Cp*Fe(dppe)(H)2〛+ cation. Hydrogen atoms (except the hydrides) and BF4– anion are omitted for clarity. Thermal ellipsoids are plotted at the 50% probability level.
2.4 Computational details
DFT calculations 〚32–35〛 were carried out using the Amsterdam Density Functional (ADF) program 〚36〛. The Vosko–Wilk–Nusair parameterisation 〚37〛 was used to treat electron correlation within the local density approximation (LDA). The non-local corrections of Becke 〚38,39〛 and of Perdew 〚40,41〛 were added to the exchange and correlation energies, respectively. The numerical integration procedure applied for the calculations was developed by te Velde et al. 〚35〛 A triple-ζ Slater-type orbital (STO) basis set was used for Fe 3d and 4s, and a single-ζ STO was used for Fe 4p. Concerning the hydrogen atoms directly bonded to the Fe centre, a triple-ζ STO basis set was employed for 1s, augmented with a single-ζ polarization function 2p. The other atoms were described by a double-ζ STO basis set for H 1s, C 2s and 2p, and P 3s and 3p, augmented with a single-ζ polarization function (2p for H, C; 3d for P). Full geometry optimisations (assuming a C1 symmetry) were carried out on each complex, using the analytical gradient method implemented by Verluis and Ziegler 〚42〛. A DFT fragment analysis, which includes a fragment MO population decomposition, was also made on each complex in the way proposed by Ziegler and co-workers 〚43–45〛.
3 Results and discussion
3.1 Preparation and spectroscopic characterisations of complexes
Protonation of the thermally stable neutral hydride derivative Cp*Fe(dppe)H (1) 〚23〛 by a slight excess (1.5 equiv) of HBF4·Et2O in diethyl ether at –80 °C affords rapidly the corresponding cationic dihydrogen complex 〚Cp*Fe(dppe)(η2-H2)〛+BF4– (2+BF4–), isolated in 95% yield as a lemon-yellow powder after work up at low temperature (T < –50 °C) (Fig. 2). Its PF6– salt dihydrogen analogue 2+PF6– was prepared in 90% yield by stirring a THF solution of the paramagnetic red 16-electron iron(II) complex 〚Cp*Fe(dppe)〛+PF6– (3+PF6–) 〚24〛 under H2 (2 atm) at –80 °C (Fig. 2). Despite their thermal instability, solid samples of 2+ can be stored for several weeks under argon at low temperature, without any signs of decomposition.
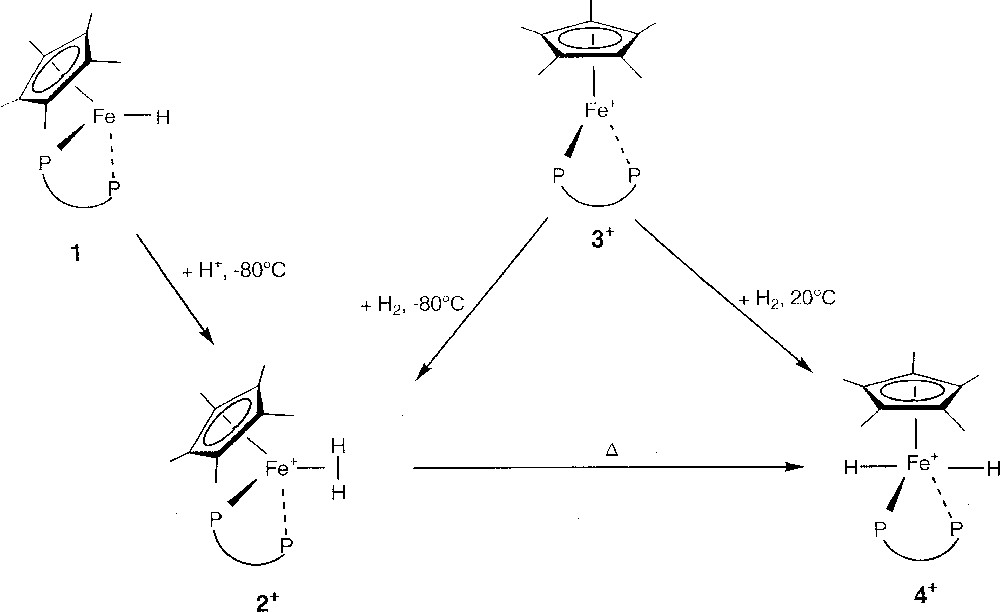
Reactional route from 1 to 4+.
In the hydride region of its 1H NMR spectrum (CD2Cl2, 193 K), complex 2+ displayed a broad resonance at δ –12.39, which integrated for 2 protons. The relaxation time of the metal bound hydride (300 MHz, shows a minimum of T1 (longitudinal relaxation time) of 7 ms at 223 K, in agreement with the formulation of complex 2+ as a dihydrogen derivative.
The HD complex 〚Cp*Fe(dppe)(η2-HD)〛BF4 (2+-d1BF4– was correspondingly prepared by protonation of the neutral iron deuteride Cp*Fe(dppe)D 〚23〛 with HBF4·Et2O. The expected 1:1:1 triplet centred at δ –12.4 was observed for 2+-d1BF4–, and the value of JH–D was determined to be 27.0 Hz, which is diagnostic of an η2-H2 bonding interaction and unequivocally establishes the structure of 2+BF4–.
Using the correlation established by Morris et al. 〚46〛 or that of Luther and Heinekey 〚47〛, it is possible to estimate the H–H distance knowing the H–D coupling within a dihydrogen complex. The value obtained in our case is 0.97 ± 0.01 Å, in good agreement with calculations (see below). Evaluation of the H–H distance within the dihydrogen complex can also be achieved using relaxation data 〚48〛. Depending upon the relative rate of the H2 ligand rotation around the M–H2 axis, two possible values for the H–H distance can be calculated from the T1 minimum values using static and fast-rotation models 〚6,49,50〛. The determination of the H–H bond lengths in the H2 ligand of the cation 2+ by the T1 minimum method using a static rotation model afforded an H–H separation of 0.98 ± 0.01 Å, a value very close to that calculated from the JHD value (0.97 Å). This distance is in agreement with the presence of a slightly stretched dihydrogen ligand in the coordination sphere of iron, due to the electron-releasing capabilities of the cationic organometallic moiety, and fully consistent with the theoretical results (see § 3.3.).
Upon warming, the dihydrogen complex 2+ converts, either in solution or in the solid state, to its respective trans-classical dihydride isomer 〚Cp*Fe(dppe)(H)2〛+ (4+), as its BF4– or PF6– salt, which is the exclusive product at room temperature (Fig. 2). Thus, pure dihydride complex 4+BF4– is isolated in 94% yield after keeping a sample of the dihydrogen complex 2+BF4– under argon at –20 °C for two days. On the other hand, complex 4+PF6– is prepared in quantitative yield by simple exposure of the 16-electron derivative 3+PF6– to H2 gas, at room temperature (Fig. 2).
The dihydrogen/dihydride transformation in solution upon warming is cleanly followed by 1H NMR spectroscopy, which reveals the appearance and the progressive increase of a sharp triplet at –7.65 ppm with the concomitant decrease and eventually complete disappearance of the broad resonance at –12.39 ppm. If the sample is cooled again to –80 °C, no dihydrogen complex reforms, which indicates that the process is gradual, complete, and irreversible, the classical dihydride complex being the thermodynamically more stable isomer.
The 4+ salts are yellow–orange crystalline materials, which are non-air- or moisture-sensitive. The IR spectra do not show bands clearly attributable to ν(FeH). As stated above, the hydridic protons of an isolated species 4+ appear on the 1H NMR spectrum in acetone-d6 as a triplet centred at –7.65 ppm due to coupling (JHP = 69 Hz) with two equivalent phosphorus nuclei. One singlet is observed at δ 90.8 on the 31P{1H} NMR spectrum, which transforms in a triplet with JPH = 69 Hz in the undecoupled spectrum. These data suggest the equivalence of the hydride ligands and the two phosphorus atoms. The classical dihydride structure for 4+BF4– is supported by the relaxation time T1 min = 175 ms (300 MHz, acetone-d6, 223 K), which rules out any bonding interaction between the hydrides. According to these data, compounds 4+ must have four-legged piano stool structure. The transoid disposition (C2v symmetry), with two orthogonal mirror planes (assuming free rotation of the C5Me5 ligand), can be confidently attributed on the basis of the simplicity of the 13C{1H} NMR spectrum. Indeed, all four phenyl groups are equivalent and give rise to three separate resonances for the four magnetically non-equivalent carbon atoms of these phenyl groups. This pattern, which is probably due to accidental degeneracy of two signals, clearly indicates a change from the Cs symmetry, invariably observed for the three-legged piano stool structure of previous compounds in this series 〚23,51,52〛 to a C2v symmetry.
These results sharply contrast with those of Brookhart et al. 〚18〛, in which the opposite situation was observed. The in-situ generated dihydrogen complexes 〚CpFe(CO)L(η2-H2)〛BAr’4 (Cp = C5H5; L = PEt3, PPh3; Ar’ = 3,5-(CF3)2(C6H3) are indeed the thermodynamically more stable isomers. The classical trans-dihydride derivative (L = PEt3) was however, characterized at –78 °C by 1H NMR spectroscopy, and no equilibrium between the dihydride and the dihydrogen forms was found. The 〚Cp*Fe(dppe)〛+ metal centre is more electron-rich than that in the 〚CpFe(CO)L〛+ moiety, thus favouring the oxidative addition of coordinated H2 through an increase back bonding in the σ* orbital of the dihydrogen ligand. This electronic difference is also illustrated in the JHD value that is equal to 32 Hz in Brookhart’s compound 〚18〛 and is consistent with a loose binding of H2 to the metal centre, as compared to the 27 Hz value found in our case. A rapid equilibrium has however been reported in this series of piano-stool structure Cp*Fe complexes 〚53〛. It occurs between the classical highly fluxional and unstable iron(IV) trihydride complex Cp*FeH3(PMe3), generated only in benzene or tetrahydrofuran solution, and its non-classical Fe(II) dihydrogen-hydride form Cp*FeH(η2-H2)(PMe3) as deduced from JHD and minimum T1 measurements. Steric protection must then play an important role in stabilizing trans-dihydride iron(IV) compounds. Complex 〚Cp*Fe(dmpe)(H)2〛+BF4– (dmpe = 1,2-bis(dimethylphosphino)ethane), which was obtained by protonation of its corresponding monohydride precursor, was found to be extremely unstable in solution 〚53〛, whereas the homologue complexes, bearing bulkier diphosphines dppe and dippe, 〚Cp*Fe(dppe)(H)2〛+ (4+) and 〚Cp*Fe(dippe)(H)2〛+BPh4– 〚17〛 are isolated at room temperature. On the other hand, coordination of dihydrogen or its homolytic splitting at metal centre greatly depends on the electron-donating capabilities of the organometallic moieties 〚8,20,21〛. Thus, when the chelating diphosphine ligand dppe is substituted for the dippe (a better σ-donor but poorer π-acceptor than the dppe) at the iron centre, Puerta et al. have reported that the stabilisation of coordinated dihydrogen is no more possible with the very electron-rich fragment 〚Cp*Fe(dippe)〛+〚17〛, whereas the dihydrogen complex 2+ is isolated at low temperature. This is in accord with the criterion for the stability of the metal–dihydrogen bond proposed by Morris, based upon the value of ν(N2) for the associated dinitrogen complex 〚54〛. The 〚Cp*Fe(dppe)〛+ fragment adds N2 to provide the end-on dinitrogen complex 〚Cp*Fe(dppe)(N2)〛+ 〚55〛, which exhibits a strong N–N stretching vibration at 2117 cm–1, whereas the 〚Cp*Fe(dippe)〛+ complex is reluctant to N2 coordination.
3.2 X-ray crystal structure determinations of trans-〚Cp*Fe(dppe)(H)2〛+BF4– (4+BF4–)
The X-ray crystal structure of 4+BF4– has been determined as outlined in the ‘Experimental’ section, confirming its formulation as a classical organo-iron(IV) dihydride. A view of the molecular structure of the organometallic cationic moiety 〚Cp*Fe(dppe)(H)2〛+ is presented in Fig. 1. Relevant interatomic distances and angles are listed in Table 2. The two hydrides were located but not refined, and as such this does not provide accurate structural information. More reliable data on the bonding within the FeH2 fragment are provided by solution 1H and 31P NMR experiments (vide supra). However, the coordination around iron can be unambiguously described as a distorted four-legged piano stool structure. The two hydride atoms are in transoid positions, with an H(1)–Fe(1)–H(2) angle of 110.5°, and the plane containing these three atoms makes an angle of 76.1° with the plane of the C5 ring. The iron–hydride bond distances Fe(1)–H(1) 1.48 Å and Fe(1)–H(2) 1.50 Å are in the normal range previously measured in other iron(IV) hydride complexes, with Fe–H distances ranging from 1.1(1) to 1.72(9) Å 〚17,56–60〛. One can note however, that in the closely related bis(diisopropylphosphino)ethane derivative 〚Cp*Fe(dippe)(H)2〛+BPh4–, the iron–hydride bond distances are somewhat shorter 1.35(6) and 1.41(5) Å 〚17〛.
Selected bond lengths (Å) and angles (°) for complex trans-〚Cp*Fe(dppe)(H)2〛+BF4– (4+BF4–).
Bond distances
| Fe(1)–Cp*CNTa | 1.728(6) | Fe(1)–C(Cp*)b | |
| Fe(1)–P(1) | 2.170(2) | Fe(1)–C(1) | 2.084(6) |
| Fe(1)–P(2) | 2.166(2) | Fe(1)–C(2) | 2.103(6) |
| Fe(1)–H(1) | 1.48 | Fe(1)–C(3) | 2.122(6) |
| Fe(1)H(2) | 1.50 | Fe(1)–C(4) | 2.116(6) |
| Fe(1)–C(1–5) av. | 2.104(6) | Fe(1)–C(5) | 2.097(6) |
| Bond angles | |||
| P(1)–Fe–P(2) | 90.73(8) | H(1)–Fe(1)–H(2) | 111 |
| P(1)–Fe(1)–H(1) | 62 | P(1)–Fe(1)–H(2) | 59 |
| P(2)–Fe(1)–H(1) | 61 | P(2)–Fe(1)–H(2) | 86 |
| Cp*CNT–Fe(1)–P(1) | 135.3 | Cp*CNT–Fe(1)–P(2) | 133.9 |
| Cp*CNT–Fe(1)–H(1) | 132 | Cp*CNT–Fe(1)–H(2) | 116 |
The other bond lengths show interesting trends. The Fe–P separations (2.166(2) and 2.170(2) Å) are the shortest never measured for complexes possessing the ‘Cp*Fe(dppe)’ framework (range 2.20–2.31 Å) 〚23,24 51,52,61〛. The C5Me5 group is planar and the Fe–Cp* centroid distance (1.728(6) Å) is also significantly shorter than usually observed (av 1.76 Å) for neutral and cationic iron species in this series 〚23,24,51,52,61〛. This Fe–P and Fe–C bond shortening can be attributed to the contraction of the Fe radius upon increase of the oxidation state from +II to +IV. Such an ionic radius effect has already been noticed in other systems 〚52, 62〛. The bite angle P(1)–Fe(1)–P(2) of 90.73(8)° matches perfectly the calculated value (90.8°) (vide infra), and is identical to that reported for the dippe analogue (90.67(9)°) 〚17〛. The plane containing the iron and the two phosphorus atoms is almost perpendicular (87.4°) to the plane of the C5 ring, as we have previously reported for the 16-electron Fe(II) complex 3+PF6– (84.8°) 〚24〛, and for the 17-electron iron(III) deuteride radical cation 〚Cp*Fe(dppe)D〛+ (88.8°) 〚16〛. All the other bond lengths and angles measured in the ligands and tetrafluoroborate anion are unexceptional.
Iron(IV) still remains relatively uncommon. This unusual oxidation state is found in coordination compounds containing donor nitrogen 〚63–65〛 and sulfur ligands 〚66–68〛. A mixed inorganic/organometallic cationic Fe(IV) derivative 〚Cp*Fe(η2-S2CNMe2)2〛PF6 has been isolated by Desbois and Astruc 〚69〛. The organometallic complex Fe(norbornyl)4 is also known 〚70〛, but as far as iron hydrides are concerned, the formal +IV oxidation state is still very unusual. The other reliably established Fe(IV) hydride systems are the neutral bis-trichlorosilyl monohydride CpFe(CO)H(SiCl3)2 〚71,72〛, the cationic dihydride 〚Cp*Fe(dippe)(H)2〛+, obtained by reaction of H2 with the 16-electron compound 〚Cp*Fe(dippe)〛+ 〚17〛, and the series of neutral dihydride trans-(η6-arene)Fe(H)2(SiRX2)2 complexes (arene = benzene, toluene, p-xylene; R = Cl, F, H, Me; X = Cl, F) resulting from oxidative addition of HSiRX2 at arene-solvated iron atoms 〚56–59〛. The crystal structure of the thermally stable and fluxional cationic trihydride derivative 〚FeH3(PEt3)4〛〚BAr’4〛 (Fe–H av. = 1.44(7) Å) has recently been reported by Berke and co-workers 〚60〛. The same structure, assumed on spectroscopic grounds, was also reported for the neutral hydrido-stannyl complex FeH3(PPh2Et)3(SnPh3) 〚73〛. Its C3 symmetric heavy atom skeleton and the fact that the metal-bound hydrogens were not located are reminiscent of the ‘Fe(PEt3)4’ core of Berke’s cationic trihydride 〚60〛.
3.3 Theoretical investigations
In order to provide a rationalisation of the structure and bonding of the title compound and to provide a comparison between its dihydride and dihydrogen forms, we have carried out DFT calculations, firstly on the simplified model 〚CpFe(dpe)H2〛+ (dpe = H2PCH2CH2PH2). Two stable conformations were found, corresponding to the hydrogen atoms lying in the trans and cis positions, respectively. The corresponding optimised structures are shown in Fig. 3. Their major metrical data are given in Table 3. Both geometries are close to the ideal Cs symmetry, which cannot be perfectly reached because of the slight distortion out of planarity of the PCCP diphosphine framework. The trans conformation corresponds to a dihydride form and its geometry is very similar to that found in the X-ray structure of 4+ (Fig. 1). The cis conformation is the dihydrogen form 〚CpFe(dpe)(η2-H2)〛+, with an H–H distance of 0.900 Å. The cis dihydrogen form is calculated to be more stable than its trans dihydride isomer by 0.19 eV. The search for other minima on the potential energy surface of 〚CpFe(dpe)H2〛+ was unsuccessful, strongly suggesting that only the two optimised trans and cis geometries are stable conformations of 〚CpFe(dpe)H2〛+. In particular, there is no trans or transoid stable dihydrogen form, neither cis nor cisoid stable dihydride form. This result showing the existence of two isomers lying close in energy, the cis dihydrogen form being the most stable, is comparable to that found experimentally by Brookhart et al. on the closely related 〚Cp(CO)(PEt3)H2〛+ compound 〚18〛. The Fe–P and Fe–C(Cp) distances are shorter in trans-〚CpFe(dpe)(H)2〛+ than in cis-〚CpFe(dpe)(η2-H2)〛+. This can be attributed to the change in the metal oxidation state when going from the dihydride to dihydrogen isomers (Fe(IV) to Fe(II)) and therefore to the concomitant increase of the atomic radius (vide supra).
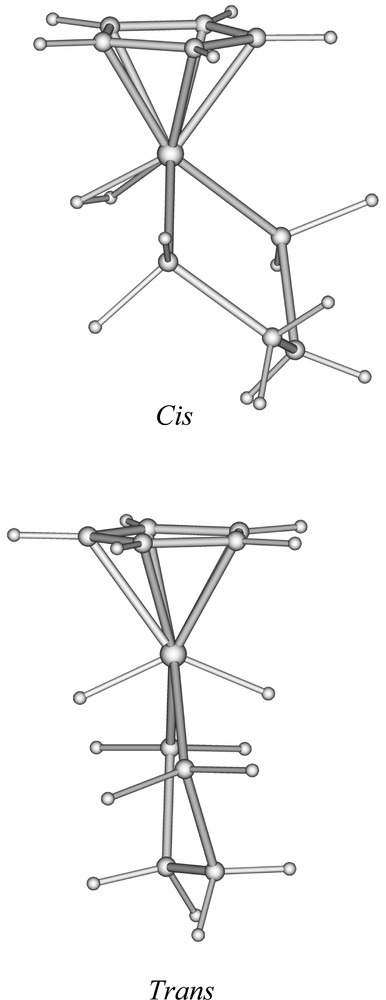
Optimised geometries of the cis- and trans- isomers of 〚CpFe(dpe)H2〛+.
Relative energies and major structural data of the optimised geometries of the cis- and trans isomers of 〚CpFe(dpe)H2〛+ and 〚Cp*Fe(dppe)H2〛+.
| cis-〚CpFe(dpe)H2〛+ | trans-〚CpFe(dpe)H2〛+ | cis-〚Cp*Fe(dppe)H2〛+ | trans-〚Cp*Fe(dppe)H2〛+ | |
| Relative energy between the cis and trans isomers (eV) | 0.000 | 0.187 | 0.190 | 0.000 |
| Fe–H(1) | 1.600 | 1.514 | 1.564 | 1.515 |
| Fe–H(2) | 1.593 | 1.512 | 1.569 | 1.510 |
| H(1)–H(2) | 0.900 | 2.764 | 0.935 | 2.733 |
| Fe–P | 2.221–2.222 | 2.191–2.190 | 2.255–2.259 | 2.202–2.207 |
| Fe–C(Cp)range | 2.117–2.138 | 2.098–2.132 | 2.127–2.214 | 2.126–2.172 |
| Fe–C(Cp)av. | 2.129 | 2.117 | 2.170 | 2.149 |
| Cpcentroid–Fe–(middle of P...P) | 143.2 | 178.7 | 150.8 | 178.8 |
| P–Fe–P | 85.3 | 90.65 | 86.2 | 90.8 |
| P–Fe–H(1) | 81.9–105.5 | 71.6–73.6 | 77.9–98.3 | 72.0–72.8 |
| P–Fe–H(2) | 103.0–82.6 | 73.1–73.6 | 105.7–79.7 | 74.5–70.50 |
| H(1)–Fe–H(2) | 32.7 | 131.9 | 34.7 | 129.2 |
| Cpcentroid–Fe–H(1) | 120.0 | 114.2 | 114.6 | 114.2 |
| Cpcentroid–Fe–H(2) | 121.5 | 113.8 | 119.9 | 116.6 |
| Cpcentroid–Fe–P | 126.2–126.0 | 133.8–135.6 | 131.5–127.6 | 134.6–134.6 |
| P–P–C–C (dppe or dpe) | 25.5 | 25.1 | 28.1 | 24.6 |
Since the dihydrogen form of the 〚CpFe(dpe)H2〛+ model was found to be slightly more stable than its dihydride isomer, and that only the dihydride form of 〚Cp*Fe(dppe)H2〛+ is isolated at room temperature, we decided to carry out DFT calculations on the real 〚Cp*Fe(dppe)H2〛+ compound, in the same manner as we did for the 〚CpFe(dpe)H2〛+ model. Similarly, two minima were identified, a trans- dihydride (4+) and a cis dihydrogen (2+) complex. Their structure, not shown here, looks very much the same as those of 〚CpFe(dpe)H2〛+ (Fig. 3). Their major structural parameters are given in Table 3. Nevertheless, some differences between the 〚CpFe(dpe)H2〛+ and 〚Cp*Fe(dppe)H2〛+ structures can be noticed. Comparing both cis-isomers, 〚Cp*Fe(dppe)(H2)〛+ has longer Fe–P and Fe–C(Cp) distances. Similarly, its H–H distance is longer (0.935 Å), while its Fe–H distances are shorter. These differences suggest a stronger π-donor ability of the 〚Cp*Fe(dppe)〛+ unit, as compared to its hypothetical 〚CpFe(dpe)〛+ homologue. Stronger π back-donation into the H2 σ*(H2) orbital reinforces the Fe–H bonds and concomitantly weakens the H–H bond 〚8〛. On the other hand, this effect occurs at the expense of π back-donation toward the other ligands, thus weakening their bonding to the metal. In fact, it is possible to get a better insight into the comparison of the bonding abilities of the 〚CpFe(dpe)〛+ and 〚Cp*Fe(dppe)〛+ units in carrying out a DFT fragment analysis of 〚CpFe(dpe)(η2-H2)〛+ and 2+ 〚43–45〛. The bonding energy between dihydrogen and the metallic unit is 1.481 and 1.495 eV in the former and the latter respectively. The stronger bond in the case of 2+ is due to a larger electron transfer into the σ(H2) orbital (0.22 vs 0.17 electron), but also to a larger donation to the metal by the σ(H2) orbital whose population is lower in the case of 2+ (1.59 vs 1.66 electron). Clearly, 〚Cp*Fe(dppe)〛+ is a better π-donor and a better σ-acceptor than 〚CpFe(dpe)〛+. If they are strong enough, both effects, especially the second one, tend to favour full dissociation of the H–H bond, i.e. to favour the dihydride form over the dihydrogen one 〚8,20,21〛 This is exactly what happens in the case of 〚Cp*Fe(dppe)H2〛+, for which, contrary to 〚CpFe(dpe)H2〛+, the trans dihydride isomer is calculated to be more stable than the cis dihydrogen one by 0.19 eV, in full agreement with all the experimental data.
The optimised geometry of 4+ is very close to that found in the X-ray crystal structure, with the DFT Fe–P separations being slightly longer, as usually observed when non-local corrections are applied. On the other hand, the optimised geometry provides a much accurate location of hydrogen atom than the X-ray data. From this point of view, it is noteworthy that, in the X-ray molecular structure of the related trans-〚Cp*Fe(dippe)(H)2〛+complex 〚17〛, the hydrogen metrical data are close to those found by DFT on trans-〚Cp*Fe(dppe)(H)2〛+.
4 Concluding remarks
We report in this article on the isolation of both the classical (4+) and non-classical (2+) dihydride iron complexes, as an illustration of the subtle balance of the steric and electronic environments around the metal in the Cp*Fe(dppe) framework. The dihydrogen derivative 2+ accommodates a slightly elongated dihapto-H2 ligand, as inferred from T1 and JHD data, thus suggesting an efficient back-bonding from the metal centre. Despite the fine tuning of the metal π-donor ability, no dihydride/dihydrogen equilibrium is observed. The dihydrogen derivative 2+ transforms irreversibly into its thermodynamically more stable trans iron(IV) dihydride isomer 4+, which has been characterised by a X-ray crystal structure. The DFT calculations on the 〚CpFe(dpe)H2〛+ model and the real 〚Cp*Fe(dppe)H2〛+ systems nicely corroborate the experimental data and show the sensitivity of the coordinated dihydrogen ligand to variations of the electron density on the metal.
Supplementary material
Crystallographic data (excluding structure factors) have been deposited with the Cambridge Crystallographic Data Centre as supplementary publication No. SUP CCDC 166568. Copies of the data can be obtained free of charge on application to the Director, CCDC, 12 Union Road, Cambridge CB2 1EZ, UK; fax: 44 + (1223) 336-033; e-mail: deposit@ccdc.cam.ac.uk.
Acknowledgements
We thank Dr S. Sabo-Étienne (Toulouse) for stimulating discussions and Dr S. Sinbandhit (Rennes) for helpful NMR assistance. Financial support from the French ‘Centre national de la recherche scientifique’ (CNRS) and of Université de Rennes-1 is acknowledged. Computing facilities were provided by the ‘Centre de ressources informatiques’ (CRI) of Rennes and the ‘Institut de développement et de ressources en informatique scientifique’ (IDRIS) of the CNRS.



