Crystal growth and classical nucleation theory

Michael C. Weinberg; W.Howard Poisl; Laszlo Granasy

doi:10.1016/S1631-0748(02)01433-9

Résumés

Anglais
Français

Calculations were performed of the crystal growth rates in lithium disilicate glass in the low-temperature regime where homogeneous nucleation is observed. The computations were executed using the gain-loss (Becker–Doring) equations that form the framework of Classical Nucleation Theory (CNT). The growth rates were obtained in several different ways, using various choices for the kinetic model, the generalized diffusion coefficient, and the physical input data. The results of these calculations are compared with recently obtained experimental values of the growth rates.

Des calculs de vitesse de croissance cristalline ont été réalisés pour un verre de disilicate de lithium, en régime de basse température, où une nucléation homogène est observée. Les calculs sur ordinateur ont été exécutés en utilisant les équations de perte de gain (Becker–Doring), qui forment le canevas de la théorie classique de la nucléation (TCN). Les vitesses de croissance ont été obtenues de différentes manières, selon divers choix de modèle cinétique, de coefficient de diffusion généralisée et de données physiques introduites. Les résultats de ces calculs sont comparés avec des valeurs de vitesse de croissance récemment obtenues.

1 Introduction

There have been many attempts to evaluate the validity of Classical Nucleation Theory (CNT) by comparing computed nucleation rates with measured values 〚1–5〛. In making such comparisons several important issues arise. First, one must decide upon the meaning of CNT. Different investigators define CNT in different manners. Second, despite one’s definition of CNT the description of nucleation experiments with a classical-type theory usual involves the simultaneous testing of several assumptions or hypotheses. In particular, the starting point of analysis is the Becker–Doring (BD) equations 〚6, 7〛. However, it is difficult to test solely the applicability of these equations for the description of nucleation experiments since they contain certain unknown functions and parameters that must be evaluated with the aid of some sort of model. For example, in order to compute the thermodynamic barrier to nucleation one must compute the work to form a critical nucleus. To execute this task one may invoke the capillarity approximation, where one assumes that thermodynamic arguments can be used to compute the surface and bulk energy contributions to the free energy of critical particle formation. Some individuals take this assumption as the definition of CNT. In addition, the kinetic prefactor that appears in the BD equations must be specified. This entails the selection of a particular model. Finally, one must determine how to treat σ, the liquid-crystal surface tension. Does one treat this parameter as a constant or allow it to be temperature dependent? It is apparent, then, that when one compares nucleation data with CNT calculations, usually one is testing many assumptions simultaneously.

The BD equations should describe crystal growth as well as nucleation. Any comparison between the measured crystal growth rates obtained from nm-sized particles and computed rates would encounter the same difficulties as those mentioned above for nucleation. However, crystal growth experiments are most conveniently performed when particles are on the size scale of microns. Under these circumstances certain simplifications ensue. For example, as a result of the large particle size, the capillarity approximation should be valid. Thus, regardless of the model employed, classical or non-classical, the thermodynamic barrier should be given by ΔG_bulk, where the latter quantity is the bulk free energy difference between crystal and liquid. Also, for some models of growth, knowledge of the liquid-crystal surface tension is not required. This constitutes a further simplification. Hence, by examining crystal growth, unlike the case in nucleation, one can test certain portions of CNT independently of others.

Most crystal growth measurements, though, are made at high temperatures that are removed from the temperature region where homogeneous nucleation occurs. However, it is desirable to have growth kinetics in the temperature regime where nucleation occurs so that one can shed light on the viability of the governing equations. Hence, one of the aims of this work will be to utilize newly gained crystal growth data, obtained in the nucleation region of a simple, pseudo-one-component, inorganic material, to compare with several versions of classical theory. Another goal of this work is to test the sensitivity of the computed crystal growth rates to the physical parameters selected. Finally, we will examine the influence of the kinetic model and the manner by which one computes the kinetic barrier on the resulting growth rate.

2 Growth models

2.1 Gain-Loss equations

If one lets n designate the number of units (e.g., atoms, molecules) in a cluster, then the rate of cluster growth can be written as 〚8〛:

d n / d t = k_{n}^{+} - k_{n}^{-}

where k⁺_n is the reaction rate for formation of a particle of size n and k^-_n is the rate of elimination of a particle of size n. If one assumes that the clusters are spherical, with radius R, and the volume/atom is v, then equation (1) can be transformed to the following:

d R / d t = {(ν / 36 π)}^{1 / 3} k_{n}^{+} n^{- 2 / 3} (1 - k_{n}^{-} / k_{n}^{+})

For large n, we have that k^-_n≈k_n+1. So, using the condition of detailed balance:

N_{n} k_{n}^{+} = k_{n + 1}^{-} N_{n + 1}

where N_n is the equilibrium number of clusters of size n, one finds:

d R / d t = {(ν / 36 π)}^{1 / 3} D_{n}^{+} (1 - \exp \{- [Φ (n) - Φ (n + 1)] / kT\})

In equation (4), Φ(n) is the free energy of a cluster of size n and D⁺_n is k⁺_nn^-2/3. The growth equation embodied by equation (4) is quite general, and relies only on the basic notions of the Becker–Doring gain-loss theory. No use of CNT has been made nor has the kinetic model for the rate coefficient been specified.

2.2 Large particle limit

If one invokes CNT, then the capillarity approximation can be used to find the free energy of a cluster. If this free energy expression is used in equation (4), then one finds:

d R / d t = {(ν / 36 π)}^{1 / 3} D_{n}^{+} (1 - \exp [(Δ G / kT) (R * / R - 1)])

In equation (5), R* is the critical radius and ΔG is the bulk free energy difference between the liquid and the crystal. When the growing particle is large, i.e. R >> R*, then the crystal growth rate reduces to:

d R / d t = {(ν / 36 π)}^{1 / 3} D_{n}^{+} [1 - \exp (- Δ G / kT)]

Although Classical Nucleation Theory was used to obtain equation (6), it is clear that this expression must be valid whenever the particle dimension, R, is much larger than the critical size. At large sizes, it is legitimate to treat the particle as a small, but macroscopic, particle and compute the free energy difference between liquid and crystal in terms of the macroscopic bulk and surface contributions. Even if at small particle sizes equation (5) is invalid due to non-classical effects, at large sizes the non-classical free energy difference must approach the classical one and equation (6) will be valid. Since crystal growth data is nearly always obtained from the growth of crystals whose sizes are far in excess of R*, equation (6) will be quite appropriate for the analysis of such experiments.

2.3 Kinetic models

Here, we shall consider two kinetic models: the Fisher–Turnbull (FT) and ballistic models 〚9, 10〛. If we denote D_n at the critical size as D^*_n, and if we suppress the plus on D⁺_n, then one may write equation (6) formally as follows:

d R / d t = {(ν / 36 π)}^{1 / 3} D_{n}^{*} \{D_{n} / D_{n}^{*}\} [1 - \exp (- Δ G / kT)]

In the FT model, D_n ∼ exp{–〚Φ(n+1) – Φ(n)〛/2k T}, so, in the large R limit it is easy to show that one obtains the following expression for the growth rate:

{(d R / d t)}_{FT} = 2 {(ν / 36 π)}^{1 / 3} D_{n}^{*} \sinh (Δ G / 2 k T)

In the ballistic model, k⁺_n∼n^2/3, so D_n = constant. Thus, the growth rate becomes:

{(d R / d t)}_{B} = {(ν / 36 π)}^{1 / 3} D_{n}^{*} (1 - \exp (- Δ G / kT))

There are several ways of computing the generalized diffusion coefficient, D^*_n. Kelton 〚5, 11〛 has expressed D^*_n in terms of the ordinary diffusion coefficient, D, as $D_{n}^{*} = 24 D / λ^{2}$ . Furthermore, if the Stokes–Einstein relation is invoked, then the generalized diffusion coefficient is given by:

D_{n}^{*} = A T / η

In equation (10), A is a constant and η is the shear viscosity. An alternative method to compute D^*_n has been discussed by Shneidman 〚12〛. If one makes the parabolic approximation to the barrier shape, then one finds:

D_{n}^{*} = Δ^{2} / 2 τ

with

Δ^{- 2} = (- 1 / 2 kT) {(d^{2} Φ (n) / d n^{2})}_{n = n *}

where τ is the nucleation transient time. The latter quantity can be found by fitting experimental nucleation data to theoretical expressions for the transient nucleation rate 〚13, 14〛.

Δ² will depend upon the manner by which one computes the free energy of an n-sized cluster. If one uses CNT, then one can show that:

Δ^{2} = 6 k T n * / Δ G

If one uses diffuse interface theory 〚4〛, then Δ^–2 is given by:

Δ^{- 2} = (Δ G / 3 k T n *) \{1 - 1 / [1 + {(T Δ s / Δ h)}^{1 / 2}]\}

In equation (13), n* is the critical number found using diffuse interface theory (DIT) and Δs, Δh are entropy and enthalpy parameters 〚15〛. Also, one observes that the number of particles in a critical nucleus differ for the CNT and DIT models. One can find (n*)_DIT by using:

{(n *)}_{Class} / {(n *)}_{DIT} = {(R_{Class}^{*})}^{3} / {(R_{DIT}^{*})}^{3}

and the expression for R^*_DIT shown below:

R_{DIT}^{*} = - (σ / Δ G) \{(Δ h / Δ h_{f}) (1 + {[T Δ s / Δ h]}^{1 / 2})\}

In equation (15), σ is the liquid-crystal surface tension and Δh_f is the enthalpy of fusion. Also, one should note that if one employs ΔG J, then Δh/Δh_f = 1.

3 Results

The physical parameters used in the calculations are shown in Table 1. Two different functions were employed to calculate the temperature variation of ΔG. One of these functions is a simple linear variation used by James 〚16〛, and henceforth will be denoted by J. The other function is a polynomial of order three that has been derived from experimental data from JANAF tables. It has been used previously by Kelton and Weinberg 〚17〛, and will be designated by KW. Also, two expressions were employed for the description of the temperature dependence of the shear viscosity, η. In both cases, a Fulcher equation was chosen, but the Fulcher parameters differed. One of the viscosity equations was used by Matusita and Tashiro 〚18〛 in their study of lithium disilicate (LS₂) crystal nucleation (denoted MT), and the other equation was given by Zanotto 〚19〛 (denoted EDZ). There have been several other reported sets of viscosity data for this system. However, the two mentioned above were selected, since they represent limiting values in that the data of most other investigators, which fall somewhere between those represented by the MT and EDZ Fulcher Equations. The experimental growth data 〚20, 21〛 for LS₂ in the lower temperature region where homogeneous nucleation has been observed was taken from the recent work of Burgner 〚20〛, while the higher temperature data was obtained from the work of Barker et al. 〚21〛.

Property	Symbol	Formula/Value*	Ref.
Viscosity (Pa s)	η MT	log η = –2.44 + 〚3370/(T – 460)〛	〚18〛
	η EDZ	log η = –2.55 + 〚3385.5/(T – 491.2)〛	〚19〛
Free Energy (J mol^–1)	ΔG J	53 370 – 39.37 T	〚16〛
	ΔG KW	48 045 – 36.81 T + 5.607 × 10^–3 T² – 4.3179 × 10^–6 T³	〚17〛
Molar Volume (m³ mol^–1)	V_M	6.15 × 10^–5	〚20〛
Surface Tension (J m^–2)	σ	0.029 11 + 0.1617 × 10^–3 T	〚16〛
Transient time (s)	τ	log τ = –28.420 + 23.291 (1000/T)	〚13〛
Entropy (J mol^–1 K^–1)	Δs	–39.37 (J)	〚16〛
Enthalpy (J mol^–1)	Δh	53 370 (J)	〚16〛
A (Kelton) (J m^–3 K^–1)	A	1.44 × 10⁶ (from 8 k/π z³, where z = 0.29 × 10^–9 m)	〚11〛

In Fig. 1, the temperature variations of both free energy functions and viscosities are shown. The MT and EDZ Fulcher plots are virtually identical at high temperatures (not shown), but there is significant deviation in the low temperature region, as observed in Fig. 1.

Fig. 1
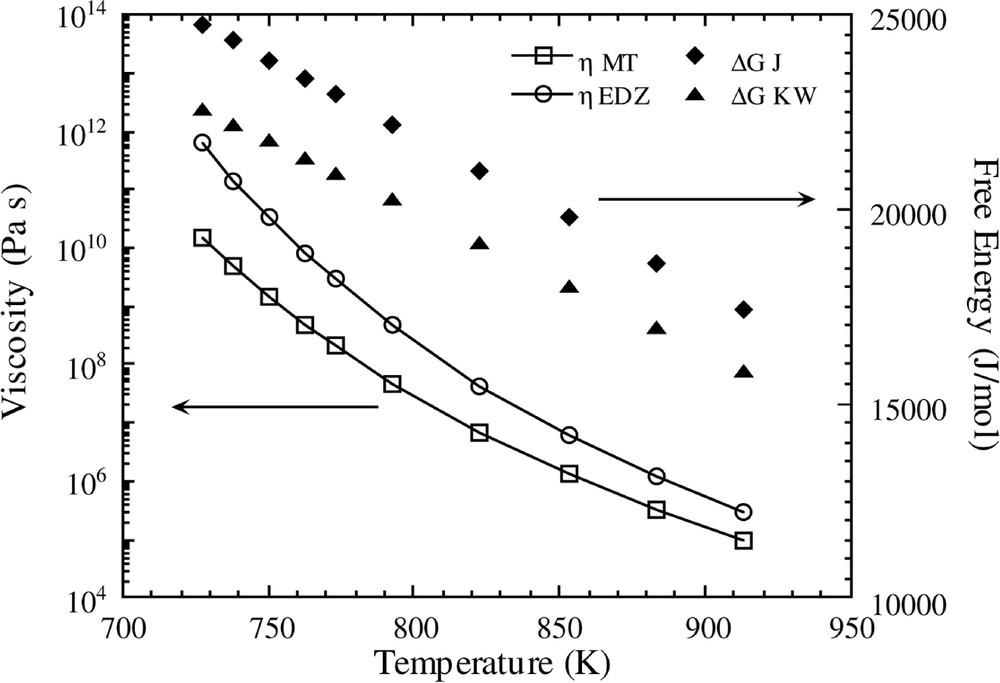
Temperature variations of viscosity and free energy relationships for the different functions shown in Table 1.

Fig. 2 shows the influence of the free energy and viscosity parameters upon the calculated growth rate, U. These calculations were performed using equations (8) and (10) and the two different free energy and viscosity equations. One observes that both free energy expressions give essentially identical results. However, use of the MT and EDZ viscosity functions lead to significantly different magnitudes of U and different temperature variations.

Fig. 2
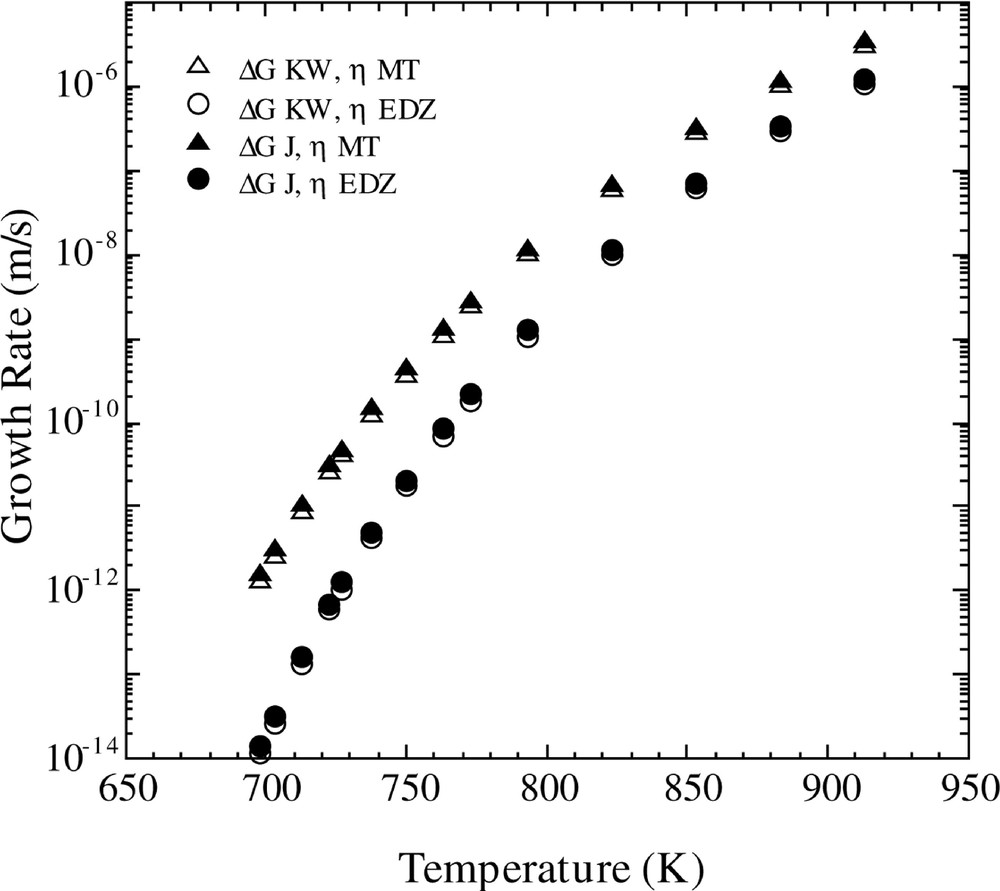
Calculated growth rate versus temperature for the Fisher–Turnbull model (equation (8)) with the Kelton expression for D^*_n (equation (10)) using the different equations for viscosity and free energy listed in Table 1.

The results of the latter calculations, using the KW free energy, are compared with experimental growth rate data in Fig 3. One observes that the calculated values of U using the MT viscosity are a couple of orders of magnitude larger than the experimental ones. However, the temperature dependence of U is given nearly precisely, as illustrated by the dashed curve which is a normalized version of the calculated U(T). On the other hand, computations of U(T) with the EDZ viscosity leads to reasonably good agreement between calculated and measured growth values in the low temperature regime where homogeneous nucleation occurs, but leads to an increasing divergence between experimental and computed values with increasing temperature.

Fig. 3
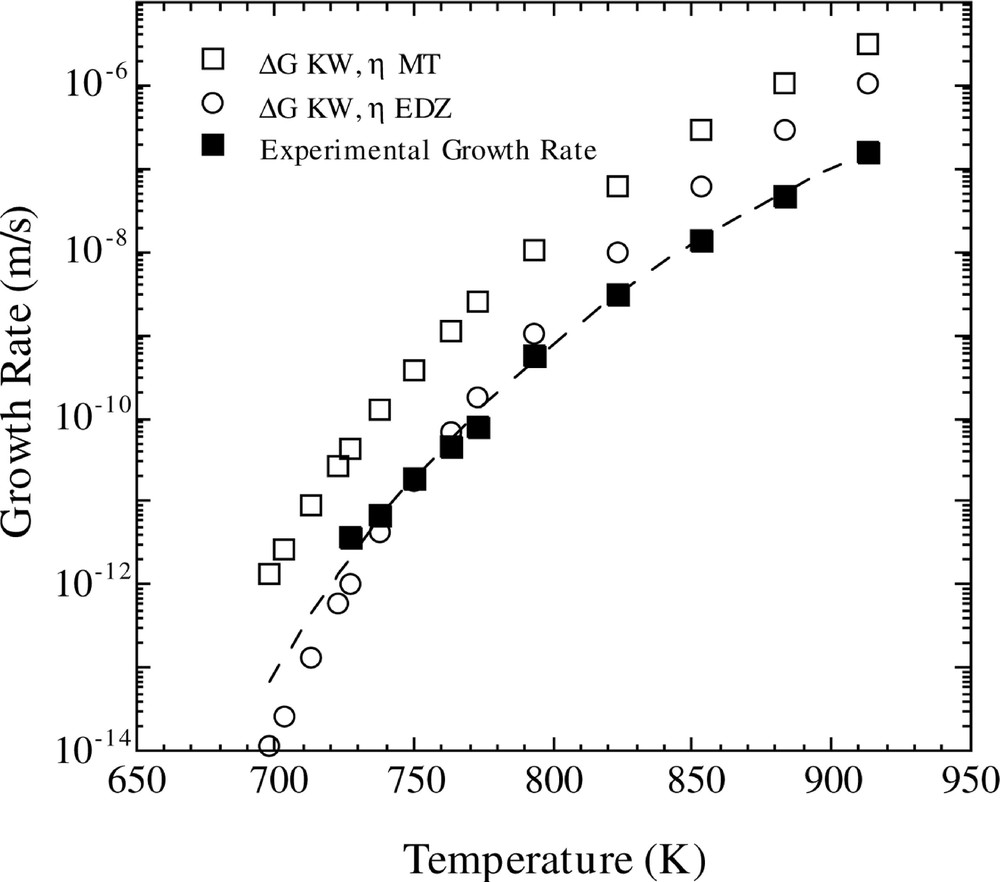
Comparison of calculated and experimental growth rates versus temperature. The calculated growth rate is for the Fisher–Turnbull model (equation (8)) with the Kelton expression for D^*_n (equation (10)), using the two different viscosity functions and the KW free energy. The dashed line shows the upper calculated growth rate (ΔG KW, η MT) divided by a constant.

In Fig. 4, the results for U(T) computed using the FT model and equations (11a,b) are shown. The open squares show the results employing the CNT model, while the open circles represent the findings using the Diffuse Interface Theory (DIT) of Granasy. It is observed that DIT and CNT give virtually identical results, and both theories give good agreement with experiment in the low temperature region, but predict growth rates that are increasingly too large as the temperature increases.

Fig. 4
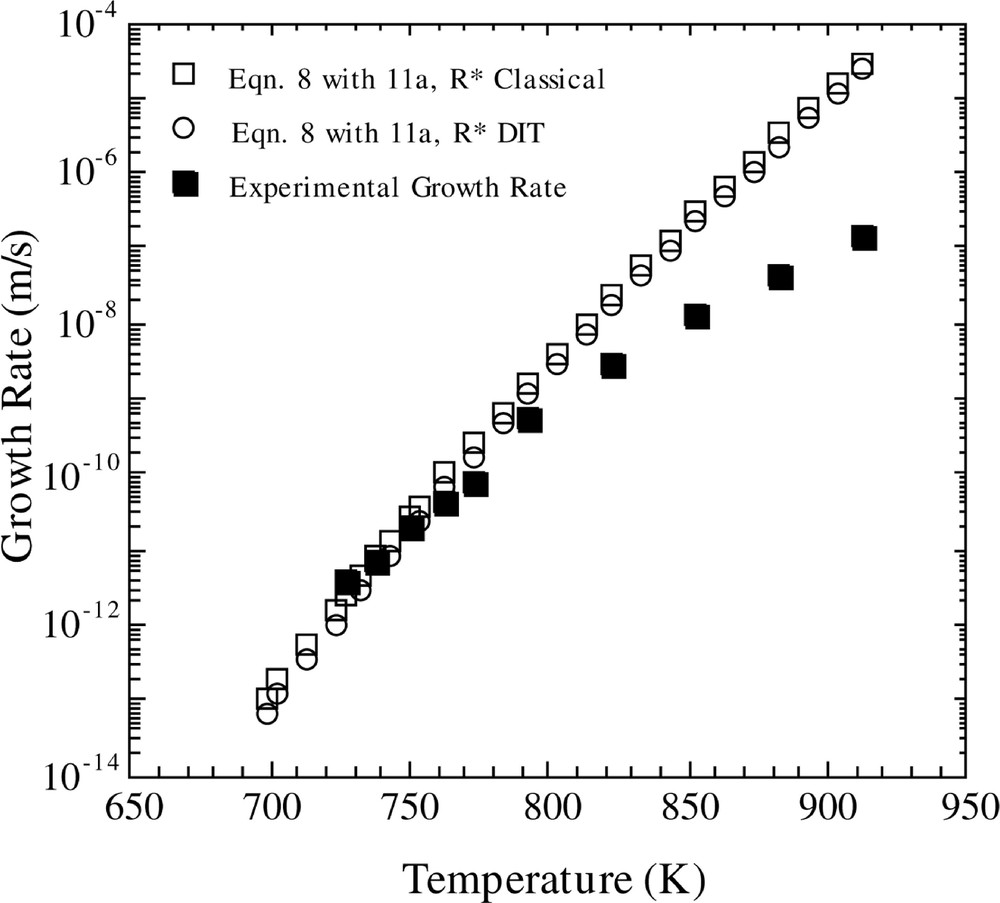
Comparison of calculated and experimental growth rates versus temperature. The calculated growth rate is for the Fisher–Turnbull model (equation (8)) with the Shneidman expression for D^*_n (equation (11a)), using the classical and DIT methods for calculating R* and the KW free energy.

The predicted crystal growth rates using the ballistic model are shown in Figs 5 and 6. In Fig 5, the temperature-dependent growth rate was calculated using equation (9), in conjunction with equations (11a) and (12). One observes that the ballistic model gives an incorrect temperature dependence of the crystal growth rate over the entire temperature region. In addition, crystal growth rates were computed using the ballistic model (equation (9)) in concert with equation (10). The results, using the viscosity fits of MT and EDZ, are shown in Fig. 6. If one employs the EDZ viscosity, then once again one notes that the ballistic model yields an erroneous temperature dependence of the growth rate. However, use of the MT viscosity expression produces a better fit of the temperature dependence of the growth rate.

Fig. 5
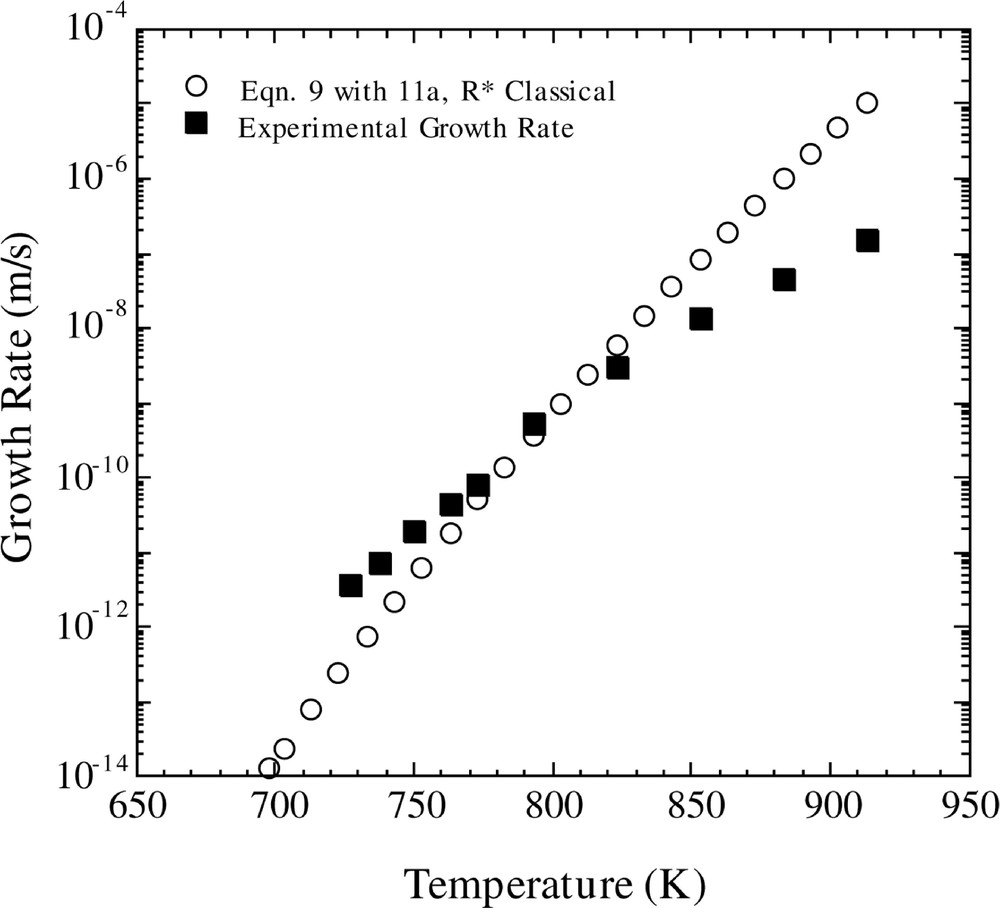
Comparison of calculated and experimental growth rates versus temperature. The calculated growth rate is for the Ballistic model (equation (9)) with the Shneidman expression for D^*_n (equation (11a)), using the classical method for calculating R* and the KW free energy.

Fig. 6
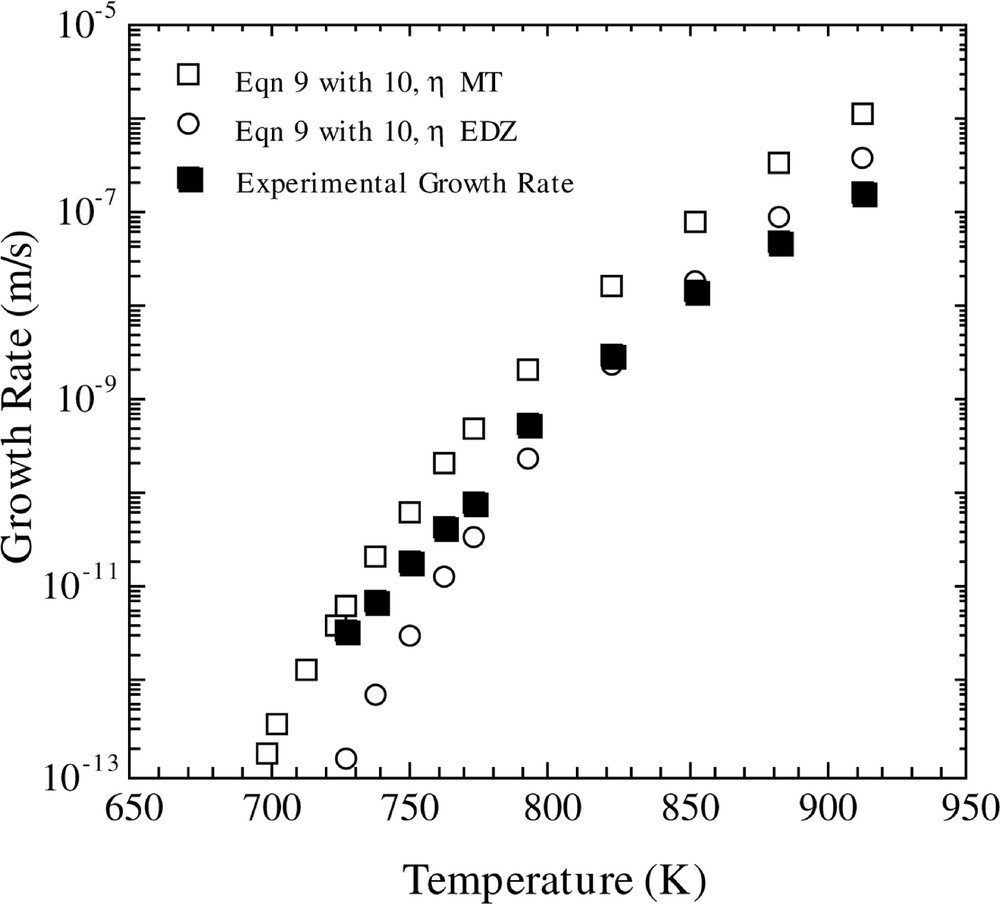
Comparison of calculated and experimental growth rates versus temperature. The calculated growth rate is for the Ballistic model with the Kelton expression for D^*_n (equation (10)), using the two different viscosity functions and the KW free energy.

4 Discussion

It has been mentioned previously that the Becker-Doring Equations that form the basis for nucleation theory should also apply to crystal growth in the temperature regime where nucleation occurs. This feature stems from the fact that nucleation and growth are not separable and independent processes. Hence comparisons between calculations and experimental data of crystal growth can shed some light on the validity of similar calculations for nucleation events.

It is almost certainly true that some form of the gain-loss equations provides an adequate description of nucleation and growth processes. However, uncertainties enter due to the selections made for certain quantities that appear in these equations and to the various approximations that are made.

Certainly, the capillarity approximation (using a thermodynamic description of a cluster) is suspect, in many situations, when applied to clusters of the size of the critical radius. However, in the case of crystal growth, one can invoke this assumption with assurance if one limits one’s attention to large clusters. Since traditional crystal growth experiments probe clusters in the micron size range, the capillarity approximation is justified.

However, there are several more choices that one must make in utilizing the gain-loss equations. First, one must choose a kinetic model. Here we have considered two such models; the FT and ballistic models. Also, one must select a way of computing the generalized diffusion coefficient. Here, we have utilized methods discussed by both Shneidman and Kelton. Furthermore, in the former approach, we have examined both classical and diffuse interface theories. Finally, we desire to ascertain the sensitivity of our conclusions to our selection of physical input parameters.

First, let us focus on the question of the kinetic model. It appears that the FT model is in better agreement with the experimental data than the ballistic model. Although there is a bit of uncertainty in this finding due to choice of input data (to be discussed), the temperature dependence of the growth rate is not in accordance with the ballistic model. Similar conclusions have been drawn from comparisons of nucleation calculations and experiments.

The generalized diffusion coefficient was computed using the Stokes–Einstein assumption and also by making use of the scheme outlined in 〚12〛 (i.e. equations (11a,b)). For the latter method, calculations were performed using both CNT and DIT. From an inspection of Fig. 4, one sees that the CNT and DIT computations give virtually identical results. Hence, one suspects that the diffuseness of the interface is not an important effect in this case. This appears to be a reasonable conclusion since the clusters are very large. The results are in good agreement with the experimental data in the lower temperature regime, but they deviate from the experimental results as the temperature increases. It is difficult to draw a firm conclusion regarding the extent of agreement between theory and experiment displayed in Fig. 4 for the following reason. Homogeneous nucleation is observed in LS₂ glass up to a temperature of approximately 800 K. One observes that, in the temperature range from about 730 to 800 K (normal nucleation regime), the agreement between theory and experiment is excellent. Hence, the question arises as to whether one would expect these calculations to be valid at higher temperatures. Burgner 〚20〛 has observed that, in the nucleation regime, the growing crystals are needle-shaped, but at a temperature of 863 K (or possibly lower), the growing particles are spherulitic. This change in morphology could signal a more complex growth mechanism that cannot be described by the simple models given here. Hence, in the temperature region where the equations appear to be most applicable, the combined use of equations (8) and (11a,b) give very good agreement with experimental growth data.

The computation of the growth rate via use of the Stokes–Einstein equation will depend upon the choice of viscosity, as seen in Fig. 3. However, neither the MT nor the EDZ viscosity appears to produce a result in agreement with experiment. The MT calculation yields growth rates that are too large, and the EDZ viscosity gives an incorrect temperature dependence of the growth rate. However, if one scales the calculation using the MT viscosity by a constant, then one obtains the dashed line shown in Fig. 4. Hence, the latter calculation reproduces the magnitude and temperature dependence of the experimental growth rate over the entire temperature range. However, in light of the discussion in the above paragraph, this agreement might only be coincidental.

We have tested the sensitivity of the calculated growth rate to two input parameters, the free energy difference function and the viscosity. We have observed that the computed crystal growth rates are rather independent of the former factor, but very sensitive to the latter. Of course, if one avoids use of the Stokes-Einstein approximation, then this dependency is no longer a problem.

Crystal growth is probably a more complex problem than envisioned in any of the existing descriptions of growth. More sophisticated and complex methods have been formulated 〚22–25〛 to describe crystal growth, but such methods cannot be applied to real systems without simplifying assumptions and/or the specification of one or more unknown parameters. Also, the agreement between theory and experiment for such methods has not been as good as that shown by the simplest gain-loss equations. Clearly, none of the existing methods seem to capture some of the essential features of growth. For example, it is known that crystal growth in LS₂ is anisotropic, and hence one must specify two growth rates. Yet, there are no geometrical features in the Becker–Doring equations. Also, it is possible that the geometric features of growing nano-clusters differ from those of the macroscopic sized clusters observed in the usual growth experiments. It has been observed that macroscopic crystals undergo morphological changes during isothermal growth 〚26〛, and thus it is possible that nano-clusters exhibit similar behavior.

5 Conclusions

From a comparison between calculated and measured crystal growth rates for LS₂, the following conclusions may be drawn.

1. 1. The FT model appears to give closer agreement with experimental results than the ballistic model.
2. 2. The computed growth rates are relatively insensitive to choice of free energy difference function, but are quite dependent upon the viscosity.
3. 3. Use of CNT or DIT gives virtually identical growth rates, both of which are in good agreement with experiment in the temperature region where homogeneous nucleation occurs.
4. 4. Due to uncertainties regarding input parameters, it is not clear which method gives the best generalized diffusion coefficient.
5. 5. Coincidence of experimental and theoretical results does not necessarily suggest the physical reality of the growth rate model.

Acknowledgements

One of us (MCW) expresses his gratitude for the support of Dr S. Slovin.