1 Introduction
Oxidoreduction equilibrium in glasses has been extensively studied in various oxide glasses containing transition-metal ions. Glasses with high concentrations of transition metals are interesting because of their semiconducting properties 〚1–5〛 and optical absorption in the visible, resulting in coloration of the glass 〚6〛. Electronic conduction can indeed occur through the electronic transfer from the low- to high-valence states. Glasses doped with transition metals also attract much attention because of their memorising and photoconducting properties 〚7–9〛. They also find potential applications in solid-state lasers 〚10〛, luminescent solar energy concentrators (LCS) and optical fibres for communication devices 〚11–15〛. Thus, it is very important to know and to control the parameters that can influence the oxidoreduction equilibrium of transition metals. The ability to control the oxidised/reduced species ratio is also important for investigating its effect on the structure and properties of glasses. The control of this ratio is very difficult, because it is influenced by many parameters: glass composition, melting conditions (including temperature and time), oxygen partial pressure in the furnace atmosphere, batch composition, addition of oxidising or reducing agents and heat treatment after melting.
In this review, we report first on TM-doped glasses since thermodynamic considerations can be used to describe the redox behaviour of these systems. Then, we describe the redox of glasses containing large amount of TM ions, in which thermodynamic concepts are no more valid. The coordination of TM ions will be then reviewed in a third chapter, first for binary compositions, and secondly for ternary glasses containing alkaline or alkaline earth oxides. For the latter ternary glasses, we consider the occurrence of complexation of TM ions, and of the condensation of the cationic polyhedra. The structural relationship between the phosphate glass network and the TM ions will be discussed in a fourth chapter.
2 Transition metals valencies in phosphate glasses
2.1 Transition metals ions as doping in phosphate glasses
Majumdar et al., in 1972 〚16〛, have determined the relative proportions of oxidised and reduced forms of TM doping in sodium metaphosphate glasses. They found that chromium, manganese, vanadium are almost completely reduced, while copper, molybdenum, titanium remain mostly in the higher valency states. These results indicate that oxidoreduction equilibrium (redox) of TM ions in glasses involves several concepts: redox, acid-base (O2– exchanges) and complexation with O2–. For instance, in vanadium doped phosphate glass, V(IV) is the main redox state, and spectroscopic data show the occurrence of VO2+ complex ion. Simple equations may then be considered:
It is possible to calculate a basicity parameter 〚18〛. This parameter, B, is calculated in terms of the coulombic force between the cation and the oxygen ion for each glass component. The reduced state of transition metal is favoured when the basicity parameter decreases because the O2– activity decreases. So, when the matrix is very basic, i.e. donor of O2–, the equilibrium is shifted towards the formation of oxidised species. In contrast, if the matrix is weakly O2–-donor (i.e. acceptor of O2–), the equilibrium is shifted towards the formation of reduced species. If one compares the basicity parameter of silica (SiO2, B = 0) 〚18〛, boron oxide (B2O3, B = 0.026), and phosphorus oxide (P2O5, B = –0.103), it can be deduced that the phosphate matrix has a higher reducing effect on the TM.
The following examples illustrate this redox behaviour.
A study of the vanadium redox in three glasses with different basicity confirms this effect 〚19〛. (33 Na2O–66 SiO2, NS), 33 NaPO3–67 Sr(PO3)3 (P) and 90 (AlF3–MgF2–CaF2–SrF2)–10 Sr(PO3)2 (FP) were doped with 0.5% mol V2O5. In the more basic silicate glass (NS), V5+ is the main redox state (V5+: 94%; V4+: 6%). By contrast, in the less basic phosphate glass, V4+ and V3+ are the predominant species. In FP, V4+ and V3+ indeed represent 90% and 10%, respectively, and in P, V4+ and V3+ represent 96% and 4%, respectively.
The oxidoreduction of Cr ions has been investigated in silicate, borate and phosphate glasses by Murato et al. 〚20〛. In silicate and borate glasses, Cr6+ and Cr3+ ions are present, with a majority of Cr6+ ions; the relative content of Cr6+ increases when the basicity increases. By contrast, only Cr3+ ions exist in the more phosphated glasses 〚20〛.
For a defined matrix, the oxidised/reduced state ratio increases with the O2– activity in silicate glasses and borate glasses, but in phosphate glasses, the TMm+/TMm+1 ratio is independent of basicity. For instance, in (25–45) MO–(40–60) P2O5–10 Al2O3 glasses with M = Ca, 2 Na or 2 Li doped with 0.5% mole Ti2O3, the relative content of Ti3+ is independent of the composition (Fig. 1) 〚18〛. The same results are observed for Cr3+ 〚20〛. For a given composition, the authors 〚18, 20〛 assume that these transition metals are incorporated into sites that involve P=O double bonds, therefore without modification of the glass basicity.
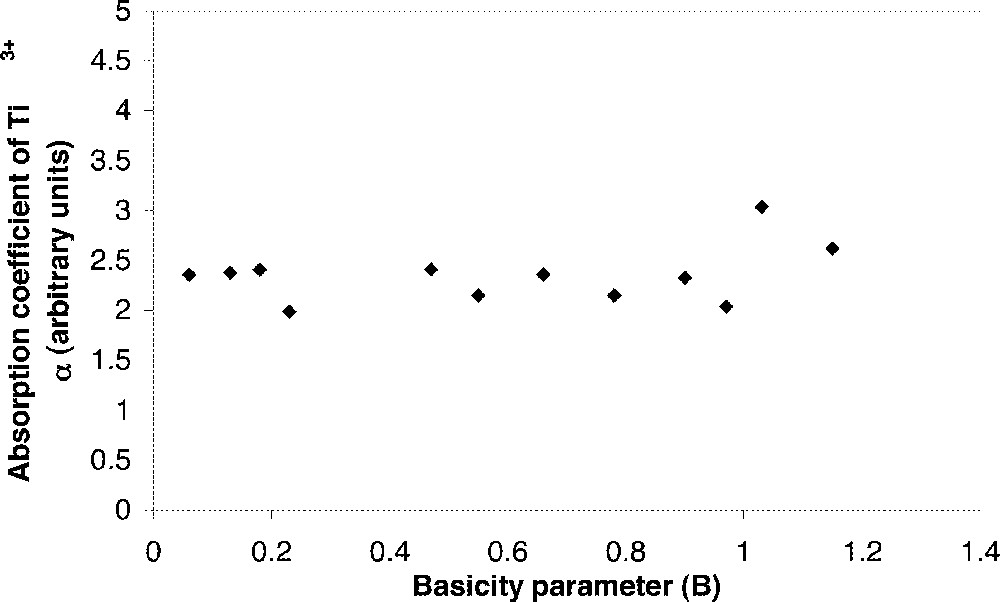
Absorption coefficient of Ti3+ versus the basicity parameter (B) of (30–50) MOn–(40–65) P2O5–10 Al2O3 glasses with M = Li, Na, K, Mg, Ca, Sr, and Ba 〚3〛.
In the case of iron 〚21〛, for the same temperature and oxygen partial pressure, the Fe3+/Fe2+ ratio is also independent of the phosphate glass composition. It is indeed the same in 50 (CaO or SrO or BaO)–50 P2O5 glasses, excepted for 50 MgO–50 P2O5 glass in which it is higher. The later phosphate glasses containing magnesium oxide are known to present anomalous structure and properties 〚22〛.
Interestingly, in sodium phosphate glasses 50 Na2O–50 P2O5 doped with x = 0.1, 0.2 and 0.3 mol% CuO 〚23〛, the copper ions exist in the glass matrix as oxidised Cu2+ ions, although the matrix has a reducing character. Matthai et al. 〚24〛 reported the same tendency: only Cu2+ exists in NaPO3–2 Sr(PO3)2 glass melted at 900 °C and doped with 1.48 mol% CuO. In silicate glasses 〚25〛 doped with CuO but melted at high temperature (1400 °C), the Cu2+ and Cu+ concentrations are approximately equal, which illustrates the temperature dependence of the oxygen redox equilibrium or means that some oxide decomposition may occur at high temperature. It is very important to take into account the experimental conditions of glass elaboration, mainly the melting temperature, because it can strongly modify the oxidoreduction equilibrium.
It is then concluded that when the reaction takes place in a glass solvent, i.e. when the glasses are doped with a small amount of transition metal, the redox reaction of TMm+/TMm+1 can be described by the equilibrium constant.
This equilibrium constant K(T) depends on the TM activity in glass, temperature, and atmosphere.
2.2 Phosphate glasses containing large concentrations of transition metals
When the concentration of the transition metal increases, the system is generally out of thermodynamic equilibrium. Even if the equilibrium is reached, it is very difficult to calculate the redox equilibrium constant of TMO in glass versus its content, because the variation of activity of an oxide with its concentration is known in only a few cases, and mainly in silicate glasses. This is why most papers report only an evaluation of the oxidised/reduced ratio of transition metal. In the following section, we describe how the temperature, the atmosphere, the concentration of TMO, and the glass basicity affect the TMm+/TM(m+1)+ ratio in phosphate glasses.
2.2.1 TMm+/TM(m+1)+ ratio versus temperature
When the temperature increases, the TMm+/TM(m+1)+ ratio is shifted towards the reduced state. For example, iron oxidoreduction 〚26〛 has been investigated for 0.4 Fe2O3–0.6 P2O5 glasses melted at different temperatures. The Fe2+/(Fe2++Fe3+) ratio increases from 0.17 to 0.5 as the melting temperatures varies from 1150 to 1400 °C. The same observation holds for Cu: the evolution of the 〚Cu+〛/(〚Cu2+〛 + 〚Cu+〛) ratio versus temperature (1000 to 1200 °C) in (1 – x) P2O5–x CuO glasses 〚27〛 is similar to that of iron, but for glasses with x = 0.5 or less CuO, the 〚Cu+〛/(〚Cu2+〛 + 〚Cu+〛) ratio is independent of the melting temperature.
2.2.2 TMm+/TM(m+1)+ ratio versus atmosphere
The copper redox state in 0.5 P2O5–0.2 Na2O–0.3 CuO glasses (mol%) melted under oxygen and air has been investigated by Shih et al. 〚28〛. The 〚Cu2+〛/(〚Cu2+〛 + 〚Cu+〛) ratio in the glass melted in flowing oxygen is higher than that melted in air. Turkdugan 〚29〛 has also observed the same behaviour for iron in iron phosphate glasses.
Addition of a reducing agent may control the oxidation and reduction of transition metal, although this synthesis is out of equilibrium. We have synthesised 0.5 CuOx–0.5 P2O5 and 0.4 CuOx–0.6 P2O5 glasses with different copper valence states by adding glucose during glass melting. For the two series of glasses, the concentration of Cu+ increases with glucose addition (Fig. 2).
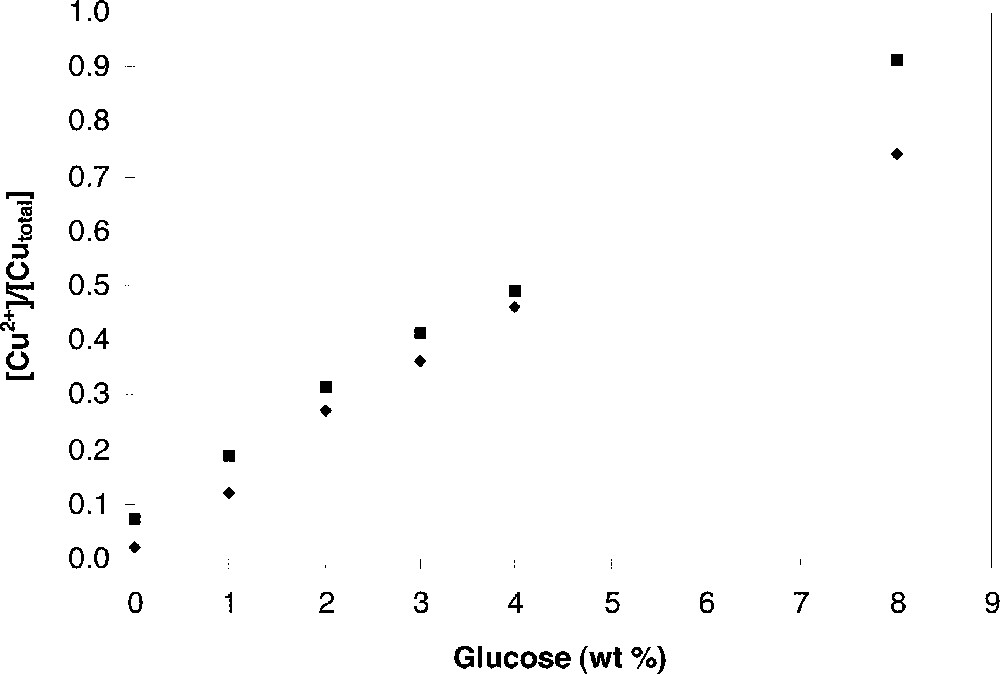
〚Cu+〛/〚CuTotal〛 ratio versus the amount of glucose added in batches: ♦ 0.5 CuOx–0.5 P2O5 and ■ 0.4 CuOx–0.6 P2O5 glasses.
2.2.3 TMm+/TM(m+1)+ ratio versus concentration of transition metal (TMO) in phosphate glasses
Fig. 3 shows the copper redox behaviour in (1–x) CuO–x P2O5 glasses. We can observe that there are contradictions concerning the evolution of the Cu2+/(Cu++Cu2+) ratio versus copper content. Bae and Weinberg 〚27〛 report that this ratio is 1, and independent of glass composition for glasses containing less than 0.5 CuO (Fig. 3). They explain this behaviour on the basis of structural constraints rather than of a redox equilibrium reaction. In contrast, Morsi et al. 〚31〛 claimed that the total copper concentration in phosphate glasses affects the ratio. The increase of the Cu2+/(Cu++Cu2+) ratio with increasing CuO content from x = 0.4 to x = 0.5 is attributed to the increase of the glass basicity (Fig. 3). For compositional range of CuO above x = 0.5 (Fig. 3), the Cu2+/(Cu++Cu2+) ratio tends to decrease. Both Bae et al. 〚27〛 and Morsi et al. 〚31〛 explain this evolution by the assumption that Cu2+ and Cu+ ions have a different coordination: copper is oxidised until all Cu2+ coordination sites are saturated (tetragonally distorted). When the copper concentration exceeds the available number of Cu2+ coordination sites, the remaining copper ions are reduced to Cu+ in trigonal distorted sites.
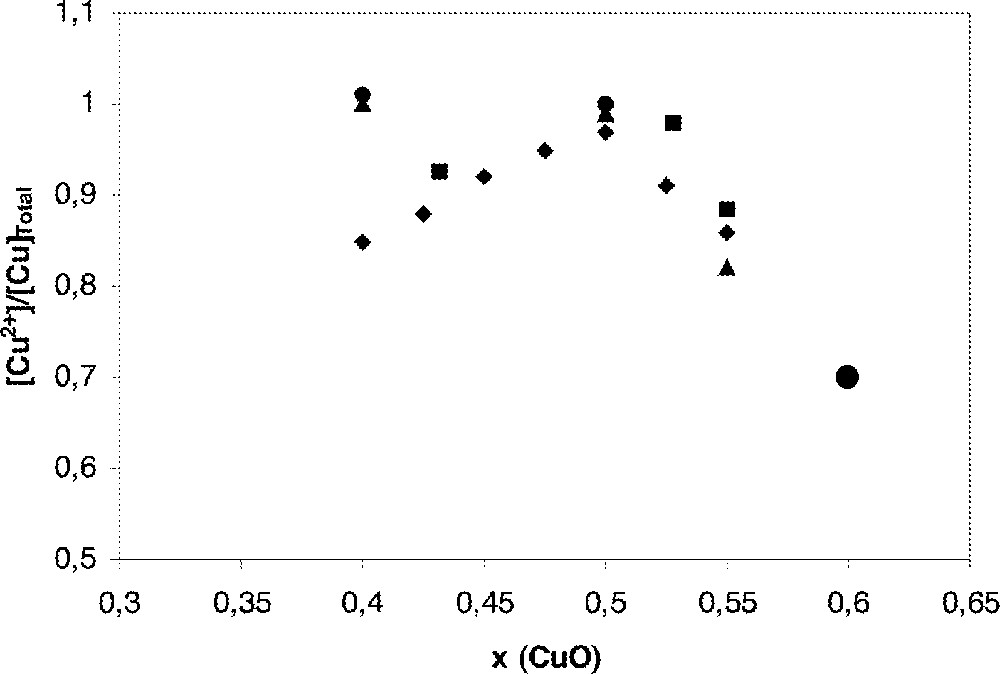
〚Cu2+〛/〚Cu〛Total ratio versus CuO content in x CuO–(1 – x) P2O5 glasses: ♦ Morsi et al. 〚31〛, ▴ Koo et al. 〚37〛, • Bae et al. 〚27〛, ■ our results 〚30〛.
Magalhaes de Abreu et al. 〚32〛 and Congas et al. 〚33〛 have investigated the iron redox behaviour in phosphate glasses. The reduced state Fe2+ is favoured when the Fe2O3 content increases. In (1 – x) NaPO3–x Fe2O3 glasses 〚33〛 with x = 0.05, 0.1 and 0.15, the Fe3+/Fe2+ ratio decreases from 0.91 to 0.87 when the Fe2O3 content increases from 0.05 to 0.15.
In iron niobophosphate glasses 〚32〛 (0.1 Nb2O5–0.4 P2O5–0.5 Li2O)–x Fe2O3 with x = 0 to 0.5, the Fe2+ population increases with the increase of Fe2O3 concentration, but for high concentrations (x > 0.3), crystallisation of Fe2O3 and LiFePO4 was observed. No structural or thermodynamic argument was proposed by the authors to explain this evolution.
The molybdenum redox behaviour in 0.25 Na2O–0.75 〚x (MoO3)2–(1–x) P2O5〛 glasses (called series 1) with x = 0.13 to 0.6, and 0.45 Na2O–0.55 〚x (MoO3)2–(1–x) P2O5〛 glasses (called series 2) with x = 0.09 to 0.55 has been investigated by Bih et al. 〚34〛. For the series 1, a maximum Mo5+/MoTotal has been evidenced for a Mo/P ratio close to 0.5 and attributed to a maximum of MoOPO4 units in the glass. For x = 0.13, 0.33 and 0.6, the Mo5+/MoTotal ratios represent 0.31, 0.33 and 0.01, respectively. For the series 2 glasses, the Mo5+/MoTotal ratios do not change with MoO3 content and remain low, i.e. for x = 0.09 and 0.55, these ratios are 0.08 and 0.01 respectively. According to Bih et al. 〚34〛, this different behaviour is due to the different Na2O concentration, because Na+ ions have aptitude to stabilise the valence +6 of molybdenum. This maximum of Mo5+/MoTotal ratio has been observed also in binary molybdenum phosphate glasses x (MoO3)–(1–x) (P2O5) 〚35〛 with x = 0.55 to 0.8.
In x V2O5–(1 – x) 〚0.6 PbO–0.4 P2O5〛 glasses with x = 0.08 to 0.8 (Fig. 4) 〚36〛, the fraction of reduced V ions V4+/(V4++V5+) (Fig. 4) decreases with increasing V2O5 concentration, in opposition to copper and iron. The formation of complex oxide ions shifts the redox equilibrium.
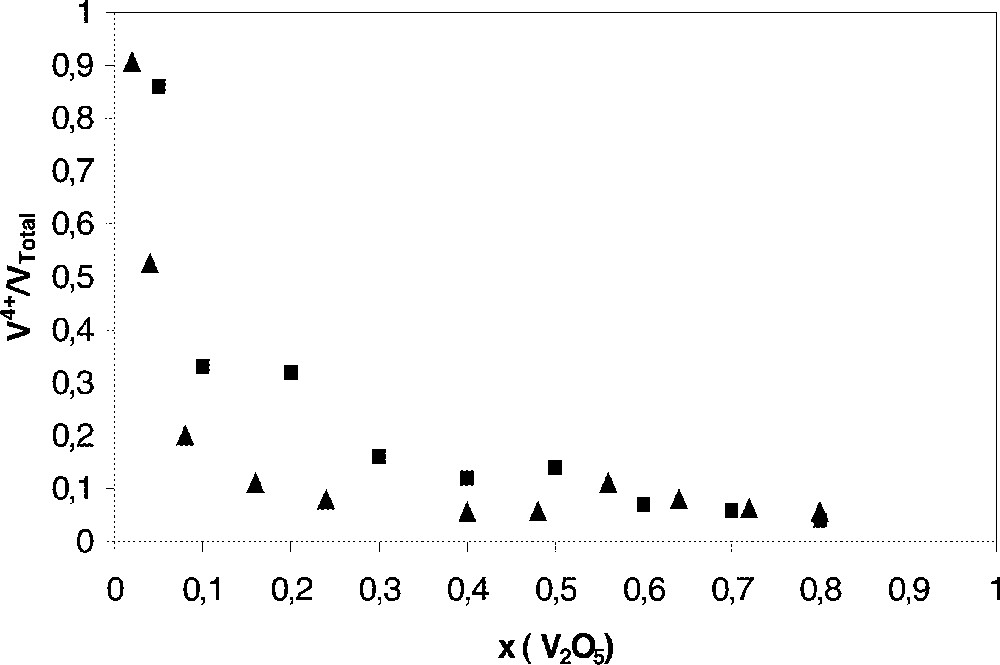
〚V4+〛/〚VTotal〛 ratio versus V2O5 content in x V2O5–(1 – x) 〚0.6 PbO–0.4 P2O5)〛 glasses. ■ Hirashima et al. 〚36〛, ▴ our results.
In conclusion, according to the transition metal, the evolution of the reduced state/oxidised state ratio versus its concentration is different. For copper and iron, the formation of reduced state is favoured when their concentration increases, but for vanadium the oxidised state is favoured. For the molybdenum, there exists a maximum for this ratio, the reduced state is favoured when the MoOPO4 units are present in glasses. So it is very difficult to predict the evolution of TMm+/TM(m+1)+ ratio versus the TMO content because structural constraints, coordination, and complex ion formation influence the redox behaviour.
2.2.4 Influence of basicity at constant TMO/P2O5
Attempts to relate redox ratios with the basicity have been made in the two following studies. The first one concerns the ternary 0.5 P2O5–0.3 CuO–0.2 MO glasses (Cu/P and O/P constant) 〚31〛 with M = 2 K, 2 Na and 2 Li or Ca and Mg. The Cu2+/(Cu2++Cu+) ratio increases in order K > Na > Li, and for alkaline earth Ca > Mg. For M = 2 K, 2 Na and 2 Li, the ratios represent 0.96, 0.94 and 0.87, respectively, and for M = Ca and Mg, the ratios represent 0.85 and 0.75, respectively. The Cu2+/CuTotal ratio is then clearly related to the basicity. The incorporation of network modifiers such as alkali and alkaline earth oxide in the glass structure increases the numbers of non-bridging oxygens, increases the basicity, and hence the oxidised state is favoured. The basicity is also related to the bond strength; when the ionic radius of the modifier increases, the bond strength between modifier and oxygen decreases, so the polarisability of oxygen ions increases.
The second study concerns the x Na2O–(1 – x) 〚0.4 (MoO3)2–0.6 (P2O5)〛 〚34〛 glasses with Mo/P constant, but with compositional changes (O/P). The Mo5+/Mo6+ ratio decreases when the Na2O content increases: for x = 0.1, 0.25 and 0.6, the Mo5+/MoTotal ratios are 0.3, 0.14 and 0.01, respectively. This redox evolution is thus in accordance with basicity considerations. Moreover, if one compares the Mo5+/MoTotal ratios of x Na2O–(1 – x) 〚0.4 (MoO3)2–0.6 (P2O5)〛 and x Li2O–(1–x) 〚0.4 (MoO3)2–0.6(P2O5), for a given composition, it is lower than in the lithium glass, which is also in agreement with what would have been expected from basicity considerations. The authors also assume that this is because Na+ ions have a higher aptitude to stabilise the +6 valency of molybdenum 〚34〛.
3 Cationic sites of transition metals (TM) in phosphate glasses
A review of the coordination of transition elements in silicate glasses 〚38〛 draws the conclusion that tetrahedral coordination is frequent for cations, and the octahedral one is restricted to the larger cations. A five-coordination, unusual in crystalline solids, appears however to be a normal coordination state in glasses for several transition elements such as nickel or titanium. In low-alkali borate glasses (< 10 mol% alkali oxides), an unusual octahedral coordination for nickel and cobalt has been reported 〚40〛. Even at high dilution, Ni, Co and Zn ions are inhomogeneously distributed within ordered domains extending to 0.6 nm 〚39〛. These domains consist of corner and edge sharing NiO6 octahedra. What happens in phosphate glasses containing transition elements?
3.1 TMOn-P2O5 phosphate glasses (TM = transition metal) without alkali or alkali-earth in the composition
3.1.1 Local environment of transition metals (TM) with a unique valence state
The most significant study found in the literature on TM-containing phosphate glasses without alkaline or alkaline earth oxides concerns zinc phosphate glasses 〚40〛. Coordination number of 4.05 is claimed for the zinc. Since NZnO is 4, ZnO4 units do not have to share terminal oxygens (OT) and clusters of Zn sites are not formed. In addition, prior EXAFS 〚41, 42〛 studies showed an increase in the zinc coordination in the binary (1 – x) ZnO–x P2O5 glass for compositions after the metaphosphate composition (x > 0.5).
3.1.2 Local environment of transition metals (TM) with various valence state
The local environment around iron in 0.4 Fe2O3–0.6 P2O5 (molar composition) melted at various temperatures or under different melting atmospheres has been investigated using 57Fe Mössbauer and X-ray-absorption fine structure spectroscopies 〚43〛. The authors indicate that Fe(III) ions occupy two distinct sites, whereas the Fe(II) ions occupy a single site. The average Fe–O coordination number extracted from EXAFS fits is close to 4.5 and corresponds, for the authors, to a mixed tetrahedral-octahedral coordination for both Fe (II) and Fe (III) ions.
In an investigation of copper in phosphate glasses, Musinu et al. 〚44〛 proposed that their results are consistent with the hypothesis that Cu(II) and Cu(I) occupy sites with different coordination geometries. Both coordination polyhedra are described from a distorted octahedron: the twofold coordinated Cu(I) originates from axial neighbours in a 2 + 4 distorted octahedron, and the fourfold coordinated Cu(II) correspond to only four equatorial neighbours in a 4 + 2 octahedron. Explanations of the evolution of physical properties with composition 〚45〛 are proposed by considering the difference in coordination and bonding states of copper: Cu(II)–O bonds are mainly ionic, meaning that CuO acts as a network modifier, thus leading to formation of non-bridging oxygens. Cu(I)–O bonds have a more covalent character; they act as links between phosphate chains, thus conferring to Cu2O a network-forming character.
Another example concerns the studies of Rao et al. 〚46, 47〛, devoted to MoO3 and WO3 in phosphate glasses. The authors proposed that in these glasses, molybdenum (mainly stabilised as Mo5+) and tungsten (W5+) are octahedrally coordinated.
3.2 TMOn–P2O5–M2O phosphate glasses (TM = transition metal and M = alkaline) or TMOn–P2O5–M’O phosphate glasses (TM = transition metal and M’ = alkaline earth)
3.2.1 The isolated octahedral site of transition metal (TM) and its distortion
Octahedral coordination appears to be the basic coordination of TM in alkaline or alkaline-earth phosphate glass chemistry 〚40〛. However, as the TM concentration increases, the proportion of distorted sites increases. Optical absorption spectra recorded for doped Ni, Mn, Cr in 20 Na2O–20 K2O–60 P2O5 glasses indicate an octahedral coordination 〚48〛. Corrias et al. 〚49〛, in a neutron diffraction study of the 30 NiO–35 Na2O–35 P2O5 glass, found a Ni–O distance centred at 0.205 nm, which is attributed to distorted octahedral coordination rather than to the fivefold coordination found in a calcium nickel silicate glass 〚38〛. However, the second difference data seem to be quite similar to those obtained for the calcium nickel silicate glasses, indicating some cation ordering in glasses 〚38〛.
For Co2+, there is evidence for an octahedral–tetrahedral equilibrium 〚49〛. The same equilibrium is found in Zn-containing phosphate glasses 〚50, 51〛. Molecular dynamics simulations were undertaken on 2 ZnO–Na2O–3P2O5 glass and leads to a zinc coordination number of 3.96.
Three sodium phosphate glasses (1 – x) NaPO3–x Fe2O3 with x = 0.05, 0.1 and 0.15 prepared in air in the same experimental conditions have been studied using 57Fe Mössbauer spectroscopy 〚33〛. High-spin ferric and ferrous iron with mean isomer shift values at 0.43–0.44 mm s–1 and 1.20–1.26 mm s–1, respectively, are characteristic of an octahedral coordination. An article 〚52〛 discusses the relationships between the composition and structure of three glass series: Na2O–Al2O3–P2O5 (NAP), Na2O–Al2O3–Fe2O3–P2O5 (NAFP) and Na2O–Fe2O3–P2O5 (NFP). The substitution of Al2O3 for Fe2O3 in (NAFP) phosphate glasses enhances the formation of pyrophosphate units, because iron has a stronger effect on the depolymerisation of metaphosphate chains than aluminium.
Copper-doped sodium metaphosphate glasses have been studied by EPR and optical absorption 〚53〛. The EPR results show that g⊥ < g∥, indicating tetragonally elongated octahedral sites for the Cu2+ ion in the glass. Cozar et al. 〚54〛 have called this local symmetry of Cu2+ an unusual tetrahedral (Td) configuration. It is admitted that the Cu coordination is higher in phosphate than in silicate and borate glasses 〚13〛.
3.2.2 Simple ion or complex ion of transition metal (TM) in phosphate glasses
As shown at the beginning of this review, complex oxide ion can be formed by the complexation of TMn+ by O2–. The complexation degree may be low like in VO2+ or high in CrO42–. The transition from simple ions to complex oxide ions occurs as a function of the oxidation state or under the influence of the glass composition.
3.2.2.1 Influence of the glass composition on the complex oxide formation
In vanadium-doped sodium metaphosphate glasses 〚53〛, V4+ is the main redox state. EPR studies show that g⊥ > g∥, indicating a tetragonally compressed octahedral site. Thus, it is to be inferred that vanadium enters the glasses as VO2+ ion. This transition from octahedral V4+ to VO2+ complex oxide ions seems to be due to the decrease of the effective charge of the surrounding oxygen ligands, which decreases their electron donating ability (σ bonds), while the charge of the central vanadium remains high. This induces the promotion of strong π bond with the two axial oxygens of the compressed octahedron.
The titanium environment has been well investigated by 〚55–60〛. The combined XANES and EXAFS data are consistent with the presence of two different kinds of titanium sites: octahedral and square based pyramids. More precisely, EXAFS analysis gives evidence for short Ti–O distances (0.161 nm–0.169 nm) that are typical of the distances usually observed in several titanates exhibiting TiO5 groups. The proportion of square-bonded pyramids increases with the titanium concentration.
3.2.2.2 Dependence of complex oxide formation upon the oxidation state
This corresponds to the well-known tetrahedral complexes such as CrO42–, VO43– and MoO43–. Murata et al. 〚20〛 report studies on chromium dopants in large series of glasses, silicate, borate, aluminate and phosphate. The Cr3+ and Cr6+ ions coexist, excepted in the phosphate glasses. Even at high alkaline concentration, the CrO42– complexes do not exist in phosphate glasses. The conclusions are identical for Cr in more complex glasses such as Na5Ga1–xCrx(PO3)8 with 0 < x < 1 〚61〛, where Cr3+ ions have an octahedral environment and move gallium ions towards tetrahedral sites. In a calcium chromium phosphate glass 〚62〛 of composition: 0.24 CaO–0.01 Cr2O3–0.75 P2O5, the chromium (III) environment is also found to be octahedral. Contrary to the chromium, discrete MoO42–entities are present in molybdenum phosphate glasses rich in alkaline oxides 〚63〛.
3.2.3 Condensation of distorted TM octahedra
As the TM concentration increases, ‘invert’ glass network is created, meaning that the glass network is formed with both PO4 tetrahedra and MOx polyhedra. In some cases, connections between TMO6 octahedra occur through oxygens not bonded to the phosphate skeleton. To obtain these invert networks, two ways are generally proposed: either by adding M2O to TMOx–P2O5 or TMOx to M2O–P2O5.
In x TiO2–(1 – x)(Na2O–P2O5) systems containing large amounts of titanium 〚64〛, EXAFS indicates the presence of titanium in the second coordination shell of a given Ti at a distance of 0.34 nm, suggesting the formation of Ti–O–Ti–O–Ti–O chains like in KTiOPO4.
In a similar way, large introductions of Nb2O5 or Ta2O5 in a borophosphate matrix (0.95 NaPO3–0.05 Na2B4O7) give rise finally to a three-dimensional association of corner-shared octahedra 〚65〛. Fargin et al. 〚56〛 suggest, for the same glass system, that the Nb–Nb distances estimated from the EXAFS analysis are typical of those found in a bronze framework (Nb–Nb = 0.32 nm and 0.4 nm). A recent 93Nb solid state NMR analysis confirmed the presence of two niobium environments in (1 – x) NaPO3–x Nb2O5 glasses 〚66〛 (Fig. 5), attributed to isolated and condensed NbO6 polyhedra bonded to a different number of PO4 tetrahedra.
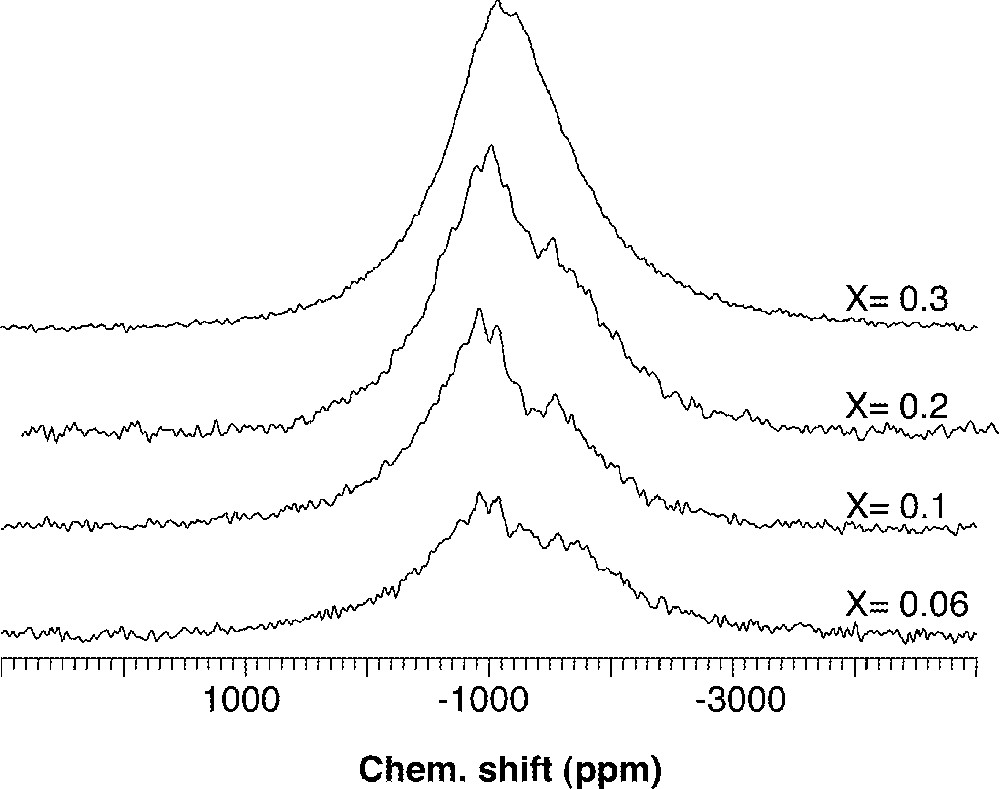
93Nb NMR spectra of (1 – x) NaPO3–x Nb2O5 glasses.
Cozar et al. 〚67〛 have found for the x V2O5–(1 – x) (P2O5–Na2O) glass system two EPR signals, one with hyperfine structure typical for isolated ions and another one consisting of a broad line without hyperfine structure characteristic of clustered ions. These clustered ions are not evidenced at low V2O5 contents (x = 0.05).
The electron paramagnetic resonance (EPR) spectra of W5+ions in Li2O–WO3–P2O5 with different amounts of oxide components have been investigated by Rhakimov et al. 〚68〛. They have shown that Li+ addition favours the formation of tungsten pairs. The mean distance between W5+ ions indeed decreases from 0.453 nm for the glass without lithium to 0.37 nm for the glass containing lithium. In the same Li2O–WO3–P2O5 glass system, Boulich et al. 〚63〛 made structural analysis using various spectroscopic techniques such as infrared, Raman and EPR. The composition of their glasses are x P2O5–y A2MO4–(1 – x – y)A2O, with x = 0.5 to 0.8 and y = 10, M = W and A = Li. These glasses contain octahedral MO6 and tetrahedral MO4 units. M2O7 dimers appear when the Li2MO4 content is increased. In 0.4 CaO–(0.6 – x) P2O5–x WO3 glasses with 0 < x < 0.15, the authors 〚69〛 reported clear evidence for WO6 and WO4 groups, identified by infrared spectroscopy. In the compositional range 0.03 < x < 0.15, when x increases, the infrared band attributed to WO6 is gradually shifted towards higher frequencies and its intensity decreases. The authors propose a different interpretation of the structural role of WO3. The WO6 octahedral concentration decreases because they are generally more strongly interconnected into 3D units than WO4. This structural organisation leads then to a decrease of the long-range disorder.
3.3 Charge balancing of distorted octahedra by alkali or alkali earth cations
Detailed studies on the charge compensation of the TM have been carried out on the K2O–TiO2–2 SiO2 glass 〚70〛. The Ti site corresponds to a square-based pyramid with four oxygens at 0.196 nm and one non-bonded oxygen at 0.168 nm. In this case, the authors propose that K atoms are charge compensators of the non-bonding titanyl bond.
In the 0.5 CaO–0.2 TiO2–0.3 P2O5 glass, Brow et al. 〚40〛 conclude that the glass network consists primarily of corner-shared orthophosphates and distorted octahedra of titanate units. In addition, the network is also constituted by five-coordinated titanate species (TiO5). Calcium ions are most likely associated with the anionic octahedral titanate species in sites similar to those occupied by sodium in crystalline Na5Ti(PO4)3 〚71〛. According to Brow 〚79〛, the problem of titanate is analogous for iron in phosphate glasses. Anionic (Fe3O12)16– clusters are formed with one Fe(II) and two Fe(III) ions, both in six-fold coordination. The (Fe3O12)16– clusters are interconnected via P2O74– groups.
Addition of TiO2, Ta2O5 or Nb2O5 removes some non-bridging oxygens from the phosphate network. Consequently, the alkali modifiers are forced near the transition metal polyhedron for balancing the charge.
4 Relationships between phosphate framework and cationic organisation
A complete description of the anionic phosphate network in x ZnO–(1 – x) P2O5 glass system 〚72–73〛 is proposed by means of two-dimensional (2D) solid and liquid states 31P NMR. Average chain length in these glasses are determined and compared to the values predicted by the Van Wazer’s theory. A large discrepancy in the phosphate groups quantification is noticed for the 0.55 ZnO–0.45 P2O5 and 0.5 ZnO–0.5 P2O5 glasses. According to the authors, a first reason is that some authors did not consider the dispropornation reactions in the model. A second reason is based on the increase of the zinc coordination. The Zn2+ ions are bonded more ionically with more of their oxygen neighbours and depolymerise more the phosphate chains. Hussin et al. 〚74〛 reported structural studies on x CdO–(1 – x) P2O5 (0.25 < x < 0.6) glasses. The local structure has been studied using 31P, 113Cd nuclear magnetic resonance. The observations are the same as those for zinc phosphate glasses.
In ternary phosphate glasses, the addition of transition metal oxide to alkali or alkali-earth condensed phosphate glasses leads to a depolymerisation of phosphate chains. X-ray diffraction has been used to study the cation coordination in three glasses with composition 0.30 TMO–0.35 Na2O–0.35P2O5 (TM = Ni, Zn, and Cu). 〚75〛. Average coordination numbers turned out to be 6 for Ni2+, 5 for Cu2+ and 4.5 for Zn2+. Anionic speciation has been investigated by IR, Raman spectroscopy for the Cu- and Ni- containing glass, and 31P MAS-NMR for the Zn- containing glass. The three glasses were found to be almost exclusively composed of diphosphate units. These observations are in agreement with the Van Wazer’s fully ionic modifying oxide model for phosphate glasses and are a priori independent of the coordination of TM.
A recent NMR study 〚76〛 details the relationships between the phosphate framework and cationic sub lattice. This study was carried out on the glass system 0.485 Na2O–0.485 P2O5–0.03 〚3 x TiO2–2 (1 – x) Bi2O3〛 with 0 ≤ x ≤1. It is assumed that Bi replaces Ti and that Bi2O3 does not act as a network former 〚77〛. The originality of this study 〚76〛 is to maintain the O/P ratio constant in the various glasses. 31P MAS NMR and 31P double quantum MAS NMR enabled the characterisation of the phosphate network. Diagonal peaks (Fig. 6) on the 31P double quantum MAS NMR indicate self correlated Qn sites 〚78〛. The occurrence of diphosphate species Q1,1(Na,Ti) at –7 ppm in the MAS dimension is early observable in the depolymerisation process 〚76〛. The second important point concerns the chemical shift of Q2,22 sites at –19 ppm, which indicates that they are only linked to Na+ ions. The Q2/Q1 ratio increases with the TiO2 content and leads to a condensation of the phosphate network although the O/P ratio is maintained constant (Figs. 7 and 8).
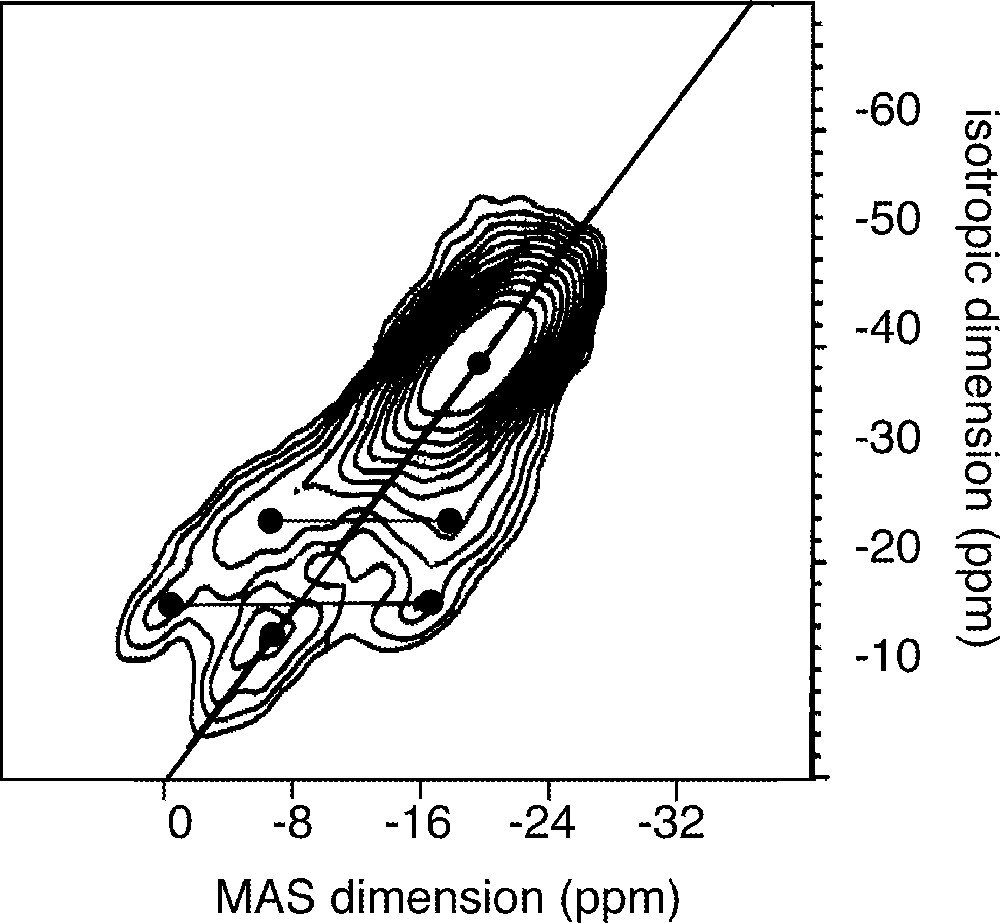
31P double-quantum filtered MAS spectrum of 0.5 Na2O–0.45 P2O5–0.03 TiO2–0.02 Bi2O3 glass.
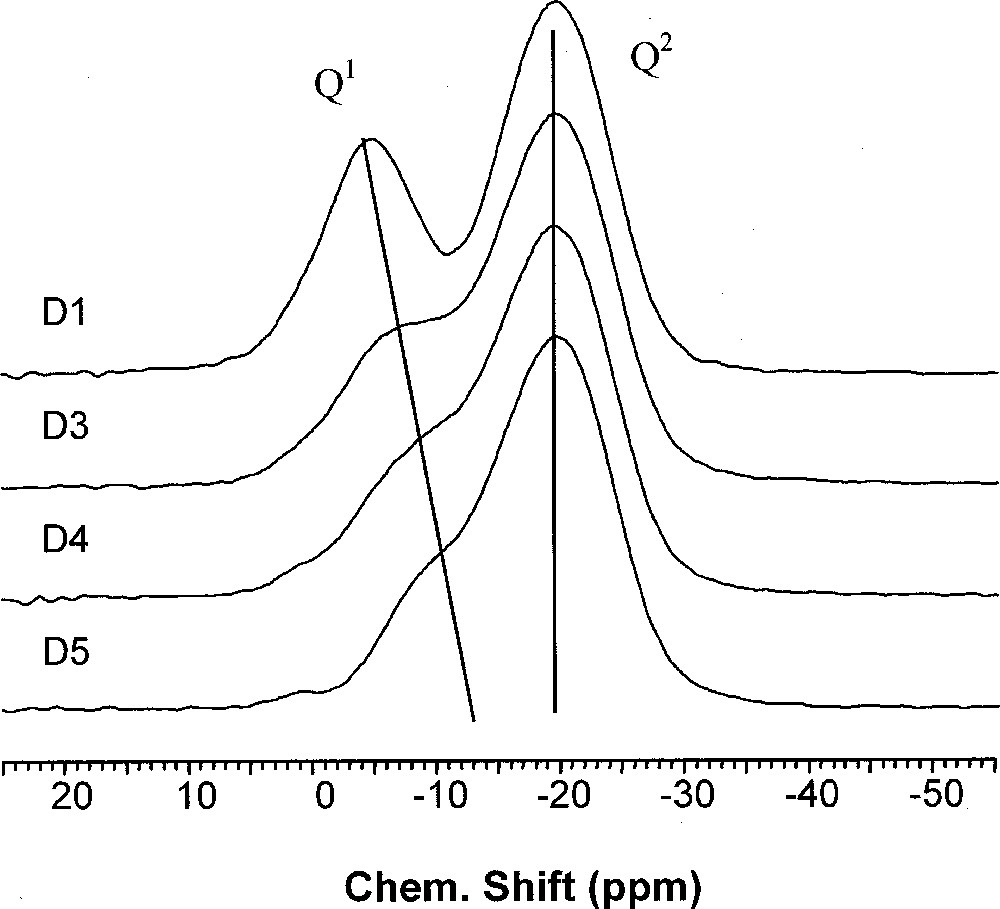
31P MAS–NMR of 48.5 Na2O–48.5 P2O5–3 〚3 x TiO2–2(1 – x) Bi2O3〛 glasses with 0 < x < 1. D1: x = 0, D3: x = 0.042, D4: x = 0.059, D5: x = 0.085.
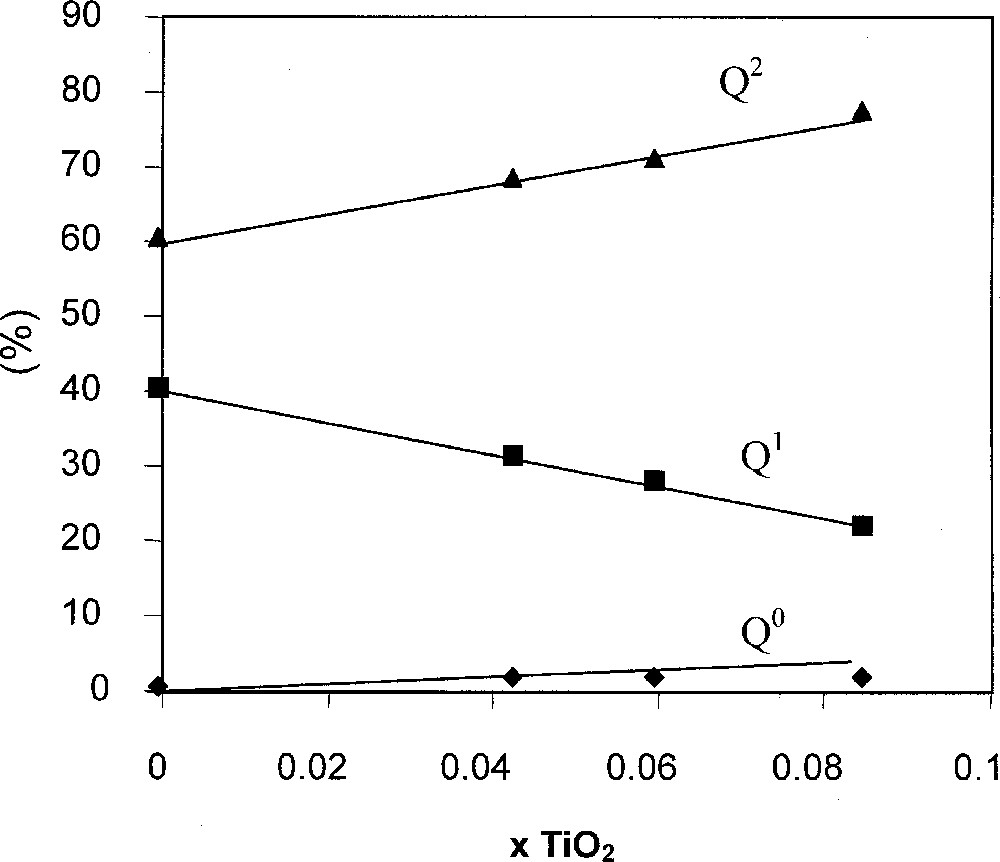
Relative amount of Qn species obtained by deconvolution of the 31P NMR spectra of Fig. 7.
The same conclusions are proposed for tantalum and niobium oxides, which act also as intermediate network former in alkali phosphate glasses and therefore eliminate some non-bridging oxygen 〚65〛. The same conclusions are also valid for Nasicon-type glasses, with the general formula AxByP3O12, where A = Li, Na or K and B = Fe, Ti, V or Nb 〚46〛. They contain diphosphate units, although the chemical formula indicates that they are orthophosphate. These non-expected condensed phosphates do not exist in the crystalline ‘Nasicon-type structure’, which is built up of corner sharing 〚BO6/2〛n– octahedra (n = 6 – the coordination of B) and 〚PO4/2〛+.
5 Perspectives
This survey is limited to transition metal in binary glasses and in alkali or alkali-earth ternary phosphate glasses and does not take in account TM in more complex systems, like halogen–phosphate glasses, like fluorophosphate glasses or phosphate glasses doped with AgI, PbO-containing phosphate glasses and finally phosphate glasses, in which redox reactions occur between two (or more) different transition metal ions. The knowledge of the cationic sites is far from being complete. It seems that interesting phosphate materials like NASICON glasses are found when the phosphate network turns into an inverted network. Further structural studies are required to develop new classes of amorphous phosphate materials containing nanophases or to understand more precisely the relationships between the local and medium-range order in phosphate glasses and their properties (optical, electrical...). Recent developments in solid state NMR spectroscopy are now able to investigate the homo-connectivities between PO4 tetrahedra, and should progress to the hetero-connectivities between PO4 and TM polyhedra.


