1 Introduction
The growing demand and future potentials of an advanced information society stimulate research for devices composing a network system with excellent flexibility and larger information capacities at much faster rates. Installation of broadband Wavelength-Division-Multiplexing (WDM) optical network system is indispensable and novel amplifier materials, which would overcome the performance of the present silica-based erbium-doped fiber amplifier (EDFA), can be a key to enable more number of channels. Among several possible choices of devices, rare-earth-doped amplifiers have implied high-power conversion efficiency than Raman and scalability of gain spectra by tailoring the host-glass composition. In telecommunication systems, the invention of the EDFA 〚1〛 can be likened to that of the transistors in electronics in terms of its technological impact. The technology to amplify the light signal directly without the conversion of light/electricity/light has been achieved by stimulated emission of 4f optical transition in rare-earth-doped fibers 〚2〛, which realizes ideal amplification with high gain and low noise. The technological development of optical telecommunication is based on the growth of technologies of fiber fabrication and those of laser diodes (LD). In fact, the invention of efficient III-V LD has also enabled efficient pumping of Er3+ with its three-level system 〚3–5〛. In addition, there exists the history of technological transition from passive fibers to active fibers 〚2〛, in which we can find a quite interesting relationship between active ions and the host glasses. Although the fiber amplifiers are already playing crucial roles in the optical networks both at 1.55 μm and at 1.3 μm bands, there exist further requirements to fully utilize the window of optical fibers with superior performance. The requirements are wide and flat gain spectrum around 1.53∼1.65 μm (C+L band) in a novel EDFA and around 1.45∼1.51 μm (S-band) in Tm3+ (TDFA) for the WDM systems 〚6〛, greater gain per pump-power at 1.31 μm in Pr3+- 〚7, 8〛 or possibly Dy3+-doped glasses 〚9–11〛.
According to the report of the Japanese Photonic Network Research Committee, the DWDM system will require 3000 channels in the year 2010 〚12〛. To enable 3000-channel WDM, we need more various amplifiers as well as a transmission fiber with a window from 1 to 1.65 μm. Fig. 1 shows a typical loss spectrum of the present silica fiber and emission bands of several rare-earth ions.
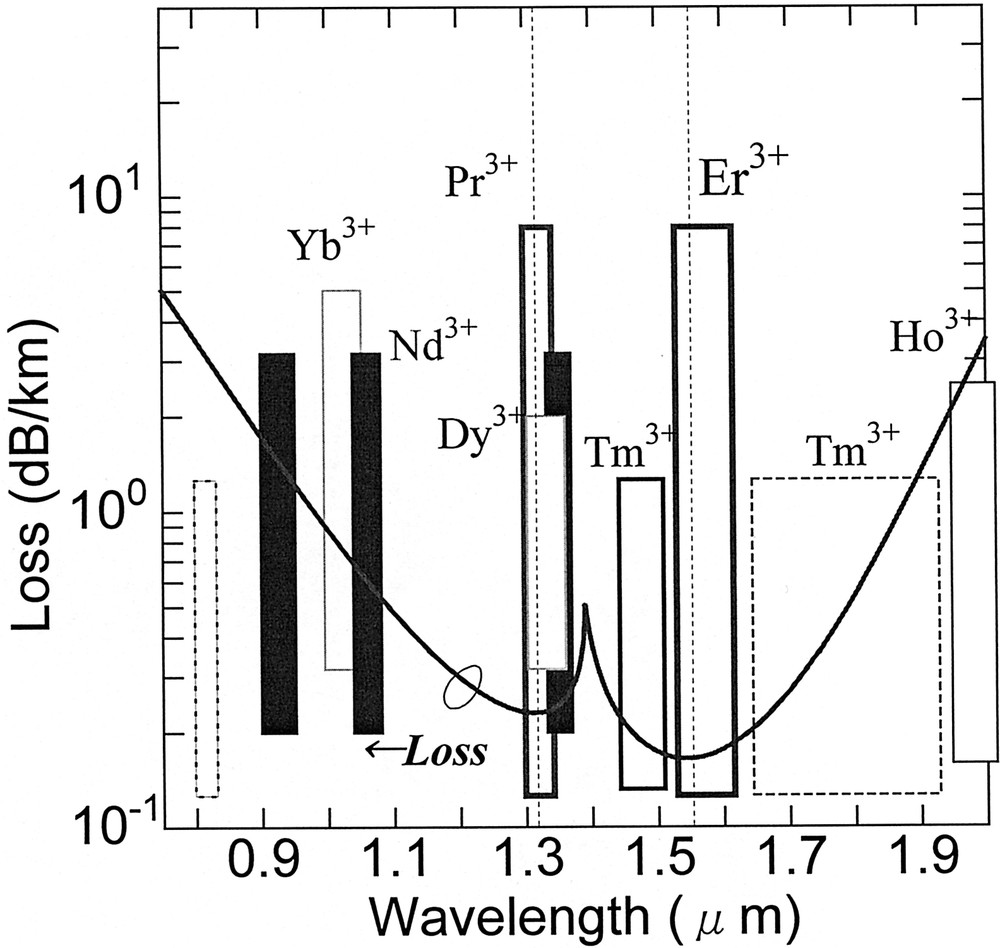
Loss characteristics of silica fiber and emission bands of some rare-earth ions.
Not only in fiber forms, planar waveguide forms will also play a role in photonic devices, since integration of optical circuits improves functions with fewer components 〚13〛. Because a shorter device length is usually expected for these waveguides, it might suffer from the problem of concentration quenching and new solutions of host materials would be required, due to the need of greater doping concentrations of rare-earth ions. In devices of either form, it is necessary to understand the 4f transitions of the ions, the structure of their sites in glass to design amplifier materials with better properties. This paper reviews some studies on the spectroscopic properties, radiative and nonradiative processes, and site structure of rare-earth ions in glasses at each wavelength.
2 Research scheme for rare-earth laser glasses
An optical amplifier works by the principle of light amplification by stimulated emission of radiation, nothing different from that of lasers. It requires a pump to create a population inversion in the amplifier medium. When an incoming signal photon stimulates an excited electron, the electron relaxes back into a lower energy state and emits a second signal photon with the same phase as the incoming photon. This process of stimulated emission amplifiers the signal. The success of the first generation silica-based EDFA is that the energy level of Er3+ ions can cause amplification to emit a photon with precisely the wavelength at which the network operates, with high efficiency, even in silica hosts having high phonon energy and poor RE solubility. The erbium was really a lucky boy to be the first, with an ideal energy level structure workable in silica and several pumping LDs available. Anyway, it is not a surprising idea to apply a research scheme for various rare-earth laser glasses to the design of novel amplifiers. To quantitatively comprehend optical phenomena of rare-earth ions in glasses, it is important to evaluate radiative and nonradiative decay process of related 4f levels. The Judd-Ofelt theory is usually adopted to obtain the radiative transition probabilities including emission by utilizing the data of absorption cross-sections of several f–f electric-dipole lines, especially for four-level emissions. The physical and chemical implement of three Ωt parameters (t = 2,4,6) are becoming clearer by combining the information of the local ligand field of doped ions by other spectroscopic techniques such as the 151Eu-Mössbauer effect 〚14〛. In some cases, the isomer shift and quadrupole splitting give us more discrete information about the rare-earth environment in glass; bond covalency and symmetry 〚15〛. The nonradiative decay rate can be evaluated experimentally by combining the lifetime measurement, which include contributions of multiphonon decay, energy transfer such as cross relaxation, cooperative upconversion, etc. In order to distinguish each contribution, systematic studies on concentration dependence of the rates are necessary. The phonon sideband spectra of Eu3+ ion can be supplementary to inclusive understanding of local structure in glass hosts, where the stretching vibrational mode of the network former bond often plays an important role 〚16〛 in the decay as well as in the phonon-assisted energy transfer 〚17〛. The above-mentioned research scheme is shown in Fig. 2. In many cases, the site selectivity of doped RE ions cannot be predicted in multicomponent glasses. However, we can feed back the several characteristics obtained for selected glasses toward a better material design based on logical direction.

Research scheme for efficient laser materials.
3 The 1.55-μm band in Er3+-doped glasses for broadband amplifiers
There is now a worldwide consensus that the WDM networking has superior functions and applications for future telecommunication systems 〚18〛 to the single channel TDM only at 1.55 μm. It offers not only large-scale information capacity, but also flexibility and transparency by utilizing the properties of light. Among various properties of EDFA, such as low-noise, broad bandwidth (not broad enough now!!) and efficient gain, the ability to amplify more than one wavelength at a time has replaced the regenerator for each channel. Although the excellent performance of the present silica-based EDFA can be used for a WDM system, but with fewer channels, there exists requirement for a larger number of channels, which could be possible by using an EDFA with a wider gain spectrum 〚6〛. From a practical standpoint, the flatness of the gain is also critically important because the light intensity for different channels would be varied by the multi-step amplifications if the gain of the amplifier were not independent of wavelengths. Therefore, the design of a host for Er3+ for wide and flat spectra of the 4I13/2–4I15/2 transition at around 1.5∼1.6 μm is a target at present.
For the transitions between the states with the difference in the total angular momentum by ΔJ = 1, there exists the contribution of the magnetic-dipole transition 〚19〛 in the 4I13/2–4I15/2. The spontaneous emission probability of this transition is given by:

Fluorescence spectra of Er3+-doped glasses; (a) Bi-silicate, (b) Bi-borate, (c) Tellurite and (d) Al-silica.
4 Tm-doped glasses for S-band amplifier
4.1 Background of S-band requirement
Due to the rapid increase of information traffic, great research effort has been paid to development of telecommunication devices for the WDM network system 〚29〛. Because the silica-based transmission fiber has a wide and low-loss window from 1.4 to 1.65 μm, there is an emergent demand for optical amplifiers, which can be used around 1.4 and 1.6 μm, in addition to the present silica-based EDFA. Tellurite-based EDFA was reported to have 80-nm-wide gain up to 1.6 μm (L-band), which also shows various excellent material properties 〚30, 31〛. For the 1.45–1.49-μm band (S+-band), the fluoride-based Tm-doped fiber (TDF) 〚32〛 can be used as an amplifier, although it still presents difficulties compared with the use of EDFA. One of the reasons for inferior performance of TDFA is a longer lifetime of the terminal 3F4 level than that of the initial 3H4 level 〚33〛. The performance of the TDFA is improved by use of an upconversion pumping scheme with a 1.06-μm laser, which produces a population inversion. Codoping of other lanthanide ion, such as Ho3+, was also found to improve the population inversion by means of the energy transfer from the 3F4 level 〚34〛. In addition, a larger branching ratio, β of the 3H4→3H6 band at 0.80 μm than that of the 1.46 μm make it difficult to realize amplification, because the fiber can easily lase at 0.80 μm, resulting in the gain saturation 〚35〛. According to the Judd–Ofelt calculation, β of 0.80 μm is nearly 90%, which is 11 times larger than that of 1.46 μm emission in most glasses 〚36, 37〛. Therefore, the suppression of the 0.80 μm amplified spontaneous emission (ASE) is desirable to avoid lasing at unexpected wavelength for improving the amplifier performance. In either case, in spite of difficulty as practical materials, nonoxide-fiber hosts with lower phonon energy have been used, because the 3H4 level is more easily quenched in high-phonon-energy environment, due to its small energy gap. However, the energy gap of the 3H4 level is not so small as that of the Pr:1G4 for 1.3-μm amplifiers and thus good performance can be expected in some oxide hosts with low phonon energy and better fiberizability.
Fig. 4 shows the relation between the multiphonon decay rate, Wp of the Tm:3H4, Pr:1G4 levels and the inverse phonon energy of various glass hosts. We can see the lower Wp of the Tm:3H4 in tellurite than that of the Pr:1G4 in ZBLAN, even with higher phonon energy.
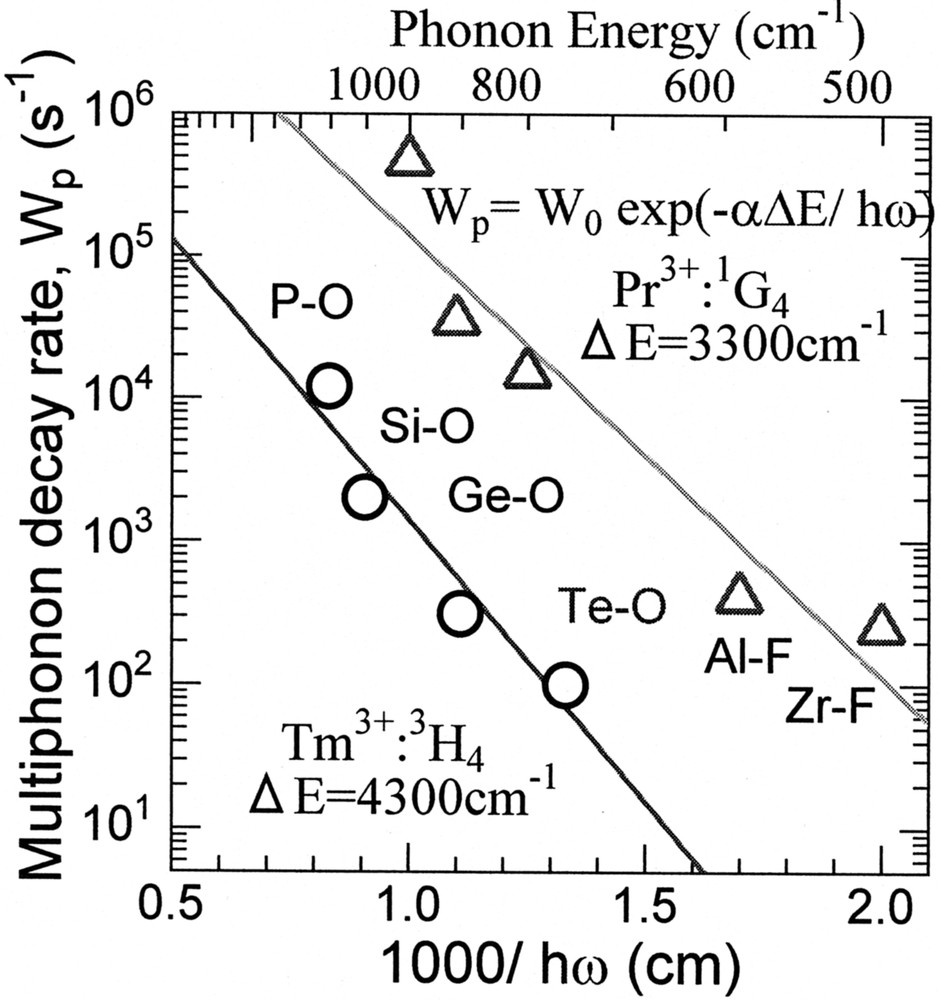
Relationship between multiphonon decay rates of Tm3+:3H4, Pr3+:1G4 levels and inverse phonon energy.
In this chapter, the tellurite glass was chosen as a host because it has relatively low phonon energy, excellent properties for fiber fabrications 〚30, 38〛, and thus can be considered as a candidate material for TDFA.
4.2 Spectroscopy of singly doped glass
4.2.1 Fluorescence spectra
Fig. 5 shows the Tm3+ energy level and a fluorescence spectrum in the tellurite glass, excited at 790 nm. The emission bands at 0.80 μm, 1.46 μm, and 1.80 μm are due to the 3H4→3H6, 3H4→3F4, and 3F4→3H6 transitions, respectively. The wavelength region longer than 1.3 μm is multiplied by 10 times. The area integration was carried out after converting the wavelength into wavenumber scale, which is directly proportional to the energy. The relative intensity ratio of 0.80 to 1.46 μm was about 11, almost unchanged with glass compositions and Tm-concentration. On the other hand, that of 1.46 to 1.80 μm was largely changed with these factors, which is due to the effect of the nonradiative relaxations.
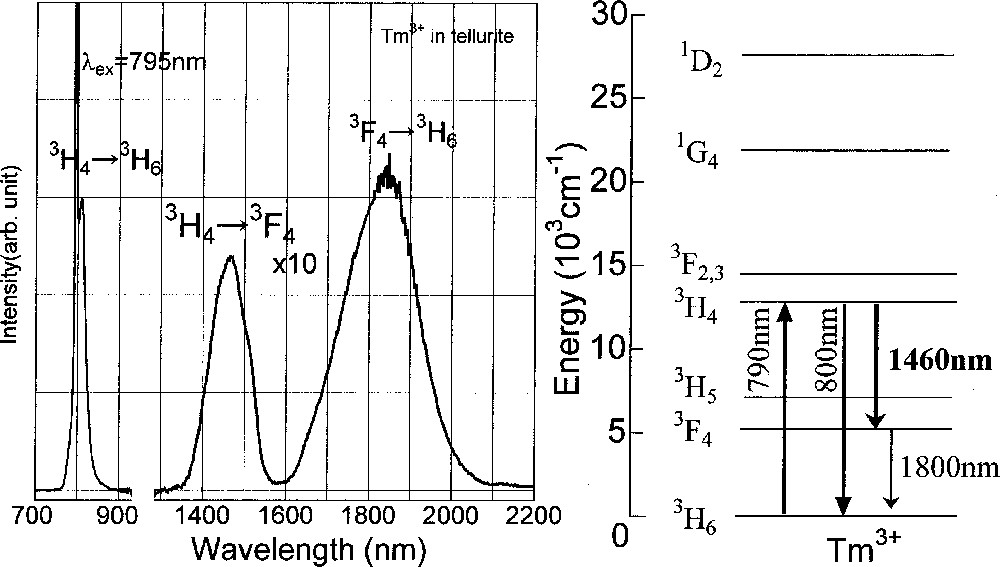
Fluorescence spectra of Tm3+-doped tellurite glass. Energy level of Tm3+ ion is also shown for assignment.
4.2.2 Judd–Ofelt analysis and quantum efficiency in tellurite
The obtained Judd–Ofelt parameters of Tm3+ in the present glass were: Ω2 = 4.69 pm2, Ω4 = 1.83 pm2, Ω6 = 1.14 pm2. Table 1 shows spontaneous emission probabilities, A and β from the 3H4 level of Tm3+ ions in the tellurite glass. The β of 0.80-μm emission is 11 times larger than that of 1.4-μm emission, which is almost similar to the case in fluoride and other oxide glasses. The calculated τR was 366 μs, while the measured lifetime was 350 μs. This indicates that the quantum efficiency of the 3H4 level is 96% in tellurite glass, which is comparable to that in ZrF4-based fluoride glasses (∼100%).
Spontaneous emission probability and branching ratios of Tm3+:3H4 level in the tellurite glass.
| Transition | Aed (s–1) | Amd (s–1) | Calculated branch ratio β(%) | Ratio of measured emission band |
| 3H4→3H6 | 2426 | – | 88.8 | ∼11 |
| 3H4→3F4 | 229 | – | 8.4 | 1 |
| 3H4→3H5 | 54 | 23 | 2.8 | – |
| Atotal = 2732 s–1, τrad = A–1 = 366 s |
4.2.3 Concentration dependence of emission
Fig. 6 shows the Tm2O3-concentration dependence of ratios of the τf(3F4)/τf(3H4) and the integrated intensity of (1.80 μm)/(1.46 μm) of fluorescence spectra. Both ratios increase drastically with increasing the Tm2O3 content. These phenomena are well understood by the so-called ‘Two-for-One Process’ 〚31〛, which is a result of the cross relaxation between two Tm3+ ions; 〚3H4,3H6〛 → 〚3F4,3F4〛 and unfavorable for population inversion between the 3H4 and 3F4 levels. Therefore, a low concentration is desirable to keep a high quantum efficiency of the 3H4 level for 1.4-μm application.
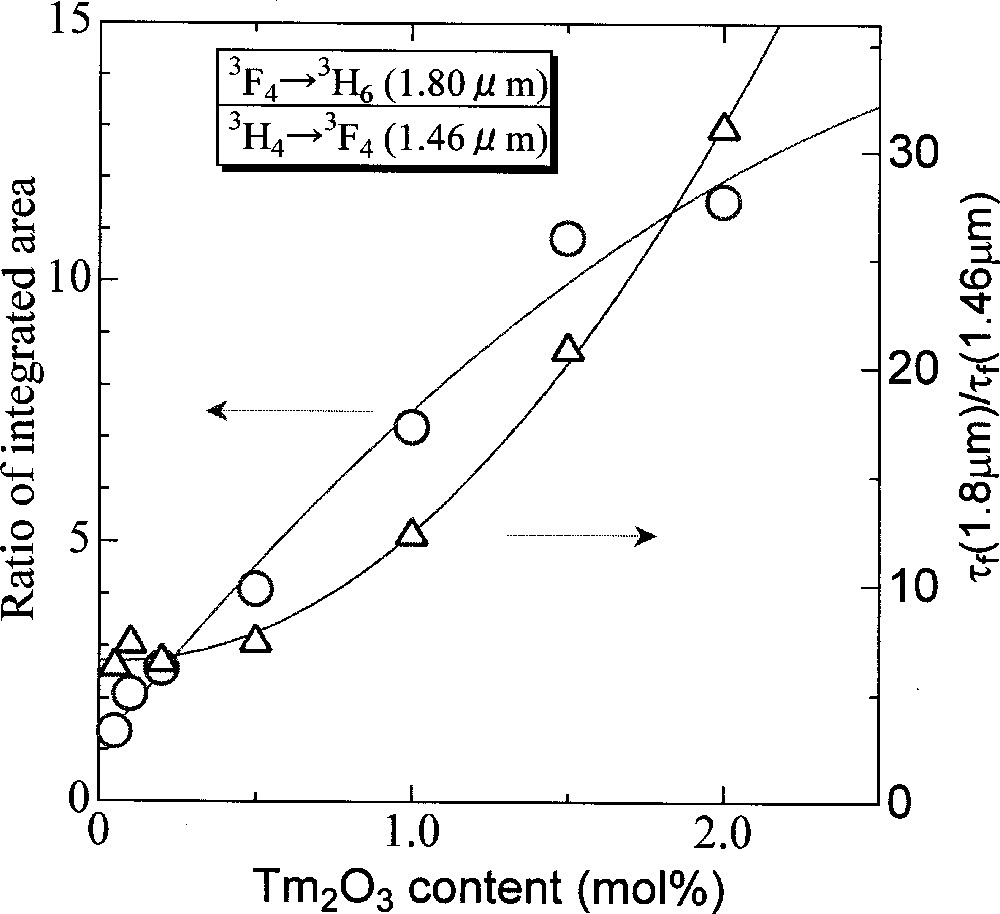
Ratio of integrated area and lifetime of 1.4 μm/1.8 μm in 72 TeO2–20 ZnO–5 Na2O–(2.9 – x) Y2O3–x Tm2O3 glasses.
4.2.4 Temperature dependence
Fig. 7 shows temperature variation of the fluorescence spectra. The peak intensity of the 1.46-μm band increases with lowering temperature, while the line shape of the 1.8-μm band becomes sharp. It can be seen that the mean wavelength of both bands shift to the longer side. The temperature dependence of integrated intensities of both bands is plotted in Fig. 8. The integrated area of the 1.46-μm band is almost unchanged at lower temperature and drops with temperature above 150 K. On the other hand, that of the 1.8-μm band increases slightly and decreases above 250 K. The tendency of the 1.46-μm emission can be explained by considering the temperature dependence of the nonradiative decay from the 3H4 level, which has smaller energy gap to the next lower level. The increasing tendency of the 1.8-μm band is ascribed to the improved population from the upper level by nonradiative processes. Therefore, the lower the temperature is, the better the population inversion becomes. Another advantage of the lower temperature can be the much-improved intensity at 1.50–1.52 μm, which is hardly obtained by conventional EDFA, though not impossible by TDFA 〚39〛.
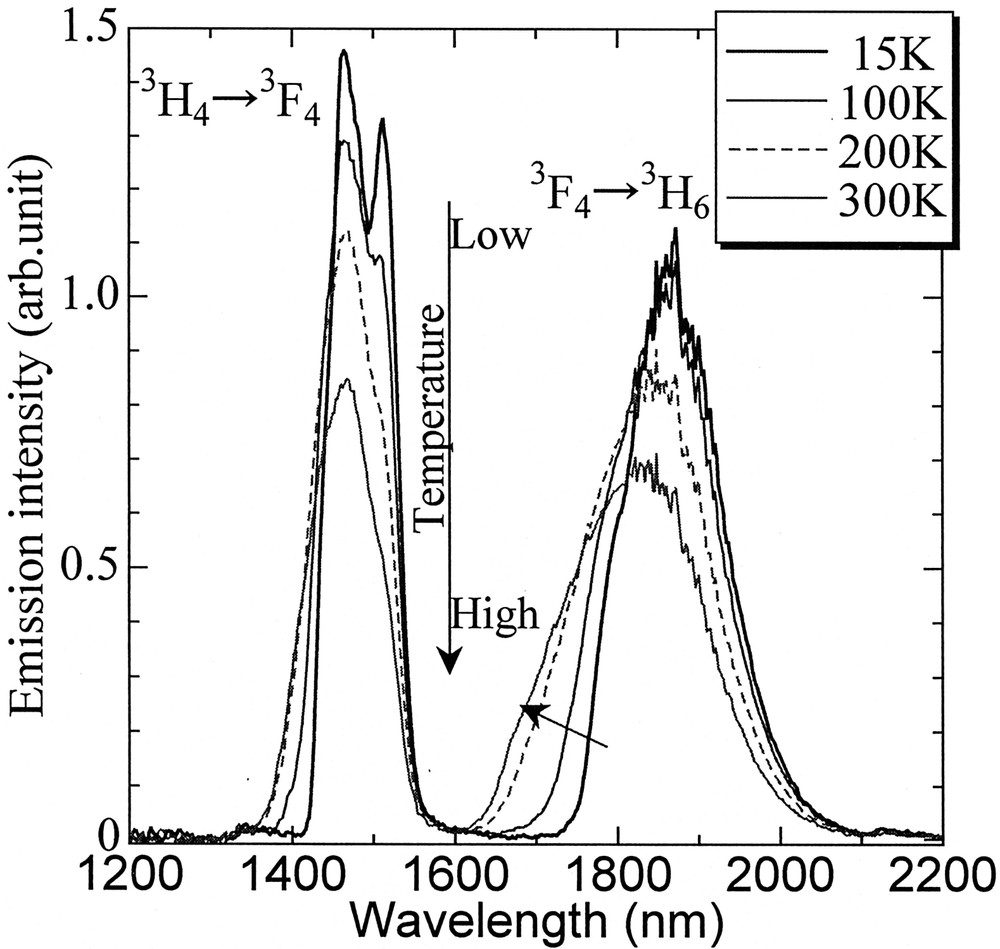
Temperature dependence of fluorescence spectra of 72 TeO2–20 ZnO–5 Na2O–2.9 Y2O3–0.1 Tm2O3 glass.
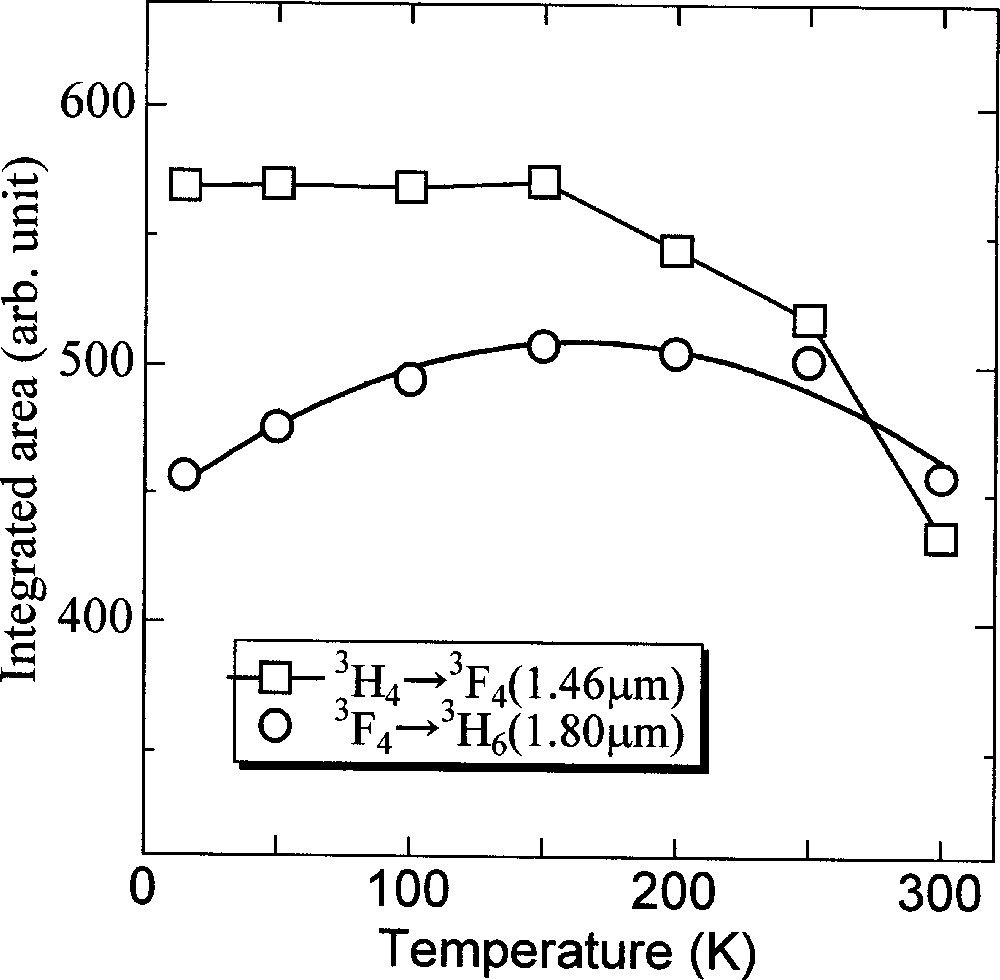
Temperature dependence of the integrated area of the 1.4-μm and 1.8-μm band in the 0.1 Tm2O3 glass.
4.3 Effect of codoping of Ho, Tb, Eu
One of the possibilities to improve the population inversion can be a selective quenching of the terminal level by codoping of other lanthanide 〚34, 40〛, because nothing is better than to pump directly the 3H4 with 0.79-μm LD of AlGaAs rather than upconversion scheme 〚35, 41〛. The role expected for a codopant is to quench the 3F4 level selectively without quenching the 3H4 level. From this viewpoint, the Eu3+, Tb3+ and Ho3+ can be a candidate among 13 4f-active lanthanide ions. The energy level diagrams of these ions are shown in Fig. 9. The Ln-concentration dependence of the lifetimes of the Tm3+:3H4 and 3F4 levels is plotted in Fig. 10. Among three codopants, the Eu3+ ion quenches both levels most significantly and the Ho3+ ion shows the best selectivity; i.e., the least effect on the 3H4 lifetime with a large quenching effect on the 3F4. The variation of the fluorescence spectra of Tm–Ho codoped tellurite glasses are shown in Fig. 11. The spectra are normalized by the intensity of 1.46-μm band, because it showed the least change. We see a drastic decrease of the 1.8-μm band and a rapid increase of the Ho3+:5I7 → 5I8 emission intensity at 2 μm. This result is an evidence of the Tm:3F4 → Ho:5I7 energy transfer.
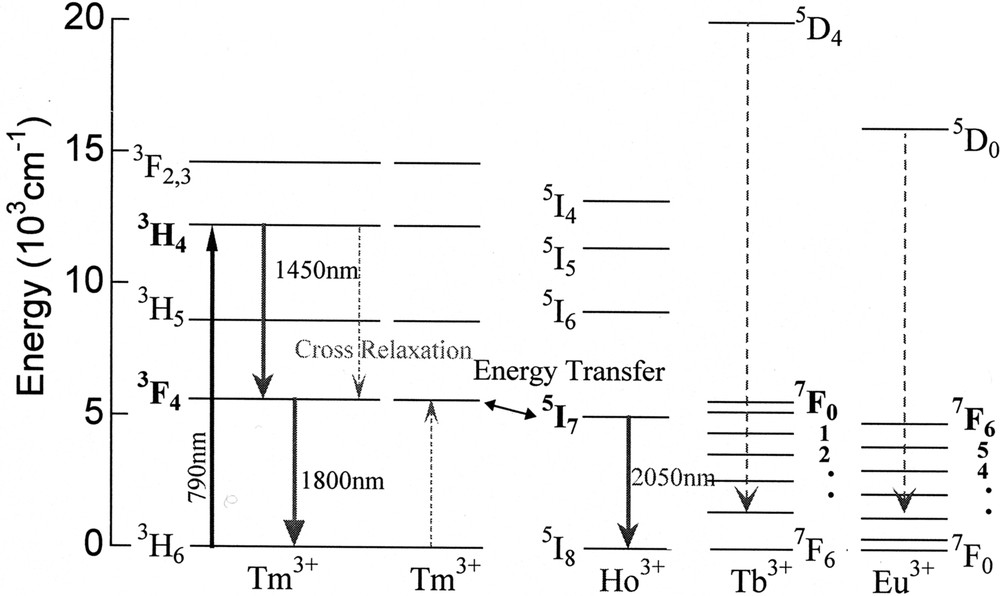
Energy level of Tm3+, Ho3+, Tb3+ and Eu3+ ion.
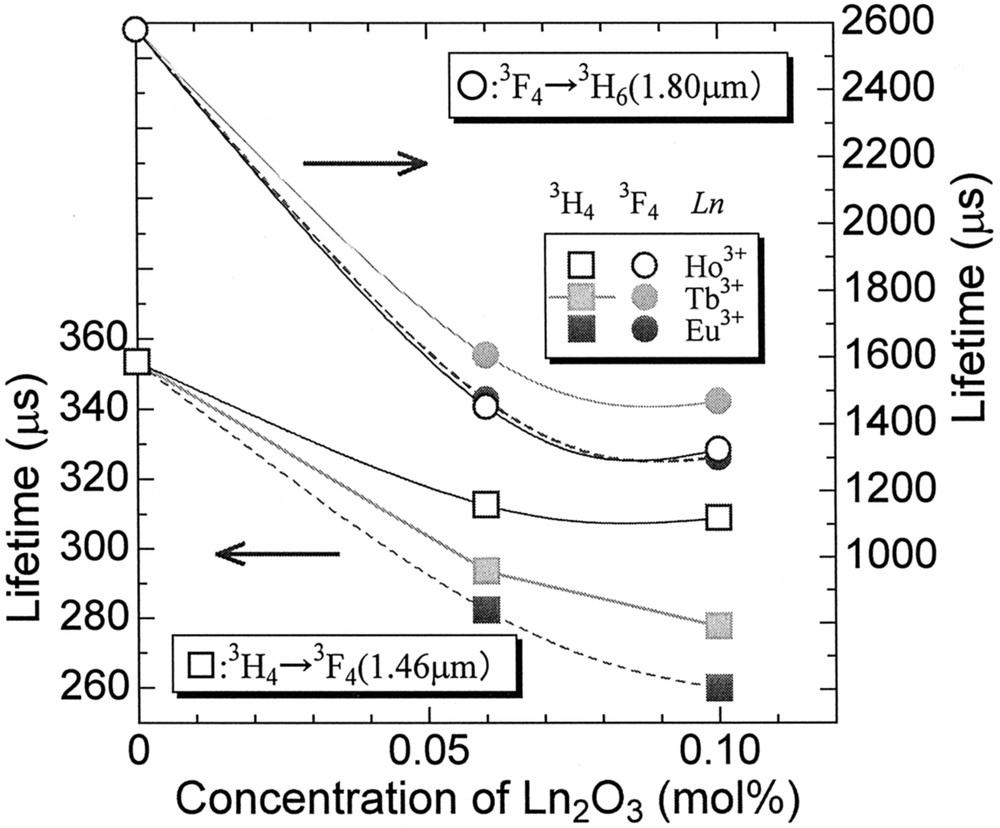
Effect of codopant on the lifetime of Tm3+ levels.
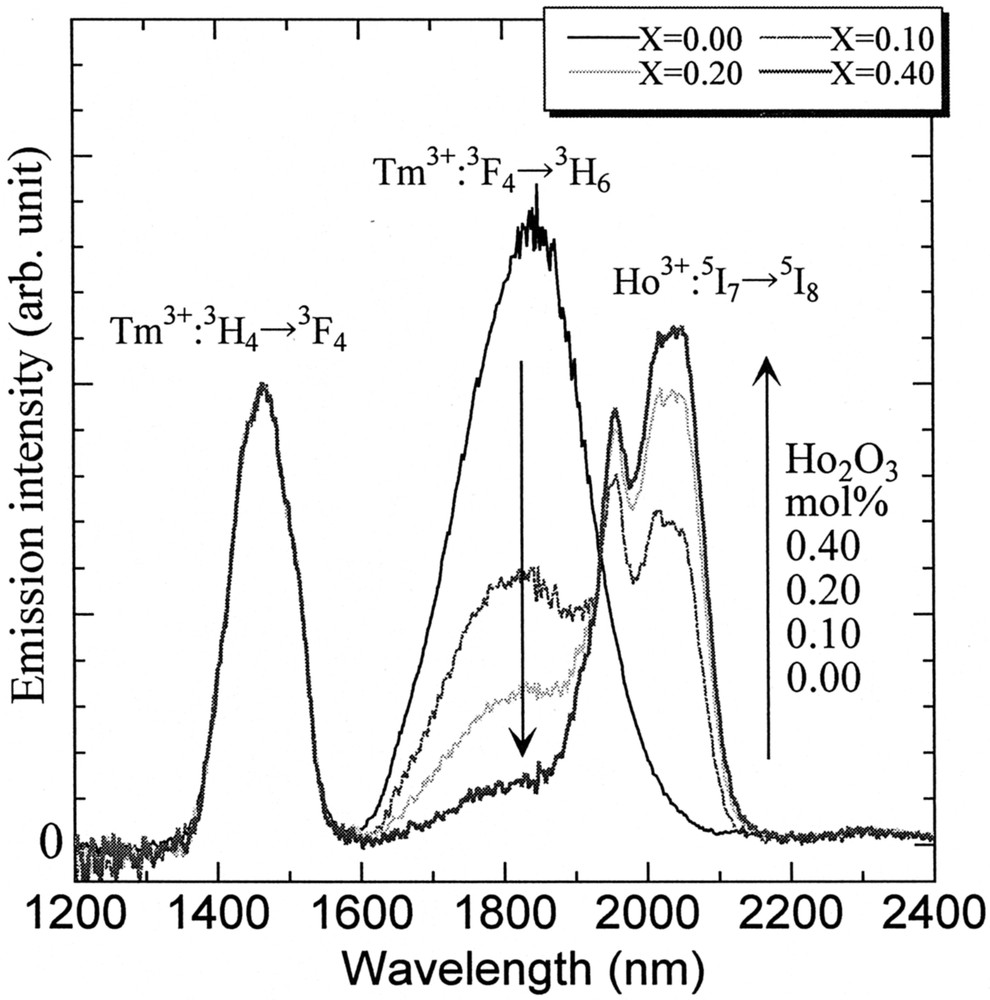
Fluorescence spectra of 72 TeO2–20 ZnO–5 Na2O–(2.9 – x) Y2O3–x Ho2O3–0.1 Tm2O3 glasses.
5 Active ions at 1.3 μm
5.1 Comparison of candidates
The world land-based optical networks installed are composed of 1.3 μm zero-dispersion silica fiber. However, no practical amplifiers have sufficient performance at 1.3-μm like EDFAs at 1.55-μm band. Fig. 12 shows the energy levels of Pr3+, Nd3+, and Dy3+ ions, which are active ions at 1.3 μm. Based on the huge amount of data on laser glasses for 1.06-μm applications 〚42〛, the Nd3+ ion was extensively studied as a candidate at first in many glasses. However, the excited state absorption from the 4F3/2 and the resulting gain shift to 1.35 μm were found to be a problem as well as a small branching ratio compared with that of 1.06 μm, which is a cause of intense amplified spontaneous emission (ASE) 〚43〛. The Pr3+ ion is probably most often studied in fluoride 〚7〛 and chalcogenide glasses 〚8〛 and practical devices have already been produced 〚44〛. The branching ratio from the 1G4 level is usually more than 60% in most glasses 〚45〛. The nonradiative loss due to the small energy gap limits the choice of host to nonoxide glasses. In addition, the small absorption cross-section of the only pumpable level (1G4) at 1.02 μm must be overcome by high-power pumping laser. Nonradiative population from the upper 1D2 level cannot be expected due to its larger energy gap. Since it is difficult to get high-quality lasers at 1.02 μm with semiconductor lasers, an 0.8 μm-LD- pumped Nd:YLiF4 solid-state laser (λ = 1047 nm) is often used as a pumping source 〚45〛. Among various glasses, the Ga–Na–S system has the highest quantum efficiency of 62% and the largest gain per pumping power at 1.34 μm 〚8〛. However, the gain at 1.31 μm is still low partly due to the peak shift to longer wavelength in sulfides 〚8〛.

Energy level of Pr3+, Nd3+ and Dy3+ ion.
Compared with these two ions, the Dy3+ has unique properties, though it is also affected by multiphonon loss. The Dy3+ ion can be pumped by 0.8 μm, 0.9 μm, 1.1 μm or 1.28 μm with large cross sections, for which the high-power LD’s can be used. Table 2 shows the reduced matrix elements of 1.3-μm emission transitions for Pr3+, Nd3+ and Dy3+ ions 〚11〛. While the transition probabilities in Pr3+ and Nd3+ ions depend most largely on Ω6, that in Dy3+ is dominated by the Ω2 parameter, which is most sensitive to the local symmetry and thus to the glass composition. The transition, the cross section of which is very sensitive to the local structure, is called ‘hypersensitive transition’ 〚46〛. The 615-nm emission of the Eu3+ ion, used for red-phosphor, is a typical example, where the <|U(2)|>2 is the largest among the three <|U(t)|>2 〚47〛.
Reduced matrix elements of 1.3-μm emission transitions for Pr3+, Nd3+ and Dy3+ ions 〚11〛.
| Ln3+ | 4fN | aJ | bJ′ | <U(2)>2 | <U(4)>2 | <U(6)>2 | λ (μm) |
| Pr3+ | 2 | 1G4 | 3H5 | 0.0307 | 0.0715 | 0.3344 | 1.32 |
| Nd3+ | 3 | 4F3/2 | 4I13/2 | 0 | 0 | 0.2117 | 1.35 |
| Dy3+ | 9 | 6H9/2 + 6F11/2 | 6H15/2 | 0.9394 | 0.8465 | 0.4078 | 1.32 |
5.2 Spectroscopy of dysprosium in glasses
5.2.1 Judd–Ofelt parameters and optical transitions
Absorption spectra of Dy3+ in the fluoride and tellurite glasses are shown in Fig. 13, where the assignment of transitions is also indicated 〚11〛. We can see that the absorption coefficients of transition peaks in this near-infrared region are not so distinct from each other for the fluoride glass. On the other hand, in the tellurite glass the intensity of 6F11/2+6H9/2 band is the largest among all transitions. The Ωt parameters obtained for the glasses are shown in Fig. 14. The Ω2 value is the largest in the sulfide and tellurite glasses and decreases in the order Ga2S3 > TeO2 > ZrF4 > InF3, whereas Ω6 increases in this order. The change in the absorption cross-section of the 6F11/2+6H9/2 band due to glass compositions can be ascribed to the set of the reduced matrix elements 〚11〛. The <6F11/2|U(2)|6H15/2>2 is the largest among three <|U(t)|>2 (t = 2, 4, 6), thus the SJJ′ of this band is dependent on the Ω2 of Dy3+ ion in the host. The <|U(2)|>2 of other transitions are small or zero and the SJJ′ of them is dependent mainly on Ω6. It is known that Ω2 is affected by the local symmetry of ligand field and bond covalency 〚15〛. The electronegativity of the anions is as follows; S < O < F 〚48〛. Therefore, the chemical bond covalency between the Dy3+ and the ligand varies with compositions: Ga2S3 > TeO2 > ZrF4 > InF3. Therefore, the opposite tendency of Ω2 and Ω6 against glass compositions can be understood in terms of the differences in the bond covalency in the glasses 〚37〛.
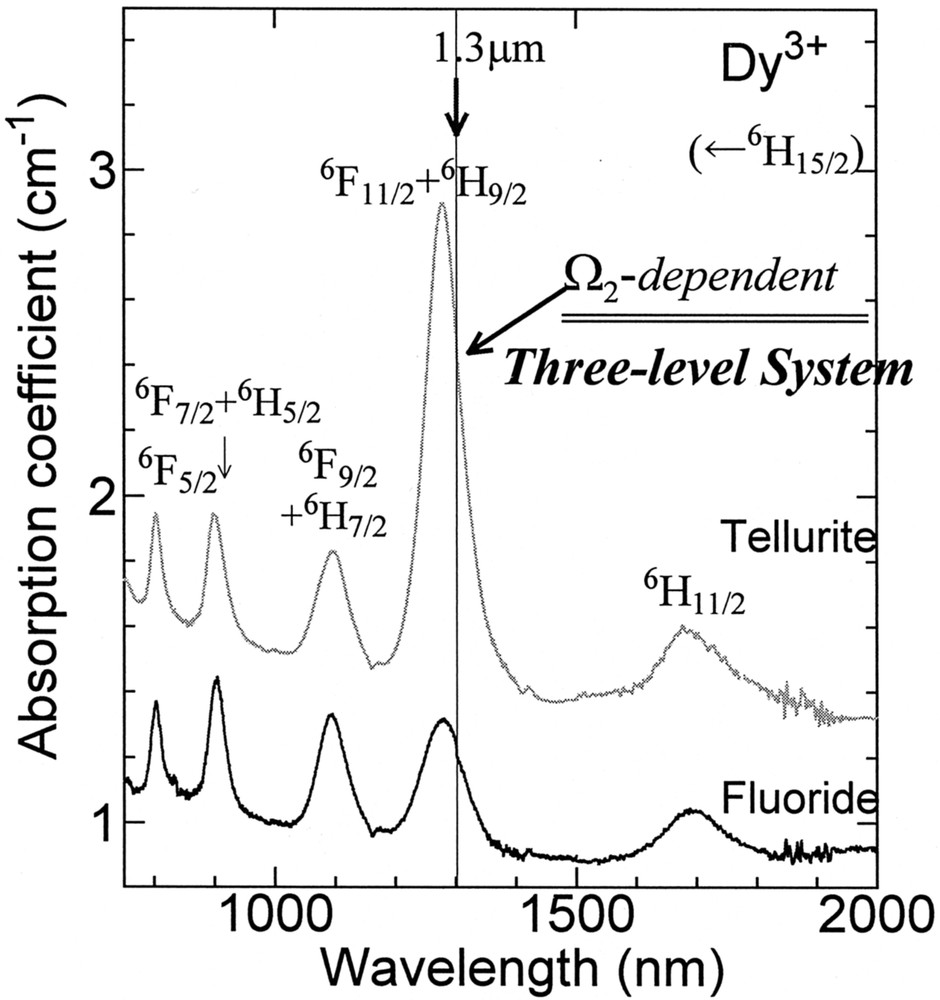
Absorption spectra of Dy3+-doped glasses.
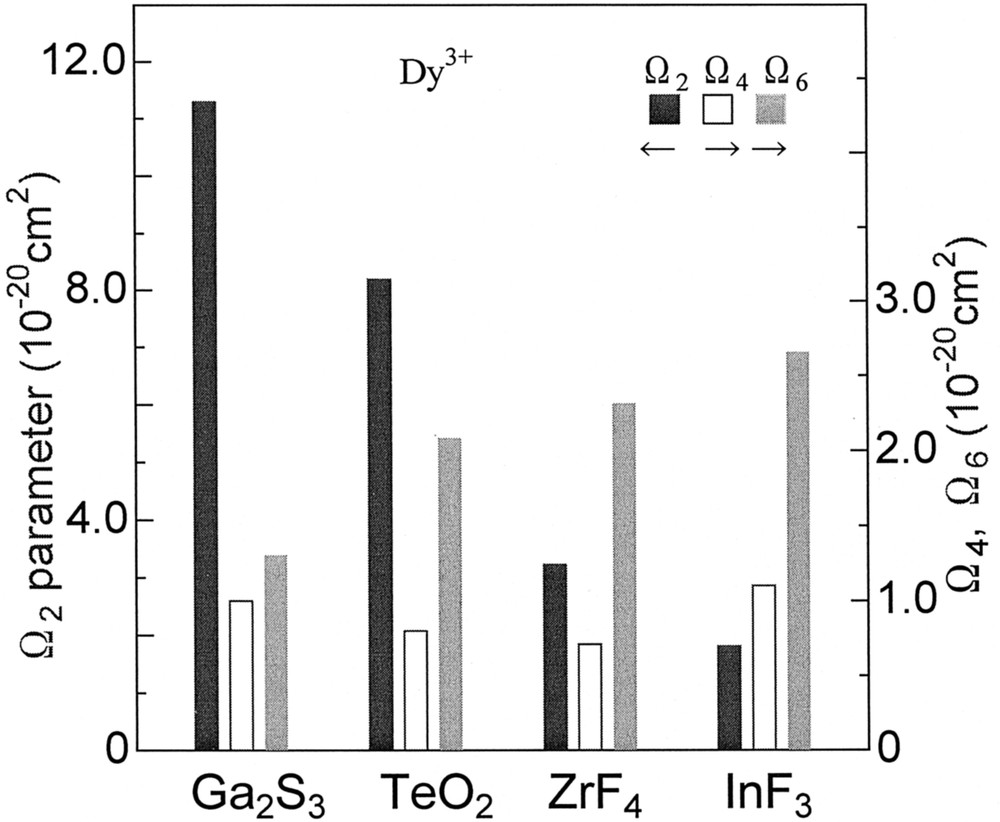
Ωt parameters of Dy3+ ions in glasses.
5.2.2 Can dysprosium be a candidate?
Because of the large branching ratio and cross section of 1.3 μm, an efficient amplifier can be expected if the nonradiative loss were reduced. Table 3 shows the lifetime and quantum efficiency of Dy3+ in several glasses. A selenide glass host can give 90% quantum efficiency 〚49〛, which is mainly due to the phonon energy being much smaller than even sulfides. This efficiency seems high enough for practical devices. Moreover, smaller electron-phonon coupling strength in chalcogenides 〚50〛 seems more promising for smaller multiphonon loss at levels with a small energy gap than in a host with comparable phonon energy, such as chlorides.
Lifetime and quantum efficiency of the Dy3+ level for 1.3-μm emission in several glass systems.
| Host | Lifetime (μs) | Quantum efficiency |
| Pb–Bi–Ga–O | 5 | 1.5% 〚53〛 |
| Ge–Ga–S | 38 | 17% 〚12〛 |
| Ga–La–S | 59 | 19% 〚13〛 |
| Ge–As–Se | 300 | 90% 〚49〛 |
One more problem of Dy3+ is bottlenecking at lower levels with longer lifetimes resulting in depression of pumping efficiency and large emission intensities at longer-wavelength side 〚51〛, because the energy gap of the lower levels is larger than that of the 1.3-μm level. If the quantum efficiency of the 1.3-μm level is large enough, the effect of bottlenecking at lower levels would be negligible, since the excited initial state relaxes directly to the ground state due to the branching ratio of more than 90% 〚52〛. There seems a great potential in Dy3+-doped chalcogenides. Further progress in the fabrication of low-loss single-mode fiber is expected.
6 Conclusions
The broad and flat spectral features of Er3+:1.55 μm transition can be obtained in novel glass compositions with a large Ω6 parameter. The Er3+ spectral change is accompanied by compositional evolution of Er–O bond ionicity and local structure.
The Tm3+:1.46 μm transition shows high quantum efficiency in heavy metal oxide glasses due to the larger energy gap of the 3H4 level than the Pr3+:1G4. Selective quenching of the terminal level is possible in a Ho-codoped system.
New materials are expected for the optical amplifiers in the future WDM network system, to control the 4f transitions of RE ions, which show a variety of spectroscopy in glasses.


