The Ising-like model applied to switchable inorganic solids: discussion of the static properties

François Varret; Sunita Arun Salunke; Kamel Boukheddaden; Azzedine Bousseksou; Épiphane Codjovi; Cristian Enachescu; Jorge Linares

doi:10.1016/S1631-0748(03)00048-1

The Ising-like model applied to switchable inorganic solids: discussion of the static properties

François Varret ¹ ; Sunita Arun Salunke ¹ ; Kamel Boukheddaden ¹ ; Azzedine Bousseksou ² ; Épiphane Codjovi ¹ ; Cristian Enachescu ¹ ; Jorge Linares ¹

¹ Laboratoire de magnétisme et d’optique, CNRS–université de Versailles–Saint-Quentin, 45, avenue des États-Unis, 78035 Versailles cedex, France
² Laboratoire de chimie de coordination, UPR 8241, CNRS, 205, route de Narbonne, 31077 Toulouse, France

Comptes Rendus. Chimie, Volume 6 (2003) no. 3, pp. 385-393.

Résumés

Anglais
Français

The Ising-like model provides a microscopic approach and a unifying description of the thermodynamic properties associated with molecular switching in inorganic solids. Applications are given for the spontaneous thermal transitions, under applied pressure or external magnetic field.

Le modèle de type Ising offre une approche microscopique et une description unifiée des propriétés thermodynamiques associées à la commutation moléculaire dans les solides inorganiques. Nous en présentons l’application aux phénomènes de transition thermique spontanée, sous pression ou sous champ magnétique.

Métadonnées

Reçu le : 2002-12-04
Accepté le : 2003-02-19
Publié le : 2003-03-01

DOI : 10.1016/S1631-0748(03)00048-1

Keywords: Full paper, inorganic solids, molecular switching, ising model, spin crossover
Mots clés : Mémoire, solides inorganiques, commutation moléculaire, modèle d’Ising, transition de spin

Affiliations des auteurs :

François Varret ¹ ; Sunita Arun Salunke ¹ ; Kamel Boukheddaden ¹ ; Azzedine Bousseksou ² ; Épiphane Codjovi ¹ ; Cristian Enachescu ¹ ; Jorge Linares ¹

¹ Laboratoire de magnétisme et d’optique, CNRS–université de Versailles–Saint-Quentin, 45, avenue des États-Unis, 78035 Versailles cedex, France
² Laboratoire de chimie de coordination, UPR 8241, CNRS, 205, route de Narbonne, 31077 Toulouse, France

@article{CRCHIM_2003__6_3_385_0,
     author = {Fran\c{c}ois Varret and Sunita Arun Salunke and Kamel Boukheddaden and Azzedine Bousseksou and \'Epiphane Codjovi and Cristian Enachescu and Jorge Linares},
     title = {The {Ising-like} model applied to switchable inorganic solids: discussion of the static properties},
     journal = {Comptes Rendus. Chimie},
     pages = {385--393},
     publisher = {Elsevier},
     volume = {6},
     number = {3},
     year = {2003},
     doi = {10.1016/S1631-0748(03)00048-1},
     language = {en},
}

TY  - JOUR
AU  - François Varret
AU  - Sunita Arun Salunke
AU  - Kamel Boukheddaden
AU  - Azzedine Bousseksou
AU  - Épiphane Codjovi
AU  - Cristian Enachescu
AU  - Jorge Linares
TI  - The Ising-like model applied to switchable inorganic solids: discussion of the static properties
JO  - Comptes Rendus. Chimie
PY  - 2003
SP  - 385
EP  - 393
VL  - 6
IS  - 3
PB  - Elsevier
DO  - 10.1016/S1631-0748(03)00048-1
LA  - en
ID  - CRCHIM_2003__6_3_385_0
ER  -

%0 Journal Article
%A François Varret
%A Sunita Arun Salunke
%A Kamel Boukheddaden
%A Azzedine Bousseksou
%A Épiphane Codjovi
%A Cristian Enachescu
%A Jorge Linares
%T The Ising-like model applied to switchable inorganic solids: discussion of the static properties
%J Comptes Rendus. Chimie
%D 2003
%P 385-393
%V 6
%N 3
%I Elsevier
%R 10.1016/S1631-0748(03)00048-1
%G en
%F CRCHIM_2003__6_3_385_0

François Varret; Sunita Arun Salunke; Kamel Boukheddaden; Azzedine Bousseksou; Épiphane Codjovi; Cristian Enachescu; Jorge Linares. The Ising-like model applied to switchable inorganic solids: discussion of the static properties. Comptes Rendus. Chimie, Volume 6 (2003) no. 3, pp. 385-393. doi : 10.1016/S1631-0748(03)00048-1. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/S1631-0748(03)00048-1/

Version originale du texte intégral

1 Introduction

Molecular switching of inorganic solids is a typical issue of the vibronic lability of molecular units, previously introduced by J.A. Ammeter [1]. We report here on several families of inorganic systems where a spin crossover is involved in the switching process between the two molecular states: spin-crossover solids (SC), photomagnetic Prussian blue analogues (PBA), valence-tautomeric system (VT) – see Table 1. A previous presentation of the concept in terms of ‘molecular bistability’ was given by O. Kahn [2], on the example of SC solids. Recent reviews on switchable inorganic solids can be found in [3–6].

System	Low-temperature state	High-temperature state	basic refs.
SC Fe^II (3d⁶)	Fe^II_LS(S = 0) = t_2g⁶	Fe^II_HS(S = 2) = t_2g⁴ e_2g²	[2, 7–10]
Fe,Co PBA	Fe^II_LS(S = 0) Co^III_LS(S = 0)	Fe^III_LS(S = 1/2) Co^II_HS(S = 3/2)	[11–16]
VT Co semiquinone*	Co^III_LS(S = 0) (sq^•)(cat)	Co^II_HS(S = 3/2) (sq^•) (sq^•)	[17–19]

The bistable properties at the molecular level are adequately described through a molecular configurational diagram, i.e. a plot of the adiabatic energies versus the distortion coordinate of the molecular system. Usually, for spin crossover, a fully symmetric distortion is considered, associated with the change in average metal–ligand distance. Due to the large atomic displacements upon spin conversion, the optical properties drastically change, so that the switching properties can be followed as well by magnetic or optical (absorption, reflectivity) techniques. In Fig. 1 we show the configurational diagram suited to spin crossover, in the case of low-spin (LS) ground state. It is noteworthy that the effect of environment in molecular solids slightly affects the configurational diagram. For example, an external pressure mainly increases the energy gap Δ, and correlatively reduces the energy barrier of the high-spin (HS) state, so as to raise the equilibrium temperature T_1/2 (see next section) and to shorten the lifetime of the HS state [20–24].

Fig. 1
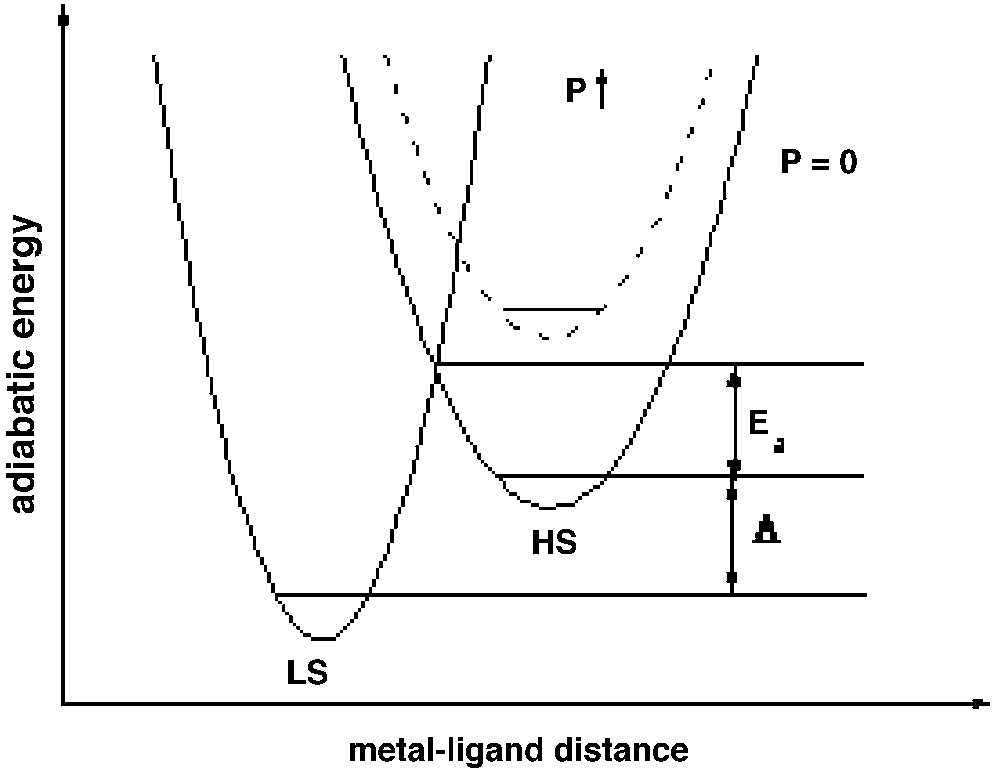
The configurational diagram of spin-crossover (after [8]), with LS ground state, and the effect of an external pressure (after [20]). Anharmonic effects have been discarded.

2 Ising-like model

A widely used model for such bistable systems is the Ising-like model [25–26], which describes interacting two-level units, the energy levels of which have different energies and degeneracies. The two-level scheme indeed is a drastic simplification of the complete vibronic level scheme, in the adiabatic approximation. However, it permits describing with amazing success most of the quasi-static properties of the SC solids [27–31]. The degeneracy ratio g = g_HS/g_LS is related to the molar entropy change upon total conversion ΔS = R ln g [29,30], and therefore can be derived from calorimetric measurements at the spin-crossover equilibrium temperature T_1/2.

A useful recent review of calorimetric data is given in ref. [4]. Because of both electronic and vibrational factors, ΔS > 0 (ΔS = 30 to 70 J K^–1 mol^–1), therefore g >> 1 [29–31]. The Ising-like model has been used and developed for describing the static [27–31] and dynamic [32–34] properties of SC mono and binuclear solids, and was applied as well to the VT compound [3]. The Ising Hamiltonian writes:

\hat{H} = (Δ / 2) \sum_{i} {\hat{σ}}_{i} - \sum_{< i, j >} J_{ij} {\hat{σ}}_{i} {\hat{σ}}_{j}

with fictitious spins

\hat{σ}

having eigenvalues +1 in the high-spin state (HS) , –1 in the low-spin state (LS), and degeneracies g_HS, g_LS. As usual, the index <i,j> stands for all pairs of sites, and the reference sign for a cooperative interaction, favouring spin-like states, is J_ij > 0. Δ = E(HS) – E(LS), denoted energy gap (or ‘fictitious field’), is the enthalpy change associated with the LS→HS conversion of one molecule. The HS fraction is expressed as a function of the ‘fictitious magnetisation’:

n_{HS} = (< \hat{σ} > + 1) / 2

A convenient form of the Ising-like Hamiltonian is the Ising equivalent form [26] obtained by rewriting the canonical partition function to get rid of the pre-exponential factors. The Ising equivalent form involves a temperature-dependent energy gap (= ‘fictitious effective field’) accounting for the degeneracy ratio:

{\hat{H}}_{equiv} = [Δ_{eff} (T) / 2] \sum_{i} {\hat{σ}}_{i} - \sum_{< i, j >} J_{ij} {\hat{σ}}_{i} {\hat{σ}}_{j}

Δ_{eff} (T) = Δ - k_{B} T \ln g

The thermodynamic properties of the Ising-like system (with the LS ground state) are merely governed by the sign of the effective field, for example the qualitative features of the thermal variation of the HS fraction are reported in Table 2 and illustrated in Fig. 2. The equilibrium temperature T_1/2 for which n_HS = n_LS = $1 ⁄ 2$ corresponds to a null effective field, irrespectively of the interactions:

Temperature	T = 0	T = T_1/2	T >> T_1/2
Δ(T)	D >0	0	Negative
$\hat{σ}$	–1	0	(g_HS– g_LS)/(g_HS+ g_LS)
n_HS	0	1/2	g_HS/(g_HS+ g_LS)

Fig. 2
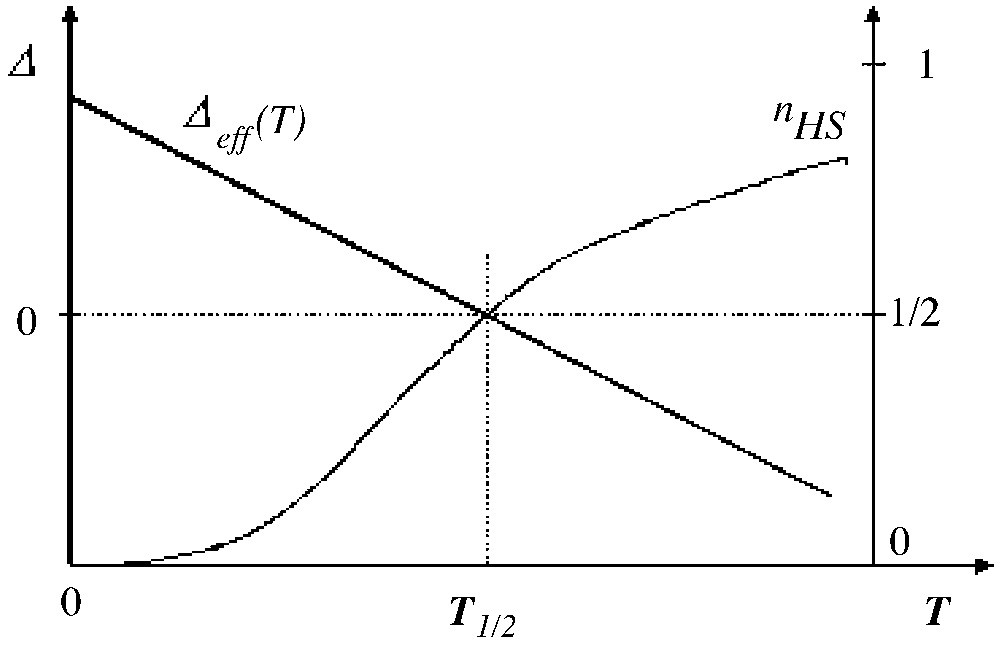
Thermal variation of the temperature-dependent fictitious field (with LS ground state) and subsequent variation of the HS fraction, in absence of interactions.

T_{1 / 2} = Δ / k_{B} \ln g

3 Spontaneous thermal hysteresis

The presence of interactions — of steric origin — makes the conversion curve n_HS(T) steeper around T_1/2. Above an interaction threshold value, the system becomes bistable at T_1/2 and thermal hysteresis occurs. The bistability condition is easily derived using the Ising equivalent form: it requires the Ising equivalent system to be ordered at the equilibrium temperature [35], i.e.:

T_{1 / 2} < T_{C}

Then the reversal of Δ_eff(T) induces the reversal of the non-null fictitious magnetisation $< \hat{σ} >,$ i.e. the thermal transition is discontinuous (in other words, the free energy as function of temperature presents a slope change = discontinuity of the first derivative δF/δT) and hysteresis can occur. This is illustrated in Fig. 3, where the hysteresis loop, resulting from a quasi-static variation of temperature, has been completed by vertical arrows.

Fig. 3
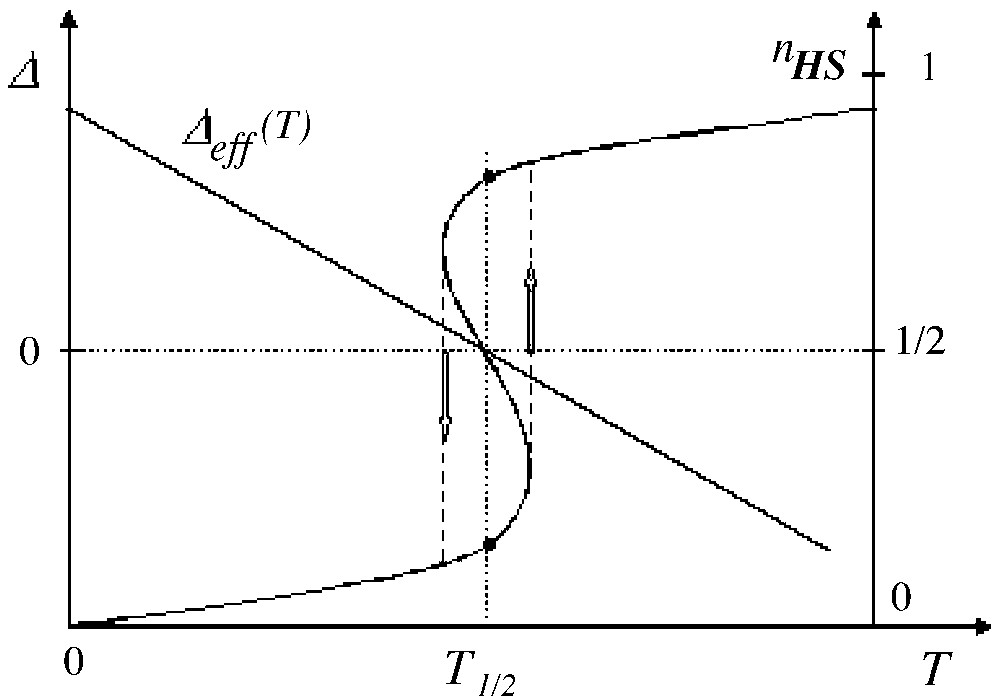
Thermal variation of the temperature-dependent fictitious field (with LS ground state) and subsequent variation of the HS fraction, in the presence of interactions larger than the threshold value.

4 Homogeneous mean-field treatment

The interaction term in Eq. (3) is re-expressed, considering:

• (i) the average effect of neighbours; the single-site Hamiltonian for site i writes:
${\hat{h}}_{i} = [Δ_{eff} (T) / 2] {\hat{σ}}_{i} - \sum_{j} J_{ij} < {\hat{σ}}_{j} > {\hat{σ}}_{i}$
• (ii) homogeneous thermodynamic properties, i.e. $< {\hat{σ}}_{j} > = < {\hat{σ}}_{i} >,$ so that a unique single-site Hamiltonian is derived, written as:
${\hat{h}}_{m . f .} = [Δ_{eff} (T) / 2] \hat{σ} - J < \hat{σ} > \hat{σ}$
where J accounts for the sum on interactions due to all neighbours.

Eq. (8) can be interpreted in terms of independent two-level systems submitted to a fictitious field dependent on the order parameter of the system:

Δ_{eff} (T, n_{HS}) = Δ - k_{B} T \ln g - 2 J < \hat{σ} > = Δ_{eff} (T, 0) - 4 {Jn}_{HS}

Straightforward self-consistent calculations, using the canonical partition function, provide the n_HS(T) dependence. It is noteworthy that an explicit expression T(n_HS) can be obtained [32]:

k_{B} T (n_{HS}) = [Δ + 2 J - 4 J n_{HS}] / [\ln (1 - n_{HS}) - \ln n_{HS} + \ln g]

The occurrence condition of hysteresis is easily derived by consideration of the slope dT/dn_HS at n_HS = 1/2 (it has to be negative), leading to:

J > Δ / \ln g = k_{B} T_{1 / 2}

Eq. (11) was previously derived from a ‘thermodynamic’ model based on the properties of regular solutions in the Bragg–Williams approach [36], later shown to be formally equivalent to the present mean-field two-level approach [37]. Eq. (11) can as well be derived from the general condition (Eq. (6)), just inserting the mean-field value T_C = J/k_B. An useful comparison can be made with the pressure effect:

Δ_{eff} (T, p) = Δ_{eff} (T, 0) + p δ V

where δV is the volume increase of the molecular unit upon LS→HS conversion. By comparing Eqs. (9) and (12), it appears that increasing n_HS induces the same effect than decreasing p, i.e. a downward shift of the HS energy well (see Fig. 1). Such an effect was previously reported by Hauser and Spiering in terms of ‘internal pressure’ [38–40] and introduced into the two-level Ising-like model in [31,41,42]. It corresponds to a cooperative effect mediated by the lattice, i.e. associated with long-range interactions: the LS→HS conversion of any molecular unit induces an increase of the lattice parameter, which in turn favours the conversion of the remaining LS units. In addition, due to the subsequent increase of the barrier energy, the lifetime of the HS metastable state is increased. To summarise, the cooperative effects correlate positively the population and the stability of the states, both statically and kinetically.

5 Two-step transitions

Two-step transitions have been reported in the case of systems combining positive and negative interactions, for example in the case of two-sublattices negatively coupled [27], or of binuclear molecular units [28,29,43].

We develop here a comparison to metamagnets, i.e. two-sublattice magnetic systems, combining intra-sublattice ferromagnetic and inter-sublattice antiferromagnetic interactions [44]. Actually metamagnetism also requires a large magnetic anisotropy, which confines the magnetic moments along the easy magnetic axis; this situation is of course suited to the Ising models. The up–up, up–down and down–down fictitious magnetisation states respectively correspond to HS–HS, HS–LS and LS–LS states. The typical magnetic behaviour of a metamagnet, i.e. the spin-flip transition obtained for positive and for negative fields, is sketched in Fig. 4 at null temperature. The two-step spin transition obviously follows, with however a smoother character, due the thermal population effect.

Fig. 4
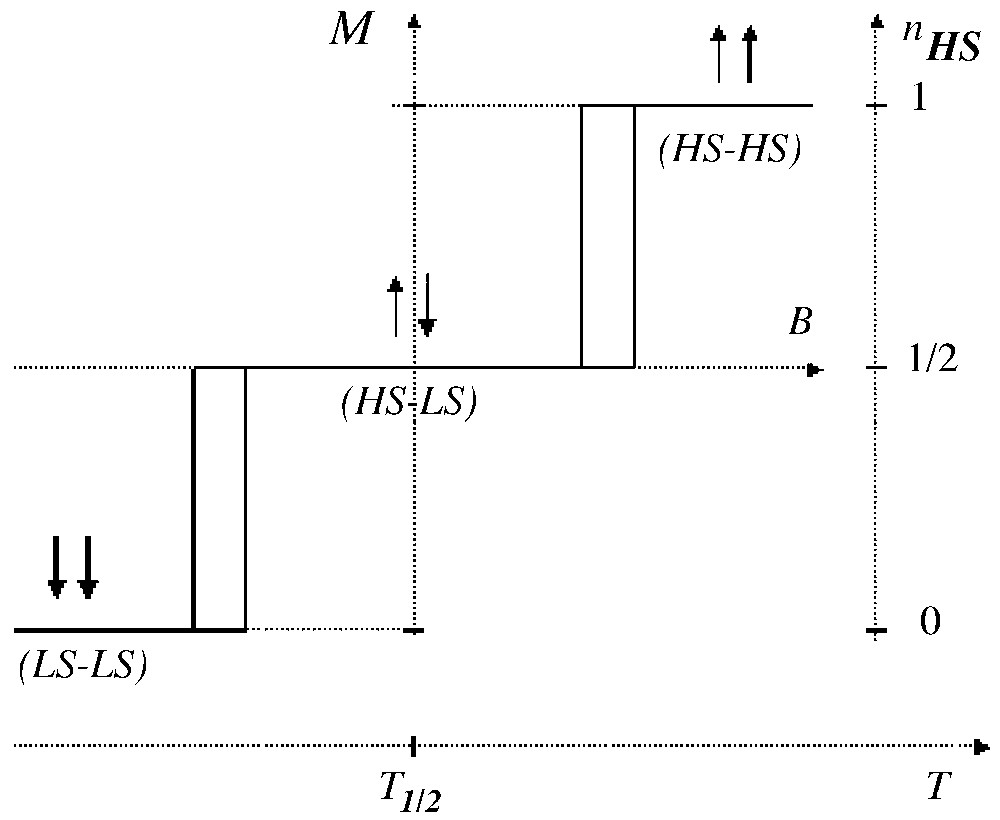
The magnetic response (at T = 0) of a metamagnet under the effect of a magnetic field applied along the easy axis. The analogy with a two-sublattice spin transition is indicated.

Alternatively, Fig. 4 can be interpreted as the response of a 3-level system under the effect of an external field. This concept also applies to the case of bi-nuclear systems [28,29,43], which indeed exhibit the two-step transition (or conversion). The key point is the relative stability of the intermediate state at zero field, i.e. the stability of the molecular HS-LS state at T_1/2, which obviously requires a negative intramolecular interaction.

6 Kinetic effects on the thermal hysteresis loop

The observation of the thermal transition requires a fast relaxation between the two states, with respect to the experimental time scale. If not, kinetic effect are to be observed, e.g. an extra-broadening of the thermal loop, in addition to the trivial heat transfer effect which has a characteristic time of some minutes in the usual temperature range of spin transitions (100–400 K).

Actually, there are not many available data for the intrinsic kinetics of the spin crossover phase transition, which seems to be rapid, and therefore should be difficult to disentangle from heat-transfer effects. On the other hand, the escape time of the macroscopic metastable state [35] in the hysteretic temperature range is expected to be very long, in agreement with the usual observation of a quasi-static hysteresis at the experimental time scale (hours, days). However, in analogy with the superparamagnetic fluctuations of nanograins, a shortening of the escape time has to be expected in the case of spin-crossover nano-crystals, due to the smaller value of the macroscopic barrier energy. Several chemistry groups presently pay a large effort in order to synthesise spin-crossover nano-crystals, and we can expect that the open question of quantum tunnelling for the spin transition will be addressed quite soon.

The situation of the Photo-magnetic Prussian Blue analogues is quite different, due to their much slower relaxation, allowing to perform an efficient photo-excitation up to ~130 K in the cases of the Cs–CoFe [45] and Na–CoFe [46] PBA systems. These systems exhibit progressive and abrupt spontaneous transitions, respectively, in the range 200–300 K. Due to the slower relaxation, the high-temperature phase can be trapped in these systems, better than in the spin-crossover solids. Indeed a partial trapping of the high-temperature phase, by thermal quenching, was previously observed in a Cs–CoFe PBA sample [45]. In a Na–CoFe PBA sample, we recently obtained a complete trapping [46]. Typical kinetic effects on the thermal loop of Na–CoFe PBA sample are reported in Fig. 5. A model for kinetic thermal hysteresis, accounting for realistic relaxation rates, was given in [32].

Fig. 5
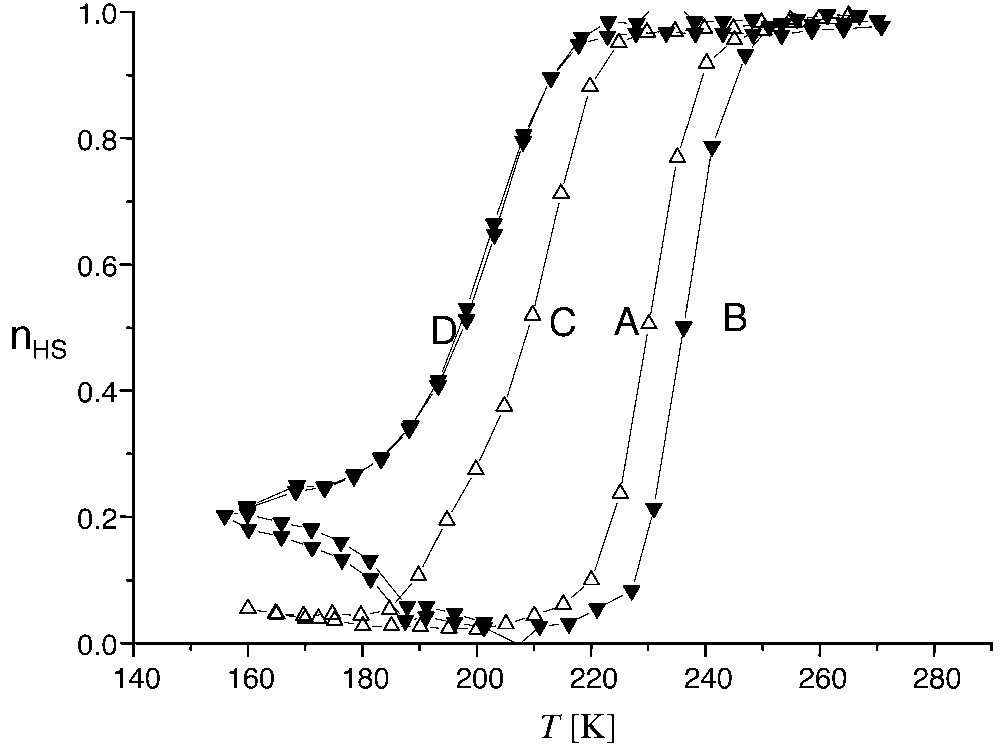
Kinetic effects on the spontaneous thermal hysteresis of Na_0.40Co[Fe(CN)₆]_0.70·3.5 H₂O: high-temperature phase fraction, deduced from magnetic measurements. Temperature sweeping rates are (A) +0.97, (B) +9.43, (C) –1.96, (D) – 11.26 K min^–1.

7 On the shape of the thermal hysteresis loop

We briefly comment on the shape of the quasi-static hysteresis loop (discarding the kinetic effects). Indeed, the usual mean-field models result in well-rounded turning points of the loop, while most of experimental data display well-marked turning points, with sometimes rather bent sides (instead of the expected jumps). The bent sides are easily reproduced by a distribution of transition temperatures. The origin of the well-marked turning points was recently elucidated [47] thanks to improved models including both long- and short-range interactions [33,34]. The detailed treatments of the extended Hamiltonian, for the static and dynamic properties, have been published for 1-D (exact solution) [48] and 2-D/3-D systems, using the Bethe or the pair approximation [33–34] or the exact (but restricted to finite size) entropic sampling approach [49–50].

We show in Fig. 6 that the shape of the hysteresis loop sensitively depends on the balance between the long-range and short-range interactions: well-marked turning points indicate the presence of short-range interactions. It is worth noting that an other important issue of short range interactions is the presence of relaxation tails, associated with a clusterisation of the system at long times: the key point is that clusters retaining the larger n_HS fraction also retain the longer lifetime, i.e. better resist against the self-accelerated relaxation process. We do not discuss here these dynamic aspects, for which the reader should refer to recent publications [32–34]. A general review involving the relaxation properties under permanent photo-excitation is in preparation [51].

Fig. 6
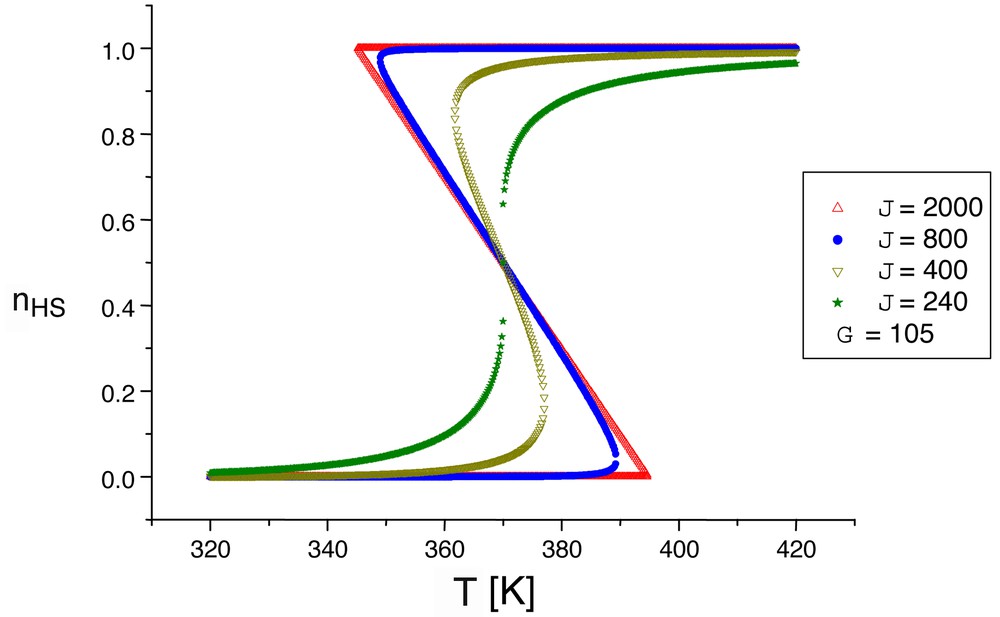
Computed thermal hysteresis loops, including the effect of short-range (J) and long-range (G) interactions (after [47]). The larger the short-range interaction, the best marked the turning points (the squarer the hysteresis loop).

8 Pressure effects

The extended expression of the temperature dependent fictitious field, accounting for both cooperative and pressure effects, is written:

Δ_{eff} (T, p, n_{HS}) = Δ_{eff} - k_{B} T \ln g + p δ V - 4 J n_{HS}

Within the present homogeneous mean-field approach, Eq. (13) introduces a linear correlation between temperature and pressure, at constant n_HS. For example, at n_HS = 1/2:

T_{1 / 2} (p) = T_{1 / 2} (0) + p δ V / k_{B} \ln g = T_{1 / 2} (0) + p Δ V / Δ S

p_{1 / 2} (T) = [T - T_{1 / 2} (p = 0)] (k_{B} \ln g / δ V) = [T - T_{1 / 2} (p = 0)] Δ S / Δ V

where ΔV = N_A δV is the molar volume increase upon total conversion. Eq. (15) defines the equilibrium pressure, i.e. the pressure which is needed, at a given temperature, to reach the equilibrium value n_HS = 1/2, starting from the HS state. A typical phase diagram built up from isobaric (T_1/2) and isothermal (p_1/2) data is shown in Fig. 7. A schematic p–T diagram derived from a straightforward application of the model is reported in Fig. 8: the biphasic domain, in-between the transition lines, is expected to decrease with increasing pressure (assuming a pressure-independent interaction parameter), and should collapse at T = T_C, according to Eq. (6). The value of δV can be derived from the average slope of the borderlines of the experimental phase diagram:

Fig. 7
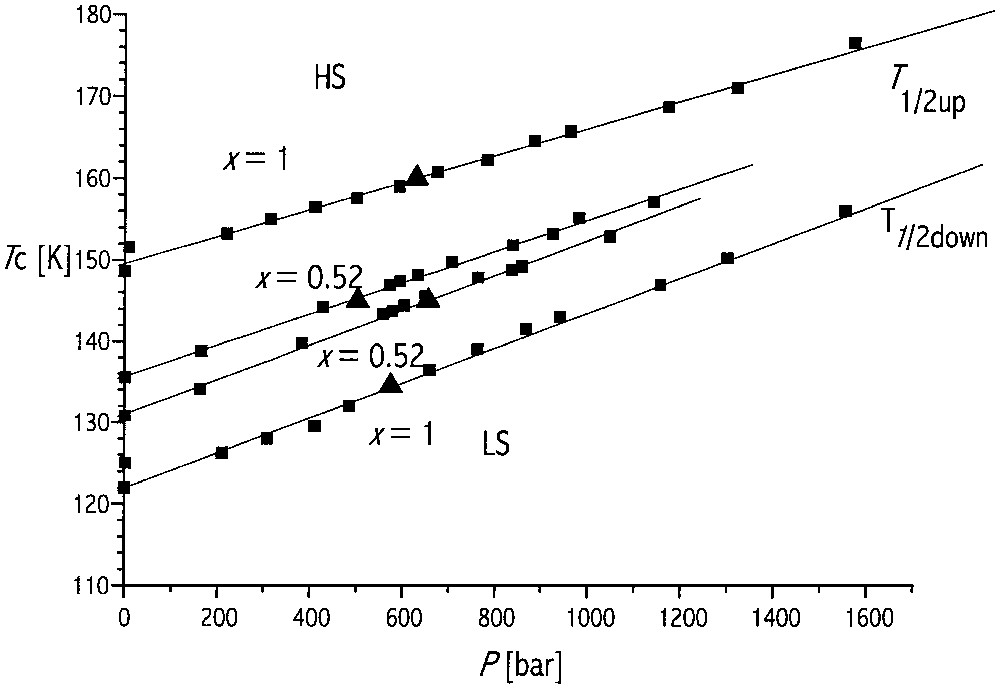
The pressure–temperature phase diagram for the spontaneous spin transition of Fe_xNi_1–_x(btr)₂(NCS)₂]·H₂O, from optical reflectivity data (λ = 600 nm), for x = 0.52, x = 1. The straight lines are associated with the transition values (■ for T_1/2, ▴ for p_1/2).

Fig. 8
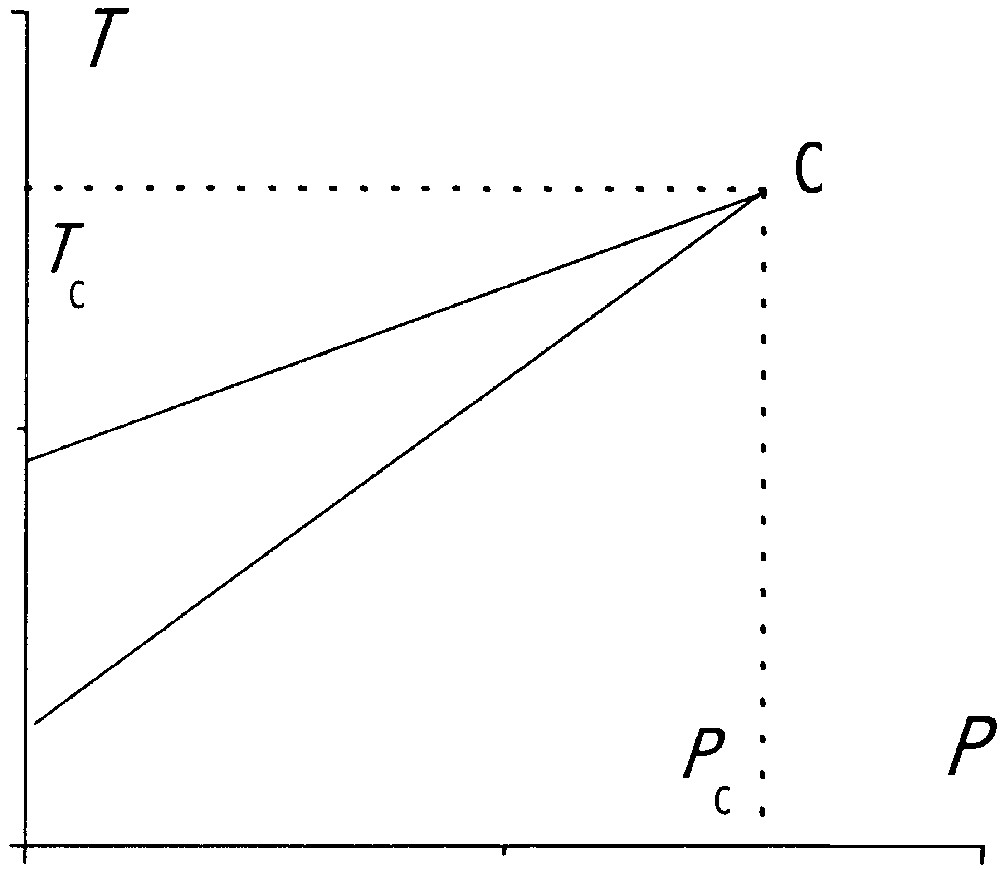
Simple schematic p–T phase diagram of the Ising-like model (assuming a pressure-independent J).

Δ V = Δ S \times (\partial T_{1 / 2} / \partial p)

Most of experimental data [6–10,21–24,41,42] for several families of spin-crossover compounds yield δV ~ 20–30 Å³. The model applies as well to the valence tautomeric transition, leading to a similar δV value, as shown in Fig. 9.

Fig. 9
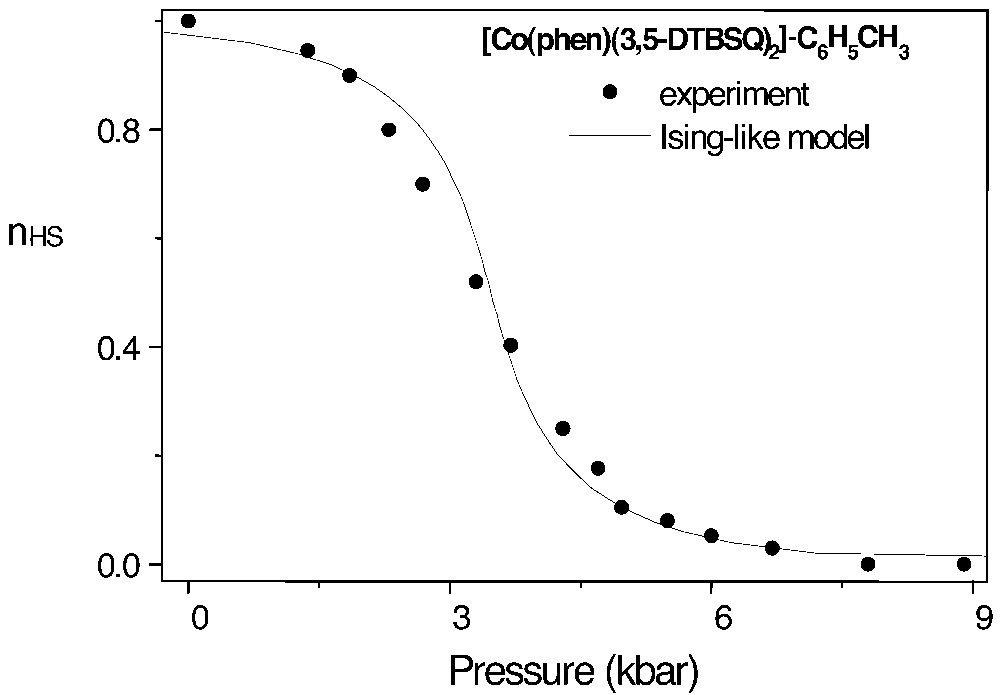
The pressure-induced valence tautomeric transition, from Co(sq^•)₂ (high-temperature phase) to Co(sq^•)(cat) (low-temperature phase). Experimental data from [52]: n_HS is the Co^II high-spin fraction. The full line was computed using the Ising-like model, with a single adjustable parameter, δV ~ 27 Å³ (after [3]).

9 Magnetic field effect

Recent experiments [53–56] under pulsed magnetic field up to 35 T, using reflectivity detection, have shown the partial or complete triggering of the SC transition. We shall not discuss here these experiments, which involve kinetic aspects inherent to the short duration of the magnetic field pulse (< 1 s). We only deal here with the quasi-static properties, analysed through a simple extension of the Ising model. The magnetic molar free energy [53,58] writes:

Δ G = G_{HS} - G_{LS} = Δ H (0) - T Δ S (0) - (χ_{HS} - χ_{LS}) B^{2} / 2 μ_{0}

where ΔH(0), ΔS(0) refer to the properties in absence of external field. Accounting for the paramagnetic properties of the HS state, it comes, for a spin S = 0→S = 2 transition:

T_{1 / 2} (B) = T_{1 / 2} (0) - 4 {(μ_{B} B)}^{2} / k_{B} Δ (0)

to which corresponds a fictitious field depending on the magnetic field, according to:

Δ_{eff} (B) = Δ_{eff} (0) - 4 (\ln g) {(μ_{B} B)}^{2} / Δ (0)

The negative sign for the gap shift means that the HS state is favoured by the coupling to the magnetic field. In the example of [53], the maximum available field, 31 T, resulted in a computed shift of the transition temperature ΔT_1/2 ~ –1.8 K, a sufficient shift for a complete triggering to be expected in the quasi-static regime. The observed incompleteness of the experimental triggering was interpreted as due to the kinetic aspect of the pulsed field experiment. These aspects were recently modelled through dynamic treatments of the Ising-like model [55–59].

10 Perspectives

Further developments or extensions of the Ising-like model have been reported: (i) static model accounting for the vibrational energy scheme of each spin state (in the Einstein model) for the quite rare case of quasi-equienergetic spin states [31], (ii) static [27–31] and dynamic models [32–34] combining short-range and long-range interactions, using Monte Carlo simulations [60–61], including magnetic field and pressure effects, and more recently based on analytical treatments and entropic sampling. An extensive investigation of several series of diluted systems, using these recent approaches, would be timely and might help to elucidate the origin of the short-range and long-range interactions. However, despite its impressive capability for reproducing detailed experimental features, the Ising-like model remains phenomenological in nature, and much work remains to be done for relating the parameter values to actual physical characteristics of the solid state (as it was initiated, for long-range interactions, in the ‘historical’ elastic model of Spiering [62,63]).

On the other hand, the Ising-like model provides a unified viewpoint of the thermodynamic properties of switchable inorganic solids, and therefore plays a unique role for developing analogies between them. No doubt it should also apply to SC systems including size reduction effects and to further switchable solids, for example those involving ligand photo-isomerisation [64], or including photo-chromic organic groups, which nowadays are actively designed and synthesized by the chemists.

Acknowledgements

M. Nogues, J. Jeftic, N. Menendez, for scientific contributions, A. Wack for technical assistance, NATO for a Cooperative Linkage Grant, CNRS and EEC (TMR TOSS program ERB-FMRX-CT98-0199) for financial supports.

Bibliographie

[1] J.H. Ammeter Nouv. J. Chimie, 4 (1980), p. 631

[2] O. Kahn Molecular Magnetism, VCH, New York, 1993

[3] F. Varret; M. Nogues; A. Goujon (J. Miller; M. Drillon, eds.), Magnetism: Molecules to Materials, vol. 2, Wiley-VCH, 2001, p. 257

[4] M. Soraï Chem. Soc. Jpn, 74 (2001), p. 2223

[5] P. Gütlich; Y. Garcia; T. Woïke Coord. Chem. Rev., 219–221 (2001), p. 839

[6] F. Varret, A. Bleuzen, K. Boukheddaden, A. Bousseksou, E. Codjovi, C. Enachescu, A. Goujon, J. Linares, N. Menendez, M. Verdaguer, Int. Conf. Solid-State Chemistry (Bratislava, Slovakia, July 2002), Proc. Pure Appl. Chem. (in press)

[7] H. Toftlund Coord. Chem. Rev., 94 (1989), p. 67

[8] E. König Struct. Bonding, 76 (1991), p. 51

[9] P. Gütlich Struct. Bonding, 44 (1981), p. 83

[10] P. Gütlich; A. Hauser; H. Spiering Angew. Chem. Int. Ed. Engl., 33 (1994), p. 2024

[11] O. Sato; T. Iyoda; A. Fujishima; K. Hashimoto Science, 272 (1996), p. 704

[12] O. Sato; Y. Einaga; T. Iyoda; A. Fujishima; K. Hashimoto J. Electrochem. Soc., 144 (1997), p. L-11

[13] A. Bleuzen; C. Lomenech; V. Escax; F. Villain; F. Varret; C. Cartier dit Moulin; M. Verdaguer J. Am. Chem. Soc., 122 (2000), p. 6648

[14] C. Cartier dit Moulin; F. Villain; A. Bleuzen; M.-A. Arrio; P. Sainctavit; C. Lomenech; V. Escax; F. Baudelet; E. Dartyge; J.-J. Gallet; M. Verdaguer J. Am. Chem. Soc., 122 (2000), p. 6653

[15] V. Escax; A. Bleuzen; C. Cartier dit Moulin; F. Villain; A. Goujon; F. Varret; M. Verdaguer J. Am. Chem. Soc., 123 (2001), p. 12536

[16] A. Goujon; O. Roubeau; M. Noguès; F. Varret; A. Dolbecq; M. Verdaguer Eur. Phys. J. B, 14 (2000), p. 115

[17] D.M. Adams; A. Dei; A.L. Rheingold; D.N. Hendrickson J. Am. Chem. Soc., 115 (1993), p. 8221

[18] D.M. Adams; Bulang Li; J.D. Simon; D.N. Hendrickson Angew. Chem. Int. Ed. Engl., 34 (1995), p. 1481

[19] D.M. Adams; D.N. Hendrickson J. Am. Chem. Soc., 118 (1996), p. 11515

[20] J. Jeftic; H. Romstedt; A. Hauser J. Phys. Chem. Solids, 57 (1996), p. 1743

[21] E. Koenig; G. Ritter; S.K. Kulshreshtha; J. Waigel; H.A. Goodwin Inorg. Chem., 23 (1984), p. 1896

[22] J. Zarembowitch; C. Roux; M.-L. Boillot; R. Claude; J.-P. Itié; A. Polian; M. Bolte J. Mol. Cryst. Liq. Cryst., 234 (1993), p. 247

[23] J. Jeftic; N. Menendez; A. Wack; E. Codjovi; J. Linares; A. Goujon; G. Hamel; S. Klotz; G. Syfosse; F. Varret Meas. Sci. Technol., 10 (1999), p. 1059

[24] M.-L. Boillot; J. Zarembowitch; J.-P. Itie; A. Polian; E. Bourdet; J.G. Haasnoot New J. Chem., 26 (2002), p. 313

[25] J. Wajnflasz; R. Pick J. Physique, 32 (1971), p. C1-C91

[26] S. Doniach J. Chem. Phys., 68 (1978), p. 4912

[27] A. Bousseksou; J. Nasser; J. Linares; K. Boukheddaden; F. Varret J. Phys., 2 (1992), p. 1381

[28] A. Bousseksou PhD thesis, University Paris-6, 1992

[29] A. Bousseksou; J. Nasser; F. Varret J. Phys., I 3 (1993), p. 1463

[30] A. Bousseksou; J. Nasser; J. Linares; K. Boukheddaden; F. Varret J. Mol. Cryst. Liq. Cryst., 234 (1993), pp. 269-274

[31] A. Bousseksou; H. Constant; F. Varret J. Phys., 5 (1995), p. 747

[32] K. Boukheddaden; I. Shteto; B. Hôo; F. Varret Phys. Rev. B, 62 (2000), pp. 14796-14806

[33] B. Hôo; K. Boukheddaden; F. Varret Eur. Phys. J. B, 17 (2000), p. 449

[34] K. Boukheddaden, J. Linares, E. Codjovi, F. Varret, V. Niel, J.A. Real, Int. Conf. Molecular Magnetic Materials (Tampa, USA, Nov. 2002), J. Appl. Phys. 93 (2003) 7103

[35] I. Shteto; K. Boukheddaden; F. Varret Phys. Rev. E, 60 (1999), p. 5139

[36] C.P. Slichter; H.G. Drickamer J. Chem. Phys., 56 (1972), p. 2142

[37] R. Zimmermann; R. König J. Phys. Chem. Solids, 38 (1977)

[38] A. Hauser; P. Gütlich; H. Spiering Inorg. Chem., 25 (1986), p. 4345

[39] A. Hauser J. Chem. Phys., 94 (1991), p. 2741

[40] A. Hauser; J. Jeftic; H. Romstedt; R. Hinek; H. Spiering Coord. Chem. Rev., 190–192 (1999), p. 471

[41] E. Codjovi; N. Menendez; J. Jeftic; F. Varret C. R. Acad. Sci. Paris, Ser. IIc, 4 (2001), p. 181

[42] G. Molnár, V. Niel, J-A. Real, L. Dubrovinsky, A.Bousseksou, J.-J. McGarvey, J. Phys. Chem. B. (submitted).

[43] J.A. Real; H. Bolvin; A. Bousseksou; A. Dworkin; O. Kahn; F. Varret; J. Zarembowitch J. Am. Chem. Soc., 114 (1992), p. 4650

[44] I.S. Jacobs J. Appl. Phys., 32 (1961), p. 619

[45] A. Goujon; F. Varret; V. Escax; A. Bleuzen; M. Verdaguer Polyhedron, 20 (2001), pp. 1339-1347

[46] S. Arun Salunke, K. Boukheddaden, E. Codjovi, K. Hashimoto, F. Varret (work in progress).

[47] J. Linares; H. Spiering; F. Varret Eur. Phys. J. B, 10 (1999), p. 271

[48] K. Boukheddaden; J. Linares; H. Spiering; F. Varret Eur. Phys. J. B, 15 (2000), p. 317

[49] I. Shteto; J. Linares; F. Varret Phys. Rev. E, 56 (1997), p. 5128

[50] J. Linares; C. Enachescu; K. Boukheddaden; F. Varret Proc. Int. Conf. Molecule-based Magnets, Polyhedron (Oct. 2002) Valencia, Spain (to appear)

[51] F. Varret, K. Boukheddaden, E. Codjovi, C. Enachescu, J. Linarès, in: P. Gütlich, H. Goodwin (Eds.), Spin Crossover in Transition Metal Compounds, Top. Curr. Chem. (to appear).

[52] C. Roux; D.M. Adams; J.-P. Itié; A. Polian; D.N. Hendrickson; M. Verdaguer Inorg. Chem., 35 (1996), p. 2846

[53] A. Bousseksou; N. Negre; M. Goiran; L. Salmon; J.-P. Tuchagues; M.-L. Boillot; K. Boukheddaden; F. Varret Eur. Phys. J. B., 13 (2000), p. 451

[54] N. Negre; M. Goiran; A. Bousseksou; J.G. Haasnoot; K. Boukheddaden; S. Askenazy; F. Varret Synth. Met., 115 (2000), p. 289

[55] N. Nègre; C. Consejo; M. Goiran; A. Bousseksou; F. Varret; J.-P. Tuchagues; R. Barbaste; S. Askénazy Physica B, 294–295 (2001), p. 91

[56] A. Bousseksou; K. Boukheddaden; M. Goiran; C. Consejo; J.-P. Tuchagues Phys. Rev. B, 65 (2002), p. 1724

[57] Y. Qi; E.W. Muller; H. Spiering; P. Gütlich Chem. Phys. Lett., 93 (1982), p. 567

[58] Y. Garcia; O. Kahn; J.-P. Ader; A. Buzdin; Y. Meurdesoif; M. Guillot Phys. Lett. A, 271 (2000), p. 145

[59] Y. Ogawa; S. Koshihara; K. Boukheddaden; F. Varret Phys. Rev. B, 66 (2002), p. 073104

[60] T. Kohlhaas; H. Spiering; P. Gütlich Z. Physik B, 102 (1997), p. 455

[61] H. Romstedt; A. Hauser; H. Spiering J. Phys. Chem. Sol., 59 (1998), p. 265

[62] N. Willenbacher; H. Spiering J. Phys. C, 21 (1988), p. 1423

[63] H. Spiering; N. Willenbacher J. Phys. Cond. Matter, 1 (1989), p. 10089

[64] M.-L. Boillot; S. Chantraine; J. Zarembowitch; J.-Y. Lallemand; J. Prunet New. J. Chem. (1999), p. 179

Commentaires - Politique