The Ising-like model applied to switchable inorganic solids: discussion of the static properties

François Varret; Sunita Arun Salunke; Kamel Boukheddaden; Azzedine Bousseksou; Épiphane Codjovi; Cristian Enachescu; Jorge Linares

doi:10.1016/S1631-0748(03)00048-1

The Ising-like model applied to switchable inorganic solids: discussion of the static properties

François Varret ¹ ; Sunita Arun Salunke ¹ ; Kamel Boukheddaden ¹ ; Azzedine Bousseksou ² ; Épiphane Codjovi ¹ ; Cristian Enachescu ¹ ; Jorge Linares ¹

¹ Laboratoire de magnétisme et d’optique, CNRS–université de Versailles–Saint-Quentin, 45, avenue des États-Unis, 78035 Versailles cedex, France
² Laboratoire de chimie de coordination, UPR 8241, CNRS, 205, route de Narbonne, 31077 Toulouse, France

Comptes Rendus. Chimie, Volume 6 (2003) no. 3, pp. 385-393.

Résumés

Anglais
Français

The Ising-like model provides a microscopic approach and a unifying description of the thermodynamic properties associated with molecular switching in inorganic solids. Applications are given for the spontaneous thermal transitions, under applied pressure or external magnetic field.

Le modèle de type Ising offre une approche microscopique et une description unifiée des propriétés thermodynamiques associées à la commutation moléculaire dans les solides inorganiques. Nous en présentons l’application aux phénomènes de transition thermique spontanée, sous pression ou sous champ magnétique.

Métadonnées

Reçu le : 2002-12-04
Accepté le : 2003-02-19
Publié le : 2003-03-01

DOI : 10.1016/S1631-0748(03)00048-1

Keywords: Full paper, inorganic solids, molecular switching, ising model, spin crossover
Mots-clés : Mémoire, solides inorganiques, commutation moléculaire, modèle d’Ising, transition de spin

Affiliations des auteurs :

François Varret ¹ ; Sunita Arun Salunke ¹ ; Kamel Boukheddaden ¹ ; Azzedine Bousseksou ² ; Épiphane Codjovi ¹ ; Cristian Enachescu ¹ ; Jorge Linares ¹

¹ Laboratoire de magnétisme et d’optique, CNRS–université de Versailles–Saint-Quentin, 45, avenue des États-Unis, 78035 Versailles cedex, France
² Laboratoire de chimie de coordination, UPR 8241, CNRS, 205, route de Narbonne, 31077 Toulouse, France

@article{CRCHIM_2003__6_3_385_0,
     author = {Fran\c{c}ois Varret and Sunita Arun Salunke and Kamel Boukheddaden and Azzedine Bousseksou and \'Epiphane Codjovi and Cristian Enachescu and Jorge Linares},
     title = {The {Ising-like} model applied to switchable inorganic solids: discussion of the static properties},
     journal = {Comptes Rendus. Chimie},
     pages = {385--393},
     publisher = {Elsevier},
     volume = {6},
     number = {3},
     year = {2003},
     doi = {10.1016/S1631-0748(03)00048-1},
     language = {en},
}

TY  - JOUR
AU  - François Varret
AU  - Sunita Arun Salunke
AU  - Kamel Boukheddaden
AU  - Azzedine Bousseksou
AU  - Épiphane Codjovi
AU  - Cristian Enachescu
AU  - Jorge Linares
TI  - The Ising-like model applied to switchable inorganic solids: discussion of the static properties
JO  - Comptes Rendus. Chimie
PY  - 2003
SP  - 385
EP  - 393
VL  - 6
IS  - 3
PB  - Elsevier
DO  - 10.1016/S1631-0748(03)00048-1
LA  - en
ID  - CRCHIM_2003__6_3_385_0
ER  -

%0 Journal Article
%A François Varret
%A Sunita Arun Salunke
%A Kamel Boukheddaden
%A Azzedine Bousseksou
%A Épiphane Codjovi
%A Cristian Enachescu
%A Jorge Linares
%T The Ising-like model applied to switchable inorganic solids: discussion of the static properties
%J Comptes Rendus. Chimie
%D 2003
%P 385-393
%V 6
%N 3
%I Elsevier
%R 10.1016/S1631-0748(03)00048-1
%G en
%F CRCHIM_2003__6_3_385_0

François Varret; Sunita Arun Salunke; Kamel Boukheddaden; Azzedine Bousseksou; Épiphane Codjovi; Cristian Enachescu; Jorge Linares. The Ising-like model applied to switchable inorganic solids: discussion of the static properties. Comptes Rendus. Chimie, Volume 6 (2003) no. 3, pp. 385-393. doi : 10.1016/S1631-0748(03)00048-1. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/S1631-0748(03)00048-1/

Version originale du texte intégral

Le texte intégral ci-dessous peut contenir quelques erreurs de conversion par rapport à la version officielle de l'article publié.

1 Introduction

Molecular switching of inorganic solids is a typical issue of the vibronic lability of molecular units, previously introduced by J.A. Ammeter [1]. We report here on several families of inorganic systems where a spin crossover is involved in the switching process between the two molecular states: spin-crossover solids (SC), photomagnetic Prussian blue analogues (PBA), valence-tautomeric system (VT) – see Table 1. A previous presentation of the concept in terms of ‘molecular bistability’ was given by O. Kahn [2], on the example of SC solids. Recent reviews on switchable inorganic solids can be found in [3–6].

System	Low-temperature state	High-temperature state	basic refs.
SC Fe^II (3d⁶)	Fe^II_LS(S = 0) = t_2g⁶	Fe^II_HS(S = 2) = t_2g⁴ e_2g²	[2, 7–10]
Fe,Co PBA	Fe^II_LS(S = 0) Co^III_LS(S = 0)	Fe^III_LS(S = 1/2) Co^II_HS(S = 3/2)	[11–16]
VT Co semiquinone*	Co^III_LS(S = 0) (sq^•)(cat)	Co^II_HS(S = 3/2) (sq^•) (sq^•)	[17–19]

The bistable properties at the molecular level are adequately described through a molecular configurational diagram, i.e. a plot of the adiabatic energies versus the distortion coordinate of the molecular system. Usually, for spin crossover, a fully symmetric distortion is considered, associated with the change in average metal–ligand distance. Due to the large atomic displacements upon spin conversion, the optical properties drastically change, so that the switching properties can be followed as well by magnetic or optical (absorption, reflectivity) techniques. In Fig. 1 we show the configurational diagram suited to spin crossover, in the case of low-spin (LS) ground state. It is noteworthy that the effect of environment in molecular solids slightly affects the configurational diagram. For example, an external pressure mainly increases the energy gap Δ, and correlatively reduces the energy barrier of the high-spin (HS) state, so as to raise the equilibrium temperature T_1/2 (see next section) and to shorten the lifetime of the HS state [20–24].

Fig. 1
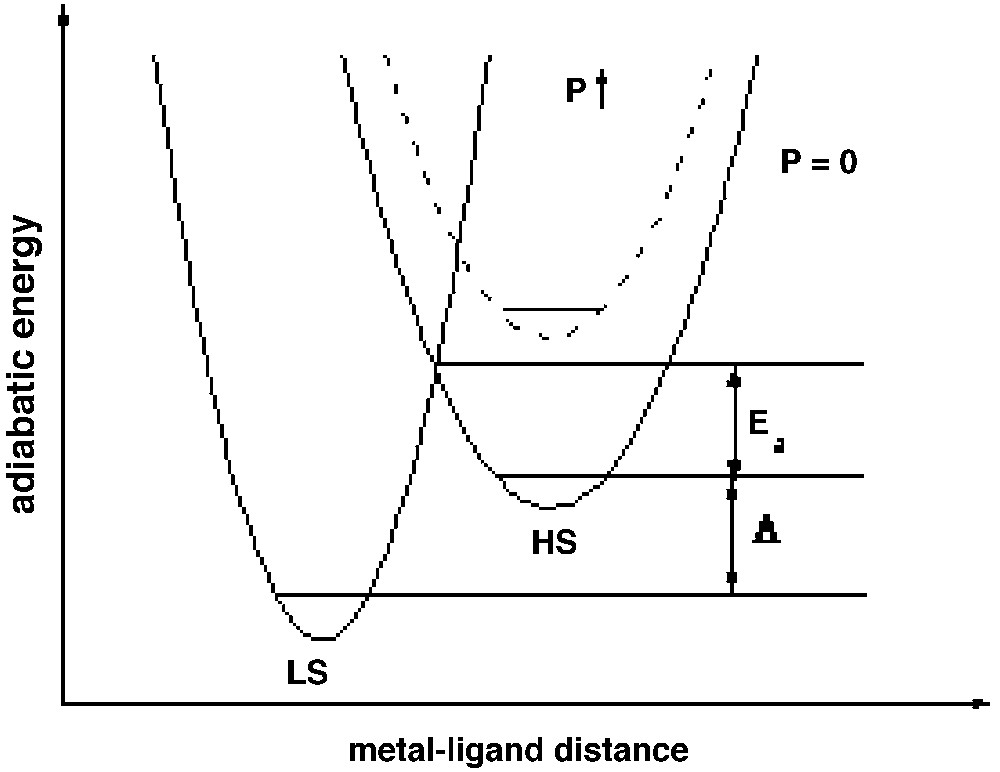
The configurational diagram of spin-crossover (after [8]), with LS ground state, and the effect of an external pressure (after [20]). Anharmonic effects have been discarded.

2 Ising-like model

A widely used model for such bistable systems is the Ising-like model [25–26], which describes interacting two-level units, the energy levels of which have different energies and degeneracies. The two-level scheme indeed is a drastic simplification of the complete vibronic level scheme, in the adiabatic approximation. However, it permits describing with amazing success most of the quasi-static properties of the SC solids [27–31]. The degeneracy ratio g = g_HS/g_LS is related to the molar entropy change upon total conversion ΔS = R ln g [29,30], and therefore can be derived from calorimetric measurements at the spin-crossover equilibrium temperature T_1/2.

A useful recent review of calorimetric data is given in ref. [4]. Because of both electronic and vibrational factors, ΔS > 0 (ΔS = 30 to 70 J K^–1 mol^–1), therefore g >> 1 [29–31]. The Ising-like model has been used and developed for describing the static [27–31] and dynamic [32–34] properties of SC mono and binuclear solids, and was applied as well to the VT compound [3]. The Ising Hamiltonian writes:

\hat{H} = (Δ / 2) \sum_{i} {\hat{σ}}_{i} - \sum_{< i, j >} J_{ij} {\hat{σ}}_{i} {\hat{σ}}_{j}

with fictitious spins

\hat{σ}

having eigenvalues +1 in the high-spin state (HS) , –1 in the low-spin state (LS), and degeneracies g_HS, g_LS. As usual, the index <i,j> stands for all pairs of sites, and the reference sign for a cooperative interaction, favouring spin-like states, is J_ij > 0. Δ = E(HS) – E(LS), denoted energy gap (or ‘fictitious field’), is the enthalpy change associated with the LS→HS conversion of one molecule. The HS fraction is expressed as a function of the ‘fictitious magnetisation’:

n_{HS} = (< \hat{σ} > + 1) / 2

A convenient form of the Ising-like Hamiltonian is the Ising equivalent form [26] obtained by rewriting the canonical partition function to get rid of the pre-exponential factors. The Ising equivalent form involves a temperature-dependent energy gap (= ‘fictitious effective field’) accounting for the degeneracy ratio:

{\hat{H}}_{equiv} = [Δ_{eff} (T) / 2] \sum_{i} {\hat{σ}}_{i} - \sum_{< i, j >} J_{ij} {\hat{σ}}_{i} {\hat{σ}}_{j}

Δ_{eff} (T) = Δ - k_{B} T \ln g

The thermodynamic properties of the Ising-like system (with the LS ground state) are merely governed by the sign of the effective field, for example the qualitative features of the thermal variation of the HS fraction are reported in Table 2 and illustrated in Fig. 2. The equilibrium temperature T_1/2 for which n_HS = n_LS = $1 ⁄ 2$ corresponds to a null effective field, irrespectively of the interactions:

Temperature	T = 0	T = T_1/2	T >> T_1/2
Δ(T)	D >0	0	Negative
$\hat{σ}$	–1	0	(g_HS– g_LS)/(g_HS+ g_LS)
n_HS	0	1/2	g_HS/(g_HS+ g_LS)

Fig. 2
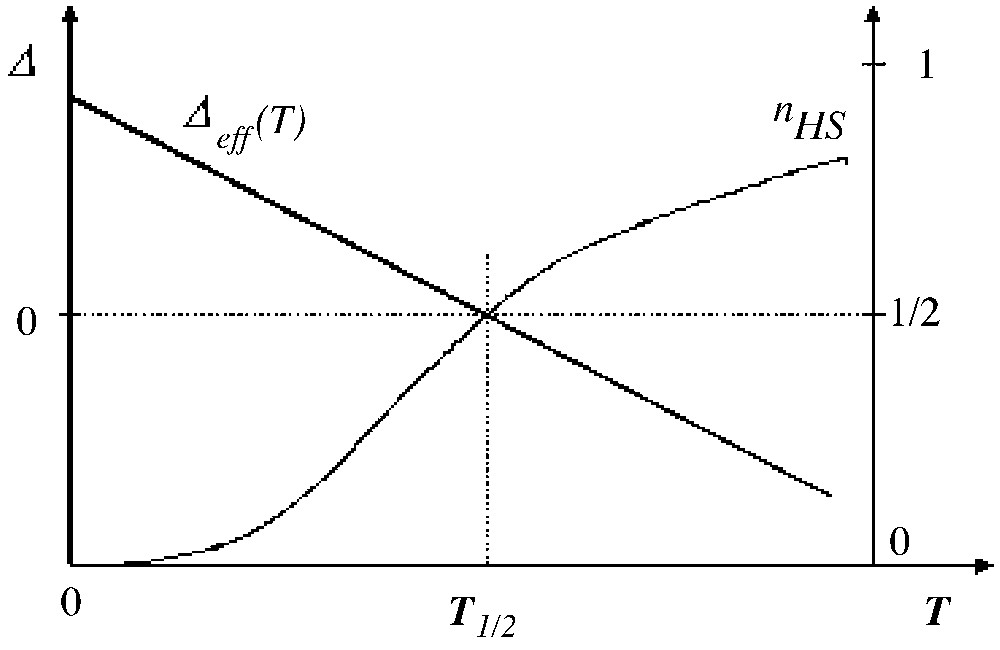
Thermal variation of the temperature-dependent fictitious field (with LS ground state) and subsequent variation of the HS fraction, in absence of interactions.

T_{1 / 2} = Δ / k_{B} \ln g

3 Spontaneous thermal hysteresis

The presence of interactions — of steric origin — makes the conversion curve n_HS(T) steeper around T_1/2. Above an interaction threshold value, the system becomes bistable at T_1/2 and thermal hysteresis occurs. The bistability condition is easily derived using the Ising equivalent form: it requires the Ising equivalent system to be ordered at the equilibrium temperature [35], i.e.:

T_{1 / 2} < T_{C}

Then the reversal of Δ_eff(T) induces the reversal of the non-null fictitious magnetisation $< \hat{σ} >,$ i.e. the thermal transition is discontinuous (in other words, the free energy as function of temperature presents a slope change = discontinuity of the first derivative δF/δT) and hysteresis can occur. This is illustrated in Fig. 3, where the hysteresis loop, resulting from a quasi-static variation of temperature, has been completed by vertical arrows.

Fig. 3
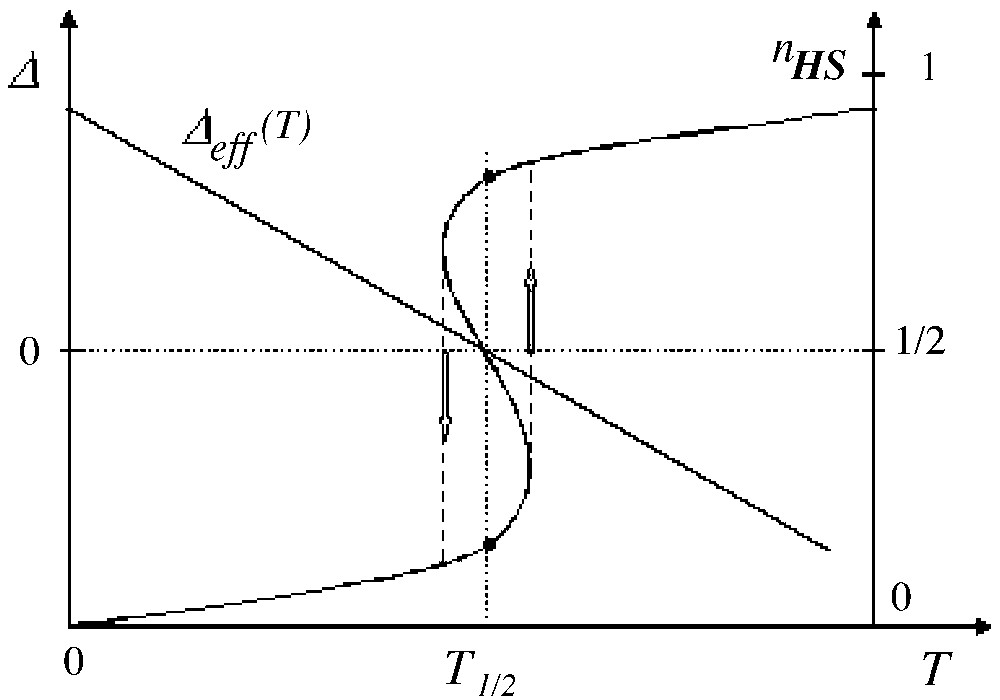
Thermal variation of the temperature-dependent fictitious field (with LS ground state) and subsequent variation of the HS fraction, in the presence of interactions larger than the threshold value.

4 Homogeneous mean-field treatment

The interaction term in Eq. (3) is re-expressed, considering:

• (i) the average effect of neighbours; the single-site Hamiltonian for site i writes:
${\hat{h}}_{i} = [Δ_{eff} (T) / 2] {\hat{σ}}_{i} - \sum_{j} J_{ij} < {\hat{σ}}_{j} > {\hat{σ}}_{i}$
• (ii) homogeneous thermodynamic properties, i.e. $< {\hat{σ}}_{j} > = < {\hat{σ}}_{i} >,$ so that a unique single-site Hamiltonian is derived, written as:
${\hat{h}}_{m . f .} = [Δ_{eff} (T) / 2] \hat{σ} - J < \hat{σ} > \hat{σ}$
where J accounts for the sum on interactions due to all neighbours.

Eq. (8) can be interpreted in terms of independent two-level systems submitted to a fictitious field dependent on the order parameter of the system:

Δ_{eff} (T, n_{HS}) = Δ - k_{B} T \ln g - 2 J < \hat{σ} > = Δ_{eff} (T, 0) - 4 {Jn}_{HS}

Straightforward self-consistent calculations, using the canonical partition function, provide the n_HS(T) dependence. It is noteworthy that an explicit expression T(n_HS) can be obtained [32]:

k_{B} T (n_{HS}) = [Δ + 2 J - 4 J n_{HS}] / [\ln (1 - n_{HS}) - \ln n_{HS} + \ln g]

The occurrence condition of hysteresis is easily derived by consideration of the slope dT/dn_HS at n_HS = 1/2 (it has to be negative), leading to:

J > Δ / \ln g = k_{B} T_{1 / 2}

Eq. (11) was previously derived from a ‘thermodynamic’ model based on the properties of regular solutions in the Bragg–Williams approach [36], later shown to be formally equivalent to the present mean-field two-level approach [37]. Eq. (11) can as well be derived from the general condition (Eq. (6)), just inserting the mean-field value T_C = J/k_B. An useful comparison can be made with the pressure effect:

Δ_{eff} (T, p) = Δ_{eff} (T, 0) + p δ V

where δV is the volume increase of the molecular unit upon LS→HS conversion. By comparing Eqs. (9) and (12), it appears that increasing n_HS induces the same effect than decreasing p, i.e. a downward shift of the HS energy well (see Fig. 1). Such an effect was previously reported by Hauser and Spiering in terms of ‘internal pressure’ [38–40] and introduced into the two-level Ising-like model in [31,41,42]. It corresponds to a cooperative effect mediated by the lattice, i.e. associated with long-range interactions: the LS→HS conversion of any molecular unit induces an increase of the lattice parameter, which in turn favours the conversion of the remaining LS units. In addition, due to the subsequent increase of the barrier energy, the lifetime of the HS metastable state is increased. To summarise, the cooperative effects correlate positively the population and the stability of the states, both statically and kinetically.

5 Two-step transitions

Two-step transitions have been reported in the case of systems combining positive and negative interactions, for example in the case of two-sublattices negatively coupled [27], or of binuclear molecular units [28,29,43].

We develop here a comparison to metamagnets, i.e. two-sublattice magnetic systems, combining intra-sublattice ferromagnetic and inter-sublattice antiferromagnetic interactions [44]. Actually metamagnetism also requires a large magnetic anisotropy, which confines the magnetic moments along the easy magnetic axis; this situation is of course suited to the Ising models. The up–up, up–down and down–down fictitious magnetisation states respectively correspond to HS–HS, HS–LS and LS–LS states. The typical magnetic behaviour of a metamagnet, i.e. the spin-flip transition obtained for positive and for negative fields, is sketched in Fig. 4 at null temperature. The two-step spin transition obviously follows, with however a smoother character, due the thermal population effect.

Fig. 4
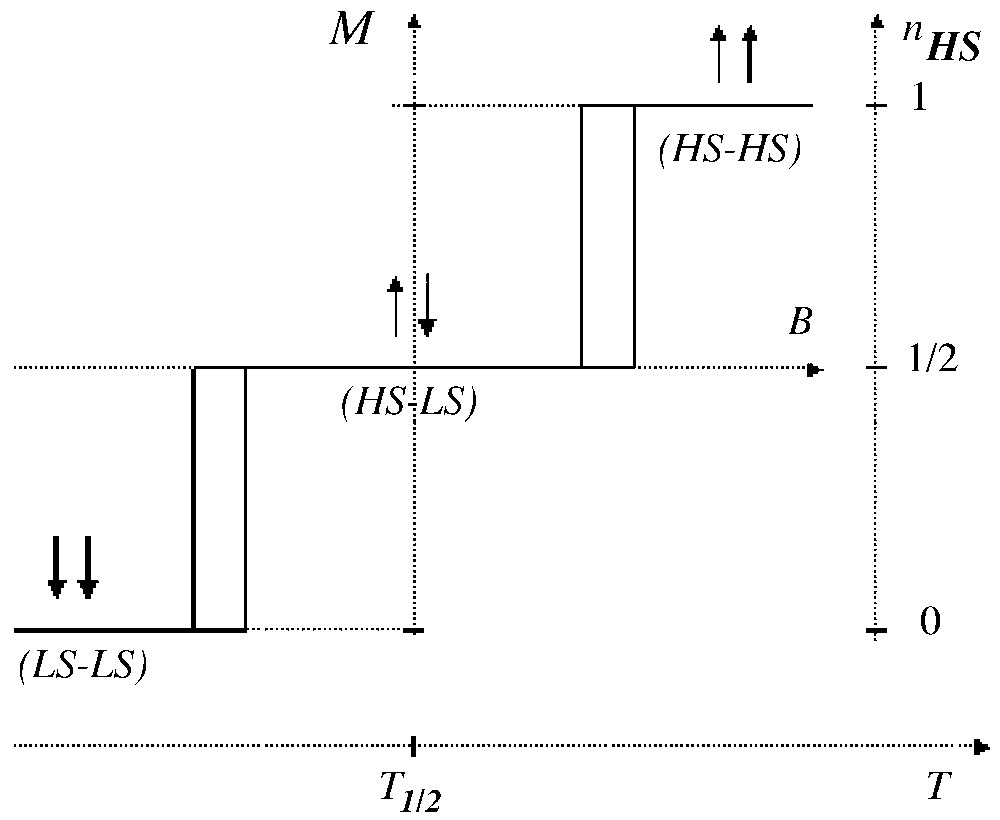
The magnetic response (at T = 0) of a metamagnet under the effect of a magnetic field applied along the easy axis. The analogy with a two-sublattice spin transition is indicated.

Alternatively, Fig. 4 can be interpreted as the response of a 3-level system under the effect of an external field. This concept also applies to the case of bi-nuclear systems [28,29,43], which indeed exhibit the two-step transition (or conversion). The key point is the relative stability of the intermediate state at zero field, i.e. the stability of the molecular HS-LS state at T_1/2, which obviously requires a negative intramolecular interaction.

6 Kinetic effects on the thermal hysteresis loop

The observation of the thermal transition requires a fast relaxation between the two states, with respect to the experimental time scale. If not, kinetic effect are to be observed, e.g. an extra-broadening of the thermal loop, in addition to the trivial heat transfer effect which has a characteristic time of some minutes in the usual temperature range of spin transitions (100–400 K).

Actually, there are not many available data for the intrinsic kinetics of the spin crossover phase transition, which seems to be rapid, and therefore should be difficult to disentangle from heat-transfer effects. On the other hand, the escape time of the macroscopic metastable state [35] in the hysteretic temperature range is expected to be very long, in agreement with the usual observation of a quasi-static hysteresis at the experimental time scale (hours, days). However, in analogy with the superparamagnetic fluctuations of nanograins, a shortening of the escape time has to be expected in the case of spin-crossover nano-crystals, due to the smaller value of the macroscopic barrier energy. Several chemistry groups presently pay a large effort in order to synthesise spin-crossover nano-crystals, and we can expect that the open question of quantum tunnelling for the spin transition will be addressed quite soon.

The situation of the Photo-magnetic Prussian Blue analogues is quite different, due to their much slower relaxation, allowing to perform an efficient photo-excitation up to ~130 K in the cases of the Cs–CoFe [45] and Na–CoFe [46] PBA systems. These systems exhibit progressive and abrupt spontaneous transitions, respectively, in the range 200–300 K. Due to the slower relaxation, the high-temperature phase can be trapped in these systems, better than in the spin-crossover solids. Indeed a partial trapping of the high-temperature phase, by thermal quenching, was previously observed in a Cs–CoFe PBA sample [45]. In a Na–CoFe PBA sample, we recently obtained a complete trapping [46]. Typical kinetic effects on the thermal loop of Na–CoFe PBA sample are reported in Fig. 5. A model for kinetic thermal hysteresis, accounting for realistic relaxation rates, was given in [32].

Fig. 5
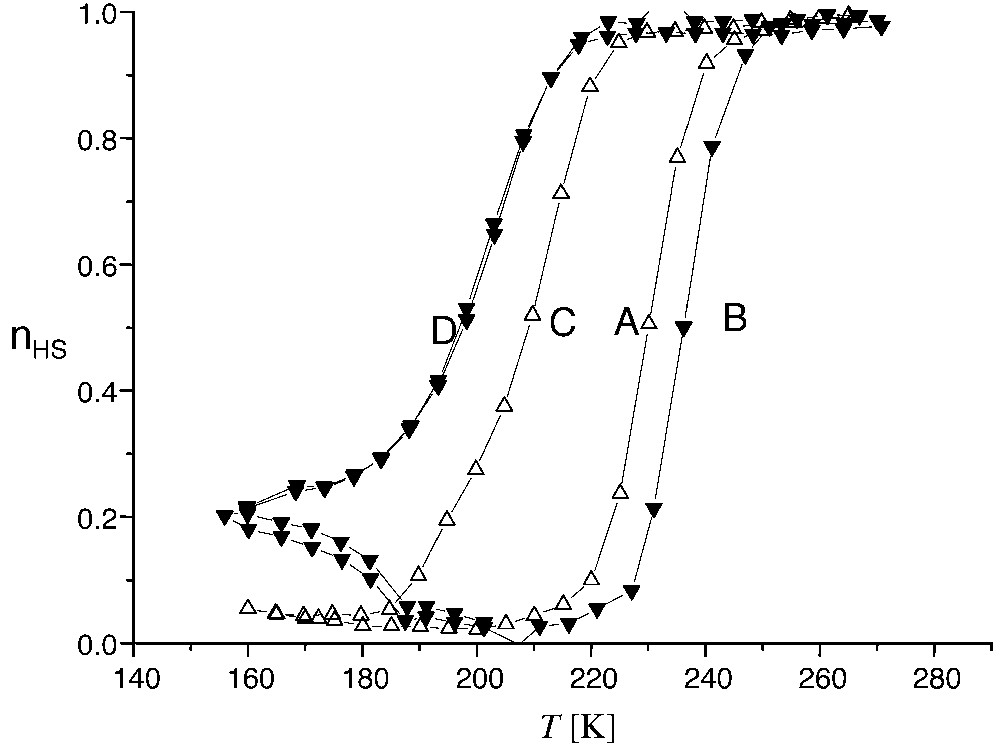
Kinetic effects on the spontaneous thermal hysteresis of Na_0.40Co[Fe(CN)₆]_0.70·3.5 H₂O: high-temperature phase fraction, deduced from magnetic measurements. Temperature sweeping rates are (A) +0.97, (B) +9.43, (C) –1.96, (D) – 11.26 K min^–1.

7 On the shape of the thermal hysteresis loop

We briefly comment on the shape of the quasi-static hysteresis loop (discarding the kinetic effects). Indeed, the usual mean-field models result in well-rounded turning points of the loop, while most of experimental data display well-marked turning points, with sometimes rather bent sides (instead of the expected jumps). The bent sides are easily reproduced by a distribution of transition temperatures. The origin of the well-marked turning points was recently elucidated [47] thanks to improved models including both long- and short-range interactions [33,34]. The detailed treatments of the extended Hamiltonian, for the static and dynamic properties, have been published for 1-D (exact solution) [48] and 2-D/3-D systems, using the Bethe or the pair approximation [33–34] or the exact (but restricted to finite size) entropic sampling approach [49–50].

We show in Fig. 6 that the shape of the hysteresis loop sensitively depends on the balance between the long-range and short-range interactions: well-marked turning points indicate the presence of short-range interactions. It is worth noting that an other important issue of short range interactions is the presence of relaxation tails, associated with a clusterisation of the system at long times: the key point is that clusters retaining the larger n_HS fraction also retain the longer lifetime, i.e. better resist against the self-accelerated relaxation process. We do not discuss here these dynamic aspects, for which the reader should refer to recent publications [32–34]. A general review involving the relaxation properties under permanent photo-excitation is in preparation [51].

Fig. 6
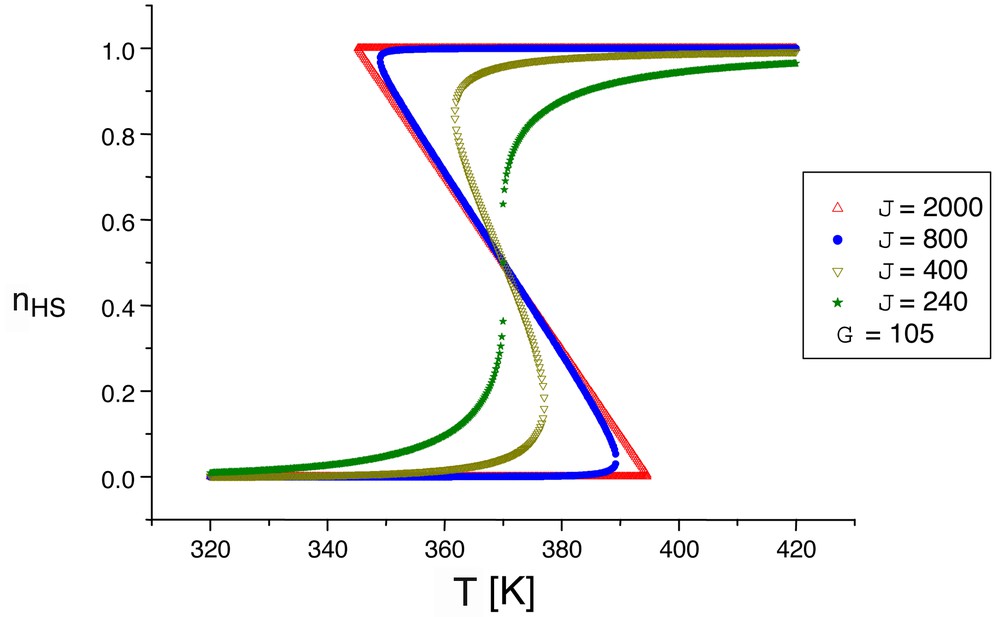
Computed thermal hysteresis loops, including the effect of short-range (J) and long-range (G) interactions (after [47]). The larger the short-range interaction, the best marked the turning points (the squarer the hysteresis loop).

8 Pressure effects

The extended expression of the temperature dependent fictitious field, accounting for both cooperative and pressure effects, is written:

Δ_{eff} (T, p, n_{HS}) = Δ_{eff} - k_{B} T \ln g + p δ V - 4 J n_{HS}

Within the present homogeneous mean-field approach, Eq. (13) introduces a linear correlation between temperature and pressure, at constant n_HS. For example, at n_HS = 1/2:

T_{1 / 2} (p) = T_{1 / 2} (0) + p δ V / k_{B} \ln g = T_{1 / 2} (0) + p Δ V / Δ S

p_{1 / 2} (T) = [T - T_{1 / 2} (p = 0)] (k_{B} \ln g / δ V) = [T - T_{1 / 2} (p = 0)] Δ S / Δ V

where ΔV = N_A δV is the molar volume increase upon total conversion. Eq. (15) defines the equilibrium pressure, i.e. the pressure which is needed, at a given temperature, to reach the equilibrium value n_HS = 1/2, starting from the HS state. A typical phase diagram built up from isobaric (T_1/2) and isothermal (p_1/2) data is shown in Fig. 7. A schematic p–T diagram derived from a straightforward application of the model is reported in Fig. 8: the biphasic domain, in-between the transition lines, is expected to decrease with increasing pressure (assuming a pressure-independent interaction parameter), and should collapse at T = T_C, according to Eq. (6). The value of δV can be derived from the average slope of the borderlines of the experimental phase diagram:

Fig. 7
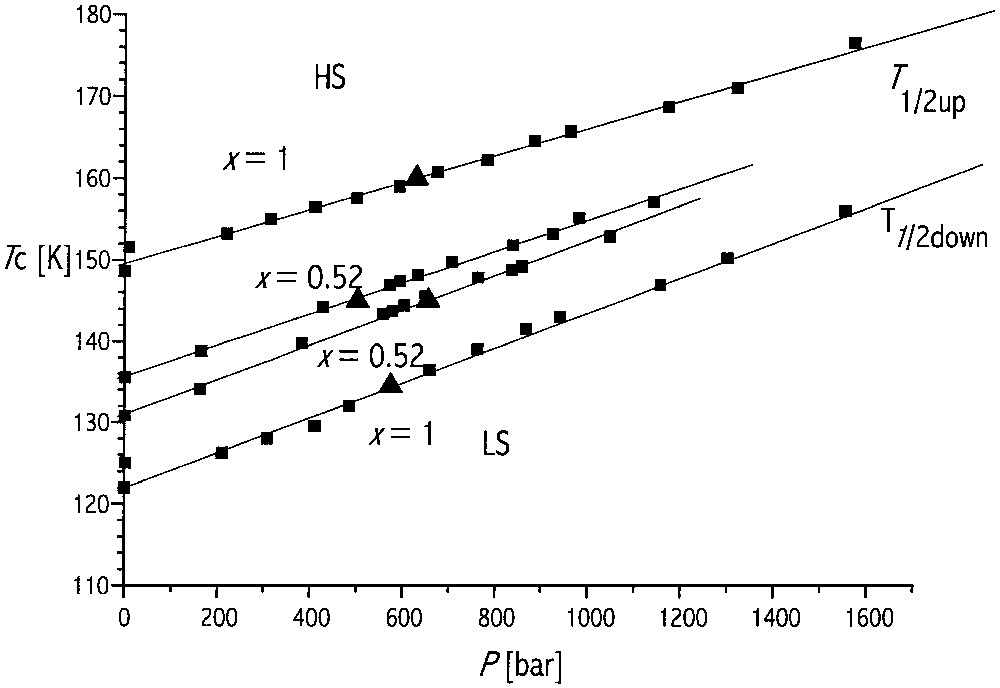
The pressure–temperature phase diagram for the spontaneous spin transition of Fe_xNi_1–_x(btr)₂(NCS)₂]·H₂O, from optical reflectivity data (λ = 600 nm), for x = 0.52, x = 1. The straight lines are associated with the transition values (■ for T_1/2, ▴ for p_1/2).

Fig. 8
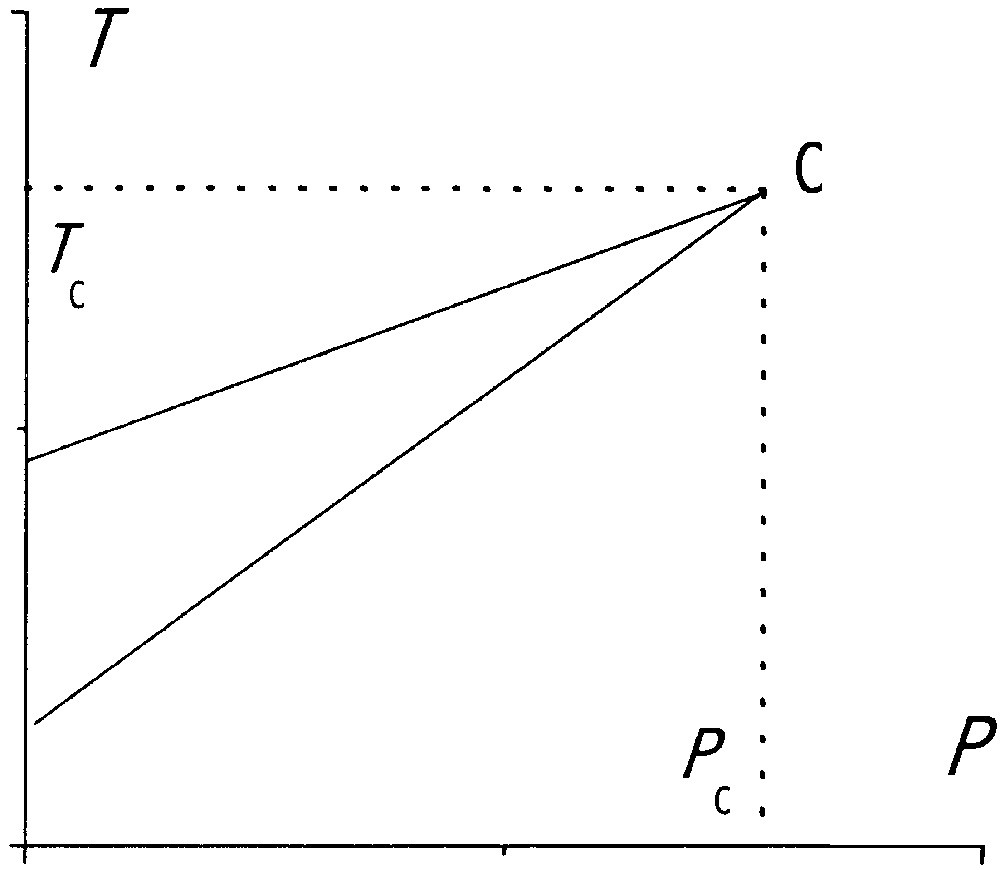
Simple schematic p–T phase diagram of the Ising-like model (assuming a pressure-independent J).

Δ V = Δ S \times (\partial T_{1 / 2} / \partial p)

Most of experimental data [6–10,21–24,41,42] for several families of spin-crossover compounds yield δV ~ 20–30 Å³. The model applies as well to the valence tautomeric transition, leading to a similar δV value, as shown in Fig. 9.

Fig. 9
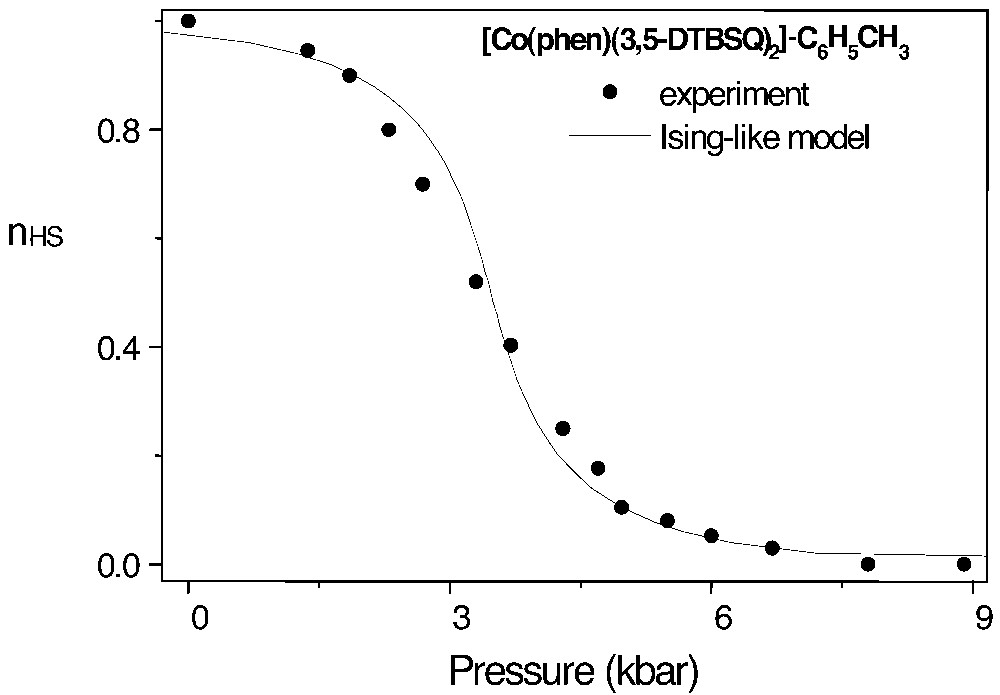
The pressure-induced valence tautomeric transition, from Co(sq^•)₂ (high-temperature phase) to Co(sq^•)(cat) (low-temperature phase). Experimental data from [52]: n_HS is the Co^II high-spin fraction. The full line was computed using the Ising-like model, with a single adjustable parameter, δV ~ 27 Å³ (after [3]).

9 Magnetic field effect

Recent experiments [53–56] under pulsed magnetic field up to 35 T, using reflectivity detection, have shown the partial or complete triggering of the SC transition. We shall not discuss here these experiments, which involve kinetic aspects inherent to the short duration of the magnetic field pulse (< 1 s). We only deal here with the quasi-static properties, analysed through a simple extension of the Ising model. The magnetic molar free energy [53,58] writes:

Δ G = G_{HS} - G_{LS} = Δ H (0) - T Δ S (0) - (χ_{HS} - χ_{LS}) B^{2} / 2 μ_{0}

where ΔH(0), ΔS(0) refer to the properties in absence of external field. Accounting for the paramagnetic properties of the HS state, it comes, for a spin S = 0→S = 2 transition:

T_{1 / 2} (B) = T_{1 / 2} (0) - 4 {(μ_{B} B)}^{2} / k_{B} Δ (0)

to which corresponds a fictitious field depending on the magnetic field, according to:

Δ_{eff} (B) = Δ_{eff} (0) - 4 (\ln g) {(μ_{B} B)}^{2} / Δ (0)

The negative sign for the gap shift means that the HS state is favoured by the coupling to the magnetic field. In the example of [53], the maximum available field, 31 T, resulted in a computed shift of the transition temperature ΔT_1/2 ~ –1.8 K, a sufficient shift for a complete triggering to be expected in the quasi-static regime. The observed incompleteness of the experimental triggering was interpreted as due to the kinetic aspect of the pulsed field experiment. These aspects were recently modelled through dynamic treatments of the Ising-like model [55–59].

10 Perspectives

Further developments or extensions of the Ising-like model have been reported: (i) static model accounting for the vibrational energy scheme of each spin state (in the Einstein model) for the quite rare case of quasi-equienergetic spin states [31], (ii) static [27–31] and dynamic models [32–34] combining short-range and long-range interactions, using Monte Carlo simulations [60–61], including magnetic field and pressure effects, and more recently based on analytical treatments and entropic sampling. An extensive investigation of several series of diluted systems, using these recent approaches, would be timely and might help to elucidate the origin of the short-range and long-range interactions. However, despite its impressive capability for reproducing detailed experimental features, the Ising-like model remains phenomenological in nature, and much work remains to be done for relating the parameter values to actual physical characteristics of the solid state (as it was initiated, for long-range interactions, in the ‘historical’ elastic model of Spiering [62,63]).

On the other hand, the Ising-like model provides a unified viewpoint of the thermodynamic properties of switchable inorganic solids, and therefore plays a unique role for developing analogies between them. No doubt it should also apply to SC systems including size reduction effects and to further switchable solids, for example those involving ligand photo-isomerisation [64], or including photo-chromic organic groups, which nowadays are actively designed and synthesized by the chemists.

Acknowledgements

M. Nogues, J. Jeftic, N. Menendez, for scientific contributions, A. Wack for technical assistance, NATO for a Cooperative Linkage Grant, CNRS and EEC (TMR TOSS program ERB-FMRX-CT98-0199) for financial supports.

Bibliographie

[1] J.H. Ammeter Nouv. J. Chimie, 4 (1980), p. 631

[2] O. Kahn Molecular Magnetism, VCH, New York, 1993

[3] F. Varret; M. Nogues; A. Goujon (J. Miller; M. Drillon, eds.), Magnetism: Molecules to Materials, vol. 2, Wiley-VCH, 2001, p. 257

[4] M. Soraï Chem. Soc. Jpn, 74 (2001), p. 2223

[5] P. Gütlich; Y. Garcia; T. Woïke Coord. Chem. Rev., 219–221 (2001), p. 839

[6] F. Varret, A. Bleuzen, K. Boukheddaden, A. Bousseksou, E. Codjovi, C. Enachescu, A. Goujon, J. Linares, N. Menendez, M. Verdaguer, Int. Conf. Solid-State Chemistry (Bratislava, Slovakia, July 2002), Proc. Pure Appl. Chem. (in press)

[7] H. Toftlund Coord. Chem. Rev., 94 (1989), p. 67

[8] E. König Struct. Bonding, 76 (1991), p. 51

[9] P. Gütlich Struct. Bonding, 44 (1981), p. 83

[10] P. Gütlich; A. Hauser; H. Spiering Angew. Chem. Int. Ed. Engl., 33 (1994), p. 2024

[11] O. Sato; T. Iyoda; A. Fujishima; K. Hashimoto Science, 272 (1996), p. 704

[12] O. Sato; Y. Einaga; T. Iyoda; A. Fujishima; K. Hashimoto J. Electrochem. Soc., 144 (1997), p. L-11

[13] A. Bleuzen; C. Lomenech; V. Escax; F. Villain; F. Varret; C. Cartier dit Moulin; M. Verdaguer J. Am. Chem. Soc., 122 (2000), p. 6648

[14] C. Cartier dit Moulin; F. Villain; A. Bleuzen; M.-A. Arrio; P. Sainctavit; C. Lomenech; V. Escax; F. Baudelet; E. Dartyge; J.-J. Gallet; M. Verdaguer J. Am. Chem. Soc., 122 (2000), p. 6653

[15] V. Escax; A. Bleuzen; C. Cartier dit Moulin; F. Villain; A. Goujon; F. Varret; M. Verdaguer J. Am. Chem. Soc., 123 (2001), p. 12536

[16] A. Goujon; O. Roubeau; M. Noguès; F. Varret; A. Dolbecq; M. Verdaguer Eur. Phys. J. B, 14 (2000), p. 115

[17] D.M. Adams; A. Dei; A.L. Rheingold; D.N. Hendrickson J. Am. Chem. Soc., 115 (1993), p. 8221

[18] D.M. Adams; Bulang Li; J.D. Simon; D.N. Hendrickson Angew. Chem. Int. Ed. Engl., 34 (1995), p. 1481

[19] D.M. Adams; D.N. Hendrickson J. Am. Chem. Soc., 118 (1996), p. 11515

[20] J. Jeftic; H. Romstedt; A. Hauser J. Phys. Chem. Solids, 57 (1996), p. 1743

[21] E. Koenig; G. Ritter; S.K. Kulshreshtha; J. Waigel; H.A. Goodwin Inorg. Chem., 23 (1984), p. 1896

[22] J. Zarembowitch; C. Roux; M.-L. Boillot; R. Claude; J.-P. Itié; A. Polian; M. Bolte J. Mol. Cryst. Liq. Cryst., 234 (1993), p. 247

[23] J. Jeftic; N. Menendez; A. Wack; E. Codjovi; J. Linares; A. Goujon; G. Hamel; S. Klotz; G. Syfosse; F. Varret Meas. Sci. Technol., 10 (1999), p. 1059

[24] M.-L. Boillot; J. Zarembowitch; J.-P. Itie; A. Polian; E. Bourdet; J.G. Haasnoot New J. Chem., 26 (2002), p. 313

[25] J. Wajnflasz; R. Pick J. Physique, 32 (1971), p. C1-C91

[26] S. Doniach J. Chem. Phys., 68 (1978), p. 4912

[27] A. Bousseksou; J. Nasser; J. Linares; K. Boukheddaden; F. Varret J. Phys., 2 (1992), p. 1381

[28] A. Bousseksou PhD thesis, University Paris-6, 1992

[29] A. Bousseksou; J. Nasser; F. Varret J. Phys., I 3 (1993), p. 1463

[30] A. Bousseksou; J. Nasser; J. Linares; K. Boukheddaden; F. Varret J. Mol. Cryst. Liq. Cryst., 234 (1993), pp. 269-274

[31] A. Bousseksou; H. Constant; F. Varret J. Phys., 5 (1995), p. 747

[32] K. Boukheddaden; I. Shteto; B. Hôo; F. Varret Phys. Rev. B, 62 (2000), pp. 14796-14806

[33] B. Hôo; K. Boukheddaden; F. Varret Eur. Phys. J. B, 17 (2000), p. 449

[34] K. Boukheddaden, J. Linares, E. Codjovi, F. Varret, V. Niel, J.A. Real, Int. Conf. Molecular Magnetic Materials (Tampa, USA, Nov. 2002), J. Appl. Phys. 93 (2003) 7103

[35] I. Shteto; K. Boukheddaden; F. Varret Phys. Rev. E, 60 (1999), p. 5139

[36] C.P. Slichter; H.G. Drickamer J. Chem. Phys., 56 (1972), p. 2142

[37] R. Zimmermann; R. König J. Phys. Chem. Solids, 38 (1977)

[38] A. Hauser; P. Gütlich; H. Spiering Inorg. Chem., 25 (1986), p. 4345

[39] A. Hauser J. Chem. Phys., 94 (1991), p. 2741

[40] A. Hauser; J. Jeftic; H. Romstedt; R. Hinek; H. Spiering Coord. Chem. Rev., 190–192 (1999), p. 471

[41] E. Codjovi; N. Menendez; J. Jeftic; F. Varret C. R. Acad. Sci. Paris, Ser. IIc, 4 (2001), p. 181

[42] G. Molnár, V. Niel, J-A. Real, L. Dubrovinsky, A.Bousseksou, J.-J. McGarvey, J. Phys. Chem. B. (submitted).

[43] J.A. Real; H. Bolvin; A. Bousseksou; A. Dworkin; O. Kahn; F. Varret; J. Zarembowitch J. Am. Chem. Soc., 114 (1992), p. 4650

[44] I.S. Jacobs J. Appl. Phys., 32 (1961), p. 619

[45] A. Goujon; F. Varret; V. Escax; A. Bleuzen; M. Verdaguer Polyhedron, 20 (2001), pp. 1339-1347

[46] S. Arun Salunke, K. Boukheddaden, E. Codjovi, K. Hashimoto, F. Varret (work in progress).

[47] J. Linares; H. Spiering; F. Varret Eur. Phys. J. B, 10 (1999), p. 271

[48] K. Boukheddaden; J. Linares; H. Spiering; F. Varret Eur. Phys. J. B, 15 (2000), p. 317

[49] I. Shteto; J. Linares; F. Varret Phys. Rev. E, 56 (1997), p. 5128

[50] J. Linares; C. Enachescu; K. Boukheddaden; F. Varret Proc. Int. Conf. Molecule-based Magnets, Polyhedron (Oct. 2002) Valencia, Spain (to appear)

[51] F. Varret, K. Boukheddaden, E. Codjovi, C. Enachescu, J. Linarès, in: P. Gütlich, H. Goodwin (Eds.), Spin Crossover in Transition Metal Compounds, Top. Curr. Chem. (to appear).

[52] C. Roux; D.M. Adams; J.-P. Itié; A. Polian; D.N. Hendrickson; M. Verdaguer Inorg. Chem., 35 (1996), p. 2846

[53] A. Bousseksou; N. Negre; M. Goiran; L. Salmon; J.-P. Tuchagues; M.-L. Boillot; K. Boukheddaden; F. Varret Eur. Phys. J. B., 13 (2000), p. 451

[54] N. Negre; M. Goiran; A. Bousseksou; J.G. Haasnoot; K. Boukheddaden; S. Askenazy; F. Varret Synth. Met., 115 (2000), p. 289

[55] N. Nègre; C. Consejo; M. Goiran; A. Bousseksou; F. Varret; J.-P. Tuchagues; R. Barbaste; S. Askénazy Physica B, 294–295 (2001), p. 91

[56] A. Bousseksou; K. Boukheddaden; M. Goiran; C. Consejo; J.-P. Tuchagues Phys. Rev. B, 65 (2002), p. 1724

[57] Y. Qi; E.W. Muller; H. Spiering; P. Gütlich Chem. Phys. Lett., 93 (1982), p. 567

[58] Y. Garcia; O. Kahn; J.-P. Ader; A. Buzdin; Y. Meurdesoif; M. Guillot Phys. Lett. A, 271 (2000), p. 145

[59] Y. Ogawa; S. Koshihara; K. Boukheddaden; F. Varret Phys. Rev. B, 66 (2002), p. 073104

[60] T. Kohlhaas; H. Spiering; P. Gütlich Z. Physik B, 102 (1997), p. 455

[61] H. Romstedt; A. Hauser; H. Spiering J. Phys. Chem. Sol., 59 (1998), p. 265

[62] N. Willenbacher; H. Spiering J. Phys. C, 21 (1988), p. 1423

[63] H. Spiering; N. Willenbacher J. Phys. Cond. Matter, 1 (1989), p. 10089

[64] M.-L. Boillot; S. Chantraine; J. Zarembowitch; J.-Y. Lallemand; J. Prunet New. J. Chem. (1999), p. 179

Cité par

Chinmoy Das; Ajana Dutta; Denisa Coltuneac; Laurentiu Stoleriu; Pradip Chakraborty Tailoring zero-point energies in nanocrystalline 3D Hofmann-type spin-crossover networks Fe1−xMx(pz)[Pd(CN)4]: impact of size, composition, and surrounding matrices, Dalton Transactions, Volume 54 (2025) no. 19, p. 7923 | DOI:10.1039/d5dt00565e
Sophia I. Klokishner; Oleg S. Reu Proton-Transfer-Coupled Spin Transitions in Mononuclear Iron(II) Compounds: Interplay of Intra- and Intercenter Interactions, The Journal of Physical Chemistry C, Volume 129 (2025) no. 7, p. 3872 | DOI:10.1021/acs.jpcc.4c07925
Nour El Islam Belmouri; Catherine Cazelles; Jorge Linares; Kamel Boukheddaden An Efficient Analytical Method for Determining Transition Temperatures in Core‐Shell Spin Crossover Nanoparticles Described by an Extended Ising‐Like Model, European Journal of Inorganic Chemistry, Volume 27 (2024) no. 35 | DOI:10.1002/ejic.202400475
Chinmoy Das; Subhadip Dey; Abhijit Adak; Cristian Enachescu; Pradip Chakraborty Variation of the Cooperativity in Diluted Hofmann-Based Spin-Crossover Coordination Solids Fe1–xMx(pz)[Pd(CN)4], Crystal Growth Design, Volume 23 (2023) no. 5, p. 3496 | DOI:10.1021/acs.cgd.3c00039
Mousumi Dutta; Shubham Bisht; Prabir Ghosh; Alexandra Ioana Chilug; Dallas Mann; Cristian Enachescu; Michael Shatruk; Pradip Chakraborty Combined Experimental and Mechanoelastic Modeling Studies on the Low-Spin Stabilized Mixed Crystals of 3D Oxalate-Based Coordination Materials, Inorganic Chemistry, Volume 62 (2023) no. 37, p. 15050 | DOI:10.1021/acs.inorgchem.3c01919
Nicolas di Scala; Nour El Islam Belmouri; Miguel Angel Paez Espejo; Kamel Boukheddaden Three-dimensional electroelastic modeling of the nucleation and propagation of the spin domains in spin-crossover materials, Physical Review B, Volume 106 (2022) no. 1 | DOI:10.1103/physrevb.106.014422
Ana Maria Toader; Maria Cristina Buta; Fanica Cimpoesu; Andrei-Iulian Toma; Christina Marie Zalaru; Ludmila Otilia Cinteza; Marilena Ferbinteanu New Syntheses, Analytic Spin Hamiltonians, Structural and Computational Characterization for a Series of Tri-, Hexa- and Hepta-Nuclear Copper (II) Complexes with Prototypic Patterns, Chemistry, Volume 3 (2021) no. 1, p. 411 | DOI:10.3390/chemistry3010031
Alexandra-Ioana Popa; Laurentiu Stoleriu; Cristian Enachescu Tutorial on the elastic theory of spin crossover materials, Journal of Applied Physics, Volume 129 (2021) no. 13 | DOI:10.1063/5.0042788
J. Linares; C. Cazelles; S. Gaci; P. R. Dahoo; K. Boukheddaden Monte Carlo Entropic sampling algorithm applied to 3D spin crossover nanoparticles: role of the environment on the thermal hysteresis, Journal of Physics: Conference Series, Volume 1730 (2021) no. 1, p. 012042 | DOI:10.1088/1742-6596/1730/1/012042
C. Cazelles; J. Linares; Y. Singh; P.-R. Dahoo; K. Boukheddaden Local mean field approximation applied to a 3D spin crossover nanoparticles configuration: free energy analysis of the relative stability of the stationary states, Journal of Physics: Conference Series, Volume 1730 (2021) no. 1, p. 012043 | DOI:10.1088/1742-6596/1730/1/012043
Catherine Cazelles; Yogendra Singh; Jorge Linares; Pierre-Richard Dahoo; Kamel Boukheddaden Three states and three steps simulated within Ising like model solved by local mean field approximation in 3D spin crossover nanoparticles, Materials Today Communications, Volume 26 (2021), p. 102074 | DOI:10.1016/j.mtcomm.2021.102074
Viktor Ivashko; Oleg Angelsky Properties of 2D hexagonal spin-crossover nanosystem: a Monte Carlo study, Applied Nanoscience, Volume 10 (2020) no. 12, p. 4487 | DOI:10.1007/s13204-020-01420-z
Teresa Delgado; Cristian Enachescu; Antoine Tissot; Andreas Hauser; Laure Guénée; Céline Besnard Evidencing size-dependent cooperative effects on spin crossover nanoparticles following their HS→LS relaxation, Journal of Materials Chemistry C, Volume 6 (2018) no. 46, p. 12698 | DOI:10.1039/c8tc04315a
J. Linares; I. Sahbani; F. Desvoix; P.R. Dahoo; K. Boukheddaden Ising-like model applied to a triangular lattice of 2D spin-crossover nanoparticles: evidence of a re-entrant phase transition, Journal of Physics: Conference Series, Volume 1141 (2018), p. 012073 | DOI:10.1088/1742-6596/1141/1/012073
Teresa Delgado; Cristian Enachescu; Antoine Tissot; Laure Guénée; Andreas Hauser; Céline Besnard The influence of the sample dispersion on a solid surface in the thermal spin transition of [Fe(pz)Pt(CN)4] nanoparticles, Physical Chemistry Chemical Physics, Volume 20 (2018) no. 18, p. 12493 | DOI:10.1039/c8cp00775f
Alexander I. Nesterov; Yuri S. Orlov; Sergey G. Ovchinnikov; Sergey V. Nikolaev Cooperative phenomena in spin crossover systems, Physical Review B, Volume 96 (2017) no. 13 | DOI:10.1103/physrevb.96.134103
Laurentiu Stoleriu; Masamichi Nishino; Seiji Miyashita; Alexandru Stancu; Andreas Hauser; Cristian Enachescu Cluster evolution in molecular three-dimensional spin-crossover systems, Physical Review B, Volume 96 (2017) no. 6 | DOI:10.1103/physrevb.96.064115
Margarethe van der Meer; Yvonne Rechkemmer; Frauke D. Breitgoff; Sebastian Dechert; Raphael Marx; María Dörfel; Petr Neugebauer; Joris van Slageren; Biprajit Sarkar Probing bistability in FeIIand CoIIcomplexes with an unsymmetrically substituted quinonoid ligand, Dalton Transactions, Volume 45 (2016) no. 20, p. 8394 | DOI:10.1039/c6dt00757k
Margarethe van der Meer; Yvonne Rechkemmer; Frauke D. Breitgoff; Raphael Marx; Petr Neugebauer; Uta Frank; Joris van Slageren; Biprajit Sarkar Multiple Bistability in Quinonoid-Bridged Diiron(II) Complexes: Influence of Bridge Symmetry on Bistable Properties, Inorganic Chemistry, Volume 55 (2016) no. 22, p. 11944 | DOI:10.1021/acs.inorgchem.6b02097
V. V. Shelest; A. V. Khristov; G. G. Levchenko The role of anharmonicity in the systems with spin crossover, Low Temperature Physics, Volume 42 (2016) no. 6, p. 505 | DOI:10.1063/1.4954782
Hong-Zhou Ye; Chong Sun; Hong Jiang Monte-Carlo simulations of spin-crossover phenomena based on a vibronic Ising-like model with realistic parameters, Physical Chemistry Chemical Physics, Volume 17 (2015) no. 10, p. 6801 | DOI:10.1039/c4cp05562d
Alexandru Atitoaie; Radu Tanasa; Alexandru Stancu; Cristian Enachescu Study of spin crossover nanoparticles thermal hysteresis using FORC diagrams on an Ising-like model, Journal of Magnetism and Magnetic Materials, Volume 368 (2014), p. 12 | DOI:10.1016/j.jmmm.2014.04.054
Catalin-Maricel Jureschi; Ionela Rusu; Epiphane Codjovi; Jorge Linares; Yann Garcia; Aurelian Rotaru Thermo- and piezochromic properties of [Fe(hyptrz)]A2·H2O spin crossover 1D coordination polymer: Towards spin crossover based temperature and pressure sensors, Physica B: Condensed Matter, Volume 449 (2014), p. 47 | DOI:10.1016/j.physb.2014.04.081
S.A. Borshch Theoretical Approaches for Spin-Crossover Phenomenon in Transition-Metal Complexes, Comprehensive Inorganic Chemistry II (2013), p. 469 | DOI:10.1016/b978-0-08-097774-4.00921-9
Ivan Šalitroš; Olaf Fuhr; Robert Kruk; Ján Pavlik; Lukáš Pogány; Bernhard Schäfer; Miroslav Tatarko; Roman Boča; Wolfgang Linert; Mario Ruben Thermal and Photoinduced Spin Crossover in a Mononuclear Iron(II) Complex with a Bis(pyrazolyl)pyridine Type of Ligand, European Journal of Inorganic Chemistry, Volume 2013 (2013) no. 5-6, p. 1049 | DOI:10.1002/ejic.201201123
Ján Pavlik; Roman Boča Established Static Models of Spin Crossover, European Journal of Inorganic Chemistry, Volume 2013 (2013) no. 5-6, p. 697 | DOI:10.1002/ejic.201201082
Cristian Enachescu; Masamichi Nishino; Seiji Miyashita Theoretical Descriptions of Spin‐Transitions in Bulk Lattices, Spin‐Crossover Materials (2013), p. 455 | DOI:10.1002/9781118519301.ch18
J. Pavlik; W. Nicolazzi; G. Molnár; R. Boča; A. Bousseksou Coupled magnetic interactions and the Ising-like model for spin crossover in binuclear compounds, The European Physical Journal B, Volume 86 (2013) no. 6 | DOI:10.1140/epjb/e2013-30613-7
Aurelian Rotaru; Jorge Linares; François Varret; Epiphane Codjovi; Ahmed Slimani; Radu Tanasa; Cristian Enachescu; Alexandru Stancu; Jaap Haasnoot Pressure effect investigated with first-order reversal-curve method on the spin-transition compounds [FexZn1−x(btr)2(NCS)2] · H2O (x=0.6,1), Physical Review B, Volume 83 (2011) no. 22 | DOI:10.1103/physrevb.83.224107
Laurentiu Stoleriu; Pradip Chakraborty; Andreas Hauser; Alexandru Stancu; Cristian Enachescu Thermal hysteresis in spin-crossover compounds studied within the mechanoelastic model and its potential application to nanoparticles, Physical Review B, Volume 84 (2011) no. 13 | DOI:10.1103/physrevb.84.134102
Aurelian Rotaru; François Varret; Epiphane Codjovi; Kamel Boukheddaden; Jorge Linares; Alexandru Stancu; Philippe Guionneau; Jean-François Létard Hydrostatic pressure investigation of the spin crossover compound [Fe(PM−BiA)2(NCS)2] polymorph I using reflectance detection, Journal of Applied Physics, Volume 106 (2009) no. 5 | DOI:10.1063/1.3202385
Haritosh Mishra; Vibha Mishra; François Varret; Rabindranath Mukherjee; Chérif Baldé; Cédric Desplanches; Jean-François Létard Opposite effects of interactions and disorder on the switching properties of the spin transition compound [FeII(L)2][ClO4]2·C7H8, Polyhedron, Volume 28 (2009) no. 9-10, p. 1678 | DOI:10.1016/j.poly.2008.10.029
L. Stoleriu; C. Enachescu; A. Stancu; A. Hauser Elastic Model for Complex Hysteretic Processes in Molecular Magnets, IEEE Transactions on Magnetics, Volume 44 (2008) no. 11, p. 3052 | DOI:10.1109/tmag.2008.2002793
W. Nicolazzi; S. Pillet; C. Lecomte Two-variable anharmonic model for spin-crossover solids: A like-spin domains interpretation, Physical Review B, Volume 78 (2008) no. 17 | DOI:10.1103/physrevb.78.174401
S. Gawali-Salunke; F. Varret; I. Maurin; C. Enachescu; M. Malarova; K. Boukheddaden; E. Codjovi; H. Tokoro; S. Ohkoshi; K. Hashimoto Magnetic and Mössbauer Investigation of the Photomagnetic Prussian Blue Analogue Na0.32Co[Fe(CN)6]0.74·3.4H2O: Cooperative Relaxation of the Thermally Quenched State, The Journal of Physical Chemistry B, Volume 109 (2005) no. 16, p. 8251 | DOI:10.1021/jp044739x
Takeshi Tayagaki; Ana Galet; Gábor Molnár; M. Carmen Muñoz; Antoine Zwick; Koichiro Tanaka; José-Antonio Real; Azzedine Bousseksou Metal Dilution Effects on the Spin-Crossover Properties of the Three-Dimensional Coordination Polymer Fe(pyrazine)[Pt(CN)4], The Journal of Physical Chemistry B, Volume 109 (2005) no. 31, p. 14859 | DOI:10.1021/jp0521611
Azzedine Bousseksou; Gábor Molnár; Galina Matouzenko Switching of Molecular Spin States in Inorganic Complexes by Temperature, Pressure, Magnetic Field and Light: Towards Molecular Devices, European Journal of Inorganic Chemistry, Volume 2004 (2004) no. 22, p. 4353 | DOI:10.1002/ejic.200400571

Cité par 37 documents. Sources : Crossref

Commentaires - Politique