1 Introduction
Over the last two decades the formation of the various latex particle morphologies that can be produced in a multi-stage emulsion polymerization process have attracted a lot of attention both in industry and in academia. There are both technical and/or environmental reasons for this interest and one example of the major driving forces is the demand to lower the volatile organic compound (VOC) emissions from coalescing agents used in coatings. It is thought that in structured latex particles, the combination of a hard non-film forming polymer together with a polymer that forms a film at ambient temperature could give a material that results in hard films formed at low temperatures without adding VOC as film forming aids. One latex particle structure often referred to that could provide a solution to this problem is the so-called core-shell morphology [1, 2]. The core-shell morphology is normally built up from a hard core surrounded by a soft shell but other examples are also available in the literature [3–6] and there are several other latex particle morphologies that could serve as adequate candidates [7, 8].
The two main factors in the formation of various latex particle morphologies are the drive for thermodynamic equilibrium [9–11] and/or kinetic restrictions, i.e., diffusivity of propagating species [2, 12–17]. Thermodynamic equilibrium morphology in this context means that incompatible polymer phases in structured latex particles are fully phase separated and that the particles have obtained their lowest value of free energy. The free energy for a structured latex particle is expressed as the combination of the free energy at surfaces and in some cases also the elastic free energy due to crosslinked seed particles [18], where the surface free energy depends on the interfacial tensions between the polymer/polymer phases as well as between the polymer/aqueous phases. Thus, the interfacial tensions are mainly affected by the presence of surfactant and/or monomer as well as the phase ratio of the two polymers and their relative polarities. Thermodynamic equilibrium latex particle morphologies are achieved when the rate of diffusion of a polymer chain is much faster than the polymerization rate, which will occur when the diffusivity in the particles is high, as in a batch process at low conversions, or a flooded semi-continuous polymerization process. On the other hand, kinetically controlled latex particle morphologies will be obtained when phase separation is slower than the polymerization, which means that the choice of polymerization conditions will affect the particle morphology to a great extent. Consequently, a high internal particle viscosity, as in the starved, second stage of polymerization, will promote kinetically controlled particle morphologies.
Recently there have been several publications regarding modeling of emulsion polymerization reaction kinetics and also the development of latex particle morphologies over the course of reaction [19–27]. At high monomer conversions in polymers having a Tg close to the reaction temperature there will be diffusion-controlled kinetics where the transition from the zero-one regime to a pseudo-bulk regime occurs. The reduced diffusion rates for all the active species in the polymerization will lead first to decreased termination rates and secondly to decreased propagation rates. Significant variations in the radical concentrations in the particles could develop, which would impact morphology development. If the particles have glassy cores it is considered that a higher radical concentration will exist at the outer shells of the latex particles, particularly with larger particles. This in turn will lead to most of the second stage polymer being formed towards the outside of the particles due to the gradient in radical concentration. The domain sizes of the second stage polymer will be dependent on the prevailing diffusion rates for both polymers.
Lovell et al. [28–30] have shown that the probability of chain transfer to polymer increases as the ratio between polymer and monomer increases. Under similar polymerization conditions, differences in the chain transfer rate due to variations in the radical lifetime and radical activity have also been observed [31]. Studies on grafted material in core-shell particles formed during multi-stage emulsion polymerizations showed that the amount of grafted material affected the properties of the dispersions [32–34] and it has also been shown that the grafted material will contribute to the interphase between the two polymers in the particles [35], which could also affect the mechanical properties of films made from such dispersions [36, 37].
In the present study we have prepared structured latex particles by a two-stage emulsion polymerization process. The first-stage polymers were non-polar poly(styrene-co-butylacrylate), p(S-co-BuA), with varying Tg ranging from 100 °C to 20 °C and the composition of the second stage polymer was held identical in all experiments and consisted of a polar poly(methyl methacrylate-co-butyl acrylate-co-methacrylic acid), p(MMA-co-BuA-co-MAA), having a Tg of 20 °C. By changing the first-stage polymer Tg we have varied the diffusivity for the propagating radicals inside the latex particles in order to see whether the amount of interphase could be correlated to the penetration depth of the incoming radicals [17, 26, 27]. The latex particle morphologies were studied using transmission electron microscopy (TEM) and the thermo-mechanical properties of the resulting latex films were investigated using differential scanning calorimetry (DSC) and dynamic mechanical analysis (DMA).
2 Experimental setup
2.1 Chemicals
Methyl methacrylate (MMA) (Merck), styrene (S) (Merck), butyl acrylate (BuA) (Merck) and methacrylic acid (MAA) (Merck) were used as supplied. Sodium persulphate (NaPS) (Merck) and sodium dodecyl sulphate (SDS) (BDH) were of analytical grade and used without further treatment. All other chemicals were used as supplied.
2.2 Emulsion polymerization
Emulsion polymerization experiments were performed in a 1-l, four-necked glass reactor equipped with a mechanical stirrer, a reflux condenser, and a thermometer. The reactor was immersed in a thermostatic water-bath for controlling the reaction temperature at (70 ± 0.5) °C. The experiments were named as ‘core Tg’ core-shell ‘shell Tg’, e.g., an experiment having a core Tg of 100 °C and a shell Tg of 20 °C would be coded as 100CS20. Polymerization details for the experiments are given in Table 1 but the same general procedure for the two-stage polymerizations was performed as follows. First, 155 g of deionized water were added to the reactor and then purged with nitrogen. When the reactor temperature was stable at 70 °C, 10 g of Emulsion-1 (see Table 1) together with Init-1 were charged to the reactor and after 15 minutes the continuous charging of Emulsion-1 and Init-2 was started. The addition time of Emulsion-1 was 110 minutes and for Init-2 the addition period lasted for 130 minutes. One hour after the end of Emulsion-1, addition of Emulsion-2 was started together with Init-2 and the addition period for Emulsion-2 was 160 minutes, while Init-2 was fed for another 180 minutes. When all the monomer and initiator had been added to the reactor the temperature was kept at 70 °C for 30 min before the reactor was cooled to room temperature. The stage ratio between the stage one polymer and the stage two polymer was 40:60 (by weight) in all experiments. Monomer conversion of the second stage polymerization was monitored by gravimetry and the particle sizes were measured by laser diffraction using a Malvern Mastersizer 2000. The minimum film formation temperature (MFT) was measured using an MFT bridge (Coesfeld, Thermostair) with a temperature gradient covering either the range from 0 °C to 32 °C or from 28 °C to 60 °C. The properties of the final latexes are given in Table 2 .
Polymerization recipes and detailed reaction conditions
| Experiment codes | |||||
| 20CS20 | 40CS20 | 60CS20 | 80CS20 | 100CS20 | |
| Reactor charge | |||||
| Water (g) | 155 | 155 | 155 | 155 | 155 |
| Emulsion-1 | |||||
| Water (g) | 141.1 | 141.1 | 141.1 | 141.1 | 141.1 |
| NaOH (g) | 0.12 | 0.12 | 0.12 | 0.12 | 0.12 |
| SDS (g) | 3.3 | 3.3 | 3.3 | 3.3 | 3.3 |
| Styrene (g) | 96 | 102.8 | 123.4 | 145.6 | 166.2 |
| BuA (g) | 76 | 68.54 | 47.98 | 25.7 | 5.14 |
| Init-1 | |||||
| Water (g) | 0.76 | 0.76 | 0.76 | 0.76 | 0.76 |
| NaPS (g) | 0.19 | 0.19 | 0.19 | 0.19 | 0.19 |
| Emulsion-2 | |||||
| Water (g) | 211.5 | 211.5 | 211.5 | 211.5 | 211.5 |
| SDS (g) | 5.3 | 5.3 | 5.3 | 5.3 | 5.3 |
| MMA (g) | 132 | 132 | 132 | 132 | 132 |
| BuA (g) | 126 | 126 | 126 | 126 | 126 |
| MAA (g) | 7.7 | 7.7 | 7.7 | 7.7 | 7.7 |
| Feed rate (g/h) | 182 | 182 | 182 | 182 | 182 |
| Init-2 | |||||
| Water (g) | 38 | 38 | 38 | 38 | 38 |
| NaPS (g) | 1.28 | 1.28 | 1.28 | 1.28 | 1.28 |
Characteristics of the structured latexes
| Sample description | MFT (°C) | Solids content (wt.%) | Particle size (nm) | ||
| Codes | Expected Tg (°C) | ||||
| stage 1 | stage 2 | ||||
| 100CS20 | 100 | 20 | 37 ± 2 | 43.6 | 149 |
| 80CS20 | 80 | 20 | 37 ± 2 | 44.3 | 150 |
| 60CS20 | 60 | 20 | 26 ± 2 | 44.0 | 113 |
| 40CS20 | 40 | 20 | 21 ± 2 | 46.2 | 95 |
| 20CS20 | 20 | 20 | 22 ± 2 | 43.9 | 141 |
2.3 Transmission Electron Microscopy (TEM)
The latexes were negatively stained with an aqueous solution of 2% uranyl acetate (UAc). In order to prepare the samples, each latex was diluted to 0.1 wt% solids and a drop of UAc was added to a 5-ml portion of the diluted solution. A drop of the resulting mixture was then placed on a formvar-coated grid and the water was removed by adsorbing it with a filter paper.
The samples were examined in a Philips CM 10 transmission electron microscope. Micrographs were recorded on negative films, which were subsequently scanned. In the micrographs the PS phase appeared as dark and the MMA-co-BuA phase as bright domains [38].
2.4 Film preparation
To prepare films, 4 g of the latex dispersions were cast on Petri dishes with similar surface areas (~ 40 cm2) and placed in a conventional oven at 35 °C. In order to slow the process of film formation, inverted Petri dishes were used to cover the drying dispersions. After 48 h, the films formed had a thickness of ~ 400 μm. In order to obtain films that could be used in the DMA the 80CS20 latex was dried at a slightly higher temperature (42 °C) using the same method as for the other latexes.
2.5 Differential Scanning Calorimetry (DSC)
Differential Scanning Calorimetry (DSC) thermograms were recorded using the TA Instruments DSC-Q1000 under a nitrogen atmosphere. The samples were first heated from room temperature to 150 °C, maintained at 150 °C for 3 minutes, and then cooled at 10 °C min–1 down to –70 °C. After 3 minutes equilibrium time at –70 °C, the samples were heated up to 180 °C with a heating rate of 10 °C min–1. The weight of the sample was about 5 mg.
2.6 Dynamic Mechanical Analysis (DMA)
The TA Instruments Dynamic Mechanical Analyzer DMA 2980 was used operating in tensile mode under isochronal conditions at the frequency of 1 Hz, to measure the temperature dependence of the complex elastic modulus E* (storage, E′, and loss, E′′, moduli). The samples were approximately 12 mm long, 5 mm wide, and 400 μm thick. The viscoelastic spectra were recorded from –110 °C to 200 °C with a heating rate of 2 °C min–1.
3 Results and discussion
All the latexes produced had solid content of 44 wt.% and particle sizes just above 100 nm. The viscosities of the dispersions were approximately 10 mPa s and there was no or very little grit formation (typically less than 0.1 wt%) during the polymerizations. For detailed dispersion properties see Table 2.
3.1 Morphology – TEM
In the present experiments there was no crosslinking monomer involved, the phase ratio between stages 1 and 2 was fixed at 40:60 and the amount and type of surfactant was the same in all of the experiments, which means that any differences in the latex particle morphologies must originate from kinetic restrictions and/or changes in the polarity of the first-stage polymer due to the compositional differences. The first-stage co-polymer, which consisted of styrene and butyl acrylate (S-co-BuA) with varying Tg, was more hydrophobic than the second stage co-polymer that consisted of equal parts of methyl methacrylate and butyl acrylate together with a small portion of polar methacrylic acid (MMA-co-BuA-co-MAA). The expected thermodynamic equilibrium latex morphology should therefore be core-shell with the non-polar p(S-co-BuA) forming the core and the more polar p(MMA-co-BuA-co-MAA) second stage polymer forming the shell. TEM micrographs showing the particle morphologies for experiments 20CS20, 60CS20, 80CS20 and 100CS20 are presented in Fig. 1 . In the micrographs the styrene-containing first-stage polymer is dark while the all-acrylic second stage polymer phase appears lighter. Negative staining using uranyl acetate (UAc) was used to define the particles if they were film forming and this is observed as a thin dark ring around the particles. The morphology inside the particles is visible because the styrene-rich phase is more stable to the electron beam [38] than the acrylic-rich phase, and therefore appears darker. In addition to simply accumulating around the particles the UAc will specifically stain carboxylic groups located at the latex particle surfaces [39], which will further enhance the contrast at the particle edges. In Fig. 1a and b, it can be seen that the expected core-shell morphology is obtained for the two experiments 20CS20 and 60CS20 (similar observations were obtained for 40CS20). However, for experiment 80CS20 (Fig. 1c), the particles appear as dark spheres having a faint thin shell but it is very hard to make any definite statements about the morphology from the micrographs. Experiment 100CS20 (Fig. 1d) resulted in particles having an uneven shell consisting of lumps of second stage polymer on the outside of the first-stage seed polymer particles. The multi-lobe structure showed that the wetting of the seed particles in 100CS20 by the second stage polymer was insufficient as compared to the other experiments despite the low Tg of the second stage polymer. However, wetting of the seed particles by the second stage polymer depends not only on the interfacial tension between the two polymers and the aqueous phase but also on the interfacial tension between the polymers themselves and a higher quantity of BuA in both polymers could promote the wetting as observed in the other experiments (Fig. 1a and b).

TEM Micrographs - latex particle morphologies: (a) 20CS20; (b) 60CS20; (c) 80CS20; (d) 100CS20.
3.2 Thermomechanical properties
Differential scanning calorimetry (DSC) and dynamic mechanical analysis (DMA) have been shown to provide relevant information for the characterization of heterogeneous polymeric systems such as block- and graft-copolymers, as well as polymer blends [40–43]. The key feature of the heterogeneity of a two-phase system on a DSC thermogram is the existence of two separate glass transitions with transition temperatures coinciding with the Tgs of the pure constituents. Similarly for the DMA, two maxima in the temperature dependence of the mechanical losses are usually found on the viscoelastic mechanical spectra of two-phase systems. Subsequently, the changes in the temperature location of the transitions (in comparison with those of the pure constituents) on DSC or DMA spectra are interpreted using a physicochemical approach including considerations about miscibility/compatibility between the polymeric species.
It is therefore of interest to consider both DSC and DMA results to explore the phase behaviour in the interfacial area of our structured latexes. In this way, Fig. 2 gives the evolution of the ΔCps, measured by DSC, as a function of the temperature for all the investigated samples (i.e. from 20CS20 to 100CS20). Also plotted on Fig. 2 are the viscoelastic mechanical properties (storage E′ and loss E′′ moduli) of the series of structured latexes. In addition, Table 3 reports on the Tg values obtained experimentally at the inflection point of the change in the ΔCp baseline (DSC traces, Fig. 2) for both hard (high-Tg) and soft (low-Tg) phases.

Thermal (ΔCp/DSC) and mechanical viscoelastic (E′ and E′′/DMA) properties of the structured latexes.
DSC data table
| Sample codes | Expected Tg (°C) | Experimental Tg (°C)* | |||
| stage 1 | stage 2 | high-Tg phase | low-Tg phase | ||
| 100CS20 | 100 | 20 | 99 ± 1 | 21 ± 1 | |
| 80CS20 | 80 | 20 | 76 ± 1 | 32 ± 1 | |
| 60CS20 | 60 | 20 | 56 ± 1 | 20 ± 1 | |
| 40CS20 | 40 | 20 | 40 ± 1 | 21 ± 1 | |
| 20CS20 | 20 | 20 | 17 ± 1 |
While it can be seen from Table 3 that the experimental Tgs of the first-stage polymers are in good agreement with the ones expected according to our latex recipes (from 100 °C to 20 °C), the main point of interest is the Tg value of the soft phase in the sample 80CS20. Whereas the Tg of the soft phases remains constant (around 20 ± 1 °C) for all the other samples, the Tg of the second-stage polymer in 80CS20 is given as equal to 32 ± 1 °C. Such a shift of Tg toward higher temperature gives important information relating to the better phase continuity in 80CS20 compared to the other structured systems. A similar anomaly can be found in the dynamic mechanical spectra of the 80CS20 sample, where both the peak of E′′ and the corresponding drop of E′ associated with the Tg of the soft phase appear at a temperature significantly higher than the one obtained for the other structured latexes.
To further investigate the information relative to the interfacial areas of our core-shell latexes, Fig. 3 gives the evolution of the derivative as a function of the temperature for the 100CS20, 80CS20 and 60CS20 samples as well as for their corresponding homopolymer latexes. In addition, Fig. 3 also shows the evolution of the loss factor tan δ, which is defined by the ratio (E′′/E′), as a function of the temperature for these samples. It can be noticed that the evolutions of both and tan δ obtained for 100CS20 and 60CS20 appear rather similar, and typical of phase-separated polymer blends. In fact, their respective DSC and DMA (tan δ) thermograms exhibit maxima at temperatures identical to those of their corresponding homopolymer latexes. On the other hand, in the case of 80CS20, it can be seen that the maximum of (as well as the one of tan δ), although distinct, is shifted and broadened toward the transition temperatures coinciding with the Tgs of the pure homopolymer latexes. Such a slight discrepancy between the DSC and DMA results (see Fig. 3b) may reflect slight morphological changes that could occur during the initial short annealing step at 150 °C.
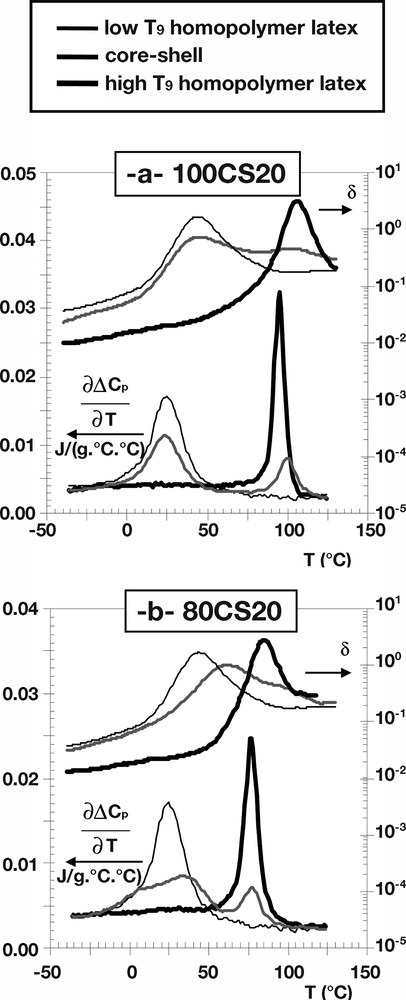
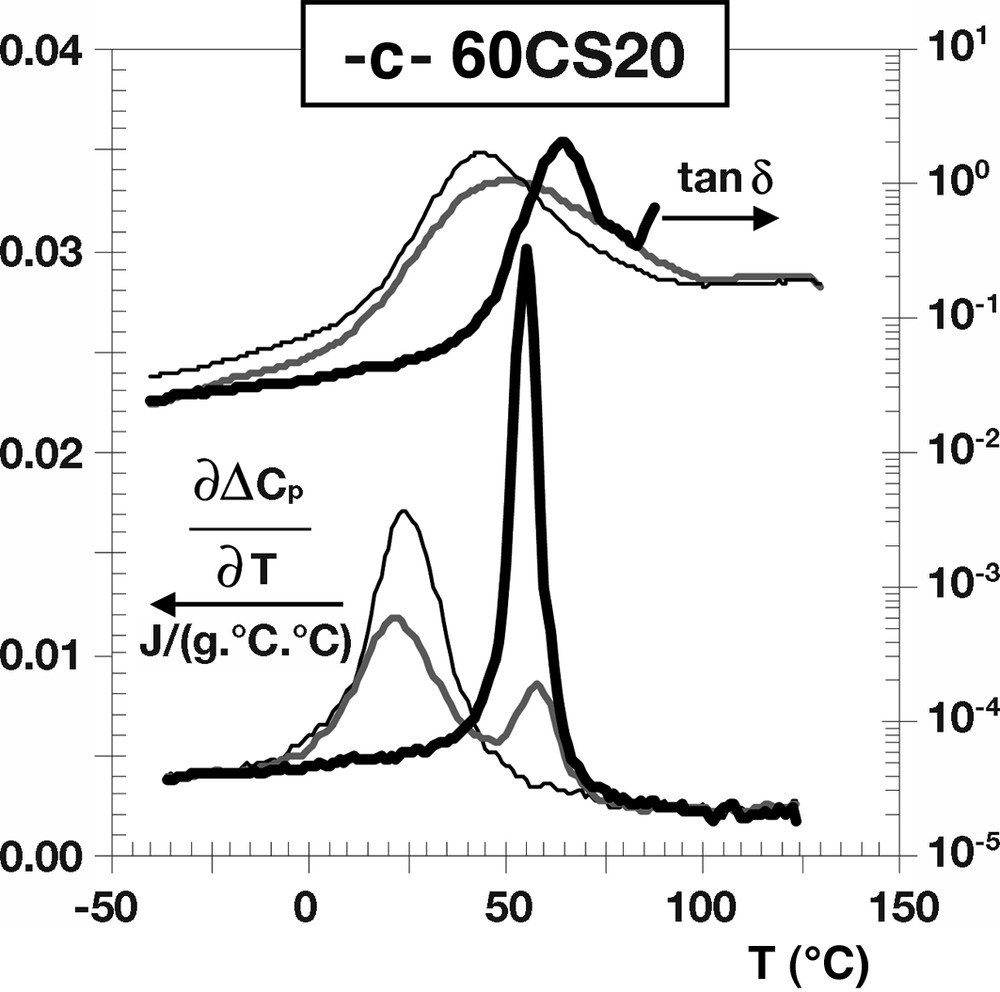
Thermal (DSC) and mechanical viscoelastic (DMA) properties of the structured latexes and their homopolymer latexes: (a) 100CS20; (b) 80CS20; (c) 60CS20.
3.3 Polymerization kinetics
Over the course of the polymerizations, samples were withdrawn for gravimetric analysis of the instantaneous monomer conversion. As can be seen in Table 4 the instantaneous monomer conversion was high in all the polymerizations and in all experiments there was on average less than 5 wt% monomer in the particles during polymerization (expressed as the monomer concentration in the particles, [M]P), which means that the diffusivity for small molecules in the first-stage polymer matrix is determined to a large extent by the difference between the reaction temperature, TR, and the first-stage polymer Tg. The diffusion rates for monomer, DM, in a polymer matrix are calculated for the experiments according to the equations presented by Karlsson et al. [44] and conversion average values of DM are given in Table 4. However, in order to be able to estimate the level of radical penetration in a latex particle, values for the diffusion coefficients of the radical species under the actual polymerization conditions are needed. Apart from TR, Tg of the first-stage polymer and [M]P, these diffusion coefficients are mainly dependent on the chain length of the diffusing radical [26, 44–47]. Under the present experimental conditions we have control of TR, Tg and [M]P, but in order to estimate the radical penetration into the latex particles, the rate at which the chain length of the radicals increases has to be known. A full explanation of how to calculate the rate at which the chains are growing would take too large a part of this paper. Instead we refer to work done by other authors that we have built the calculations of propagation rates and termination rates upon [23, 48, 49] and only present the essential equations for propagation reactions by anticipating that pseudo-bulk kinetics are valid at the high instantaneous monomer conversion prevailing in this study [8, 24, 25, 48]. The propagation reactions have both a chemically controlled, kpcop,p [50], as well as a diffusion controlled, kpdiff, contribution according to the model proposed by Russel et al. [48]:
| (1) |
| (2) |
| (3) |
Calculated kinetic coefficients and experimental parameters used
| [M]p | DM | kp | kt | t | |
| (mol l–1) | (cm2 s–1) | (l mol–1 s–1) | (l mol–1 s–1) | (s) | |
| 20CS20 | 0.3 | 1.12 × 10–6 | 17 000 | 8.30 × 106 | 1 |
| 40CS20 | 0.1 | 3.01 × 10–9 | 17 000 | 30 000 | 15 |
| 60CS20 | 0.1 | 1.46 × 10–10 | 14 000 | 4000 | 50 |
| 80CS20 | 0.1 | 1.87 × 10–12 | 800 | 1000 | 80 |
| 100CS20 | 0.2 | 2.04 × 10–13 | 100 | 1000 | 100 |
The diffusion controlled (kt,ijdiff) and residual termination (ktres) terms [52] are given by:
| (4) |
| (5) |
It has been shown that at high conversion the so-called ‘short long' approximation, which states that a majority of the termination events will involve a relatively short, mobile chain and a longer entangled one [49], will be valid. In the present study we have made the assumption that one of the radicals is always long, while the other one has a maximum length of 30 monomer units. Using the values for DM as discussed above, the diffusion for a radical of length i is estimated by equation (6) [45]
| (6) |
These equations, together with literature data for the coefficients used [53] and the data extracted from the polymerization, now make it possible to estimate the lifetime of a radical, t, expressed as t = 1/kt[R] where [R] is the radical concentration and is calculated as [17]:
| (7) |
3.4 Radical penetration depth
Sundberg et. al. presented a concept, whereby the depth to which polymer radicals can penetrate into seed particles was estimated by defining a so-called fractional penetration value [17, 26], defined as the distance diffused by the radical divided by the particle radius. It has proven to be a useful tool with which to estimate the latex particle morphology development at given experimental conditions. For example, a calculated fractional penetration value less than unity indicates a limited radical penetration, which would then result in a core-shell morphology. In the present study we have not calculated the actual fractional penetration values but we have used the concept. From the calculated diffusion rates and averaged rate coefficients together with the roughly estimated radical life times (see Table 4), the penetration depth of the growing radicals into the seed particles was ranked in three classes. Class 1 will allow full penetration, Class 2 will have partial penetration and finally in Class 3 there will be very limited penetration of incoming radicals. In the original concept of fractional penetration the radicals were non-polar entering a polar seed and the thermodynamic equilibrium morphology in that system was an inverted core shell. In the present study the situation was the opposite, i.e., polar radicals entering non-polar seed polymer which resulted in a core-shell morphology being the thermodynamic equilibrium structure. The experiments 20CS20 and 40CS20 were considered to belong to Class 1 because of their rather high kp and kt and short radical life times. In the micrographs in Fig. 1 the particle core-shell morphology for 20CS20 is shown while not shown in the figure, but also similar, was the morphology for 40CS20. This type of penetration calculations is intended for non-equilibrium conditions and if the diffusion of dead polymer is significant, then it is likely that the morphology will be controlled by thermodynamic driving forces, and the equilibrium morphology based on minimization of the interfacial energies should be considered instead. This was also what was observed in the TEM micrographs for these experiments and the thermo-mechanical analysis confirmed that there were two distinct polymer phases present in the particles. Finally, the MFT values for 20CS20 and 40CS20 agreed well with the Tg of the second stage, which also indicated that the second stage polymers were located on the outside of the particles and that the film formation process was unhindered by the first-stage polymer.
Experiments 60CS20 and 80CS20 were judged to belong to Class 2 even though a core-shell structure was observed in the TEM micrographs for 60CS20 (Fig. 1b). The Class 2 assessment was based on the long lifetime of the radicals, and also that the diffusion rates in the first-stage polymer were low and would almost correspond to values representing the Tg for the first-stage polymer. In addition, the MFT values (see Table 2) for these two experiments were higher than the second stage Tg, which further indicated a morphological difference compared to the 20CS20 and 40CS20 experiments. In the 60CS20 and 80CS20 experiments, it is not unlikely that the polar second stage oligo-radicals could still have penetrated into the existing particles to some extent before the newly formed second stage polymer was phase separated into its own phase. Depending on both the Tg of the polymer and the concentration of free monomer in the system the ability to both penetrate and to find the equilibrium latex morphology will be affected. The TEM micrograph for 80CS20 (Fig. 1c) is difficult to interpret but there seems to be a thin shell of second stage polymer also in these particles. However, when the thermo-mechanical properties were compared (Figs. 2 and 3b) there was a significant difference between 80CS20 and all the other experiments. As explained earlier, the phases exhibited a large extent of mixing and they seemed more compatible than in the other experiments. This behavior was not observed in the Class 3 experiment 100CS20 where the TEM analysis showed multi-lobed structures (Fig. 1d) and the kinetic analysis showed (Table 4) that the diffusivity even for a monomer molecule was lower than 10–11 cm2 s–1 that is anticipated as the value for the diffusion rate of a small molecule in a polymer matrix at the Tg [44]. The thermo-mechanical analysis did not show any tendency towards phase mixing in these particles and two distinct Tg having the expected values were observed (Fig. 3a). However, the same MFT value of 37 °C for 100CS20 and 80CS20 (Table 2) indicated some morphological similarities and the possibility that a portion of the second stage polymer could be confined inside the seed polymer and not contributing to the film formation also could not be excluded in 100CS20.
It seems most likely that the incoming radicals in the experiments 20CS20, 40CS20 and 60CS20 were able to fully penetrate the seed particles, then they were terminated the polymers could diffuse to the outside of the particles and build up a shell of second-stage polymers. As the second stage polymerization continued there would be a substantial shell thickness and incoming radicals would have a higher compatibility with the polymer in the shell. As we pointed out earlier the calculations for the lifetimes and termination rates were based on conditions in the first-stage polymer but as the second stage polymer shell was built up the situation would change and the kinetics would be dominated by the prevailing conditions in the second stage polymer. This change will have a larger impact in experiment 60CS20 than in 20CS20 and 40CS20 due to the reduced penetration rate in the first-stage polymer in this experiment. Furthermore, even if the TEM micrograph showed a core-shell morphology the higher MFT value for 60CS20 indicated small morphological differences. On the other hand, the situation is very different in 100CS20 in which the radicals were hardly able to penetrate the seed particles and the second stage polymer mostly remained on the outside during the whole experiment. In the 80CS20 there was yet another situation where the radicals could partly penetrate the seed particles, but this time when the chains terminated they remained stuck in that position. Due to the shifted Tgs in 80CS20 the thermo-mechanical analysis also indicated a great deal of mixing between the phases, which to a large extent could be explained by the dead second stage polymer chains confined inside the first-stage polymer, thus forming a large amount of interphase.
An additional factor in the case of 60CS20 and 80CS20 was that the decrease of kp at high conversion together with the decreased termination rate would provide a good environment for grafting onto existing polymers via chain transfer to polymer, ktrp [28]. As shown in Table 4, the radicals were long-lived and the probability of grafting to polymer would increase greatly during the late stages of a conventional polymerization, or when the monomer was starve-fed during the whole second step, as in the present case. Lovell et al. [29, 30, 54, 55] have shown that the probability of a propagating chain undergoing transfer to polymer rather than propagation can be expressed as:
| (8) |
4 Concluding remarks
A series of heterogeneous latexes was prepared by two-stage emulsion polymerization at 70 °C. The weight ratio between the first and second stage polymers was held constant at 40:60 in all the experiments. The first-stage polymers were non-polar styrene-co-butyl acrylate (S–BuA) with Tgs varying from 100 °C to 20 °C while the composition of the second stage polymer was held identical in all experiments and consisted of a polar methyl methacrylate-co-butyl acrylate-co-methacrylic acid (MMA–BuA–MAA) having a Tg of 20 °C.
The latex particle morphologies were studied using transmission electron microscopy (TEM) and the thermomechanical properties of the resulting latex films were studied using differential scanning calorimetry (DSC) and dynamic mechanical analysis (DMA). In the experiments using a first-stage polymer having a Tg below the reaction temperature the observed latex particle morphologies were the nonpolar core/polar shell expected from a thermodynamic standpoint. However, when the first-stage polymer had a Tg above the reaction temperature the observed particle structures diverged from a core shell morphology and the particles had an irregular shape due to lumps of second stage polymer which did not form a complete shell. These irregular shells resulted in a higher minimum film formation temperature than in the experiments having regular core shell morphology. The amount of interphase between the stage one and stage two polymers was studied using both DMA and DSC. The largest amount of interphase was found in the structured particles having a first-stage polymer Tg close to the polymerization temperature, and this was likely due to the low diffusivity in the seed polymer and the long lifetime of the growing propagating radicals. As the radicals grew longer they could penetrate the seed polymer but as dead polymer chains they could not diffuse out of the seed polymer. The long lifetime for the growing radicals inside the seed polymer most likely increased the probability of chain transfer to the seed polymer.
Acknowledgements
The authors thank the Center for Amphiphilic Polymers from Renewable Resources (CAP), Lund University, for their financial support, and Simon Dennington for his dictionary knowledge and helpful suggestions.


